Abstract
Objectives
The goal of this study was to develop a system model of type 1 diabetes for the purpose of in silico simulation for the prediction of long-term glycemic control outcomes.
Methods
The system model was created and identified on a physiological cohort of virtual type 1 diabetes patients (n = 40). Integral-based identification was used to develop (n = 40) insulin sensitivity profiles.
Results
The n = 40 insulin sensitivity profiles provide a driving input for virtual patient trials using the models developed. The identified models have a median (90% range) absolute percentage error of 1.33% (0.08–7.20%). The median (90% range) absolute error was 0.12 mmol/liter (0.01–0.56 mmol/liter). The model and integral-based identification of SI captured all patient dynamics with low error, which would lead to more physiological behavior simulation.
Conclusions
A simulation tool incorporating n = 40 virtual patient data sets to predict long-term glycemic control outcomes from clinical interventions was developed based on a physiological type 1 diabetes metabolic system model. The overall goal is to utilize this model and insulin sensitivity profiles to develop and optimize self-monitoring blood glucose and multiple daily injection therapy.
Keywords: blood glucose, compartmental models, decision support, diabetes, hyperglycemia, insulin, simulation, subcutaneous injection
Introduction
The control of type 1 diabetes is a widely studied and experimented research field. Previously published control methods are diverse, using different routes of insulin administration and glucose measurement. Since the 1970s, the closed-loop artificial endocrine pancreas has been heralded as the solution (as reviewed in Bequette1). While no commercial product currently exists, the systems in current clinical use that are likely to constitute the components of an extracorporeal artificial pancreas are the continuous subcutaneous insulin infusion (CSII) pump and a continuous glucose measurement (CGM) device. Advanced control algorithms and methods to “close the loop” have also been widely studied (as reviewed elsewhere2–4), despite early and ongoing limitations in sensors and pumps. Currently, the use of open-loop CGM and/or CSII has resulted in, at best, a modest clinical advantage over conventional methods of insulin administration or multiple daily injection (MDI) (as reviewed elsewhere5,6). Additionally, these systems are only used by a small population of type 1 diabetic patients because of high upfront costs, costs of consumables, complexity, and the extensive health care infrastructure and support required. The prevalence of CSII use is as low as 2% of the type 1 diabetes population in the United Kingdom and up to 15–20% elsewhere and in the United States.7
Hence, there is a more practical and urgent need to address the large majority of the type 1 diabetes population using conventional glucose measurement, i.e., self-monitoring blood glucose (SMBG), and insulin administration, i.e., MDI methods, and for whom current conventional or intensive therapies are failing to deliver recommended levels of glycemic control.8 In the United States, over 50% of diagnosed diabetics aged 20–64 are deemed “out of control.9” The higher accuracy of bedside capillary blood glucose meters10,11 and the latest insulin analogues for MDI therapy,12 coupled with better control methods, have the potential to provide better care to the majority of outpatient or ambulatory type 1 diabetics than currently observed. Such techniques must necessarily be simple to implement to ensure broad clinical uptake by the diabetes population.
This study reports the development of a system model of the type 1 insulin–glucose regulatory system and its identification on a virtual patient cohort. The models utilized have several novel and unique features. In particular, the insulin model used is unique and captures the insulin kinetics of multiple insulin types in a single pharmacokinetic model for all shared physiological spaces. The pharmacodynamic model used has not been reported previously but bears components of a similar nature to other such models used in this field due to the need to capture similar physiology. This study is the basis for a novel model-based application to develop a simple and practical adaptive method for clinical glycemic control of type 1 diabetes using multiple daily injection and self-monitoring blood glucose measurements. In addition, the modeling of long-term clinical outcomes of glycemic control and their corroboration against clinical expectations and studies are explored further in a subsequent in silico simulation on a virtual patient cohort, which is also reported in this issue. Later, the complex interaction of all quantifiable errors in protocol application is investigated in a Monte Carlo study to test the robustness of the developed protocol in effectiveness and safety.13
Model Development
The system model shown in Equation (1) is an evolution of the model of Chase et al.14 and Wong et al.15
| (1) |
where G(t) is plasma glucose concentration (mmol/liter), CNS is central nervous system glucose uptake (mmol/liter·min), EGP0-G is endogenous glucose production extrapolated to zero plasma glucose concentration (mmol/liter·min), pG is glucose effectiveness (min−1), SI is insulin sensitivity (liter/min·mU), Q(t) is interstitial (effective) insulin concentration (mU/liter), RGC(t) is renal glucose clearance (mmol/liter·min), and P(t) is meal plasma glucose rate of appearance (mmol/liter·min).
This glucose model differs mathematically from the model developed by Chase et al.14 and Wong et al.15 in removal of insulin effect saturation and addition of the renal glucose clearance rate, RGC(t). These two studies were done on highly dynamic, critically ill patients with high effective insulin resistance who were treated with intravenous insulin doses. Removal of the insulin effect saturation was deemed suitable for modeling more compliant, insulin-sensitive and stable type 1 diabetes patients treated with subcutaneously administered insulin.
| (2) |
where RGC(t) is renal glucose clearance (mmol/liter·min), GFR is glomerular filtration rate (liter/min), G(t) is plasma glucose concentration (mmol/liter), RGT is renal glucose threshold (mmol/liter), Vp is glucose distribution volume (liter/kg), and mb is body mass (kg).
Referring to Equation (2), the renal glucose clearance rate, RGC(t), models glucose removal by the kidney above the renal glucose threshold, RGT, using a linear relationship proportional to the glucose concentration above RGT and the glomerular filtration rate, GFR. From the study by Johansen and colleagues,16 this linear approximation is acceptable. Linear models have also been used in AIDA17 by Lehmann et al.18 and by Arleth et al.19
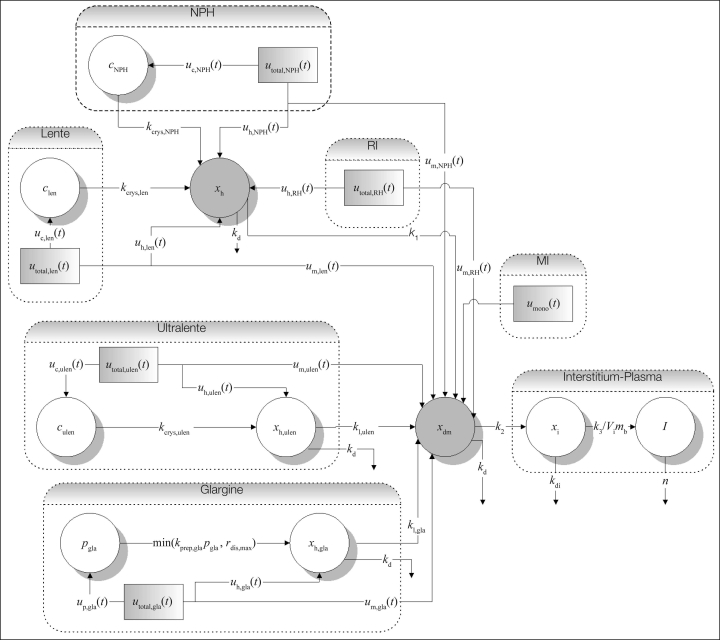
Insulin absorption from subcutaneous injection or infusion has been widely studied since Binder.20 A novel, compartmental model of subcutaneous insulin absorption kinetics specifically developed for diabetes decision support has been presented.21,22 The model accounts for the volume and concentration dependence of regular human insulin absorption and models the absorption kinetics of six insulin types, including monomeric insulin and insulin glargine. Additionally, insulin injected or infused subcutaneously or intravenously can also be modeled. A schematic of the model adapted from Wong and colleagues22 is shown in Figure 1. This model is used in this study, which is the first application of the developed model in the control of type 1 diabetes.
Figure 1.
Structure of the subcutaneous insulin absorption kinetic model. The model is characterized by a common hexameric state compartment for regular insulin (RI), neutral protamine Hagedorn (NPH) insulin, and lente insulin (xh), whereas those for insulins glargine and ultralente (xh,ulen and xh,gla) are separate. A crystalline state compartment for NPH (cNPH), lente (clen), and ultralente (culen) insulins and a precipitate compartment for insulin glargine (pgla) model these protraction mechanisms. All insulin flows through a common a dimeric–monomeric state compartment (xdm), interstitium compartment (xi), and finally into the plasma (I). Adapted from Wong et al.22
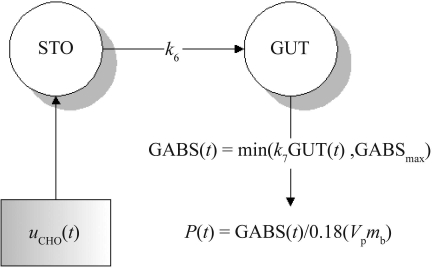
Modeling of the meal glucose rate of appearance (Ra), including digestion, absorption, and transport of glucose, is a complex process not widely studied.23 Meal carbohydrate amount and type are the main factors affecting meal glucose Ra or P(t) in Equations (1) and (6).24,25 However, clinical models of glucose Ra almost universally accept input of meal glucose amount only.18,26 Glucose equivalent carbohydrate introduced by Yates and Fletcher23 to express carbohydrate values as monosaccharide equivalents necessarily depends on an a priori known content of the carbohydrate type within the meal to be consumed, which is typically unavailable. Carbohydrate counting is a technique27–29 commonly taught by diabetes care providers to improve glycemic management. Glycemic index, a measure of the effect of carbohydrate type, is not easily calculable for mixed meals30 nor as readily available as carbohydrate content. The minimal models of meal glucose Ra by Worthington31 and Lehmann et al.17,18 form the basis of the model used in this study. Referring to Figure 2 and Equations (3)–(5), the model consists of two compartments for the stomach and gut, with linear gastric emptying and gut-absorption rates to describe the plasma glucose Ra in Equation (6).Another simplification is the expression of meal carbo-hydrate content (in grams) as equivalent to the same mass of glucose monosaccharide regardless of the meal carbohydrate type.23 Again, such meal data are typically unavailable in a clinical setting. As such, the complex digestion processes, such as the hydrolysis of poly-saccharides, are assumed linear and lumped into the simplified processes given earlier.
| (3) |
| (4) |
| (5) |
| (6) |
where STO(t) is mass of carbohydrate/glucose in the stomach (g), GUT(t) is mass of carbohydrate/glucose in the gut (g), GABS is gut carbohydrate/glucose absorption rate (g/min), GABSmax is maximum gut carbohydrate/glucose absorption rate (g/min), k6 is carbohydrate/glucose gastric emptying rate (min−1), k7 is carbohydrate/glucose gut-absorption rate (min−1), uCHO(t) is meal carbohydrate/glucose input (g/min), P(t) is meal plasma glucose rate of appearance (mmol/liter·min), Vp is glucose plasma distribution volume (liter/kg), and mb is body mass (kg).
Figure 2.
Structure of the meal glucose rate of the appearance model. The model is characterized by a delta function to describe meal glucose input [uCHO(t)], linear gastric emptying (k6), and gut absorption (k7) rates and saturable gut absorption (GABSmax).
Worthington31 found that the one-compartment model with time delay had the smallest fitting error. However, this result was obtained with a model fit to plasma glucose data and is dependent on the model of glucose kinetics used. Lehmann and colleagues18 used a “complex” function to describe the gastric emptying rate from the stomach compartment. This study used a linear transport rate, k6, while the glucose input into the stomach compartment, uCHO(t), is described by a delta function. Similar to the saturable gastric emptying rate of Lehmann et al.,18 this study incorporated a saturable gut-absorption rate, GABSmax. Saturable gut absorption has been postulated by Korach-Andre and colleagues32 in experiments using relatively large starch meals. However, this difference is likely to be small considering the minimal nature of both models. Referring to Figure 3, the effective gut-absorption rate is shown as a function of the mass of carbohydrate/glucose in the GUT compartment. Addition of the saturable term GABSmax effectively makes the gut absorption rate nonlinear as a function of the amount of carbohydrate in the gut. This dynamic is similar to that of the nonlinear three-compartment model of Dalla Man et al.,26 which consists of dual stomach compartments with a nonlinear gastric emptying rate with four identified parameters. The nonlinear gastric emptying term is described by a hyperbolic tangent function as a function of the proportion of the consumed carbohydrate remaining in the stomach. There is no saturation term considered for large, absolute meals.
Figure 3.
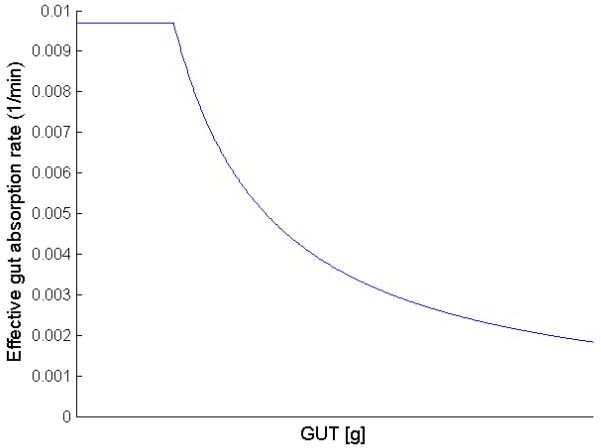
Qualitative plot of the effective gut absorption rate as a function of the mass of carbohydrate/glucose in the GUT compartment. While the process of gastric emptying is linear, addition of the saturable gut absorption term, GABSmax, of 1.1 g/min effectively makes the process of gut absorption, and hence meal glucose Ra, nonlinear. At low glucose levels in the gut, the effective gut absorption rate is 0.0097 liter/min.
Referring to Table 1, the values of patient-independent model population constants are a priori identified from literature. The renal glucose threshold, RGT, has been shown to vary considerably in type 1 diabetes,16 but median values of 10 mmol/liter have been widely reported. The glucose distribution volume, Vp, is taken to be 0.22 liter/kg, the same value used by Lehmann et al.18 The glomerular filtration rate, GFR, is taken as 0.12 liter/min or 120 ml/min, which reflects the average adult GFR of 125 ml/min.33
In a study by Dalla Man et al.,34 the maximum meal Ra (Ra meal) was ∼8–9 mg/kg·min after an oral dose of 1 g/kg glucose. In the study by Korach-Andre et al.,32 the exogenous meal Ra (Ra exo) was approximately 7–9 mg/kg·min for a meal of 4 g/kg of starch (∼4.4 g/kg glucose). Despite the fourfold increase in glucose load, the maximum Ra remains at ∼9 mg/kg·min or ∼0.72 g/min for an average adult. In a study by Noah et al.,35 a higher figure still of 11 mg/kg·min was reported in a porcine model. The maximum value of the rate of gut absorption is taken as 1.1 g/min using the Noah et al.35 study as a basis, assuming a 100-kg body weight.
The proportion of glucose lost to first-pass splanchic uptake is still being debated, with proportions from negligible36,37 to as high as 30% reported in some studies.38 As there will be no tracer data in the intended application of the model, negligible losses from first-pass splanchnic sequestration and complete absorption are assumed for simplicity39 with complete absorption of meal glucose. The values of k6 and k7 are optimized using nonlinear least squares to model-independent, mixed-meal tracer glucose Ra data34 (results not shown).
The values of CNS, EGP0-G, and pG are derived from results of studies done by Del Prato et al.40,41 Like the minimal model of Bergman and colleagues,42 the model is unable to differentiate noninsulin-mediated glucose uptake from production, which is lumped into a linear relationship with glucose. Referring to Figures 4 and 5, total body glucose uptake (TBGU) and hepatic glucose production (HGP) data described elsewhere40,41 are used to identify CNS, EGP0-G, and pG. Data at glucose exceeding the approximate RGT of 10 mmol/liter are ignored to eliminate the need to evaluate renal glucose clearance, RGC, and associated errors. Under fasting and insulinopenic conditions, the P(t) and SIG(t)Q(t) terms of Equation (1) can be further eliminated. By the linear definition of the effect of hyperglycemia on TBGU, CNS can then be derived as the “virtual” y intercept of the linear TBGU curve. The term “virtual” is used, as no glucose uptake is theoretically possible at zero glucose. The central nervous system glucose uptake CNS is saturated at 3.3 mmol/liter and is relatively insensitive to insulin and glucose.43,44 At euglycemia, CNS accounts for ∼70% of all noninsulin-mediated glucose uptake,45 and this proportion is likely to increase with hypoglycemia. Hence, use of the term CNS for the virtual y intercept of the linear TBGU curve is justified.
Figure 4.
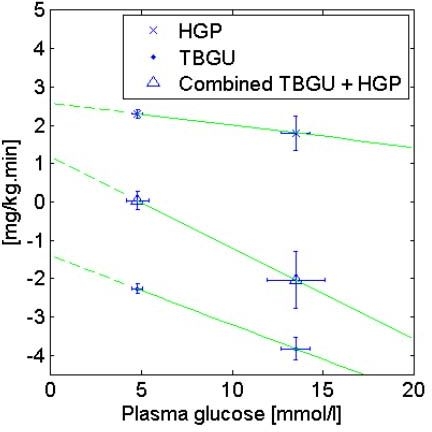
Using HGP and TBGU data from Del Prato and colleagues41 for an insulinopenic normal cohort, values of CNS = 1.4 mg/kg·min, EGP0-G = 2.6 mg/kg·min, and pG = 0.006 min−1 can be calculated by linear regression.
Figure 5.
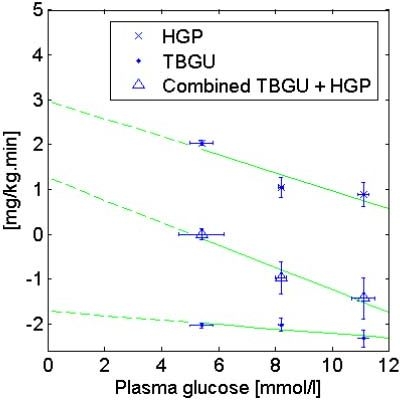
Using HGP and TBGU data of Del Prato and colleagues40 for an IDDM cohort under basal insulin, values of CNS = 1.7 mg/kg·min, EGP0-G = 3.0 mg/kg·min, and pG = 0.006 min−1 can be calculated by linear regression.
Similarly, by the linear definition of the effect of hyperglycemia on HGP, EGP0-G is the y intercept of the linear HGP curve and pG is the slope of the combined TBGU and HGP curve. Hence, pG is similar to the minimal model glucose effectiveness, SG, but is defined under conditions of insulinopenia or subbasal insulin rather than basal insulin.46
Unlike the minimal model, the insulin model in this study models the absolute insulin concentration, not insulin concentration above basal. In type 1 diabetes, conditions of basal insulin are not necessarily met all the time. Using data from Del Prato and colleagues41 for an insulinopenic normal cohort (Figure 4), values of CNS = 1.4 mg/kg·min, EGP0-G = 2.6 mg/kg·min, and pG = 0.006 min−1 are obtained compared to CNS = 1.3 mg/kg·min, EGP0-G = 3.0 mg/kg·min, and pG = 0.009 min−1 under basal insulin conditions (figure not shown). Compared to insulinopenia, the presence of basal insulin results in overestimation of pG, although this value is still approximately half that of published values of the minimal model SG for a normal cohort ∼0.024 min−1.46
Using data of Del Prato et al.40 for an insulin-dependent diabetes mellitus (IDDM) cohort under basal insulin (Figure 5), values of CNS = 1.7 mg/kg·min, EGP0-G = 3.0 mg/kg·min, and pG = 0.006 min−1 were obtained. Hence, pG of the normal, insulinopenic cohort41 is similar to the IDDM cohort under basal insulin.40 This result is logical, as SG is decreased in IDDM,46 whereas basal insulin increases SG, either by increased glucose uptake44 or by suppression of endogenous glucose production.41 In IDDM, the pG obtained is also approximately half that of published SG values of ∼0.013 min−1.46 One explanation is the elimination of data at high glucose concentrations from the pG analysis, which, if unaccounted for, would include the effect of urinary glucose excretion, thereby increasing the “effective” glucose uptake. From this investigation, it can be deduced that for an IDDM cohort under conditions of insulinopenia, pG must have an upper bound of 0.006 min−1, which is assumed in this study. The values of CNS obtained are in agreement with other results,45,47,48 and the assumption that CNS is approximately equal to the virtual y intercept of the linear TBGU curve is valid. A summary of the values of the model constants is shown in Table 1.
Table 1.
A Priori Identified Model Constants Obtained from the Literature Except Linear Gastric Emptying and Gut Absorption Rates (k6 and k7, Respectively), Which Were Optimized Using Nonlinear Least Squares to Model-Independent, Mixed-Meal Tracer Glucose Ra Data34
| Model constants | Values (units) |
|---|---|
| GABSmax | 1.1 (g/min) |
| pG | 0.0060 (min−1) |
| CNS | 1.7 (mg/kg·min) |
| EGP0-G | 3.0 (mg/kg·min) |
| GFR | 0.12 (liter/min) |
| RGT | 10 (mmol/liter) |
| VP | 0.22 (liter/kg) |
| k6 | 0.0388 (min−1) |
| k7 | 0.0097 (min−1) |
Methods
Patient Cohort
Patient data used in this study were obtained from AIDA on-line2, the Web-based version of the AIDA educational diabetes program.49 AIDA on-line2 incorporates the physiological model developed by Lehmann et al.18 and can simulate glycemic levels for any insulin or meal stimuli over a period of 1 day. Patient data (n = 40) for this study were obtained from sample diabetes case scenarios available with AIDA on-line2. Referring to Table 2, each patient case is unique in body weight, meals/carbohydrates consumed, and insulin treatment. Each patient also has unique clinical variables of hepatic and peripheral insulin sensitivity, glucose renal threshold, and glomerular filtration rate. Hence, the AIDA on-line2 cohort represents a broad range of patients and possible clinical behavior. To retrieve blood glucose, plasma insulin, and meal glucose absorption rates from AIDA on-line2, the “Advanced” display is selected to output data in text format. A sample of these data is shown in Figure 6.
Table 2.
Details of Patient Cohort (n = 40) from AIDA2 On-line Showing Body Weight, Total Carbohydrate Consumed, Total Prandial Insulin Dose, Total Basal Insulin Dose, and Unique Clinical Variables of Hepatic and Peripheral Insulin Sensitivity, Glucose Renal Threshold, and Glomerular Filtration Rate
| Case number | Body weight (kg) | Total carbohydrate consumed (g) | Total prandial insulin dose (U) | Total basal insulin dose (U) | Renal threshold | Renal function | Hepatic insulin sensitivity | Peripheral insulin sensitivity |
|---|---|---|---|---|---|---|---|---|
| 1 | 70 | 130 | 7 | 30 | Normal | Normal | Reduced | Reduced |
| 2 | 68 | 180 | 13 | 10 | High | Normal | Increased | Increased |
| 3 | 70 | 120 | 9 | 13 | Normal | Normal | Normal | Increased |
| 4 | 60 | 180 | 13 | 12 | Normal | Normal | Increased | Increased |
| 5 | 98 | 180 | 12 | 12 | Normal | Normal | Normal | Normal |
| 6 | 76 | 120 | 8 | 28 | Normal | Normal | Reduced | Increased |
| 7 | 70 | 90 | 7 | 24 | Normal | Normal | Increased | Reduced |
| 8 | 70 | 120 | 10 | 20 | Normal | Normal | Reduced | Increased |
| 9 | 70 | 180 | 12 | 12 | High | Normal | Normal | Increased |
| 10 | 70 | 120 | 15 | 8 | Normal | Normal | Normal | Increased |
| 11 | 70 | 205 | 16 | 22 | Normal | Normal | Normal | Increased |
| 12 | 70 | 185 | 24 | 20 | Normal | Normal | Reduced | Increased |
| 13 | 76 | 100 | 8 | 26 | Normal | Normal | Normal | Increased |
| 14 | 65 | 70 | 5 | 20 | Normal | Normal | Reduced | Normal |
| 15 | 99 | 115 | 6 | 42 | Normal | Normal | Reduced | Normal |
| 16 | 70 | 180 | 9 | 32 | Normal | Normal | Reduced | Increased |
| 17 | 70 | 110 | 10 | 24 | Normal | Normal | Reduced | Increased |
| 18 | 60 | 165 | 18 | 36 | High | Normal | Reduced | Increased |
| 19 | 60 | 180 | 12 | 12 | Normal | Normal | Normal | Increased |
| 20 | 70 | 105 | 8 | 36 | Normal | Normal | Normal | Increased |
| 21 | 98 | 295 | 34 | 40 | Normal | Normal | Reduced | Reduced |
| 22 | 75 | 70 | Biphasic 40 | Normal | Normal | Reduced | Reduced | |
| 23 | 87 | 177 | 38 | 12 | Normal | Normal | Reduced | Increased |
| 24 | 76 | 95 | 7 | 24 | Normal | Normal | Normal | Increased |
| 25 | 70 | 120 | 18 | 28 | Normal | Normal | Reduced | Normal |
| 26 | 80 | 170 | Biphasic 20 | Normal | Normal | Normal | Increased | |
| 27 | 70 | 120 | 9 | 13 | Low | Normal | Normal | Normal |
| 28 | 75 | 85 | 5 | 40 | Normal | Normal | Normal | Increased |
| 29 | 83 | 60 | 12 | 25 | Normal | Normal | Reduced | Normal |
| 30 | 80 | 165 | 16 | 36 | Normal | Normal | Reduced | Increased |
| 31 | 99 | 220 | 29 | 14 | Low | Normal | Normal | Increased |
| 32 | 90 | 70 | 0 | 28 | Normal | Normal | Reduced | Reduced |
| 33 | 98 | 180 | 0 | 18 | Normal | Normal | Normal | Increased |
| 34 | 60 | 175 | 17 | 13 | High | Normal | Normal | Increased |
| 35 | 60 | 170 | 22 | 10 | Normal | Normal | Normal | Increased |
| 36 | 70 | 100 | 8 | 32 | Normal | Normal | Reduced | Increased |
| 37 | 70 | 105 | 9 | 36 | High | Normal | Reduced | Reduced |
| 38 | 70 | 95 | Biphasic 26 | Normal | Normal | Normal | Reduced | |
| 39 | 70 | 110 | 12 | 35 | High | Normal | Reduced | Increased |
| 40 | 76 | 100 | 7 | 30 | Normal | Normal | Normal | Normal |
Figure 6.
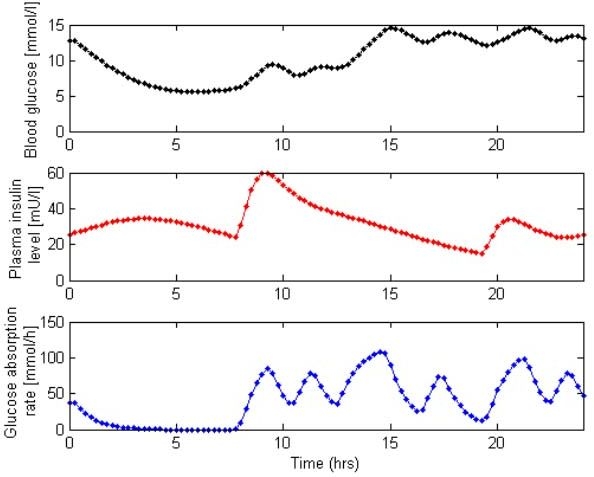
Sample raw blood glucose, plasma insulin level, and glucose absorption rate data from AIDA on-line2.49
Simulation Method
For in silico simulation, the virtual patient method is used.50,51 This method has been utilized to develop effective glycemic control protocols by simulating the physiological glycemic response to glucose and insulin stimuli.50–52 The glycemic responses are generated with patient-specific SI(t) profiles derived from retrospective data. This clinically validated method50 enables extensive simulations to be performed in a short time for rapid development and testing of any control methodology. In silico simulation was performed using MATLAB® (The Mathworks, Natick, MA) implemented on a personal computer notebook (Pentium M 1.7 GHz).
To obtain the retrospective SI(t) patient data profiles, the model is first fitted to data using the linear and convex, integral-based parameter identification method.53 Equation (1) can be expressed in a generic integral form [Equation (7)] for period ti-1 to ti, which can then be rearranged into a set of linear equations as shown in Equation (9). All quantities in Equation (7) are modeled and, as such, are known except for G(t).
| (7) |
| (8) |
AIDA on-line2 uses a first-order Euler integration method with a 15-minute step size to solve the plasma glucose model equation.54 To determine G(t) to solve Equation (7), AIDA on-line2 glucose data are interpolated linearly to obtain a piecewise linear G(t) function [Equation (8)].
The ti – ti-1 time interval for the optimization of SI(t) is chosen arbitrarily as 10 minutes. Equation (8) is solved using a proprietary MATLAB linear solver. Referring to Figure 7 and Equations (9) and (10), a stepwise, time-variant SI(t) with a 10-minute step interval is obtained.
| (9) |
where
| (10) |
Figure 7.
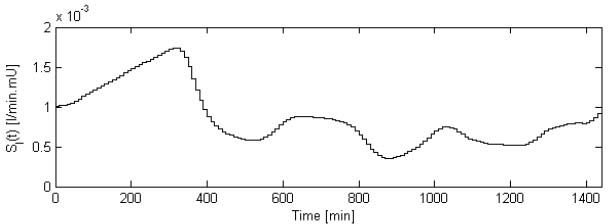
Sample patient SI(t) profile as obtained from model fit. Note the 10-minute interval for fitting the stepwise, time-variant SI(t).
A proprietary MATLAB numerical ODE solver is used to solve the model equations with a 1-minute time step. Biphasic insulin preparations are treated as in AIDA with the insulin response assumed to be a superposition of the individual components of the preparation.18 This is an acknowledged simplification considering the large variety and lack of data on such preparations.
The numerical solution to the model equations forms the in silico simulation tool. With the set of 40 virtual patient SI(t) profiles, any meal or subcutaneous insulin input and its effect on glycemia can be simulated with the assumption that SI is independent of the inputs administered, i.e., the virtual patient. This opens the possibility of simulating any glycemic control protocol, even current clinical methods.55–57 An initial validation would be to replicate long-term glycemic control outcomes, e.g., hemoglobin A1c.
Results
To gauge the model fit to data, absolute and absolute percentage errors of the G(t) model fit to the AIDA on-line2 patient data cohort are shown in Tables 3 and 4. In Table 3, per patient errors are shown, whereas total errors over the entire cohort are shown in Table 4. A sample G(t) fit is also shown in Figure 8.
Table 3.
Per Patient Absolute and Absolute Percentage G(t) Model Fit Errors to Patient Cohort Data (n = 40) from AIDA On-line2
| Absolute % G(t) fit error | Absolute G(t) fit error (mmol/liter) | |||||
|---|---|---|---|---|---|---|
| Case number | Median | 5th percentile | 95th percentile | Median | 5th percentile | 95th percentile |
| 1 | 0.84 | 0.08 | 2.87 | 0.10 | 0.01 | 0.43 |
| 2 | 1.28 | 0.05 | 7.14 | 0.10 | 0.00 | 0.50 |
| 3 | 1.19 | 0.02 | 3.56 | 0.12 | 0.00 | 0.37 |
| 4 | 1.72 | 0.05 | 7.84 | 0.12 | 0.00 | 0.42 |
| 5 | 0.94 | 0.11 | 3.24 | 0.11 | 0.01 | 0.36 |
| 6 | 1.25 | 0.04 | 4.89 | 0.13 | 0.00 | 0.53 |
| 7 | 1.93 | 0.11 | 4.52 | 0.07 | 0.00 | 0.20 |
| 8 | 0.96 | 0.05 | 4.46 | 0.09 | 0.00 | 0.49 |
| 9 | 1.03 | 0.10 | 2.94 | 0.12 | 0.01 | 0.39 |
| 10 | 1.92 | 0.28 | 4.27 | 0.17 | 0.02 | 0.39 |
| 11 | 3.09 | 0.20 | 14.04 | 0.20 | 0.01 | 2.39 |
| 12 | 1.23 | 0.05 | 8.78 | 0.13 | 0.00 | 0.70 |
| 13 | 1.08 | 0.09 | 4.80 | 0.07 | 0.00 | 0.26 |
| 14 | 0.47 | 0.04 | 3.43 | 0.05 | 0.00 | 0.47 |
| 15 | 1.00 | 0.12 | 3.84 | 0.08 | 0.01 | 0.29 |
| 16 | 1.61 | 0.11 | 5.84 | 0.18 | 0.01 | 0.59 |
| 17 | 1.31 | 0.06 | 4.38 | 0.13 | 0.00 | 0.38 |
| 18 | 3.34 | 0.32 | 7.84 | 0.21 | 0.03 | 0.80 |
| 19 | 1.23 | 0.09 | 4.14 | 0.16 | 0.01 | 0.52 |
| 20 | 2.89 | 0.17 | 21.39 | 0.13 | 0.00 | 0.89 |
| 21 | 2.73 | 0.49 | 7.17 | 0.32 | 0.06 | 0.93 |
| 22 | 0.88 | 0.11 | 3.95 | 0.09 | 0.01 | 0.50 |
| 23 | 1.50 | 0.03 | 4.96 | 0.11 | 0.00 | 0.33 |
| 24 | 1.98 | 0.21 | 6.67 | 0.14 | 0.01 | 0.43 |
| 25 | 1.37 | 0.02 | 7.44 | 0.09 | 0.00 | 0.59 |
| 26 | 0.67 | 0.09 | 2.48 | 0.07 | 0.01 | 0.31 |
| 27 | 0.69 | 0.08 | 2.74 | 0.06 | 0.01 | 0.27 |
| 28 | 0.81 | 0.09 | 6.27 | 0.05 | 0.00 | 0.36 |
| 29 | 0.81 | 0.15 | 4.48 | 0.07 | 0.01 | 0.40 |
| 30 | 9.36 | 0.98 | 37.10 | 0.72 | 0.06 | 2.56 |
| 31 | 1.16 | 0.11 | 8.67 | 0.08 | 0.01 | 0.44 |
| 32 | 0.60 | 0.06 | 2.36 | 0.06 | 0.01 | 0.28 |
| 33 | 0.93 | 0.13 | 2.72 | 0.10 | 0.01 | 0.29 |
| 34 | 1.84 | 0.01 | 5.93 | 0.15 | 0.00 | 0.44 |
| 35 | 3.30 | 0.18 | 11.70 | 0.26 | 0.01 | 1.06 |
| 36 | 1.36 | 0.19 | 5.05 | 0.12 | 0.01 | 0.39 |
| 37 | 0.94 | 0.03 | 3.38 | 0.12 | 0.00 | 0.46 |
| 38 | 0.73 | 0.08 | 3.07 | 0.08 | 0.01 | 0.40 |
| 39 | 1.29 | 0.04 | 5.53 | 0.11 | 0.00 | 0.51 |
| 40 | 1.70 | 0.20 | 7.20 | 0.10 | 0.01 | 0.31 |
| Median | 1.24 | 0.09 | 4.85 | 0.11 | 0.01 | 0.43 |
| Range | 0.47–9.36 | 0.01–0.98 | 2.36–37.10 | 0.05–0.72 | 0.00–0.06 | 0.20–2.56 |
Table 4.
Total Absolute and Absolute Percentage G(t) Model Fit Errors to Patient Cohort Data (n = 40) from AIDA On-line2
| Absolute % G(t) fit error | Absolute G(t) fit error (mmol/liter) | ||||
|---|---|---|---|---|---|
| Median | 5th percentile | 95th percentile | Median | 5th percentile | 95th percentile |
| 1.33 | 0.08 | 7.20 | 0.12 | 0.01 | 0.56 |
Figure 8.
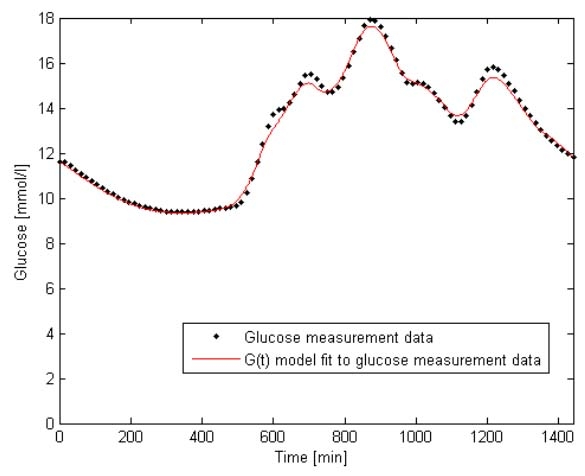
G(t) model fit to glucose measurement data for Patient 1 shown with glucose measurement data from AIDA on-line2.
From Table 3, the per patient median (95% range) absolute percentage error in G(t) is 1.24% (0.09–4.85%), which translates into a per patient absolute error in G(t) of 0.11 mmol/liter (0.01–0.43 mmol/liter). Over the entire cohort the figures are 1.33% (0.08–7.20%) and 0.12 mmol/liter (0.01–0.56 mmol/liter), which are similar. The errors reported are extremely low and within the measurement errors of clinical methods of glucose measurement in current use. This shows that the model and SI identification method is capable of capturing all patient G(t) dynamics, which will produce a more physiologically accurate simulation.
Conclusions
An in silico simulation tool was presented that utilizes an extended model of glucose kinetics, a simple glucose rate of appearance model, and the novel application of a subcutaneous insulin pharmacokinetic model. Models are identified to a physiological cohort of type 1 diabetes virtual patients. To corroborate the approach initially, an in silico simulation with data from the patient cohort using the virtual patient simulation method is planned.
Acknowledgements
The authors acknowledge Dr. Eldon Lehmann and AIDA on-line2 for the use of patient data in this study.
Abbreviations
- CGM
continuous glucose measurement
- CSII
continuous subcutaneous insulin infusion
- HGP
hepatic glucose production
- IDDM
insulin-dependent diabetes mellitus
- MDI
multiple daily injection
- SMBG
self-monitoring blood glucose
- TBGU
total body glucose uptake
References
- 1.Bequette BW. A critical assessment of algorithms and challenges in the development of a closed-loop artificial pancreas. Diabetes Technol Ther. 2005;7(1):28–47. doi: 10.1089/dia.2005.7.28. [DOI] [PubMed] [Google Scholar]
- 2.Bellazzi R, Nucci G, Cobelli C. The subcutaneous route to insulin-dependent diabetes therapy. IEEE Eng Med Biol Mag. 2001;20(1):54–64. doi: 10.1109/51.897828. [DOI] [PubMed] [Google Scholar]
- 3.Steil GM, Rebrin K, Darwin C, Hariri F, Saad MF. Feasibility of automating insulin delivery for the treatment of type 1 diabetes. Diabetes. 2006;55(12):3344–3350. doi: 10.2337/db06-0419. [DOI] [PubMed] [Google Scholar]
- 4.Steil GM, Panteleon AE, Rebrin K. Closed-loop insulin delivery–the path to physiological glucose control. Adv Drug Deliv Rev. 2004;56(2):125–144. doi: 10.1016/j.addr.2003.08.011. [DOI] [PubMed] [Google Scholar]
- 5.Klonoff DC. Continuous glucose monitoring: roadmap for 21st century diabetes therapy. Diabetes Care. 2005;28(5):1231–1239. doi: 10.2337/diacare.28.5.1231. [DOI] [PubMed] [Google Scholar]
- 6.Guidance on the use of continuous subcutaneous insulin infusion for diabetes. Technology Appraisal Guidance No. 57, National Institute for Clinical Excellence. 2003. Available from: www.nice.org.uk.
- 7.Position statement on insulin pump therapy. Position statement on insulin pump therapy, Diabetes UK. [cited 2007 Aug 8]. Available from: www.diabetes.org.uk.
- 8.ADA. Standards of medical care in diabetes-2006. Diabetes Care. 2006;29:S4–S42. [PubMed] [Google Scholar]
- 9.Mainous AG, 3rd, Diaz VA, Saxena S, Baker R, Everett CJ, Koopman RJ, Majeed A. Diabetes management in the USA and England: comparative analysis of national surveys. J R Soc Med. 2006;99(9):463–469. doi: 10.1258/jrsm.99.9.463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cohen M, Boyle E, Delaney C, Shaw J. A comparison of blood glucose meters in Australia. Diabetes Res Clin Pract. 2006;71(2):113–118. doi: 10.1016/j.diabres.2005.05.013. [DOI] [PubMed] [Google Scholar]
- 11.Guerci B, Floriot M, Böhme P, Durain D, Benichou M, Jellimann S, Drouin P. Clinical performance of CGMS in type 1 diabetic patients treated by continuous subcutaneous insulin infusion using insulin analogs. Diabetes Care. 2003;26(3):582–589. doi: 10.2337/diacare.26.3.582. [DOI] [PubMed] [Google Scholar]
- 12.Gerich JE. Novel insulins: Expanding options in diabetes management. Am J Med. 2002;113(4):308–316. doi: 10.1016/s0002-9343(02)01176-2. [DOI] [PubMed] [Google Scholar]
- 13.Wong J, Chase JG, Hann CE, Lotz TF, Lin J, Le Compte A, Shaw GM. Monte Carlo analysis of an adaptive protocol for the clinical control of type 1 diabetes. Diabetes Sci Technol. 2008;2(3) in preparation. [Google Scholar]
- 14.Chase JG, Shaw GM, Lin J, Doran CV, Hann C, Robertson MB, Browne PM, Lotz T, Wake GC, Broughton B. Adaptive bolus-based targeted glucose regulation of hyperglycaemia in critical care. Med Eng Phys. 2005;27(1):1–11. doi: 10.1016/j.medengphy.2004.08.006. [DOI] [PubMed] [Google Scholar]
- 15.Wong XW, Singh-Levett I, Hollingsworth LJ, Shaw GM, Hann CE, Lotz T, Lin J, Wong OS, Chase JG. A novel, model-based insulin and nutrition delivery controller for glycemic regulation in critically ill patients. Diabetes Technol Ther. 2006;8(2):174–190. doi: 10.1089/dia.2006.8.174. [DOI] [PubMed] [Google Scholar]
- 16.Johansen K, Svendsen PA, Lørup B. Variations in renal threshold for glucose in Type 1 (insulin-dependent) diabetes-mellitus. Diabetologia. 1984;26(3):180–182. doi: 10.1007/BF00252403. [DOI] [PubMed] [Google Scholar]
- 17.Lehmann ED, Deutsch T, Carson ER, Sönksen PH. Aida: an interactive diabetes adviser. Comput Methods Programs Biomed. 1994;41(3–4):183–203. doi: 10.1016/0169-2607(94)90054-x. [DOI] [PubMed] [Google Scholar]
- 18.Lehmann ED, Deutsch T. A physiological model of glucose-insulin interaction in type 1 diabetes mellitus. J Biomed Eng. 1992;14(3):235–242. doi: 10.1016/0141-5425(92)90058-s. [DOI] [PubMed] [Google Scholar]
- 19.Arleth T, Andreassen S, Federici MO, Benedetti MM. A model of the endogenous glucose balance incorporating the characteristics of glucose transporters. Comput Methods Programs Biomed. 2000;62(3):219–234. doi: 10.1016/s0169-2607(00)00069-9. [DOI] [PubMed] [Google Scholar]
- 20.Binder C. Absorption of injected insulin. A clinical-pharmacological study. Acta Pharmacol Toxicol (Copenh) 1969;27(Suppl 2):1–84. doi: 10.1111/j.1600-0773.1969.tb03069.x. [DOI] [PubMed] [Google Scholar]
- 21.Wong J, Chase JG, Hann CE, Shaw GM, Lotz TF, Lin J, Le Compte AJ. A subcutaneous insulin pharmacokinetic model for computer simulation in a diabetes decision support role: validation and simulation. J Diabetes Sci Technol. 2008 doi: 10.1177/193229680800200418. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wong J, Chase JG, Hann CE, Shaw GM, Lotz TF, Lin J, Le Compte AJ. A subcutaneous insulin pharmacokinetic model for computer simulation in a diabetes decision support role: model structure and parameter identification. J Diabetes Sci Technol. 2008 doi: 10.1177/193229680800200417. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yates TL, Fletcher LR. Prediction of a glucose appearance function from foods using deconvolution. Ima J Math Appl Med Biol. 2000;17(2):169–184. [PubMed] [Google Scholar]
- 24.Wolever TM, Bolognesi C. Source and amount of carbohydrate affect postprandial glucose and insulin in normal subjects. J Nutr. 1996;126(11):2798–2806. doi: 10.1093/jn/126.11.2798. [DOI] [PubMed] [Google Scholar]
- 25.Wolever TM, Bolognesi C. Prediction of glucose and insulin responses of normal subjects after consuming mixed meals varying in energy, protein, fat, carbohydrate and glycemic index. J Nutr. 1996;126(11):2807–2812. doi: 10.1093/jn/126.11.2807. [DOI] [PubMed] [Google Scholar]
- 26.Dalla Man C, Camilleri M, Cobelli C. A system model of oral glucose absorption: validation on gold standard data. IEEE Trans Biomed Eng. 2006;53(12 Pt 1):2472–2478. doi: 10.1109/TBME.2006.883792. [DOI] [PubMed] [Google Scholar]
- 27.Bruttomesso D, Pianta A, Crazzolara D, Capparotto C, Dainese E, Zurlo C, Minicuci N, Briani G, Tiengo A. Teaching and training programme on carbohydrate counting in Type 1 diabetic patients. Diabetes Nutr Metab. 2001;14(5):259–267. [PubMed] [Google Scholar]
- 28.Warshaw HS, Kulkarni K. 2nd ed. Virginia: American Diabetes Association; 2004. Complete guide to carb counting: how to take the mystery out of carb counting and unlock the secrets to blood glucose control. [Google Scholar]
- 29.Gregory RP, Davis DL. Use of carbohydrate counting for meal planning in type I diabetes. Diabetes Educ. 1994;20(5):406–409. doi: 10.1177/014572179402000507. [DOI] [PubMed] [Google Scholar]
- 30.Flint A, Møller BK, Raben A, Pedersen D, Tetens I, Holst JJ, Astrup A. The use of glycaemic index tables to predict glycaemic index of composite breakfast meals. Br J Nutr. 2004;91(6):979–989. doi: 10.1079/bjn20041124. [DOI] [PubMed] [Google Scholar]
- 31.Worthington DR. Minimal model of food absorption in the gut. Med Inform (Lond) 1997;22(1):35–45. doi: 10.3109/14639239709089833. [DOI] [PubMed] [Google Scholar]
- 32.Korach-André M, Roth H, Barnoud D, Péan M, Péronnet F, Leverve X. Glucose appearance in the peripheral circulation and liver glucose output in men after a large 13C starch meal. Am J Clin Nutr. 2004;80(4):881–886. doi: 10.1093/ajcn/80.4.881. [DOI] [PubMed] [Google Scholar]
- 33.Guyton AC, Hall JE. 10th ed. London: Saunders; 2000. Textbook of medical physiology. [Google Scholar]
- 34.Dalla Man C, Caumo A, Basu R, Rizza R, Toffolo G, Cobelli C. Minimal model estimation of glucose absorption and insulin sensitivity from oral test: validation with a tracer method. Am J Physiol Endocrinol Metab. 2004;287(4):E637–E643. doi: 10.1152/ajpendo.00319.2003. [DOI] [PubMed] [Google Scholar]
- 35.Noah L, Krempf M, Lecannu G, Maugère P, Champ M. Bioavailability of starch and postprandial changes in splanchnic glucose metabolism in pigs. Am J Physiol Endocrinol Metab. 2000;278(2):E181–E188. doi: 10.1152/ajpendo.2000.278.2.E181. [DOI] [PubMed] [Google Scholar]
- 36.Mari A, Wahren J, DeFronzo RA, Ferrannini E. Glucose absorption and production following oral glucose: comparison of compartmental and arteriovenous-difference methods. Metabolism. 1994;43(11):1419–1425. doi: 10.1016/0026-0495(94)90038-8. [DOI] [PubMed] [Google Scholar]
- 37.Ferrannini E, Bjorkman O, Reichard GA, Jr, Pilo A, Olsson M, Wahren J, DeFronzo RA. The disposal of an oral glucose load in healthy subjects. A quantitative study. Diabetes. 1985;34(6):580–588. doi: 10.2337/diab.34.6.580. [DOI] [PubMed] [Google Scholar]
- 38.Capaldo B, Gastaldelli A, Antoniello S, Auletta M, Pardo F, Ciociaro D, Guida R, Ferrannini E, Saccà L. Splanchnic and leg substrate exchange after ingestion of a natural mixed meal in humans. Diabetes. 1999;48(5):958–966. doi: 10.2337/diabetes.48.5.958. [DOI] [PubMed] [Google Scholar]
- 39.Livesey G, Wilson PD, Dainty JR, Brown JC, Faulks RM, Roe MA, Newman TA, Eagles J, Mellon FA, Greenwood RH. Simultaneous time-varying systemic appearance of oral and hepatic glucose in adults monitored with stable isotopes. Am J Physiol. 1998;275(4 Pt 1):E717–E728. doi: 10.1152/ajpendo.1998.275.4.E717. [DOI] [PubMed] [Google Scholar]
- 40.Del Prato S, Matsuda M, Simonson DC, Groop LC, Sheehan P, Leonetti F, Bonadonna RC, DeFronzo RA. Studies on the mass action effect of glucose in NIDDM and IDDM: evidence for glucose resistance. Diabetologia. 1997;40(6):687–697. doi: 10.1007/s001250050735. [DOI] [PubMed] [Google Scholar]
- 41.Del Prato S, Riccio A, Vigili de Kreutzenberg S, Dorella M, Tiengo A, DeFronzo RA. Basal plasma insulin levels exert a qualitative but not quantitative effect on glucose-mediated glucose uptake. Am J Physiol. 1995;268(6 Pt 1):E1089–E1095. doi: 10.1152/ajpendo.1995.268.6.E1089. [DOI] [PubMed] [Google Scholar]
- 42.Bergman RN, Ider YZ, Bowden CR, Cobelli C. Quantitative estimation of insulin sensitivity. Am J Physiol. 1979;236(6):E667–E677. doi: 10.1152/ajpendo.1979.236.6.E667. [DOI] [PubMed] [Google Scholar]
- 43.Siesjö BK. Hypoglycemia, brain metabolism, and brain damage. Diabetes Metab Rev. 1988;4(2):113–144. doi: 10.1002/dmr.5610040203. [DOI] [PubMed] [Google Scholar]
- 44.Best JD, Taborsky GJ, Jr, Halter JB, Porte D., Jr Glucose disposal is not proportional to plasma glucose level in man. Diabetes. 1981;30(10):847–850. doi: 10.2337/diab.30.10.847. [DOI] [PubMed] [Google Scholar]
- 45.Baron AD, Brechtel G, Wallace P, Edelman SV. Rates and tissue sites of non-insulin- and insulin-mediated glucose uptake in humans. Am J Physiol. 1988;255(6 Pt 1):E769–E774. doi: 10.1152/ajpendo.1988.255.6.E769. [DOI] [PubMed] [Google Scholar]
- 46.Best JD, Kahn SE, Ader M, Watanabe RM, Ni TC, Bergman RN. Role of glucose effectiveness in the determination of glucose tolerance. Diabetes Care. 1996;19(9):1018–1030. doi: 10.2337/diacare.19.9.1018. [DOI] [PubMed] [Google Scholar]
- 47.Scheinberg P. Observations on cerebral carbohydrate metabolism in man. Ann Intern Med. 1965;62:367–371. doi: 10.7326/0003-4819-62-2-367. [DOI] [PubMed] [Google Scholar]
- 48.Boyle PJ, Scott JC, Krentz AJ, Nagy RJ, Comstock E, Hoffman C. Diminished brain glucose metabolism is a significant determinant for falling rates of systemic glucose utilization during sleep in normal humans. J Clin Invest. 1994;93(2):529–535. doi: 10.1172/JCI117003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Reed K, Lehmann ED. Diabetes website review: www.2aida.org. Diabetes Technol Ther. 2005;7(5):741–754. doi: 10.1089/dia.2005.7.741. [DOI] [PubMed] [Google Scholar]
- 50.Chase JG, Shaw GM, Lotz T, LeCompte A, Wong J, Lin J, Lonergan T, Willacy M, Hann CE. Model-based insulin and nutrition administration for tight glycaemic control in critical care. Curr Drug Deliv. 2007;4(4):283–296. doi: 10.2174/156720107782151223. [DOI] [PubMed] [Google Scholar]
- 51.Chase JG, Wong XW, Singh-Levett I, Hollingsworth LJ, Hann CE, Shaw GM, Lotz T, Lin J. Simulation and initial proof-of-concept validation of a glycaemic regulation algorithm in critical care. Control Eng Pract. In press 2008. [Google Scholar]
- 52.Lonergan T, Le Compte A, Willacy M, Chase JG, Shaw GM, Wong XW, Lotz T, Lin J, Hann CE. A simple insulin-nutrition protocol for tight glycemic control in critical illness: development and protocol comparison. Diabetes Technol Ther. 2006;8(2):191–206. doi: 10.1089/dia.2006.8.191. [DOI] [PubMed] [Google Scholar]
- 53.Hann CE, Chase JG, Lin J, Lotz T, Doran CV, Shaw GM. Integral-based parameter identification for long-term dynamic verification of a glucose-insulin system model. Comput Methods Programs Biomed. 2005;77(3):259–270. doi: 10.1016/j.cmpb.2004.10.006. [DOI] [PubMed] [Google Scholar]
- 54.Lehmann ED, Deutsch T. AIDA2: a Mk. II automated insulin dosage advisor. J Biomed Eng. 1993;15(3):201–211. doi: 10.1016/0141-5425(93)90116-g. [DOI] [PubMed] [Google Scholar]
- 55.BD Diabetes Learning Centre. Insulin therapies. Managing diabetes with insulin. 2006 Available from: http://www.bddiabetes.com/us/main.aspxcat=1&id=151. [Google Scholar]
- 56.Walsh J, Roberts R. The pocket pancreas: your diabetes guide for improved blood sugars. Diabetes Services Inc. 1994 [Google Scholar]
- 57.Hanas R. New York: Marlowe & Company; 2005. Type 1 diabetes: a guide for children, adolescents, young adults and their caregivers. [Google Scholar]