Mathematical Model of the Drosophila Circadian Clock: Loop Regulation and Transcriptional Integration

Abstract

Eukaryotic circadian clocks include interconnected positive and negative feedback loops. The clock-cycle dimer (CLK-CYC) and its homolog, CLK-BMAL1, are key transcriptional activators of central components of the Drosophila and mammalian circadian networks, respectively. In Drosophila, negative loops include period-timeless and vrille; positive loops include par domain protein 1. Clockwork orange (CWO) is a recently discovered negative transcription factor with unusual effects on period, timeless, vrille, and par domain protein 1. To understand the actions of this protein, we introduced a new system of ordinary differential equations to model regulatory networks. The model is faithful in the sense that it replicates biological observations. CWO loop actions elevate CLK-CYC; the transcription of direct targets responds by integrating opposing signals from CWO and CLK-CYC. Loop regulation and integration of opposite transcriptional signals appear to be central mechanisms as they also explain paradoxical effects of period gain-of-function and null mutations.

Introduction

Circadian clocks exhibit 24-h behavioral and transcriptional oscillations. These oscillations are generated by interconnected transcriptional feedback loops. In particular, the Drosophila circadian clock has one positive and two negative loops that interconnect at CLK-CYC, a heterodimer of the clock (CLK) and cycle (CYC) proteins. CLK-CYC binds canonical E-box sequences to activate the transcription of direct targets clockwork orange (cwo), period (per), timeless (tim), vrille (vri), and par domain protein 1 (Pdp1, Fig. 1 a) (1–6). Clockwork orange (CWO) is a recently defined negative transcriptional regulator that directly targets the same genes as CLK-CYC (Fig. 1 a). The presence of circadianly expressed cwo orthologs in mouse (dec1 and dec2) suggests that a similar feedback mechanism exists in mammals (7); this view may also extend to other animal systems (8).

Figure 1.

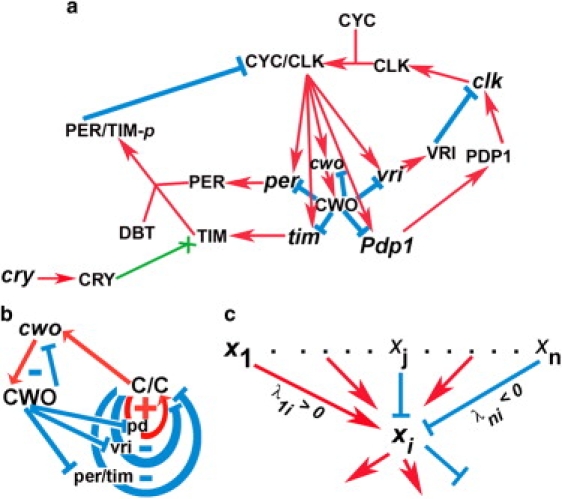
The network of the Drosophila circadian clock. (a) Cartoon depicting the Drosophila circadian molecular network; protein and mRNA are represented by capital letters and lower case, respectively. Red arrows and cyan lines indicate stimulatory and inhibitory interactions, respectively. The green arrow ending in X indicates that CRY protein enhances the degradation of TIM. The amounts of CYC and DBT are assumed to be constant. (b) Loop diagram of the network showing the CWO autorepressive loop (cwo, CWO), the per/tim and vri negative loops, and the Pdp1 (pd) positive loop. (c) Cartoon depicting a hypothetical example of molecules x_j, where 1 ≤ j ≤ n, regulating the state of molecule x_i by positive (red arrows) or negative (cyan lines) interactions. Positive and negative real parameters are regulatory weights that simulate stimulation and repression, respectively (see Eq. 1).

Because CWO represses the transcription of cwo, per, tim, vri, and Pdp1, one expects cwo mutants to exhibit higher peak levels of all direct-target mRNAs compared to wild-type flies (wt). Both Matsumoto et al. (9) and Richier et al. (10) show that the peak levels of per, tim, Pdp1, and vri are lower in cwo-mutant flies compared to wt flies. Lim et al. also show that the peak levels of per, Pdp1, and vri are lower in cwo-mutant flies than in wt flies (the peak level of tim was not studied) (11). The results of Kadener et al. are consistent with those above, except in the case of Pdp1 (8). The reasons why a cwo null mutation has these unusual effects on direct target genes are not known.

Glossop et al. described two negative interlocked feedback loops within the Drosophila circadian oscillator: 1), a per/tim loop that is activated by CLK-CYC and repressed by the period-timeless (PER-TIM) dimer; and 2), the vri/clk loop, consisting of the CLK-CYC heterodimer activating VRI, which represses clk transcription (6,12–14). The Pdp1/clk positive loop, which also interconnects at CLK-CYC, includes PDP1 acting as a transcriptional activator of clk mRNA (Fig. 1 b) (15–17). PER-TIM represses the transcriptional ability of CLK-CYC by inhibiting its DNA binding activity (18–21); furthermore, double-time (DBT) kinase appears to mediate these effects on CLK-CYC by phosphorylating PER and CLK (22–24). DBT is incorporated in our model as a positive and necessary regulator of the PER-TIM dimer.

Mathematical models of the circadian clock typically use the Michaelis-Menten and Hill-type equations, which require several parameters to model a single regulatory reaction. Furthermore, several equations are needed to model the ability of a molecule to regulate the state of another (15–17,25–28). Here, we introduce a new system of nonlinear ordinary differential equations that model regulatory networks such that regulatory weights are represented by single parameters. The system is generic in the sense that it is applicable to mRNA, protein, protein dimer formation, or protein phosphorylation. We construct a new mathematical model of the Drosophila circadian clock and demonstrate that it is faithful in the sense that it replicates biological results. The model is then applied to study the regulatory effects of CWO and to suggest a resolution of the paradox of the effects of CWO on direct target genes. The model predicts that the actions of CWO on the interconnected loops elevate the level of CLK-CYC; the latter generates positive transcriptional signals on per, tim, vri, and Pdp1 that outweigh the direct repressive actions of CWO. In the Results section, using the regulatory weights introduced by the new system of differential equations, we suggest a method for quantifying transcriptional signals. These ideas are applied to analyze simulations of per gain-of-function and null mutations.

Methods

Numerical computations

Simulations are performed in MATLAB (The MathWorks, Natick, MA); the system of ordinary differential equations is solved numerically by the subroutine “ode45” (see the Supporting Material for MATLAB functions).

Results

Interconnected positive and negative loops

A loop (a₁,…,a_n) is a sequence of interacting molecules such that 1), each of its molecules is figured only once; 2), for 1 < k ≤ n, a_k-1 is the only molecule that directly regulates a_k (either negatively or positively); and 3), a_n regulates a₁ (either negatively or positively). A loop is positive if it contains an even number of negative regulations, including zero, and is negative otherwise. For example, the loops (CYC-CLK, Pdp1, PDP1, clk, CLK) and (CYC-CLK, vri, VRI, clk, CLK) are positive and negative, respectively (Fig. 1 a).

The network shown in Fig. 1 a can be reduced to the loop diagram shown in Fig. 1 b, which includes three main loops that intersect at CLK-CYC. These are the (CLK-CYC, per/tim, PER-TIM, PER/TIM-p) and (CLK-CYC, vri, VRI, clk, CLK) negative loops and the (CLK-CYC, Pdp1, PDP1, clk, CLK) positive loop. Henceforth, we will refer to these loops as per/tim, vri, and Pdp1 loops, respectively. The network also includes a negative auto-repressive loop (cwo, CWO); notice that this negative loop, which includes two molecules, cwo and CWO, doesn't interconnect at CLK-CYC. Recall that CLK-CYC binds to E-box sequences leading to transcriptional activation of direct targets, including cwo. The CWO protein specifically binds and represses the promoter elements/E-box sequences of direct targets, including cwo (9,11).

System of ordinary differential equations

We introduce a nonlinear, autonomous, first-order system of ordinary differential equations (Fig. 1 c). Assuming that genes/proteins j ∈ {1,…, n} regulate the production of gene/protein i, we use the following type of differential equations as a general model:

$$\frac{d{x}_i\left(t\right)}{dt}={\rho }_{i}g\left(\sum _{j=1}^n{\lambda }_{ji}{x}_j\left(t\right)-{\delta }_i{x}_i\left(t\right)\right)x_i\left(t\right)\left(s_i-x_i\left(t\right)\right),1\le j\le n,$$ (1)

where x_i is the state vector representing the concentration of molecule i at its site of action. The real parameters, λ_ji, are regulatory weights that encode the effects of molecule j on the production rate of molecule i. Positive and negative λ_ji are interpreted as j activating or repressing, respectively, molecule i. The absolute value of λ_ji reflects the strength of stimulation or repression. Notice that λ_ji is applicable to several biochemical reactions, such as the formation of a protein dimer (i.e., CLK-CYC), the effects of a kinase (i.e., DBT), the effects of a transcription factor on a promoter (i.e., the effect of CLK-CYC or CWO on direct target genes), and mRNA translation to protein (i.e., PER or TIM).

The sum of the regulatory influences is modulated by an odd sigmoid function, $g:\mathbb{R}\to \mathbb{R}$, of the form

$$g\left(u\right)=\frac{u}{\sqrt{1+u^2}}=\tanh \left(\ln \left(u+\sqrt{1+u^2}\right)\right),$$

together with a real parameter ρ_i > 0 that indicates the maximum rate of formation of i. The model incorporates logistic terms ((x_i)(s_i − x_i)), where constants s_i ≥ 0 indicate the saturation level of molecule i. The real parameter δ_i is the decay rate of i. Notice also that because x_i denotes the concentration of molecule i at the site of its action, the parameters model not only direct stimulation or repression, but also the cumulative effects of transport and diffusion across cellular compartments. The actual equations and parameters are provided in MATLAB functions and pdf copies in the Supporting Material.

Parameters and simulations

The parameters are optimized to yield a numerical solution such that the clock oscillates with a 24-h period both in light-dark (LD) and dark-dark (DD) cycles indefinitely and with timely peaks of direct targets (see Fig. 2, a–c, and Supporting Material). The period exhibits minimum variations, and the amplitudes are effectively constant; in particular, the period ranges from 23.9718 h to 24.0292 h in LD and from 23.9633 h to 24.0483 h in DD conditions (Fig. 2 d). CRY is a light-regulated cryptochrome that leads TIM to its subsequent degradation. To account for different photoperiods (i.e., LD), the model uses oscillations of cry mRNA obtained from published microarray expression data (see Fig. S1 in the Supporting Material) (8). The cry mRNA oscillations, approximated by fitting with linear elements, keep the Zeitgeber time (ZT; i.e., time mod(24) in LD). DD conditions are simulated by annulling the effects of CRY on TIM (i.e., λ_{CRY, TIM} = 0).

Figure 2.

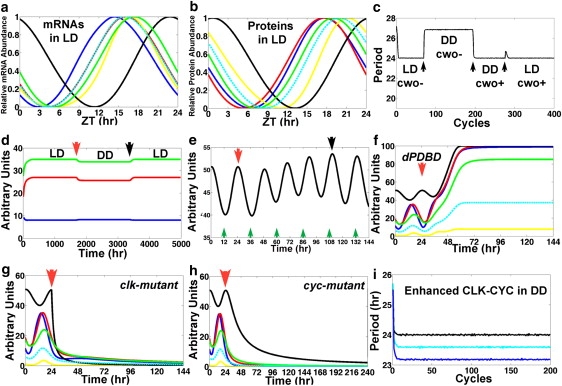
The model replicates biological results. (a) Plot of the results of model simulations in LD of the concentrations of clk (black; peak, 22.8 h), per (blue; peak, 14.4 h), tim (red; peak, 16.1 h), cwo (yellow; peak, 16.8 h), Pdp1 (green; peak, 17.4 h), and vri (cyan; peak, 15.9 h). (b) Plot of the results of model simulations in LD of the concentration of the CLK (black; peak, 0.7 h), PER (blue; peak, 17.7 h), TIM (red; peak, 17.6 h), CWO (yellow; peak, 21.2 h), PDP1 (green; peak, 19 h), and VRI (cyan; peak, 20 h). Relative abundance is determined by (x − min)/(max − min). The Zeitgeber reference time is described in LD conditions only. To define a time reference in DD conditions we set time 0 at −0.7 h of the peak of the CLK protein so that the latter peaks at the same time in both LD and DD. The peak times of the direct-target genes and proteins in DD are as given in a except for TIM, which peaks at 16.6 h. (c) Plot of the period (time between the peaks of per mRNA) in an experiment where the model cycles first in LD with cwo mutation (cwo−), then in DD with cwo mutation, then in DD with wt cwo (cwo+), and finally in LD with wt cwo. Transitions are applied at ZT = 0 (arrows). Notice the minimum variability of the 24-h period in both DD and LD in wt cwo simulations. (d) Plot of the peak (green) and trough (blue) levels and the amplitude (peak − trough, red) of per mRNA, computed from an experiment where the model cycles first in LD (0 to red arrow), then in DD (red arrow to black arrow), and finally in LD. Transitions from LD to DD and from DD to LD are applied at ZT = 0. (e) The model clock resets (black arrow) 4.5 days after a shift of +12 h is applied at the red arrow. Notice that CLK evolves to a peak around midnight of the previous time zone (black arrow). Green arrows point to ZT = 12 h of the previous time zone. (f–h) Plots of the simulated dynamics of dPDBD (in DD) (f), clk (in LD) (g), and cyc (in DD) (h) null mutations applied at time = 24 h (red arrows). Notice the elevated and constant levels of per (blue) and tim (red) mRNAs in simulated dPDBD mutants and the low levels of per and tim mRNAs in clk- and cyc-null mutants. The mRNA levels of per, tim, cwo, Pdp1, and vri are shown in blue, red, yellow, green, and cyan, respectively. The CLK protein is shown in black. (i) Plot of the period of the wt model (black) and the simulations where all the positive regulatory weights of CLK-CYC on direct-target genes are increased by 15% (cyan) or 30% (blue) in DD conditions.

The timing of the peaks of the oscillating direct-target mRNAs and proteins is consistent with biological observations (Fig. 2, a and b). In particular, the model predicts that per, tim, PER, and TIM peak at ZT = 14.4, 16.1, 17.7, and 17.6 h, respectively, in LD. These results are within range of published results for per (13–16 h), tim (13–16 h), PER (18–20 h), and TIM (17–18 h). The predicted times of the peak of CLK (0.7 h) and the period between the peaks of clk and CLK (1.9 h) are also within range of those in the literature (1,8,10,29–34). The oscillations of mRNAs and proteins in DD have the same phases as in LD conditions except for the TIM protein, which peaks 1 h earlier in DD (16.6 h versus 17.6 h).

The model replicates biological observations

Once the model was established as described in the previous section, the next step was to test whether it could predict the effects of unfitted perturbations. A major characteristic of the circadian clock is its capacity to respond to different time zones. TIM degradation is the main response of the clock to light; this effect is mediated by CRY (Fig. 1 a) (35,36). We study the response of the model to a 12-h time shift (simulating the effects of time-zone changes in LD). This is done by advancing the level of cry mRNA at ZT = 0 to its level at ZT = 12 h (i.e., LD, DL, DL,…). The outcome of the numerical experiment is that the molecular clock is reentrainable by light, i.e., the CLK protein evolves smoothly from peaking at ZT = 12 h, which is ZT = 0 h in the previous time zone, to peaking at ZT = 0 h in the new time zone, although the transition takes 4.5 days to complete (see Fig. 2 e). This entrainment is valid for all mRNAs. These results are in concordance with the behavior of the mammalian clock in response to shifting the light/dark cycle by 12 h (LD to DL); Chen et al. showed near-complete phase reversal (11.55 h) of behavioral and molecular phase shifts after 5 days of DL (37).

We next tested whether or not the model can predict accurately the molecular effects of mutations in the core clock components. Null mutations are simulated by setting the appropriate λ_ji = 0. For example, clk mutations are simulated by setting λ_{clk, CLK} = 0. A mutation of the DBT binding domain on PER (dPDBD) is simulated by λ_{DBT, PER/TIM-p} = 0. Fig. 2 f plots a simulation of the dPDBD mutation in DD, showing the absence of oscillations with elevated levels of per and tim mRNA. These results are largely consistent with biological data for dPDBD from the literature, which are arrhythmic with elevated PER and TIM (23,38–40). Furthermore, simulations of cyc- and clk-mutant flies are also consistent with biological data showing that the mutant flies are arrhythmic with low levels of PER and TIM (Fig. 2, g–h) (1,5).

Kadener et al. analyzed the effects of enhancing the activity of the CLK-CYC by generating CYC-VP16, a well studied construct that imparts strongly enhanced activity of the CLK-CYC-VP16 complex (41). This experimental design is simulated by increasing the positive regulatory effects of CLK-CYC on direct-target genes. The model replicates the biological outcome by yielding a higher peak level of per mRNA (data not shown) and a shorter period in DD (Fig. 2 i). The ability of the model system to replicate biological results for which it was not fit gives a certain level of confidence in its overall faithfulness. The results of simulations of per-null and gain-of-function mutations are discussed below.

Modeling the actions of CWO

With the aim of understanding the role of CWO in the circadian molecular network, we instituted in silico cwo-null mutations. Consistent with biological data, mutations in this gene lead to low mRNA peak levels of per, tim, vri, and Pdp1 in both LD and DD conditions. It is interesting to note that the model also predicts that, as compared to wt RNA, the peak level of cwo mRNA is higher in the cwo-mutant model in both LD and DD conditions (see Fig. S2 and Fig. S3). The model predicts a period of 26.8 h in cwo-mutants in DD conditions (Fig. 2 c). These results are consistent with biology, since the experimentally measured period is ∼26.5 h (8,10). Furthermore, as in biological observations, the cwo-mutant model yields a period of 24 h in LD conditions. This satisfactory outcome further enhances our confidence in the model.

Direct-target genes receive two opposing signals, a direct stimulus from CLK-CYC and a direct repressive action by CWO (see Fig. 1 a). In addition, CWO regulates the level of the CYC-CLK, presumably through its actions on each of three main loops (i.e., the per/tim and vri negative loops and the Pdp1 positive loop (Fig. 1 b)). It is therefore uncertain how the absence of CWO affects direct-target genes. We hypothesized that the behavior of the network may be deduced from its loop structure.

CWO is a loop regulator

The in silico experiments detailed in this section are performed to elucidate the mechanism of CWO action. Recall that in addition to its autorepressive effects, CWO has three repressive loop actions at 1), the per/tim negative loop, 2), the vri negative loop, and 3), the Pdp1 positive loop (Fig. 1 b). To optimize the presentation, the experiment begins from a baseline absence of any CWO function (i.e., mutant cwo (Fig. 3, black line)), then proceeds by turning on either single or combinations of repressive actions of CWO in DD conditions. Figs. 3 and 4 plot the mRNA levels of the direct-target genes as well as that of CLK-CYC in response to the targeted parameter perturbations; each panel represents a molecule and the results of the experiments are shown in color. It can be intuited that repressing a single positive or negative loop would yield lower and higher peak levels of CLK-CYC, respectively.

Figure 3.

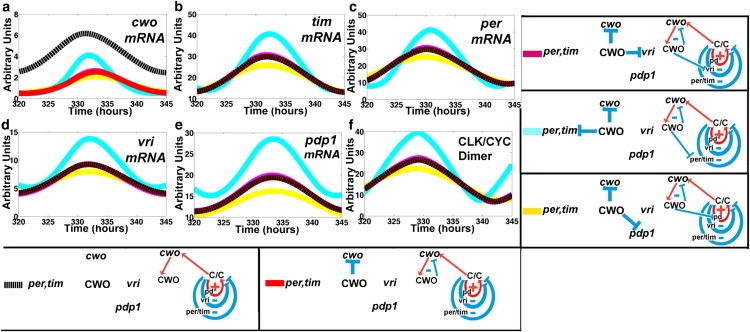
Actions of CWO on the loops. (a–f) mRNA concentrations of cwo, tim, per, vri, pdp1, and CLK-CYC in response to selective activation of the repressive actions of CWO in DD conditions. Dotted black lines represent the mutant model. The red line denotes the selective activation of the CWO autorepressive loop (cwo, CWO) only. Magenta, cyan, and yellow lines indicate the activation of two repressive actions, the CWO autorepressive loop plus one of either the vri or per/tim negative loops, or the Pdp1 positive loop (pd), respectively.

Figure 4.

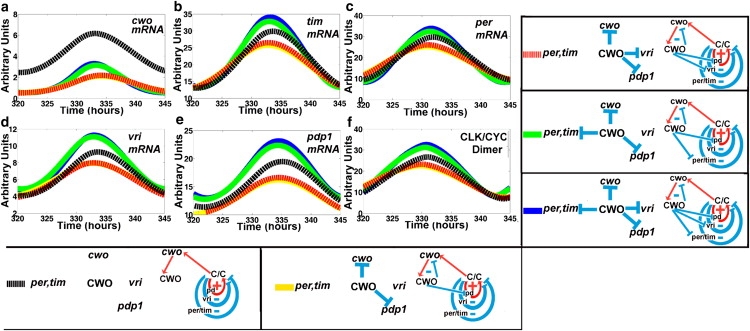
CWO regulates the loops. (a–f) mRNA concentrations of cwo, tim, per, vri, pdp1, and CLK-CYC in response to selective activation of the repressive actions of CWO in DD conditions. Blue and black lines represent the wt and mutant models, respectively. The yellow line denotes the selective activation of the CWO autorepressive loop (cwo, CWO) and the Pdp1 positive loop (pd). Red and green lines denote the activation of three CWO-repressive actions, the CWO autorepressive loop plus the Pdp1 positive loop plus one of either the vri (red) or the per/tim (green) negative loops, respectively.

Starting from a baseline of no CWO action, then selectively turning on the CWO autorepression, causes the peak level of cwo mRNA to decrease (Fig. 3 a, black versus red), but the mRNA peak levels of the other direct target genes remain unchanged (Fig. 3, b–f). This is expected, because this configuration isolates the (cwo, CWO) autorepressive loop from the other components of the clock (Fig. 1 b). Next, we turn on two repressive actions:1), the CWO autorepression, and 2), one of either the Pdp1 (positive), vri (negative), or per/tim (negative) loops. The results confirm that downregulating a positive or a negative loop lowers (Fig. 3, red to yellow) and elevates (Fig. 3, red to cyan or red to magenta), respectively, the peaks of the CYC/CLK dimer and all direct-target genes.

Next, we turn on three CWO-mediated repressive actions, namely 1), the CWO autorepression; 2), repression of the Pdp1 positive loop; and 3), repression of either the vri or the per/tim negative loops (Fig. 4). It is interesting that downregulating the per/tim negative loop is more effective than downregulating the vri loop in elevating the peak levels (Fig. 4, yellow to green versus yellow to red), suggesting that the per/tim negative loop is more repressive than the vri negative loop. The results provide a confirmation of the idea that repression of a positive or a negative loop by a molecule located outside the loop (i.e., CWO) causes negative and positive effects, respectively, on the elements of the loop.

Actions of CWO on direct targets

The next experiments are done to understand the cumulative effects of CWO on the three loops that interconnect at CLK-CYC in LD and DD conditions (see Fig. S4 and Fig. S5). Specifically, we start from the baseline, where CWO selectively represses its own transcription (Fig. S4 and Fig. S5, red), and turn on all three loop-repressive actions of CWO (i.e., the wt model (Fig. S4 and Fig. S5, blue)). The results reveal that the peak levels of CLK-CYC are higher in the wt than in the cwo-mutant model (Fig. S4 f and Fig. S5 f, red to blue). Recall that each direct-target gene receives positive and negative transcriptional stimuli from CLK-CYC and CWO, respectively. Notice that the increase in CLK-CYC (referred to as $\Delta x_{\text{C/C}}=x_{\text{C/C}}-x_{\text{C/C}}^{\text{cwo-mutant}}$) causes a positive effect on the transcription of per, tim, vri, and Pdp1, despite the repressive effects of CWO (blue versus red). This suggests that the positive effects of Δx_C/C outweigh the repressive actions of CWO on the transcription of per, tim, vri, and Pdp1.

To understand how cwo integrates the opposing transcriptional effects of Δx_C/C and CWO, we examine the models of 1), null-mutant cwo (i.e., no CWO actions (Fig. S4 and Fig. S5 a, black dotted line); 2), cwo acted on by CWO only (Fig. S4, and Fig. S5 a, red); and 3), cwo acted on by both CWO and Δx_C/C (wt model, Fig. S5 a, blue). The results reveal that the positive transcriptional effects of Δx_C/C partially reverse the repressive effects of CWO because they elevate the transcription of cwo (blue versus red) but not to the level seen in the mutant cwo model (blue versus dotted black). These findings suggest that unlike the other direct-target genes, the outcome of the opposing transcriptional actions of Δx_C/C and CWO at cwo favors repression.

Modeling the integration of opposing transcriptional signals

Our next goal is to elucidate the law that governs the integration of the opposing transcriptional effects of Δx_C/C and CWO on a direct-target gene (g) at the time of its peak (t_g). We examine 1), the “wiring” as reflected by the regulatory weights λ_{C/C, g} and λ_{CWO, g}, and 2), Δx_C/C and the concentration level of the CWO protein (x_CWO). Recall that the parameters λ_{C/C, g} and λ_{CWO, g} are positive and negative and that their absolute values reflect the strength/weight of transcriptional enhancement and repression, respectively. The difference between the peak concentrations of direct-target gene g in the wt and cwo-mutant models ($\Delta Y_g=Y_g^{}-Y_g^{\text{cwo-mutant}}$) can be expressed as (see Supporting Material)

$$\text{sign}\left(\Delta Y_g\right)=\text{sign}\left[\Delta x_{\text{C/C}}\left(t_g\right){\lambda }_{\text{C/C},g}-x_{\text{CWO}}\left(t_g\right)\left|{\lambda }_{\text{CWO},g}\right|\right]\text{.}$$ (2)

Hence, a transcriptional signal at the peak of a direct-target gene can be modeled by the product of the concentration of the transcriptional modulator (i.e., Δx_C/C(t_g) or x_CWO) and the absolute values of the weights of the transcriptional regulation (i.e., |(λ_C/C,g)| or |λ_CWO,g|). Furthermore, the transcription of a direct-target gene at its peak is enhanced (ΔY_g > 0) or repressed (ΔY_g < 0) when the positive signal, Δx_C/C(t_g)λ_C/C,g, is larger or smaller, respectively, than the negative transcriptional signal, [x_CWO(t_g)|λ_CWO,g|] (Fig. 5). We conclude that the integration of the actions of CWO on the loops causes an elevation of CLK-CYC (Δx_C/C > 0). In the wt model, each direct-target gene integrates a positive signal from Δx_C/C and a negative signal from CWO. The peak levels of tim, per, vri, and Pdp1 are higher in the wt than in the cwo-mutant model because the positive transcriptional signals outweigh the negative ones (i.e., Δx_C/C(t_g) λ_C/C,g > x_CWO(t_g)|λ_CWO,g|, Fig. 5). However, the transcription of cwo is repressed in the wt model because the negative transcriptional signal is dominant (i.e., $\Delta x_{\text{C/C}}\left(t_{cwo}\right){\lambda }_{\text{C/C},cwo}<x_{\text{CWO}}\left(t_{cwo}\right)\left|{\lambda }_{\text{CWO},cwo}\right|$). The fact that the integration of transcriptional signals on direct targets was not considered when Eq. 1 was constructed gives additional confidence in its overall faithfulness.

Figure 5.

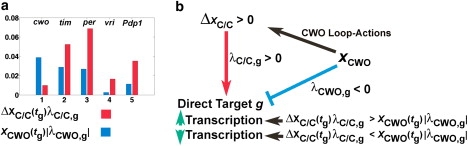
Integration of opposite transcriptional signals. (a) Bar plot of the absolute values of the positive (Δx_C/C(t_g)λ_C/C,g; red) and negative (x_CWO(t_g)|λ_CWO,g|; blue) transcriptional signals at the peak of each direct-target gene in the wt model in LD. (b) The cumulative effects of the actions of the CWO protein on the three loops cause an increase in peak levels of CLK-CYC (Δx_C/C > 0), which leads to higher peaks of vri, Pdp1, per, and tim, because the values of the positive signals are larger than those of the negative signals. The transcription of cwo is repressed because the negative signal is dominant. The term x_CWO(t_g) refers to the concentration of CWO protein at the time of the peak of a direct-target gene.

To understand the effects of CWO on the period, we examine simulations where individual repressive weights of CWO are increased or decreased by 10% in DD conditions. Recall that by repressing Pdp1, per, tim, and vri, CWO acts on the loops that interconnect at CLK-CYC, namely, the Pdp1 positive loop and the per/tim and vri negative loops. The results reveal that perturbations that increase or decrease the level of CLK-CYC shorten and elongate the period, respectively (Fig. 6). Notice that these findings are consistent with the outcome of the simulation where the activity of CLK-CYC is enhanced (Fig. 2 i). In particular, by repressing Pdp1, CWO downregulates the activity of the Pdp1 positive loop in the sense that the level of CLK/CYC decreases. Similarly, by repressing per or vri, CWO downregulates the per/tim and vri negative loops as the levels of CLK-CYC increase. Thus, by repressing the transcriptional levels of per, vri, and Pdp1, CWO regulates the activity of the three main loops by making the positive loops “less positive” and the negative loops “less negative.”

Figure 6.

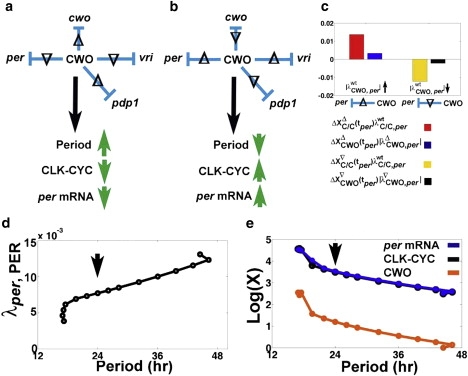
Effects of single repressive effects of CWO on the period in DD. (a and b) Summary of how the period and peak levels of CLK-CYC and per mRNA react in simulations where the absolute value of a single repressive regulatory weight of CWO is increased (Δ) or decreased (∇) by 10% in DD. Neither CLK-CYC nor the period is affected by similar perturbations of the repressive actions of CWO on tim. (c) Bar graph from an experiment where $\left|{\lambda }_{\text{CWO},per}^{\text{wt}}\right|$ is increased ($\left|{\lambda }_{\text{CWO},per}^{\Delta }\right|$) or decreased ($\left|{\lambda }_{\text{CWO},per}^{\nabla }\right|$) by 10% in DD, leading to higher ($\Delta x_{\text{C/C}}^{\Delta }\left(t_{per}\right)>0$ and $\Delta x_{\text{CWO}}^{\Delta }\left(t_{per}\right)>0$) and lower ($\Delta x_{\text{C/C}}^{\nabla }\left(t_{per}\right)<0$ and $\Delta x_{\text{CWO}}^{\nabla }\left(t_{per}\right)<0$) levels of CLK-CYC and CWO, respectively. The symbol t_per refers to ZT at the peak of per. In the case of ${\lambda }_{\text{CWO},per}^{\Delta }$, the positive transcriptional signal for per outweighs the negative one ($\Delta x_{\text{C/C}}^{\Delta }\left(t_{per}\right){\lambda }_{\text{C/C},per}^{\text{wt}}>\Delta x_{\text{CWO}}^{\Delta }\left(t_{per}\right)\left|{\lambda }_{\text{CWO},per}^{\Delta }\right|$). In the case of ${\lambda }_{\text{CWO},per}^{\nabla }$, the positive transcriptional signal for per is smaller than the negative one ($\Delta x_{\text{C/C}}^{\nabla }\left(t_{per}\right){\lambda }_{\text{C/C},per}^{\text{wt}}<\Delta x_{\text{CWO}}^{\nabla }\left(t_{per}\right)\left|{\lambda }_{\text{CWO},per}^{\nabla }\right|$). (d) Response of the period to the titration of λ_{per, PER}. Notice the apparent linear relation in the interval λ_{per, PER} ∈ [0.0069, 0.0123]; y = 2 × 10^-4 × x + 0.0029 (norm of residuals = 2.7312 × 10^-4). (e) Based on the data plotted in d, and Plots of log(X) versus period, where X denotes the level of CLK-CYC (black), per (blue), or CWO (orange). The arrows in d and e indicate the wt model.

The results of the perturbation experiments also demonstrate that per mRNA reacts in the same direction as CLK-CYC (Fig. 6 a). However, it appears paradoxical that increasing the repressive activity of CWO on per elevates the level of per mRNA instead of suppressing it (Fig. 6). This paradox is easily resolved when we consider the idea of loop regulation and the method for integrating opposite transcriptional signals detailed in Fig. 5 (see Fig. 6 c). In particular, increasing the strength of CWO-mediated repression of the per/tim negative loop ($\left|{\lambda }_{\text{CWO},per}^{\Delta }\right|>\left|{\lambda }_{\text{CWO},per}^{\text{wt}}\right|$) elevates CLK-CYC, a positive regulator of CWO (i.e., $\Delta x_{\text{C/C}}^{\Delta }\left(t_{per}\right)>0$ and $\Delta x_{\text{CWO}}^{\Delta }\left(t_{per}\right)>0$). After integrating the two opposing signals, the peak level of per increases because the positive transcriptional signal ($\Delta x_{\text{C/C}}^{\Delta }\left(t_{per}\right){\lambda }_{\text{C/C},per}^{\text{wt}}$) outweighs the negative one ($\Delta x_{\text{CWO}}^{\Delta }\left(t_{per}\right)\left|{\lambda }_{\text{CWO},per}^{\Delta }\right|$). In a similar way, decreasing the strength of the CWO-mediated repression of the per/tim negative loop (i.e., $\left|{\lambda }_{\text{CWO},per}^{\nabla }\right|<\left|{\lambda }_{\text{CWO},per}^{\text{wt}}\right|$) lowers both CLK-CYC and CWO (i.e., $\Delta x_{\text{C/C}}^{\nabla }\left(t_{per}\right)<0$ and $\Delta x_{\text{CWO}}^{\nabla }\left(t_{per}\right)<0$). However, the level of per decreases because the positive transcriptional signal ($\Delta x_{\text{C/C}}^{\nabla }{\lambda }_{\text{C/C},per}^{\text{wt}}$) is smaller than the negative signal ($\Delta x_{\text{CWO}}^{\nabla }\left(t_{per}\right)\left|{\lambda }_{\text{CWO},per}^{\nabla }\right|$). Finally, the results highlight the usefulness of the regulatory network introduced in Eq. 1 in advancing our understanding of the complex actions of cwo, in simulating how the network integrates the actions of CWO on multiple loops, and in uncovering a method for integrating opposite transcriptional signals at each direct-target gene (Eq. 2).

Simulations of per mutations

Flies with chromosomal deletions of the per locus are arrhythmic (39,42). The per⁰¹ is a per mutation with an early stop codon corresponding to position 464 of the amino acid sequence (43). The levels of per mRNA are inversely correlated with period length, so that flies with the lowest levels of per have slow-running biological clocks (44,45). Based on these observations, Baylies et al. suggest that per⁰¹ is a null mutation (43). Notice that the perturbation experiments of Fig. 6, a–c, are consistent with the idea that low levels of per are associated with long periods. To investigate how the model reacts to per mutations, we titrate λ_{per, PER} and examine the levels of per, CLK-CYC, and CWO, and the period in DD (Fig. 6 d). The results reveal an apparent linear correlation between λ_{per, PER} and the period within bounds and confirm that per mRNA levels are inversely correlated to period length (Fig. 6, d and e). Nonetheless, our simulations suggest a conclusion different from that of Baylies et al. Specifically, the results of simulations of PER gain of function in LD and DD (λ_{per, PER} is increased by 25%) reveal persistent oscillations of per, tim, and cry mRNAs with lower peaks compared to the wt model; the period is 24 h in LD (Fig. 7, a and b). The peak levels of both per and tim in LD and DD are at 78% and 57%, respectively, of the levels in the wt model (Fig. 7 a). In addition, clk shows minute oscillations close to the trough level of the wt model (Fig. 7 a). Simulations of PER gain of function in DD reveal further depression of the amplitudes leading to minute oscillations in per, tim, and clk (Fig. 7 b). These results in PER gain-of-function experiments are strikingly similar to the behavior of per, tim, and clk in per⁰¹ flies (2,29,32,38,39,43,46,47). Furthermore, simulation of a per-null mutation predicts that the clock is arrhythmic with elevated levels of per and tim (Fig. 7 c). If we assume that the network topology shown in Fig. 1 a is accurate, the model suggests that per⁰¹ could be a gain-of-function mutation rather than a null mutation in the sense that it leads to enhanced repression of CLK-CYC. The clock is arrhythmic in the per-null mutant model because all the eigenvalues of the flow matrix have negative real parts and only two have nonzero conjugate and constant imaginary parts (see Fig. 7, d–g). The real and imaginary parts of the eigenvalues in the cwo-mutant model are shown in Fig. S6.

Figure 7.

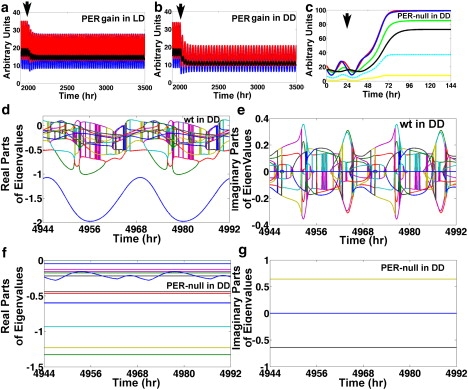
Simulations of PER gain and loss of function. (a and b) Reactions of per (blue), tim (red), and clk (black) mRNAs when λ_{per, PER} is increased by 25% (PER gain of function) at the arrows in LD and DD, respectively. (c) Results of a simulation where a per-null mutation (λ_{per, PER} = 0) is applied at the arrow for per (blue), tim (red), clk (black), cwo (yellow), vri (cyan), and Pdp1 (green) direct-target genes. (d and e) Real and imaginary parts, respectively, of the eigenvalues (colored lines) of the flow matrix of the wt model in DD; observe that the real parts cross the x axis. (f and g) Real and imaginary parts of the eigenvalues (colored lines) of the flow matrix of the per-null model in DD; all the real parts are negative and only two conjugate imaginary parts are nonzero. Notice that times 4944 h, 4968 h, and 4992 h correspond to ZT = 0 h, and times 4956 h and 4980 h correspond to ZT = 12 h.

Comment

Sabhouri-Ghomi et al. have discussed some of the limitations of the Michaelis-Menten equations (48). The authors find that the Michaelis-Menten kinetics may be misleading in modeling protein interaction networks. A practical limitation of detailed kinetic reactions is that individual parameters don't all directly relate to measurable interactions within the network. We have been inspired by the gene circuits of Reinitz and colleagues (49–56). The system shown in Eq. 1 has several advantages, namely that its parameters model regulatory effects within the network and that it is generic in the sense that it is applicable to transcriptional, translational, as well as posttranslational mechanisms (57). In particular, the use of regulatory weights in Eq. 1 set the stage for Eq. 2, which models transcriptional signals and integration.

Loops are present in many molecular systems like the mammalian circadian clock, the cell cycle, NF-kB and p53 responses, calcium spikes, and the sinoatrial pacemaker. Negative feedback aligns dose responses and the design of positive-plus-negative feedback achieves a widely tunable frequency and stable amplitudes (58,59). The network of the Drosophila clock includes interconnected positive and negative loops. The network model shown in Fig. 1 replicates a range of outcomes, including oscillations with a 24-h period, timely peaks, and entrainment in response to time shifts, and it reacts in harmony with the results of experimental mutations and perturbations (Fig. 2). The findings uncover the principle that large molecular networks may be reduced to a few positive and negative loops (see Fig. 1). In fact, the results demonstrate that the dynamical behavior of the whole system can be predicted by simple rules, such as suppressing negative and positive loops leads to positive and negative effects, respectively (see Figs. 3 and 4).

Transcription is a dynamic process that involves continuous tuning of mRNA production in response to opposing signals. Equation 2 quantifies transcriptional signals and the integration of opposite signals. The idea that transcription reacts in harmony with the outcome of weighing opposite signals is intuitive. The fact that such a relatively simple model has predictive power opens the door for further simulations in pursuit of greater understanding of the underlying molecular network. The same principles should apply to other molecular networks like the mammalian circadian clock and signaling pathways.

Both biological observations and the cwo-mutant model reveal that the Drosophila clock continues to oscillate with a 24-h period in LD in the absence of CWO, albeit with a change in amplitude. The question of the unique and essential contribution of CWO to the dynamics of the oscillating molecular circuit of the clock remains open.