Protein Stabilization and the Hofmeister Effect: The Role of Hydrophobic Solvation

Abstract

Using the IGg binding domain of protein L from Streptoccocal magnus (ProtL) as a case study, we investigated how the anions of the Hofmeister series affect protein stability. To that end, a suite of lysine-to-glutamine modifications were obtained and structurally and thermodynamically characterized. The changes in stability introduced with the mutation are related to the solvent-accessible area of the side chain, specifically to the solvation of the nonpolar moiety of the residue. The thermostability for the set of ProtL mutants was determined in the presence of varying concentrations (0–1 M) of six sodium salts from the Hofmeister series: sulfate, phosphate, fluoride, nitrate, perchlorate, and thiocyanate. For kosmotropic anions (sulfate, phosphate, and fluoride), the stability changes induced by the cosolute (encoded in $m_3=\delta \Delta G_{}^0/\delta C_3$) are proportional to the surface changes introduced with the mutation. In contrast, the m₃ values measured for chaotropic anions are much more independent of such surface modifications. Our results are consistent with a model in which the increase in the solution surface tension induced by the anion stabilizes the folded conformation of the protein. This contribution complements the nonspecific and weak interactions between the ions and the protein backbone that shift the equilibrium toward the unfolded state.

Introduction

Upon addition of inorganic salts, a plethora of physicochemical properties can be sorted unequivocally based on the Hofmeister series (1–3). In living organisms, biomolecular interactions, protein stability upon unfolding, and protein solubility are affected by the presence of salts according to this invariant trend (4). Despite the striking fact that such disparate phenomena obey the same series, a universal mechanism for this effect remains elusive (5). Originally, these cosolutes were classified as kosmotropic or chaotropic, depending on their ability to constructively or destructively modify the structure of water (6). However, recent experimental developments have emphasized that the influence of denaturants and stabilizers on the structure of bulk water (7–9) is small, and the mechanistic models for the Hofmeister effect point toward the existence of nonspecific interactions between the macromolecular surface and the solvated ion (more specifically, between the ion and the first hydration shells) (10,11). In this context, recent molecular dynamics simulations (12) and theoretical developments (13–16) have highlighted the role that dispersion forces may play in the Hofmeister effect.

The influence of salts on protein stability was first observed in the changes in midpoint denaturation temperature (T_m) and solubility of proteins and DNA (5,17). From the thermodynamic perspective, this interaction can be globally addressed by the well known preferential interaction (or exclusion) coefficient, accessible from equilibrium dialysis experiments (18,19) and other experimental techniques (20). A detailed thermodynamic treatment has been reported (20,21). According to the linkage function theory (22), the cosolute effects on protein stability depend on the properties of the folded and unfolded states and, therefore, are expected to be proportional to the change in solvent-exposed area upon unfolding (ΔASA) (18,23).

At the molecular level, distinct mechanisms have been suggested for the salt interaction with the polar and nonpolar moieties of the protein (4), reflecting the heterogeneous nature of the polypeptide chain. The denaturant effect of certain salts is attributed to the nonspecific (weak) interactions between the cosolute and the polar regions of the protein, in particular with the protein backbone (24–28), and strong experimental evidence for the interaction between ions and macromolecules has recently been reported (10,29). Such interactions seem to be mediated by interfacial water molecules (11,30,31). However, this mechanism is insufficient to explain the switch between chaotropic and kosmotropic ions observed in the Hofmeister series. An additional contribution from the solvation of the hydrophobic moiety of the molecule can be estimated from the work necessary to create a cavity whose surface is equal to the solvated nonpolar surface (cavity model) (4,32,33) when adapted for the specific geometry of the protein surface (34,35). Almost all the ions in the Hofmeister series increase the surface tension of the solution, which results in stabilization of the folded conformation, since the denatured state has a larger surface exposed to the solvent. Experiments measuring the transfer free energy of model compounds in the presence of salts (36,37) and experiments with globular proteins in the presence of other osmolytes (i.e., trehalose and lysine hydrochloride) (38,39) fit well with this model, but its validity has not been fully explored for the Hofmeister series of ions in a protein system.

Here, we address the effect of Hofmeister anions on protein stability using the midpoint denaturation temperature, T_m, as a reporter of the changes in stability and the immunoglobulin G binding domain of protein L from Streptoccocus magnus (ProtL) as a model system (40,41). Previous studies have shown that this protein unfolds reversibly by a two-state process (42), that its thermal stability is sensitive to salts, and that the order of stability change with salt follows the Hofmeister series (43). A suite of surface mutations was designed and characterized in the absence and presence of a set of inorganic salts. First, we structurally demonstrate that these mutants alter the amount of nonpolar protein surface accessible to solvent. Second, we experimentally show that the effect of kosmotropic anions on protein stability is sensitive to these surface modifications. Our results are in reasonable agreement with the idea that Hofmeister anions increase ProtL stability by changing the surface tension of the solution.

Materials and Methods

Site-directed mutagenesis and protein sample preparation

Site-directed mutagenesis was performed by using the QuiaChange II Kit (Quiagen, Venlo, The Netherlands) with custom-made oligonucleotides as primers (Invitrogen, Carlsbad, CA). Freshly transformed Escherichia coli BL21 DE(3) cells were used for protein expression. Samples were grown in the appropriate media for the experiment: lysogeny broth-rich media for circular dichroism (CD) and fluorescence experiments, and M9 minimal media (employing ¹⁵NH₄Cl and ¹³C₆-glucose) for relaxation measurements and NMR structure determination of K×5Q ProtL. Since ProtL samples contain no additional tag, protein purification was achieved by a thermal shock followed by gel filtration chromatography. In all experiments, sample pH was adjusted to 6.0 by addition of 20 mM sodium phosphate buffer.

CD and fluorescence experiments

Data were collected on a J-810 spectropolarimeter (JASCO, Tokyo, Japan), using a quartz cuvette of 1-cm path length. Samples were used at a concentration of 4 μM; the thermal melts were run at 1°C/min and monitored at 214 nm with a bandwidth of 4 nm, and data were collected every 0.2°. The thermal range of the experiment was optimized for every sample, assuring the proper determination of the baselines for the folded and unfolded states.

Thermal denaturation curves monitored by fluorescence spectroscopy were collected at a concentration of 1 μM, with measuring conditions equivalent to those in the CD experiments except for the use of a 4-nm excitation bandwidth centered at 280 nm and recording the emission at 350 nm. In all cases, the CD and fluorescence signal recovery after the thermal melt was monitored, and was found to be no lower than 95%. Between four and six independent measurements were obtained from CD and fluorescence data at each experimental condition, and duplicate experiments were used to obtain an estimation of the error.

Data analysis was completed with in-house-built scripts programmed in MATLAB (The MathWorks, Natick, MA). CD and fluorescence spectroscopy thermal denaturation data were processed assuming the linear extrapolation method (63), where the molar ellipticity at each point of the transition can be described as a linear combination of the expected values for the folded ((θ_F) and unfolded (θ_U) states. The values for θ_F and θ_U were obtained from extrapolations of the linear baselines.

NMR measurements and structure calculation

NMR experiments for the chemical-shift assignment and collection of conformational restraints were performed on a single, uniformly ¹⁵N, ¹³C-labeled 300-μM protein sample dissolved in 93% H₂O/7% D₂O (v/v). NMR experiments were collected at 300 K on an Avance 800 MHz spectrometer (Bruker, Billerica, MA) equipped with a cryoprobe. Chemical-shift assignments for 98% of nonlabile ¹H, 97% of ¹⁵N, and 94% of ¹³C were obtained using a combination of standard triple-resonance experiments. Assignments were checked for consistency with three-dimensional (3D) ¹⁵N-edited [¹H,¹H] nuclear Overhauser effect spectroscopy (NOESY) and ¹³C-edited [¹H,¹H] NOESY. The 3D NOESY spectra were recorded using a mixing time of 140 ms.

The 3D structures of the K×5Q mutant were determined by combined automated NOESY crosspeak assignment and structure calculations in torsion-angle space with the software CYANA 2.1 (64). The 20 conformers with the lowest final CYANA target function values were further refined by restrained energy minimization in a water shell with the program OPALp (65) using the AMBER force field (66). MOLMOL (67) was used for analysis and visualization of the structures. The 20 conformers that represent the solution structure of the K×5Q mutant were deposited in the Protein Data Bank with the accession code 2JZP.

Mutant structure modeling and solvent-accessible area calculation

All the single K-to-Q mutants of ProtL were modeled using the Swiss Model Workspace (47) and the Protein Homology/analogY Recognition Engine (Phyre) (48). The ensemble constituted by the 12 lowest energy conformations from the solution NMR structures of wild-type ProtL (2PTL) (44) (without the his-tag tail) and the 20 lowest energy conformations for the K×5Q ProtL (2JZP), as well as the modeled mutant variants, were employed for solvent accessibility calculations using the MOLMOL program (67) with a probe radius of 1.4 Å. The solvent-accessible values reported for the K41Q and K7Q mutants correspond to the average of the values from the two programs employed. In the nonpolar area calculations necessary to estimate $A_{\text{np}}^{\text{Q}},A_{\text{np}}^{\text{K}},{\chi }_{\text{WT}}^{\text{F}},\text{and}{\chi }_{\text{Mut}}^{\text{F}}$, α–ɛ (α–γ) positions were considered for the lysine (glutamine) side chains. Error bars arise from the variations in area calculated for the 12 conformations in the manifold of the solution NMR structure and for the two differently modeled structures (K41Q and K7Q).

NMR relaxation data

The ¹⁵N side-chain relaxation rates were measured on the NHD isotopomer to circumvent the contribution from proton dipole-dipole cross-correlation (68). To avoid signal overlap in the region of interest, four ¹⁵N isotopically labeled samples were obtained: K7Q ProtL, K61Q ProtL, a K×2Q ProtL (K41Q and K42Q), and a K×3Q ProtL (K23Q, K54Q, and K28Q). Protein samples were lyophilized and resuspended in 50% D₂O to maximize the population of the NHD isotopomer. Spectra were recorded in a two-dimensional mode with relaxation times of 0, 20, 60 (×2), 120, 240, 400, 550, and 700 ms for the T1 and 0, 5, 40 (×2), 80, 160, 200, and 240 ms for the T2 spectra. Experimental data were adjusted to exponential decays to obtain the relaxation constants (T1 and T2). The nOe rates correspond to the intensity ratio between an equilibrium experiment (no irradiation, 12-s recovery delay) and an experiment where the proton region is irradiated (5-s irradiation, 7-s recovery delay). The model-free approach (69,70) with a local correlation time (71) was employed to obtain the generalized order parameter (S²) from the experimental relaxation rates.

Results

Surface mutations affect ProtL stability by modulating solvation contribution

We chose the lysine residue because its side chain is unbranched and possesses a large hydrophobic area. The solution structure of wild-type ProtL (44) reveals that its seven lysines are largely exposed to the solvent (43% on average) with no evidence for interresidue hydrogen bonding or participation in salt bridges.

We have expanded a previously described set of mutations (45) to obtain all the individual lysine (K)-to-glutamine (Q) replacements, as well as selected multiple K-to-Q mutants (see Table S1 of the Supporting Material). For up to five glutamine substitutions, the expression yield was high enough to perform NMR studies, and we obtained the high-resolution solution structure for the K×5Q ProtL variant (K23Q, K28Q, K42Q, K54Q, and K61Q). Table S2 includes a summary of the experimental restraints used in the structure elucidation process, and Fig. 1 A shows the resulting structure (overlay of the 20 lowest energy conformations), with the introduced mutations highlighted. Consistent with conservative mutational design, the fold of the K×5Q variant is almost identical to the wild-type fold (backbone root mean-squared deviation of 0.77 Å with respect to the 1HZ6 structure (46); see Table 1). Further analysis of the structure reveals that the glutamine side chains are placed in an orientation similar to that of the wild-type lysines (Fig. 1 B, red side chains). In addition, no new interresidue interactions could be observed. The modifications do not alter the surface side-chain packing in positions other than the mutated ones, highlighting the high degree of independence among the mutations.

Figure 1.

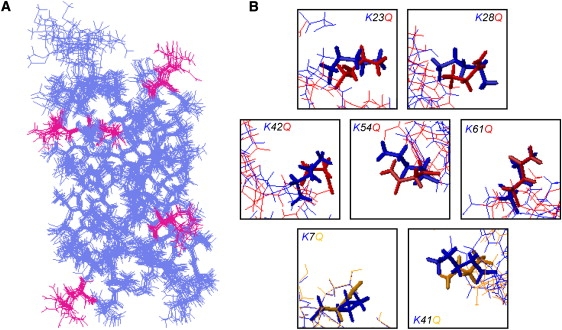
(A) View of the 20 lowest energy conformers that represent the solution structure for the K×5Q ProtL variant. The mutated glutamines are highlighted in magenta. (B) Close-up of the protein regions where the side chains were mutated. The side chains for wild-type ProtL are shown in blue, whereas the side chains for the mutants are shown in red, for those experimentally determined by NMR, or yellow for those computationally modeled.

Table 1.

Generalized order parameters (S²) for the side-chain H-N bond of the seven introduced glutamines

Glutamine	7	23	28	41	42	54	61
S2∗	0.28 ± 0.03	0.24 ± 0.02	0.23 ± 0.03	0.31 ± 0.01	0.32 ± 0.03	0.36 ± 0.04	0.30 ± 0.05

^∗Model-free approach (69) with a local correlation time (71) was employed to obtain the generalized order parameter (S²) from the experimental relaxation rates. The average value for the correlation time is 4.05 ± 0.3 ns.

In addition to the NMR structure of the K×5Q variant, each of the single mutations has been modeled in silico, making use of two software programs: the Swiss Model Workspace (47) and Phyre (48). The K×5Q variant was modeled using the same software. The modeled structure is in good agreement in the glutamine side-chain arrangement compared to the solution structure (data not shown). Based on this validation, the modeled conformations for K7Q and K41Q (Fig. 1 B, yellow side chains) are taken as reference structures for the subsequent analysis.

$T_{\text{m}}^{}$ values were obtained from thermal denaturation experiments for each of the single K-to-Q mutant proteins and for the multiple mutants (K×2Q–K×6Q). In all cases, reversible thermal denaturation according to a two-state model was found. Duplicate data from CD and fluorescence spectroscopy were combined to obtain a single average value. Experimental $T_{\text{m}}^{}$ values were converted into the relative changes in free energy with respect to the wild-type protein ($\Delta \Delta G_{\text{Mut}/\text{WT}}^{0,\text{U}-\text{F}}$) using the equation (49)

$$\Delta \Delta G_{\text{Mut}/\text{WT}}^{0,\text{U}-\text{F}}=\Delta H_{\text{m},\text{WT}}^{0,\text{U}-\text{F}}\times \left(1-\frac{T_{\text{m},\text{WT}}^{}}{T_{\text{m},\text{Mut}}}\right),$$ (1)

where $T_{\text{m},\text{WT}}^{}$ and $T_{\text{m},\text{Mut}}^{}$ are the T_m values for wild-type and mutant ProtL, respectively, and $\Delta H_{\text{m},\text{WT}}^{0,\text{U}-\text{F}}$ is the denaturation enthalpy (53 ± 4.8 kcal·mol⁻¹) (43).

In a K-to-Q substitution, a new carbonyl group is introduced and the side chain is reduced by one methylene unit. The change in stability for the single variants ranges from +0.11 ± 0.18 to −1.1 ± 0.12 kcal·mol⁻¹ and is dependent on the location of the mutated side chain. Although the charge of the molecule decreases by one unit upon mutation, the similarity in stability in the presence of 1 M sodium chloride for wild-type ProtL (43) and the set of K-to-Q mutants (data not shown) suggests that electrostatic effects do not significantly contribute to $\Delta \Delta G_{\text{Mut}/\text{WT}}^{0,\text{U}-\text{F}}$.

Analysis of the protein structures reveals that the new glutamine side-chain amides are largely exposed to the solvent (between 80% and 100%). The order parameters (S²) for the side-chain H-N bonds have been independently determined for each of the seven glutamines from ¹⁵N relaxation data (see Materials and Methods for details) and are reported in Table 1. The low S² values indicate the existence of large reorientational angles and highly dynamic behavior for the H-N bonds, consistent with a solvated local environment for the side-chain amide group. All these data suggest that the polar heads of the side chain contribute in a similar way to protein stability regardless of the mutated position. Hence, the variation in free energy among the variants arises from the solvation of the hydrophobic part of the side chain. The change in nonpolar solvent-accessible area upon unfolding introduced by the mutation ($\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$) was estimated by employing the expression

$$\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}=\left({\chi }_{\text{np},\text{Mut}}^{\text{U}}-{\chi }_{\text{np},\text{Mut}}^{\text{F}}\right)\times A_{\text{np}}^{\text{Q}}-\left({\chi }_{\text{np},\text{WT}}^{\text{U}}-{\chi }_{\text{np},\text{WT}}^{\text{F}}\right)\times A_{\text{np}}^{\text{K}},$$ (2)

where $A_{\text{np}}^{\text{Q}}$ and $A_{\text{np}}^{\text{K}}$ are the nonpolar areas for the glutamine and lysine side chains, respectively, and${\chi }_{\text{np}}^{}$ corresponds to the fraction of nonpolar area buried to solvent at the mutation site (a residue with fully buried nonpolar area should have ${\chi }_{\text{np}}^{}$ = 1, whereas ${\chi }_{\text{np}}^{}$ = 0 for a totally exposed side chain). The values employed in the calculations are listed in Table S4: ${\chi }_{\text{np},\text{WT}}^{\text{U}}$ and ${\chi }_{\text{np},\text{Mut}}^{\text{U}}$ were obtained from simulations of the average solvent accessibility for the unfolded state (50,51), whereas $A_{\text{np}}^{\text{Q}},A_{\text{np}}^{\text{K}},{\chi }_{\text{WT}}^{\text{F}},\text{and}{\chi }_{\text{Mut}}^{\text{F}}$ were obtained from the solution structures (WT and K×5Q) or the modeled structures (K7Q and K41Q). A positive value of $\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ was found in all the protein variants but two (K28Q and K41Q), meaning that these mutants expose less area to the solvent upon unfolding than does the wild-type (i.e., the mutant has a lower contribution to the overall hydrophobic effect). In K28Q and K41Q, the opposite is true due to the large buried fraction of the glutamine side chains.

Fig. 2 A shows the empirical correlation obtained between $\Delta \Delta G_{\text{Mut}/\text{WT}}^{0,\text{U}-\text{F}}$ and $\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ for the mutation set. The correlation indicates that the variations in stability agree well with the differential solvation of the side chains. As expected, the mutants that present a higher reduction in nonpolar area are the most destabilizing, whereas small variations in $\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ result in negligible changes in protein stability.

Figure 2.

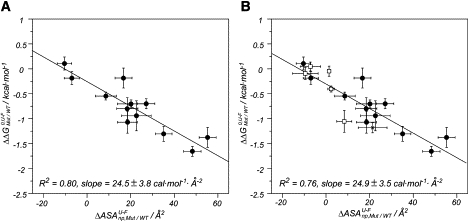
Correlation between the change in nonpolar surface area introduced by the mutation ($\Delta {\text{ASA}}_{\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$) and the change in stability of the mutants ($\Delta \Delta G_{\text{Mut}/\text{WT}}^{0,\text{U}-\text{F}}$) for (A) the K-to-Q mutant set only and (B) all mutant types considered: K-to-Q (solid circles), K-to-A (star), and D-to-E (open squares). Error bars in $\Delta {\text{ASA}}_{\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ arise from the values calculated for the 12 conformations in the manifold of the solution NMR structure and for the two differently modeled structures (K41Q and K7Q). R² corresponds to the coefficient of determination.

To validate this hypothesis, we considered alternative mutational designs: K to alanine (A) to increase the change in nonpolar area upon mutation, and glutamic acid (E) to aspartic acid (D), where the reduction in one methylene is not accompanied by a protein charge variation. In total, six additional surface replacements were studied: K23A, E2D, E3D, E21D, E32D, and E46D. For each of these mutants, the melting temperatures were converted into free energies by using Eq. 1, and their $\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ values were estimated from homology models (see Table S3). Fig. 2 B shows the correlation between $\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ and $\Delta \Delta G_{\text{Mut}/\text{WT}}^{0,\text{U}-\text{F}}$ obtained for the 18 mutants (12 K-to-Q, 5 E-to-D, and 1 K-to-A). Almost identical slopes are obtained using the full set (Fig. 2 B, line) or the K-to-Q mutant subset (Fig. 2 A, line). The correlations shown in Fig. 2 connect protein stability upon unfolding with the nonpolar area changes introduced with the mutation and highlight the role of solvation in the side-chain packing of ProtL surface. After the detailed structural and thermodynamic characterization, the K-to-Q mutant set becomes an appropriate model to evaluate the influence of the protein surface on the protein stability changes induced by cosolutes.

Protein surface modifications and the Hofmeister effect

The changes in $T_{\text{m}}^{}$ for the set of K-for-Q substitutions in ProtL (seven single and five multiple mutants) were measured at increasing concentrations (0–1 M) of a suite of sodium salts, representative of the Hofmeister series: sulfate, fluoride, nitrate, perchlorate, and thiocyanate, in addition to the phosphate that is partially taken from a previous study (45). Data are listed in Table S5, Table S6, Table S7, Table S8, Table S9, and Table S10). Fig. 3 shows the melting temperatures as a function of the cosolute concentration and the subsequent regressions, assuming a linear dependence of $T_{\text{m}}^{}$ on the anion molarity. Stabilizing agents (sulfate, phosphate, and fluoride) result in positive slopes, whereas denaturants (nitrate, thiocyanate, and perchlorate) show the opposite trend.

Figure 3.

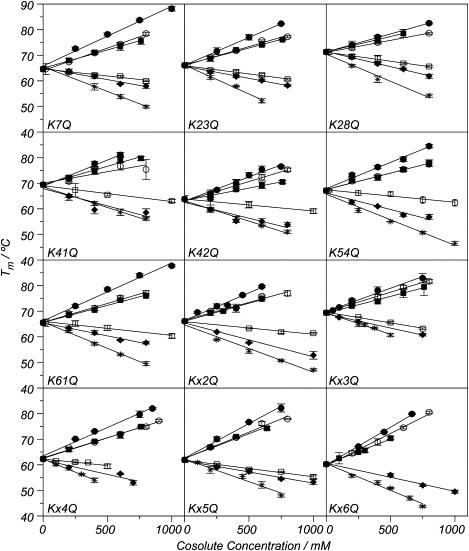
Dependence of the denaturation midpoint temperature (T_m) on the cosolute concentration. The lines correspond to the linear regression of the data for sulfate (solid circles), phosphate (open circles), fluoride (solid squares), nitrate (open squares), perchlorate (solid diamonds), and thiocyanate (stars). The error bars correspond to the standard deviation obtained from at least four independent measurements.

The changes in free energy caused by the cosolute ($\Delta \Delta G_3^{0,\text{U}-\text{F}}$, where subscript 3 represents the cosolute (52)) were estimated from the $T_{\text{m}}^{}$ values by using the Gibbs-Helmholz equation (43,49),

$$\Delta \Delta G_3^{0,\text{U}-\text{F}}=\Delta H_{\text{m},3}^0\times \left(1-\frac{T_{\text{m},0}^{}}{T_{\text{m},3}^{}}\right)-\Delta C_{\text{p},3}^{}\times \left[\left(T_{\text{m},3}^{}-T_{\text{m},0}^{}\right)+T_{\text{m},0}^{}\ln \left(\frac{T_{\text{m},0}^{}}{T_{\text{m},3}^{}}\right)\right],$$ (3)

where subscripts 3 and 0 refer to the value in the presence or absence, respectively, of cosolute. Hence, $\Delta H_{\text{m},3}^0$ and $\Delta C_{\text{p},3}^{}$ are the midpoint denaturation enthalpy and the apparent heat capacity in the presence of cosolute. These parameters have been measured for all the anions (43).

The $\Delta \Delta G_3^{0,\text{U}-\text{F}}$ values also show linear trends with the molar salt concentration, and their slopes ($m_3^{}$) reflect the dependence of protein stability on the cosolute concentration. For a given mutant, slopes are positive (negative) for kosmotropic (chaotropic) anions, and their magnitudes follow the trend of the Hofmeister series. The slopes of these plots ($m_3^{}$) have been related to the change in solvent-accessible area upon unfolding for denaturant agents (53) and for other osmolytes as well (54). Based on the structural analysis of the mutations (see above), the $m_3^{}$ values for the six sodium salts were plotted against the changes in nonpolar area at the protein surface introduced upon mutation ($\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$) (Fig. 4). The $m_3^{}$ values for wild-type ProtL (43) are also plotted in Fig. 4 (solid squares). Stabilizing anions (sulfate, phosphate, and fluoride) show positive slopes ($\eta =\partial m_3/\partial \Delta AS{A}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$) with high correlation coefficients (R ≥ 0.86). In contrast, negligible η values (R ≤ 0.31) are obtained for nitrate, perchlorate, and thiocyanate. The correlation coefficient is not an accurate descriptor of the goodness of fit when both variables are subject to experimental uncertainties. Therefore, the error bars of the $m_3^{}$ values were propagated to yield a distribution of η values for each anion. Such distributions are compared to η = 0 in the insets of Fig. 4. Consistent with the R analysis, kosmotropic anions have a slope η > 0, whereas for denaturants, η ≈ 0. Thus, despite the small changes in the surface introduced upon mutation (within a range of 70 Ų), the stabilizing effect of the kosmotropic anions depends on the changes in area introduced in the protein surface. Mutants showing a larger change in ASA become more stabilized by kosmotropic anions, and vice versa.

Figure 4.

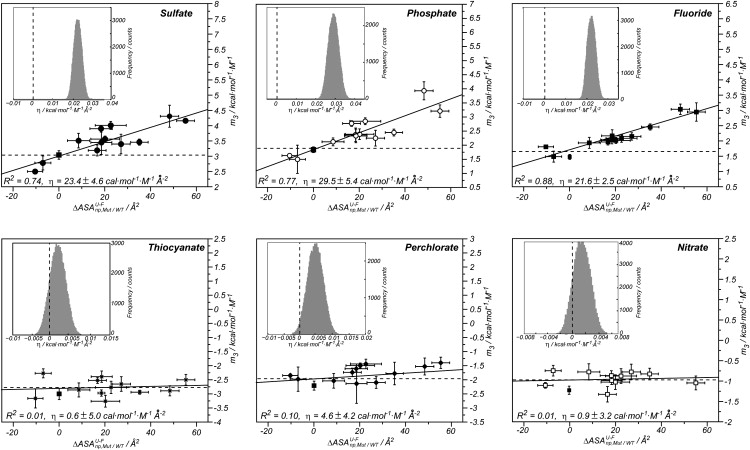
Dependence of m₃ on the change in nonpolar surface introduced with the mutation ($\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$) for sulfate (solid circles), phosphate (open circles), fluoride (solid squares), nitrate (open squares), perchlorate (solid diamonds), and thiocyanate (stars). The error bars for the m₃ values correspond to the standard deviation of the slopes in a plot of $\Delta \Delta G_{\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ versus the cosolute concentration, and R² corresponds to the coefficient of determination. The slope for the wild-type is shown as a solid square in each panel. (Insets) Gaussian distributions of η values (η =$\delta m_3^{}/\partial {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$) obtained from Monte Carlo propagation of the error from experimental data. Dashed vertical line highlights the value of η = 0.

The positive η values found for kosmotropic agents reflect the dependence of m₃ on surface modifications that alter the nonpolar exposed surface (Fig. 4). According to the cavity model, the work that must be done to solvate the nonpolar area is proportional to the surface tension of the solution. Fig. 5 shows the correlation between the change in surface tension and η. Although the degree of correlation is moderate (R = 0.83), it is clear that larger surface tensions and η values are produced by kosmotropes and smaller surface tensions and lower η values by chaotropes.

Figure 5.

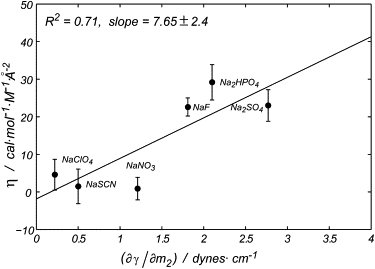
Comparison between η and $\delta \gamma /\delta C_3^{}$ values for each anion (taken from Pegram and Record (61)). The error bars correspond to the standard deviations of the linear fittings. R² is equal to the coefficient of determination. Na₂SO₄, sodium sulfate; Na₂HPO₄, sodium phosphate; NaF, sodium fluoride; NaSCN, sodium thiocyanate; NaCIO₄, sodium perchlorate; NaNO₃, sodium nitrate.

Discussion

Several studies with osmolytes (39,55) and ions (10,36,56) have compared data from model peptides (36) or polymers (57) in attempts to understand the stabilizing role of cosolutes. Here, we have studied the contribution of nonpolar area to salt-induced protein stabilization using a globular protein system. To that end, conservative modifications were introduced in the surface to minimize structural perturbation. High-resolution NMR data establish the link between the structural modifications introduced upon mutation and the subsequent changes in free energy. Modulation of the solvation contribution from the nonpolar side chain emerges as the main cause for the variations in stability observed upon mutation (regardless of whether the amino acid change varies the charge (Fig. 2)). Thus, the interaction between residue side chains and water molecules drives surface packing in ProtL. This is complementary to other systems in which charged residues stabilize the protein through a network of interresidue electrostatic interactions (58–60).

The effect of salts on stability was evaluated for the set of mutants. The plots shown in Fig. 3 show linear dependence with the molar concentration of salt, and the subsequent slopes follow the Hofmeister series. Such values are in reasonable agreement with the salting-in coefficients (see Table S11 for a representative example), underlining the role of nonspecific interactions in protein stabilization by the Hofmeister effect (4,26,36).

The structure-stability relationship obtained for the mutation set allowed a detailed study of the effect of salts on ProtL stability. Despite the conservative mutation design, the structural perturbations introduced are large enough to alter the m₃ value. NMR in combination with molecular modeling was used to correlate the distribution of m₃ values with the changes in nonpolar solvent-accessible area. The relationship between the m₃ value and $\Delta {\text{ASA}}_{}^{\text{U}-\text{F}}$ is well established for denaturants (53) and osmolytes (28) and mainly attributed to the interactions between the cosolute and the protein backbone (26). Here, the dependence between m₃ and $\Delta {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$ found in kosmotropic anions contrasts with the invariability of m₃ upon mutation in chaotropic agents.

Our results suggest a connection between the anion modulation of the solution surface tension and protein stability in that 1), the anion effect on protein stability (reported in $m_3^{}$) depends on the surface modifications (Fig. 4); 2), positive η values (η =$\delta m_3^{}/\partial {\text{ASA}}_{\text{np},\text{Mut}/\text{WT}}^{\text{U}-\text{F}}$) were obtained for all the salts considered, suggesting that the same mechanism applies for chaotropes and kosmotropes; and 3), a correlation was observed between η and the increase in the solution surface tension induced by the anion (Fig. 5). In a recent study, Record and co-workers analyzed the effect of the Hofmeister ions at the air-water interface, a simplified model for the protein-solvent interface (61). Their results show that the changes in the surface tension introduced by the ions result in a reduced concentration of the cosolutes at the air-water interface due to the higher dehydration energy involved. In support of this idea, a certain degree of correlation between η and the partition coefficients at the air-water interface was also found. Moreover, in a study of the effect of inorganic salts on the stability of the H2A-H2B histone dimer, a correlation between $m_3^{}$ and the salt increase in the solution surface tension was also found (62). Finally, a lowered concentration of stabilizing cosolutes in the surroundings of the ProtL surface is also in full agreement with the dominant preferential exclusion term for these anions, obtained from a mechanistic analysis of the effect of the anions on wild-type ProtL stability (43).

In summary, we have shown that the changes in stability introduced by a suite of conservative mutations in the protein surface can be rationalized in terms of the changes in nonpolar solvent-accessible area. This set of proteins allowed us to explore the influence of the Hofmeister anions on protein stability. Our results are consistent with a model in which an increase in solution surface tension plays an important role in protein stabilization. This mechanism is complementary to the destabilizing interactions with the polar moiety (4,26). Taken together, these data help to explain the modulation of protein stability exerted by the Hofmeister salts.