Abstract
We consider different models of inositol 1,4,5-trisphosphate (IP3) receptor (IP3R) channels in order to fit nuclear membrane patch clamp data of the stationary open probability, mean open time, and mean close time of channels in the Xenopus oocyte. Our results indicate that rather than to treat the tetrameric IP3R as four independent and identical subunits, one should assume sequential binding-unbinding processes of Ca2+ ions and IP3 messengers. Our simulations also favor the assumption that a channel opens through a conformational transition from a close state to an active state.
The dynamics of inositol 1,4,5-trisphosphate (IP3) receptor (IP3R) channels is an important issue in cellular physiology and is central to many problems of cellular signaling. Models for calcium channels are widely used to investigate a variety of topics such as calcium oscillations and excitation-contraction coupling in cardiac cells. In particular, the mechanism that permits cells to organize regular calcium spikes in response to increased IP3 levels is an intriguing issue of great interest for both the biological and physical communities. A crucial step in the analysis of IP3 channels is the study of channel dynamics under (nonphysiological) conditions without Ca2+ feedback. Our work builds on recent patch clamp experiments for single IP3 channels located in the nuclear membrane. We discuss different traditional and new IP3R models by fitting their parameters to the stationary data of patch clamp recordings. Our analysis not only suggests that sequential binding-unbinding processes by Ca2+ ions and IP3 messengers should be assumed but also supports the recent incorporation into the gating model of a ligand-independent conformational transition. An understanding of the single channel gating is fundamental to any further modeling approach of intracellular and intercellular calcium dynamics. This fact gives a central importance to the results presented in this work.
INTRODUCTION
Calcium is one of the most important messengers in the cytosol of living cells.1 It can trigger and modulate a wide variety of calcium dependent signaling events and reaction cascades. A major mechanism of calcium signaling involves the liberation of Ca2+ ions from the endoplasmic reticulum (ER) through IP3Rs.2 Structurally, the IP3R is a homomer with four subunits forming a single ion-conducting channel. The opening of the channel requires the binding of second messenger inositol 1,4,5-trisphosphate, which is generated in the cytoplasm in response to the binding of extracellular ligands to plasma membrane receptors. Gating of IP3R is biphasically modulated by Ca2+ ions, such that small elevations of cytosolic Ca2+ concentration promote channel opening, whereas higher Ca2+ concentrations result in inactivation of the channel. This Ca2+ feedback, in addition to the clustered distribution of functioning IP3Rs on the ER membrane, results in complex spatiotemporal Ca2+ signals, including Ca2+ puffs, saltatory waves, spreading waves, and spiral waves.3
Models of calcium signals play an important role to elucidate quantitatively the complex dynamics of various Ca2+ patterns generated by the IP3 pathway. Because of the crucial role of IP3R channels for the generation of calcium signals, an accurate IP3R channel model is fundamental in order to simulate the calcium system properly.4 Several IP3R models4, 5, 6, 7, 8, 9 have been developed to describe experimental data obtained from IP3R reconstituted in a bilayer membrane invitro,10 with the De Young–Keizer5 model in particular being widely applied.
The intracellular calcium signals involve liberation through IP3R from the ER. Although there is no single-channel experiment by now with IP3R located on the ER membrane, IP3R data were measured in different environments. Most recently patch-clamp recordings from native IP3R in Xenopus oocyte nuclei have been obtained.11, 12 The experimental results indicate that there are significant differences in behavior of the reconstituted IP3R in bilayer membrane10 versus that of IP3R in their native environment of the nuclear envelope in the Xenopus oocyte.11, 12 Although we do not know what exactly can be expected for IP3R behavior on the ER versus that on the nuclear membrane, we take the available data as the closest estimate of the ER behavior. This assumption is supported by the fact that the ER membrane is physically connected to the nuclear membrane.
Therefore, we think that a suitable IP3R model should be based on the recent data obtained on the nuclear membrane. By now, only a few models have incorporated nuclear membrane data. Among these, an allosteric four-plus-two-conformation model was considered by Mak et al.13 That model postulates that each of the four IP3R monomers has one IP3-binding site and three different functional Ca2+-binding sites on the cytoplasmic side of the channel. Another model was developed by Baran,14 consisting of one activation module and one inhibition module, both allosterically operated by Ca2+, IP3, and adenosine triphosphate (ATP), together with one adaptation module driven by IP3 and Ca2+. However, these models can predict only the steady-state gating properties and not the kinetics of individual channel openings and closings. A kinetic model, including an explicit dependence of channel gating with luminal calcium, was suggested by Fraiman and Dawson15 to simulate a monomeric IP3R. A further model, recently proposed by Shuai et al.,16 contains a conformational change but is otherwise based on the De Young–Keizer model. The model successfully reproduces experimental estimates including the open probability, mean open and close times, and the multiexponential distributions of open and close time durations.
In this paper, we consider different types of IP3R models and compare their data fitting to patch clamp data of IP3R on the nuclear membrane in Xenopus oocyte.11, 12, 13 In detail, in this study, we compare the data matching of various models to the open probability, mean open time, and mean close time of the channel as a function of calcium concentration and IP3 concentration. We explore the behavior of IP3R models by using the deterministic matrix transition analysis.17, 18 Our discussion suggests the inadequacy of De Young–Keizer-type models, which propose four independent and identical subunits. We conclude that the tetramerically structured IP3R shows a sequential binding-unbinding process with Ca2+ ions and IP3 messengers.
EXPERIMENTAL DATA OF IP3R IN XENOPUS OOCYTE
The experimental data for IP3R type-1 channels in nuclear membrane in the Xenopus oocyte have been obtained at various calcium concentrations C and IP3 concentrations I.11, 12, 13 The open probability PO shows the following attributes. (1) At saturating IP3 concentration, i.e., I=10 μM, the channel exhibits a steep responding dynamics around C=0.2 μM, changing from PO=0.13 at C=0.08 μM to PO=0.73 at C=0.56 μM. (2) At I=10 μM, for a large range of calcium concentration from C=0.7 μM to 25 μM, the channel shows a flat but large open probability around PO∼0.8, indicating that calcium concentrations in this region are optimal. (3) At I=10 μM, the channel shows a steep decrease in open probability with higher calcium concentration around C=50 μM. (4) The channel also shows a very sensitive response to unsaturating IP3 concentration around I=0.02 μM, changing from PO=0.02 at I=0.01 μM to PO=0.67 at I=0.033 μM at calcium concentration around 1 μM.
The channel mean open time τO and mean close time τC were measured for saturating IP3 concentration. The mean open times typically scatter around 8 ms at various calcium concentrations, except for the two extreme values at large and small calcium concentrations where the observed open times are small. For those two parameter regimes, however, the standard deviations are large. Thus, it is difficult to define a clear curve for τO as a function of C. As suggested by Mak et al.,12, 13 τO first increases monotonically with C, and after reaching the maximum around C=2 μM, it monotonically deceases with C. However, in Ref. 15, the authors interpreted it simply as a constant τO, which is independent of C.
THE FITTING OF MODELS TO EXPERIMENTAL DATA
We consider various models by fitting the stationary open probability, mean open time, and mean close time to data obtained in experiments. To find an optimal fitting, all the model parameters were changed systematically in a reasonable region and the fitting results were judged by an evaluation function. In order to calculate the open probability, the only parameters we need are the reaction dissociation constants, while to determine the open time and close time, binding∕unbinding rates are needed. For the experimental data, the open probability is given at varying Ca2+ concentrations with four different IP3 concentrations, while the mean open and close times are given at I=10 μM only.
For the open probability PO we consider the mismatch function
| (1) |
to obtain the optimal fitting parameters of all the reaction dissociation constants in the model. The mismatch values for PO fitting with various IP3R models are given in Table 1. Further, we use the mismatch function
| (2) |
for τO and τC at I=10 μM to obtain the optimal fitting parameters of the binding rates. We notice that the open time duration experimentally is of the order of 10 ms, while the close time duration is distributed in the range of 1–2000 ms. To balance the contributions of open and close time in Eq. 2, we rescale the errors between the experimental and numerical data by the experimental results.
Table 1.
The mismatch value for PO fitting of the eight models. Here the value has been rescaled by the averaged open probability of the channel for the experimental data.
| Model | 8-state | 6-state | 9-state | 7-state | 13-state | 20-state | 21-state | 46-state |
|---|---|---|---|---|---|---|---|---|
| Mismatch value | 0.188 | 0.188 | 0.168 | 0.169 | 0.128 | 0.177 | 0.150 | 0.132 |
THE DE YOUNG–KEIZER IP3R MODELS
In many numerical simulations of Ca2+ signals, a widely applied IP3R model is the De Young–Keizer model5 as well as its simplified versions.19, 20 Therefore, in this section we will first discuss the fitting of the modified De Young–Keizer model to experimental data.
Model 1: IP3R model with four 8-state subunits
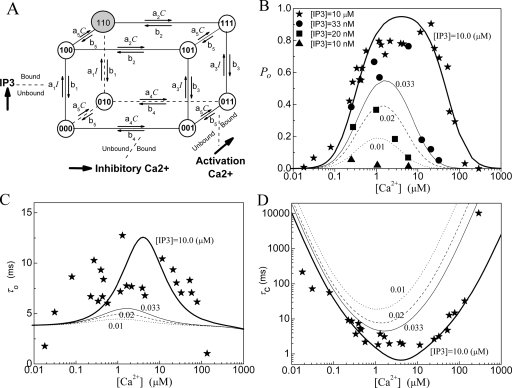
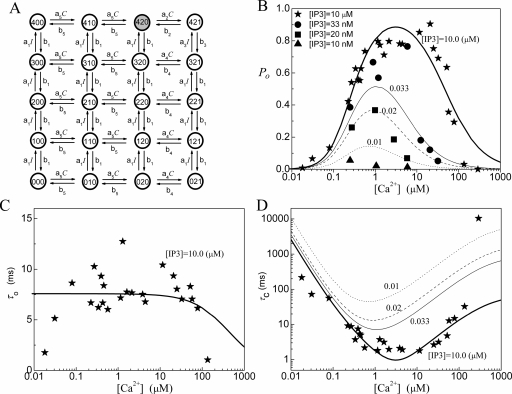
The De Young–Keizer IP3R model5 comprises four identical and independent subunits. In each subunit, there are two independent Ca2+ binding sites (i.e., an activating binding and inhibitory binding site) and an IP3 binding site. The state of each subunit is denoted as (ijk), where the index i represents the IP3 binding site, j the activating Ca2+ binding site, and k the inhibitory Ca2+ binding site. An occupied site is represented by 1, and a nonoccupied site by 0. A schematic picture of the state transitions for De Young–Keizer IP3R subunit is shown in Fig. 1. The channel is open when three or four subunits are in the (110) state.
Figure 1.
Model 1: (a) The structure of the De Young–Keizer IP3R subunit model. The graph shows the dependence of (b) the open probability PO, (c) the mean open time τO, and (d) the mean close time τC as a function of Ca2+ concentration for different concentrations of IP3. The lines show the results calculated with the deterministic transition matrix theory and the symbols show the results obtained from single-channel patch clamp from IP3R on native nuclear membranes (Refs. 11, 12, 13). Here, thick lines and stars are for [IP3]=10 μM, thin lines and circles are for 0.033 μM, dashed lines and squares are for 0.02 μM, and dotted lines and triangles are for 0.01 μM. Same notations are used in the following figures. The parameters used in the model are K1=0.0072 μM, K2=78 μM, K3=0.22 μM, K4=K1K2∕K3, K5=0.21 μM, a1=500 μM−1 s−1, a2=0.01 μM−1 s−1, and a5=400 μM−1 s−1.
For all binding∕unbinding loops given in Fig. 1, the thermodynamic constraint of detailed balance requires that the reaction dissociation constants satisfy the relation K1K2=K3K4. In the model, each subunit has eight different states with transitions governed by second-order rate constants ai for binding processes and first-order rate constants bi for unbinding processes [Fig. 1a]. In order to calculate the channel open probability, the necessary parameters are the reaction dissociation constants, i.e., Ki=bi∕ai, while the calculation of mean open time and mean close time requires the values of binding and unbinding rates. Parameter values needed for PO, τO, and τC are given in the legend of Fig. 1.
Now we apply the deterministic matrix transition method17, 18 to analyze the channel open probability, mean open time, and mean close time. The probability of an IP3R subunit being in state (ijk) is denoted by Pijk with ∑Pijk=1. By mass action kinetics, the equations describing the subunit dynamics are
| (3) |
where Q is the generator matrix of transition rates and P is the vector of probability of subunits.
Mathematically, the equilibrium state is defined as dP∕dt=0. The equilibrium vector w satisfies wQ=0 according to the transition matrix theory. Detailed balance is imposed so that we can solve for the vector w easily. This is done by calculating the probabilities in terms of their probabilities relative to state (000) along the shortest binding∕unbinding path. These unnormalized probabilities are denoted as qijk with q000=1. As an example, the equilibrium probability (q110) of state (110) relative to that of state (000) is just the product of forward to backward rates along any of the shortest paths connecting (000) to (110) (i.e., either through state 100 or state 010) given as
| (4) |
Then the normalized equilibrium probability for state (ijk) is
| (5) |
where Z is the normalization factor defined by Z=∑qijk and given as
| (6) |
Thus, the normalized equilibrium probability for state (110) is as follows:
| (7) |
For the tetrameric IP3R model, the channel opens when three out of four subunits are in state (110), so the channel open probability is written as
| (8) |
with and .
Because channel states (110, 110, 110, not −110) are the only open states that connect to closed channel states by any one of three (110) states changing to the other three states, i.e., 100, 010, or 111 with rate b5, b1, or a2[Ca2+], we can directly write the equilibrium probability flux between open and close states as follows:
| (9) |
The mean open and close times are then given by
| (10) |
The fittings of the channel model to the experimental data are shown in Figs. 1b, 1c, 1d for PO, τO, and τC. For the fitting of PO at I=10 μM, the model does not provide a flat PO for calcium concentrations changing from C=0.7 to 25 μM. The model also fails to give a steep response to IP3 concentration changes around I=0.02 μM. A calcium concentration dependent τO is clearly obtained from the model.
Model 2: IP3R model with four 6-state subunits
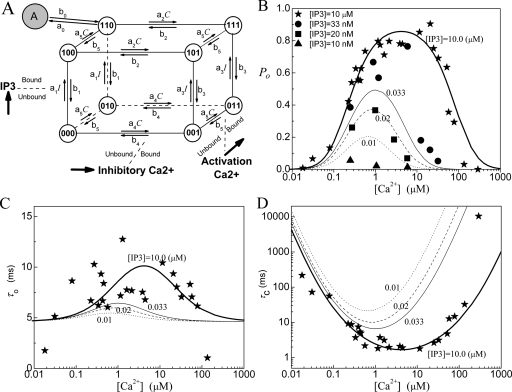
Now we consider a simplified De Young–Keizer IP3R model in which each subunit has six states only, as shown in Fig. 2. The channel is open when three or four identical and independent subunits are in the (110) state.
Figure 2.
Model 2: (a) The subunit structure of the channel model, (b) the open probability PO, (c) the mean open time τO, and (d) the mean close time τC. In the model K1=0.008 μM, K2=78 μM, K3=0.22 μM, K4=K1K2∕K3, K5=0.21 μM, a1=400 μM−1 s−1, a2=0.01 μM−1 s−1, and a5=400 μM−1 s−1.
For this model, the normalization factor is written as
| (11) |
The other formulas are the same as those for model 1.
The fittings of the channel model to the experimental data are given in Figs. 2b, 2c, 2d for PO, τO, and τC. One can see that the fitting results of this model are quite similar to the fittings of model 1. As given in Table 1, the mismatch values for PO fitting are 0.188 for both model 1 and model 2. It appears that the states and transitions omitted in the derivation of model 2 from model 1 are not essential for the gating behavior.
IP3R MODELS WITH CONFORMATIONAL CHANGE DYNAMICS
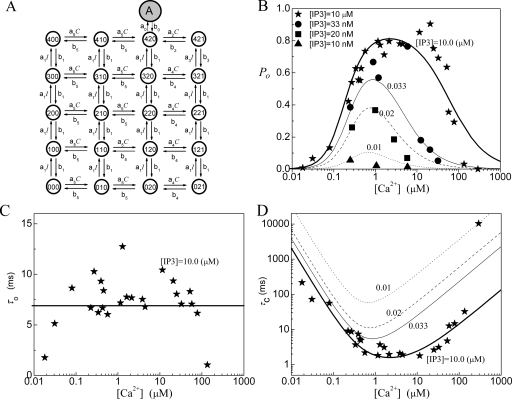
Model 3: IP3R model with four 9-state subunits
In Ref. 16, we have proposed a modified De Young–Keizer IP3R model. The model comprises four identical and independent subunits. Two independent Ca2+ binding sites for each subunit (i.e., an activating binding and inhibitory binding site) and an IP3 binding site, are assumed for each subunit. The model further includes a conformational change whereby a subunit in the (110) state (one IP3 and one activating Ca2+ bound) is “inactive” and must change through a conformational transition to an “active” (A) state before it can contribute to channel opening. This conformational step is analogous to the well-characterized behavior of nicotinic acetylcholine receptors21 and further implies that the active state is locked with respect to agonist binding and dissociation. The model also assumes that the channel is open when either three or four subunits are in active state. A schematic picture of the state transitions for a subunit is shown in Fig. 3a and the fitting results are shown in Figs. 3b, 3c, 3d. Notice that the parameters obtained here are slightly different from those in Ref. 16, where the optimized fitting process was not used. As shown in Table 1, the open probability is better fitted with this model than with the models 1 and 2. This supports our assumption that a channel opens through a conformational transition from a close state to an active state.
Figure 3.
Model 3: (a) The subunit structure of the channel model. A conformational transition to an active state (state-A) occurs before the subunit can contribute to channel opening. (b) The open probability PO, (c) the mean open time τO, and (d) the mean close time τC. In the model K1=0.0054 μM, K2=17.6 μM, K3=0.64 μM, K4=K1K2∕K3, and K5=1.04 μM. For the conformational change, K0=0.135 μM and a0=535 μM−1 s−1.
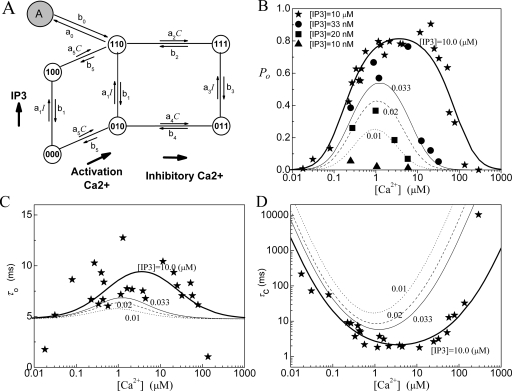
Model 4: IP3R model with four 7-state subunits
Now we consider a simplified IP3R model based on model 3. In the model, each subunit has seven states, as shown in Fig. 4. For this model, the equilibrium probability for the active state (i.e., A-state) is given as
| (12) |
with
| (13) |
The equilibrium probability flux between open and close states is given as
| (14) |
The other formulas are the same as those for model 1.
Figure 4.
Model 4: (a) The subunit structure of the channel model, (b) the open probability PO, (c) the mean open time τO, and (d) the mean close time τC. In the model K1=0.018 μM, K2=24 μM, K3=0.4 μM, K4=K1K2∕K3, K5=0.56 μM, and K0=0.194 μM with a0=360 μM−1 s−1.
The fittings of the channel model to the experimental data are given in Figs. 4b, 4c, 4d for PO, τO, and τC. In fact, the fittings of this model are quite similar to the fittings of model 3. Compared to the results given by model 1 and model 2, model 3 and model 4 give a better fitting of PO at optimal calcium concentrations around C=2 μM at I=10 μM. However, the model also fails to give a sensitive response to IP3 concentrations around I=0.02 μM. Again, model 3 and model 4 give a similar approximation of the experimental data, suggesting that the two omitted states are inessential.
Model 5: IP3R model with four 13-state subunits
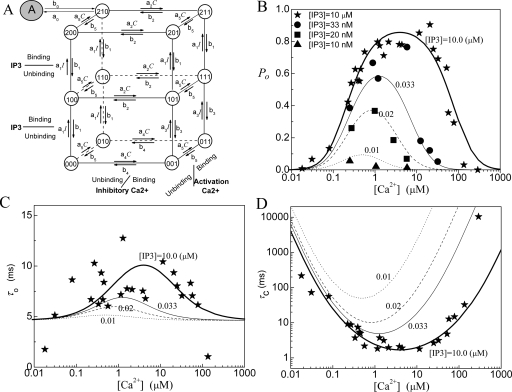
The above four models all show a low sensitivity in response to I around 0.02 μM. In order to obtain a sensitive response of the channel to IP3 concentration, we consider a 13-state subunit IP3R model.
The model comprises four identical and independent subunits. We still consider two independent Ca2+ binding sites for each subunit, i.e., an activating binding site and an inhibitory site. However, in order to account for the observed strongly cooperative dependence of IP3R channel opening on I, we assume that there are two IP3 sequential binding sites in each subunit. A schematic picture of the transitions among 13 states for each subunit is shown in Fig. 5a. The channel is open when either three or four subunits are in the active state.
Figure 5.
Model 5: (a) The subunit structure of the channel model, (b) the open probability PO, (c) the mean open time τO, and (d) the mean close time τC. In the model K1=0.005 μM, K2=15.6 μM, K3=2.25 μM, K4=K1K2∕K3, K5=1.01 μM, and K0=0.135 μM with a0=535 μM−1 s−1.
For this model, the normalization factor Z is a sum of 13 terms that can be easily written out and we have
| (15) |
The other formulas are the same as those for model 4. The fittings of the channel model to the experimental data for PO, τO, and τC are given in Figs. 5b, 5c, 5d. As a comparison of Fig. 5 with Figs. 1234, one can see that a more sensitive response of the channel for PO to IP3 concentration can be obtained with model 5. As shown in Table 1, compared to the previous four models, a better fitting for the open probability is obtained with this model.
Each monomer of the tetrameric channel complex has two IP3 binding sites with different dissociation constants, as has also been suggested in Ref. 6. However, the molecular structure study of the IP3R indicates that there is one IP3 core binding domain and several calcium binding sites for each monomer.2, 22 Thus the experimental data do not favor the assumption of two IP3 binding sites for each subunit. However, this model clearly shows that a sequential binding of IP3 messengers can give a steep change in PO versus I.
SEQUENTIAL BINDING IP3R MODELS
Model 6: 20-state IP3R model
In contrast to the five models discussed above—with the assumption of four independent units—we will now consider the tetrameric IP3R channel as a single unit with sequential binding processes. In the model, we assume that there are only two sequential activating Ca2+ binding sites and only one inhibitory Ca2+ binding site. There are four sequential IP3 binding sites. We assume that only after the two activating binding sites are occupied by Ca2+ ions, the inhibitory Ca2+ binding site becomes available. Further, only after the inhibitory Ca2+ binding site becomes empty, the unbinding processes for activating Ca2+ ion can occur sequentially. The Ca2+ binding∕unbinding processes are independent of the IP3 binding∕unbinding processes. A schematic picture for the transitions among the 20 channel states is shown in Fig. 6a. The channel is open when it is in state (420) with four IP3 messengers bound to the IP3 sites and two Ca2+ ions bound to the activating sites.
Figure 6.
Model 6: (a) The state structure of the sequential binding IP3R model, (b) the open probability PO, (c) the mean open time τO, and (d) the mean close time τC. In (c), the mean open time is independent of IP3 concentration. In the model K1=0.009 μM, K2=48 μM, K3=0.3 μM, K4=K1K2∕K3, K5=0.18 μM, a1=240 μM−1 s−1, a2=0.3 μM−1 s−1, and a5=720 μM−1 s−1.
For this model, the normalization factor Z is a sum of 20 terms and we have
| (16) |
Obviously, we also have
| (17) |
| (18) |
and so
| (19) |
The fittings of the channel model 6 to the experimental data are given in Figs. 6b, 6c, 6d for PO, τO, and τC. For the fitting of PO at I=10 μM, the model could not supply a flat PO at optimal calcium concentration. The model fails to exhibit a steep decreasing PO with large C at I=10 μM. With this model, as given by Eq. 19, τO almost stays constant for C<2 μM and then decreases at large C.
Model 7: 21-state IP3R model
Next, based on model 6, we furthermore consider the conformational change dynamics at state (420) for the channel to become open. A schematic picture for the transitions among the 21 states is shown in Fig. 7a. With J=b0PO, we have a simple result for the mean open time as τO=1∕b0, which is independent of any concentrations.
Figure 7.
Model 7: (a) The state structure of the sequential binding IP3R model, (b) the open probability PO, (c) the mean open time τO, and (d) the mean close time τC. In the model K1=0.016 μM, K2=8 μM, K3=0.3 μM, K4=K1K2∕K3, K5=0.44 μM, and K0=0.151 μM with a0=960 μM−1 s−1.
The fittings of the channel model 7 to the experimental data are shown in Figs. 7b, 7c, 7d for PO, τO, and τC. After considering the conformation change, the model can provide a flat PO at optimal calcium concentration and also increases the sensitivity of PO to I at optimal C. However, the model still fails to give a steep decreasing PO with large C at I=10 μM. This failure occurs because only one inhibitory Ca2+ binding site is assumed in the model.
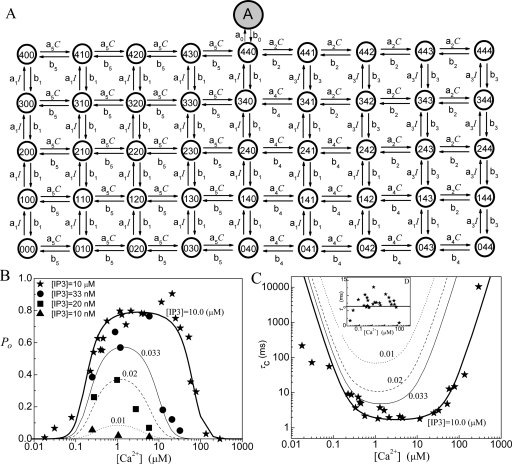
Model 8: 46-state IP3R model
In this model, we consider four sequential activating Ca2+ binding sites, four sequential inhibitory Ca2+ binding sites, and four sequential IP3 binding sites. Thus each monomer has one activating Ca2+ binding site, one inhibitory Ca2+ binding site, and one IP3 binding site. We assume that only after the four activating binding sites are occupied sequentially by Ca2+ ions, the four inhibitory Ca2+ binding sites become available sequentially. Only after the inhibitory Ca2+ binding site becomes empty sequentially, the unbinding processes for activating Ca2+ ion can occur sequentially. The Ca2+ binding∕unbinding processes and the IP3 binding∕unbinding processes are independent. We furthermore consider the conformational change dynamics at state (440) (i.e., with four activating Ca2+ and four IP3 bound on the channel) for the channel to become open. Thus there are in total 46 states in this model. A schematic picture for the transitions among the 46 channel states is shown in Fig. 8a. Similar to model 7, with J=b0PO a constant mean open time is given as τO=1∕b0.
Figure 8.
Model 8: (a) The state structure of the sequential binding IP3R model, (b) the open probability PO, and (c) the mean close time τC. The inset figure in (c) is the plot of the mean open time τO. In the model K1=0.02 μM, K2=53 μM, K3=0.2 μM, K4=K1K2∕K3, K5=0.21 μM, and K0=0.233 μM with a0=155 μM−1 s−1.
For this model, there are two dissociation constants for the inhibitory Ca2+ binding, K2 and K4. At the bottom of Fig. 8a, i.e., without any IP3 bound, the dissociation constants for four inhibitory Ca2+ bindings all equal K4, and at the top of Fig. 8a, i.e., with four IP3 bound, the dissociation constants for four inhibitory Ca2+ bindings all equal K2. In between, with increasing number of IP3 bindings, the dissociation constant K4 at the most right side will be replaced by K2 one by one.
The fittings of the channel model 8 to the experimental data are given in Figs. 8b, 8c for PO, τO, and τC. It can be seen that this model can reproduce the following characteristics of the experimental data. (1) The model provides a flat PO at optimal calcium concentration at I=10 μM. (2) The model gives a sensitive response of PO to I at optimal C. (3) The model exhibits a steep increasing response and a steep decreasing response of PO to C at saturating I. As shown in Table 1, a small mismatch value is obtained for PO fitting with this model. Thus, except for the 13-state model, this model gives the best fitting for the channel open probability among the seven models. However, compared to all other models discussed above, this model is much more complex.
DISCUSSION
The IP3R channel model plays a key role for the simulation of intracellular calcium signals. Different IP3R models have been proposed in the past.5, 6, 7, 8, 9, 13, 14, 15, 16, 19, 20 We here suggest that a proper IP3R model should reflect the tetrameric structure of the channel and we fit the IP3R patch clamp data recorded in their native environment of the nuclear membrane. As an example, we consider the fitting of patch clamp data of IP3R on the nuclear membrane in Xenopus oocytes. Different types of IP3R models are discussed in the paper in order to fit the experimental data of the open probability, mean open time, and mean close time of the channel as a function of calcium concentration and IP3 concentration. Our discussion indicates that rather than possessing four independent and identical subunits, an IP3R channel shows a sequential binding-unbinding process with Ca2+ ions and IP3 messengers. Our simulations also favor the assumption that a channel opens through a conformational transition from a close state to an active state.
At saturating IP3 concentration stimulus, the observation that the channel shows a steep increase in open probability at small Ca2+ concentration favors a sequential binding of activating Ca2+ ions, while the observation that the channel shows a rapid decrease in open probability at large Ca2+ concentration favors a sequential binding of inhibitory Ca2+ ions. Similarly, the sensitivity of the channel open probability to small IP3 stimuli requires a sequential binding dynamics of IP3 messengers on the channel. At the optimal Ca2+ concentration, the open probability shows a flat behavior, which can be easily matched by assuming a conformational change with constant rates leading to the opening of the channel. Without the conformational change, a flat behavior can only be achieved at PO=1 for the channel model.
By considering the tetrameric IP3R which consists of four independent and identical subunits, both the number of model states and the number of model parameters can be largely reduced. This provides an advantage for any IP3R simulations. However, if we consider a structurally symmetric channel with dynamically sequential binding IP3R, both the number of model states and the number of model parameters are large. For example, if considering one IP3 binding site and two Ca2+ binding sites for activating and inhibitory processes each, at least a 45-state channel should be implemented, which is similar to model 8. As a result, the sequential IP3R model will complicate simulations.
On the other hand, relaxing requirements to obtain a handy model, one may consider that even a model as simple as model 2 can roughly fit the experimental data. Thus in some situations the model 2 may be sufficient for calcium signaling simulations. In that sense, in order to simplify the numerical process in the modeling, the De Young–Keizer model may still be regarded a good choice for calcium signaling studies.
For the De Young–Keizer model, model 1, we cannot fix the values of the binding rates a3 and a4 with stationary data of PO, τO, and τC. A similar limitation that the steady state results of PO, τO, and τC are not sufficient to determine all the binding parameters in the models holds also for the other seven models. In this paper, parameters of the models are chosen to fit the steady state experimental data, and the different models are compared based on such fittings. In Ref. 23, three IP3R models have been compared by fitting them to the dynamic data of IP3R responding to step increases in Ca2+ and IP3 concentrations, rather than the stationary data at steady Ca2+ and IP3 concentrations. With the original De Young–Keizer model, the peak of the bell-shaped curve moves to the right with increasing [IP3], while when the best-fit parameters are used in the De Young–Keizer model for dynamic data, a left moving peak is obtained. In biologically realistic situations, the IP3R channels typically respond to oscillating Ca2+ concentration. It was argued in Ref. 23 that during an oscillation, the steady-state response is less important than the response to a changing Ca2+ concentration, and the receptors seldom experience a steady Ca2+ concentration except at resting state. Thus the important question is posed as to what extent the steady-state data should be used to constrain the parameter fitting of the model. On the other hand, another conclusion drawn in Ref. 23 is that time-dependent responses to steps of Ca2+ and IP3 concentrations alone are insufficient to determine the model parameters unambiguously. Thus, a reasonable modeling approach in the future should incorporate both the steady state11, 12, 13 and dynamic data.24, 25
Here we did not address the kinetic feedback of calcium, i.e., the physiological condition that released calcium may bind back to the channel. As shown, for instance, in Ref. 26 such feedback leads to largely increased open probabilities and bursts of channel openings∕closings. Under those conditions, details of the single channel model, such as the conformational transition, further affect gating dynamics. To give an example, release bursts for models with this transition may occur independent of momentary calcium concentration.26 The bursts are therefore different from the bursts for earlier models, where the opening∕closing transition involves calcium binding∕unbinding. We expect that our kinetic parameter fittings will be useful for further analysis of integrative calcium release models.
ACKNOWLEDGMENTS
This work was supported by National Institutes of Health Grant No. 2R01GM065830-06A1 for J.S. and J.P. J.S. also acknowledges the support from the National Science Foundation of China under Grant No. 10775114.
References
- Berridge M. J., Lipp P., and Bootman M. D., Nat. Rev. Mol. Cell Biol. 1, 11 (2000). 10.1038/35036035 [DOI] [PubMed] [Google Scholar]
- Foskett J. K., White C., Cheung K. H., and Mak D. O., Physiol. Rev. 87, 593 (2007). 10.1152/physrev.00035.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lechleiter J., Girard S., Peralta E., and Clapham D., Science 252, 123 (1991). 10.1126/science.2011747 [DOI] [PubMed] [Google Scholar]
- Sneyd J. and Falcke M., Prog. Biophys. Mol. Biol. 89, 207 (2005). 10.1016/j.pbiomolbio.2004.11.001 [DOI] [PubMed] [Google Scholar]
- De Young G. W. and Keizer J., Proc. Natl. Acad. Sci. U.S.A. 89, 9895 (1992). 10.1073/pnas.89.20.9895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atri A., Amundson J., Clapham D., and Sneyd J., Biophys. J. 65, 1727 (1993). 10.1016/S0006-3495(93)81191-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaftan E. J., Ehrlich B. E., and Watras J., J. Gen. Physiol. 110, 529 (1997). 10.1085/jgp.110.5.529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swillens S., Champeil P., Combettes L., and Dupont G., Cell Calcium 23, 291 (1998). 10.1016/S0143-4160(98)90025-2 [DOI] [PubMed] [Google Scholar]
- Sneyd J. and Dufour J. F., Proc. Natl. Acad. Sci. U.S.A. 99, 2398 (2002). 10.1073/pnas.032281999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezprozvanny I., Watras J., and Ehrlich B. E., Nature (London) 351, 751 (1991). 10.1038/351751a0 [DOI] [PubMed] [Google Scholar]
- Mak D. O. and Foskett J. K., J. Gen. Physiol. 109, 571 (1997). 10.1085/jgp.109.5.571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak D. O., McBride S., and Foskett J. K., Proc. Natl. Acad. Sci. U.S.A. 95, 15821 (1998). 10.1073/pnas.95.26.15821 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak D. O., McBride S. M., and Foskett J. K., J. Gen. Physiol. 122, 583 (2003). 10.1085/jgp.200308809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baran I., Biophys. J. 84, 1470 (2003). 10.1016/S0006-3495(03)74960-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraiman D. and Dawson S. P., Cell Calcium 35, 403 (2004). 10.1016/j.ceca.2003.10.004 [DOI] [PubMed] [Google Scholar]
- Shuai J., Pearson J. E., Foskett J. K., Mak D. O., and Parker I., Biophys. J. 93, 1151 (2007). 10.1529/biophysj.107.108795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruno W. J., Yang J., and Pearson J. E., Proc. Natl. Acad. Sci. U.S.A. 102, 6326 (2005). 10.1073/pnas.0409110102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Bruno W. J., Hlavacek W. S., and Pearson J. E., Biophys. J. 91, 1136 (2006). 10.1529/biophysj.105.071852 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y. and Rinzel J., J. Theor. Biol. 166, 461 (1994). 10.1006/jtbi.1994.1041 [DOI] [PubMed] [Google Scholar]
- Keizer J. and De Young G., J. Theor. Biol. 166, 431 (1994). 10.1006/jtbi.1994.1038 [DOI] [Google Scholar]
- Hille B., Ion Channels of Excitable Membranes, 3rd ed. (Sinauer Associates, Sunderland, MA, 2001). [Google Scholar]
- Bezprozvanny I., Cell Calcium 38, 261 (2005). 10.1016/j.ceca.2005.06.030 [DOI] [PubMed] [Google Scholar]
- Sneyd J., Falcke M., Dufour J.-F., and Fox C., Prog. Biophys. Mol. Biol. 85, 121 (2004). 10.1016/j.pbiomolbio.2004.01.013 [DOI] [PubMed] [Google Scholar]
- Dufour J. -F., Arias I. M., and Turner T. J., J. Biol. Chem. 272, 2675 (1997). 10.1074/jbc.272.5.2675 [DOI] [PubMed] [Google Scholar]
- Mak D. -O. D., Pearson J. E., Loong K. P. C., Datta S., Fernandez-Mongil M., and Foskett J. K., EMBO Rep. 8, 1044 (2007). 10.1038/sj.embor.7401087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rüdiger S., Shuai J. W., Huisinga W., Nagaiah C., Warnecke G., Parker I., and Falcke M., Biophys. J. 93, 1847 (2007). 10.1529/biophysj.106.099879 [DOI] [PMC free article] [PubMed] [Google Scholar]