The role of hydrogen bonding in tethered polymer layers

Abstract

A molecular theory to study the properties of end tethered polymer layers, in which the polymers have the ability to form hydrogen bonds with water is presented. The approach combines the ideas of the single-chain mean-field theory to treat tethered layers with the approach of Dormidontova (Macromolecules, 2002 35,987) to include hydrogen bonds. The generalization includes the consideration of position dependent polymer-water and water-water hydrogen bonds. The theory is applied to model poly ethylene oxide (PEO) and the predictions are compared with equivalent polymer layers that do not form hydrogen bonds. It is found that increasing the temperature lowers the solubility of the PEO and results in a collapse of the layer at high enough temperatures. The properties of the layer and their temperature dependence are shown to be the result of the coupling between the conformational entropy of the chains, the ability of the polymer to form hydrogen bonds, and the intermolecular interactions. The structural and thermodynamic properties of the PEO layers, such as the lateral pressure-area isotherms and polymer chemical potentials, are studied as a function of temperature and type of tethering surface. The possibility of phase separation of the PEO layer at high enough temperature is predicted, due to the reduced solubility induced by breaking of polymer-water hydrogen bonds. A discussion of the advantages and limitations of the theory, together with how to apply the approach to different hydrogen bonding polymers is presented.

1 Introduction

Poly(ethylene oxide) (PEO)^1,2, also called Poly(ethylene glycol) (PEG)³, has a wide range of applications. These include prevention of particle aggregation^4,5, modification of surfaces for bio-compatibility^6-9, and drug delivery^10,11. In many of these applications, the polymers are tethered to surfaces at one of their ends. For example, PEO grafted layers^12-14 are used for the prevention of nonspecific adsorption of proteins on surfaces to reduce immunological responses^15-22 In supported membrane systems, PEO layers are used as soft polymer cushions to maintain structural and dynamical properties of biomembranes^23-25.

The good solubility of PEO in water at room temperature, as well as the flexibility of the polymer chains, are believed to be the source for the ability of PEO to prevent/reduce protein adsorption. The solubility is related to the ability of oxygen in the ethylene oxide segments to form hydrogen bonds with water molecules. The formation of hydrogen bonds is the main source for the temperature dependence of the solubility of PEO. Namely, that the solubility of PEO decreases with increasing temperature and then the solution shows a lower critical temperature for phase separation^26-38. In polymers where the quality of the solvent is determined by Van der Waals interactions, the solubility decreases with decreasing temperature and an upper critical solution temperature is obtained³⁹. The phase diagram of PEO solutions displays a closed loop, implying that at very high temperatures the solubility of PEO in water increases again. This interesting and rich phase behavior has attracted a great amount of study, including experiments^26-30, theories^31-38,40-42 and computer simulations^43-46.

Theoretically, mostly two state models have been employed^{32-37,41-43,47,48} to study PEO solutions. In these models, the segments are assumed to exist into two interconverting states. Usually, polymers segments are separated into hydrogen bonded and non-bonded segments. Two state models have been proposed by Karlström³³, Matsuyama and Tanaka³⁴, and Bekiranov et al.³⁵, to study PEO solutions and all obtained a closed-loop phase behavior. Those models provide only qualitative agreement with experiments. A common feature of those models is that they only included hydrogen bonds between water and PEO, but they lacked the treatment of water-water hydrogen bonds. A recently developed mean-field theory by Dormidontova³⁸ and computer simulations^44-46 showed that the inclusion of both PEO-water as well as water-water hydrogen bonds is essential to accurately describe the phase behavior of PEO-solutions. The predicted phase diagrams are in quantitative agreement with experimental observations^26,27,29. Therefore a correct description of PEO solutions should include both PEO-water and water-water association. Also noteworthy is that Baulin and Halperin^36,37,47,48 successfully combined various two state models^33-35 by introducing an effective interaction parameter χ_eff (T, ϕ). This formulation is important because this effective χ-parameter is related to the measured χ-parameter. The model proposed by Dormidontava exhibits an effective χ-parameter which is in good agreement with experiments unlike, for example, the Karlström model.

Although a large amount of studies have focused on PEO solutions, far less have been devoted to a molecular level understanding of the formation of hydrogen bonds in polymeric systems. Most theoretical studies^33-37,47,48 of PEO-solutions are based on a coarse-grained description of the PEO-chains, including few molecular details. However, the formation of hydrogen bonds is significantly influenced by the conformations adopted by the PEO chains^46,49. It is necessary to include more molecular details to properly describe hydrogen bonding in PEO systems. Most of the theoretical studies have focused on the phase behavior of PEO solutions. Hence they study the solutions at high temperatures, where the phase transitions occurs. Depending on the molecular weight of PEO, the lower critical solution temperature (LCST) is well above 100°C^26,27. Around room temperature PEO is soluble in water and forms a homogenous solution. In many bio-related practical applications where PEO end-tethered layers are used, slightly above room temperature is the relevant regime. Therefore, it is important to investigate the behavior of tethered PEO layers near room temperature by explicitly including hydrogen bonding and the coupling that exists between the conformational statistics of the chain molecules and their ability to hydrogen bond with the surrounding water in a highly inhomogeneous environment.

In this paper, we present a molecular theory to study tethered PEO layers in water. The theory has been used previously to study the thermodynamics and structural properties of tethered polymers^50,51, and has been shown to be in quantitative agreement with simulations and experimental observations^52-56. In this work, we generalize the theory to include the ability of the polymers to form hydrogen bonds with water molecules. The ability to form hydrogen bonds is introduced following the ideas of Dormidontova³⁸. Our aim is to explore the mechanism of hydrogen bonding in PEO layers based on a molecular description of the polymers, and establish which factors influence the formation of hydrogen bonds. We focus attention to conditions near room temperature. Observable structural and thermodynamics quantities obtained from our theoretical calculations are presented. As will be demonstrated, these macroscopic observables depend largely on the microscopic hydrogen bonding of PEO with water.

The paper is organized as follows. First, we describe the molecular theory. Then we present relevant results, concentrating on the differences between PEO layers and non-hydrogen bonding polymer layers, and establish a number of important factors influencing the formation of hydrogen bonds. In the last section, we draw conclusions on hydrogen bonding of PEO layers and discuss the limitations of the theory and how to extend it to other hydrogen bonding polymers.

2 Molecular Theoretical Approach

We generalize a molecular theory^50-53, that considers the size, shape, and conformation of every molecular type explicitly with the inclusion of hydrogen bonding. The system is composed of a surface of area A that spans the x-y plane at the origin of the z axis. There are N_p polymer molecules tethered onto the surface. They are only allowed in the z ≥ 0 half-space. The number of tethered chains per unit area, or surface coverage is σ = N_p/A. Each polymer has N segments and each segment has a volume v_p. The polymer modified surface is immersed in water. The number of water molecules is N_w, each with a volume v_w, which is the unit of volume used throughout the paper. The existence of the surface induces an inhomogeneous distribution of all the molecular species. We assume that the only inhomogeneous direction is the one perpendicular to the surface, i.e., the z-direction.

The Helmholtz free energy per unit area of a polymer layer in an aqueous solution is given by

$$\frac{\beta F}{A}=\frac{S_p}{k_{B}A}+\frac{\beta F_{\mathit{inter}}}{A}-\frac{S_w}{k_{B}A}+\frac{\beta F_{\mathit{assoc}}}{A}+\frac{\beta U_{\mathit{surf}}}{A}\frac{\beta U_{\mathit{rep}}}{A}.$$ (1)

The first term in Eq. (1) denotes the entropy of polymer chains, which is given by

$$\frac{-S_p}{k_{B}A}=\sigma \underset{\alpha }{\Sigma }P\left(\alpha \right)\ln P\left(\alpha \right)+\sigma \ln \sigma ,$$ (2)

where the first term accounts for the conformational entropy of the chains, and the second corresponds to the translational entropy of the chains. In the case of polymers chemically grafted to the surface, the second term in Eq. (2) should be excluded since the polymers lack the ability to move on the surface. P(α) is the probability distribution function (pdf) of finding a chain in conformation α. Given the pdf we can calculate any thermodynamical and average structural quantity of the polymers. For example, the polymer volume fraction profile is given by

$$\langle {\varphi }_p\left(z\right)\rangle \mathrm{d}z=\sigma \underset{\alpha }{\Sigma }P\left(\alpha \right)v_p(z;\alpha )\mathrm{d}z,$$ (3)

where v_p(z; α)dz denotes the volume that a polymer chain in conformation α contributes in the layer between z and z + dz.

The second term of the free energy, Eq. (1), describes the effective intermolecular interaction between the polymer segments and the water molecules.

$$\frac{\beta F_{\mathit{inter}}}{A}=\frac{\chi }{v_w}\int \mathrm{d}z{\varphi }_p\left(z\right){\varphi }_w\left(z\right).$$ (4)

where χ is the interaction parameter measuring the strength of the water-polymer effective repulsions, i.e. determines the quality of the solvent in the absence of hydrogen bonds³⁹. ϕ_p(z) ≡ 〈ϕ_p(z)〉 and ϕ_w(z) are the position dependent volume fractions of the polymer and the water respectively. The volume fraction of water is given by ϕ_w(z) = ρ_w(z)v_w, where ρ_w(z) corresponds to the number density of water molecules at z. Similarly, the polymer volume fraction is related to the number density of the polymer segments by ϕ_p(z) = ρ_p(z)v_p.

The third term in Eq. (1) is the z-dependent translational (mixing) entropy of the water molecules, which is given by

$$\frac{-S_w}{k_{B}A}=\int \mathrm{d}z{\rho }_w\left(z\right)[\ln {\rho }_w\left(z\right)v_w-1].$$ (5)

The fourth term in the free energy expression, Eq. (1), is the contribution from the formation of hydrogen bonds. According to Ref.38 for homogeneous PEO solutions, the contribution to the free energy arises from the association of polymer and water molecules and can be written as

$$\beta F_{\mathit{assoc}}=-\ln Z_{\mathit{assoc}},$$ (6)

where Z_assoc is a partition function equal to

$$Z_{\mathit{assoc}}=P_{\mathit{comb}}{W}_p\exp \left(\beta \Delta E_p{n}_p\right)W_w\exp \left(\beta \Delta E_w{n}_w\right),$$ (7)

where P_comb is a combinatorial factor, which describes the number of ways to form n_p hydrogen bonds between PEO and water and n_w water-water hydrogen bonds. Assuming that each oxygen of a PEO segment, acting as a proton acceptor, can participate in the formation of two hydrogen bonds and that each water molecule, acting as proton acceptor as well as proton donor, can participate in the formation of hydrogen bonds either with a PEO segment or with another water molecule. Consequently, the combinatorial factor is given by^38,57

$$P_{\mathit{comb}}=\frac{\left(2N_{p}N\right)!}{(2N_{p}N-n_p)!n_p!}\frac{\left(2N_w\right)!}{(2N_w-n_w)!n_w!}\frac{\left(2N_w\right)!}{(2N_w-n_p-n_w)!}.$$ (8)

In equation (7) W_p is the probability of finding a water molecule (donor) and a PEO segment (acceptor) in the vicinity of each other and in the correct orientation to form of a hydrogen bond, W_w is similarly defined for the water-water hydrogen bond. These probabilities are given as^38,40,57

$$W_i={\left(\frac{v_{\mathit{hb}}^i}{V}\right)}^{n_i},$$ (9)

where $v_{\mathit{hb}}^p$ is the volume of a PEO-water and $v_{\mathit{hb}}^w$ the volume of a water-water hydrogen bond and V is the total volume of the system. The last two terms in the partition function, (7), −ΔE_p and −ΔE_w are the energetic gain associated with the formation of a hydrogen bond between PEO and water and between water and water, respectively.

The above formalism was developed for homogenous PEO solutions. Here we generalize the approach to allow for spatial inhomogeneities in the z-direction, i.e., the contribution to the free energy at a particular z can be represented by a term −lnZassoc(z), where Zassoc(z) is given by the position dependent counterpart of the one presented in equation 6. Therefore, the total free energy contribution associated with the formation of hydrogen bonds can be expressed as

$$\frac{\beta F_{\mathit{assoc}}}{A}=-\frac{1}{V}\int \mathrm{d}z\ln Z_{\mathit{assoc}}\left(z\right),$$ (10)

where the position dependent partition function is given by

$$Z_{\mathit{assoc}}\left(z\right)=P_{\mathit{comb}}\left(z\right)W_p\exp \left(\beta \Delta E_p{n}_p\left(z\right)\right)W_w\exp \left(\beta \Delta E_w{n}_w\left(z\right)\right).$$ (11)

with

$$P_{\mathit{comb}}\left(z\right)=\frac{\left(2N_p\left(z\right)N\right)!}{(2N_p\left(z\right)N-n_p\left(z\right))!n_p\left(z\right)!}\frac{\left(2N_w\left(z\right)\right)!}{(2N_w\left(z\right)-n_w\left(z\right))!n_w\left(z\right)!}\frac{\left(2N_w\left(z\right)\right)!}{(2N_w\left(z\right)-n_p\left(z\right)-n_w\left(z\right))!}.$$ (12)

Note that quantities such as the number of polymers, number of water molecules, and the number of hydrogen bonds all have become position dependent.

The fifth term in the free energy, Eq. (1), describes the interaction between the surface and polymer segments. We approximate this interaction by a square well potential of range δ and thus the total attraction of the polymer segments with the surface is given by

$$\frac{\beta U_{\mathit{surf}}}{A}=\sigma \beta \epsilon \underset{\alpha }{\Sigma }P\left(\alpha \right)n(\alpha ;0),$$ (13)

where n(α, 0) denotes the number of polymer segments within distance δ from the surface and ε is the depth of the square well potential.

The last term in the total free energy expression, Eq. (1), represents the repulsive interactions of the system. These are modeled as hard-core repulsions and can be written in the form

$$\frac{U_{\mathit{rep}}}{A}=\beta \int \mathrm{d}z\pi \left(z\right)({\varphi }_p\left(z\right)+{\varphi }_w\left(z\right)-1),$$ (14)

where π(z) represents the position dependent repulsive interaction field. This field is determined by the requirement that the total volume is filled with either polymer or solvent, i.e. we impose packing constraints associated with the excluded volume interactions which are position dependent and have the form

$$\langle \varphi \left(z\right)\rangle +{\varphi }_w\left(z\right)=1.$$ (15)

The total Helmholtz free energy per unit area now becomes:

$$\begin{array}{cc}\hfill \frac{\beta F}{A}=& \sigma \underset{\alpha }{\Sigma }P\left(\alpha \right)(\ln P\left(\alpha \right)+\beta \epsilon n(\alpha ;0))+\sigma \ln \sigma \hfill \\ \hfill & +\int \mathrm{d}z{\rho }_w\left(z\right)[\ln {\rho }_w\left(z\right)v_w-1]\hfill \\ \hfill & +\frac{\chi }{v_w}\int \mathrm{d}z{\varphi }_p\left(z\right){\varphi }_w\left(z\right)\hfill \\ \hfill & +\int \mathrm{d}z2{\rho }_p\left(z\right)[x_p\left(z\right)\ln x_p\left(z\right)+(1-x_p\left(z\right))\ln (1-x_p\left(z\right))-x_p\left(z\right)\beta \Delta F_p]\hfill \\ \hfill & +\int \mathrm{d}z2{\rho }_w\left(z\right)[x_w\left(z\right)\ln x_w\left(z\right)+(1-x_w\left(z\right))\ln (1-x_w\left(z\right))-x_w\left(z\right)\beta \Delta F_w]\hfill \\ \hfill & +\int \mathrm{d}z2{\rho }_w\left(z\right)[1-x_w\left(z\right)-x_p\left(z\right)\frac{{\rho }_p\left(z\right)}{{\rho }_w\left(z\right)}]\ln [1-x_w\left(z\right)-x_p\left(z\right)\frac{{\rho }_p\left(z\right)}{{\rho }_w\left(z\right)}]\hfill \\ \hfill & -\int \mathrm{d}z2{\rho }_w\left(z\right)[x_w\left(z\right)+x_p\left(z\right)\frac{{\rho }_p\left(z\right)}{{\rho }_w\left(z\right)}]\ln \frac{2{\rho }_w\left(z\right)v_w}{e}\hfill \\ \hfill & +\beta \int \mathrm{d}z\pi \left(z\right)({\varphi }_p\left(z\right)+{\varphi }_w\left(z\right)-1),\hfill \end{array}$$ (16)

where −βΔF_i is the gain in free energy of forming a single hydrogen bond, which includes the energetic gain and entropic loss of forming the hydrogen bond: βΔF_i = βΔE_i − ΔS_i, with i = p for PEO-water and i = w for water-water hydrogen bonds. In our study, ΔE_p/k is fixed at 2000K, and ΔE_w/k at 1800K. The entropic loss is related to $v_{\mathit{hb}}^i$ and given by $\Delta S_i=-\ln \left(\frac{1-\mathit{cos}{\Delta }_i}{2}\right)$, with Δ_p = π/8.35 and Δ_w = π/4.75. These parameters are identical to those derived by Dormidontova in Ref38 to describe the phase diagram of aqueous PEO solutions. We like to stress that these parameters are not freely adjustable but have clear physical meaning and are fixed throughout all calculations. For PEO-water solutions the above values gave very good agreement between theoretical predictions and experimental results^{26,27,38,58-61}. In Eq.(16), we have introduced two additional variables: the local fraction of PEO-water hydrogen bonds, x_p(z), and the local fraction of water-water hydrogen bonds, x_w(z). They are defined as

$$x_p\left(z\right)=\frac{n_p\left(z\right)}{2N_p\left(z\right)N}\text{and}{x}_w\left(z\right)=\frac{n_w\left(z\right)}{2N_w\left(z\right)}.$$ (17)

To determine the probability distribution function P(α) of the polymer conformations, the solvent density ϕ_w(z), the local fraction of PEO-water hydrogen bonds x_p(z), and the local fraction of water-water hydrogen bonds x_w(z), we minimize the free energy.

Minimization of the free energy with respect to P (α) yields:

$$\begin{array}{cc}\hfill P\left(\alpha \right)=\frac{1}{q}\exp [-\beta \int \phantom{]}\mathrm{d}z\pi \left(z\right)n(\alpha ,z)v_p-\frac{\chi }{v_w}\int \mathrm{d}z& {\varphi }_w\left(z\right)n(\alpha ,z)v_p\hfill \\ \hfill & -2\int \mathrm{d}\mathit{zn}(\alpha ,z)\ln (1-x_p\left(z\right))-\beta \epsilon n\phantom{[}(\alpha ;0)].\hfill \end{array}$$ (18)

Here q is a normalization constant ensuring that ΣαP(α) = 1. Note that the excluded volume interactions, the polymer-water interaction and surface interaction enters into the pdf via the expected energetic Boltzmann factor. However the ability to form the polymer-water hydrogen bonds is represented by an entropic-like term: ln(1 − x_p(z)). In reality this term in the pdf is a generic feature that arises when the states of a system are coupled to a chemical like-equilibrium. For example, a similar term appears in the pdf for weak polyelectrolytes^62,63, where there is equilibrium between charged and uncharged states of the polymer segments.

The water volume fraction is given by:

$${\varphi }_w\left(z\right)=\exp [-\beta \pi \left(z\right)v_w-\frac{\chi }{v_w}{\varphi }_p\left(z\right)v_w-2\ln (1-x_w\left(z\right))-2\ln (1-x_w\left(z\right)-x_p\left(z\right)\frac{{\rho }_p\left(z\right)}{{\rho }_w\left(z\right)})].$$ (19)

The local fraction of PEO-water, x_p(z), and the local fraction of water-water hydrogen bonds, x_w(z), are given by the following chemical equilibrium like equations

$$x_p\left(z\right)=2\exp \left(\beta \Delta F_p\right)(1-x_p\left(z\right))(1-{\varphi }_p\left(z\right))(1-x_w\left(z\right)-x_p\left(z\right)\frac{{\rho }_p\left(z\right)}{{\rho }_w\left(z\right)}),$$ (20)

$$x_w\left(z\right)=2\exp \left(\beta \Delta F_w\right)(1-x_w\left(z\right))(1-{\varphi }_p\left(z\right))(1-x_w\left(z\right)-x_p\left(z\right)\frac{{\rho }_p\left(z\right)}{{\rho }_w\left(z\right)}).$$ (21)

From Eq. (18) and (19), we observe that the density of PEO segments depends on the local fraction of PEO-water and water-water hydrogen bonds, while Eqs. (20) and (21) indicate that the formation of hydrogen bonds depends on the local density of PEO segments. So the polymer density and the local fractions of hydrogen bonds are coupled in a non-linear way. Dividing Eq.(20) by Eq. (21), we find that x_p(z) and x_w(z) obey the following relation

$$\frac{x_p\left(z\right)}{(1-x_p\left(z\right))}=\exp \left[\beta (\Delta F_p-\Delta F_w)\right]\frac{x_w\left(z\right)}{(1-x_w\left(z\right))}.$$ (22)

This equation shows that the difference between the two local fractions of hydrogen bonds originates from the difference in the free energy associated with formation of a single PEO-water and a single water-water hydrogen bond. If ΔF_p−ΔF_w < 0 then x_w(z) is larger than x_p(z), which implies that the formation of water-water hydrogen bonds is more favorable than the formation of PEO-water hydrogen bonds. Converse, if ΔF_p − ΔF_w > 0, the association of PEO-water is more favorable. The two types of hydrogen bonding compete with each other because water is a common source of proton donors.

Substituting the expression for the pdf, Eq. (18), the water volume fraction, Eq. (19), the local fractions of PEO-water, Eq. (20), and water-water hydrogen bonding, Eq. (21), into the Helmholtz free energy gives the minimal free energy:

$$\begin{array}{cc}\hfill \frac{\beta F_{\mathit{min}}}{A}=& -\sigma \ln q+\sigma \ln \sigma -\beta \int \mathrm{d}z\pi \left(z\right)-\frac{\chi }{v_w}\int \mathrm{d}z{\varphi }_p\left(z\right){\varphi }_w\left(z\right)-\int \mathrm{d}z{\rho }_w\left(z\right)\hfill \\ \hfill & +\int \mathrm{d}z[2{\rho }_w\left(z\right)x_w\left(z\right)+2{\rho }_p\left(z\right)x_p\left(z\right)].\hfill \end{array}$$ (23)

The free energy, Eq. (23), represents the thermodynamic potential of the system and therefore all other thermodynamic quantities of interest can be obtained by taking the appropriate derivative. The most important quantities are the lateral pressure Π and the chemical potential μ since they determine the phase equilibrium in the system.

The lateral pressure can be directly measured experimentally using a Langmuir trough⁵⁵ and is given by $\Pi =-\left(\frac{\partial F}{\partial A}\right)N_p,N_s,T$. Using Eq.(23), the lateral pressure of PEO layer becomes:

$$\begin{array}{cc}\hfill \beta \Pi =& \sigma +\frac{\sigma {\mathit{Nv}}_p}{v_w}+\beta \int \mathrm{d}z\pi \left(z\right)+\frac{\chi }{v_w}\int \mathrm{d}z{\varphi }_p\left(z\right){\varphi }_w\left(z\right)+\int \mathrm{d}z\frac{1-2x_w\left(z\right)}{v_w}\hfill \\ \hfill & +\sigma \int \mathrm{d}z\left[2{\rho }_w\frac{1+x_w\left(z\right)}{x_w\left(z\right)}\frac{\partial x_w\left(z\right)}{\partial \sigma }-2{\rho }_p\frac{x_p\left(z\right)}{1-x_p\left(z\right)}\frac{\partial x_p\left(z\right)}{\partial \sigma }\right].\hfill \end{array}$$ (24)

The chemical potential, $\mu =\left(\frac{\partial F}{\partial N_p}\right)T,A$, is given by

$$\begin{array}{cc}\hfill \beta \mu =& -\ln q+\ln \sigma +\int \mathrm{d}z\frac{2{\rho }_p\left(z\right)}{\sigma }[-\frac{v_p}{v_w}{x}_w\left(z\right)+x_p\left(z\right)+\frac{v_p}{v_w}]\hfill \\ \hfill & +\int \mathrm{d}z\left[2{\rho }_w\left(z\right)\frac{1+x_w\left(z\right)}{x_w\left(z\right)}\frac{\partial x_w\left(z\right)}{\partial \sigma }-2{\rho }_p\left(z\right)\frac{x_p\left(z\right)}{1-x_p\left(z\right)}\frac{\partial x_p\left(z\right)}{\partial \sigma }\right].\hfill \end{array}$$ (25)

The unknowns in the above equations are the position dependent repulsive fields and fraction of hydrogen bonded moieties. These quantities are determined by substituting Eq.(18)-(21) into the packing constraints, Eq.(15). In practice, we discretize space and thereby convert the integral equations into a set of coupled nonlinear equations, which are solved numerically. The input necessary to solve those equations include the set of conformations for the polymer chains, the polymer surface coverage, the bare free energies for the formation of hydrogen bonds between water and PEO and water and water and the interaction parameter χ. Details concerning the discretization and numerical methodology can be found in the Appendix and in Refs.^52,63

Before showing the results we should comment on the particular form that we consider for the χ interaction parameter. In the results presented in the next section we consider only an interaction parameter of the form χ = B/T, with B = 100K. Thus, we do not include an entropic dependent term, as it is in general done, and as it has been used by Dorminotova³⁸. The reason for this choice is that we are developing a molecular theory where, in principle, all the entropic and interaction terms are explicitly considered. Thus, it will be inconsistent to have an entropic contribution in the χ parameter. It is clear, that we are using many assumptions in deriving and applying the molecular theory. However, keeping the approximations consistent will enable us to determine which assumptions are valid and which are not.

3 Results

In this section we present some representative results for the role of hydrogen bonding on the structural and thermodynamic properties of tethered PEO layers. To describe the salient features that arise from the incorporation of PEO-water hydrogen bond, we compare the results with polymer layers that do not have the ability to hydrogen-bond with water. We call these polymers non-HB polymers.

First, we study the distribution of tethered PEO segments around room temperature. In Figures 1(a) and (b) the volume fractions of PEO layers and non-HB polymer layers are presented. Figure 1(a) shows that the tethered PEO chains are more stretched than similar polymers that do not form hydrogen bonds with the water, as Figure 1(b) shows. This is because the energetical favorable hydrogen bonds between PEO segments and water molecules can compensate the loss of entropy due to chains stretching and the repulsive intermolecular interactions measured by χ. PEO chains tend to adopt more extended conformations for the formation of PEO-water hydrogen bonds. For non-HB polymers, the equilibrium structure of the polymer layer is determined by the balance between the opposing forces arising from the chain stretching and the polymer-solvent interactions. In order to minimize the repulsive polymer-solvent interactions, the polymer chains shrink, thereby reducing the number of unfavorable solvent polymer contacts. However, the ability of the PEO to form hydrogen bonds enables the chains to stretch in order to maximize, within the balance of the other interactions, the number of hydrogen bonds formed. Therefore, the effective intermolecular repulsions are reduced by the PEO-water hydrogen bonds, and as a result the solubility of PEO chains increases which causes PEO layers to swell.

Figure 1.

The average volume fraction of the grafted chains as a function of the distance from the surface for (a) PEO layers, and (b) non-HB polymer layers. The different lines correspond to different temperatures: full line, T = 10°C; dotted line, T = 20°C; dashed line, T = 30°C. For all cases the molecular weight of the polymer chain equals M_w = 5000, which corresponds to N = 114 segments. The surface coverage is σ = 0.1nm⁻².

An interesting result from Figure 1 is the temperature dependence of the structure of the polymer layers. In the case of non-HB polymer layers, Figure 1(b), the profiles are very similar for the three temperatures shown, manifesting the fact that in the absence of hydrogen bonds the solvent is marginally good in this temperature range. The inclusion of hydrogen bonds however, makes the profiles of the model PEO layers to show two important features as compared to the non-HB. First, the layers are much more stretched, showing that the addition of hydrogen bonds at this temperature makes the water to be a better solvent than without hydrogen bonds. Second, the component that is responsible for improving the solubility is energetic and therefore as the temperature decreases the HB become more favorable and the quality of the solvent improves, resulting in a more stretched PEO layer. The comparison between the model PEO, Figure 1(a), and the non-HB polymers, Figure 1(b), demonstrates that around room temperature, the role of hydrogen bonds is more important that the dispersion interactions modeled with the χ parameter.

To understand in more detail the role of hydrogen bonds and how temperature affects the properties of tethered PEO chains, we investigated the variation in the number of hydrogen bonds as a function of temperature. As we have discussed in the theory section the polymer-water and water-water HB are position dependent, therefore to describe the overall behavior of the layer we define the average fraction of PEO-water hydrogen bonds, $\langle x_p\rangle =\frac{\int \mathrm{d}{\mathit{zx}}_p\left(z\right){\varphi }_p\left(z\right)}{\int \mathrm{d}z{\varphi }_p\left(z\right)}$, and the average fraction of water-water hydrogen bonds, $\langle x_w\rangle =\frac{\int \mathrm{d}{\mathit{zx}}_w\left(z\right){\varphi }_w\left(z\right)}{\int \mathrm{d}z{\varphi }_w\left(z\right)}$. The integration extends only over the region where there are polymers, because we are interested in the effect of the polymers layer on the hydrogen bonding. If the integration is extended to infinity, 〈x_w〉 would become equal to the average fraction of water-water hydrogen bonds of pure water, since the bulk solution is infinitely large compared to the surface.

The role of temperature on the properties of the PEO layer is due to the competition between the polymer-water and the water-water hydrogen bonds. The formation of hydrogen bonds is always accompanied by a gain in free energy, i.e. both −ΔF_p and −ΔF_w are negative. However, we also have ΔF_p−ΔF_w < 0 and therefore whenever possible water would prefer to form HB with another water molecule over the PEO. This effect is demonstrated in the variation of the fraction of hydrogen bonds with temperature, in the range of [10°C, 80°C], for polymers and water as shown in Figure 2. Both fractions decrease with increasing temperature, but the average fraction of PEO-water hydrogen bonds, 〈x_p〉, decreases slightly faster. Moreover, the average fraction of water-water hydrogen bonds, 〈x_w〉, is always larger than the average fraction of PEO-water hydrogen bonds, 〈x_p〉, because the free energy gain for forming water-water hydrogen bonds is larger then the gain in free energy for forming PEO-water hydrogen bonds: ΔF_p −ΔF_w < 0. This can also be inferred from Eq. (22) which shows that the local fraction of water-water hydrogen bonds, x_w(z), must be larger than the local fraction of PEO-water hydrogen bonds x_p(z), for ΔF_p − ΔF_w < 0, and as a result 〈x_w〉 > 〈x_p〉. Consequently, the solubility of PEO decreases and the polymer layer becomes more compact, as will be shown next (see Fig. 3). Similar results have been obtained in theoretical investigations³⁸ and MD simulations⁴⁶ of PEO solutions.

Figure 2.

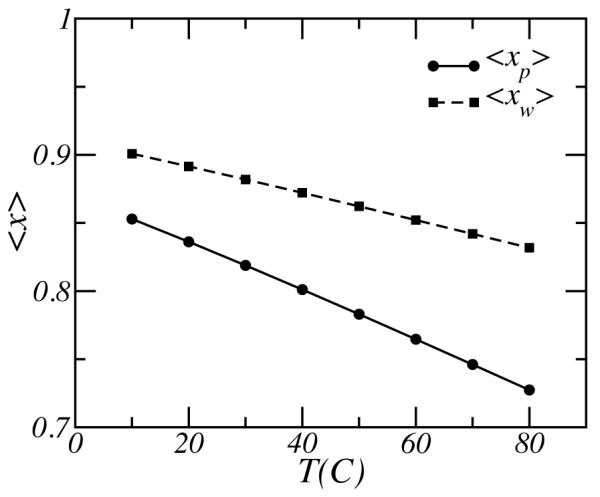
The average fraction of PEO-water and water-water hydrogen bonds as a function of temperature. The solid line with the circles correspond to the average fraction of PEO-water hydrogen bonds 〈x_p〉, and the dotted line with the square symbols shows the average fraction of water-water hydrogen bonds 〈x_w〉. The molecular weight of the polymer is M_w = 5000, and the surface coverage is σ = 0.1 nm⁻².

Figure 3.

The height of the polymer layers as a function of temperature. The dotted line with square symbols corresponds to a PEO layer, while the solid line with circles correspond to a nonHB polymer layer, The molecular weight of the polymer is M_w = 5000, and the surface coverage is σ = 0.1 nm⁻².

We define the height of the tethered layer by $\langle H\rangle =\frac{\int \mathrm{d}\mathit{zz}{\varphi }_p\left(z\right)}{\int \mathrm{d}z{\varphi }_p\left(z\right)}$ and it measures the amount of stretching of the tethered polymers. Figure 3 presents the height as a function of temperature for PEO and non-HB polymers. The height of the PEO layer decreases with increasing temperature while the height of the non-HB polymer layer slightly increases with increasing temperature. This result is expected from the temperature dependence of the polymer layer density profiles presented in Figure 1. The effect of the HB is to make the solvent (water) poorer as the temperature increases resulting in the decrease of the height with temperature. On the other hand, for non-HB polymers increasing the temperature makes the solvent better and therefore the polymer layer stretches. It is interesting to note that hydrogen bonds make the temperature dependence much stronger than in the absence of HB as can be seen in the sharper variation of 〈H〉 with T for PEO as compared to non-HB layers. This implies that in the competition between HB and χ in determining the quality of the solvent, the hydrogen bonds make a large contribution in the relevant temperature range.

To better quantify the coupling that exists between the two components that determine the quality of the solvent, Figure 4 shows the average fraction of PEO-water hydrogen bonds as a function of the χ parameter. It is important to point out that we vary the χ = B/T by changing the value of B and keeping the temperature constant. Therefore, the results in Figure 4 represent the direct competition between HB and Van der Waals interactions at fixed temperature.

Figure 4.

The average fraction of PEO-water, 〈x_p〉, and water-water (insert), 〈x_w〉, hydrogen bonds as a function of χ, for a temperature of T = 20°C. The molecular weight of the polymer chain is M_w = 5000, and the surface coverage is σ = 0.1 nm⁻2.

The results in Figure 4 demonstrate that there is a weak dependence of the number of polymer-water hydrogen bonds on χ, and that as the Van der Waals interactions between the polymer and the solvent become less favorable, the number of hydrogen bonds very slightly decreases. Increasing the number of PEO-water hydrogen bonds leads to a gain in the free energy, which is balanced by the loss of conformational entropy of the chain due to chain stretching and the increased number the intermolecular repulsions. This additional cost to the free energy hinders further PEO-water association, which is shown by a decreasing 〈x_p〉 with increasing χ in Figure 4. On the other hand over the range of investigated values of χ the change in the number of PEO-water hydrogen bonds is very low. As shown in the inset of Figure 4 the formation of water-water bonds is almost independent of χ. These results show that the behavior of PEO layers at room temperature is determined by the conformational entropy of the PEO-chains and the free energy associated with the hydrogen bond formation. The influence of the energetic repulsions between water and PEO around room temperature, in comparison, is small. The variation of χ gives us an estimate of the sensitivity at room temperature of the presented results against a particular choice of the χ-parameter. This is important because reported χ-parameters tend to vary considerable.³⁸. Regularly, also entropic contributions are included in the χ-parameter, i.e., χ = B/T + A, as we have discussed in the Theory section the entropic term is to account for the lack of proper description of the conformation statistics of the chain and their molecular structure⁶⁴. Since the theory presented here accounts explicitly for the conformational statistics of the chains, and their coupling to HB and the interactions, the only consistent form of the interactions parameter within this framework is without the temperature independent term.

To complete the role of the different variables in the ability of PEO to form hydrogen bonds, Figure 5 presents the dependence of the fractions of hydrogen bonds on polymer surface coverage. Both PEO-water and water-water hydrogen bonds decrease with increasing surface coverage. This result is similar to results obtained in previous theoretical calculations³⁸ and MD simulations⁴⁶ of PEO solutions. For bulk PEO solutions, the number of hydrogen bonds decreases with increasing bulk polymer concentration. The local density within the PEO layers increases with increasing surface coverage. This in turn results in a decrease of the probability of PEO-water and water-water association.

Figure 5.

The average fraction of PEO-water hydrogen bonds, 〈x_p〉, and average fraction of water-water hydrogen bonds, 〈x_w〉, as a function of the surface coverage at a fixed temperature T = 20°C. The molecular weight of the polymer is M_w = 5000, and the surface coverage is σ = 0.1 nm⁻2.

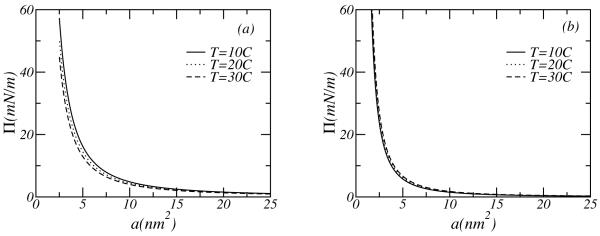
We now turn to the thermodynamical behavior of PEO layers. In particular, we concentrate our attention on the lateral pressure and the chemical potential of the polymers in the tethered layers. The lateral pressure can be directly measured experimentally using the Langmuir trough and it provides a direct measure of the lateral interactions within the polymer layer. The chemical potential provides the thermodynamic stability of the polymer layers. Figures 6(a) and 6(b) show the lateral pressure as a function of the area per polymer, a = 1/σ, for PEO layers and non-HB polymer layers. The lateral pressure increases with decreasing area per polymer (or increasing surface coverage) reflecting the dominant role of the interpolymer repulsions and the osmotic pressure at these temperatures. Comparison of Figures 6(a) and 6(b) shows that the lateral pressure is much larger for PEO layers, especially in the case of large surface coverage. The formation of PEO-water hydrogen bonds results in a larger excluded volume of the solvated PEO segments, leading to larger repulsions in PEO layers. As the temperature increases the lateral pressure for non-HB polymers increases slightly, while for PEO the pressures are lower. This opposite tendency of the lateral pressure isotherms is related to the structural behavior presented above for non-HB polymers as compared to PEO, and it is a direct indication of the quality of solvent and its temperature dependence. Namely, for PEO the quality of the solvent decreases with increasing temperature, i.e. the attractions become more important and as a result the pressure decreases. On the other hand, for non-HB polymers the quality of the solvent improves with increasing temperature and thus, the lateral pressure increases.

Figure 6.

Lateral pressure-area isotherms of PEO layers (a), and non-HB polymer layers (b). The solid line corresponds to a temperature of T = 10°C, the dashed line to T = 20°C and the dotted line to T = 30°C. The molecular weight of the polymer is M_w = 5000.

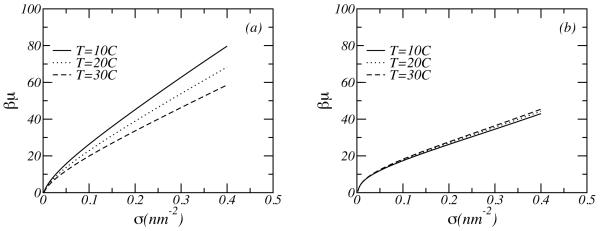
Figure 7(a) and (b) presents the chemical potential of the polymer as a function of the surface coverage for PEO layers and non-HB polymer layers, respectively. The chemical potential increases monotonically in both cases, which implies that the tethered layers are stable in the presented regime of temperatures and surface coverages. The temperature dependence of the chemical potential of the polymer in Figure 7(a) and (b) shows an opposite temperature tendency for PEO and non-HB polymer layers, similar to the one observed for the lateral pressure as well as the structural properties and reflecting the changes in the quality of solvent with temperature for each case. The chemical potential of the polymer measures the amount of work required to bring a polymer from the bulk solution into the surface. Actually, because the system is incompressibly the chemical potential is an exchange chemical potential; the insertion of polymer molecules requires removing water molecules. Thus, when inserting polymers also the free energy cost associated with the formation of polymer-water and the breaking of water-water hydrogen bonds needs to be overcome. Consequently the (exchange) chemical potential of a PEO layer is larger as compared to a non-HB polymer layer. Moreover, like the lateral pressure, the number of hydrogen bonds between polymer segments and water molecules drops with increasing temperature. This makes it easier to insert polymers hence the chemical potential decreases with increasing temperature.

Figure 7.

Chemical potential of the polymer as a function of the surface coverage, for (a) PEO layers and (b) non-HB polymer layers. The solid line corresponds to T = 10°C; the dotted line to T = 20°C and the dashed line to T = 30C°. The molecular weight of the polymer is M_w = 5000.

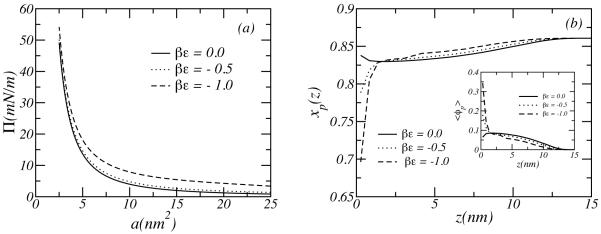
There is ample experimental evidence that PEO adsorbs to hydrophobic surfaces⁶⁵. Namely, there is an effective attraction between the polymer segments and the surface. Different surfaces are characterized by different strengths for the attraction, i.e., ε. It has clearly been shown experimentally and predicted theoretically, that PEO adsorbs to the water-air interfaces^55,66 and the strength of the EO monomer interface attraction is of the order of the thermal energy⁵⁵. To show the role of surface-monomer attraction on the behavior of the layers, Figure 8(a) displays pressure-area isotherms of PEO layers for different surface attraction. The pressure-area isotherms show larger values of the pressures at all areas as the surface-monomer attraction increases. This can be understood by looking at Figure 8(b), where the fraction of polymer-water hydrogen bonds and the polymer density profiles (inset) are shown. The surface attraction increases the monomers of EO close to the interface. This enhanced density results in two effects. One is that the interpolymer repulsions increase and second that the polymer-water hydrogen bonds decreases close to the interface, while it increases at distances away from the surface. Both effects are responsible for the increase in lateral pressure. The dominant effect however, is the increase of polymer local density.

Figure 8.

(a) Lateral pressure-area isotherms of PEO layers on attractive surfaces with different attractive strength. (b) Fraction of PEO-water HB as a function of the distance from the surface. The inset shows the volume fractions of PEO layers. Different curves represent different attraction strength ε: solid line: βε = 0; dotted line: βε = −0.5; dashed line: βε = −1.0. The molecular weight of the polymer is M_w = 5000, the surface coverage is σ = 0.1 nm⁻2, and the temperature is T = 20°C.

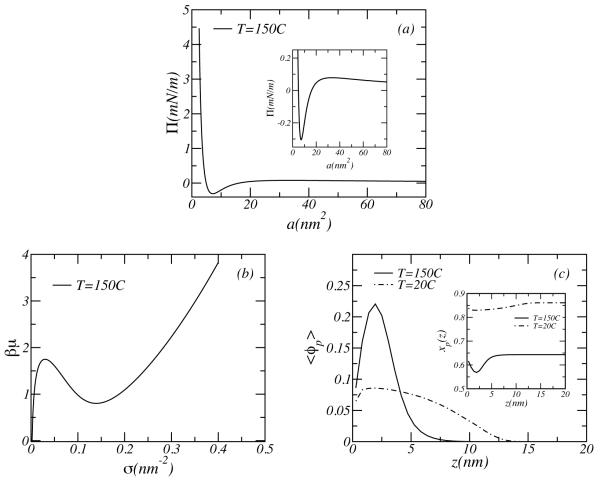
It is well known that PEO solutions present closed-loop phase behavior at high temperatures. The LCST is due to ability of the polymer to form hydrogen bonds and the USCT to the dispersion (Van der Waals) interactions. The theoretical approach developed by Dormidontova³⁸ predicts both with very good agreement with experimental observations. For example, EO solutions with a molecular weight of M_w = 5000 undergo phase separation around T = 130°C for polymer concentrations between approximately 0.0 and 0.5 volume fractions^26,27,38. In the case of tethered polymers however, the situation is rather different. First, experimentally it is very hard to observe phase separation on PEO tethered layers, due to the technical difficulties associated with working at high temperatures with water-air interfaces. Second, in order to tether the polymers to the interface, usually a second polymer block is used. This block is highly hydrophobic and it contributes significantly to the phase behavior^52,55. In order to elucidate what to expect at high temperatures, we have calculated the PEO contribution to the pressure-area isotherms and the PEO chemical potential above the expected LCST of the bulk polymer. This is presented in Figures 9. The shape of the lateral pressure as well as the chemical potential show a clear Van der Waals loop that is characteristic of a phase separated system. This behavior is qualitatively different than the one discussed above for room temperature conditions, see e.g., Fig. 6. The phase separation predicted at these high temperatures is driven by the variation of hydrogen bonds at high temperatures and it is mostly entropically driven. It is interesting to note that the increasing temperature results in a collapse of the PEO layer as can be seen in Figure 9(c). Clearly, the chains at low temperature are highly stretched, while those at high temperature collapse. This is completely due to the role of hydrogen bond in determining the solubility.

Figure 9.

(a) Lateral pressure-area isotherms, and (b) chemical potential versus the surface coverage of the PEO layer at a temperature of T = 150°C. (c) The volume fraction of the PEO layer with a surface coverage of σ = 0.1nm⁻2 at two different temperatures. The solid line corresponds to T = 150°C, and the dashed line is T = 20°C. The inset shows the fraction of PEO-water hydrogen bonds as a function of distance from the surface. The molecular weight of the polymer is M_w = 5000.

As mentioned above, it is hard to directly study the phase behavior of tethered PEO layers. One possibility, to avoid addition of the anchoring block, is to directly graft the polymers to the surface by a chemical bond. In this case however, the fixed grafting prevents phase separation to occur over macroscopic length scales due to the lack of translational degrees of freedom and the system may microphase separate. In those cases the pressure will not show the typical Van der Waals loop, but rather a minimum that indicates negative isothermal compressibility and therefore instability towards lateral microphase segregation⁶². However, the systematic study of the phase behavior of tethered and grafted PEO layers is beyond the scope of this work.

4 Summary and Conclusions

We presented a molecular theory that enables the study of hydrogen bonding between polymers and water (solvent) molecules in inhomogeneous environments. In particular, we studied hydrogen bonding of tethered PEO chains in aqueous solutions. The theory considers both PEO-water and water-water hydrogen bonding and its explicit coupling to the polymer conformations, i.e. the polymer volume fraction. The competition between the two types of hydrogen bonds and the coupling with the polymer concentration is essential for a correct description in inhomogeneous environments of water soluble polymers in general and of PEO in particular. The hydrogen bonding between PEO-water and water-water molecules are both changed from their bulk value, because of the inhomogeneous distribution of the molecules due to the presence of the surface and the polymers tethered to it.

The theoretical approach presented in this work is based on an extension of the molecular theory that we have used to study tethered polymer layers^50,52 combined with a position dependent version of the hydrogen bond treatment done for PEO solutions by Dormidontova³⁸. Our theory couples the conformational degrees of freedom of the chains with the thermodynamic state and the ability to form hydrogen bonds. Furthermore, the position dependent description of the polymer-water and water-water hydrogen bonds enables the study of the large variations of HB fractions as a function of distance from the surface. This effect indicates that an average description may not be enough to properly capture the behavior of hydrogen-bonding polymers in inhomogeneous environments.

We have systematically studied the structural and thermodynamic behavior of PEO layers using the molecular theory. The results are compared with non-HB tethered polymers. PEO and non-HB polymer layers show opposite behavior with respect to temperature changes, for both structural and thermodynamic properties. This opposite temperature dependence is due to the fact that hydrogen bonding is entropically dominated. We have also shown how surface interactions affect the formation of hydrogen bonds. Finally, the collapse of PEO layers and its tendency to phase separate are predicted at high temperatures, consistent with the bulk solution behavior of PEO.

It is important to mention at this point that we have previously predicted quantitatively the properties of end-tethered PEO layers, as compared with experimental observations for thermodynamic and structural properties^53,55 as well as the ability of PEO layers to prevent proteins adsorption^15,52,56. In all those studies however, we have not included the ability of PEO layers to form hydrogen bonds. The reason that the we could properly describe the layers without HB is that we only considered a single temperature and therefore the role of HB was capture in an effective monomer-monomer interaction parameter. The new theoretical approach should enable us to study the role of temperature, hopefully, with the same level of predictive power.

The theoretical approach presented on this work is general and it can be applied to other molecular systems. The changes that need to be made is to have the proper molecular model to generate the conformations of the given polymer chain and also needed are the strength of the interaction parameter and the polymer segment-water HB free energy. For example, poly(N-isopropylacrylamide) (PNIPAM)^67,68 is an interesting system since its LCST is at around 37 degrees, and therefore this molecules have great potential applications in biomaterials. Furthermore, we are considering the role of salt in the properties of hydrogen bonding polymer layers to be able to describe the salting out effect observed in PEO⁶⁹ and PNIPAM⁷⁰.

The molecular approach enables the study of HB, acid-base equilibrium⁶³, ligand-receptor binding⁷¹, electrostatic interactions⁶² and counterion binding⁷² for a rather complete description of polymer molecules in confined environments. However, it is important to emphasize that the theoretical approach it is still based on averaging of the interactions, i.e. it is mean-field approach. The good predictive power of the theory is due to the fact that in most cases that we studied the correlations that are not accounted for by the theory seem not to be the most important contributions determining the behavior of the system. In any case, there are several things that can be done in order to improve the theory. First, we need to develop a systematic way to build the molecular models for different types of molecules. This can be achieved in a systematic way by using bulk molecular dynamic simulations and from them, build the specific coarse grained model for the chains, depending on their chemistry, and their effective interaction parameters, i.e. the free energy of the polymer segment water HB as well as the χ. Second, we need to solve the theory taking into account three dimensional inhomogeneities. We have done steps in this direction^63,73,74 and we plan to extend the approach, in particular to study domain formation and microphase segregation. The improvement of the theory, combined with experimental observations, will enable the molecular design of surfaces modified for a large variety of applications.

5 Appendix

Numerical methodology

Here we present an outline of the numerical method used to solve the equations derived from the molecular theory. A numerical solution for the position dependent osmotic pressure π(z), fraction of polymer-water hydrogen bonds x_p(z) and fraction of water-water hydrogen bonds x_w(z) is obtained by discretization of the packing constraint Eq. (15) and the two equations governing the position dependent hydrogen bond fractions Eq. (21) and Eq. (20). This is done by dividing the z-axis into parallel layers of thickness δ. Functions are assumed to be constant within a layer, hence integrations can be replaced by summations. The i^th layer is defined as the region between (i −1)δ ≤ z < iδ. The packing constraint, Eq. (15), in discrete form for layer i reads

$$\frac{\sigma }{\delta }\underset{\alpha }{\Sigma }P\left(\alpha \right)n(\alpha ,i)v_p+{\varphi }_w\left(i\right)=1$$ (26)

Eqs. (18), (19), (20) and (21) in discrete form are given by

$$\begin{array}{cc}\hfill P\left(\alpha \right)=& \frac{1}{q}\prod _{i=1}^{i=i_{\max }}\exp [-\beta \pi \left(i\right)n(\alpha ,i)v_p-\frac{\chi }{v_w}{\varphi }_w\left(i\right)n(\alpha ,i)v_p\hfill \\ \hfill & -2n(\alpha ,i)\ln (1-x_p\left(i\right))-\beta \epsilon n(\alpha ;1)],\hfill \end{array}$$ (27)

$$\begin{array}{cc}\hfill {\varphi }_w\left(i\right)=& \exp [-\beta \pi \left(i\right)v_w-\frac{\chi }{v_w}{\varphi }_p\left(i\right)v_w-2\ln (1-x_w\left(i\right))\hfill \\ \hfill & -2\ln (1-x_w\left(i\right)-x_p\left(i\right)\frac{{\rho }_p\left(i\right)}{{\rho }_w\left(i\right)})],\hfill \end{array}$$ (28)

$$x_p\left(i\right)=2\exp \left(\beta \Delta F_p\right)(1-x_p\left(i\right))(1-{\varphi }_p\left(i\right))(1-x_w\left(i\right)-x_p\left(i\right)\frac{{\rho }_p\left(i\right)}{{\rho }_w\left(i\right)}),$$ (29)

and

$$x_w\left(i\right)=2\exp \left(\beta \Delta F_w\right)(1-x_w\left(i\right))(1-{\varphi }_p\left(i\right))(1-x_w\left(i\right)-x_p\left(i\right)\frac{{\rho }_p\left(i\right)}{{\rho }_w\left(i\right)}).$$ (30)

where 1 ≤ i ≤ i_max (i_max is the total number of layers considered in the system). Substituting Eqs. (27), (28), (29) and (30) into the constraint equation (26), results in a set of coupled nonlinear equations that are solved by standard numerical methods.

Finally, the chain model, we employ to generate the chain conformations, is a three-state RIS-model⁷⁵. In this model, each bond has three different isoenergetic states. The conformations are generated by a simple sampling method and all are self-avoiding and cannot penetrate into the surface. We generated a set of 2 × 10⁶ independent conformations. The same set of conformations is used in all calculations presented in this paper. The molecular weight of polymer is chosen as M_w = 5000, which corresponds to a degree of polymerization N = 114. Each segment of the polymers has a length l_seg = 0.3 nm, and a volume v_p = 0.065 nm³ which is chosen according to the partial molar volume of PEO in water⁷⁶. The volume of a water molecule is v_w = 0.03 nm³. The interaction parameter is fixed at χ = 100/T. The layer thickness is δ = 0.5 nm, which is sufficient to obtain accurate solutions for the given set of equations.