A sequence-compatible amount of native burial information is sufficient for determining the structure of small globular proteins

Abstract

Protein tertiary structures are known to be encoded in amino acid sequences, but the problem of structure prediction from sequence continues to be a challenge. With this question in mind, recent simulations have shown that atomic burials, as expressed by atom distances to the molecular geometrical center, are sufficiently informative for determining native conformations of small globular proteins. Here we use a simple computational experiment to estimate the amount of this required burial information and find it to be surprisingly small, actually comparable with the stringent limit imposed by sequence statistics. Atomic burials appear to satisfy, therefore, minimal requirements for a putative dominating property in the folding code because they provide an amount of information sufficiently large for structural determination but, at the same time, sufficiently small to be encodable in sequences. In a simple analogy with human communication, atomic burials could correspond to the actual “language” encoded in the amino acid “script” from which the complexity of native conformations is recovered during the folding process.

During the last two decades, a physical picture of the folding process has emerged with the advent of energy landscape theory (1–5) but, despite many recent advances, a general solution to the problem of structure prediction from sequence has remained elusive. Most attempts in this direction have assumed sequences to encode partial information about many structural properties, such as likelihood of tertiary contacts or secondary structure propensities, that could eventually be combined to provide a general predictive algorithm (6–10). An alternative scheme would assume a single (or few) conformational property to be directly encoded in sequences, resulting in a small number of sequence-dependent parameters, whereas other conformational features would arise from sequence-independent constraints. The importance of such constraints has been recently emphasized by Banavar and collaborators (11).

The amount of information provided by a putative single property dominating the code should satisfy two conditions: It should be sufficiently large for structural determination but sufficiently small for being encodable in sequences (12). The widely recognized importance of hydrophobic interactions on protein structure formation (13, 14) suggests atomic burials to constitute a natural candidate for this putative dominant property. There has been some discussion, in the simplified context of lattice models, on the possibility that intrinsically unspecific hydrophobicity could satisfy the first condition (15), including a dependence on the choice of native conformation (16, 17). Encouraging results from recent Monte Carlo simulations, on the other hand, indicate that the first condition is satisfied by atomic burials, as measured by distances from the molecular geometrical center, for small globular proteins represented by off-lattice, geometrically realistic, all-heavy-atom models (12). In the present study, we estimate the amount of this required burial information and suggest that the second condition may also be satisfied.

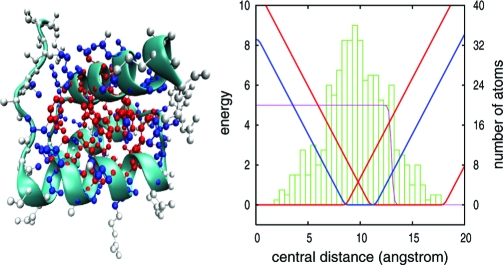
We perform molecular dynamics simulations of an all-heavy-atom protein model with a chosen number of natively constrained central distances in order to enforce the burial condition. Each atom i receives information about the native structure in the form of a radial force toward the center of a flat-bottomed, spherically symmetric, burial-potential well. The total distribution of central distances is divided in a chosen number L of equiprobable disjoint “layers”. Every atom in each layer is governed by the same burial potential centered at r_i*±δ_i, whose native-dependent parameters are the layer-central distance and width, respectively. Simulations were performed for L = 10, L = 5, L = 3 and L = 2. The limiting case of exact burials (r_i* = r_i^nat, δ_i = 0) was also investigated. An upper bound, in bits/atom, for the provided information (18, 19) is log₂(L). The actual value must be smaller because of unavoidable correlations between burials in a chain of covalently linked atoms. Viable compact conformations are enforced by native-independent additional constraints in the form of geometrically realistic covalent bonds, atomic excluded volume, side-chain chirality, and a strong penalty for backbone oxygen and nitrogen atoms to be buried unless geometrically defined hydrogen bonds are formed, independently of partners. The general procedure is described in the Materials and Methods section and summarized in Fig. 1.

Fig. 1.

Description of the computational experiment. The plot on the Right shows the histogram of the actual burial distribution for 1ENH. Burial-potential wells used for the simulations with three layers, L = 3, are shown in red (inner and outer layers) and blue (middle layer). Atoms in each of these layers are shown in red, blue, and white in the schematic representation on the Left. Note that the layers have different thickness, δ_i, in order to accommodate the same number of atoms. Energies are measured in units of the simulation temperature. The slope of the nonflat region of the potential determines the burial force modulus, k_i, which varies during the simulation. All backbone oxygen and nitrogen atoms receive an energetic penalty when getting closer to the geometrical center without forming a hydrogen bond, shown by the step-like curve (purple). Hydrogen bond formation is quantified for all combinations of donors (nitrogen) and acceptors (oxygen) from the concomitant satisfaction of three geometrical requirements: N–O distance h < 3.0 Å, angle with N–H bond θ < 0.5 rad and angle with C=O bond η < 0.6 rad.

Results and Discussion

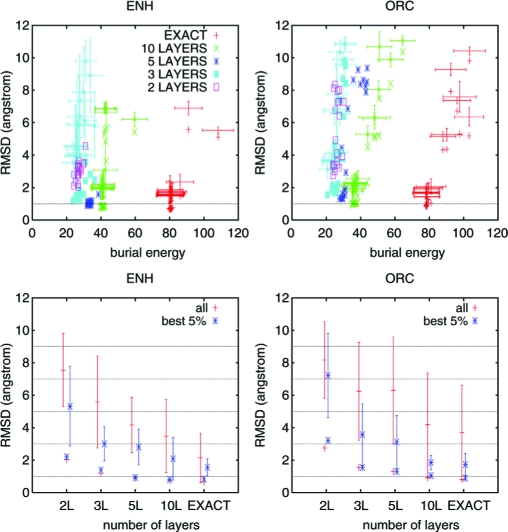
The Upper Left frame of Fig. 2 shows results for the small α-helical engrailed homeodomain [Protein Data Bank (PDB) code 1ENH]. Conformations with C_α root mean square deviation, (RMSD), from the PDB file smaller than 1 Å are sampled in the majority of trajectories when exact or L = 10 burials are used. Minimal RMSDs are around 1 Å for L = 5, between 1 Å and 2 Å for L = 3, and between 2 Å and 4 Å for L = 2. Conformations clearly similar to the PDB structure are therefore sampled even for L = 2, whereas virtually native conformations are sampled for L ≥ 3. When a sufficiently large amount of information is provided, most trajectories are actually uniformly close to the native structure. This closeness is apparent from the the small average RMSD and corresponding standard deviation for exact burials and L = 10. When the amount of provided information is reduced, the behavior of different trajectories is less uniform, and RMSD averages become significantly larger than their minimal values (for example L = 3). In the low-information regime, information increase is reflected almost completely on a decrease of RMSD and almost no change in the average burial energy. In the high-information regime, on the other hand, burial-energy increase is the major response to additional provided information.

Fig. 2.

Results for two small globular proteins. Several long trajectories were performed for all- α 1ENH (Left) and α+β 1ORC (Right). Both proteins were previously investigated in a recent Monte Carlo study (12). Temperature was kept constant while burial force modulus for all atoms, k_i, was gradually increased from k_i = 0 to k_i = 1, in energy units per angstrom. All other energy parameters were kept constant. The initial conformation is a completely extended structure generated with the program MOLMOL (27) by using standard residue and peptide geometries. Present analysis is restricted to trajectories corresponding to final conformations of each simulation (0.9 ≤ k_i ≤ 1.0). Minimal RMSD values observed in these final conformations, as a function of average trajectory burial energy, are shown in the upper plots. Different colors are used for each group of trajectories: exact, L = 10, L = 5, L = 3, and L = 2. For clarity, average RMSD as a function of average burial energy, with respective standard deviations plotted as error bars, are shown only for the exact, L = 10, and L = 3 groups. Lower plots show average RMSD and corresponding standard deviation as a function of provided information for all conformations in each group, independent of specific trajectory. The same quantities are also shown for the subgroup with the 5 % lowest burial energy. Minimal values in each group are shown by single points. The final value of k_i = 1 determines the effective half-width of each potential well, due to thermal fluctuations, to be ≈δ_i + 1 Å at the simulation temperature, which results in a stable native structure for exact burials. The effective cooling rate provided by its gradual increase is sufficiently slow to result in successful folding in these conditions for around 90% of trajectories for the α-helical 1ENH, as shown in the Upper Left frame. A lower fraction of successful trajectories for 1ORC under identical conditions, as seen in the Upper Right frame, results from slower overall kinetics for the α+β protein.

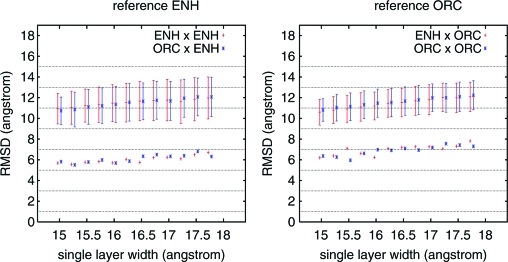
An apparent correlation between RMSD and average burial energy suggests that a simple-selection criterium based on burial energy could eventually improve structural predictions. For the small α-helical engrailed homeodomain, this expectation is corroborated by the Lower Left frame of Fig. 2. This frame compares the average RMSD over all conformations in each group, independent of trajectory, to the same quantity restricted to the subgroup with the lowest 5 % burial energy. The lowest-energy subgroups reflect more closely the general behavior of minimal RMSD values. This is true even if the actual global RMSD minimum is not in this subgroup. For L = 3, for example, although the overall average lies between the overall averages for L = 5 and L = 2, the lowest energy subgroup and minimal RMSD are very similar to the corresponding values for L = 5 and much smaller than for L = 2. These results suggest that the minimal amount of provided information required to recover identifiable native-like conformations lies somewhere between L = 2 and L = 3. The Right frames of Fig. 2 show analogous results, with exactly the same parameters for all native-independent constraints, for the α+β monomeric version of the cro factor (PDB code 1ORC). These additional results suggest that this surprisingly small amount of required information is not an exclusive property of simple α-helical domains. In negative controls shown in Fig. 3 for both proteins, with all atoms subjected to identical burial potentials shaped as a single, central well with width ranging from 15–18 Å, average and minimal RMSDs never go below 10 Å and 5 Å, respectively. Furthermore, as shown in the same figure, no specific structural information appears to be provided by the sequence-specific excluded volume interactions present in these simulations, as indicated by similar RMSDs for 1ENH and 1ORC trajectories with respect both to 1ENH and 1ORC native structures.

Fig. 3.

Results for a single layer, L = 1. Long trajectories were also performed for 1ENH and 1ORC with a single burial layer, L = 1, to explore the effect of simple compaction on structure formation with no native-dependent burial information. Both the temperature and force modulus k_i = 1.0 were kept constant during these simulations. The width of the single layer was different in each trajectory, ranging from 15–18 Å. Average C_α RMSD, corresponding standard deviations for each 1ENH trajectory (red) and 1ORC trajectory (blue), with respect to both 1ENH PDB file (Right) and 1ORC PDB file (Left), are shown with error bars, and minimal value are shown by single points.

In order to compare our results with the information of amino acid sequences, we estimate the actual amount of provided burial information by its corresponding Shannon entropy (18, 19) for different numbers of layers, H_L(B), in bits/residue. Because burial correlations between covalently linked atoms are present, smaller values than the maximal H_L^max(B) = log₂(L) bits/atom can be anticipated. Furthermore, an expected increase in the correlation range with protein globule size suggests a possible dependence of provided information on chain length. Fig. 4 shows entropy estimates obtained from burial frequencies in a set of small (between 50 and 100 residues) globular proteins. In this kind of analysis [e.g. Brenner and collaborators (20)], we compute entropies for “fragments”, or “blocks”, from sequences of burials of linearly connected atoms and estimate the entropy per atom from the resulting dependence on block size. The entropy per backbone atom is computed from burials of linearly connected backbone atoms. Nitrogens, α-carbons, and carbonyl carbons are considered indistinguishable. Assuming correlations along the backbone direction to be on average similar to correlations along side-chain directions, we then estimate the entropy per residue simply by multiplying the backbone value by the average number of atoms per residue.

Fig. 4.

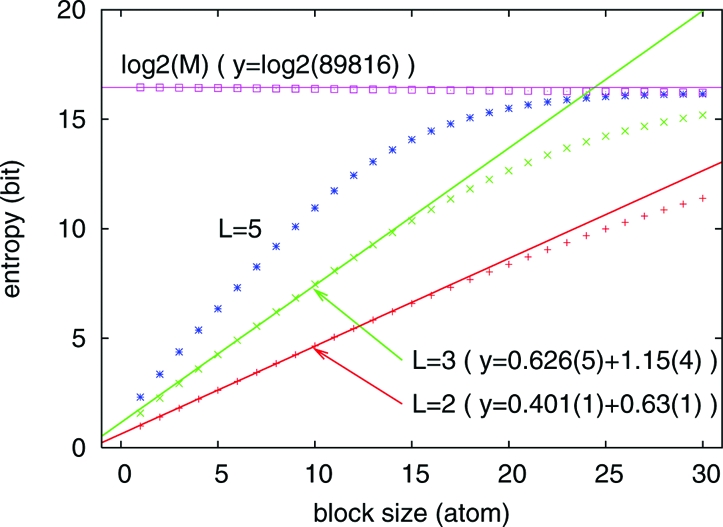
Shannon entropies for blocks of burials of linearly connected backbone atoms. Short range (along the chain) correlations are reflected in the deviation from linearity for small blocks. Deviation from linearity for large blocks is an artifact from the finite size of the data bank that imposes an upper limit for the estimated entropy of log₂(M) (purple points), where M is the total number of blocks in the bank. M becomes slightly smaller than the total number of residues (89,816) for larger blocks because of chain-length effects. This decrease in the number of blocks is noticed by the slight deviation of the purple points from the horizontal purple line. Entropies per atom are obtained from linear fits to regions of intermediate block sizes (4 to 14) for L = 3 and L = 2. Fitted equations are shown with the uncertainty on the last significant digit of each coefficient in parenthesis. Entropies per residue are obtained by a simple multiplication of the adjusted slopes by the average number of atoms per residue, taken as 7.8.

Block entropies for L = 2, L = 3, and L = 5 are shown in Fig. 4 for our set of small proteins. An appropriate chain size range varying between 50 and 100 residues was used. Measuring the slope of the linear fits to regions with intermediate block sizes, we determine backbone entropies to be H₂(B) ≈ 0.4 and H₃(B) ≈ 0.6 bits/atom, or H₂(B) ≈ 3.1 and H₃(B) ≈ 4.7 bits/residue. These values can now be compared with the entropy of protein sequences H(Q) ≈ 4.2 bits/residue (20, 21). It must be noted that the actual amount of structural information obtainable from sequences is not given by sequence entropy itself but by the somewhat smaller mutual information between sequences and structures (18, 19). Although this difference has not been estimated, evidence for its significance comes from several empirical observations. For example, many sequences fold into the same 3D structure (22, 23), and also, foldable chains can be constructed from reduced amino acid alphabets (24–26). Even considering a reasonable, more restrictive value—like something around 3 bits/residues—together with unavoidable uncertainties on all estimates, burial and sequence entropies are found to be strikingly similar. Furthermore, our values for required burial information must be considered as upper estimates because future improvements on native-independent model constraints cannot be ruled out.

These surprising results not only confirm that native conformations are recoverable from burial information alone, but they also indicate that the required amount of information could be sufficiently small to be encoded by the linear sequence of amino acids. Other conformational properties, such as secondary structures or even pairwise contact interactions, would arise as a consequence of crucial but sequence-independent constraints. The resulting connection between burials and sequence suggests a simple analogy with human communication. Atomic burials could correspond to the actual “language” directly encoded in the “script” of amino acids. Specific atomic burials would constitute the “literature” transmitted by sequences whereas other conformational properties would arise from the “grammar” governing the language. The practical prediction problem could in principle be solved by a sequence-dependent, probably knowledge-based, potential capable of “reading” burial patterns in the amino acid script. Sequence-independent constraints, similar to the native-independent terms used in the present study, would convert burials into a 3D structure, “speaking” the protein folding burial language.

Materials and Methods

We perform standard molecular dynamics simulations of an all-heavy-atom protein model. Native-independent standard constraints are enforced by harmonic potentials on distances, angles, rigid dihedrals (in peptide bonds and aromatic rings), and side-chain chirality. Minima positions are taken from an extended conformation generated with program MOLMOL (27), by using standard residue and peptide geometries. The side-chain chiral angle is always constrained to 2.5 rad. Excluded volumes arise from a repulsive potential for distances smaller than 2.5 Å between any pair of atoms except for C_β and backbone O atoms, in which case a larger distance of 3.0 Å is used. All simulations were performed with an adaptation of the molecular dynamics program previously used with structure-based models (28). Nonstandard terms, detailed below, correspond to the native-dependent atomic burial potential and to additional native-independent constraints resulting from hydrogen bond formation.

Native-Dependent Atomic Burial Potential.

Different atoms i contribute to the potential energy function with a simple burial term that depends on its central distance, E_i^bur(r), attaining its minimal value of zero everywhere inside the 2δ_i long interval (r_i*−δ_i,r_i* + δ_i) and increasing linearly outside this interval with slope ±k_i, except for small quadratic sections of length δ_q required to maintain differentiability at every point, including r = 0:

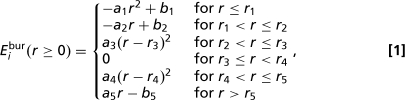with atom-dependent r₁,…,r₅,a₁,…,a₅,b₁,b₂,b₅ ≥ 0 defined in terms of r_i*, δ_i, k_i and δ_q. Usually, therefore, r_i*−r₃ = r₄ − r_i* = δ_i, r₁ = r₃ − r₂ = r₅ − r₄ = δ_q and a₂ = a₅ = k_i, and remaining terms are obtained from continuity and differentiability requirements. For sufficiently small values of r_i*, appropriate modifications of r₁, r₂, r₃, and a₂ might also be necessary. In the present study, we divide the total distribution of central distances in a chosen number L of equiprobable disjoint “layers” and assign to every atom in each layer the same r_i* and δ_i values, given respectively by the central position and half-width of the layer. We use L = 10, L = 5, L = 3, and L = 2 layers, in addition to the limiting cases of L = 1, corresponding to simple compaction with no native-dependent burial information, and of exact burial (r_i* = r_i^nat and δ_i = 0), which is the continuous function corresponding to the burial potential of ref. 12. k_i for all atoms gradually increases during the simulation from 0 to 1, in energy units per angstrom, where the energy unit is defined by the constant temperature of the simulation, except for L = 1, in which case k_i was kept constant at 1. We have used δ_q = 0.5 Å. Fig. 1 shows the three final burial-energy wells used for simulations with three layers, L = 3, superimposed to the actual burial distribution.

Native-Independent Hydrogen Bonds.

For each of the N₁ × N₂ combinations of N₁ possible donors and N₂ possible acceptors, we have a putative hydrogen bond quantified by the product of three Fermi functions

with F(α) = 1/(1 + exp(β_α(α−μ_α))), which changes abruptly but continuousy from 1 to 0 as any of three controlling variables exceeds a specific threshold. These three controlling variables are computed from the coordinates $\{\overrightarrow{r_1},\dots ,\overrightarrow{r_5}\}$ of the following five atoms: the acceptor carbonyl oxygen, the donor nitrogen, the two atoms adjacent to this nitrogen, and the carbon adjacent to the acceptor oxygen, in this order. These coordinates define three convenient vectors: $\overrightarrow{v_1}=\overrightarrow{r_2}-\overrightarrow{r_1}$, $\overrightarrow{v_2}=\overrightarrow{r_3}+\overrightarrow{r_4}-2\overrightarrow{r_2}$, and $\overrightarrow{v_3}=\overrightarrow{r_1}-\overrightarrow{r_5}$. In terms of these vectors, $h=\left|\overrightarrow{v_1}\right|=\sqrt{{(v_1^x)}^2+{(v_1^y)}^2+{(v_1^z)}^2}$ is the norm of $\overrightarrow{v_1}$, η is the angle between $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$, or $\cos \eta =(\overrightarrow{v_1}\cdot \overrightarrow{v_2})/(\left|\overrightarrow{v_1}\right|\left|\overrightarrow{v_2}\right|)$, and θ is the angle between $\overrightarrow{v_1}$ and $\overrightarrow{v_3}$ or $\cos \theta =(\overrightarrow{v_1}\cdot \overrightarrow{v_3})/(\left|\overrightarrow{v_1}\right|\left|\overrightarrow{v_3}\right|)$. In the present study, the energetic contributions of the donor and acceptor in a given hydrogen bond is allowed to depend explicitly on their coordinates $\overrightarrow{r_i}$, in addition to λ, as

In the present scheme, therefore, hydrogen bond formation does not result in a simple decrease in energy because it is only within a region around the center, defined by the inflection position of the Fermi function F(r), that it is unfavorable for potential donors and acceptors not to form hydrogen bonds. The resulting continuous dependence on local geometry and global burial is similar in spirit to previous discrete environment-dependent hydrogen bond models (12, 29), which are motivated by the increased probability for exposed groups of hydrogen bond formation with the solvent. We have used ɛ_hb = 10, μ_r = 13 Å and β_r = 10 Å ⁻¹, with the resulting penalty function shown in Fig. 1 superimposed to the actual burial-distribution and burial-potential wells. All backbone nitrogen and oxygen atoms were considered possible hydrogen bond donors and acceptors, respectively. The same parameters were used for all putative bonds: ɛ_h = 3 Å, β_h = 100 Å ⁻¹, ɛ_η = 0.5 rad, β_η = 100 rad ⁻¹, ɛ_θ = 0.6 rad, and β_θ = 100 rad ⁻¹.

Computation of Burial Entropies.

Shannon entropies for burial blocks of size N, or N-blocks, of linearly connected backbone atoms for a given number of layers L, H_L(B^N) are computed from the basic Shannon entropy equation (18, 19):

where the probabilities P_L(B^N) of different N -blocks, for given number of layers L, are estimated from their frequencies in the data bank. Frequencies were computed in a set of 392 small globular proteins, with sizes varying between N = 50 and N = 100 residues, derived from a recent release (November 2008) of the PDBSLECT database (30). Globular structures were selected from the condition $R_g/\sqrt[3]{N}<2.9$ Å (31). Because the probability for any burial level at each position in the N-block is simply 1/L, statistical independence between burials at different positions would result in equal block probabilities of (1/L)^N, and the block entropy would reduce to its maximal value Nlog₂(L). The entropy per atom or entropy density, H_L(B), formally corresponds to the limit of the ratio between block entropy and block length as length increases (18, 19):

In the present study, this ratio is estimated from the slope of H_L(B^N) as a function of N for intermediate values of N, as shown in Fig. 4, to avoid artifacts from the finite size of the data bank on probability and entropy estimates for large N. Correlations between burials, as expected in a chain of connected atoms, are reflected in smaller block entropies and reduced entropy density when compared with the maximal value corresponding to uncorrelated burials, or H_L^max(B) = log₂(L) bits/atom.