Abstract
We describe here the use of several spectroscopies, such as fluorescence emission, circular dichroism, and differential quenching by acrylamide, in examining the equilibrium and kinetic folding of proteins. The first section regarding equilibrium techniques provides practical information for determining the conformational stability of a protein. In addition, several equilibrium-folding models are discussed, from two-state monomer to four-state homodimer, providing a comprehensive protocol for interpretation of folding curves. The second section focuses on the experimental design and interpretation of kinetic data, such as burst-phase analysis and exponential fits, used in elucidating kinetic folding pathways. In addition, simulation programs are used routinely to support folding models generated by kinetic experiments, and the fundamentals of simulations are covered.
1. Introduction
Protein folding is a central theme in structural biochemistry and in biotechnology. While the forces that stabilize protein structure have been examined for more than one hundred years (Clark, 2008), protein chemists still are unable to predict the native structure of a protein from a known amino acid sequence. Under physiological conditions, proteins exist in equilibrium between ensembles of unfolded states (U) and native states (N), where each ensemble is characterized by a closely related set of structures that fluctuate around a local (or global) energy minimum. Protein function depends on attaining the native conformation. While the forces that drive proteins to adopt their native conformations are, in general, defined as the difference between the unfavorable chain entropy and the favorable enthalpic interactions, the stability of protein native structures can vary drastically. Moreover, the kinetic pathway a protein utilizes to adopt its native conformation can vary from a relatively simple two-state process, where only the native and unfolded ensembles are populated significantly, to more complex reactions in which the structure passes through one or more nonnative, partially folded intermediates before reaching the native conformation. It has been well documented that the pathways can be sequential, in which the intermediates are found between the unfolded and native ensembles, or parallel, in which multiple intermediates form simultaneously and eventually coalesce to the native ensemble (Wallace and Matthews, 2002). In addition, not all intermediates lead to the native conformation but rather can lead to misfolded, or off-pathway, structures (Ikai and Tanford, 1971). Finally, proteins have been shown to fold over a wide range of time regimes, from microseconds to hours (Creighton, 1990). Consequently, characterizing the kinetic and thermodynamic folding of proteins can be a daunting task. However, the benefits to understanding the folding process can prove invaluable, for example, in revealing motifs or regions of the protein that are critical to function, as potential drug targets, or in determining the mechanisms for protein misfolding or aggregation (Cohen and Kelly, 2003; Soto, 2003)
Outlined in this chapter is practical information for characterizing the thermodynamic and kinetic folding properties of a protein by exploiting intrinsic probes such as fluorescence emission and circular dichroism. One should note other excellent sources that describe the use of extrinsic probes in protein folding (Lakowicz, 2006; Weber, 1951; Waggoner, 1995). Fluorescence techniques are extremely useful for this application, and the advantages of fluorescence emission over other techniques make it an attractive method to examine protein tertiary structure. These include high sensitivity, the use of low protein concentrations, the ability to selectively monitor regions or motifs within a protein, and the use of a multitude of solution conditions (Eftink, 2000). Circular dichroism also is employed to examine the protein secondary structure and/or tertiary structure during unfolding and refolding and to validate the findings from the fluorescence emission experiments. While proteins can be unfolded using a variety of agents, the focus here is on a well-identified chaotrope, urea. The equilibrium-unfolding studies described here allow for the calculation of the conformational free energy, revealing the stability of the native conformation and intermediates (where applicable). The kinetic techniques aid in deciphering the folding pathway and in examining intermediates that may not be detectable in equilibrium experiments.
This chapter aims to provide a comprehensive protocol for examining the thermodynamic and kinetic folding properties of simple systems, so-called two-state, as well as more complex systems where multiple intermediates are present. More complex analyses for parsing the conformational free energy into component parts (entropy, enthalpy, heat capacity) as well as studies of the transition state can be found elsewhere (Dill, 1990; Privalov, 1989; Royer, 2008). Often, it is of interest to examine the conformational stability not only of wild-type proteins but also of mutants or other proteins that differ slightly in structure. This type of analysis can be useful in comparing proteins within the same family or comparing structural motifs in general. Such studies have revealed critical residues and regions of proteins that make significant contributions to the overall stability (Wilson and Wittung-Stafshede, 2005). The protocols outlined in this chapter also are useful for comparing multiple proteins in a family.
2. Equilibrium Unfolding
2.1. Practical considerations
Equilibrium unfolding is the process of disrupting the protein’s native structure in favor of the unfolded ensemble by increasing the concentration of denaturant, either urea or guanidinium hydrochloride, GdmHCl, in a stepwise manner such that the protein reaches a balance between native and unfolded conformations. For this discussion, urea will be used as the denaturant; however, similar methodologies apply when using GdmHCl (to further investigate the properties and advantages and disadvantages of urea and GdmHCl, see Pace, 1986). Increased temperature is another common technique used to induce unfolding. While the protocol is not outlined here, a thorough description of the technique and data analysis exists elsewhere (Pace and Sholtz, 1997; Pace et al., 2005). There are many factors to consider prior to setting up folding reactions and taking measurements. Is unfolding reversible? That is, do the unfolding and refolding data overlay to validate reversibility? This is important because the experiments yield thermodynamic information on the stability of the protein. Is the folding reaction equilibrated? Because equilibrium experiments are being performed, sufficient time must be given to allow each reaction to come to equilibrium. It is common for proteins, even single-point mutants, to vary greatly in equilibration times. While there are various methods for determining equilibration times, two are described subsequently. Other factors to consider include incubation temperature, the use of reductants, and the number of aromatic side chains in the protein. Temperature must be considered carefully, as the time required for the reaction to equilibrate can be temperature dependent (Pace, 1986). The experiments described here include the addition of 1 mM reducing agent because of the presence of free sulfhydryl groups and the possibility of forming disulfide bonds. We use dithiothreitol (DTT) routinely, but it is important to note that DTT degrades quickly. Therefore, if long incubation times are required (more than 24 h), then β-mercaptoethanol or tris(2-carboxyethyl)phosphine (TCEP) would serve well (Zahler and Cleland, 1968). If free sulfhydryls are not an issue, the reducing agent can be left out.
It is very important to obtain an accurate determination of the protein concentration because fluorescence emission is a sensitive technique. If the extinction coefficient is known for the protein of interest, the concentration of the native stock can be readily obtained by measuring the absorbance of the protein at 280 nm. If the extinction coefficient is unknown, then the protocol outlined by Pace and Schmid (1997) explains in great detail how to determine this parameter. The concentration of the protein required for equilibrium unfolding experiments is typically in the low micromolar range but depends on the number of aromatic residues present in the protein. Protein fluorescence emission is dominated by tryptophans and tyrosines because of their high quantum yield at the wavelength of excitation (Schmid, 1997).
Finally, there are a variety of buffers that one may use for fluorescence and CD measurements. The absorbance properties of the buffer must be taken into consideration to assure that it does not absorb in the spectral region of the protein. Buffer blanks (the sample without protein) should be scanned with each experiment and subtracted from the protein sample to remove artifacts that may be introduced by the buffer and urea.
Typically, the following steps are used to set up an equilibrium-unfolding experiment, and several steps are described in detail subsequently.
Prepare 10 M urea stock.
Confirm that the protein is completely unfolded.
Optimize instrument settings using native and unfolded protein in their respective buffers.
Set up unfolding and refolding samples in varying concentrations of denaturant.
Establish equilibration times and reversibility.
Perform equilibrium-unfolding and equilibrium-refolding experiments.
Repeat experiments at different protein concentrations as needed.
2.2. Instrumentation
For the studies described here, fluorescence emission is measured using a PTI C-61 spectrofluorometer (Photon Technology International, Birmingham, NJ), and circular dichroism is measured using a PiStar spectropolarimeter (Applied Photophysics, Surrey, UK). Both instruments are equipped with water jackets to maintain a constant temperature during the experiment. It is useful to monitor unfolding by different techniques because intermediates not revealed by one technique may appear using another. In general, if the equilibrium-unfolding curves from multiple techniques coincide, then the data from one technique is sufficient to determine the conformational free energy. Conversely, deviation in the unfolding curves, or noncoincidence of the data, from one technique to another implies intermediates are present under equilibrium conditions. General parameters and considerations for each technique are listed below. Note that quality quartz cuvettes are used in both techniques.
2.2.1. Fluorescence emission
Certain features can be instrument and/or software specific; however, the same general parameters apply to the setup regardless of the instrument used. Adjustment of the slit width allows only the desired amount of light to enter the sample chamber and/or detector and, in part, determines the signal-to-noise ratio. Protein concentration will have the greatest effect on this setting. The reader is referred to the manufacturers’ guidelines for setting slit widths. Emission scans are acquired between 300 nm and 400 nm, following excitation at 280 nm and at 295 nm. The former provides information on the environmental changes of both tryptophan and tyrosine side chains due to the absorption wavelengths of both amino acids (280 nm and 275 nm, respectively). The latter provides a method to follow tryptophan emission selectively because there is little absorbance of tyrosines at 295 nm (Lackowicz, 2006).
In general, there are two methods for collecting equilibrium unfolding data using fluorescence emission. In the first, one will obtain an emission spectrum for the native and unfolded samples (described subsequently). Then one will choose a single wavelength that provides the largest difference in the two samples (Fig. 1.1A). In subsequent experiments, one will examine fluorescence emission intensity at the prescribed wavelength versus urea, where the signal typically is averaged for 30 s. In the second method, one will obtain an emission spectrum at each concentration of denaturant and calculate the average emission wavelength (AEW) for each sample (Royer et al., 1993). A description of the advantages and disadvantages of using AEW is provided by Eftink (1994).
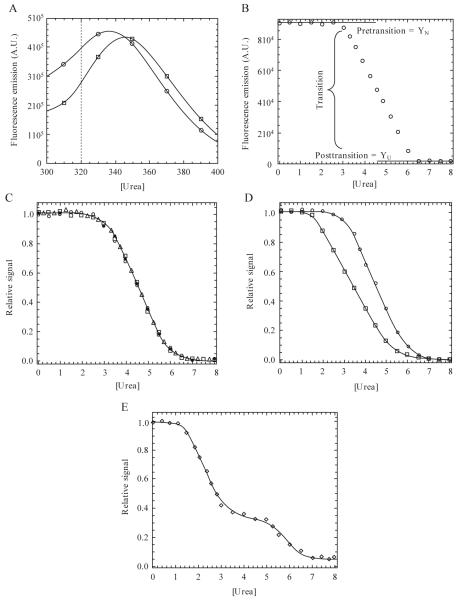
Figure 1.1.
(A) Emission spectra following excitation at 280 nm. Data for 0 M (○) and 8 M (□) urea are shown. In this example, the dotted line indicates a wavelength at which unfolding may be monitored due to a large difference in signal between the native and unfolded protein. (B) Equilibrium unfolding curve monitored by fluorescence emission at 320 nm (excitation at 280 nm). The pretransition, transition, and posttransition regions are indicated. (C) Normalized data demonstrating three probes used in the unfolding experiments. Unfolding was monitored by fluorescence emission following excitation at 280 nm (○) or 295 nm (□) or by CD (Δ). Refolded protein (●) demonstrates reversibility. (D) Noncoincidence of the unfolding curves when monitored by different spectroscopic techniques, suggesting a more complex folding mechanism than the two-state model suggested by a single technique. (E) Example of a three-state equilibrium-unfolding curve. Continuous lines in panels C-E represent fits of the data either to a two-state (panels C and D) or three-state (panel E) monomer unfolding model as described in the text.
2.2.2. Circular dichroism
Secondary structure is monitored during unfolding by CD. Minima at 208 nm and 222 nm indicate α-helical structure, whereas a minimum at 217 nm is characteristic of β-sheet (Woody, 1995). Circular dichroism is strongest at the aforementioned wavelengths; however, light scattering by buffer components may require monitoring CD at somewhat higher wavelengths. We routinely monitor CD at 228 nm, which allows for detection of secondary structural changes in urea while avoiding amplification of the voltage at higher denaturant concentrations. As described previously for fluorescence emission, however, one should determine the wavelength that provides the greatest difference in signal between the native and unfolded protein samples. Slit width and scanning speeds should be adjusted according to the manufacturers’ specifications.
2.3. Preparation of 10 M urea stock
This protocol, adapted from the method described by Pace (1986), describes the preparation of 100 mL of 10 M urea stock containing 50 mM potassium phosphate buffer, pH 7.5. One should use an analytical balance that measures accurately to ± 0.1 mg. Potassium phosphate buffer is prepared separately in a volumetric flask (100 mL) using the chemicals in step 1 below and distilled, deionized water.
Separately weigh 191 mg of potassium phosphate monobasic, KH2PO4, and 650 mg of dibasic, anhydrous dipotassium hydrogen phosphate, K2HPO4, on weigh paper.
Weigh 60.0 g of ultra pure urea (purity >99%) in a weigh boat.
Combine both phosphates in a beaker with a minimum capacity of 200 mL; add a clean, dry stir bar; place on a scale and tare. Add the urea into the beaker and record the weight.
Add distilled, deionized water into the beaker to a weight of 114.6 g. Record the weight.
Cover the beaker and stir until the urea dissolves. One should expect this to take 3 to 4 h.
When dissolved, check the pH using a recently calibrated pH meter. If the pH needs to be adjusted, then correct to pH 7.5, accordingly.
Filter before use.
Once the urea stock is prepared, the molarity is determined based on the recorded weights from steps 3 and 4 and from the refractive index, as described by Pace (1986). If the difference in the calculated molarity from each method is less than 10%, then the urea may be used. If it is greater than 10%, then the urea must be prepared again. Upon completion, the urea may be stored at -80 °C until used. A reducing agent such as DTT is added from a stock solution to the buffer and urea just prior to use. Methods for making stock urea in other buffers is described by Pace and Scholtz (1997).
2.4. Confirm that the protein is completely unfolded
Before starting an equilibrium unfolding experiment, it is important to confirm that the unfolded sample has reached equilibrium and that the protein is completely unfolded, because many of the experiments begin with the unfolded protein. If insufficient time is allowed for the protein to unfold, or if one uses too low a denaturant concentration to fully unfold the protein, then subsequent experiments would begin with a species other than the unfolded state, and the data may be incorrect.
To confirm the protein is completely unfolded after a certain incubation period, add native protein to 8 M urea-containing buffer, as shown subsequently, so that the final protein concentration is 1 μM and the final volume is 1 mL.
Urea (800 μL of 10 M urea stock)
DTT (10 μL of a 0.1 M stock)
Buffer (185 μL)
Native protein (5 μL of a 200 μM stock)
A second sample should be prepared in which the urea is replaced with buffer. Take a fluorescence emission scan from 300-400 nm of the native protein (no urea) and of the unfolding sample. Place the samples back in the reaction tube and incubate at the desired temperature (typically 25 °C) for 10 min. Take a second emission scan of the unfolded protein. Repeat this process until no change in signal is observed. If the protein is resistant to chemical denaturation, longer incubation times may be required between scans. Also, it is recommended that an additional scan be taken after the sample has incubated in urea for 24 h. One considers the protein equilibrated when no further signal change is observed. Depending on the protein, one might expect a red shift in the emission peak of unfolded protein with respect to the native protein (Fig. 1.1A), which shows that the protein tertiary structure is disrupted by the denaturant.
In separate experiments, the samples should be excited at 280 nm and at 295 nm, as described previously. Also, one should verify the results using CD to examine changes in secondary structure. Repeat the experiments as described above until no further change in CD is observed.
Finally, the fluorescence and CD experiments should be repeated at several final urea concentrations in order to determine the concentration of urea that is sufficient to unfold the protein. The example shown here uses 8 M urea-containing buffer, but the protein may unfold at much lower urea concentrations. Conversely, if the protein does not unfold fully at high urea concentrations (≈9 M), then one should use a different denaturant, such as GdmHCl.
2.5. Establishing equilibration times and reversibility for folding reactions
2.5.1. Method 1
This protocol would serve well when no prior information on the folding of the protein of interest is available. The main purpose of this experiment is to determine the amount of time required to equilibrate the protein incubated in intermediate concentrations of urea. In general, this method requires one to set up unfolding and refolding samples and to monitor fluorescence emission over time until equilibrium is observed, that is, when the signal from the unfolding and refolding reactions are identical. Similar experiments also should be done using CD, as noted earlier.
The unfolding samples are set up following the protocol shown in Table 1.1. The refolding samples are set up similarly with the exception that the starting material is unfolded protein, as shown in Table 1.2, in 8 M urea-containing buffer. In both cases, the final protein concentration is 1 μM. One should note that the urea in the unfolded protein stock must be accounted for in the setup of the refolding samples. We typically set up the experiments in 2-mL siliconized Eppi tubes to prevent protein from sticking to the tube. All samples should be incubated at the desired temperature in a water bath. Once the unfolding and refolding samples are assembled, fluorescence emission scans are taken for each sample from 300 nm to 400 nm. In separate experiments, the samples are excited at 280 nm and at 295 nm, as described previously. If the signals of the unfolding and refolding samples are identical, then the reaction has reached equilibrium. If the signals differ, then place each sample back in the reaction tube and incubate for longer time periods. Following incubation, take another emission scan, and repeat this process until the unfolding and refolding signals match for each final urea concentration, at which point equilibrium has been reached. As stated previously, equilibration may take only a few minutes, or it could potentially take several hours or days. The experiments should be repeated by monitoring CD, as described previously.
Table 1.1.
Unfolding reaction setup
| Urea (μL) |
Phosphate buffer (μL) |
DTT (μL) |
Native protein (μL) |
Final urea [M] |
|---|---|---|---|---|
| 0 | 985 | 10 | 5 | 0 |
| 50 | 935 | 10 | 5 | 0.5 |
| 100 | 885 | 10 | 5 | 1.0 |
| 150 | 835 | 10 | 5 | 1.5 |
| 200 | 785 | 10 | 5 | 2.0 |
| 250 | 735 | 10 | 5 | 2.5 |
| 300 | 685 | 10 | 5 | 3.0 |
| 350 | 635 | 10 | 5 | 3.5 |
| 400 | 585 | 10 | 5 | 4.0 |
| 450 | 535 | 10 | 5 | 4.5 |
| 500 | 485 | 10 | 5 | 5.0 |
| 550 | 435 | 10 | 5 | 5.5 |
| 600 | 385 | 10 | 5 | 6.0 |
| 650 | 335 | 10 | 5 | 6.5 |
| 700 | 285 | 10 | 5 | 7.0 |
| 750 | 235 | 10 | 5 | 7.5 |
| 800 | 185 | 10 | 5 | 8.0 |
Calculations are based on stock concentrations of 200 μM native protein, 10 M urea, 100 mM DTT, and 50 mM phosphate buffer, pH 7.5. The final protein concentration is 1 μM.
Table 1.2.
Refolding reaction setup
| Urea (μL) |
Phosphate buffer (μL) |
DTT (μL) |
Unfolded protein (μL) |
Final urea [M] |
|---|---|---|---|---|
| 0 | 927.5 | 10 | 62.5 | 0.5 |
| 50 | 877.5 | 10 | 62.5 | 1.0 |
| 100 | 827.5 | 10 | 62.5 | 1.5 |
| 150 | 777.5 | 10 | 62.5 | 2.0 |
| 200 | 727.5 | 10 | 62.5 | 2.5 |
| 250 | 677.5 | 10 | 62.5 | 3.0 |
| 300 | 627.5 | 10 | 62.5 | 3.5 |
| 350 | 577.5 | 10 | 62.5 | 4.0 |
| 400 | 527.5 | 10 | 62.5 | 4.5 |
| 450 | 477.5 | 10 | 62.5 | 5.0 |
| 500 | 427.5 | 10 | 62.5 | 5.5 |
| 550 | 377.5 | 10 | 62.5 | 6.0 |
| 600 | 327.5 | 10 | 62.5 | 6.5 |
| 650 | 277.5 | 10 | 62.5 | 7.0 |
| 700 | 227.5 | 10 | 62.5 | 7.5 |
| 750 | 177.5 | 10 | 62.5 | 8.0 |
Calculations are based on an unfolded protein stock of 16 μM in 8 M urea-containing buffer, 10 M urea stock, 100 mM DTT stock, and 50 mM phosphate buffer, pH 7.5. The final protein concentration is 1 μM.
2.5.2. Method 2
The longest equilibration times are those at the transition midpoint(s) because the rates of folding and unfolding are approximately equal (Pace, 1986). Therefore, one can monitor fluorescence emission over time for protein incubated in urea concentrations near the midpoint of the transition. One sample includes native protein in urea-containing buffer (unfolding sample). The second sample contains unfolded protein in urea-containing buffer (refolding sample). In both samples, the final urea concentration is identical and is close to the midpoint for unfolding. The samples are incubated as described earlier, and fluorescence emission scans of both samples are collected until the signals are identical. This method provides a quick and efficient approach for determining equilibration times when some information is known concerning the protein of interest.
2.6. Equilibrium unfolding
In general, equilibrium unfolding experiments are set up in one of two ways. First, the simplest method is to use a titrator that accurately adds protein and urea-containing buffer into the cuvette. For this method, one need prepare only two solutions, native protein in buffer and unfolded protein in urea-containing buffer. The two solutions are prepared and allowed to reach equilibrium before data are collected. In this way, the protein concentration remains constant, but the urea concentration changes with each mixing. This method is preferred for proteins with short equilibration times. Second, for proteins with longer equilibration times (several minutes to hours), individual sample tubes are set up in the same manner as described previously. A typical experimental setup is shown in Tables 1.1 and 1.2. In this case, the final protein concentration is 1 μM and the final urea concentration is varied between 0 and 8 M. One should note that the protocol should be adjusted for each protein in order to maximize the number of samples in the transition region. The reactions are incubated for the established equilibration time prior to measurements of fluorescence emission and CD.
Three data sets are obtained from each sample shown in Tables 1.1 and 1.2, one each from fluorescence emission following excitation at 280 nm or 295 nm and one from far-UV CD.
If the protein under study is a monomer, then only one protein concentration will be needed for the final analysis. Several concentrations should be tested, however, to verify that the protein does not oligomerize at higher protein concentrations. For a monomer, there should be no difference in the unfolding curves from one protein concentration to the next. If this is the case, then the data may be averaged. If the protein is a dimer or higher-order oligomer, then multiple protein concentrations should be examined in order to determine the concentration-dependent transition. Typically, protein concentrations over a ten-fold range (at least) are used.
2.7. Interpretation of equilibrium-unfolding curves
The two-state equilibrium folding mechanism has been described in detail by Pace and others (Greene et al., 1974; Pace, 1986; Scholtz, 1995; Saito and Wada, 1983), where the native and unfolded ensembles are present in the absence of well-populated intermediate conformations. The goal of this section is to provide a comprehensive outline for analyzing and interpreting the data from an equilibrium folding experiment. We describe fitting for the following folding models: two-state monomer, three-state monomer, two-state dimer, three-state homodimer, three-state heterodimer, and four-state homodimer. More complicated mechanisms have been described for some proteins, such as the four-state monomeric model described by Enoki (2006), for example, but they are not considered here. While we will not derive the equations used in fitting the data, Tables 1.3 and 1.4 show the equations used in the fitting process for each respective model and the definition of each molar fraction. In addition, the references provided describe derivations for the models discussed here.
Table 1.3.
Equilibrium-folding models for monomeric proteins
| Mechanism | 2-state model |
3-state model |
|---|---|---|
| Equilibrium constants and total protein concentration | ||
| Definition of molar fraction fN = | ||
| Definition of molar fraction fI = | — | |
| Definition of molar fraction fU = | ||
| Fitting equation | Y = YNfN + YUfU | Y = YNfN + YIfI + YUfU |
Notes: N, native state; I, intermediate state; U, unfolded state; PT, total molar concentration of the protein; fN, fI, fU, are the mole fractions of the respective species. YN, YI, and YU are the amplitudes of the spectroscopic signal for the specified species.
Table 1.4.
Equilibrium-folding models for homodimeric proteins
| Mechanism | 2-state model |
3-state model (monomeric intermediate) |
|---|---|---|
| Equilibrium constants and total protein concentration | ||
| Definition of molar fraction fN2 = | 1 - fU | 1 - fI - fU |
| Definition of molar fraction fI2 = | — | — |
| Definition of molar fraction fI = | — | |
| Definition of molar fraction fU = | K2fI | |
| Fitting equation | Y = YN2fN2 + YUfU | Y = YN2fN2 + YIfI + YUfU |
| Mechanism |
3-state model (dimeric intermediate) |
4-state model |
| Equilibrium constants and total protein concentration | ||
| Definition of molar fraction fN2 = | 1 - fI2 - fU | 1 - fI2 - fI - fU |
| Definition of molar fraction fI2 = | ||
| Definition of molar fraction fI = | — | |
| Definition of molar fraction fU = | ||
| Fitting equation | Y = YN2fN2 + YI2fI2 + YUfU | Y = YN2fN2 + YI2fI2 + YIfI + YUfU |
Notes: Abbreviations used are the same as described for Table 1.3, with the representing addition of the N2 native homodimer and I2 representing the homodimeric intermediate. fN1 and fI2 are the mole fraction of the homodimer and of the dimeric intermediate, respectively, and YN2 and YI2 are the amplitudes of the spectroscopic signal for the specified species.
During the following discussion we will refer the reader to several unfolding curves that were generated for visualization purposes and that describe what one may expect from a typical unfolding experiment. Raw data, corrected for buffer background (Fig. 1.1B), are normalized between zero (unfolded) and one (native), as shown in Eq. 1.1, in order to visualize different spectroscopic signals on a single scale.
| (1.1) |
In this case, Yx is the signal being normalized, YU is the signal of the unfolded protein, and YN is the signal of the native protein. The latter two signals are in the absence of urea, where YN and YU are determined from linear fits of data in the pre- and posttransition regions and extrapolated to zero denaturant, as shown in Fig. 1.1B. A plot of the normalized signal versus the denaturant concentration generates the denaturation or unfolding curve (Fig. 1.1C) for each of the spectroscopic probes. When analyzing denaturation curves, there are three regions one must take note of, regardless of the mechanism. The pretransition region shows the dependence of the native protein signal on denaturant concentration and is represented in the unfolding curve in Fig. 1.1B between 0 and ≈2.5 M urea. The transition region represents a mixture of the native ensemble and the unfolded ensemble (or intermediate if present). Once again, examining the data in Fig. 1.1B, this region is observed between 3 and 6 M urea. The posttransition region represents the denaturant concentrations where the unfolded ensemble is largely populated. This region occurs between 6 and 8 M urea in Fig. 1.1B. The posttransition must be sufficiently defined for two reasons. First, and most important, it shows that the protein is unfolded. Second, fits of the data will be inaccurate if no posttransition region is present. If a posttransition region is not observed, then one must use higher concentrations of denaturant or a stronger chaotrope to ensure that the protein is completely unfolded.
2.7.1. Monomeric models
The simplest mechanism by which a protein unfolds is a two-state process, where the native protein cooperatively unfolds to the unfolded ensemble, as shown in Eq. 1.2.
| (1.2) |
In this model, N represents the native ensemble, U represents the unfolded or denatured ensemble, and Keq represents the equilibrium constant for the reaction. As shown in Fig. 1.1C, the denaturation curve displays one cooperative transition between 3 and 6 M urea. The closed circles represent the refolding reaction, demonstrating that the protein folds reversibly. While the data imply a two-state mechanism, the model should be validated by employing other techniques to monitor unfolding. For example, the equilibrium-unfolding techniques described previously illustrate three probes for monitoring unfolding, two for tertiary structure, and one for secondary structure. Agreement among the different spectroscopic probes implies a two-state mechanism (Fig. 1.1C), while noncoincidence of the folding curves indicates a more complex unfolding mechanism, typically due to the population of nonnative, partially folded, intermediates (Fig. 1.1D). One should note, however, that agreement in the unfolding curves is only consistent with a two-state mechanism and does not prove this model with certainty (Lumry, 1966).
A biphasic unfolding curve demonstrates a three-state unfolding mechanism, where the native protein unfolds through a partially structured intermediate before completely unfolding (Fig. 1.1E). A general three-state model of equilibrium unfolding can be described by Eq. 1.3.
| (1.3) |
Here, N, I, and U represent the native, intermediate, and unfolded ensembles respectively, and K1 and K2 represent the equilibrium constants for the two reactions. A typical biphasic unfolding curve is shown in Fig. 1.1E, where a plateau is observed between 3 M and ≈5.5 M urea in this example. The data demonstrate two transitions that correspond to the transition of N to I (1 M to 3 M urea) and of I to U (5.5 M to 7 M urea).
2.7.2. Dimeric Models
Overall, the unfolding reaction must begin with the native dimer, N2, and end with two unfolded monomers. However, the pathway by which the dimer unfolds can include one or more intermediates (two-state dimer vs. three-state dimer mechanism). In addition, the intermediate can be dimeric or monomeric. The most basic model for dimer unfolding resembles the simple two-state mechanism for the monomer (Eq. 1.2), where the native dimer dissociates to the two unfolded monomers in a single transition, as shown in Eq. 1.4.
| (1.4) |
In this model, N2 represents the native dimer, 2U corresponds to the unfolded monomers, and Keq represents the equilibrium constant for the reaction. Fig. 1.2A shows the expected sigmoidal unfolding curve for a dimer, where a single transition is observed. The apparent stability of the dimer is dependent on the concentration of monomer. In other words, as the concentration of protein increases, the equilibrium shifts toward N2. Therefore, one observes a shift to higher transition midpoints at higher protein concentrations (Fig. 1.2A). To validate a two-state dimer model, we recommend examining several structural probes as outlined above in section 2.7.1 for a two-state monomer.
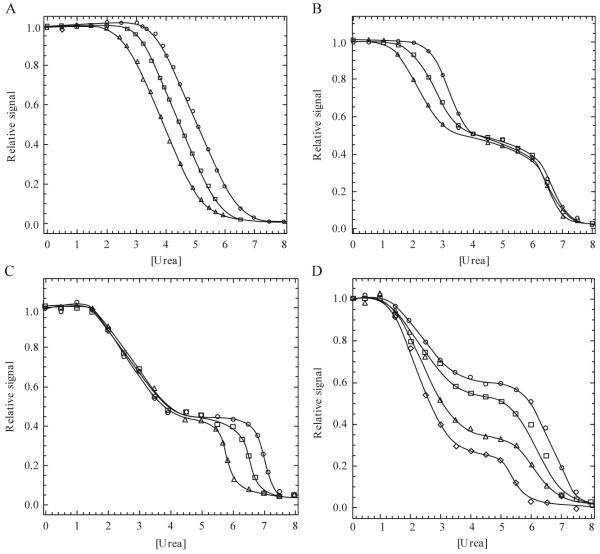
Figure 1.2.
(A) Example of an equilibrium-unfolding curve for a dimeric protein that follows a two-state unfolding model. Protein concentration dependence is demonstrated by an increase in the transition midpoint as the protein concentration is increased (○ > □ > Δ). (B) Example of a three-state dimer-unfolding model in which the protein concentration dependence is observed in the first transition, demonstrating the presence of a monomeric intermediate. (C) Example of a three-state dimer-unfolding model in which the protein concentration dependence is observed in the second transition, demonstrating the presence of a dimeric intermediate. (D) Example of a four-state dimer-unfolding model. (I) In this case, the midpoint of the first transition is the same for each protein concentration, while the second transition midpoint increases with increasing protein concentration (○ > ◇). The relative signal observed between 3 M and 5 M urea also increases with increasing protein concentration revealing a four-state unfolding process as described in the text.
If one establishes that the protein of interest follows a three-state model, then there are two pathways by which the protein can unfold. In the first case, a monomeric intermediate is populated (Eq. 1.5), and in the second case, a dimeric intermediate is populated (Eq. 1.6).
| (1.5) |
| (1.6) |
Here, N2 represents the native dimer, 2I represents the monomeric intermediate, I2 represents the dimeric intermediate, 2U represents the unfolded monomers, and K1 and K2 represent the equilibrium constants for each transition. A biphasic unfolding curve would be expected in each case if the intermediate is well populated, and one of the two transitions will be dependent on the protein concentration (Fig. 1.2B-C). If the first step is protein concentration dependent (Eq. 1.5, Fig. 1.2B), then the dimer dissociates in the first transition to yield a monomeric intermediate. In contrast, protein concentration dependence in the second transition indicates that subunit dissociation occurs after formation of a dimeric intermediate (Eq. 1.6, Fig. 1.2C).
While we present several unfolding models for homodimers in Table 1.4, one should note that similar models exist for heterodimers, depending on how the subunits of the heterodimer are treated. In equilibrium studies of the heterodimeric bacterial luciferase (Clark et al., 1993) and of the histone H2A/H2B (Placek et al., 2005), for example, the subunits were assumed to be identical. In this case, the data are then treated as one would for a homodimer. Only when the subunits of the heterodimer are treated differently will the data analysis vary from that of a homodimer.
If one establishes the presence of two intermediates in the equilibrium-unfolding pathway of the dimer, then there are three possible four-state models. For these models, dimer dissociation occurs as the first step (Eq. 1.7), the second step (Eq. 1.8), or the third step (Eq. 1.9) in unfolding.
| (1.7) |
| (1.8) |
| (1.9) |
For these models, N2 represents the native dimer, I2 represents the dimeric intermediate, 2I represents the monomeric intermediates, 2U represents the unfolded monomers, and K1 - K3 represent the equilibrium constants for the three transitions. Examples are known for the first two models, but we are not aware of examples in the literature for dimer dissociation in the third step (Eq. 1.9). The dimer of glycyl tRNA synthetase was shown to dissociate in the first step of unfolding, as described by Eq. 1.7 (Dignam et al., 2001), while the dimer of procaspase-3 was shown to dissociate in the second unfolding step, as described by Eq. 1.8 (Bose and Clark, 2001). The unfolding data for procaspase-3 suggest a minimum three-state unfolding mechanism because two transitions are observed (Fig. 1.2D). However, when the experiments are carried out at several protein concentrations, one observes that the signal for the plateau shifts to higher values at higher protein concentrations. The curves in Fig. 1.2D represent increasing concentration of procaspase-3, between 0.25 μM and 2 μM. Thus, the native dimer isomerizes to a dimeric intermediate , followed by dissociation of the dimer to two monomers (3-5 M urea). The monomers then unfold at higher urea concentrations (6-8 M urea). All together, these data reveal two important points. First, dimerization is considered a folding event because dimerization occurs as a result of the association of two monomeric intermediates. Second, fitting of the data to Eq. 1.8 reveals that dimerization contributes significantly to the overall stability of the protein (see subsequent section for further explanation of data fitting).
2.8. Data analysis
2.8.1. Equilibrium constants and fractions of species
For the monomeric folding models described by Eqs. 1.2 and 1.3, the equilibrium constants for the transitions are related to free energy as shown in Eq. 1.10.
| (1.10) |
Here, R is the gas constant and T is the temperature in degrees Kelvin. If one assumes that the free energy change for each step of the reaction is linearly dependent on the denaturant concentration (Pace, 1986), then one may calculate the free energy change in the absence of denaturant, as shown in Eq. 1.11.
| (1.11) |
In this case, ΔGH2O represents the free energy change in the absence denaturant, and m represents the cooperativity index associated with reaction. While not discussed here, m is related to the solvent surface area for each transition, and a comparison of m-values of for related proteins has been shown to be quite informative (Myers et al., 1995).
For the two-state monomer described by Eq. 1.2, the sum of the fraction of N (fN) and of the fraction of U (fU) is one, and the total protein concen tion is the sum of the concentrations of N and U (PT = [N] + [U]) at a given concentration of urea (Table 1.3). As a result, the apparent fractio species is shown by Eq. 1.12. In thi case, Y represents the signal obtained at each urea concentration.
| (1.12) |
Taking into account Eqs. 1.10-1.12 and solving for Y, one can derive Eq. 1.13, as described previously (Santoro and Bolen, 1988).
| (1.13) |
Here, mN and mU account for changes in the signals of the pre- and posttransition regions with changes in denaturant, if any. YN’ and YU’ represent the signal of the native and unfolded species, respectively, in the absence of denaturant. Inherent is this description, as well as the subsequent ones, is that the measured signal is the sum of the fractional contribution of each species.
Thus, Eq. 1.13 is used to describe the simple two-state model for equilibrium unfolding of a monomeric protein. Eqs. for the three-state equilibrium-folding model for a monomer are provided in Table 1.3, taking into account both equilibrium constants in terms of the fractions of the three species.
Using a similar analysis, the data for homodimeric proteins are analyzed to obtain the free energy change with each step in unfolding. Equations. are provided in Table 1.4 for the two-state Eq. 1.4 (Bowie and Sauer, 1989; Gloss and Matthews, 1997), three-state Eqs. 1.5 and 1.6 (Clark et al., 1993; Grimsley et al., 1997; Harder et al., 2004; Hornby et al., 2000; Park and Bedouelle, 1998), and four-state Eq. 1.8 (Bose and Clark, 2001) models.
2.8.2. Fitting equilibrium-unfolding data
There are a multitude of programs available for fitting protein-folding data, and certain features vary depending on the software. Simple fitting procedures, such as that for the two-state monomer (Eq. 1.2 and Table 1.3) are readily performed in spreadsheet programs, such as Kaleidagraph (Synergy Software), SigmaPlot (Systat Software), or Excel (Microsoft). However, fitting multiple data sets should be done globally. For example, data collected from the three spectroscopic probes described here, and especially data that suggest more complicated folding mechanisms (Eqs. 1.4-1.9, Table 1.4) should be fit simultaneously to one of the models shown in Tables 1.3 and 1.4, or another appropriate model to describe the data. The advantage to global fitting is that parameters that are constant to all data sets, ΔG and m-values, for example, are linked, whereas other parameters are set locally, such as YN’ and YU’ (Eq. 1.13), as they vary between data sets.
3. Measuring Folding Kinetics
In contrast to the equilibrium experiments described previously, kinetic experiments examine refolding or unfolding processes by monitoring changes in a spectroscopic signal over time following the initiation of the reaction. A number of methods have been developed to examine protein folding kinetics, from continuous flow instruments, which measure reactions on the microsecond time scale (Shastry et al., 1998), to stopped-flow instruments, which measure reactions on the millisecond to minute time scale. Stopped-flow instruments, the focus of this section, can employ absorbance, fluorescence emission, circular dichroism, or other spectroscopies as a detection method. We describe here experimental protocols and data-fitting procedures for kinetic folding experiments utilizing stopped-flow fluorescence emission and circular dichroism spectroscopies.
3.1. Experimental protocol
3.1.1. General considerations
Kinetic experiments with a stopped-flow instrument require rapid mixing of two solutions. For both refolding and unfolding studies, one routinely uses asymmetric mixing, 1:10 for example, either to dilute (refolding) or increase (unfolding) the amount of denaturant to span the unfolding or refolding transition region that was determined from equilibrium-folding experiments. The 1:10 ratio is obtained typically by using one small drive syringe (e.g., 250 μL) and one large drive syringe (e.g., 2.5 mL). One should consult the instrument manufacturer to determine the mixing dead-time, which is the shortest time at which one can measure the kinetic signal due to the time required to mix the two solutions, typically 1-10 ms.
While the instrumental setup will vary depending on the manufacturer, there are several parameters common to all instruments, including signal detection, temperature, slit widths, wavelengths, and time scale. Each parameter will be discussed briefly. As described previously, it is recommended to use multiple spectroscopic probes to study protein folding because each detection method provides different information about the structures formed during refolding or unfolding. For fluorescence emission studies, there are two options available. The detection photomultiplier tube can be attached directly to the sample handing unit, or it can be attached to a monochromator. The advantage to the latter method is that it allows the user to select a particular detection wavelength. The disadvantage is that the overall signal will be decreased because other emission wavelengths are filtered out such that only a fraction of the total emission is detected. In contrast, a cutoff filter is used if the photomultiplier tube is attached to the sample-handling unit. For this case, there are a variety of filters available, where the most common for intrinsic protein fluorescence emission use cutoff wavelengths of 305 nm or 320 nm.
It is important to maintain a constant temperature around the observation cell and drive syringes. The most common temperature for kinetic folding experiments reported in the literature is 25 °C (Maxwell et al., 2005; Zarrine-Afsar and Davidson, 2004). This is because 25 °C is slightly above room temperature, which allows easy control with heating, and it is an adequate endpoint for temperature-jump studies. If a reaction is too fast to be detected by a stopped-flow instrument, it may be helpful to slow the chemistry by lowering the temperature. One should note that studies at low temperatures (<10 °C) will require low temperature syringes to prevent sample leakage during injections.
Kinetic traces should be collected until the signal reaches that of the native or unfolded control in order to examine the full time course for the reaction. Depending on the protein, equilibration could occur in milliseconds or in hours. One should note that longer collection times can result in artifacts due to remixing of solutions of different densities in the observation cell and flow lines. One can test for mixing artifacts using various fluorescent compounds, such as tryptophan. Hand mixing experiments, which are performed on a steady-state instrument set for time-based data collection, also can verify slow reactions.
All experiments described below should be completed at multiple protein concentrations in (at least) duplicate experiments in order to verify the apparent kinetic rates and amplitude changes. One should use a ten-fold or greater variation in protein concentration, which will allow for the identification of protein concentration-dependent steps if the protein is an oligomer. If the protein is a monomer, then the apparent rate(s) should not depend on the protein concentration. If one observes this experimentally, then the data from the various protein concentrations can be averaged. If one observes a protein concentration-dependent rate during the folding or unfolding of a monomer, then the data indicate that the protein forms aggregates during the reaction.
3.1.2. Initial parameterization
Two samples are used to determine the initial parameters (final protein concentration and slit widths) needed for a kinetic experiment: native protein in buffer and unfolded protein in urea-containing buffer. First, native protein stock is placed in the small syringe, mixed with buffer (from the large syringe), and data are collected for several seconds. Second, unfolded protein stock is placed in the small syringe, mixed with urea containing buffer (from the large syringe) such that there is no dilution of the urea, and data are collected for several seconds. For each experiment, there should be no change in signal over time because the samples serve as controls for the native and unfolded signals. The unfolded protein stock should contain the same final urea concentration as the urea-containing buffer to which it is mixed. The general procedure for these initial experiments is to examine one protein concentration and slit width for various time scales, then to change the slit widths and repeat the experiment until the maximum difference is observed between the native and unfolded control samples. One may find that the optimized slit widths and protein concentrations are similar to those used in equilibrium unfolding experiments. In general, total volumes of 1 mL of protein and 10 mL of buffer solutions are sufficient for determining one set of parameters (e.g., slit width and voltage used for a particular final protein concentration).
In the experiments described subsequently, unfolded protein will be mixed with different urea-containing buffers in order to examine refolding at several final urea concentrations. The number of urea steps and volumes required will vary, depending on the protein and on the refolding conditions. The procedure outlined here is useful for examining burst-phase kinetics, apparent rates and amplitudes of observable phases, and for generating chevron plots of the apparent rate constants.
3.1.3. Sample preparation for measuring refolding and unfolding kinetics
First, one should determine the final urea and protein concentrations. Eq. 1.14 describes the necessary calculation assuming a 1:10 mixing ratio.
| (1.14) |
For example, if the protein stock solution is in 8 M urea-containing buffer (1 part = 250 μL syringe) and is mixed with a 0 M urea-containing buffer (10 parts = 2.5 mL syringe), then the final urea concentration will be 0.73 M using Eq. 1.14. Similar calculations are used to determine the final protein concentration as well.
To measure refolding kinetics, one should prepare two stock protein samples (unfolded and native protein) and various urea-containing buffers that encompass the refolding transition. For example, in a typical experiment that measures the refolding of procaspase-3, we routinely use 17 urea concentrations between 0 M and 8 M at 0.5 M increments, and we average ≈20 injections per urea step. This requires 10 mL of urea-containing buffer for each final urea concentration and 15 mL of protein stock. Table 1.5 shows the procedure for preparing urea-containing buffer solutions as well as the final urea concentration calculated using Eq. 1.14. If necessary, the urea concentrations should be adjusted in order to cover all regions of the equilibrium-unfolding curve. Table 1.6 shows the calculations for making the unfolded and native protein stocks, assuming that the protein unfolds in 8 M urea-containing buffer and that the final protein concentration in the observation cell is 5 μM.
Table 1.5.
Example calculations for urea and 0.77 M acrylamide/urea stock solutions
| 10 M Urea stock (mL) |
Buffer (mL) |
8 M Acrylamide stock (mL) |
Final urea concentration (M) |
|
|---|---|---|---|---|
| Urea stocks (M) | ||||
| 0 | 0 | 10 | 0.73 | |
| 1 | 1 | 9 | 1.64 | |
| 2 | 2 | 8 | 2.55 | |
| 3 | 3 | 7 | 3.45 | |
| 4 | 4 | 6 | 4.36 | |
| 5 | 5 | 5 | 5.27 | |
| 6 | 6 | 4 | 6.18 | |
| 7 | 7 | 3 | 7.09 | |
| 8 | 8 | 2 | 8 | |
| 0.77 M Acrylamide/Urea stocks (M) | ||||
| 0 | 0 | 9.037 | 0.963 | 0.73 |
| 1 | 1 | 8.037 | 0.963 | 1.64 |
| 2 | 2 | 7.037 | 0.963 | 2.55 |
| 3 | 3 | 6.037 | 0.963 | 3.45 |
| 4 | 4 | 5.037 | 0.963 | 4.36 |
| 5 | 5 | 4.037 | 0.963 | 5.27 |
| 6 | 6 | 3.037 | 0.963 | 6.18 |
| 7 | 7 | 2.037 | 0.963 | 7.09 |
| 8 | 8 | 1.037 | 0.963 | 8 |
Table 1.6.
Example calculations for 55 μM procaspase-3 protein stock solutions for refolding/unfolding kinetic experiments experiments
| Protein stock solutions |
10 M Urea (mL) |
1 M DTT (μL) |
825 μM Proteina (μL) |
Buffer (mL) |
|---|---|---|---|---|
| Unfolded control (1 mL) | 0.8 | 1 | 66.7 | 0.1323 |
| Native (15 mL) | 0 | 15 | 1000 | 13.985 |
| Native control (1 mL) | 0.073 | 1 | 66.7 | 0.8593 |
| Unfolded (15 mL) | 12 | 15 | 1000 | 1.985 |
Initial protein concentration of 825 μM is diluted to 55 μM for kinetic folding experiments.
A native protein stock is used as a control in order to determine the final signal in the refolding process (Table 1.6). The native stock should contain the same buffer as the final refolding sample: 0.73 M urea-containing buffer in this example. Incubate the protein samples for the predetermined equilibration time, and then follow the subsequent instrument procedure.
To measure unfolding kinetics, one will mix native protein with different urea-containing buffers. The sample preparation basically is the same as for the refolding experiment except for the initial protein stock. Prepare the urea-containing buffers as described above (Table 1.5) and the unfolded protein and controls as shown in Table 1.6. Note that the unfolded control should contain the same urea concentration as the final unfolding sample, 8 M in this example. Incubate the protein samples for the predetermined equilibration time, and then follow the subsequent instrument procedure.
3.1.4. Instrument procedure
The general procedure for a kinetic refolding experiment on a stopped-flow instrument is outlined here. The experimental protocol for unfolding follows the same steps except that one starts with native rather than unfolded protein. The basic idea is to refold or unfold the protein at several final ureaconcentrations and to monitor the signal until no further change occurs. Final signals for the lowest and highest urea concentrations should match those of the controls (native and unfolded protein).
Flush the system with distilled, deionized water and then with buffer. Make sure that the drive syringes contain no air bubbles, as this will cause mixing artifacts in the data. For 1:10 asymmetric mixing, about ten injections are required to move samples and/or buffers completely through the system, depending on the tubing length and stop syringe volume.
Place the unfolded protein stock in the small drive syringe and the 8 M urea-containing buffer in the large drive syringe.
Fill the drive syringes and flush the system.
Set the instrument parameters determined previously (wavelength, temperature, slit width, signal detection of choice, voltage).
Obtain data by acquiring multiple injections at one set of conditions. The goal is to collect enough repetitions to average, the final number of which will depend on the signal-to-noise ratio. The averages also depend on the final protein concentration and detection method. Collect data for various time frames, such as 1, 10, 100, and 500 s, as needed.
Once the unfolded control sample is completed, remove the 8 M urea-containing buffer. For a refolding experiment, fill the large drive syringe with the next urea-containing buffer, in this case 7.5 M urea. One should note that whenever the solution conditions are drastically changed, one should rinse the syringe either with distilled, deionized water or with buffer to remove any remaining solution in the syringe.
Flush the system and acquire data as in step 5.
Continue to change the urea-containing buffer in the large drive syringe and acquire data by repeating steps 5-7 until the final buffer (0 M urea) is reached.
Remove unfolded protein and buffer solutions from the syringes.
For the native control, add the native protein (Table 1.6) to the small syringe and 0.73 M urea-containing buffer to the large syringe.
Flush the system and acquire data as in step 5.
Once the experiment is complete, clean the instrument by removing the protein and urea-containing buffer solutions from the reservoir syringes. Flush the system with buffer and distilled, deionized water as before.
3.2. Differential quenching by acrylamide
Differential quenching describes the relative solvent accessibility of aromatic residues during refolding or unfolding compared to the same residues in the native or unfolded states. The technique of differential quenching may allow one to identify and characterize folding intermediates not detected by other methods such as stopped-flow fluorescence emission or CD spectroscopies. For example, Vanhove et al. (1998) used this technique to investigate a nonnative intermediate formed during the refolding of TEM-1 β-lactamase. Four tryptophan residues are located on the protein surface in the native state, and it is proposed that the tryptophans are less accessible to solvent during refolding than in the native state. This group verified, through quenching by acrylamide and other techniques, the presence of a hydrophobic collapse in the nonnative intermediate.
One should first identify the quencher of choice. It is desirable to use a quencher that reacts differentially to the native and unfolded states of the protein. Equilibrium quenching measurements should be conducted first to provide the optimal concentration of quencher for use in kinetic studies. In the case of procaspase-3, for example, it was shown that 0.7 M acrylamide provided the greatest difference between quenching of native and unfolded protein fluorescence emission (Bose et al., 2003). In kinetic experiments, however, it is important to verify that the quencher does not affect the kinetic folding process. One should test a variety of quencher concentrations and, if necessary, different quenchers. Also, if an ionic quencher (e.g., iodide) is used, it is important to verify that the increased ionic strength has no effect on the folding process. One can do this simply by increasing the ionic strength in the folding experiments described earlier (in the absence of quencher).
3.2.1. Sample preparation
Sample preparation for differential quenching by acrylamide is performed as described previously for the refolding and unfolding experiments except that acrylamide is included in the urea-containing buffers (Table 1.5). Protein stock solutions should be prepared as described in Table 1.6. Equation 1.14 is used to determine the initial concentration of acrylamide needed in the urea-containing buffers. Using procaspase-3 as a model, a final acrylamide concentration of 0.7 M requires the initial concentration to be 0.77 M, so the 0.77 M acrylamide urea-containing buffers are made as shown in Table 1.5. The acrylamide stock solution (8 M) is made by weighing 11.37 g of acrylamide (wear a mask) and bringing the volume up to 20 mL with buffer.
3.2.2. Experimental procedure
The experimental procedure for stopped-flow differential quenching is the same as those for the refolding and unfolding experiments described previously for stopped-flow fluorescence emission. Briefly, unfolded or native protein (Table 1.6) is placed in the small syringe and is mixed 1:10 with acrylamide- and urea-containing buffers (Table 1.5). Data also are collected for controls of native and unfolded protein (Table 1.6). In the examples shown here, the fluorescence emission of the native protein control is examined in 0.7 M acrylamide, 0.73 M urea-containing buffer, and that of the unfolded protein control is examined in 0.7 M acrylamide, 8 M urea-containing buffer. The excitation wavelength should be set to 295 nm in order to avoid inner-filter effects from acrylamide (Lakowicz, 2006).
The kinetic data in the presence of quencher and at various final urea concentrations are plotted with the native and unfolded controls, which also are in the presence of quencher (Fig. 1.3A). In this way, one observes the differential quenching of tryptophan fluorescence emission during refolding or unfolding as compared to the quenching of the native and unfolded proteins.
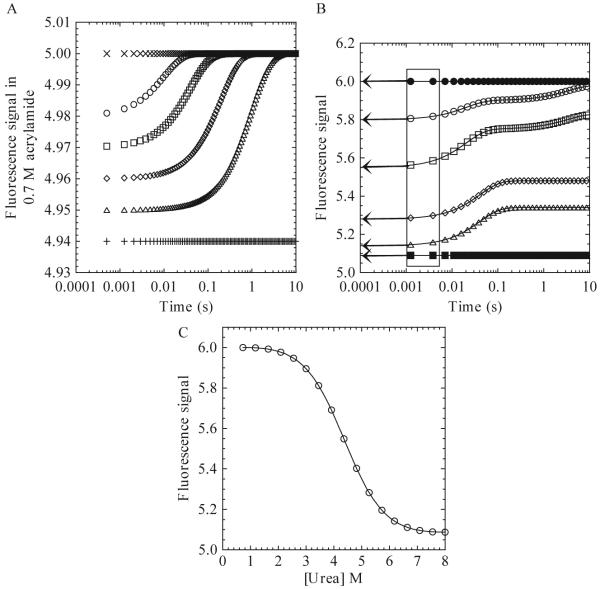
Figure 1.3.
(A) Hypothetical plot of fluorescence signal in the presence of 0.7 M acrylamide versus time for a refolding reaction. The unfolded (+) and native (x) protein signals in the presence of acrylamide are shown. Data at several final urea concentrations are shown (Δ, ◇, □, ○). (B) Hypothetical plot of the fluorescence emission signal versus time for a refolding reaction. The unfolded (■) and native (●) protein signals are shown. Final urea concentrations of 3.45 M (○), 4.36 M (□), 5.27 M (◇), and 6.18 M (Δ) are shown. The boxed area marks the time from 1-5 ms. The arrows show the extrapolation of the signal to time zero. (C) Plot of burst phase signal versus final urea concentration. The continuous line represents a fit to a two-state equilibrium-folding model as described in the text.
3.3. Data analysis
The first step in data analysis is to determine the number of kinetic phases in the experimental data. To achieve this, there are multiple data analysis programs available including KaleidaGraph (Synergy Software), Excel (Microsoft), and Origin (Origin Lab).
A phase is defined here as any change in signal over time. A phase can be described by a single rate constant, or, in the case of a burst phase, a change in amplitude. In order to determine the number of kinetic phases, plot the signal versus time in seconds. A logarithmic scale can be used for short times (1 to 100 ms) or for combining multiple time scales. An example of a refolding experiment is shown in Fig. 1.3B, which shows the signal acquired versus time at six different final urea concentrations. One should note that the data will vary for different proteins. In this hypothetical refolding experiment, three phases are detected and are referred to here as the burst, fast, and slow phases in order to illustrate the following analysis. The burst phase occurs within the mixing dead time for the instrument and is observed at all final urea concentrations shown here. The fast phase, from ≈2 ms to ≈100 ms, occurs at 3.45, 4.36, 5.27, and 6.18 M urea. The slow phase, from ≈200 ms to ≈10 s, occurs at 3.45 and 4.36 M urea.
3.3.1. Burst phase
The burst phase is defined as the change in signal that occurs during the mixing dead time, and while illustrated here, not all kinetic experiments will display a burst phase. If the data display a change in the initial signal with different final urea concentrations, as shown in Fig. 1.3B, then one should plot the burst phase signal versus final urea concentration (Fig. 1.3C). In order to determine the signal, extrapolate the data from ≈1-5 ms (the boxed area in Fig. 1.3B) to a time of 0 s (arrows in Fig. 1.3B). These times are chosen because the signal typically is too noisy at shorter times.
A plot of the burst phase signals versus urea (Fig. 1.3C) may show linear or nonlinear transitions. A linear transition indicates a noncooperative process and simply may represent a change in signal for the unfolded protein with a change in final urea concentration. In contrast, a nonlinear transition (Fig. 1.3C) indicates a cooperative folding process. In this case, one can determine the free energy and m-value for the formation of the burst phase species by fitting the data to a relevant equilibrium-folding model. Typically, one uses a two-state equilibrium model (Eq. 1.13), although more complicated models also can be used. An examination of data determined by fluorescence emission, following excitation at 280 nm and 295 nm, CD, and/or differential quenching may show whether multiple species form in the burst phase (Georgescu et al., 1998; Zaidi et al., 1997). By comparing the free energy and m-values to those obtained from equilibrium unfolding experiments, one will obtain further information regarding the species formed during the burst phase.
3.3.2. Exponential fits
Most observable phases comprise exponential increases or decreases in signal. Therefore, this section will focus on the use of multiple exponential equations to fit the experimental data. Two valuable pieces of information will be obtained from these fits: the amplitude and the apparent rate of each phase. The amplitude provides information on the change in signal with each phase and is related to the population of species that occurs in a phase (Wallace and Matthews, 2002). The apparent rate constant provides the rate at which the transition occurs. One should note that because only the rate-limiting step is detected, a single phase may consist of multiple transitions with multiple rate constants. In addition, the amplitude of a particular phase may differ depending on the detection method used, while the rate will be consistent between all methods (so long as the phase is detected by each method). As stated previously, kinetic measurements are collected until the equilibrium signal is reached. So, in general, the total change in amplitudes of the kinetic phases should equal the difference in signals between native and unfolded control proteins.
The data are fit as a sum of exponentials, as shown in Eq. 1.15:
| (1.15) |
In this case, A(t) is the amplitude at time t, A(∞) is the offset value, Ai is the change in signal for phase i, k is the apparent rate, and t is time (Bieri and Kiefhaber, 2000; Utiyama and Baldwin, 1986). To fit exponential phases, it is best to use a nonlinear least squares fitting program, such as those mentioned previously. Two and three (or more) exponential equations have the same format as a single exponential but with additional terms to account for the total number of phases. That is, data that contain more than one phase are fit to a sum of exponentials.
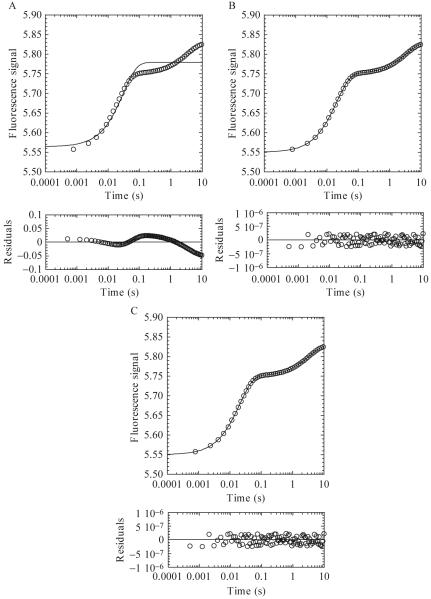
As an example, for the refolding experiment shown in Fig. 1.3B, each urea step is plotted and analyzed individually. Fig. 1.4 shows a plot of data collected at a final urea concentration of 4.36 M fit to either a one (Fig. 1.4A), two (Fig. 1.4B), or three (Fig. 1.4C) exponential equation. An analysis of the residuals to the fits (below each plot) shows the difference between the fit and the experimental data, where the distribution of the points should be random around zero. A single exponential (Fig. 1.4A) does not adequately describe the data, and the residuals for the three exponential fit (Fig. 1.4C) are not significantly different from those of the two exponential fit (Fig. 1.4B). Thus, using the simplest model, one would describe the experimental data as containing two phases, each defined by an apparent rate constant and amplitude.
Figure 1.4.
The 4.36 M refolding data from Fig. 1.3B were fit to a one (A), two (B), or three (C) exponential equation. Residuals to the fits are shown below each panel. (A) A single exponential fit of the data provides an amplitude of 0.22 and rate of 33 sec-1. (B) A two exponential fit of the data provides amplitudes of 0.20 and 0.08 and rates of 50 and 0.3 sec-1, respectively. (C) A three exponential fit of the data provides amplitudes of 0.2, 0.08, and 0.05 and rates of 50, 0.3 and 3.3 × 10-7 sec-1, respectively.
Continue the fitting process until all of the urea steps are analyzed, and then plot the rates and amplitudes from the different phases and detection methods versus denaturant concentration. Using a monomeric protein as a simple example (all observed phases are first-order reactions), we generated a plot of the log of apparent rate constant versus denaturant concentration. The data display a V-shape, and this plot is referred to as a chevron plot (Fig. 1.5A). The chevron analysis has been described extensively for a simple two-state folding model (Ferguson et al., 1999; Parker et al., 1995; Wallace and Matthews, 2002; Zarrine-Asfar and Davidson, 2004), and the reader is referred to previous reviews on the subject. The information obtained from the chevron analysis includes the folding rates (both refolding and unfolding) in the absence of denaturant, the m-values for refolding and unfolding, and information on the transition state for folding.
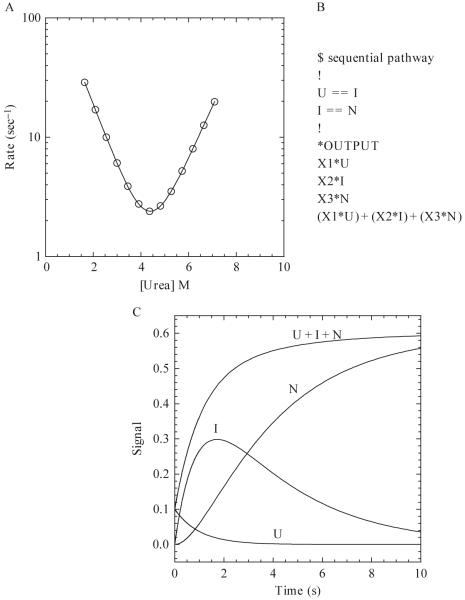
Figure 1.5.
(A) Hypothetical chevron plot of the apparent refolding and unfolding rates versus the final urea concentration. The continuous line represents a fit to a two-state kinetic folding model (Ferguson et al., 1999) with the following parameters: , , mN-TS = 0.7, mU-TS = 0.6, ΔGH2O = 5.62 kcal/mol, m-value = 1.3 kcal/mol/M, . (B) Example of a sequential pathway with one on-pathway intermediate written in the text format for KINSIM. X1, X2, and X3 are the extinction coefficients of U, I, and N, respectively. (C) Hypothetical example of a refolding reaction of 10 μM protein for 10 s. The populations of species, shown by the continuous lines, are labeled as U, I, N, and U + I + N. The rates of the U to I and I to N transitions are 1 and 0.3 sec-1, respectively. The values of X1, X2, and X3 are 0.01, 0.05, and 0.06, respectively.
For an oligomeric protein, the phase in which the protein forms the oligomer will display a protein concentration dependence to the apparent rate constant. For a dimeric protein, for example, the apparent rate will be second order with regard to the protein concentration. To determine the rate of dimerization, plot the apparent rate (sec-1) versus the protein concentration (μM). The second-order rate plot should show a linear dependence on protein concentration, with a slope equal to the rate of dimerization (Jaenicke and Rudolph, 1986).
3.3.3. Simulations
Creating a kinetic folding model is outside of the scope of this article but is covered in other reviews (Bieri and Kiefhaber, 2000; Creighton, 1988; Utiyama and Baldwin, 1986; Wallace and Matthews, 2002). Once a model is created, it can be tested using other stopped-flow techniques, such as sequential mixing (Eftink and Shastry, 1997; Schmid, 1986; Wallace and Matthews, 2002). The protein-folding mechanism could be very complex, depending on the number of kinetic phases and the oligomeric properties of the protein, and analysis of the data may yield several possible folding mechanisms. The overall goal is to devise the simplest mechanism that adequately explains the experimental data. In this regard, simulation programs are useful for distinguishing between possible mechanisms. It is important to note that simulations cannot prove a mechanism, but rather they allow one to determine whether a mechanism is supported by the experimental data. This section will describe the use of the simulation program KINSIM (Barshop et al., 1982), but other programs also are available, such as KinTekSim (KinTek Corp.), KINFITSIM (Svir et al., 2002), and DynaFit (BioKin).
There are various examples in the literature of the use of KINSIM in the field of protein folding, ranging from determining if an intermediate is on- or off-pathway (Heidary et al., 2000) to examining the complex parallel folding pathway of a homodimeric protein (Mallam and Jackson, 2006). KINSIM is a free program available at http://www.biochem.wustl.edu/cflab/message.html, where there also is a help manual with instructions for the program, but a brief overview will be described here.
KINSIM allows the user to define a mechanism in a text file. A simple example is shown in Fig. 1.5B for the folding of a monomer with one on-pathway intermediate (U ↔ I ↔N). In this sequential mechanism, the unfolded protein (U) folds to an intermediate species (I) before forming the native structure (N). As shown in Fig. 1.5B, a reversible reaction is described by two equal signs (==). The concentration of each species is multiplied by an output factor (X1-X3 in Fig. 1.5B), and the signal observed is the sum of the contribution of each species.
Once the mechanism is loaded into KINSIM, the user can change protein concentration (μM), rate constants (sec-1), output factors (signal/[protein]) and simulation time (sec). The protein concentration and simulation time are chosen on the basis of the experimental conditions. The rate constants determined from fits of the experimental data (described previously) are used as initial guesses for the simulated rate constants. For example, if the data analysis reveals a rate of 50 sec-1 for the transition of U to I, then one would use 50 for k1. Output factors are calculated by dividing the signal of the species, taken from the experimental data, by the protein concentration. Finally, one can output any combination of species. As an example, using the sequential mechanism in Fig. 1.5, the simulation screen will show four lines based on the four specified outputs, U, I, N and U + I + N (Fig. 1.5C). Experimental data also can be uploaded in order to examine the agreement between simulated and real data, which allows the user to fine-tune rate constants and output factors and to distinguish between possible mechanisms.
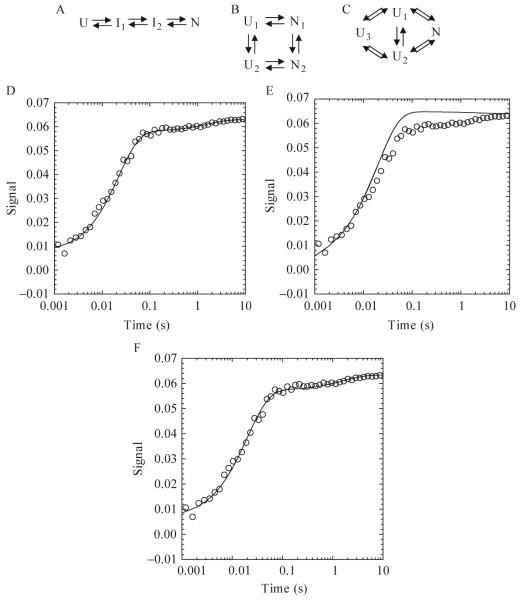
As an example, KINSIM simulations were used to investigate several potential kinetic folding pathways of the caspase recruitment domain (CARD) of apoptotic protease activating factor 1 (Apaf-1) (Milam et al., 2007). Apaf-1 CARD is a small (<100 amino acids), monomeric protein consisting of six α-helices arranged in an α-Greek key folding topology (Weber and Vincenz, 2001). One sequential (Fig. 1.6A) and two parallel (Fig. 1.6B-C) kinetic mechanisms were proposed on the basis of three phases present in the experimental data (burst, fast, and slow). In order to demonstrate the ability of KINSIM to discriminate between possible mechanisms, this brief discussion will focus on simulations of the slow phase in the Apaf-1 CARD kinetic folding pathway. In the sequential folding model (Fig. 1.6A), the unfolded protein folds through two intermediates before forming the native conformation. KINSIM simulations with this mechanism agree with the experimental data (Fig. 1.6D). However, more complicated mechanisms were proposed on the basis of stopped-flow sequential mixing studies that showed the presence of multiple unfolded species (Milam et al., 2007). The proposed parallel mechanisms, shown in Figs. 1.6B and 1.6C, consist of multiple unfolded and/or native conformations. In the model shown in Fig. 1.6B, two unfolded conformations, U1 and U2, form two native conformations, N1 and N2, and the unfolded and native species are able to interconvert. Simulations with this mechanism were not able to recapitulate the slow phase of refolding, assuming that the slow phase was due to the interconversion of U1 to U2 or of N1 to N2 (Fig. 1.6E). As a result, the folding model in Fig. 1.6C was proposed, with the inclusion of a third unfolded species, U3. In this parallel pathway, both unfolded conformations, U1 and U2, can form the native species (N). The conversion of U3 to U1 or to U2 represents the slow phase, as shown in Fig. 1.6F. Therefore,the models in Figs. 1.6A and 1.6C adequately explain the single mixing stopped-flow data (Fig. 1.6D and 1.6F, respectively), but only the model in Fig. 1.6C agrees with the sequential mixing stopped-flow data, which showed multiple unfolded species.
Figure 1.6.
One sequential (A) and two parallel folding pathways (B and C) used in KINSIM simulations. (A) The unfolded species folds through two intermediates before forming the native species. (B) Two unfolded and native species exist and interconvert. (C) Three unfolded species exist, where U1 and U2 fold to the native state and U3 interconverts with U1 or U2. (D-F) Plots of an Apaf-1 CARD refolding reaction in 3.64 M urea. KINSIM simulations for each plot are shown as a continuous line. For pathway A, the concentration of I1 was 10 μM. The extinction coefficient for U, I1,I2, and N were 0, 0.0007, 0.0058, and 0.0063, respectively. The rates for I1 to I2 and I2 to N were 45 and 0.6 sec-1, respectively. For pathway B, the concentrations of U1 and U2 were 1 and 9 μM, respectively. The extinction coefficients for N1 and N2 were 0.0074 and 0.0064. The rates of U1 to N1, U1 to U2, U2 to N2, and N1 to N2 were 500, 100, 50, and 0.4 sec-1, respectively. For pathway C, the concentrations of U1, U2, and U3 were 0.7, 8.3 and 1 μM. The extinction coefficient of N was 0.0086. The rates of U1 to N, U2 to N and U3 to U1 or U2 were 5000, 37 (back rate of 13) and 0.6 (back rate of 0.01) per second.
REFERENCES
- Barshop BA, Wrenn RF, Frieden C. Analysis of numerical methods for computer simulation of kinetic processes: Development of KINSIM—a flexible, portable system. Anal. Biochem. 1983;130:134–145. doi: 10.1016/0003-2697(83)90660-7. [DOI] [PubMed] [Google Scholar]
- Bieri O, Kiefhaber T. Kinetic models in protein folding. In: Pain RH, editor. Mechanisms of Protein Folding. Oxford University Press; 2000. pp. 34–64. [Google Scholar]
- Bose K, Clark AC. Dimeric procaspase-3 unfolds via a four-state process. Biochem. 2001;40:14236–14242. doi: 10.1021/bi0110387. [DOI] [PubMed] [Google Scholar]
- Bose K, Pop C, Feeney B, Clark AC. An uncleavable procaspase-3 mutant has a lower catalytic efficiency but an active site similar to that of mature caspase-3. Biochem. 2003;42:12298–12310. doi: 10.1021/bi034998x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowie JU, Sauer RT. Equilibrium dissociation and unfolding of the arc repressor dimer. Biochem. 1989;28:7139–7143. doi: 10.1021/bi00444a001. [DOI] [PubMed] [Google Scholar]
- Clark AC. Protein folding: Are we there yet? Arch. Biochem. Biophys. 2008;469:1–3. doi: 10.1016/j.abb.2007.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark AC, Sinclair JF, Baldwin TO. Folding of bacterial luciferase involves a non-native heterodimeric intermediate in equilibrium with the native enzyme and the unfolded subunits. J. Biol. Chem. 1993;268:10773–10779. [PubMed] [Google Scholar]
- Cohen FE, Kelley JW. Therapeutic approaches to protein-misfolding diseases. Nature. 2003;426:905–909. doi: 10.1038/nature02265. [DOI] [PubMed] [Google Scholar]
- Creighton TE. Toward a better understanding of protein folding pathways. Proc. Natl. Acad. Sci. 1988;85:5082–5086. doi: 10.1073/pnas.85.14.5082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Creighton TE. Protein folding. Biochem. J. 1990;270:1–16. doi: 10.1042/bj2700001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dignam JD, Qu X, Chaires JB. Equilibrium unfolding of bombyx mori glycyl-tRNA synthetase. J. Biol. Chem. 2001;276:4028–4037. doi: 10.1074/jbc.M006840200. [DOI] [PubMed] [Google Scholar]
- Dill KA. Dominant forces in protein folding. Biochem. 1990;29:7133–7155. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- Eftink MR. The use of fluorescence methods to monitor unfolding transitions in proteins. Biophys. J. 1994;66:482–501. doi: 10.1016/s0006-3495(94)80799-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eftink MR. Use of fluorescence spectroscopy as thermodynamics tool. Methods Enzymol. 2000;323:459–473. doi: 10.1016/s0076-6879(00)23378-8. [DOI] [PubMed] [Google Scholar]
- Eftink MR, Shastry MCR. Fluorescence methods for studying kinetics of protein-folding reactions. Methods Enzymol. 1997;278:258–286. doi: 10.1016/s0076-6879(97)78014-5. [DOI] [PubMed] [Google Scholar]
- Enoki S, Maki K, Inobe T, Takahashi K, Kamagata K, Oroguchi T, Nakatani H, Tomoyori K, Kuwajima K. The equilibrium unfolding intermediate observed at pH 4 and its relationship with the kinetic folding intermediates in green fluorescent protein. J. Mol. Biol. 2006;361:969–982. doi: 10.1016/j.jmb.2006.07.009. [DOI] [PubMed] [Google Scholar]
- Ferguson N, Capaldi AP, James R, Kleanthous C, Radford SE. Rapid folding with and without populated intermediates in the homologous four-helix proteins Im7 and Im9. J. Mol. Biol. 1999;286:1597–1608. doi: 10.1006/jmbi.1998.2548. [DOI] [PubMed] [Google Scholar]
- Georgescu RE, Li JH, Goldberg ME, Tasayco ML, Chaffotte AF. Proline isomerization-independent accumulation of an early intermediate and heteroge-neity of the folding pathways of a mixed alpha/beta protein, Escherichia coli thioredoxin. Biochem. 1998;37:10286–10297. doi: 10.1021/bi9805083. [DOI] [PubMed] [Google Scholar]
- Gloss LM, Matthews CR. Urea and thermal equilibrium denaturation studies on the dimerization domain of Escherichia coli trp repressor. Biochem. 1997;36:5612–5623. doi: 10.1021/bi970056e. [DOI] [PubMed] [Google Scholar]
- Greene RF, Pace CN. Urea and guanidine hydrochloride denaturation of ribonuclease, lysozyme, alpha-chymotrypsin, and beta-lactoglobulin. J. Biol. Chem. 1974;249:5388–5393. [PubMed] [Google Scholar]
- Grimsley JK, Scholtz JM, Pace CN, Wild JR. Organophosphorus hydrolase is a remarkably stable enzyme that unfolds through a homodimeric intermediate. Biochem. 1997;36:14366–14374. doi: 10.1021/bi971596e. [DOI] [PubMed] [Google Scholar]
- Harder ME, Deinzer ML, Leid ME, Schimerlik MI. Global analysis of three-state protein unfolding data. Protein Sci. 2004;13:2207–2222. doi: 10.1110/ps.03229504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidary DK, O’Neill JC, Roy M, Jennings PA. An essential intermediate in the folding of dihydrofolate reductase. Proc. Natl. Acad. Sci. 2000;97:5866–5870. doi: 10.1073/pnas.100547697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornby JA, Luo JK, Stevens JM, Wallace LA, Kaplan W, Armstrong RN, Dirr JM. Equilibrium folding of dimeric class mu glutathione transferases involves a stable monomeric intermediate. Biochem. 2000;39:12336–12344. doi: 10.1021/bi000176d. [DOI] [PubMed] [Google Scholar]
- Ikai A, Tanford C. Kinetic evidence for incorrectly folded intermediate states in the refolding of denatured proteins. Nature. 1971;230:100–102. doi: 10.1038/230100a0. [DOI] [PubMed] [Google Scholar]
- Jaenicke R, Rudolph R. Refolding and association of oligomeric proteins. Methods Enzymol. 1986;131:218–250. doi: 10.1016/0076-6879(86)31043-7. [DOI] [PubMed] [Google Scholar]
- Lakowicz JR. Principles of fluorescence spectroscopy. Springer; New York: 2006. [Google Scholar]
- Lumry R, Biltonen R, Brandts J. Validity of the “two-state” hypothesis for conformational transitions of proteins. Biopolymers. 1966;4:917–944. doi: 10.1002/bip.1966.360040808. [DOI] [PubMed] [Google Scholar]
- Mallam AL, Jackson SE. Probing nature’s knots: The folding pathway of a knotted homodimeric protein. J. Mol. Biol. 2006;359:1420–1436. doi: 10.1016/j.jmb.2006.04.032. [DOI] [PubMed] [Google Scholar]
- Maxwell KL, Wildes D, Zarrine-Afsar A, De Los Rios MA, Brown AG, Friel CT, Hedberg L, Horng JC, Bona D, Miller EJ, Vallee-Belisle A, Main ERG, et al. Protein folding: Defining a “standard” set of experimental conditions and a preliminary kinetic data set of two-state proteins. Protein Sci. 2005;14:602–616. doi: 10.1110/ps.041205405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milam SL, Nicely NI, Feeney B, Mattos C, Clark AC. Rapid folding and unfolding of Apaf-1 CARD. J. Mol. Biol. 2007;369:290–304. doi: 10.1016/j.jmb.2007.02.105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers JK, Pace CN, Scholtz JM. Denaturant m values and heat capacity changes: Relation to changes in accessible surface areas of protein unfolding. Protein Sci. 1995;4:2138–2148. doi: 10.1002/pro.5560041020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace CN. Determination and analysis of urea and guanidine hydrochloride denaturation curves. Methods Enzymol. 1986;131:266–280. doi: 10.1016/0076-6879(86)31045-0. [DOI] [PubMed] [Google Scholar]
- Pace CN, Grimsley GR, Scholtz JM. Denaturation of proteins by urea and guanidine hydrochloride. In: Buchner J, Kiefhaber T, editors. Protein Folding Handbook. Wiley-VCH; Weinheim: 2005. pp. 45–69. [Google Scholar]
- Pace CN, Schmid FX. How to determine the molar absorption coefficient of a protein. In: Creighton TE, editor. Protein Structure: A Practical Approach. Oxford University Press; New York: 1997. pp. 253–259. [Google Scholar]
- Pace CN, Scholtz JM. Measuring the conformational stability of a protein. In: Creighton TE, editor. Protein Structure: A Practical Approach. Oxford University Press; New York: 1997. pp. 299–321. [Google Scholar]
- Park YC, Bedouelle H. Dimeric tyrosyl-tRNA synthetase from Bacillus stearothermophilus unfolds through a monomeric intermediate. J. Biol. Chem. 1998;273:18052–18059. doi: 10.1074/jbc.273.29.18052. [DOI] [PubMed] [Google Scholar]
- Parker MJ, Spencer J, Clarke AR. An integrated kinetic analysis of intermediates and transition states in protein folding reactions. J. Mol. Biol. 1995;253:771–786. doi: 10.1006/jmbi.1995.0590. [DOI] [PubMed] [Google Scholar]
- Placek BJ, Harrison LN, Villers BM, Gloss LM. The H2A.Z/H2B dimer is unstable compared to the dimer containing the major H2A isoform. Protein Sci. 2005;14:514–522. doi: 10.1110/ps.041026405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Privalov PL. Thermodynamic problems of protein structure. Ann. Rev. Biophys. Biophys. Chem. 1989;18:47–69. doi: 10.1146/annurev.bb.18.060189.000403. [DOI] [PubMed] [Google Scholar]
- Royer CA. The nature of the transition state ensemble and the mechanisms of protein folding. Arch. Biochem. Biophys. 2008;469:34–45. doi: 10.1016/j.abb.2007.08.022. [DOI] [PubMed] [Google Scholar]
- Royer CA, Mann CJ, Matthews CR. Resolution of the fluorescence equilibrium unfolding profile of Trp aporepressor using single tryptophan mutants. Protein Sci. 1993;2:1844–1852. doi: 10.1002/pro.5560021106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito Y, Wada A. Comparative study of GuHCl denaturation of globular proteins. I. Spectroscopic and chromatographic analysis of the denaturation curves of ribonuclease A, cytochrome c, and pepsinogen. Biopolymers. 1983;22:2105–2122. doi: 10.1002/bip.360220909. [DOI] [PubMed] [Google Scholar]
- Santoro MM, Bolen DW. Unfolding free energy changes determined by the linear extrapolation method. 1. Unfolding of phenylmethanesulfonyl α-chymotrypsin using different denaturants. Biochem. 1988;27:8063–8068. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- Schmid FX. Fast-folding and slow-folding forms of unfolded proteins. Methods Enzymol. 1986;131:70–82. doi: 10.1016/0076-6879(86)31035-8. [DOI] [PubMed] [Google Scholar]
- Schmid FX. Optical spectroscopy to characterize protein conformation and conformational changes. In: Creighton TE, editor. Protein Structure: A Practical Approach. Oxford University Press; New York: 1997. pp. 261–297. [Google Scholar]
- Scholtz JM. Conformational stability of HPr: The histidine-containing phospho-carrier protein from Bacillus subtilis. Protein Sci. 1995;4:35–43. doi: 10.1002/pro.5560040106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shastry MCR, Luck SD, Roder H. A continuous-flow capillary mixing method to monitor reactions on the microsecond time scale. Biophys. J. 1998;74:2714–2721. doi: 10.1016/S0006-3495(98)77977-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soto C. Unfolding the role of protein misfolding in neurodegenerative diseases. Nat. Rev. Neurosci. 2003;4:49–60. doi: 10.1038/nrn1007. [DOI] [PubMed] [Google Scholar]
- Svir IB, Klymenko OV, Platz MS. “KINFITSIM”: A software to fit kinetic data to a user selected mechanism. Computers and Chemistry. 2002;26:379–386. doi: 10.1016/s0097-8485(02)00014-1. [DOI] [PubMed] [Google Scholar]
- Utiyama H, Baldwin RL. Kinetic mechanisms of protein folding. Methods Enzymol. 1986;131:51–70. doi: 10.1016/0076-6879(86)31034-6. [DOI] [PubMed] [Google Scholar]
- Vanhove M, Lejeune A, Guillaume G, Virden R, Pain RH, Schmid FX, Frere JM. A collapsed intermediate with nonnative packing of hydrophobic residues in the folding of TEM-1 beta-lactamase. Biochem. 1998;37:1941–1950. doi: 10.1021/bi972143c. [DOI] [PubMed] [Google Scholar]
- Waggoner A. Covalent labeling of proteins and nucleic acids with fluorophores. Methods Enzymol. 1995;246:362–373. doi: 10.1016/0076-6879(95)46017-9. [DOI] [PubMed] [Google Scholar]
- Wallace LA, Matthews CR. Sequential vs. parallel protein-folding mechanisms: Experimental tests for complex folding reactions. Biophys. Chem. 2002;101-102:113–131. doi: 10.1016/s0301-4622(02)00155-2. [DOI] [PubMed] [Google Scholar]
- Weber CH, Vincenz C. The death domain superfamily: A tale of two interfaces? TRENDS Biochem. Sci. 2001;26:475–481. doi: 10.1016/s0968-0004(01)01905-3. [DOI] [PubMed] [Google Scholar]
- Weber G. Polarization of the fluorescence of macromolecules. Biochem. J. 1951;51:145–155. doi: 10.1042/bj0510145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ, Wittung-Stafshede P. Role of structural determinants in folding of the sandwich-like protein Pseudomonas aeruginosa azurin. Proc. Natl. Acad. Sci. 2005;102:3984–3987. doi: 10.1073/pnas.0501038102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woody RW. Circular dichroism. Methods Enzymol. 1995;246:34–71. doi: 10.1016/0076-6879(95)46006-3. [DOI] [PubMed] [Google Scholar]
- Zahler WL, Cleland WW. A specific and sensitive assay for disulfides. J. Biol. Chem. 1968;243:716–719. [PubMed] [Google Scholar]
- Zaidi FN, Nath U, Udgaonkar JB. Multiple intermediates and transition states during protein folding. Nat. Struct. Biol. 1997;4:1016–1024. doi: 10.1038/nsb1297-1016. [DOI] [PubMed] [Google Scholar]
- Zarrine-Afsar A, Davidson AR. The analysis of protein folding kinetic data produced in protein engineering experiments. Methods. 2004;34:41–50. doi: 10.1016/j.ymeth.2004.03.013. [DOI] [PubMed] [Google Scholar]