The interwinding nature of protein–protein interfaces and its implication for protein complex formation

Abstract

Motivation: Structural features at protein–protein interfaces can be studied to understand protein–protein interactions. It was noticed that in a dataset of 45 multimeric proteins the interface could either be described as flat against flat or protruding/interwound. In the latter, residues within one chain were surrounded by those in other chains, whereas in the former they were not.

Results: A simple method was developed that could distinguish between these two types with results that matched those made by a human annotator. Applying this automatic method to a large dataset of 888 structures, chains at interfaces were categorized as non-surrounded or surrounded. It was found that the surrounded set had a significantly lower folding tendency using a sequence based measure, than the non-surrounded set. This suggests that before complexation, surrounded chains are relatively unstable and may be involved in ‘fly-casting’. This is supported by the finding that terminal regions are overrepresented in the surrounded set.

Availability: http://cib.cf.ocha.ac.jp/DACSIS/

Contact: yura.kei@ocha.ac.jp; sjh@cmp.uea.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Protein–protein interactions, both transient and permanent including the interactions forming supramolecules, play an essential role in biological function (Alberts, 1998; Gavin et al., 2006). Prominent examples are RNA polymerase for transcription, spliceosome for mRNA maturation and the ribosome for translation. Knowledge of the components of these complexes and determination of their atomic structures is essential for understanding mechanism to function. The components of the complexes can be identified by mass spectroscopy, yeast two-hybrid systems and other related methods (Gavin et al., 2006; Krogan et al., 2006) and their structures can be solved by X-ray crystallography (Dutta and Berman, 2005). Accumulation of structural data enables the study of protein–protein interfaces, leading to the prospect of being able to predict complexed structures given only the structures of the individual components. Recent studies have demonstrated that the chemical characteristics of interfaces, namely hydrophobicity and complementarity, are important for prediction (Janin et al., 2008).

Visual inspection of some of protein complex structures reveals that there is a feature of protein–protein interfaces that has received little attention, namely that the backbone of one chain protrudes into other subunits or interwinds with the backbone of other subunits. The small heat shock protein (sHSP) from wheat, involved in disaggregation of thermally denatured proteins (van Montfort et al., 2001), forms a dodecamer. For some monomer crystallographic structures, 42 residues at the N-terminal are disordered, whereas the corresponding residues form a coil and a helix in the complexed structure. In addition the C-terminal end of each subunit protrudes into the neighbouring subunit (van Montfort et al., 2001). Both N- and C-termini seem to tether the subunits together, strengthening subunit interactions. This is supported by a C-terminal truncation mutant of homologous Hsp104 from Saccharomyces cerevisiae which has a defect in oligomerization indicating a crucial role of the C-terminal region in the oligomerization process (Mackay et al., 2008).

These protruding/interwound regions at interfaces may be a remnant of docking that involves a process called fly-casting (Levy et al., 2005; Shoemaker et al., 2000). Fly-casting was proposed to speed up the recognition of interaction partners while forming an oligomer or protein–DNA complex. The Go-model simulation of protein/protein and protein/DNA recognition showed that an unfolded region in a monomer helps speed up the docking process by reeling in the partner once the initial contact between the monomers has been made (Shoemaker et al., 2000). It is plausible that unfolded N- or C-terminal regions in uncomplexed monomers could fulfill this role. If so, the N- or C-terminal regions are likely to remain attached to the other subunit in the complexed structure.

Analysis of the structures of subunit interfaces mentioned above may pave the way for understanding both static and dynamic features of protein–protein interactions. There is, however, no automatic method to identify protruding/interwound regions at interfaces, and hence no way to assess the significance of these features in protein–protein interactions. Here, we devised a method to automatically detect protruding/interwound regions at protein–protein interfaces and applied it to a set of complexed structures from the protein structural database. We found that a high proportion of protein interfaces have regions that are protruding/interwound. These regions are often located at the termini of individual subunits, although sometimes they are located at non-terminal loops. Analysing their sequences showed that these regions have a greater propensity to be unfolded than non-interwound/protruding regions. We further speculate on the role of these regions in protein complexation.

2 DATA AND METHODS

2.1 Collection of protein oligomer 3D structures and subunit interfaces

Protein oligomer 3D structures from the March 2007 release of the Protein Databank (PDB) (Berman et al., 2007) were selected by the following procedure. First, an entry from the PDB with two or more polypeptides was selected. An entry with DNA/RNA molecules was discarded. To make sure that the polypeptides form a complexed structure, all the distances of atoms from each polypeptide were calculated and when 40 or more pairs of atoms were located within 4.5 Å, then the two polypeptides were considered to be in complexed state. An oligomer is defined as a set of polypeptides with each polypeptide having, at least, another polypeptide that forms a complex with it. Second, the most similar amino acid sequence from UniProt (The UniProt Consortium, 2008) against one of the sequences in the oligomer was selected using BLAST (Altschul et al., 1997) with default parameters. Each UniProt entry contains a description of the number of biologically relevant subunits in the comment line. The number of chains in the oligomer and the number of subunits described in UniProt were compared, and when the number was different, the oligomer entry was discarded. Taking advantage of the systematic nomenclature of UniProt entry ID, the oligomers with homologous amino acid sequences were grouped. The nomenclature of UniProt entry ID is a shortened form of the protein family name followed by an underscore and a shortened species name. Therefore, oligomers with the same protein family name could be grouped using the UniProt entry ID. Each group was then represented by a single oligomer: the one with the highest resolution and fewest disordered atoms. Entries with missing atoms in the subunit interfaces were discarded.

2.2 Measuring the degree of surroundedness of residues at the interfaces; surroundedness factor

The extent to which residues within one chain were protruding/interwound with other chains was quantified in the following manner. We extended and modified the method named CX (Pintar et al., 2002), which was developed to identify atoms protruding into the solvent, in order to identify protruding/interwound segments at subunit interfaces. The i-th residue along the sequence at the interface was represented by its Cα atom, and the number of non-hydrogen atoms belonging to the same polypeptide (N_s) and the number of non-hydrogen atoms belonging to a different polypeptide (N_d), both located within a fixed distance R from the Cα atom, were counted. We defined the surroundedness factor (SF) of residue i at the interface as

where L governs the amount of smoothing along the amino acid sequence around the i-th residue. L relates to a window length as W = 2L + 1. If the interfaces of both subunits are flat, then SF would be close to 1.0, and if the interface is protruding into, or interwound with, chains of other subunits, then SF would be much greater than 1.0. A value of 12 Å was used for R close to the 10 Å default value used for CX (Pintar et al., 2002) and a value of five residues was used for W. The best threshold value of SF to distinguish between flat and protruding/interwound segments was a parameter to be determined.

2.3 Measuring the folding tendency of a fragment

The folding of the polypeptide at the subunit interface may have been induced by subunit interactions. We predicted whether part of the sequence at the interface was intrinsically unfolded using FoldIndex (Prilusky et al., 2005; Uversky et al., 2000). FoldIndex I_F^KD is a simple measure to predict whether the amino acid sequence is likely to be folded or intrinsically unfolded based on the mean net charge and the mean hydrophobicity of the sequence:

where 〈H〉 is the sum of all residue hydrophobicities divided by the total number of residues, and |〈R〉| is the absolute value of the difference between the number of positively charged residues and the number of negatively charged residues at pH 7 divided by the total number of residues. The hydrophobicity was measured using the Kyte and Doolittle (1982) scale, with parameters between 0.0 and 1.0. When I_F^KD is positive, the sequence is likely to fold, and when it is negative, the sequence is likely to be intrinsically unfolded (Prilusky et al., 2005).

3 RESULTS

3.1 The number of oligomer 3D structures

We gathered 888 PDB entries with multi-subunit structures. In these entries, there were 976 unique subunits based on our standard described in Section 2. Of the 888 entries, 580 entries were dimers (2), 72 were trimers (3), 162 were tetramers (4), nine were pentamers (5), 43 were hexamers (6), two were heptamers (7), eight were octamers (8), two were decamers (10), one was undecamer (11), six were dodecamers (12), one tetradecamer (14), one hexadecamer (16) and one tetracosamer (24). Of the 888 entries, 815 entries were homo-oligomers and 73 entries were hetero-oligomers. We used one chain from each homo-oligomers and 161 non-homologous chains from hetero-oligomers, hence 976 chains were analysed. Further details on the 888 structures and 976 chains can be found at http://cib.cf.ocha.ac.jp/DACSIS/.

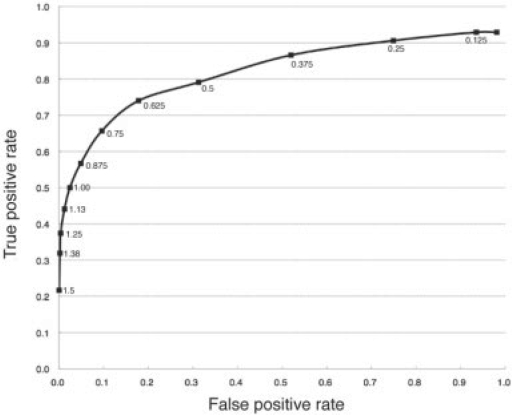
3.2 Determination of threshold value for SF

SF was newly introduced to automatically measure the degree of protruding/interwound segments in protein–protein interfaces. In order to determine a good threshold for SF to distinguish between a segment with a flat-against-flat interface (not surrounded) and one with a protruding/interwound interface (surrounded), 45 examples were selected at random from the 888 structures. Of these 45 complexes, segments of the polypeptide at the subunit interfaces were categorized by visual inspection using molecular graphics, as being surrounded by the other subunit. Excluding equivalent residues in symmetry related subunits, 17 segments comprising 254 residues from 13 complexes were put in the ‘surrounded’ set. In the remaining 32 complexes, interface residues were identified as those that had SF > 0, with R = 6 Å and W = 1. Removing symmetrically equivalent residues gave 1395 residues in 189 segments in the ‘non-surrounded’ set. SF, now with R = 12 Å and W = 5 residues, was calculated for each of these residues in each of these sets. For the non-surrounded set the mean SF value was 0.421 [standard deviation (SD) 0.238] and for the surrounded set the mean SF value was 1.085 (SD 0.68). A two-sample t-test gave a t-value of 15.4 [probability(t > 15.4) ≪ 10⁻⁶] which shows a highly significant difference between the two sets. The difference between the two sets is also supported by a Mann–Whitney U-test [U = 62 812, z = 16.38, probability(z) ≪ 10⁻⁶]. Figure 1 shows the receiver operating characteristic (ROC) curve where the true positive rate (proportion of surrounded set greater than threshold SF value) is plotted against the false positive rate (proportion of non-surrounded set greater than threshold SF value) and each point represents a threshold value for SF. Based on this curve and with a view that the number of false positives should be as practically low as possible, a threshold value of 1.25 for SF was selected. Even though only about one-third of the residues in the surrounded set were correctly identified, when considering whole segments, this threshold value gave a good result: for the 17 segments in the surrounded set, 14 had at least one residue with a SF value ≥1.25, whereas for the non-surrounded set, only two segments out of 189 had at least one residue with a SF value ≥1.25. Thus a threshold value of 1.25 for SF is able to automatically distinguish between surrounded and non-surrounded segments in a way that conforms to a human annotator using molecular graphics. This allows us to use SF to distinguish surrounded and non-surrounded regions in the much larger set of protein complexes.

Fig. 1.

ROC curve for the determination of the SF threshold. Below 1.25, the false positive rate is practically zero. The horizontal axis is the proportion of the non-surrounded set greater than the threshold SF value (false positive rate) and the vertical axis is proportion of surrounded set greater than the threshold SF value (true positive rate). Each threshold value is shown on the plot.

3.3 Application of SF to the whole data

The SF calculation was applied to 976 chains in 888 oligomer entries. The 976 chains comprise 257 831 residues of which 137 865 residues (53.4%) have non-zero SF values. These residues are defined as interface residues. All the data is available at http://cib.cf.ocha.ac.jp/DACSIS/. The SF data is presented in raw format as well as graphically. In addition, the 3D structures of proteins with the high SF segments can be viewed using the molecular graphics software Jmol (http://www.jmol.org/).

3.4 High SF segments occur with high significance in terminal regions

Out of the whole data, segments were selected that contained the longest run of consecutive residues with SF ≥ 1.25. The two residues on the N-terminal flank and the two residues on the C-terminal flank were also included. We added two residues on both termini of the segment, because SF of the segment is calculated with W = 5. We identified 562 segments of high SF (≥1.25) in 362 chains out of the whole set comprising 976 chains (Table 1). These are the surrounded set for the whole dataset. Of the 562 segments, 113 segments are located within a 10-residue range of the N-terminal and 112 segments within 10-residue range of the C-terminal. The remaining 337 segments are located in the internal region of the chain. To check whether this distribution is not random, our null hypothesis would be that the non-zero SF residues are randomly located on the protein chains. We performed the following test in the count of residues, not in the count of segments for simplicity. Since a non-zero SF residue is only found at an interface, high SF segments should be evenly distributed in the interfaces according to the null hypothesis. The 976 chains contain 137 865 residues with non-zero SF value. The number of residues in terminal regions is 15 616 (= 8 × 976 × 2) (Table 1). Note that since W = 5, two residues on both termini cannot be assigned a SF value. Thus the expected number of residues with high SF values in terminal regions is ∼ 165.2 [=(2686/253 927)×15 616]. A χ²-test of the observed distribution of the residues in terminal regions with high SF values [780 (=374 (N-terminus) +406 (C-terminus)] showed that the distribution is extremely skewed and not random [χ²=2288 probability(χ²>2288) ≪10⁻⁶]. It should be noted, however, that 337 segments, a non-negligible number (Table 1), with high SF values are located in the internal regions, mostly as loops.

Table 1.

Distribution of high SF in the terminal regions

Location	High SF segmenta	High SF residue	Count of residue
N-terminal	113 (20.1%)	374 (13.9%)	7808 (3.1%)
Middle	337 (60.0%)	1906 (71.0%)	238 311 (93.8%)
C-terminal	112 (19.9%)	406 (15.1%)	7808 (3.1%)
Total	562 (100%)	2686 (100%)	253 927 (100%)

^aTerminal region is defined as 10-residue range from the terminal residue. When one of the residues in high SF segment is located within the region, it is counted.

3.5 Example of high SF segment at the terminal region and in the loop

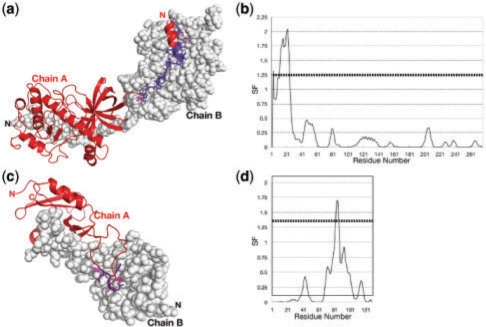
SF was calculated on protein kinase domain of a trp Ca-channel, ChaK (PDB ID: 1IA9) as one of the examples (not used for the adjustment of the threshold). Applying the threshold value for SF (≥ 1.25) to automatically detect the protruding/interwound segments in the interface worked well as shown in Figures 2a and b. Visual inspection shows that only the N-terminal residues of subunit A are surrounded by subunit B (Fig. 2a), corresponding to the automatic method where only the N-terminal residues 3 and 12–24 have SF values ≥1.25 (Fig. 2b). At a glance, exclusion of the N-terminal half of the helix seems unreasonable. However, the whole helix is not inserted into chain B and the N-terminal part of the helix is located far from chain B. The N-terminal residues before the helix are very close to chain B. Hence the SF calculation with the threshold value of 1.25 gives a reasonable result in this case.

Fig. 2.

Result of SF calculation on the kinase domain of Trp Ca-channel, ChaK (PDB ID: 1IA9) homodimer (a and b) and C-type lectin CRD domain bound to coagulation factor IX-binding protein (PDB ID: 1BJ3) (c and d). SF was calculated on one of the subunits only (chain A). (a) Residues with SF ≥ 1.25 on ChaK protein are with side chains and coloured in deep purple. Other residues are coloured in red. (b) SF values of ChaK chain A. (c) Residue with SF ≥1.25 on C-type lectin CRD domain. (d) SF values on C-type lectin CRD domain.

SF was also calculated on C-type lectin CRD domain bound to coagulation factor IX-binding protein (PDB ID: 1BJ3) as an example with the high SF region in a loop (Fig. 2c and d). Residues 82–86 of C-type lectin CRD domain are located on the tip of a long loop and extensively interact with the other subunit. Other regions of the loop are relatively exposed to the solvent.

3.6 FoldIndex indicates that surrounded segments are more likely to be disordered than non-surrounded

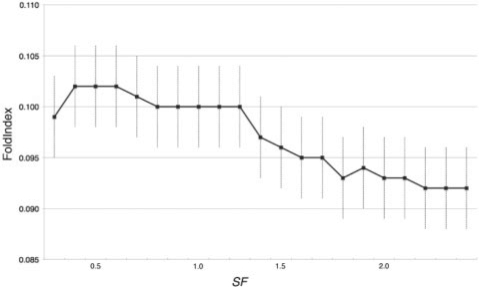
A surrounded set segment was defined at the beginning of Section 3.4. A non-surrounded set segment was defined as one that contained the longest run of consecutive residues with 0 < SF < 1.25 plus the two residues on the N-terminal flank and the two residues on the C-terminal flank (thus the minimum fragment length is five residues as W = 5). There are 562 segments in the surrounded set and 5557 segments in the non-surrounded set. Protruding/interwound segments in the surrounded group have substantial interactions with other subunits, hence before complexation, the segment does not have these interactions and evidently does not assume the same structure as the one observed in the complexed structure. Therefore, a likely scenario is that the segments are unfolded before complexation. If so, a measure of intrinsic liability to fold should indicate a difference between these two groups. FoldIndex is a simple sequence-based measure that is supposed to measure a segment's intrinsic liability to fold or remain unfolded (Prilusky et al., 2005; Uversky et al., 2000). If its value is positive it indicates a polypeptide that has a propensity to fold, whereas if its value is negative it indicates a polypeptide with a propensity to remain unfolded. We applied FoldIndex to the two groups and found that its average value for the non-surrounded group was 0.1193 (SD = 0 .23 from 5557 segments), whereas for the surrounded group it had an average value of 0.0286 (SD = 0.33 from 562 segments) (Table 2). This result was tested using a two-sample t-test and found to be highly significant [t = 6.4, probability(t > 6.4) ≪ 10⁻⁶]. The significant difference between the two groups is also supported by a Mann–Whitney U-test [U = 1.69 × 10⁶, z=10.37, probability(z) ≪ 10⁻⁶]. The average length of the segments in the surrounded group is 8.7 residues, whereas the average length of the segments in the non-surrounded group is 28.0 residues (The length distribution is shown in Supplementary Materials). This calculation weights equally, short and long segments which could introduce a bias. In order to overcome this, a sliding window with five-residue length was applied to each segment thus creating a set of sequences each of equal length. FoldIndex was then applied to each of the pentapeptide sequences in the two groups. The average value for the surrounded group was 0.0122 (SD = 0.432 from 2657 pentapeptides), whereas for the non-surrounded group it had an average value of 0.0399 (SD = 0.4694 from 133 416 pentapeptides). Again this result was tested using a two-sample t-test and also found to be highly significant [t = 3.3, probability(t > 3.3) ≈0.05%]. The difference between the two groups is also supported again by a Mann–Whitney U-test [U = 1.84 × 10⁸, z > 10², probability(z) ≪ 10⁻⁶]. The statistical tests above suggest that there is a negative correlation between SF and FoldIndex. This is verified in the cumulative graph of Figure 3. In this cumulative graph, the point at SF = 1.0, for instance, means the average value of all the FoldIndex values of segments with SF ≤ 1.0. As the upper limit on SF gets higher, so the average of the FoldIndex value gets lower. The cumulative graph shows a sharp drop between SF = 1.2 and 1.3 which corresponds to the threshold value for automatically detecting surrounded regions. As a lower FoldIndex value indicates a greater tendency to be disordered, this negative correlation supports our hypothesis that the surrounded set is less ordered in the uncomplexed state than the non-surrounded set.

Table 2.

Correlation of SF and FoldIndex

SF	Count	FoldIndex (SD)a
<1.25	5557	0.119 (±0.23)
≥1.25	562	0.0286 (±0.33)
Total	6119

^aA two-sample t-test result in t = 6.4 (P ≪ 10⁻⁶).

Fig. 3.

Cumulative distribution of average FoldIndex values against SF. Each point indicates an average value (with standard error) of FoldIndex of the segments with SF values less than the specified value.

3.7 Application of SF to a different data set

The data set we built may contain non-biological interfaces, even though we cross-validated with UniProt (Section 2). We cannot rule out the possibility that the biological interface is located between unit cells. Another possibility is that our dataset does not represent the true distribution of the interfaces, because we did not take symmetric units into account. We, therefore, applied our SF and FoldIndex analysis to the set of protein interfaces presented by Keskin et al. (2004) which took crystal symmetry into account (3799 entries). We found the same significant difference in the FoldIndex of the surrounded and non-surrounded sets for this dataset [probability(t > 9.2) ≪ 10⁻⁶, U = 2.73 × 10⁷, z > 10², probability(z) ≪ 10⁻⁶] and negative correlation between SF and FoldIndex almost exactly reproduces what is seen in Figure 3. Hence, the results presented here are likely to be free from dataset bias.

4 DISCUSSION

We have used simple and easily reproducible methods to analyse properties at subunit–subunit interfaces with the aim of understanding processes involved in the formation of protein complexes. We showed that segments with high SF values have a significantly lower FoldIndex than those with low SF values. This suggests that segments that protrude into, or interwind with, a neighbouring subunit may have a lower propensity to fold. A possible explanation is that segments with high SF values are disordered in non-complexed state, but adopt a definite 3D structure in the complexed state. Truly disordered proteins or disordered protein segments should have negative FoldIndex values. However, the high SF regions have an average positive FoldIndex values close to zero suggesting that these regions may have intermediate propensities for being ordered and disordered. This may relate to so-called ‘dual personality’ fragments in proteins (Zhang et al., 2007). Dual personality fragments are those that have been found to have a well-defined structure in one X-ray experiment, but found to be unresolvable in another. An example given in the paper (Zhang et al., 2007) concerns cyclin dependent kinase, which has unresolved fragments in one structure, but these fragments have definite structure in another when it is phosphorylated and bound to another protein (cyclin). The maximum SF values of the two fragments, namely Ile35-Val44 and Leu148-Glu162 (PDB ID: 1QMZ chain A), are 1.14 and 0.97, respectively, which are high, although below the cutoff of 1.25 used here. Their FoldIndex values are −0.09 and −1.15, respectively, indicating a small tendency to be disordered in the former and a strong tendency to be disordered in the latter. Although phosphorylation may play a role in this example, it is clear that the cyclin protein also plays a role, as the fragments' SF values are relatively high. Thus, this example of dual personality fragments is surely related to the hypothesis that partially unfolded regions are involved in protein–protein interactions and adopt a protruding structure upon complexation with a partner protein.

These protruding/interwound segments at interfaces may be a remnant of the fly-casting process (Levy, et al., 2005; Shoemaker et al., 2000), whereby an unfolded region in a monomer makes the initial contact with the partner biomolecule and reels itself in as the unfolded region folds. A possible scenario would involve an unfolded region, which is part of a largely folded monomer. This would increase probability of capture by increasing the search radius. The folding of the unstructured region would then occur as a final stage in the docking process, leaving the initially unstructured region as a remnant, now structured and having substantial contacts with the partner. It is easier to imagine that this occurs in a partially folded protein by fly casting an unfolded terminal region rather than an unfolded loop and this would explain the high proportion of N- and C-termini in the surrounded dataset.

Segments in the surrounded set were found in 362 (see Section 3.4) out of 976 chains (see Section 3.3) suggesting that in more than one third (= 362/976) of known protein complexes, disordered segments of a protein play a substantial role in complex structure formation. Of those 362 chains, we found 562 (see Section 3.4) segments in the surrounded set indicating that in some cases multiple segments are involved in the fly-casting process.

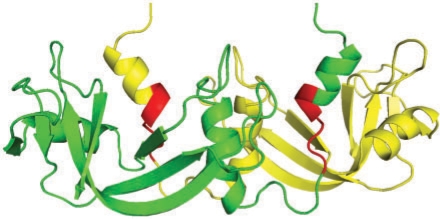
A similar process would also be expected to occur in domain swapping where part of a monomer structure becomes unfolded and interwinds with another identical monomer to form a dimer in an oligomerization process (Rousseau et al., 2003). The interfaces, especially the subunit-crossing linkers, are unlikely to be complementary and so in order to make a stable multimer, there needs to be some interwinding as can be seen in the examples given in Figure 2 of the paper by Rousseau et al. We have taken as an example the case of bovine seminal ribonuclease from Figure 2 of the paper. The protein is the first RNase found to swap domains and we found high SF regions in a C-terminal part of the swapped N-terminal α helix (Fig. 4). The N-terminal region of the α helix protrudes into solvent and the high SF region which precedes it is surrounded by the other subunit (average SF = 1.42). Based on our findings we would expect the high SF region (with the sequence: FERQHMDSGN) to have a low FoldIndex which indeed it has (−0.42). We speculate therefore that the pre−folded α helix on the N-terminus is fly-casted by this unfolded segment to the other subunit, which it reels in until the unfolded segment is attached appropriately to the main part of the other subunit resulting in an exchange of α helices.

Fig. 4.

Example of SF in domain swapping found in the homo-dimer of bovine seminal ribonuclease (PDB ID: 11BA). One of the monomers is in green and the other in yellow. The high SF region is in red. N-terminal α helices are swapped.