Emergent gene order in a model of modular polyketide synthases

Abstract

Polyketides are a class of biologically active heteropolymers produced by assembly line-like multiprotein complexes of modular polyketide synthases (PKS). The polyketide product is encoded in the order of the PKS proteins in the assembly line, suggesting that polyketide diversity derives from combinatorial rearrangement of these PKS complexes. Remarkably, the order of PKS genes on the chromosome follows the order of PKS proteins in the assembly line: This fact is commonly referred to as “collinearity”. Here we propose an evolutionary origin for collinearity and demonstrate the mechanism by using a computational model of PKS evolution in a population. Assuming continuous evolutionary pressure for novel polyketides, and that new polyketide pathways are formed by horizontal transfer/recombination of PKS-encoding DNA, we demonstrate the existence of a broad range of parameters for which collinearity emerges spontaneously. Collinearity confers no fitness advantage in our model; it is established and maintained through a “secondary selection” mechanism, as a trait which increases the probability of forming long, novel PKS complexes through recombination. Consequently, collinearity hitchhikes on the successful genotypes which periodically sweep through the evolving population. In addition to computer simulation of a simplified model of PKS evolution, we provide a mathematical framework describing the secondary selection mechanism, which generalizes beyond the context of the present model.

Polyketides are found in bacteria, protozoa, plants, and animals where these secondary metabolites mediate a variety of interactions between cells and their environment (1). Polyketides function as messengers in cell-to-cell communication (2), as antimicrobial agents against competitors, and as immunosuppressors or virulence factors (3) in pathogens. The extensive structural and functional diversity of natural polyketides may be the result of an interspecies and host–pathogen chemical “arms race”. Alternatively, the ability to generate chemical diversity might be an end in itself, increasing the likelihood of discovering biologically potent molecules (4).

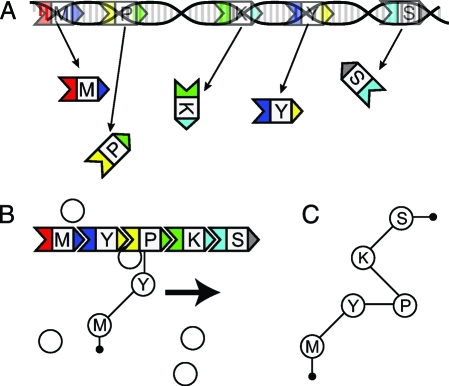
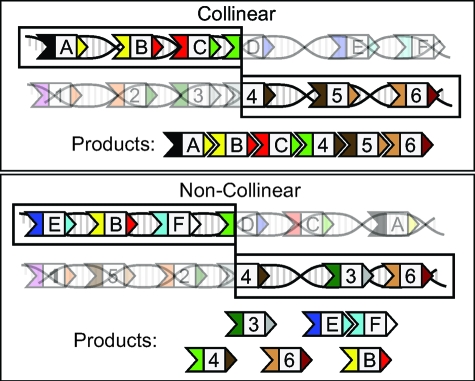
In bacteria, the diversity of polyketides is achieved through a unique combinatorial biosynthesis mechanism. A large class of bacterial polyketides is constructed by ordered complexes of modular polyketide synthase (PKS) proteins via sequential polymerization of acylthioester monomers such as malonyl-CoA (5). Each step of chain extension is performed by a single PKS catalytic module. These modules include three obligatory catalytic domains involved in sequential elongation of the nascent chain. The “minimal” three-domain PKS leaves the added monomer as a keto group. Three more-complex modules include up to three reductive domains (keto reductase, dehydratase, enoyl reductase) which sequentially modify the chemical form of the added monomer. The assembly of modules into the synthetic complex is directed by specific interactions between C- and N-terminal docking domains (6 –10) as shown in Fig. 1.

Fig. 1.

A schematic representation of the DNA → PKS → polyketide conduit by which genetic information becomes a functional polyketide. (A) The translation of the PKS genes into PKS proteins. The head and tail domains are colored; binding is exclusive between corresponding domains of the same color. The flavor of chain extension performed by the PKS is represented here by a letter. (B) PKSs assemble into multiprotein complexes, which catalyze polyketide production. Individual PKS proteins perform one cycle of chain extension and then pass the result to the next PKS in line. The result, seen in C, is a product polyketide analagous to the functional complex of PKS proteins.

The order of catalytic modules determines the chemical pathway and hence chemical structure of the product polyketide. This modularity allows, in principle, the synthesis of at least 4^L different polyketides by rearrangement of the four flavors of catalytic modules (L being the length of the polyketide). Additional levels of complexity, such as chirality and alternative acylthioester monomers, further increases this combinatorial potential (11). Realization of this diversity depends crucially on the observed substrate tolerance of catalytic modules (5). The experimental effort to exploit the combinatorial potential of this biosynthetic pathway is an active area of research (12, 13).

Remarkably, the order of catalytic modules in the biosynthetic complex is closely reflected in the chromosomal order of the underlying genes—a property known as the “collinearity rule” (14). This order holds within PKS operons, and it implies that most physically interacting PKS proteins are encoded contiguously (9). Collinearity of PKSs stands out because although gene order is conserved between closely related bacterial species, its conservation is rapidly lost as species diverge, even for genes within operons (15, 16). Typically gene order is considered selection-neutral, with degree of conservation even used to estimate phylogenetic distance (17). Yet physically interacting proteins have been noted to conserve gene order for longer times (15), suggesting an intuitively plausible tendency for interacting proteins to form “genetic modules”. Aside from the possible explanation in terms of common transcriptional regulation, formation of such modules could be driven by evolutionary forces. R.A. Fisher argued that chromosomal proximity of genes encoding interacting proteins is favored by the reduced probability of coadapted genes to be separated by recombination (18). The “selfish operon” hypothesis explains genetic clustering by its role in facilitating horizontal gene transfer (HGT) between bacteria (19).

Functional and genetic modularity of the polyketide biosynthesis system suggests that it evolves via combinatorial exploration of biochemical space facilitated by gene duplication, recombination, and horizontal gene transfer (9). Because PKS protein domains from different organisms retain a high degree of sequence identity, homology-preferring recombinant processes are expected to drive the shuffling of PKS genes between DNA strands. This expectation is supported by the evidence from comparative genomics (1, 20, 21) including several examples of HGT events that have been inferred from sudden transitions in sequence identity along PKS gene clusters (1). If one accepts the hypothesis that HGT and homologous recombination are the main drivers of the search for novel polyketides, it becomes interesting to consider how natural selection might augment the modular features of the system that facilitate its adaptation to changing circumstances, or, in other words, make it more “evolvable” (22).

Here we shall use existing understanding of the modular PKS system summarized above to construct a theoretical model of evolution of a combinatorial pathway under continuous selective pressure for novelty. In this model, genetic collinearity will emerge spontaneously as a chromosomal architecture that facilitates adaptive evolution. Specifically, we shall assume PKS evolution to be driven by a “Red Queen” (RQ)-type paradigm (23) of a continuous arms race between polyketides and the environmental pressures they ameliorate. Thus, the fitness benefit of existing polyketides decays with time, giving individuals synthesizing novel polyketides a selective advantage. In our model, novel pathways are produced by recombination-induced shuffling of synthase genes. Collinearity facilitates the creation of new, long, synthetic pathways and is established and maintained by hitchhiking on the successful pathway genotypes it helps create. We shall define the model and use numerical simulations to determine a “phase diagram” that describes the conditions under which “secondary selection” maintains collinearity as a function of key parameters such as the rate of HGT/recombination and the rate of fitness decay. We shall then provide a probabilistic description of the dynamics that quantitatively explains the action of secondary selection on collinearity.

The Model

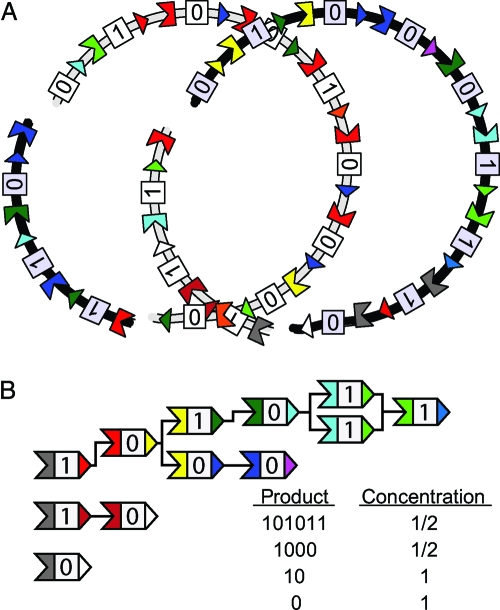
We consider a radically simplified model of the modular PKS system that retains three key features: (i) modularity and combinatorial diversity; (ii) generation of novel biosynthetic pathways by recombination; and (iii) selective pressure favoring novel products. To reflect the simplification and abstraction inherent in our model, we shall speak of multiflavored “synthases” and combinatorial chain “products” rather than PKS proteins and polyketides. Our synthases consist of three regions: head and tail docking domains and a central catalytic module taking on two “flavors” (Fig. 2). The associated gene is arranged likewise, head and tail domains flanking the catalytic module. The two-flavor catalytic module restriction allows products to be represented as binary strings as seen in Fig. 2 B. Docking domains belong to K different classes: heads and tails bind exclusively when they are of the same class.

Fig. 2.

Representation of recombination in the model of PKS system. (A) Two model chromosomes, one gray and one black, undergoing recombination. The genes for synthases are represented by the same arrows as the synthase proteins themselves. The circular chromosomes exchange homologous sections of DNA to form recombinant offspring. Note that because circular chromosomes can recombine upon an arbitrary rotation relative to one another, many outcomes are possible even as a product of two identical parental chromosomes. (B) The products of one of the recombinant offspring are shown with their associated concentrations. The fitness is a sum of the fitness effects of those four products weighted by concentration.

The fitness of an individual synthesizing product k is given by f = 1 + Δf _k(t) (this readily generalizes to the case when more than one product is produced; see Fig. 2 B and Materials and Methods). Selection for novelty is introduced by assuming that the fitness contribution of a new product k subsequently decays with time Δf _k(t) = Δf _k(0)e ^−t/τ. We call the time constant τ the “environmental decorrelation time.” This decay is motivated by considering an archetypal antibiotic, the effectiveness of which decreases as its targets gain resistance. The consequence is selective advantage for novel products. One expects that beneficial products must have sufficient complexity and hence be sufficiently long (e.g. most polyketides need to cyclize), an assumption supported by the observed length distribution of polyketides seen in Fig. S1. We shall consider in detail a particularly simple fitness landscape where only products of certain length L* have a fitness benefit s, so that Δf _k(0) = sδ(|k| − L*). In simulations shown, L* = 7 and s = .1, but results are qualitatively similar for different L*,s and are expected to hold for more general fitness functions.

We consider the evolution of a population of size N with model individuals appearing in the next generation in proportion to their fitness and recombining with rate r (see Materials and Methods). In this model, variation arises solely by recombinant shuffling of synthases. However, because of fixation, allelic diversity will decay unless replenished by mutations. To maintain the diversity of head/tail domains, in order to study long-time behavior, we introduce a “comutation” process in which a head/tail pair on an individual chromosome change class together. This comutation represents the accumulation of correlated changes in the interacting head/tail domains, which preserve their specific interaction (9). Comutation is phenotypically invisible: It is still the case that all phenotypic diversity is due to recombination. The results we report below are insensitive to this process, provided that it occurs at a rate sufficient to prevent terminal decrease in the number of head/tail alleles.

It is natural to quantify collinearity in terms of mean chromosomal distance d (see Materials and Methods) between interacting heads and tails because this is proportional to the likelihood of recombination affecting the pathway. Collinearity of an individual “genome,” y, is then defined by y =1 −d/d̄, where d̄ is the average d in the ensemble of all possible genome rearrangements. If the chromosomal order of synthases follows their order in the pathway perfectly, then d = 0 and y = 1. On the other hand, without selection on gene order, population average 〈d〉 relaxes to the random ensemble value d̄, driving the population average 〈y〉 to zero. As we shall see, when subjected to selective pressure to evolve novel products, the population will acquire a positive average collinearity reflecting emergent order.

Results

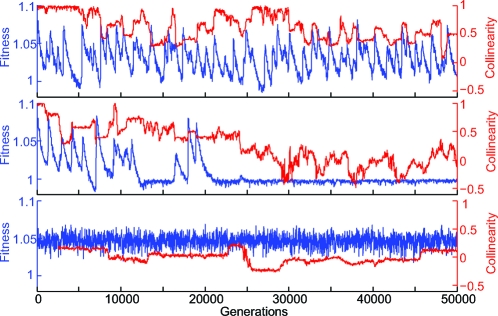
Our model exhibits three fundamental regimes of behavior dependent on population parameters. The first is the continuously evolving RQ regime, which is characterized by populations with high average fitness and emergent collinearity. The second is a “quiescent” regime with low average fitness and no collinearity. The third regime obtains in the special case of a time-independent environment and, hence, time-independent fitness (τ → ∞).

The evolving RQ state exhibits a characteristic saw-tooth behavior in the population-averaged fitness (Fig. 3 A). This fitness trajectory is produced by successive selective sweeps of the population by genomes encoding novel products of length L*. After a sweep, the population is dominated by individuals expressing a particular L* product. Subsequently, the average fitness decays, tracking the decay of the fitness granted by the swept product. Decreasing average fitness increases the relative advantage of individuals expressing novel L* products, thereby increasing the chance that recombinants expressing such a product will spread. Once a new beneficial genotype escapes low-number stochasticity, a selective sweep occurs and the cycle continues.

Fig. 3.

Population-averaged evolutionary trajectories characteristic of the three dynamical behaviors exhibited by the model. (A) The evolving (RQ) behavior; genotypes encoding novel products are repeatedly created and sweep the population, maintaining high fitness and collinearity. (B) Here, environmental decorrelation time τ is reduced by a factor of two (to 500 generations). The faster fitness decay results in the population eventually failing to find a novel product quickly enough to avoid the effects of drift, causing a transition to the Q state. Consequently, the initial collinearity decays away and then fluctuates around the random ensemble average of y = 0. (C) Environmental change has been removed, τ → ∞, and static behavior is observed.

If enough time passes after a sweep without a novel product found and established in the population, exponential decay of fitness will reduce the strength of selection below that needed to “purify” the population of disruptive recombinants. This reduction occurs once drift dominates over selection, at a postsweep time t ≈ τlog(Ns). The result is an accumulation of genotypes that have lost the ability to produce L*-long products. We call this the quiescent (Q) state: Individuals have few interacting head/tail pairs, pathways are broken into short segments, and only short products are produced. In a fitness landscape in which minimum product length is necessary for fitness benefit, this state is essentially permanent: The population is finite and the likelihood to create L*-long pathway chains out of the short fragments is exponentially suppressed with L*. Fig. 3 B shows a population undergoing this transition.

The case of an unchanging environment (τ → ∞) provides a useful reference. In the “static” (S) state, the purifying effect of selection preserves the pathway producing the beneficial L* product. However, because functionality of the pathway does not depend on the order of genes on the chromosome, genes are continuously reshuffled, resulting in 〈y〉 = 0. The only fitness effect relevant to population averages is the recombination load. Accounting for the recombination load, we expect an average fitness of approximately 〈f〉 = (1 + s)(1 − r), consistent with what we observe in Fig. 3 C.

Collinearity emerges spontaneously and is maintained in the evolving RQ state. The evolving population in Fig. 3 A maintains high collinearity through repeated selective sweeps. Moreover, if the population is initialized with no collinearity present, it is generated over time. Excursions to noncollinear genetic realizations do occur but are temporary. Long-time average of collinearity in the RQ state is 〈y〉 ≈ .38. This number depends on L* and the chromosomal architecture of our model but is essentially independent of r, τ, N parameters that instead determine the stability of the RQ state.

Populations that transition into the Q state do not maintain collinearity, even if initially present. In Fig. 3 B we see preexisting collinearity decay away after such a transition because of genomic reshuffling. As we shall discuss in Secondary Selection and Collinearity, maintenance of collinearity requires the population to be repeatedly swept by high-fitness genotypes, which does not occur in the Q state. A similar situation obtains in the static state where selective pressure maintains a particular high-fitness L* pathway. Because its fitness does not decay with time there is no pressure for generation of new products and the static state does not maintain high collinearity.

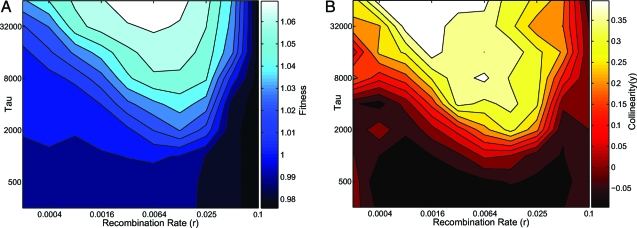
The two key parameters controlling the long-term behavior of the populations are the recombination rate r and the environmental decorrelation time τ. In Fig. 4 we display time-averaged fitness and collinearity of populations evolved in a range of r, τ. There is clear separation into two regimes: a high-fitness, high-collinearity regime corresponding to the evolving RQ state, and a low-fitness, noncollinear regime corresponding to the Q state. The regime boundaries derive from the dual effects of recombination in this system. Recombination load is dominant at high r: The spread of individuals encoding a novel product is hindered by the dissociative action of recombination. A novel individual has a nonzero chance of sweeping only if r < s, which limits the domain of the RQ. On the other hand, recombination is the sole source of phenotypic novelty. The persistence of evolving behavior requires that novel genotypes encoding L* products be created in sufficient number so that at least one sweeps the population before entry into the Q state, which occurs in a time proportional to τ. There are Nr novel genotypes created each generation, and the probability of one sweeping, once created, is approximately s. Hence, the persistence of evolving behavior requires that Nrsτ > C for some constant C, which describes the second boundary in Fig. 4. This inequality contains the dependence of the RQ regime boundaries on the population size N and strength of selection s. We emphasize that this boundary is not a real transition but a cross-over, low Nrsτ corresponds to a high probability to transition into a Q state before a given time T (i.e. before the end of the simulation). This probability decreases rapidly as Nrsτ increases.

Fig. 4.

Long-time averages of population fitness (A) and collinearity (B) as a function of recombination rate (r) and decorrelation time (τ). Darker color corresponds to lower values of average fitness (A) and collinearity (B). Individual points are averages taken over 100 replicates of our simulation, each running for 10⁶ generations. The region of high collinearity corresponds to the region of high fitness, which is also the region of (r,τ) parameter space in which populations maintain evolving behavior.

Secondary Selection and Collinearity

The emergence of collinearity is interesting because collinearity has no phenotypic effect in our model. Genomic reshuffling by recombination brings collinearity down to the random ensemble level. Hence, in order to persist, it must be constantly reinforced. This reinforcement is a consequence of collinear genomes, or portions of genomes, making better building blocks for constructing new, long pathways via recombination, as shown schematically in Fig. 5. Novel recombinant genomes that encode long pathways, and hence have high fitness, exhibit higher-than-average collinearity. Selective sweeps by such genomes amplify collinearity and counteract the attenuating action of recombinant reshuffling.

Fig. 5.

Collinearity increases the likelihood of recombination forming novel products. Recombination between two collinear parents produces a long and potentially high-fitness product. When nonsyntenic parents recombine, many head/tail bonds are cut and the recombinant offspring contains only fragmentary synthase complexes.

Let us quantify the dynamics of collinearity in a population as it moves from one selective sweep to the next. Consider the initial conditions obtaining after a sweep in which the population is approximately clonal. We assume that the sweep time scale of log(N)/s is small compared with the other time scales in the problem, assign time zero to the sweep event, and consider the subsequent dynamics of the population. Let the population distribution of collinearity be ξ(y,t) with the initial condition ξ(y,0) = δ(y − y ₀), where y ₀ is the collinearity of the genotype that swept at time t = 0. Recombination induces variation in y, which is described by

Γ(y|y′,y″) describes the probability of a recombinant offspring of parents with collinearity y′,y″ to have collinearity y. At long times, this equation describes relaxation of ξ(y,t) toward the distribution of y in randomly shuffled genomes, ρ(y), which is well approximated by a Gaussian centered on y = 0 (see Fig. 6).

Fig. 6.

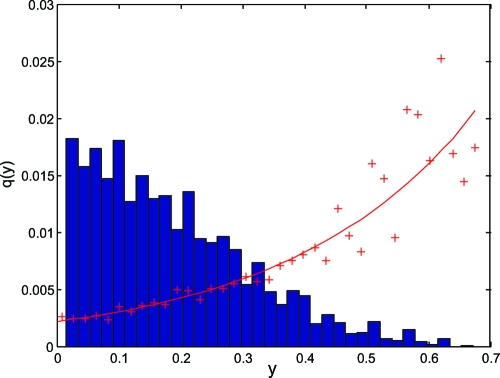
The probability of a recombinant individual encoding a novel L*-long pathway in our model depends on its collinearity (y). This dependence, determined numerically by sampling individuals with collinearity y generated by recombinations between parents of similar collinearity, is shown with red crosses and is approximately exponential, as shown with a solid red line. The blue histogram represents the relative frequency, ρ(y), with which collinearity y appears in the ensemble of randomly ordered genes. This frequency distribution is well fit by a Gaussian centered on y = 0.

We introduce q(y)—the probability that a recombinant with collinearity y encodes a novel L* product (see SI Text). We expect this function to increase monotonically with y. This expectation is confirmed by determining it numerically for our model in silico, as shown in Fig. 6. The process of sweep generation is two-fold: A novel, high-fitness genotype must arise and avoid stochastic extinction before the deterministic selective sweep can occur. In each generation, there will be, on average, rN recombinants with approximately q(y) chance of having high fitness. The probability of a novel recombinant escaping immediate extinction is given by

Here, χ[x] = x/(1 + x) for x > 0 and is zero otherwise. p _es becomes nonzero when the fitness advantage relative to the mean fitness of the population s − s̄(t)exceeds r. The time dependence of mean fitness, s̄(t)=se ^−t/τ, corresponds to the exponential decay of the fitness benefit of products extant in the population.

We can now write the probability of the next sweep occurring at time t after the sweep of an individual with y = y ₀:

with

Note that p _es(t) in this expression effectively introduces a waiting time before the next sweep can occur: The fitness must decay sufficiently that novel individuals have a relative selective advantage exceeding r.

We can now consider a “recurrence relation,” the probabilistic mapping of the collinearity obtaining in a particular sweep to the collinearity of the next sweep. In particular, we are interested in the expected change in collinearity from one sweep to the next. Let us assume that ξ(y,t) changes slowly on the time scale of an interval between successive sweeps. This consequence of purifying selection holds in the RQ state (with τ < ∞) and is confirmed by simulations. We can then approximate the population distribution in y with its initial condition (delta function at y ₀) and write an expression for the sweep to sweep change in y:

The first integral on the right hand side of Eq. 5 is positive, the sign of the expected change in y is determined by the second term. The latter integral involving Γ will quite generally decrease, with increasing y ₀ crossing zero at certain y*, which defines a stable fixed point of collinearity attained upon repeated selective sweeps. This property can be illustrated by a simple approximation where Γ(y|y′,y″) = ρ(y) corresponding to the case in which offspring collinearity follows the random distribution independent of parental values y′,y″. In that case, $y^{*}=\int dyyq(y)\rho (y)/\int dyq(y)\rho (y)\approx 0.18$. A more realistic and general analytic form of Γ(y|y′,y″), described in the SI Text, also yields a fixed point. A direct numerical average over Γ(y|y ₀,y ₀), obtained by sampling recombinant chromosomes within our model, yields y* = 0.32, which is comparable with the collinearity observed in the RQ state.

Interestingly, the existence of the fixed point depends solely on Γ(y|y′,y″) and q(y). Other model parameters (e.g. r,τ,s,N) determine only whether the population undergoes the repeated sweeps that drive it towards the fixed point. This separation between the existence of repeated sweeps and their ultimate effect is important, it allows the generalization of our analysis to other systems—such as real PKSs, in which details assuredly differ.

Discussion

Our analysis has been based on a model which, instead of attempting a faithful representation of all aspects of PKS pathways, focused on distilling several key features and investigating their consequences. These features are: (i) modularity and combinatorial diversity of pathways; (ii) the capacity to generate the combinatorial diversity through recombination; and (iii) continuous evolutionary pressure to generate new products. Certain details of our model were motivated by computational expediency rather than biological reality; we must ask if our conclusions are in any way dependent on our choices. In particular, our model used two (rather than four) synthase flavors, used a small, circular chromosome consisting solely of synthase genes, and chose a fitness landscape that differentiated between products solely on the basis of length. These details affect the likelihood of recombinants being novel and fit, and consequently have quantitative implications on the cross-over between the RQ and Q regimes and the level of collinearity maintained in the RQ state. These details do not affect the qualitative behavior of the model, in particular the existence of an RQ regime in which repeated sweeps produce emergent collinear ordering of synthase genes.

Perhaps the most significant difference between our model and the real PKS system lies not in the model representation of the PKS pathway but in the differences in population structure. Modular PKSs occur widely in bacteria and it is the totality of these bacteria that constitute the “population” in which they evolve. In contrast to the panmictic population we consider, real PKSs evolve in a “highly structured” population subject to differing environmental pressures and isolated by interspecies barriers violated by occasional HGT events. Our model representation of HGT as recombination occurring with a certain rate is reasonable as long as the number of HGT events that occur on the time scale of environmental change (and hence of evolution) is large. On the other hand, the heterogeneity of selection on different species and subpopulations will result in much greater genetic diversity than is maintained in our panmictic population. Additionally, real bacterial populations maintain under selection not one but many distinct polyketide products. This heightened diversity of PKS pathways and evolutionary targets reinforces the basic mechanism of creation of and selection for novelty implemented in our model. We expect its qualitative conclusions, i.e. the existence of a continuous evolving RQ regime with emergent genetic collinearity, to continue to apply.

We note that gene order in our model was driven not by the pressure to reduce the rate with which interacting docking domains are separated by recombination (18) but by the selection for rapid generation of new pathways. It should not be surprising that we find a regime in which recombination is beneficial when our fitness function changes quickly enough with time; previous models incorporating environmental variability and epistasis have shown similar behavior (24). Our goal here has been less to investigate the conditions favoring recombination, which is itself an interesting question discussed by many authors (25), but to examine a possible evolutionary connection between recombination and genomic architecture. The latter is particularly interesting in the case of strong interactions between genes, also known as physiological epistasis (26), which through interplay with recombination can create selective pressure for modularity in gene arrangement (27, 28). The PKS system (and our simplified model of it) represent an interesting special case of epistasis associated with the requirement for multiple coadapted synthases inherent in the biosynthetic architecture.

The framework we employ here to describe the secondary selection on collinearity is generalizable to other systems and genetic characteristics. One such characteristic that suggests itself is modularity, and much significant work has been done exploring its role in the evolutionary process. Tailed phages are thought to be an example of modular evolution (29, 30) with “easy and continual access to… variety” being suggested as the reason for the existence of their modular architecture (31). A seemingly different class of genetic characters subject to secondary selection are the mutator strains (32, 33). In contrast to collinearity, mutator strains have a direct, negative contribution to fitness because of the increased mutation load. Yet mutator genotypes can become established in a population (32) because of the increased access to novelty provided by higher mutation rates. All of these cases can be reformulated and analyzed in the framework of secondary selection that we have developed here.

The relevance of the present work to PKS evolution will be best assessed by bioinformatic analysis of PKS pathways with the goal of assembling evidence of HGT, gene duplication, and domain swapping in PKS genes and pathways. This work has begun (1, 20); however, current studies are still limited by genomic data—an impediment that is being increasingly overcome. It is clear that the collinearity effect exists (14, 34) and is a quantifiable phenomenon (9). Still, if our proposed mechanism has substantially contributed to this effect, we have some further expectations for modular PKS systems. Genetic mosaicity in these complexes should be common and widespread. Not only will mosaic PKS genes exist but so will mosaic pathways. Recombination joints will often correspond to protein domain boundaries, as has been observed in phages (35) as well as in PKSs (20). Collinearity will be present, but will not be perfect. We would like to further constrain the relative contribution of different evolutionary modes, such as mutation and gene duplication, which have also been observed in PKS evolution (36). Further systematic phylogenetic analysis at the gene and protein domain level in modular PKSs will continue to be interesting and informative as to their evolutionary history, allowing better use of the predictions from models such as ours.

Materials and Methods

Simulated population dynamics used a geometric offspring distribution with the expected number given by an individual's fitness normalized by the population average fitness. Individuals propagate in discrete, nonoverlapping generations. Average population size was N = 10³. Model individuals have circular chromosomes (or “plasmids”) with M synthase genes. Each member of the offspring generation has probability r to recombine with another member so chosen. Recombination is reciprocal and homologous in the sense that exchanged segments are the same length and begin and end with the same genetic region, as seen in Fig. 2 A. This property ensures that the size and structure of chromosomes is constant under recombination. All relative rotations of recombining chromosomes are equally likely.

Head and tail domains (H _i, T _j) are drawn from a set of K + 1 different classes with K = 15. H _i = 0 and T _j = 0 are terminator domains, which do not bind. An individual's fitness is determined by summing over the fitness effects of all products synthesized by the chain assemblies of its M synthases. Specifically, $f=1+\sum _k{C}_k\Delta f_k$ where k labels the products. The fitness contribution Δf _k is weighted by C _k, which is the probability of assembling the corresponding synthase complex with the assumption of equiprobable binding of cognizant H/T pairs. Fig. 2 B shows the products and associated C _k of a sample individual. We suppress looping complexes by assigning them zero fitness.

The mean distance between interacting H/T pairs, d, is defined in terms of the distance along the chromosome dist(H _i,T _j). Adjacent H/T pairs are at distance zero. Maximal distance on our circular chromosome, is M/2. Average H/T pair distance, normalized to the length of the chromosome, is

The sum is over all heads and tails, and δ_HiTj = 1 if H _i and T _j belong to the same class (i.e., bind) and is zero otherwise. Average d in the equiprobable ensemble of all possible gene arrangements is d̄ =1/4.