An investigation of the MC-SIMEX method with application to measurement error in periodontal outcomes

SUMMARY

Measurement error is pervasive in medical research. In periodontal research studies, one measure of disease status is the probed pocket depth (PPD), the depth of the space between a tooth and the surrounding gum. In larger studies, these assessments are made by multiple examiners, each having distinct measurement error characteristics. Because PPD is recorded in whole millimeters, it may be regarded as discrete and its associated error as misclassification error. This study investigates the impact of this measurement error when evaluating the effect of periodontal disease status on levels of inflammatory markers in gingival crevicular fluid (GCF). The marker readings are either left or right censored, due to quantities that are either too small to be reliably quantified or so large that they saturate the detector. Additionally, marker readings from multiple periodontal sites within a subject's mouth are correlated. These considerations give rise to a clustered survival model for the marker readings in which the discrete predictor of interest is misclassified. Associations between the GCF markers and periodontal assessments are corrected for misclassification error using the MC-SIMEX method. Simulation studies reveal the impact of varying degrees of misclassification error on associations of interest. Analysis of pilot data from a periodontal study, for which examiner misclassification rates are estimated from calibration studies, further illustrates the approach.

1. INTRODUCTION

Measurement error is pervasive in medical research. Carroll et al. [1, §1.6] discuss examples arising from nutrition research, in which nutrition intake instruments (24-hour recall or food frequency questionnaires) are well known to be error prone; coronary kidney disease, in which an estimated glomerular filtration rate is often substituted for a genuine laboratory measurement; and pollution exposure studies, in which particulate concentrations at specified locations are used as surrogates for personal exposure. There is a large body of work addressing CD4 counts as noisy predictors for AIDS onset or progression (e.g. [2, 3, 4, 5, 6, 7, 8] ), and, in an analogous context, Lin et al. [9] handle prostate-specific antigen levels as noisy predictors for prostate cancer onset. Applications such as these have motivated statistical methods for handling measurement error in a wide variety of models, including linear regression, generalized linear mixed models [10, 11, 12], kernel smoothing [6], Cox proportional hazards models [4], frailty models [13, 14] and accelerated failure time models [15]. This paper addresses an application arising from oral health research that leads to a clustered survival outcome (subject to either left or right censoring) and a discrete covariate measured with error. The approach combines the clustered survival measurement error models of Li and Lin [14] (and also [13]) with the misclassification covariate error of [16].

In periodontal research studies, disease status is determined using multiple periodontal assessments, e.g. probed pocket depth (PPD) and clinical attachment loss. In larger studies, these assessments are made by multiple examiners, each subject to distinct measurement error characteristics. This study investigates the impact of this measurement error when evaluating the effect of periodontal disease status on levels of inflammatory markers in gingival crevicular fluid (GCF). The levels of the inflammatory markers, specific cytokines, are determined by an assay described briefly in Section 2.2 that has both a lower limit of detection and a quantitation limit, hence leading to observations potentially censored either below or above.

Variability in PPD determination is well known and has led to the established practice of training and calibrating multiple examiners for larger oral health studies. While trained examiners generally exhibit a high degree of agreement (over 95%) within one millimeter in PPD, exact agreement is less impressive. Hence methods that incorporate PPD as an explanatory variable are subject to the effects of measurement error in PPD. The simulation-extrapolation (SIMEX) algorithm [17] provides a means to correct for the bias attributable to measurement error. The SIMEX method empirically determines the relationship between the degree of measurement error and the estimate of the coefficient of interest. A bias correction for the estimated coefficient is obtained by extrapolating this relationship to the situation of zero measurement error. The approach is quite flexible as it requires only a consistent estimator when no measurement error is present and an estimator or known distribution for the measurement error.

Küchenhoff et al. [16] introduced the misclassification SIMEX (MC-SIMEX) algorithm for applying the simulation-extrapolation method to discrete variables measured with error. In a series of simulation studies in the context of logistic regression models, they demonstrated the ability of MC-SIMEX to substantially reduce bias in parameter estimates relative to naive methods (i.e. methods that ignore measurement error). They further illustrated their methods using data from a longitudinal study of caries experience, in which the binary assessment of caries was subject to measurement error. Subsequent work derived an estimate of the asymptotic variance of the bias-corrected coefficient [18] and provided an R [19] package [20, 21] that implements SIMEX and MC-SIMEX for a number of common statistical models.

Motivated by the context of assessing the association between GCF cytokine levels and PPD, this paper describes a statistical model for the cytokine levels that accommodates within-mouth correlation and both left and right censoring. Because PPD is recorded as the largest whole millimeter less than the value observed on the probe, PPD is handled as a discrete predictor, subject to measurement error, i.e. misclassification. The structure of the measurement error is specific to each oral examiner. A simulation study investigates the ability of MC-SIMEX to correct for bias in the context of this model and data.

Section 2 describes briefly the study context and data motivating this work. Section 3 describes the statistical model of interest relating the PPD of a periodontal site to the concentration of cytokines in GCF obtained from that site. The application of MC-SIMEX in this model and implementation are discussed. A simulation investigating the ability of MC-SIMEX algorithm to recover the association between PPD and cytokine concentration is presented in Section 4. Analyses of the pilot periodontal study data are presented in Section 5, and the paper concludes with discussion in Section 6.

2. MOTIVATING DATA

A cross-sectional study was performed to investigate the association between periodontal disease status and the concentrations of specific inflammatory markers in gingival crevicular fluid. The study population consisted of African American Gullah with diabetes. The Gullah are descendants of Africans brought to the US from the rice-growing regions of West Africa who now inhabit the Low Country, especially the Sea Islands, of South Carolina and Georgia. Demographic information including age, gender, body mass index, and smoking status, as well as glycosylated hemoglobin levels (HbA1c) and a full periodontal examination were obtained for all study participants. Patient recruitment and additional study details are available elsewhere [22, 23, 24, 25]. The work described in this paper was initiated with a pilot sample of 43 subjects to investigate the effects of measurement error in periodontal pocket depth readings on analyses of the association with GCF cytokine levels.

2.1. Oral examination and examiner calibration

A full periodontal examination was performed on all study participants. Three oral examiners were trained by a standard examiner for measurements of probed pocket depth (PPD) and the distance from the cemento-enamel junction to the gingival margin (CEJ-GM). PPD was recorded in whole millimeters (mm) as the floor of the value observed on the probe up to a maximum of 15 mm. A subsequent calibration study established the degree of agreement between the study examiners and the standard examiner. The calibration study was designed to achieve estimates of agreement between study and standard examiners with high precision; additional details, including the rationale behind its design, are described by Hill et al. [26]. The results for agreement within one mm in PPD were 97% with 95% confidence interval (CI) (96%, 99%), 96% with CI (95%, 98%) and 99% with CI (98%, 99%), for the three study examiners. Exact agreement between the three study examiners and the standard examiner was 55% (48%, 61%), 52% (45%, 59%), and 55% (50%, 61%), respectively. Thus, relative to the standard examiner, there is measurement error in the PPD recorded by the study examiners. Although this measurement error is often within one mm, the simulation in Section 4 demonstrates that such measurement error nonetheless may impact conclusions regarding association of PPD with other variables such as the cytokine concentration levels considered here.

2.2. Determination of cytokine levels

The inflammatory markers of interest were cytokines previously linked to diabetes and/or periodontal disease. Prior to the periodontal examination, gingival crevicular fluid (GCF) samples were collected from up to 17 sites (periodontal pockets) in each participant's mouth, as described in [22]. These samples were assayed in duplicate with a SearchLight™ multiplex sandwich ELISA (enzyme-linked immunosorbent assay) [27]. For each GCF sample, the assay simultaneously yields chemiluminescent signals for all cytokines studied. These signals are recorded as an image and then quantified (using software [28]) into an optical density reading for each cytokine.

The optical density (OD) is related to the cytokine concentration through the four-parameter logistic ELISA function:

$$\mathrm{OD}=D+\frac{A-D}{1+{\left(\frac{x}{C}\right)}^B},$$ (1)

where x is the cytokine concentration in pg/ml, A is the asymptote as x → 0 for B > 0, D is the asymptote as x → ∞, C is the concentration at 50% inhibition, and B is a slope related parameter. The parameters A, B, C and D are determined separately for each cytokine and for each run of the multiplex assay; details are given in [22]. When plotted after performing log-transformations on both the concentration and optical density, the function has an S shape with horizontal asymptotes at log A and log D.

Investigators seek a dilution of the patient samples such that the majority of OD readings will fall on the linear part of the standard curve. OD values near the asymptotes are not well determined and may be marked as falling below the detection limit or above the quantification limit of the assay. Because there is only enough GCF available for one assay (in duplicate) from each site from each patient, further dilution is not possible, leading to the need to accommodate censoring due to the detection and/or quantification limits in analyses.

3. STATISTICAL MODEL

Consider a single cytokine of interest and let Y_ij, i = 1, 2, . . . , n, j = 1, 2, . . . , m_i be the (natural) logarithm of the cytokine concentration obtained for the jth periodontal site for the ith study subject. Although the study protocol called for GCF to be collected from 17 designated periodontal sites, not all subjects provided samples from all sites due to missing teeth or other reasons, hence the number of GCF samples collected varies from subject to subject. In part because cytokine concentrations must be nonnegative, they exhibit right skewness, and the log transformation serves to pull in the right tail and stabilize the variance. On this scale, a plausible model is based on a Gaussian distribution for {Y_ij} with random effects {α_i} serving to induce correlation among the cytokine concentrations obtained from the same subject:

$$\begin{array}{cc}\hfill Y_{ij}& ={\beta }_0+{\beta }_1{\mathrm{PPD}}_{ij}+{\beta }_2{\mathbf{X}}_{ij}+{\epsilon }_{ij}+{\alpha }_i\hfill \\ \hfill {\epsilon }_{ij}& ~N(0,{\sigma }^2)\mathrm{iid}\hfill \\ \hfill {\alpha }_i& ~N(0,{\sigma }_{\alpha }^2)\mathrm{iid};\left\{{\alpha }_i\right\},\left\{{\epsilon }_{ij}\right\}\text{mutually independent}.\hfill \end{array}$$ (2)

In equations (2), X_ij represents all covariates other than PPD, including potentially site-level covariates such as whether the GCF was obtained from a molar, premolar or incisal tooth, and subject-level covariates such as gender, age and smoking status. With the iid errors {ε_ij} in equations (2), the random effects {α_i} induce the compound symmetry correlation structure on the marginal distribution of the cytokine concentrations. Thus, Corr(Y_ij, Y_ij′) is the same value $({\sigma }_{\alpha }^2∕({\sigma }^2+{\sigma }_{\alpha }^2))$ for all j, j′, and cytokine measurements from different subjects are independent.

3.1. Limit of detection for cytokine concentration

Because the quantity of GCF obtained from a periodontal site was often low, it was important to accommodate censoring of the cytokine level at the lower limit of detection. The lower limit of detection advertised by the manufacturer of the SearchLight™ ELISA was determined for analyses of serum, urine, or other situations where abundant sample is available and hence potentially not appropriate for the low quantities of GCF available in our study. In other work [22], we investigated a number of approaches to determining the appropriate lower limit of detection, including the manufacturer's recommendation and multiple methods derived from statistical modeling. For this manuscript, we use the minimum detectable concentration (MDC) [29], defined as the minimum concentration, x_MDC, such that the predicted OD, OD_MDC = OD(x_MDC), is statistically significantly greater than the OD at cytokine concentration zero. To determine x_MDC, the variation in the fitted standard curve is used to form a 95% confidence interval for the predicted average of two OD replicates (because our samples were run in duplicate) at concentration x = 0 pg/ml. The upper limit of this confidence interval is then back transformed through the fitted standard curve to obtain x_MDC.

GCF samples producing a cytokine concentration less than the MDC are treated as censored in our analyses. Note that, because the standard curve, and correspondingly the MDC, is determined for each cytokine for each assay run, a GCF sample that yields a censored value for one cytokine may produce detectable quantities for other cytokines. Moreover, the same OD reading may yield a censored cytokine concentration for one subject, but a well-determined concentration for another.

3.2. Quantitation limit for cytokine concentration

Though rare for our data, cytokine concentration determinations were also subject to censoring above due to the quantitation limit of the ELISA procedure. The quantitation limit was determined as follows: On the log-log scale, the S-shape of the fitted standard curve implies an inflection point, which is a function of the 50% inhibition parameter C for the assay. The tangent to the fitted curve through this inflection point will intersect the upper asymptote (log A). The quantitation limit is determined by the point on the fitted standard curve (on the log-log scale) nearest (in Euclidean distance) to this point of intersection.

3.3. Measurement error in PPD

Let ${\mathrm{PPD}}_{ij}^T$ and ${\mathrm{PPD}}_{ij}^O$ be the true and observed (error-prone) PPD values for the jth site from the ith subject. The classical measurement error model, for which ${\mathrm{PPD}}_{ij}^O$ is a perturbed version of ${\mathrm{PPD}}_{ij}^T$, is appropriate; we further assume that the measurement error is nondifferential [1, §2.5], so that the distribution of {Y_ij} given {${\mathrm{PPD}}_{ij}^T$, ${\mathrm{PPD}}_{ij}^O$, X_ij} does not depend on {${\mathrm{PPD}}_{ij}^O$}, i.e. given the true unobserved values {${\mathrm{PPD}}_{ij}^T$}, the observed values {${\mathrm{PPD}}_{ij}^O$} contain no additional information about {Y_ij}. This assumption is consistent with work addressing measurement error in caries determination [16]. ${\mathrm{PPD}}_{ij}^O$ is recorded to the largest whole mm in the range {0, 1, . . . , 15} less than what the examiners observe on the probe. Thus, PPD is discrete and the measurement error may be conceptualized as misclassification error. Suppose that subject i was seen by examiner E, and let π_E be the K × K (K = 16) misclassification matrix associated with the examiner E, then ${\left[{\Pi }_E\right]}_{k\ell }=\mathrm{Pr}({\mathrm{PPD}}_{ij}^O=k\mid {\mathrm{PPD}}_{ij}^T=\ell ),k,\ell \in \{0,1,\dots ,15\}$.

The desired relationship is that between the response Y_ij and ${\mathrm{PPD}}_{ij}^T$, so that the first line of equations (2) becomes

$$Y_{ij}={\beta }_0+{\beta }_1^T{\mathrm{PPD}}_{ij}^T+{\beta }_2{\mathbf{X}}_{ij}+{\epsilon }_{ij}+{\alpha }_i,$$

where ${\beta }_1^T$ quantifies the effect of the true (i.e. error-free) value of PPD on the transformed cytokine level. Naive estimation substitutes ${\mathrm{PPD}}_{ij}^O$ for ${\mathrm{PPD}}_{ij}^T$ as predictor and yields the naive estimator ${\widehat{\beta }}_1^O$, which, for linear models, is attenuated relative to ${\beta }_1^T$. The values of the remaining parameters in the model, e.g. β₀, β₂, σ, are also a ected by substitution of ${\mathrm{PPD}}_{ij}^O$ for ${\mathrm{PPD}}_{ij}^T$, but this has been notationally suppressed since interest focuses on β₁.

To see that measurement error among examiners with even a relatively high degree of agreement in PPD readings can lead to substantial effects on inferences, consider the simplified model Y_ij = 0.5 PPD_ij+α_i+ε_ij, i = 1, 2, . . . , 40, j = 1, 2, . . . , 20 with σ² = 0.25 and correlation among responses within a subject of 0.6 (i.e. ${\sigma }_{\alpha }^2$ = 0.375). Data were simulated as described in Section 4 with each of the 40 subjects randomly assigned to one of three examiners whose misclassification was such that the recorded PPD values exhibited overall exact agreement with the true PPD as 85.6% and agreement within one mm of 88.8%. Regression on the simulated true PPD yields a slope estimate of ${\widehat{\beta }}_1^T=0.51$ (se = 0.01), however regression on the misclassified PPD gives the naive slope estimate ${\widehat{\beta }}_1^O=0.33(\mathrm{se}=0.01)$. Correction using the MC-SIMEX method as described below in Section 3.4 yields an estimate of ${\widehat{\beta }}_{1,\mathrm{SIMEX}}=0.44$ (se = 0.03) – certainly an improvement over the naive estimator, but nonetheless attenuated relative to the true slope of 0.5.

3.4. Application of MC-SIMEX

Let π be the misclassification matrix associated with PPD and define the mapping G(λ) : λ → β₁(λ), where β₁(λ) is the coefficient of interest when the predictor is PPD^λ, a further perturbation of the error-prone predictor (PPD^O) according to the misclassification matrix π^λ. Thus λ ≥ 0 quantifies the degree of misclassification error so that π⁰ = I_K×K and, correspondingly, ${\beta }_1\left(0\right)={\beta }_1^O$. Analogous to SIMEX, MC-SIMEX empirically determines the form of G(·) though a simulation step followed by an extrapolation step. Briefly, for a fixed grid 0 = λ₀ < λ₁ < λ₂ < . . . < λ_m, the simulation step consists of generating, for each λ_k, k = 1, 2, . . . , m, B new pseudo data sets with {PPD^λ_k,b} a π^λ_k-misclassified version of {PPD^O}, b = 1, 2, . . . , B. The estimate ${\widehat{\beta }}_1{\left({\lambda }_k\right)}_b$ is obtained by naively fitting the model of interest with {PPD^λ_k,b} as predictor, and β₁(λ_k) is estimated using ${\widehat{\beta }}_1\left({\lambda }_k\right)=\frac{1}{B}{\sum }_{b=1}^B{\widehat{\beta }}_1{\left({\lambda }_k\right)}_b$, k = 1, 2, . . . , m. Note that with λ₀ = 0, ${\widehat{\beta }}_1\left(0\right)\equiv {\widehat{\beta }}_1^O$.

The extrapolation step then consists of fitting a parametric model $\mathcal{G}(\lambda ,\theta )$ to the points $\{({\lambda }_k,{\widehat{\beta }}_1\left({\lambda }_k\right)),k=0,1,\dots ,m\}$ and extrapolating this fit back to λ = –1. Because λ = 0 corresponds to the amount of misclassification error in the observed data {PPD^O}, λ = –1 corresponds to the error-free situation. The MC-SIMEX estimator of ${\beta }_1^T$ is ${\widehat{\beta }}_{1,\mathrm{SIMEX}}=\mathcal{G}(-1,\widehat{\theta })$. Küchenhoff et al. [16] investigated linear, quadratic and log-linear forms for the extrapolant function $\mathcal{G}$, and found that while linear is clearly inadequate, both quadratic and log-linear performed well.

An asymptotic estimate of the variance ${\widehat{\beta }}_{1,\mathrm{SIMEX}}$ has been derived by [18]. The simex R package [20, 21] additionally implements a jackknife variance estimate based on the work of Cook and Stefanski [17].

3.5. Implementation

Model (2) with {PPD^O} or a perturbed version {PPD^λ_k,b} as primary predictor of interest, together with censoring of the response either below or above, is fit using maximum likelihood estimation using the survreg function in the survival [30] package for R [19]. In this framework, the cytokine concentration is viewed as a clustered duration outcome subject to censoring. The function survreg fits the fully parametric log-normal model with the random effects {α_i} handled as frailties, yielding the naive estimator ${\widehat{\beta }}_1{\left({\lambda }_k\right)}_b$ for each error-inflated realization of {PPD^λ_k,b}.

Implementation of the MC-SIMEX algorithm requires the misclassification matrix π_E for each of the three oral examiners, E ∊ {A, B, C}. Estimates of these matrices are readily available from the examiner calibration study described in Section 2.1, where the recordings from the standard examiner are regarded as truth. As described by Küchenhoff et al. [16], estimated misclassification matrices may not satisfy the conditions needed so that π^λ exists for each λ > 0. In these situations, the approach of Israel et al. [31] can produce a matrix close to the estimated misclassification matrix for which powers do exist.

The implementation of the MC-SIMEX algorithm in the R package simex [20] was used with the quadratic extrapolant $\mathcal{G}$, the jackknife estimate of the variance of ${\widehat{\beta }}_{1,\mathrm{SIMEX}}$ (ignoring the variability in the estimates of the misclassification matrices π_A, π_B and π_C), and B = 100 generated perturbed data sets at each value of λ ∊ {.25, .5, 1, 1.5, 2}.

4. SIMULATION

The illustration in Section 3.3 showed that MC-SIMEX has the potential to at least partially correct for the attenuation due to misclassification error in the context of our model. A more extensive simulation study was performed to investigate the ability of MC-SIMEX to recover the underlying true association parameter in situations that reflect the realities of periodontal research. The sample size was fixed at 40 subjects, each having 20 periodontal sites from which PPD and GCF were obtained (similar to our data). Primary interest focused on the effect of the degree of misclassification error.

True PPD values were generated such that $\text{log}{\mathrm{PPD}}_{ij}^T=\text{log}4+{\gamma }_i+{\epsilon }_{ij}$ with γ_i ~ N(0, 0.15²) iid and ε_ij ~ N(0, 0.30²) iid and independently of {γ_i}, inducing a correlation among log PPD^T from the same subject of 0.2. After setting any generated log PPD^T less than zero to 0.1 and then exponentiating, values were floored to the largest integer among {0, 1, . . . , 15} to yield the simulated {${\mathrm{PPD}}_{ij}^T$}.

Three examiners, E = A, B, and C, were modeled as having the same misclassification probabilities. Hence one misclassification matrix π was used for each of the three examiners, created as follows: for a specified value of exact agreement with truth, p_exact = Pr(PPD^O = j | PPD^T = j), assumed constant for j = 0, 1, . . . , 15, the jth column of π was first computed as π_ij p_exact · ρ^|i–j|, i = 0, 1, . . . , 15, and then the entries excluding the jth were renormalized so that all entries in the column summed to one. The value of ρ was set to 0.8, and p_exact ∊ {.95, .90, .80, .70, .60, .50}.

Cytokine levels were generated as Gaussian on the log scale according to (2), $Y_{ij}={\beta }_1^T{\mathrm{PPD}}_{ij}^T+{\alpha }_i+{\epsilon }_{ij},i=1,2,\dots ,40$, j = 1, 2, . . . , 20, with ${\beta }_1^T=0.5$, ${\sigma }_{\alpha }^2=0.375$ and σ² = 0.25, inducing a within-subject correlation of 0.6, and then subject to censoring below. The Y_ij were censored below at log(6.25), which resulted in a censoring rate of about 50%.

For each value of p_exact, M = 50 replications were run, acknowledging the computationally intensive nature of the MC-SIMEX algorithm. For each replication, the estimated slope coefficients ${\widehat{\beta }}_1^T$, ${\widehat{\beta }}_1^O$, and ${\widehat{\beta }}_{1,\mathrm{SIMEX}}$ were obtained from the regressions on PPD^T, PPD^O, and via the MC-SIMEX correction, respectively. The MC-SIMEX algorithm was used as described in Section 3.5. The empirical bias and mean squared error of the coefficient estimates were determined as

$$\text{Bias}\left({\widehat{\beta }}_1\right)=\frac{1}{M}\sum _{r=1}^M({\widehat{\beta }}_{1,r}-{\beta }_1^T)\text{and}\mathrm{MSE}\left({\widehat{\beta }}_1\right)=\frac{1}{M}\sum _{r=1}^M{({\widehat{\beta }}_{1,r}-{\beta }_1^T)}^2$$

for each of the estimators ${\widehat{\beta }}_1={\widehat{\beta }}_1^T,{\widehat{\beta }}_1^O$, and ${\widehat{\beta }}_1$. The empirical bias and MSE were also computed for the estimates of the regression intercept and error standard deviation σ using each of the three approaches.

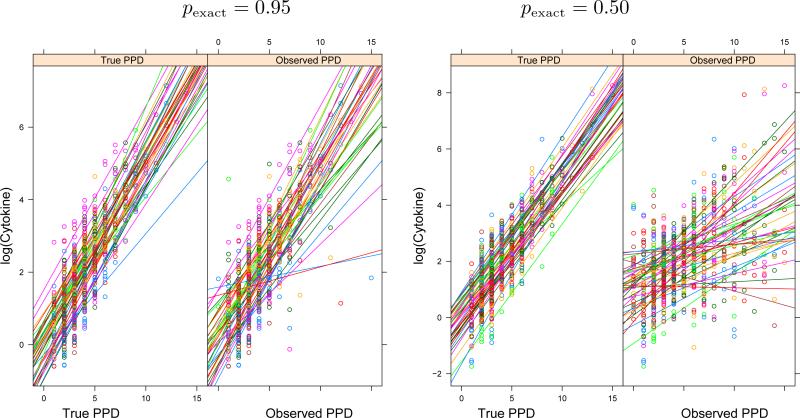
Figure 1 shows plots of Y versus PPD^T and PPD^O for p_exact = 0.95, 0.50. The influence of the degree of misclassification error on the observed association is apparent. Figure 2 shows the empirical bias and MSE for each of the estimators as a function of p_exact when the censoring rate in the response is 50%. As the misclassification error decreases, i.e. p_exact increases, the bias and MSE of both the naive and MC-SIMEX estimators decrease. In particular, the bias associated with the naive estimator of the slope decreases from –0.32 (or 60% of ${\beta }_1^T=0.5$) to –0.07 (14% of ${\beta }_1^T$), and the MSE drops from 0.11 to 0.01 as p_exact increases from 0.50 to 0.95. For this same increase in p_exact, the bias of the MC-SIMEX estimate of the slope decreases from –0.21 (40% of ${\beta }_1^T$) to –0.003 (0.7% of ${\beta }_1^T$), and the MSE decreases from 0.05 to 0.0007. This pattern of decreasing bias and MSE also holds for the estimates of the intercept and error standard deviation parameters. Note that the naive estimate of the standard error is inflated compared to the MC-SIMEX estimate and the true value. Although the MC-SIMEX corrected estimators exhibit less bias than the naive estimators, it is apparent that unless the agreement among examiners is extremely good (i.e. p_exact = 0.95) considerable bias remains.

Figure 1.

Behavior of the simulated data when p_exact = 0.95 (left panel) and 0.50 (right panel). In each panel, the first graph shows {Y_ij} plotted versus {${\mathrm{PPD}}_{ij}^T$} with simple linear regression fits for each subject overlaid. The right graph is similar, except that {PPD_ij}^O is predictor. Censored values have been omitted in these plots.

Figure 2.

Empirical bias and MSE for intercept, slope and error standard deviation estimates from simulation study. The true values of these parameters were β₀ = 0, ${\beta }_1^T=0.5$ and σ = 0.5.

The simulation was repeated with no censoring of the response and also with approximately 75% censoring below. Table I reports the bias and MSE of the parameter estimates, including also the estimates of the frailty standard deviation σ_α, when p_exact = 0.50, 0.95 for the three censoring rates. At higher levels of censoring and with less misclassification error (p_exact = 0.95), the bias in the regression parameters β₀ and β₁ increases moderately and the estimates become less precise. From Table I, it is also apparent that MC-SIMEX provides only a small adjustment to the estimate of σ_α.

Table I.

Empirical bias and MSE for the parameter estimates for 3 levels of censoring and two values of p_exact from the simulation study. The true values of these parameters were β₀ = 0, ${\beta }_1^T=0.5$, σ_α = 0.612 and σ = 0.5.

pexact = 0.50		True		Naive		MC-SIMEX
Censoring		Bias	MSE	Bias	MSE	Bias	MSE
0%	β 0	0.0103	0.0107	1.2607	1.6016	0.8740	0.7848
	β 1	0.0004	0.0001	–0.3488	0.1220	–0.2472	0.0622
	σ α	0.1046	0.0179	0.1585	0.0329	0.1381	0.0274
	σ	–0.1260	0.0160	0.3721	0.1398	0.2705	0.0749
50%	β 0	0.0517	0.0137	0.9962	1.0139	0.6029	0.3872
	β 1	–0.0068	0.0002	–0.3241	0.1053	–0.2130	0.0460
	σ α	0.1013	0.0154	0.2155	0.0567	0.1767	0.0404
	σ	–0.1336	0.0183	0.5073	0.2602	0.3740	0.1430
75%	β 0	0.1256	0.0307	0.8118	0.6984	0.4424	0.2414
	β 1	–0.0133	0.0004	–0.3046	0.0933	–0.1912	0.0378
	σ α	0.0688	0.0081	0.1893	0.0482	0.1403	0.0317
	σ	–0.1527	0.0238	0.5724	0.3360	0.4119	0.1789

pexact = 0.95		True		Naive		MC-SIMEX
Censoring		Bias	MSE	Bias	MSE	Bias	MSE
0%	β 0	0.0168	0.0117	0.3331	0.1287	0.0782	0.0270
	β 1	0.0003	0.0001	–0.0903	0.0087	–0.0175	0.0012
	σ α	0.1072	0.0158	0.1116	0.0173	0.1034	0.0159
	σ	–0.1279	0.0165	0.0390	0.0030	–0.0760	0.0087
50%	β 0	0.0523	0.0165	0.2172	0.0675	0.0374	0.0205
	β 1	–0.0042	0.0002	–0.0682	0.0051	–0.0034	0.0008
	σ α	0.1124	0.0193	0.1344	0.0261	0.1163	0.0214
	σ	–0.1362	0.0189	0.0494	0.0042	–0.1053	0.0151
75%	β 0	0.1256	0.0307	0.2293	0.0780	0.1263	0.0387
	β 1	–0.0133	0.0004	–0.0746	0.0061	–0.0216	0.0013
	σ α	0.0688	0.0081	0.1052	0.0176	0.0861	0.0151
	σ	–0.1527	0.0238	0.0843	0.0118	–0.0788	0.0149

5. APPLICATION

As described in Section 2, the pilot data were obtained from n = 43 African American subjects with diabetes, each undergoing a full periodontal examination with GCF collected from up to 17 periodontal sites per subject. Among these 43 subjects, GCF was collected from a total of 412 periodontal sites. Table II summarizes information on subjects’ PPD, gender, age, HbA1c and smoking status.

Table II.

Characteristics of the n = 43 subjects for analysis.

Variable	Summary
	mean	median	min	max
Perio sites (count)	9.6	9.0	1.0	17.0
PPD (mm)	2.6	2.0	1.0	8.0
Age (yrs)	54.5	56.0	36.0	73.0
HbA1c (%)	8.0	8.0	6.0	11.6
Gender	32 female, 11 male
Smoking	6 current, 6 past, 31 never

The periodontal exams and GCF collection were performed by three trained study examiners, A, B and C, who examined 21, 17 and 5 subjects, respectively. Prior to recruitment of subjects, the calibration study described in Section 2.1 provided estimates of the misclassification matrices for each examiner. Although each of the estimated misclassification matrices Π was a valid transition probability matrix, Π^λ did not exist for some λ used in the MC-SIMEX fits (i.e. λ ∊ {.25, .5, 1, 1.5, 2}), hence the method of Israel et al. [31] was used to obtain misclassification matrices similar to those from the calibration study for which the desired powers did exist. These misclassification matrices, used in the analyses, are shown in Appendix I.

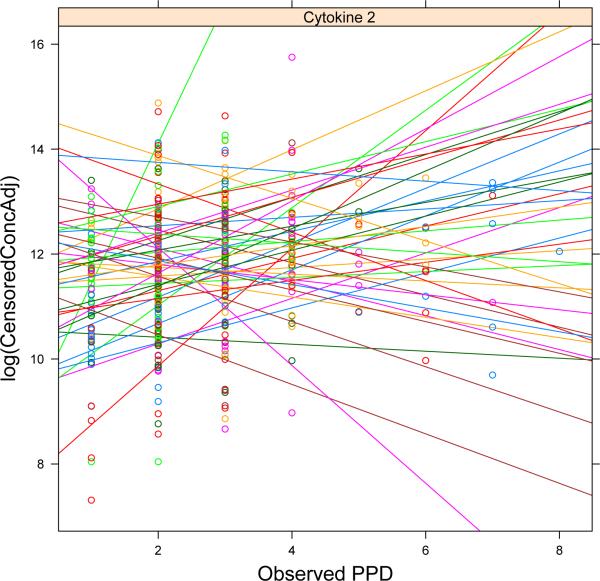
The GCF samples from each periodontal site from a subject were analyzed for the concentrations of 13 cytokines of interest. The purpose of this analysis was to examine the effect of misclassification error on assessment of the association between PPD and cytokine levels in a pilot dataset. Biological conclusions were not to be drawn, pending analyses of the full periodontal study data. Hence the identity of the cytokines was masked in these results. Table III gives the percentages of readings censored below and above for each of the 13 cytokines. Cytokines 2, 3, 4, and 8 have over 10% of readings censored below, with cytokine 4 having 37%, and cytokine 10 has over 10% censored above. Hence it is important to accommodate this censoring so as to utilize all information available in the data. Figure 3 shows a scatter plot of the log concentration levels for cytokine 2 versus the measured PPD with simple linear regression fits for each subject overlaid. There is considerable variation in the trends, similar to the behavior of the simulated data as shown in Figure 1.

Table III.

Percentage of the 412 observations censored among the cytokine concentrations.

Cyotkine	Censored Above	Not Censored	Censored Below
1	0.7	98.8	0.5
2	0.0	82.8	17.2
3	1.0	84.2	14.8
4	0.0	62.9	37.1
5	0.0	98.8	1.2
6	3.2	95.4	1.5
7	0.0	98.5	1.5
8	0.0	80.6	19.4
9	3.6	96.4	0.0
10	13.6	86.4	0.0
11	0.0	99.3	0.7
12	1.0	99.0	0.0
13	0.0	94.7	5.3

Figure 3.

Scatter plot of concentration levels for cytokine 2 versus measured PPD values. Simple linear regression fits for each subject have been overlaid. Censored values have been omitted.

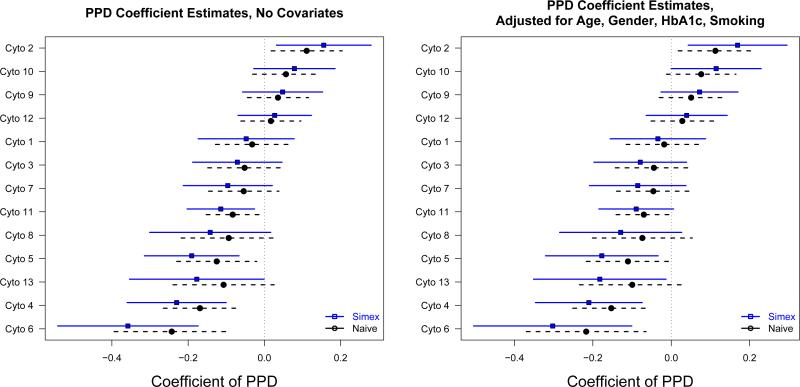
Analyses were performed both with and without adjustment for the covariates age, gender, HbA1c and smoking status. Figure 4 shows the naive and MC-SIMEX estimates of the coefficient associated with PPD, together with approximate 95% confidence intervals. The cytokines are sorted according to the MC-SIMEX esimator in the adjusted analyses. The attenuation of the naive estimators is apparent in that all naive point estimates are nearer to zero than the bias-corrected estimates. Consistent with the notion of variance-bias tradeoff, the confidence intervals are wider for the MC-SIMEX estimates. Substantive conclusions regarding the statistical significance of the association between PPD and cytokine concentrations are the same for both naive and MC-SIMEX estimates, however, with the exception of cytokine 13, especially in the covariate-adjusted analysis, for which the bias correction leads to a confidence interval that does not cover zero, despite its greater width.

Figure 4.

Naive (dashed) and MC-SIMEX (solid) estimates and 95% confidence intervals for the coefficient associated with PPD in the cytokine analyses. Left panel is without adjustment for covariates, while right panel is with adjustment.

6. DISCUSSION

The model that we have described accommodates a clustered Gaussian response that may be censored either below or above and a discrete covariate subject to misclassification error. Although the Gaussian assumption suggests adaptation of the measurement error methods of Wang et. al [10] for generalized linear mixed models to accommodate censoring and misclassification error, a survival analysis perspective permits application of the simex package for R, which incorporates the MC-SIMEX algorithm of Küchenhoff et al. [16]. Periodically evaluating and recalibrating examiners is standard practice in oral health research and provides information about the distribution of misclassification error in periodontal assessments.

The simulation study in Section 4 was designed to mimic the sample size and level of agreement among examiners in our pilot periodontal study data. The results indicate that even with the adjustment for bias afforded by the MC-SIMEX algorithm, considerable bias remains unless examiner agreement is extremely good. Hence the magnitude of the effect of PPD on the log cytokine levels is likely substantially underestimated in our pilot data. It would be desirable to provide, for a given amount of misclassification and noise variation, the sample size required for a specified reduction in relative bias of the MC-SIMEX estimator relative to the naive estimator. Such guidance may be derived from asymptotic bias and variance expressions such as those in [13, 14, 18].

In computing the standard errors associated with the parameter estimates for the pilot periodontal study data, we have ignored the variance associated with estimation of the misclassification matrices from the examiner calibration study. Hence our reported standard errors are low. A bootstrap procedure could be used to incorporate this variability, though this would be quite computationally intensive on top of the considerable demands of the MC-SIMEX approach. Alternatively, a model and inference stemming from full specification of the joint distribution of the error-prone covariate and its associated underlying true value permits the propagation of variability from the examiner calibration data directly. Such a model was developed by Mwalili et al. [32] for an ordinal caries outcome influenced by misclassification; inference in the Bayesian framework seamlessly incorporated uncertainty in the distributions of examiner misclassification. The model (2) can be made more flexible by adopting a semiparametric approach – the survival analysis perspective easily accommodates an unspecified baseline hazard function for the log cytokine readings. In addition to handling the correlation among response values from the same subject, inferences potentially could be strengthened by analyzing the panel of cytokine levels from a periodontal site as a multivariate response.

Our work demonstrates that measurement error in periodontal assessments can influence the interpretation of analyses using these assessments. Taken together with the work of Küchenhoff et al. [16] who drew attention to measurement error in caries determination, there is ample justification for considering measurement error in the design and analysis of oral health studies and for diligently maintaining the established practice of on-going examiner training and calibration.

APPENDIX

I. Misclassification matrices

The examiner misclassification matrices used for application of the MC-SIMEX method to the pilot periodontal study data are given in Table IV. These matrices resulted from application of the method of Israel et al. [31] to the estimated misclassification matrices obtained from the examiner calibration study described in Section 2.1. Given an estimated misclassification matrix, this method generates an approximately equal transition probability matrix for which powers exist using a series approximation (see their Theorem 2.1) and then, if needed, applying numerically stabilizing corrections.

Table IV.

The examiner misclassification matrices used for MC-SIMEX analysis of the pilot periodontal study data. Only the upper left portion of the 16×16 matrices is shown, the remainder being nearly ones on the diagonal with off-diagonal entries < 0.01 such that the columns sum to one.

Examiner A	Standard Examiner PPDT
PPDO	0	1	2	3	4	5	6	7. . .
0	.33	.09	.01	0	0	0	0	0
1	.62	.80	.17	.03	.04	.02	.01	0
2	.05	.10	.68	.24	.08	.08	.06	0
3	0	.01	.12	.62	.39	.15	.17	0
4	0	0	.01	.11	.45	.33	.19	0
5	0	0	0	0	.03	.42	.39	0
6	0	0	0	0	0	0	.18	0
7	0	0	0	0	0	0	0	1

Examiner B	Standard Examiner PPDT
PPDO	0	1	2	3	4	5	6	7. . .
0	.82	.07	0	0	0	0	0	0
1	.09	.86	.07	0	0	0	0	0
2	0	.03	.70	.07	.02	0	0	0
3	0	0	.01	.66	.05	0	0	0
4	0	0	0	.01	.59	.04	0	0
5	0	0	0	0	.01	.43	.13	.01
6	0	0	0	0	0	.01	.78	.01
7	0	0	0	0	0	0	0	.98

Examiner C	Standard Examiner PPDT
PPDO	0	1	2	3	4	5	6	7. . .
0	.81	.09	.02	.04	.02	.02	0	0
1	.17	.83	.26	.09	.12	.05	0	0
2	.01	.08	.65	.36	.12	.16	0	0
3	0	0	.06	.42	.27	.07	0	0
4	0	0	.01	.09	.42	.19	0	0
5	0	0	0	.01	.06	.52	0	0
6	0	0	0	0	0	0	.50	.50
7	0	0	0	0	0	0	.50	.50