Reversal of the Myosin Power Stroke Induced by Fast Stretching of Intact Skeletal Muscle Fibers

Abstract

Force generation and movement in skeletal muscle result from a cyclical interaction of overlapping myosin and actin filaments that permits the free energy of ATP hydrolysis to be converted into mechanical work. The rapid force recovery that occurs after a step release imposed on a muscle is thought to result from a synchronized tilting of myosin lever arms toward a position of lower free energy (the power stroke). We investigated the power stroke mechanism in intact muscle fibers of Rana esculenta using a fast stretch to detach forcibly cross-bridges. Stretches were applied either with or without a conditioning step release. Cross-bridge rupture tension was not significantly influenced by the release, whereas sarcomere elongation at the rupture point increased immediately after the release and returned to the prerelease condition within 15–20 ms, following a slower time course compared to the recovery of tension. These observations suggest that the rupture force of a bridge is unaltered by a conditioning release, but rupture must first be preceded by a power stroke reversal, which restores the prepower stroke state. The sarcomere extension at the rupture point indicates both the extent of this power stroke reversal and the time course of strained bridge replenishment.

Introduction

Force generation and shortening in skeletal muscle occur, at the molecular level, through the cyclical interaction of thick filament myosin cross-bridges with active sites on the thin (actin) filaments. It has been proposed that the force recovery that occurs after a fast length step consists of rapid swinging of the actin-bound myosin heads (the power stroke), which stretches series elasticity and generates force (1,2). The length step alters the stress on myosin heads and promotes their synchronized movement, which extends or compresses the half-sarcomere elasticity, and some or all of the original tension is recovered. The elasticity within the cross-bridges and myofilaments allows head rotation to occur without a contemporaneous filament sliding. It is now widely assumed that, rather than being caused by a movement of the whole myosin head, the power stroke results from a swinging of the myosin lever arm domain while the motor domain remains firmly attached to actin (2,3). Experimental results from both mechanical and x-ray diffraction work during the quick force recovery support many aspects of this theory (4–6), and crystallographic data have shown the existence of at least two myosin head conformations, before and after the power stroke, characterized by a different orientation of the myosin lever arm (7,8). In this work, we investigated the power stroke mechanism by using fast stretches that induced the forced detachment of cross-bridges.

It is known that a mechanical force applied to a chemical bond induces an exponential increase of the detachment rate constant, which leads to a rapid bond rupture (9). Important properties of the bond have been determined in single-molecule experiments by means of force spectroscopy (10,11). We recently showed that the rupture kinetics of a single bond can be extended to the ensemble of parallel bonds constituted by cross-bridges acting in parallel within each half-sarcomere (12). This allowed us to obtain the properties of the actomyosin bond in an intact skeletal muscle fiber by analyzing the force response to fast ramp stretches, which were large enough to induce the forced rupture of the cross-bridge ensemble. The same fast ramp stretching technique was applied here to investigate the mechanism of the power stroke. Stretches were applied to tetanized single skeletal muscle fibers of the frog during the time course of the quick force recovery that occurs after a conditioning step release and is thought to result from a synchronized power stroke. The results showed that 1) the rupture force of the cross-bridge ensemble was almost constant during the whole quick recovery period, independently of the force developed by the fiber; and 2) the sarcomere elongation required to detach the cross-bridges increased immediately after the conditioning step release to a value that remained approximately constant for 1–2 ms and then started to fall with a time constant of ∼4.5 ms toward the prerelease value, which was reached after 15–20 ms. These effects can be explained by assuming that the forced cross-bridge rupture induced by the stretch is preceded by the reversal of the myosin power stroke.

Materials and Methods

Frogs (Rana esculenta) were killed by decapitation followed by destruction of the spinal cord, in accordance with the guidelines of the Animal Care and Use Committee of the University of Florence and the official regulations of the European Community Council (directive 86/609/EEC). Single intact fibers, dissected from the tibialis anterior muscle (4–6 mm long, 60–120 μm diameter), were mounted by means of aluminum foil clips between the lever arms of a force transducer (natural frequency 40–60 kHz) and a fast electromagnetic motor (minimum stretch time 100 μs) in a thermostatically controlled chamber provided with a glass floor for both white and laser light illumination. Stimuli of alternate polarity, 0.5 ms duration, and 1.5 times threshold strength were applied transversely to the fiber by means of platinum-plate electrodes, at the minimum frequency necessary to obtain fused tetanic contractions. Sarcomere length was measured using a striation follower device (13) in a fiber segment (1.2–2.5 mm long) selected for striation uniformity in a region as close as possible to the force transducer. This eliminated the effect of tendon compliance and reduced the effects of mechanical wave propagation on the sarcomere length measurements. Fast ramp-shaped stretches (duration 0.3–0.5 ms and amplitude 15–28 nm hs⁻¹, corresponding to ∼30–90 fiber length s⁻¹) were applied to one end of the fiber while the force response was measured at the other. Since fibers developing maximum tetanic tension can be easily damaged by the stretches used here, we performed our experiments on the tetanus rise at a mean tension, P_t0, of ∼0.54 ± 0.016 (mean ± SE) of maximum tetanic tension, P₀, where fiber damage was very much reduced. Usually, >50 normal contractions could be obtained before any sign of damage appeared. The experimental temperature was set to 5°C and the resting sarcomere length was ∼2.1 μm.

Stretch application induced an almost linear force increase up to a peak representing the cross-bridge rupture force. This phase was usually preceded by a small and faster force rise (lasting <0.1 ms) at the start of the stretch, the amplitude of which was roughly proportional to the stretching speed. This phase, which was very variable from one fiber to the other, most likely arises from the passive properties of the activated fiber, such as inertia or viscosity (14), and therefore the peak force was corrected for it. To that end, the slower linear part of the force rise was extrapolated back to the starting time of the stretch, and the intercept on the ordinate was considered zero tension. Stretches were applied alone and 0.2, 0.4, 0.6, 0.8, 1, 2, 5, 10, 15, and 20 ms after a conditioning step release of 3.89 ± 0.12 nm hs⁻¹ amplitude and 150 μs duration. In five fibers, a smaller step release of 2.11 ± 0.05 nm hs⁻¹ was also used, but the stretch was applied only at 2 ms after the release. The passive force response was negligible and no correction was made for it. Measurements of the rupture tension, P_c, were corrected for the increase of tension that occurred between the quick release and the stretch application on the basis of the fixed ratio between P_c and isometric tension, as found previously (15). The same correction was also applied to tension and sarcomere length records. These corrections are significant only for delays from the conditioning step > 5 ms. A correction was also performed for the effects of the quick recovery on the force response during the stretch. This was done by subtracting the waveform of the step release from that of the step release plus ramp stretch.

Ringer's solution was used with the following composition (mM): NaCl, 115; KCl, 2.5; CaCl₂, 1.8; NaH₂PO₄, 0.85; Na₂HPO₄, 2.15. Force, fiber length, and sarcomere length signals were measured with 10 μs resolution with a digital oscilloscope (4094; Nicolet, Madison, WI) and transferred to a personal computer for further analysis.

Results

Stretch on the tetanus rise

Fig. 1 shows the force response to a fast ramp stretch applied to a fiber on the tetanus rise at tension P_t0 of 57% of maximum tetanic tension, P₀. Tension rises almost linearly during the stretch, reaches a critical force P_c, and then falls despite the continued stretching (Fig. 1 B). This indicates that the half-sarcomere compliance increases suddenly at the tension peak due to forced detachment of the cross-bridge ensemble (15–19). Actually, the rapid tension fall after the peak indicates that fiber compliance becomes “negative,” which is a clear indication of a complex nonelastic response such as cross-bridge rupture. The sharpness of the force peak indicates that the cross-bridge rupture occurs abruptly and simultaneously among half-sarcomeres throughout the fiber. With the stretch amplitude used here, the tension after cross-bridge detachment did not fall below the isometric value. This is most likely due to fast myosin head reattachment after rupture (20,21).

Figure 1.

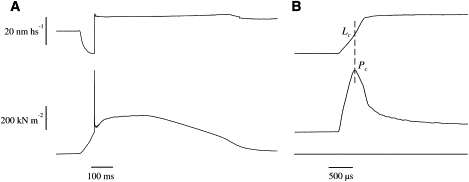
Force response to a fast ramp stretch (26.8 nm hs⁻¹ amplitude, 290 μs time to tension peak) applied to a single fiber at a tension of 0.57 P₀ on the tetanus rise. (A) Slow time base record. (B) Fast time base of a portion of A. Upper traces: sarcomere length; lower traces: tension. Tension rises quickly during the stretch up to a peak (P_c) and then falls despite the continued stretching. This peak represents the force needed to detach the cross-bridge ensemble. The intercept of the vertical dashed line in B with the upper trace indicates the sarcomere length (critical length, L_c) at which the rupture of the cross-bridge ensemble occurs. Fiber length: 4250 μm; segment length: 1767 μm; sarcomere length: 2.11 μm.

The P_c/P_t0 ratio measured in six experiments was 3.49 ± 0.18 (mean ± SE). This means that to detach the cross-bridges, it was necessary to apply a force 3.49 times greater than the tension developed, in agreement with previous data (19). The average sarcomere elongation required to detach the cross-bridges (critical length, L_c) was 11.90 ± 0.65 nm hs⁻¹.

Previous experiments with stretches applied at tetanus plateau at various sarcomere lengths (16) during tetanus rise, tetanus relaxation, and submaximal tetanic contractions in the presence of 2,3-butanedione monoxime (BDM) (15) showed that P_c was linearly correlated with tension development, whereas L_c was independent of tension, as would be expected from the parallel disposition of cross-bridges. These findings suggest that P_c can be used as a measure of attached cross-bridge number.

Stretches during the quick force recovery after a step release

To investigate the mechanism behind the quick force recovery, we applied a series of test ramp stretches similar to that shown in Fig. 1 to the contracting fiber. The force response to the control stretch, applied without a conditioning release, was compared with the force responses to stretches applied at various delays (0.2–20 ms) after a conditioning step release. An example of the records obtained is shown in Fig. 2. It can be seen that the peak tension required to detach the cross-bridge ensemble, P_c, was about the same under control conditions or during the tension recovery after the release. This occurred despite the substantial changes in the tension, P_t, developed by the fiber at the time of the stretch.

Figure 2.

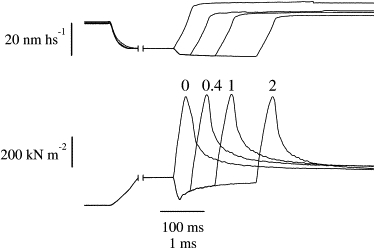
Force and sarcomere length records during ramp stretches applied with and without a conditioning step release. Upper traces: sarcomere length; lower traces: tension. Stretches were applied in the absence of any conditioning length change (0) or 0.4, 1, and 2 ms after a step release applied at ∼0.5 P₀. Peak force does not change significantly during the quick force recovery. Step release, 3.91 nm hs⁻¹ amplitude, 170 μs duration. The same fiber as in Fig. 1. Fast sampling starts at the interruption on the traces.

In contrast to P_c behavior, the critical length, L_c, changed substantially, increasing immediately after the stretch and gradually returning toward its prerelease value within 15–20 ms.

The time courses of the mean P_c, L_c, and tension are shown in Fig. 3, B–D. Changes in the relative critical force P_c/P_t0, which we suggest measures the cross-bridge number, were small. Compared to the prerelease value, P_c decreased by 5% at 2 ms after the release and reached the maximum decrease of 8% at 5 ms after the release. This means that, in agreement with previous suggestions (22,23), the cross-bridge number remains almost constant during the quick tension recovery. In contrast, L_c was strongly affected by the release, increasing from the prerelease value of 11.90 ± 0.65 nm hs⁻¹ to 16.24 ± 0.75 nm hs⁻¹ within 0.2 ms of the release. L_c then remained almost constant: after a 2 ms delay, it was 16.20 ± 0.64 nm hs⁻¹, and then it decreased toward the prerelease value. The increase of L_c at 2 ms delay (the end of the quick recovery), compared to the prerelease value, was similar to the release amplitude. This effect also occurred in five experiments in which a smaller release amplitude of 2.11 ± 0.05 nm hs⁻¹ was used: L_c increased by 2.24 nm hs⁻¹ from the prerelease value to 14.14 ± 0.64 nm hs⁻¹.

Figure 3.

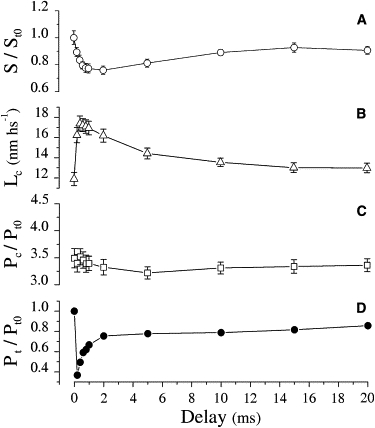
Time course of chord stiffness, S (A), critical length (B), critical force (C), and relative isometric force (D) after a conditioning step release of 3.89 ± 0.12 nm hs⁻¹ (n = 7), which reduced isometric tension to 0.19 ± 0.02 P_t0. Force recovered to 0.76 P_t0 in ∼2 ms. S values are expressed relatively to the isometric value, S_t0, corresponding to 0.21 P_t0/nm hs⁻¹ ((3.49 − 1)/11.90 nm hs⁻¹). The main changes occurred in S and L_c, whereas P_c was only slightly affected by the step release. L_c fell immediately after the step release, whereas S attained the minimum value 2 ms later. Return of both S and L_c to the prerelease value occurred in 15–20 ms, with a time course much slower than the tension. Average values ± SE.

It is not surprising that L_c increased when the stretch was applied 0.2 ms after the release. During such a short time interval, the quick recovery has no time to proceed appreciably, and therefore the critical length needs to be greater to compensate for the effects of the previous release. This simple elastic effect on L_c disappears progressively within 2 ms, when most of the tension loss due to the release is recovered. However, our measurements show that at this time, L_c was still 4.29 nm hs⁻¹ greater than the prerelease value. This means that the L_c increase cannot be explained by the elastic effect alone, and some other mechanism must also be involved. To reveal this mechanism, we investigated the changes in the half-sarcomere chord stiffness, S (measured as the ratio (P_c − P_t)/L_c) that accompanied the quick recovery. Although chord stiffness is inversely proportional to L_c, it is unaffected by the elastic increase of L_c because of the accompanying fall in P_t. This causes an increase of the numerator (P_c − P_t) in proportion to that of L_c and maintains S constant. The results are shown in Fig. 3 A. In contrast to the L_c time course, S started to decrease gradually after the release to reach a maximum drop of 24% after 2 ms. From this point, S started to increase again exponentially, with a time constant of ∼4.5 ms, toward the prerelease value. Thus, the quick force recovery is associated with a decrease in the half-sarcomere chord stiffness. This effect is illustrated in the records of Fig. 4, which show the instantaneous stress-strain relationships of the half-sarcomere elasticity during stretches applied either without the step release or 0.2 ms, 2 ms, and 15 ms after the release, when S has returned to near its prerelease value. In comparison with the prerelease condition, the relation obtained at a 2 ms delay (dotted line) shows two important changes: 1) due to the greater L_c needed to reach the same P_c, the average slope (the chord stiffness of the half-sarcomere) is significantly smaller; and 2), the relationship is more curved downward, suggesting that the half-sarcomere stiffness decreases significantly during the stretch itself. Both of these effects can be explained by assuming that the stretch, before detaching the cross-bridges, reverses the power stroke.

Figure 4.

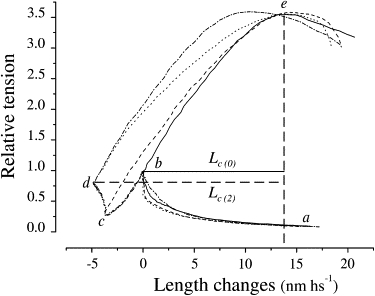
Instantaneous length-tension relations during ramp stretches. Stretches were applied either without a conditioning release (continuous trace) or after a conditioning release of 3.84 nm hs⁻¹ after 0.2 ms (dashed trace), 2 ms (dotted trace), or 15 ms (dot-dashed trace). Letters on the figure indicate the following events: a–b, isometric tension rise before any applied length change; b–c, step release; c–d, tension rise during the quick recovery; b–e, stretch before the release; and d–e, stretch at 2 ms delay. Note that isometric, 0.2 ms, and 2 ms delay records all reach the peak at the same absolute sarcomere length (vertical dashed line). L_c(0) and L_c(2), are critical lengths before and 2 ms after the release, respectively. After 15 ms, the shift of the force peak to the left reduces L_c to the prerelease value. A zero value on the abscissa corresponds to the sarcomere length at P_t0 (2.07 μm). Fiber length: 4090 μm; segment length: 1410 μm; sarcomere length: 2.10 μm.

The time courses in Fig. 3 show that 15–20 ms after the release, both L_c and S recovered to their isometric values. This means that whatever modifications were induced by the step release disappeared within 15–20 ms. We suggest that postrecovery cross-bridges detach and within 15–20 ms are replaced by other freshly formed cross-bridges with the prerelease configuration.

Model

To investigate the validity of the above hypothesis, we analyzed the responses of a model that uses the formalism of Eisenberg et al. (24). For details, see the Supporting Material.

The responses of the model to stretches alone and at 0.2 and 2 ms after a release of 4 nm hs⁻¹ are shown in Fig. 5. Force is plotted against length to compare the model responses with the experimental results shown in Fig. 4. In agreement with the experiments, the model response shows that 1) P_c is about constant in all of the force responses; 2) L_c increases immediately after the release by an amount equal to the release amplitude and remains elevated when the stretch is applied 2 ms after the release, when the quick recovery is over; and 3) the tension rise during the stretch applied 2 ms after the release has more of a downward curve compared to the other responses.

Figure 5.

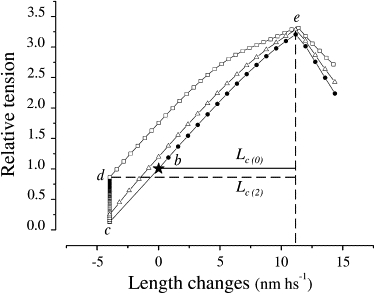
Length-tension plot calculated with the model. Stretches were applied either without the step release (circles) or at intervals of 0.2 ms (triangles) and 2 ms (squares) after a step release of 4 nm hs⁻¹. The star indicates the isometric tension before the release. L_c(0) and L_c(2) are critical lengths before and 2 ms after the release, respectively. Letters on the traces indicate the following events: b–c, step release; c–d, quick recovery; b–e, stretch before the release; and d–e, stretch 2 ms after the release. Compare with the experimental results of Fig. 5.

The model does not include the filament compliance. This may be compensated for by reducing the separation between free-energy minima by an amount equivalent to the series filament compliance, and by increasing the steepness of the parabolas appropriately. Changes regarding the replacement of detaching bridges with newly formed bridges, which account for the return to prerelease conditions, are also not considered in the model.

Discussion

A small step length change applied to an activated muscle fiber produces an elastic force change followed by a rapid (∼1 ms) force recovery. Because this force recovery occurs with no pronounced change in muscle stiffness, an index of the number of actin-bound S1 (the motor subfragment of myosin), it is believed to arise from force exerted by cross-bridges present immediately before the stretch. It represents a synchronized redistribution of the S1-actin population between at least two S1 structural isomers that are associated with different axial forces (1). Huxley (2) proposed that cross-bridge force depends on the average tilt of actin-bound S1 isomers, and that changes in tilt of an S1 moiety attached perpendicularly to the thin filament could explain the fall in intensity of the meridional M3 x-ray reflection (which arises from the axial periodicity of S1 projections from the thick filament) in response to both step stretches and releases (5). Crystallographic structures of S1 revealed that the orientation of the lever arm domain (linking the actin-binding motor domain to the S2 myosin moiety) depends on the occupancy of the S1 catalytic site (25), providing a plausible mechanism for this tilting. Irving et al. (26) further showed that the M3 intensity response to a length step was split between the elastic and the recovery force transients, and that by modeling the crystallographic S1 structure, this intensity response can be accounted for by displacement of the lever arm through a combination of passive tilting during the elastic response and a synchronized active tilting during the force recovery (27). In addition, optical probes attached to the S1 lever arm domain were reported to change their orientation during the quick recovery of force (28), which is also consistent with the “tilting cross-bridge” model of the power stroke and the notion of a force-dependent distribution of at least two different force-bearing states of the S1-actin complex.

It was previously shown that fast ramp stretches forcibly detached cross-bridges (15–19). Here we determined the effect of the transition from the pre- to post-power-stroke state on the force and half-sarcomere strain required to rupture the S1-actin bond, and we used this effect to investigate the kinetics of the transition between pre- and post-power-stroke states.

We investigated the actomyosin bond properties by analyzing the force responses of single muscle fibers to stretches applied either alone and at various times (up to 20 ms) during the quick force recovery subsequent to a conditioning step release. Although force recovery also occurs after a step stretch, the analysis reported here was limited to the release because of the well-known nonlinear cross-bridge behavior in response to a quick stretch (22).

Because of the very fast stretches used here (stretching time 300–500 μs), we assumed throughout the study that the cross-bridge attachment and detachment during the stretch itself, up to the tension peak, were negligible. This is consistent with the results of our model simulations, which reproduce the most essential aspects of the experimental results without assuming any cross-bridge cycling. Previous results from modeling of force responses to slow stretches (29,30) are also consistent with negligible cross-bridge cycling during the stretch.

Our experiments were performed at a mean tension of 0.54 P₀ on the tetanus rise rather than at the tetanus plateau. This was done both to reduce damage caused by the fast ramp stretches to the fiber and to improve the uniformity of the force distribution between the individual cross-bridges along the fiber (12). It should be pointed out that conditions under which single fibers develop subtetanic forces in vivo are entirely physiological.

Critical force

The critical force, P_c, is the force needed to detach the cross-bridge ensemble in activated muscle fibers. Under our conditions, in which all cross-bridges act in parallel, P_c is proportional to the cross-bridge number and individual bond rupture force (12). Previous results obtained during isometric contraction, isotonic shortening, and submaximal tetanic contractions in the presence of BDM (15) were well explained by assuming that the individual rupture force was constant. Thus, P_c was assumed to be directly proportional to the number of myosin heads attached (15). It is clear that P_c is independent of the elasticity in series with the cross-bridges, including the myofilament elasticity.

Our results show that, in comparison with the prerelease conditions, the greatest P_c change during the force recovery from a step release of 3.89 nm hs⁻¹ was an 8% reduction that occurred 5 ms after the release. This means that the cross-bridge population changed little during the quick recovery, in agreement with previous conclusions (22,23). Thus, force changes that occur during the quick recovery are almost entirely accounted for by changes in the strain of the individual cross-bridge. The independence of P_c from the tension developed by the fiber differs from previous results on the tetanus rise, where P_c was directly proportional to the tension developed (15). This difference is consistent with our assumption that P_c measures the number of cross-bridges, as well as with the mechanism of quick recovery. The increase of force during the tetanus rise is in fact due to the progressive cross-bridge formation in proportion to tension, whereas the quick force recovery after a release is mainly due to the increased strain of the same cross-bridge population (22,23).

Critical length

The critical length, L_c, represents the half-sarcomere elongation needed to detach the cross-bridges. Since the cross-bridges are disposed in parallel, L_c, in contrast to P_c, is expected to be independent of the cross-bridge number but dependent on the cross-bridge strain. For example, if the cross-bridges are less strained, they will develop less force, and a greater elongation will be needed to elevate their force up to the rupture tension. L_c is influenced by the myofilament elasticity.

In contrast to P_c, L_c increased immediately after the release and decreased only slightly during the quick force recovery. An increase of ∼4 nm hs⁻¹ was already present 0.2 ms after the step release. This increase is easily explained by the cross-bridge and myofilament strain reduction due to the previous release, which then requires a greater elongation to reach the critical tension. This elastic effect disappears 2 ms after the release, when the tension (P_t) has almost returned to the prerelease values, but L_c is still ∼4 nm hs⁻¹ greater than the prerelease value. This observation is hard to reconcile with models of a strain-independent power stroke equilibrium constant (31).

Since P_c did not change, the greater L_c resulted in a decrease of fiber chord stiffness compared to the prerelease and immediate postrelease values. In principle, this stiffness reduction could be due to a decrease in cross-bridge number or an increase in myofilament compliance. However, because of the constancy of P_c, it is unlikely that the cross-bridge number is reduced. An increase in myofilament compliance is also unlikely, since the tension developed by the fiber is about the same as before the release and the filament compliance is expected to be the same.

Reversal of the power stroke and cross-bridge rupture

We propose that the greater critical length required to detach cross-bridges 2 ms after the release is due to a stretch-induced reversal of the power stroke after a conditioning release and a redistribution in the population of pre- and post-power-stroke states. The forced cross-bridge rupture would occur only after completion of the power stroke reversal. According to this view, our results can be explained as follows: at the end of the quick recovery, most of the myosin heads have moved into the postrecovery state. The ramp stretch, through the elasticity of the half-sarcomere, progressively increases the load on the actomyosin bonds, which in turn increases the reaction rate for the reversal of the power stroke. Thus, during the stretch itself, myosin heads progressively swing back to the prerecovery configuration. This backward movement reduces the strain on both the bond and the filament elasticity, requiring a greater stretch to elevate force to the critical value. These changes are shown schematically in Fig. 6. This hypothesis and our modeling predict that the backward movement induced by the stretch should be similar to the power stroke and therefore to the step release. This is actually close to what we found. At a 2 ms delay, L_c increased by 4.29 nm hs⁻¹ when the release was 3.89 nm hs⁻¹, and by 2.24 nm hs⁻¹ when the release was 2.11 nm hs⁻¹. Thus, by measuring the increase of L_c, we can quantify the average power stroke movement.

Figure 6.

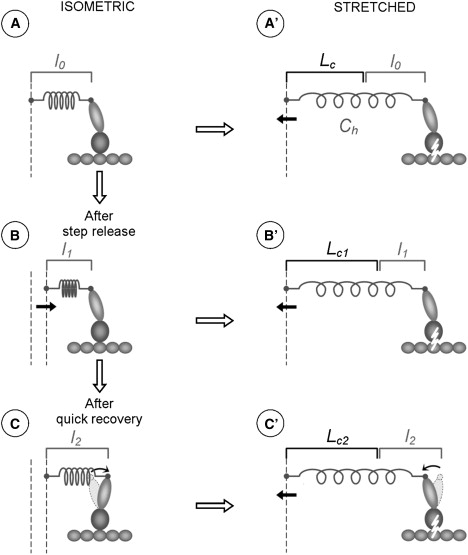
Schematic disposition of the myosin head before (left column) and after the ramp stretch at rupture tension (right column): (A and A′) before a conditioning step release, (B and B′) immediately after the step release, and (C and C′) 2 ms after the step release, at the end of the quick force recovery. The spring indicates the half-sarcomere compliance (for clarity, the half-sarcomere compliance is assumed to be located entirely outside the myosin head); l₀, l₁, and l₂ are the half-sarcomere extensions before the stretch, after the quick release, and at end of the quick recovery, respectively (the values shown on the right column are taken from the left column); L_c, L_c1, and L_c2 are the corresponding sarcomere elongations needed to detach the cross-bridges.

All the above findings suggest that cross-bridge rupture only occurs when cross-bridges are forced by the stretch to populate the same high-energy “detachable” state that is reached after the backward rotation of the lever arm. It is evident that when the stretch is applied 2 ms after the step release, the stretch must also compensate for the forward head movement that occurred during the quick recovery, which explains the greater L_c compared to the prerelease condition. This effect appears as a reduction of the half-sarcomere chord stiffness, whereas the progressive backward movement of myosin heads produces the downward curvature (increased compliance) of the instantaneous tension-length plot of the experimental curve and the model simulation. This effect also explains the long-standing finding that when a series of ramp stretches and releases is applied to a fiber, cross-bridge detachment occurs only during the first ramp stretch, and not after the second stretch that is preceded by the release (20). The release, in fact, makes necessary a greater stretch to induce the detachment. A similar effect was also found by Flitney and Hirst (32) during the application of a double cycle of much slower stretch and release at tetanus plateau. The reversal of power stroke by the stretch was also suggested by previous data obtained with much lower stretching velocities in both intact muscle fibers (30) and single-molecule experiments (33), and its effects on force response were observed in modeling of slow stretches by Månsson (29) and Pinniger et al. (30).

If detachment occurs only when cross-bridges are forced to populate the same detachable state, independently of the state in which they were at the time of the stretch, the rupture force of the individual bond will be the same; only the critical length will be different. This is consistent with our previous observations (15,17).

Fig. 4 shows that the average force developed during the whole course of the stretch is about the same under isometric conditions and 2 ms after the step release, when the sarcomere lengthening necessary to induce bond rupture is 4.29 nm hs⁻¹ greater. This means that, compared to state 1 bonds (see the model in the Supporting Material), more external energy is required to break the bonds that have transformed into state 2.

Crystallographic work has shown that myosin heads exists in at least two configurations (7,8), and switching from one position to the other produces a movement at the tip of the lever arm of ∼11 nm hs⁻¹. It has been suggested that the myosin structure may be able to flop easily between these states and take up any intermediate position depending on the force applied to it (7). Our observation that the position of the myosin lever arm at the end of the quick recovery depends on the step length change applied indicates that power stroke amplitude is modulated by the force on the cross-bridges, consistent with the above hypothesis.

Recovery of the prerelease condition

At 2 ms after the step release, the chord stiffness, S, starts to recover exponentially toward the isometric value with a time constant of ∼4.5 ms. This recovery process can be explained as follows: after the step release, actomyosin bonds progressively enter the postrecovery state characterized by a mean L_c of ∼16 nm hs⁻¹, and they start to detach. At the same time, other myosin heads, which are brought into a more energetically favorable position by the release, attach afresh to actin. These new heads bind to actin with the prerelease configuration characterized by the average L_c of ∼12 nm hs⁻¹. Thus, there exist two mixed cross-bridge populations: one with a longer L_c that decreases with time, and one that grows with time, characterized by the shorter isometric L_c. Hence, the average L_c declines progressively from the postrelease value to the prerelease value in ∼20 ms. At this time, all of the heads that have gone through the power stroke are detached and have been replaced by fresh ones, causing prerelease conditions to be reestablished. The attachment of new heads and the detachment of old ones occur at about the same rate, since the overall number of attached heads, as measured by P_c, remains almost constant. Considering that cross-bridge kinetics on the tetanus rise are faster than at plateau (34,35), the time constant of this recovery process of ∼4.5 ms is similar to the time constant of the repriming process described previously (36). Thus, T₂ relation recovery (1,36) and L_c recovery are probably both different aspects of the same phenomenon, i.e., the recovery of the original fiber conditions after the perturbation induced by the step length change. The relatively fast head attachment after the step, compared to the tetanus rise and the ATPase rate, could be justified, as suggested previously, if the freshly attached heads are the companion heads of the detaching ones (37). However, other explanations are possible (36,38).

In conclusion, in agreement with the theory, the postrecovery cross-bridge state is characterized by a lower potential energy compared to the isometric state. The individual cross-bridge rupture force does not change, and therefore the lower potential energy of the postrecovery state manifests itself as a greater lengthening necessary for the detachment.

The forced rupture of the actomyosin bond, produced by fast stretches, is preceded by the reversal of the power stroke. Thus, by measuring the critical length, one can estimate the movement of the myosin lever arm during the power stroke.

Supporting Material

Model theory, equations, a figure, acknowledgment, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01464-7.