Helix/Coil Nucleation: A Local Response to Global Demands

Abstract

A complete description of protein structure and function must include a proper treatment of mechanisms that lead to cooperativity. The helix/coil transition serves as a simple example of a cooperative folding process, commonly described by a nucleation-propagation mechanism. The prevalent view is that coil structure must first form a short segment of helix in a localized region despite paying a free energy cost (nucleation). Afterward, helical structure propagates outward from the nucleation site. Both processes entail enthalpy-entropy compensation that derives from the loss in conformational entropy on helix formation with concomitant gain in favorable interactions. Nucleation-propagation models inherently assume that cooperativity arises from a sequential series of local events. An alternative distance constraint model asserts there is a direct link between available degrees of freedom and cooperativity through the nonadditivity in conformational entropy. That is, helix nucleation is a concerted manifestation of rigidity propagating through atomic structure. The link between network rigidity and nonadditivity of conformational entropy is shown in this study by solving the distance constraint model using a simple global constraint counting approximation. Cooperativity arises from competition between excess and deficiency in available degrees of freedom in the coil and helix states respectively.

Introduction

According to the IUPAC Compendium of Chemical Terminology (1), a cooperative transition is defined as, “A transition that involves a simultaneous, collective displacement or change of state of the atoms and/or electrons in the entire system.” For example, in a perfectly cooperative four-spin system, only the states (↑↑↑↑) and (↓↓↓↓) can exist because three of the spins are dependent on one reference spin, making mixed states nonexistent. Cooperativity is the hallmark of myriad protein folding and functional mechanisms (2–4). For example, cooperativity is present in the folding of protein domains. Most domains exhibit first-order (i.e., two-state) folding transitions that define folding units (5). The ensemble of accessible states at temperatures near the melting point (T_m) is composed of a subensemble of proteins that are native-like, and a subensemble that is unfolded. When thermodynamic response is highly cooperative, the free energy landscape can be expressed accurately in terms of a single order parameter, and the system will exhibit hysteresis at intermediate temperatures where two stable basins are separated by an intermediate free energy barrier. In the limit of a perfectly cooperative transition, every residue in a folding unit is either folded or unfolded because the foldedness of each residue is 100% dependent on the others.

Folding-cooperativity within the helix/coil transition is well described by a nucleation event, followed by a zipper-like propagation mechanism (6–9). In these models, there is a large conformational entropy, S_conf, cost associated with the formation of an initial helical structure within a polypeptide that is otherwise unfolded in a coil state. Once an initial helical structure is formed, the helix propagates more readily because the nucleation cost has been paid already. The details of the nucleation/propagation mechanism differ between various helix/coil models, but the common element within these models is they all use a free energy decomposition (FED) scheme. That is, enthalpy and entropy contributions are assigned to various local states tied to structure, such as the backbone conformational state of a residue (6) or the presence of a hydrogen bond (H-bond) along the backbone (8). These models build in a high entropic cost to form an initial section of helix, but cooperativity through local consecutive coupling of residues overcomes improbable random noncooperative helical formation. For example, an explicit coupling term that favors helical structure is invoked after ∼3 consecutive helical residue states along the backbone or ∼3 consecutive H-bonds to account for nucleation. This local cooperativity mechanism accounts for enthalpy/entropy compensation, where the high cost in entropy associated with a large reduction in the number of accessible conformational states is balanced by the formation of a localized group of favorable interactions. Further reduction in S_conf is not as severe as more favorable interactions form to propagate helical structure.

The helix/coil transition is also qualitatively well described by a thermodynamic argument based on a two-state model given by Schellman (10). The assumption of a two-state model implies perfect cooperativity, which is a global property of the system. Therefore, without a proposed microscopic mechanism, estimates of enthalpy and entropy of the helix and coil states leads to an estimate for the transition temperature. Schellmann's approach is a global view that is independent of the mechanistic aspects that helix/coil models offer. Conversely, helix/coil models lose generality because they are tied to a FED scheme limited to a specific type of localized coupling between residues. Yet, helix/coil models invoking different detailed mechanisms are equivalent in their predictive power for average helix content, because cooperativity is the key aspect these models capture. The influence of the global property of cooperativity diminishes the need for a specific local mechanism, perhaps explaining why the nucleation process remains unclear (11). Therefore, it is important to evaluate carefully the thermodynamics of underlying mechanisms responsible for observed cooperativity. From a thermodynamic point of view, coupling between subsystems is the source of nonadditivity in the FED (12). In particular, entropy has been identified as an intrinsically nonadditive property of coupled subsystems (12,13). In contrast, additivity in free energy and entropy of subsystems occurs only when all subsystems are independent. Therefore, cooperativity implies nonadditivity. This simple fact generically explains why standard additive FED schemes miss cooperative effects, and why they are largely unsuccessful at predicting thermodynamic behavior in proteins (12).

A distance constraint model (DCM) restores the utility of a FED scheme by explicitly addressing the critical issue of nonadditivity when the free energy of a system is reconstituted (14). The DCM uses a generic FED where enthalpy and entropy components are associated with various interaction types. Unlike all prior FED schemes, interactions are also associated with distance constraints. The distinct feature of the DCM is that total free energy is not simply a sum over all components. A nonlinear free energy reconstitution (FER) algorithm is used to explicitly account for nonadditivity within entropic components (14–16). Although the total enthalpy remains additive as a sum over all enthalpic components, only the entropic components associated with independent constraints, as identified by efficient network rigidity graph algorithms (17,18), are summed. Specifically, the nonadditive aspect of the FER involves identifying a proper subset of constraints that are independent based on the properties of network rigidity. The salient feature of the DCM is that network rigidity is regarded as an underlying mechanical interaction that links mechanical and thermodynamic response as an enthalpy-entropy compensation mechanism. In addition, cooperativity originates from the propagation of rigidity/flexibility through molecular structure, which depends strongly on global properties of the system. The DCM has been able to recapitulate a number of experimental results, including the effects of co-solutes on helix/coil transitions (19), protein folding/unfolding C_p curves (15,16), protein fragment stability (20), and protein flexibility characteristics (21–23). It was used also to explain seemingly confounding sets of folding kinetics data from the enzyme thioredoxin (20).

The relationships between cooperativity, nonadditivity in S_conf and rigidity have unfortunately been masked by the complexity of solving the DCM. In this study, the helix/coil transition is described using a DCM that is solved under a simplifying mean-field approximation of global constraint counting. In this approximation, fluctuations in excess or deficiency of constraints within local regions are suppressed. Despite model simplicity and severity of the approximation, the helix/coil transition within a polypeptide is well described in terms of global demands on the system in a thermodynamic sense (i.e., minimum in free energy). Juxtaposed to the Zimm and Bragg (8) and Lifson and Roig (6) helix/coil models, the DCM is void of explicit nucleation and propagation parameters because the nucleation-propagation mechanism is a consequence of enthalpy-entropy compensation. We show how available degrees of freedom (based on distance constraints originating from interactions) are fundamentally linked to S_conf nonadditivity, and why this connection serves as a universal and concerted mechanism responsible for the onset of cooperativity. As such, the nucleation event can be considered a local response to global demands.

The Theoretical Model

The DCM begins by constructing a FED scheme to characterize interactions that impose distance constraints between interacting pairs of atoms, which form a constraint network. An entropy spectrum rank orders by entropy all interactions within the network. The procedure to calculate total S_conf is to test which interaction is independent starting from the lowest entropy, and working toward the highest entropy listed in the spectrum. Only independent constraints contribute to S_conf, which makes the DCM mathematically complex. However, following the approach used previously (24), we use a mean-field approximation that assumes constraints are uniformly distributed within the network, meaning local density fluctuations are ignored. This simplifying assumption allows us to replace the complicated rigidity algorithms that identify independent constraints with Maxwell counting (25). This Maxwell counting DCM will be referred to as McDCM from here onward. Maxwell counting assumes all constraints are independent when the constraint network is globally flexible, whereas the network is globally rigid when the number of constraints is equal to or greater than some threshold.

A framework, F, (i.e., graph) is used to represent a subensemble of conformations that span all accessible atomic geometries that share the same set of interactions (i.e., same constraint topology defined by F). Whereas the frameworks are based on short-range interactions, long-range communication propagates through the network due to the mechanical properties of rigidity (17). This observation has led to many successful applications of the concept of network rigidity based on the native structure of a protein (18,26–28). However, the key limitation in characterizing network rigidity of a single interaction network is that thermal fluctuations are not modeled. Dealing with temperature in the standard way prescribed by statistical mechanics, the DCM considers an ensemble of frameworks. The ensemble is derived from all fluctuating interactions.

An accurate free energy is reconstituted from the FED by accounting for the nonadditivity in S_conf during the process of summing over independent entropy contributions. Assuming each interaction of type i is identical, the total enthalpy and entropy of a framework are calculated by

$$H_{\text{total}}\left(F\right)=\sum _i^{N_{\text{int}}}{n}_i{\varepsilon }_i\text{and}{S}_{\text{total}}\left(F\right)=\sum _i^{N_{\text{int}}}{I}_i{\sigma }_i,$$ (1)

where ɛ_i and σ_i represent the enthalpy and entropy, respectively, of interaction i, and N_int indicates the number of interaction types. In qualitative terms, ɛ_i describes the depth of the potential energy minima, whereas σ_i describes the amount of phase space associated with the breadth of the energy basin. The total enthalpy of F is simply the sum over the contributions from each interaction type for which there are n_i instances of interaction type i. However, only the independent constraints, I_i, corresponding to the ith interaction type contribute to the total entropy (note that I_i ≤ n_i). In this way, total entropy is based on a local decomposition that is tabulated, whereas global demands are maintained by using network rigidity to account for long-range couplings that would otherwise be hidden.

In most works (15,16,20–23), we have used a minimal DCM (mDCM) that only considers two types of fluctuating interactions in the FED: H-bonds and torsion angle forces. Salt bridges are considered a special case of H-bonds. In addition, covalent bonds are modeled as quenched (always present) constraints, which are important for the rigidity analysis, but need not be parameterized in terms of enthalpy and entropy contributions. In principle, the partition function for the ensemble must account for all possible frameworks. To reduce the combinatorics of calculating the partition function, only native-like H-bonds are assumed accessible. Torsion angles are classified as either native or disordered. Despite this Go-like simplification, the size of the partition function state space remains much too large to completely enumerate for proteins (∼2⁹⁰⁰ for a typical 150 residue protein). In prior work, the free energy of each macrostate (N_HB, N_NT) is evaluated using a free energy functional that takes into account nonadditivity (15,16). Monte Carlo sampling generates distinct frameworks with N_HB H-bonds and N_NT native torsions. For each framework, a rigidity calculation is carried out to determine the conditional probability of interaction i to be independent, which is related to I_i as the cumulative sum of these conditional probabilities.

The synopsis given above on the process used to solve the mDCM is straightforward, but unfortunately the conceptual link between rigidity and S_conf gets lost in the details. Within the McDCM, Maxwell counting reduces the mathematical analysis to a simple counting exercise that does not require Monte Carlo sampling. This procedure maintains the essential element that rigidity is used to properly account for nonadditivity within S_conf components of a FED. The crucial aspect of the McDCM is that the spatial locations of constraints within the network are not considered. Rather, the entropy spectrum (Fig. 1 a) provides all required information for Maxwell counting to be conducted. In addition, the M_l defines the minimum number of constraints that need to be present that signifies the global transition from flexible to rigid. Based on the entropy spectrum, constraints are introduced in the network according to lowest to highest entropy rank order. When the jth constraint is placed in the network at or below the Maxwell level (i.e., j ≤ M_l), the constraint removes an available degree of freedom (thus it is independent) and contributes to S_conf. Constraints introduced into the network above the Maxwell level (i.e., j > M_l) are redundant because the network is already rigid, and do not contribute to S_conf. Differences between exact graph rigidity calculations used in previous work (14,15) and the Maxwell approximation are exemplified by an illustrative example in Fig. 1 b.

Figure 1.

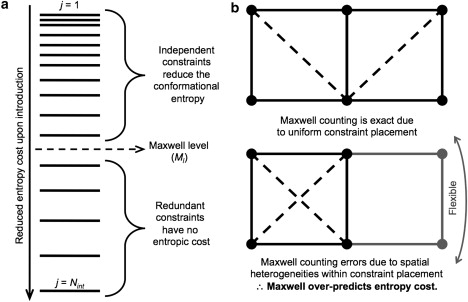
(a) Generic entropy spectrum. All interactions present in a network are rank-ordered by their entropy components (from top to bottom of the spectrum, j = 1 to N_int). A cutting line defines the Maxwell level, which defines the rigidity transition. Interactions ranked-ordered before the Maxwell level (i.e., j ≤ M_l) reduce S_conf, whereas interactions past it (i.e., j > M_l) do not. The type of interaction is not indicated in this schematic because sorting is based solely on entropy ranking. (b) The Maxwell counting approximation is explained by a simple edge-sharing quadrilateral in two-dimensions (rigid substructures are black, whereas flexible substructures are gray). In the top example, both quadrilaterals are isostatically rigid (meaning, rigid but no redundant constraints). In this case, two identical fluctuating interactions are present (shown as dashed lines), and each pays an entropic cost (e.g., a total cost of 2γ). Here, the entropy cost calculated by Maxwell equals the true network rigidity result due to uniformity. However, in the bottom example, the true entropy cost is only γ because one of the interactions is redundant. However, Maxwell assumes all interactions up to M_l are independent irrespective of their location in the network, which results in overprediction (again, 2γ) of the S_conf cost.

For a given framework, the Boltzmann weight is given by exp(S_total/R)exp(−βH_total), where S_total and H_total are given in Eq. 1. In this study, the random coil defines the reference state, whereas vacuum served as the reference state in prior works. Therefore, it follows S_total = S_coil − S_cost, where S_cost is associated with the entropy reduction accompanying the addition of interactions to a flexible chain in which all dihedral angle interactions are disordered, and no cross-linking H-bonds are present. Thus, the entropy cost parameter for the ith interaction is given by γ_i = σ_dis − σ_i. Only interactions that satisfy σ_dis > σ_i need to be considered, because otherwise they will never pay an entropy cost. In other words, σ_dis > σ_i implies γ_i > 0, which indicates that this interaction will reduce S_conf (relative to the coil state) provided other interactions have not already rigidified its local region. In all previous work, we directly used σ_i as characterizing the absolute entropy of the interaction with respect to the vacuum state. Although there is no mathematical difference, this change was made to conceptually emphasize there is greater entropy reduction associated with stronger interactions. Consequently, positive values reported here for γ_i indicate a loss in entropy, and, in applying Maxwell counting, constraints associated with greatest entropy loss are placed in the network before other constraints having lower entropy loss. Because S_coil is constant, we set it to zero with no loss of generality in calculating thermodynamic response functions, such as average energy or heat capacity. Therefore, the Boltzmann weight for a given framework within the McDCM simplifies to exp(−S_cost/R)exp(−βH_total). Note that we need to use the correct value of S_coil only to calculate absolute entropy and absolute free energy.

The McDCM presented here has a similar FED to the mDCM described above. Namely, the fluctuating interaction types are based on fluctuating H-bond and native torsion force interactions. Each H-bond is modeled as consisting of three constraints, whereas each native torsion force interaction is modeled as one constraint. Each native torsion force constraint contributes energy ɛ_NT, and when independent, there is an entropy cost of γ_NT. To keep the McDCM presented in this study to be as simple as possible, all H-bonds are treated as identical, having energy ɛ_HB, and each of its constraints, when independent, are associated with an entropy cost of γ_HB. Unlike the mDCM, the energy parameter for H-bonds implicitly accounts for a competition with H-bonds to solvent. In general, a DCM can account for additional free energy components using a more complete FED. For example, as we have done previously for polypeptides (19) and proteins (15,16), solvent terms that are expected to be independent can simply be added to the enthalpy and entropy expressions in Eq. 1. Here, all solvent effects are implicitly expressed by the four effective model parameters (e.g., ɛ_HB describes that net enthalpy change from forming an intramolecular versus solvent H-bond).

It is instructive to introduce two preliminary examples of extreme limits where all fluctuating interactions are either: 1), 100% independent; or 2), 100% redundant. For a system having 100% independent constraints, each interaction contributes to the total S_conf cost, so the Boltzmann weight of a given framework is given by $\text{exp}\left[-\left(N_{\text{NT}}{\gamma }_{\text{NT}}+3N_{\text{HB}}{\gamma }_{\text{HB}}\right)\right]\text{exp}\left[-\beta \left(N_{\text{NT}}{\varepsilon }_{\text{NT}}+N_{\text{HB}}{\varepsilon }_{\text{HB}}\right)\right]$. Conversely, in the case of 100% redundant constraints, the Boltzmann factor is given by $\text{exp}\left[-\beta \left(N_{\text{NT}}{\varepsilon }_{\text{NT}}+N_{\text{HB}}{\varepsilon }_{\text{HB}}\right)\right]$ because redundant constraints pay no entropic cost. The latter case serves only as a hypothetical example because not all fluctuating constraints can be redundant because the coil state is flexible, not rigid. It is convenient to introduce elementary statistical weights, where e_x = exp(−βɛ_x) and g_x = exp(−γ_x) for x = HB or NT. The Boltzmann weight must take into account that both independent and redundant constraints are present. For example, the Boltzmann weight of a protein that contains N_HB H-bonds and N_NT native torsion force interactions, for which I_HB H-bond distance constraints and I_NT native torsion constraints are independent, is given by ${\left[g_{\text{NT}}\right]}^{I_{\text{NT}}}{\left[g_{\text{HB}}\right]}^{I_{\text{HB}}}{\left[e_{\text{NT}}\right]}^{N_{\text{NT}}}{\left[e_{\text{HB}}\right]}^{N_{\text{HB}}}$, where the macrostate is given by (N_HB, N_NT). In the McDCM, the Boltzmann weight of a microstate is expressed solely as a function of its macrostate (N_HB, N_NT) because constraint locations are irrelevant. Thus, the McDCM partition function is calculated by considering all possible arrangements of constraints to obtain degeneracy factors related to entropy of mixing (e.g., which H-bond is present or absent given there are N_HB H-bonds in the network).

The general strategy of solving the partition function, Q, within the McDCM is to express it as a sum of Boltzmann factors, all being some powers of elementary statistical weights. The expression must count all accessible permutations of constraint networks for which the fluctuating interactions can explore. In addition, the number of independent constraints (i.e., I_HB and I_NT) must be related to M_l, which can be determined based on the entropy spectrum. Within an α-helix, the maximal number of H-bonds, n_HB, is equal to N_res − 4, whereas the maximal number of native torsion angle forces is given by n_NT = 2N_res − 2. The helix becomes rigid on introduction of all native torsion interactions, thus M_l = 2N_res − 2. The complete McDCM partition function is compactly expressed as:

$$Q=\left\{\sum _{k=0}^{\left[\frac{M_l}{b}\right]}\left(\begin{array}{c}{n}_{\text{HB}}\\ k\end{array}\right)g_{\text{HB}}^{kb}{e}_{\text{HB}}^k\left(\sum _{i=0}^{M_{\text{l}}-\text{kb}}\left(\begin{array}{c}{M}_{\text{l}}\\ i\end{array}\right)g_{\text{NT}}^i{e}_{\text{NT}}^i+g_{\text{NT}}^{M_{\text{l}}-\text{kb}}\sum _{i=M_{\text{l}}-\text{kb}+1}^{M_{\text{l}}}\left(\begin{array}{c}{M}_{\text{l}}\\ i\end{array}\right)e_{\text{NT}}^i\right)\right\}+\left\{\sum _{k=\left[\frac{M_l}{b}\right]+1}^{n_{\text{HB}}}\left(\begin{array}{c}{n}_{\text{HB}}\\ k\end{array}\right)g_{\text{HB}}^{M_{\text{l}}}{e}_{\text{HB}}^k\sum _{i=0}^{M_{\text{l}}}\left(\begin{array}{c}{M}_{\text{l}}\\ i\end{array}\right)e_{\text{NT}}^i\right\},$$ (2)

where b = 3 represents the number of constraints per H-bond and the square brackets indicates that the ratio (a real number) is truncated to the proceeding integer. This expression enumerates all constraint networks in the ensemble making use of the permutation factors, while appropriately grouping powers of the elementary Boltzmann weights. The expression of Eq. 2 assumes γ_HB ≥ γ_NT, meaning a H-bond constraint reduces S_conf more than restricting a dihedral to native-like fluctuations. The free energy of a particular framework of a polypeptide is obtained by exploring accessible rigidity states. In the context of Maxwell counting, Fig. 2 illustrates some examples of accessible macrostates that the partition function of Eq. 2 captures, which is calculated analytically by Maple. Once the partition function is calculated, the free energy is given by G = −RTlnQ, and C_p is obtained by appropriate derivatives of the free energy.

Figure 2.

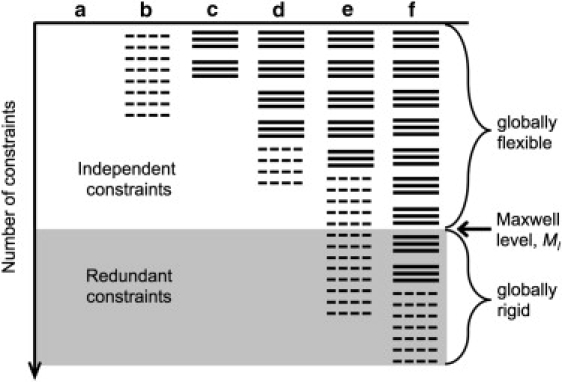
Schematic showing global dependence of Boltzmann factors due to Maxwell counting. Dashed lines represent torsion force constraints. Solid lines represent H-bond constraints, for which there are three per H-bond. Because H-bond constraints have greater entropy cost than torsion force constraints, they are placed in the network first. Six example cases (a–f) show different macrostates accessible to the polypeptide. Constraints are independent when the polypeptide is globally flexible (white) and redundant for a rigid polypeptide (gray). The left-hand bracket of Eq. 2 accounts for example cases a–e. (a) No constraints are present, which defines the random coil reference state. (b) No H-bonds formed, but some helical structure is present. (c) No helical structure formed, despite some H-bonds have formed. (d) Both helical structure and H-bonds have formed. In cases a–d the polypeptide is flexible with as many available degrees of freedom given by the gap between where the last independent constraint is shown, and the Maxwell level. (e) All H-bonds are independent, but the torsion force constraints associated with helical structure exhibit a mixture of being independent and redundant. (f) All torsion force constraints are redundant, but the H-bond constraints exhibit a mixture of being independent and redundant.

Results and Discussion

The McDCM reproduces heat capacity

The excess C_p for the helix/coil transition quantifies equilibrium fluctuations in energy that occur over an ensemble of polypeptide conformations. Therefore, measured C_p is an excellent thermodynamic response function to parameterize the McDCM. Because the McDCM presented in this study does not discriminate between residues, its four free parameters {ɛ_HB, γ_HB, ɛ_NT, γ_NT} are associated with an effective homogenous polypeptide. These parameters must be obtained by fitting to some experimental data (helix content or, as done here, C_p). This approach of fitting to experimental data on a case-by-case basis (due to nontransferable parameters) is exactly the same as used by the classic helix-coil models of Lifson and Roig (6) and Zimm and Bragg (8). We find that experimental C_p data are reproduced markedly well via fitting by inspection using Maple. Four typical examples using published C_p data for the A4, V5, and A6 polypeptides (29) and peptide I (30) are shown in Fig. 3. The McDCM parameters obtained by fitting to these experimental data are summarized in Table 1. Although there is enough freedom in the McDCM to fit well to a given C_p curve, the model is too simple for transferability in parameters. Specifically, parameter differences reflect portions of the FED that are not explicitly considered (i.e., solvent effects) and the accuracy of the homogeneous polypeptide assumption. Interestingly, the parameters of the A4, V5, and A6 polypeptides (that are of similar amino acid composition, length, and are from identical solvent conditions) are nearly transferable. Conversely, the parameters are significantly shifted in Peptide I to account for its increased length, alternate composition (specifically, altered spacing between Glu and its basic residue), and differing solvent conditions. Considering FED differences between our various models and systems (i.e., β-hairpin, α-helix, and a diverse variety of proteins), the parameters obtained here are within ranges that are qualitatively consistent. Parameter transferability is expected to increase as more complete FEDs are developed.

Figure 3.

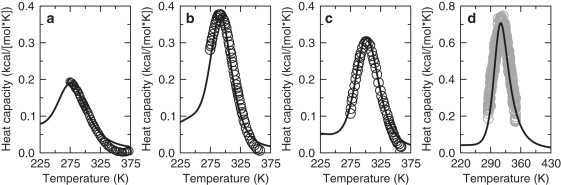
McDCM fits to excess heat capacity markedly well. Open circles denote experimental C_p data for the (a) A4, (b) V5, and (c) A6 polypeptides (29). In each case, the solid line is the corresponding McDCM best fit. (d) Light gray open circles denote experimental C_p data for peptide I from Scholtz et al. (30), and the solid line is the corresponding McDCM best fit.

Table 1.

McDCM parameters used in this study^∗

Parameter	Physical interpretation	A4 Y(AEARA)4Nres = 21	V5† Y(XEARA)6Nres = 31	A6 Y(AEARA)6Nres = 31	Peptide I Ac-Y(AEAAKA)8F Nres = 50
ɛHB	H-bond energy	−0.83	−0.83	−0.60	−1.14
ɛNT	Native torsion force energy	−0.50	−0.40	−0.45	−0.09
γHB	H-bond pure entropy cost	1.19	1.13	1.07	0.94
γNT	Native torsion force pure entropy cost	0.75	0.75	0.90	0.35

^∗Values were determined by fitting to the DSC data in Richardson and Makhatadze (29) for A4, V5, A6, and Scholtz et al. (30) for peptide I. The fits are shown in Fig. 3. The units of the energy parameters are kcal/mol, and the entropy parameters are unitless.

^†In the V5 polypeptide, X = A in repeats 1–4 and 6, whereas X = V in the fifth repeat.

Nucleation emerges as a local response to global demands

In our previous work on the helix/coil transition, an exact transfer matrix method was used to solve the DCM (14,19,31) where the FED followed closely the original model of Lifson and Roig (6). That is, each residue was considered to be in a helix or coil state. If in a helix state, then both the PHI and PSI angles were considered to simultaneously have a native torsion force constraint present. The helix or coil conformational state for each of three consecutive residues defined a local cooperative unit. Moreover, H-bonds were modeled in a similar way as done in the Zimm and Bragg model (8), and a local relationship for the energy and entropy parameters of a spanning H-bond as a function of the local conformational state of each of the three residues the H-bond spanned was constructed. The important point to note here is that the helix/coil FED used in our prior works was designed to provide accuracy and transferability of parameters, but it sacrificed simplicity. In contrast, in the FED used here, a H-bond does not couple to native torsions within residues that it spans, and all H-bonds are treated to be identical, independent of their local environment. The PHI and PSI torsion interactions within a residue are independent of one another. Moreover, Maxwell counting removes all spatial correlations. Taken together, all local couplings are eliminated. The McDCM can only exhibit cooperativity from global properties. Note that we are not implying that global demands made by rigidity are the only important aspect to nucleation and folding. Rather, the simplified McDCM is valid in a certain limit that allows us to understand the hidden nature of nucleation and cooperativity as a universal mechanism.

We first verify that there is no transition and no cooperativity if rigidity is ignored. The affect of network rigidity is easily removed by modifying the statistical weights in Eq. 2 to produce two hypothetical cases. Although interactions can form when all constraints are treated as independent, they now always give rise to a reduction of S_conf (that is, of course, incorrect). This is equivalent to changing I_i in Eq. 1 to n_i, which is the standard FED assumption of additivity. Second, we treat all constraints as redundant, which is equivalent to ignoring entropy effects altogether (i.e., γ_HB = γ_NT = 0). We then proceed to account for the observed helix-coil transition using only the two free energy parameters {ɛ_HB, ɛ_NT}. In both incorrect cases, the quality of the C_p fits shown in Fig. 3 was unattainable. It is noted that a similar null result would occur if the nucleation parameter were eliminated from the Zimm and Bragg (8) or Lifson and Roig (6) model. These results show the DCM and traditional helix/coil models exhibit cooperativity as a direct manifestation of free energy nonadditivity, regardless of its origins (local versus global). However, there is an important difference when the origin of cooperativity is identified. The nucleation/propagation models are not applicable to anything but the helix/coil transition. In contrast, the concerted (not sequential) origin of cooperativity in the DCM is a universal mechanism, and the McDCM is useful to highlight how cooperativity emerges as a consequence of a global enthalpy/entropy mechanism related to concerted properties of network rigidity.

Cooperativity requires nonadditivity

The two hypothetical cases above are analyzed further to glean insight into limiting behavior of the McDCM in states that are globally rigid or flexible. The case that all constraints are treated as 100% independent may be an acceptable approximation when the polypeptide is in the coil state. In fact, many published results of FEDs are given in tables that suggest additivity is, at times, an acceptable assumption (32,33). Therefore, we calculate the partition function using the same parameters from the McDCM given in Table 1 for the A6 polypeptide, but treating all constraints as independent. Fig. 4 shows the free energy landscape from this calculation has only one basin. It is seen that there is too much of a S_conf cost to allow the helix state to be a competitive alternative in minimizing the free energy of the system. Using the same parameters in the second case that all constraints are treated as redundant, we again calculate the partition function. Again, Fig. 4 shows the free energy landscape from this calculation has only one basin. No entropy cost is required to form favorable interactions; therefore, no entropy can be gained when these interactions break. As a result, there is no mechanism to gain enough S_conf to promote the transition by overcoming the energy cost when favorable interactions break. The free energy landscapes associated with these two extreme limits shift in location (number of constraints at the bottom of the basin) by a small amount as temperature changes.

Figure 4.

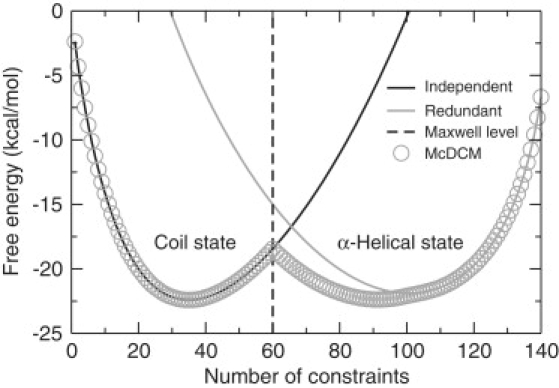
One-dimensional free energy landscapes at fixed temperature (T = 302 K) are shown as a function of number of constraints. All curves were generated with McDCM parameters for the A6 polypeptide. The (black, gray) curves show free energy landscapes with a single basin centered on the (left, right) side when all constraints are modeled as either (independent, redundant). Open circles show a free energy landscape with a double basin predicted by the McDCM, indicating cooperativity arises from a competition between microstates that are primarily flexible in the coil state and rigid in the α-helical state. The vertical dash-dotted line denotes the Maxwell level (i.e., the number of constraints needed to make the polypeptide just rigid), which indicates the polypeptide is globally (flexible, rigid) to its (left, right).

The corresponding C_p curves in the above limits do exhibit a peak (data not shown). A peak appears because of the combinatorial factors that are part of the partition function. These combinatorial factors play a critical role in defining the parabolic shape of each of the single free energy basins considered, and they represent the mixing entropy related to how many different ways N_hb H-bonds and N_nt native torsions can be arranged within the structure. However, as is well known, finding a peak in the heat capacity is not a foolproof indicator of a phase transition. A peak in C_p only reflects when the energy fluctuations are the greatest, but this does not necessarily imply cooperativity or a change of state. Tracking the free energy landscape as a function of temperature confirms that no transition occurs when the constraints are assumed to be either 100% independent or 100% redundant.

Informatively, the two limiting cases each mimic a specific aspect of the McDCM, which correctly predicts a first-order phase transition. Fig. 4 shows that there is considerable overlap between the 100% independent free energy basin and the coil basin of the McDCM. In addition, there is overlap between the 100% redundant free energy basin and the α-helix basin of the McDCM. The high degree of overlap in the two basins has important implications. Formation of H-bonds and native torsion forces in the coil state generally pay a high entropy cost. The high overlap with the single basin free energy landscape characterizes a flexible structure in a noncooperative environment where additivity prevails. In the α-helix state, H-bonds do not generally pay an entropic cost on formation because of the cooperativity that is created by having many H-bonds present in the structure. Although the physical reason why the α-helical state is stable is because of the cooperativity among interactions (i.e., dense formation of H-bonds along the backbone and native torsion forces) the mathematical exercise of enforcing 100% redundancy is analogous to enforcing the presence of the helix state, irrespective of how many H-bonds are present. As such, under this hypothetical situation, the change in free energy on formation of a H-bond is independent of whether other H-bonds are present or not. Thus, the single basin free energy landscape describing the case when all constraints are 100% redundant represents a noncooperative environment, where all free energy components are additive.

A statistical mechanical model of enthalpy/entropy compensation

Conceptually, perfect cooperativity can be thought to arise from the competition between two thermodynamic states, each representing a subensemble of conformations, where one state has low enthalpy and low entropy, whereas the other state has high enthalpy and high entropy. At low temperatures, the enthalpic stabilization of forming many interactions outweighs the entropic cost of forming those interactions. The situation is reversed as temperature increases, which gives rise to the abrupt (cooperative) transition between folded and unfolded states. This two-state thermodynamic description was used by Schellman (10) to successfully explain the helix/coil transition. Schellman gave remarkably good estimates for the enthalpies and entropies for the coil and helical states as a function of chain length to explain the dependency of melting temperature on chain length. By working with global stability estimates of end states (coil or helical structure) a model for the nucleation mechanism is not needed. Although McDCM is a statistical mechanics model, it captures the essence of Schellman's thermodynamic approach because it does not incorporate local cooperativity effects responsible for a local nucleation event. Nevertheless, as shown in Fig. 4, the free energy landscape (near the T_m) predicted by the McDCM exhibits a classic profile that contains two basins separated by a barrier. Finally, a traditional indicator of cooperativity in the helix/coil transition is that the T_m increases as a function of chain length until a point of saturation. Schellman explained the reason for this length dependence by carefully taking into account boundary effects, which in part relies on knowing the maximum number of H-bonds that can form in the α-helical structure is four less than the number of residues in the chain (10). The important point is that cooperativity can be captured as a global property of the system (total enthalpies and entropies) without invoking a microscopic mechanism for nucleation. As shown in Fig. 5, McDCM predicts T_m increases as the chain length increases until a saturation length is reached. The details of this length dependence are buried in Eq. 2 because the chain length affects the M_l, Maxwell counting and the degeneracy factors that appear in the partition function. However, the McDCM predicts the same trend as Schellman did, namely the effects of the ends become less important as the chain length increases.

Figure 5.

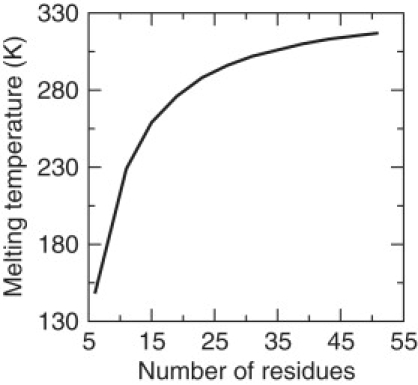
Dependence of cooperativity on chain length. Based on parameters for the A6 polypeptide, the McDCM predicts the melting temperature initially increases with chain length, until a saturation level is reached.

Perfect cooperativity, as Schellman approximated using a two-state model, does not exist in the McDCM because the partition function of Eq. 2 accounts for all possible constraint arrangements, consisting of a total of 2^3Nres-6 accessible states. The convex shape of the basins arises from combinatorial factors that account for mixing, but this does not diminish the accuracy of a two-state model. More interestingly, the α-helix basin does not completely trace the minimum of the corresponding noncooperative limiting case. This is an indication that microstates with appreciable fraction of independent constraints appear. The asymmetry in shape between the basins is a consequence that there is no natural symmetry in the problem. Of potential concern is that the α-helix basin is broader (having less curvature) than the coil basin. This is abnormal because greater fluctuations are represented in a broader basin. Prior works with the mDCM (15,16) typically result in the unfolded and folded basins to be broader and narrower, respectively. It is the favorable coupling interactions that are present in real polypeptides that suppress fluctuations in the α-helix basin. However, no local coupling interactions are modeled in the McDCM to void any type of local cooperativity.

The McDCM recapitulates the thermodynamic reasoning Schellman used to explain the helix/coil transition nearly 55 years ago, which remains sound. Thermodynamic arguments are often the most powerful because they are independent of knowing specific microscopic mechanisms. On the other hand, statistical mechanics models provide greater insight into why the thermodynamics works the way it does. The McDCM has been specifically designed here as a simple, yet informative statistical mechanics model that focuses on the microscopic reason for the cooperative behavior that is observed in thermodynamic response. Global stability issues have been demonstrated to be directly linked to network rigidity, its role in reconstituting total free energy of a system, with cooperativity being a consequence of nonadditivity appearing in S_conf via enthalpy/entropy compensation. Network rigidity places a global demand on a system to form a local nucleation event. This is because once the available degrees of freedom become marginal, near M_l, a small group of interactions forming or breaking will become highly cooperative. More generally, beyond the Maxwell counting mean-field approximation, fluctuations in constraint density play a critical role in how the global demands manifest themselves in local response.

Transition state and the rigidity threshold

As shown in Fig. 4, the McDCM predicts a transition state at the apex of the free energy barrier separating the two basins. The interesting feature is that the transition state is located precisely at M_l. The system is less stable close to the rigidity threshold separating the system from being globally rigid or globally flexible. The mechanism of enthalpy/entropy compensation is too balanced, and small fluctuations will fiercely drive the system to one basin or the other to obtain a lower free energy. The McDCM will always associate the rigidity threshold to the thermodynamic transition state, for the reasons just described. However, we showed previously that the rigidity threshold and the thermodynamic transition state are generally not collocated (15,16,23). The rigidity threshold can appear on either side of the transition state. In particular, network rigidity will have fluctuations, where some regions will be rigid, whereas other regions will be flexible. Different regions will exhibit different degrees of cooperativity depending on the nature of how rigidity/flexibility propagates through the molecular structure. These latter details manifest into a cooperativity mechanism specific to a given polypeptide (14,19,31) or protein (15,16,21–23), but the universal aspect is the link between thermodynamic and mechanical response.

Beyond a two-state model

The Maxwell counting approximation forces the entire system to be 100% rigid or 100% flexible, but this enforcement is artificial. Although lifting this mean-field approximation makes solving the DCM mathematically complicated, the approach remains tractable and computationally efficient. Network rigidity provides a universal mechanism to track nonadditivity within component entropies, thus leading to cooperative behavior. The McDCM is maximally cooperative (compared to prior DCMs) because spatial fluctuations within constraint placement, which suppress cooperativity, are not considered (cf. Fig. 1 b). In fact, the general DCM does not force two-state behavior, as both continuous and multi-phasic transitions have been successfully predicted. Across length scales (i.e., polypeptides to protein complexes), cooperativity naturally arises by accounting for nonadditivity within S_conf. The McDCM presented in this study provides an intuitive enthalpy/entropy compensation mechanism that occurs from the competition between redundant and independent states. As shown here for the McDCM, the driving force within all DCMs, despite their nuanced differences, is that nucleation emerges as a local response to global demands.

Conclusions

The DCM is a unique modeling paradigm that restores the utility of FED schemes. By accounting for S_conf nonadditivity, the general DCM strategy provides a universal mechanism for the concerted (not sequential) onset of cooperativity. Specifically, the DCM uses rigidity graph algorithms to identify (independent, redundant) constraints that (contribute, do not contribute) to the total S_conf. Although conceptually straightforward, previous DCMs are couched in a rather mathematically complex formulism that obfuscates its simplicity. As such, we have developed a mean-field DCM based on the Maxwell counting approximation that considers all constraints to be uniformly distributed throughout the system. Application of this McDCM to the helix/coil transition problem clearly highlights how cooperativity concertedly results from a competition between a collapsed state with many redundant constraints and an extended coil state where most constraints are independent. Despite its simplicity, the McDCM retains the essential physics to quantitatively reproduce experimental C_p curves. Namely, thermodynamic stability is directly linked to network rigidity, which serves as a universal mechanism for reconstituting the total free energy of a system. Cooperativity is a manifestation of nonadditivity appearing in S_conf via enthalpy/entropy compensation governed by propagation of rigidity and flexibility though molecular structure. Due to the long-range nature of rigidity, helix nucleation is a local response to global demands.