Simulation of Cyclic Dynein-Driven Sliding, Splitting, and Reassociation in an Outer Doublet Pair

Abstract

A regular cycle of dynein-driven sliding, doublet separation, doublet reassociation, and resumption of sliding was previously observed by Aoyama and Kamiya in outer doublet pairs obtained after partial dissociation of Chlamydomonas flagella. In the work presented here, computer programming based on previous simulations of oscillatory bending of microtubules was extended to simulate the cycle of events observed with doublet pairs. These simulations confirm the straightforward explanation of this oscillation by inactivation of dynein when doublets separate and resumption of dynein activity after reassociation. Reassociation is augmented by a dynein-dependent “adhesive force” between the doublets. The simulations used a simple mathematical model to generate velocity-dependent shear force, and an independent elastic model for adhesive force. Realistic results were obtained with a maximum adhesive force that was 36% of the maximum shear force. Separation between a pair of doublets is the result of a buckling instability that also initiates a period of uniform sliding that enlarges the separation. A similar instability may trigger sliding initiation events in flagellar bending cycles.

Introduction

In cilia and eukaryotic flagella, dynein motor enzymes, arrayed along the nine outer doublets of the axoneme, produce interdoublet sliding that can generate a wide variety of bending movements. How the action of these dyneins is coordinated to produce useful bending patterns is still not understood. In particular, the fundamental mechanism for oscillation to produce cyclic bending has not been established. However, there is one situation in which dyneins produce oscillatory movements that appear to be easily explained. These movements are found in partially disintegrated flagella, where the outer doublets remain attached together at the basal end of the flagellum. Dynein activity on just one doublet can produce sliding between a pair of doublets. If the doublets were to remain closely associated, the pair would be expected to bend and ultimately stabilize with the active shear force balanced by the elastic resistance of the bent doublets. With partially disintegrated doublets, the sliding is accommodated more easily by splitting of the doublet pair on the basal side of the sliding region. Further sliding enlarges the separation between the doublets. The distal end of the separated region propagates to the distal end of the doublets, and the doublets separate completely. This is followed by reassociation, beginning from the basal end. This cycle of sliding, separation, reassociation, and more sliding can be repeated at a regular frequency. This behavior was described in detail for Chlamydomonas flagella by Aoyama and Kamiya (1) after earlier observations (2,3). A somewhat similar cyclic behavior was observed in sea urchin sperm flagella (4). These examples of oscillation were explained by the simple assumption that dyneins are inactivated by separation between the doublets and resume activity when the doublets reassociate.

In these experimental situations, the partial dissociation of the doublets appeared to result from breakage of elastic interdoublet linkages (sometimes referred to as nexin linkages) by proteases. After protease treatment, the dyneins may be the remaining source for the forces that hold two doublets together, as well as for producing sliding. To better understand these dynein functions, computer programming was developed to simulate the oscillatory behavior seen in the experiments with partially dissociated flagella. This computer modeling considers dyneins on just one outer doublet (referred to as doublet A) interacting with sites on another outer doublet (doublet B). In the examples studied by Aoyama and Kamiya (1), doublet B was not straight, although there was very little bending of doublet B during the cycle, while doublet A underwent extensive bending and movement. The work presented here considers only the case in which doublet B does not bend during the cycle. The case in which both doublets can bend will require substantially new computational methods and a separate study. In this study, dynein force generation was simulated by simple and independent mathematical relations for a velocity-dependent shear force and an elastic adhesive force. Modeling with more realistic kinetic models for dynein force generation also remains to be performed in future studies.

Methods

As in previous work, beginning with that of Machin (5), the bending movement of a long flexible filament is obtained by solving a moment balance equation. This work considers a two-dimensional model, with two outer doublets represented by two thin filaments that remain in a single plane as they bend. It is convenient to describe the shape of a filament by its curvature, κ (s), where s is the distance measured along the filament. Given a shape at time t, the moment balance equation is solved to obtain rates of bending, ∂κ(s)/∂t, and the shape can then be updated to time t + Δt by κ(t + Δt) = κ(t) + ∂κ(s)/∂t Δt. Repeated iterations then lead to a complete history of bending of the filament through time. For numerical analysis, the length of the filament is divided into segments of length Δs, and κ and ∂κ/∂t are defined at the joints between each segment. This converts the moment balance equation from a partial differential equation to a set of linear equations that is solved to obtain the values of ∂κ/∂t. Each filament is clamped at its basal end, so that no displacement or rotation of its basal end can occur. Consequently, the distance (60 nm) between the filaments at the basal end remains constant, with no shear between filaments at the basal end. In flagellar modeling, a constant distance between doublets at all points along the length is assumed, and active dynein force density is easily converted to active shear moment density, which is integrated along the length to obtain active bending moment. For a single doublet, or for a doublet pair with variable interdoublet spacing, the relationship between the dynein force and the active bending moment on each filament is determined by the shape of the filament. This procedure was described in an earlier modeling study of bending movements of individual microtubules over a surface coated with motor enzymes (6).

Dynein sliding forces can be simulated by a simple mathematical model used in earlier studies (6–9). When there is no sliding, this model produces a tangential force density per unit length along doublet A, f₀. A short sliding displacement at a velocity V_L causes a reduction in force, as if the force were produced by an elastic resistance: df/dt = −f₀ E_SCB V_L, where E_SCB is a stiffness constant equal to the reciprocal of the sliding distance required to reduce the force to 0. When f is less than f₀, the force recovers toward f₀ with a first-order rate constant k. If f₀ and V_L are constant, the steady-state solution gives the force density, f:

$$f=f_0\left(1-E_{\text{SCB}}{V}_{\text{L}}/k\right)\text{.}$$

The force decreases linearly with sliding velocity to zero, where the sliding velocity V₀ = k/E_SCB. The moment balance equations can be developed with the steady-state solution, where the velocity-dependent term acts like a longitudinal viscous resistance, and f₀/V₀ is simply added to the longitudinal viscous drag coefficient, C_L, in the equations. A non(steady-state) version used in previous modeling studies (6–8) was also examined, with E_SCB = 0.1 nm⁻¹. Both versions give nearly identical results over most of the range of parameters examined, and unless stated otherwise, the reported results represent the results from both methods. The steady-state version effectively assumes dynein kinetics that rapidly follow changes in switching, whereas the rate constant k in the non(steady-state) version introduces a delayed response to switching. Agreement between the two versions suggests that this simple model for force generation is acceptable. When the two versions do not agree, the results must be considered tentative, pending future exploration of models that incorporate realistic kinetics for dynein attachment to and detachment from substrate sites.

If doublet A is perfectly straight, a longitudinal force will produce no bending moments, and the doublet will remain straight indefinitely. To avoid this situation, all of the simulations include a small symmetry-breaking curvature, usually 1 × 10⁻⁸ rad μm⁻¹. A more complete presentation of these methods is provided in the Supporting Material.

New features required for modeling an interacting doublet pair

In this work, the dynein shear force constant, f₀, is assumed to be modulated by the distance between the two filaments, such that it is completely eliminated when this distance becomes too great. There is also assumed to be force normal to filament A, which attempts to maintain a constant spacing between the filaments. This force has been termed the adhesive force (10,11), and is suspected to be provided by the dyneins. This force is derived from a linear elastic resistance constant, E_N. Functional relationships between these forces and the separation distance between the filaments, measured normal to doublet A and relative to the fixed separation at the basal end, are governed by four constants: C₁ is the separation distance at which f₀ increases from 0 (for separations <C₁) to a constant value; C₂ is the separation distance at which f₀ starts to decrease linearly to 0 at separation distance C₃; and C₄ is a multiplier of E_N for separation distances <0. E_N is constant from separation = 0 to C₂, and then also falls to 0 at C₃. Values used for these constants are given in Table 1. Modulation of dynein forces over a range of 8 nm is guided in part by observations of 10 nm differences in interdoublet spacing between bent and straight regions of Chlamydomonas flagella (12). The primary new development in this work is that the separation distance and relative velocities between interacting regions of the two filaments, each described by its own κ(s) variables, are computed. This is described in detail, along with computer code for the core portions of the programming, in the Supporting Material.

Table 1.

Parameter values used for examples A and B

Elastic bending resistance, EB (pN nm2)	1 × 107
Dynein adhesive elastic constant, EN (pN nm−2)	0.005
Longitudinal viscous drag coefficient, CL (pN s nm−2)	3.24 × 10−9
Active sliding force density, f0 (pN nm−1)	0.11
Doublet length (nm)	12000
Drag coefficient ratio, CN/CL	1.8
Active sliding velocity at 0 force, V0 (nm s−1)	14000
Lower separation limit for active force, C1(nm)	−2
Separation at which dynein active force and elasticity start to decrease, C2(nm)	8
Separation at which dynein active force and elasticity become 0, C3 (nm)	16
Dynein elasticity multiple for separation < 0, C4	40

Results

Typical results

Configuration series from typical simulations with a doublet length of 12 μm are shown in Fig. 1. Movies in the Supporting Material provide a more complete picture of the movement. These examples are designed to simulate the results previously obtained with a dissociated Chlamydomonas flagellum, as shown in Fig. 2 and Movie S1 of Aoyama and Kamiya (1). Example A (Fig. 1 A and Movie S1) shows the results obtained when doublet B is straight. This restriction creates a simpler situation in which the effects of the model parameters can be understood more easily. For example B (Fig. 1 B and Movie S2), doublet B is given a constant curvature of 0.05 rad μm⁻¹, and the elastic rest position of doublet A is concentric to doublet B, with a radius that is 60 nm greater. These specifications are not sufficient to precisely match the experimental results, because there is some bending of doublet B during the cycles of bending observed by Aoyama and Kamiya (1). The parameters used for the simulations in Fig. 1 are given in Table 1.

Figure 1.

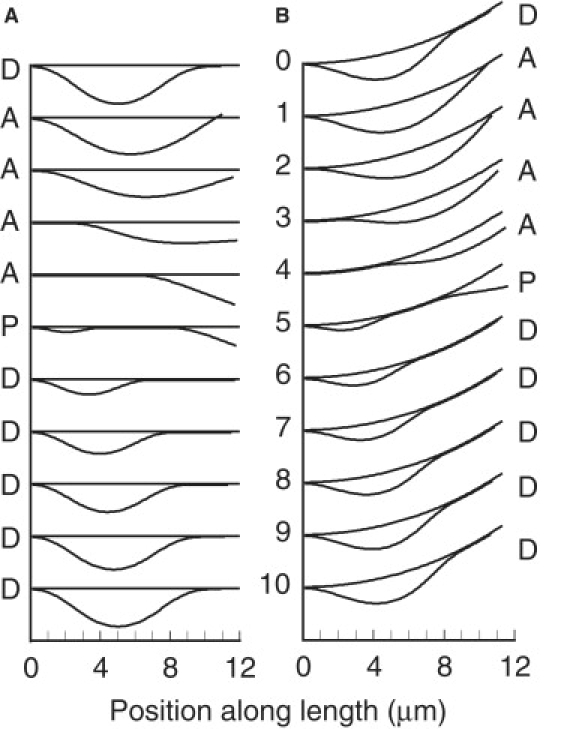
Panel A shows a sequence of images covering one cycle of oscillation of example A, a typical simulation of a doublet pair with doublet B straight and stationary. Images 0 and 10 should be identical. Association, propagation, and dissociation phases are indicated by the letters A, P, and D, respectively. Panel B shows a similar sequence for example B, in which doublet B has a fixed curvature of 0.05 rad μm⁻¹. The parameters used for these models are given in Table 1. For example A, the time interval between images is 14.9 ms and the frequency is 6.7 s⁻¹. For example B, the time interval between images is 9.8 ms and the frequency is 10.2 s⁻¹.

Figure 2.

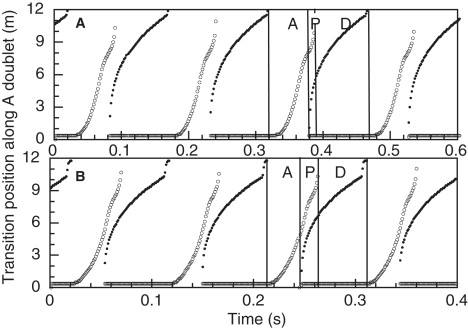
Positions of transition points on doublet A, plotted as a function of time, for simulation examples A and B. The positions of association transitions, at the basal end of a separated region, are shown as open circles. The positions of dissociation points, at the distal end of a separated region, are shown as solid circles. The solid vertical lines demarcate the A, P, and D phases for one cycle of oscillation. These plots can be compared with Fig. 4 of Aoyama and Kamiya (1).

For their experimental example, Aoyama and Kamiya (1) also presented a plot (their Fig. 4) showing the propagation of association and dissociation points along the doublets as a function of time. Similar plots for simulation examples A and B are shown in Fig. 2. For an association transition, these points are taken to be the points at which the separation between the doublets causes the dynein shear force density f₀ to switch from below half to above half of its full value. Similarly, the dissociation points are for switching of f₀ in the opposite direction. There is probably only an approximate relationship between these criteria and those used to distinguish transitions in the previous video recordings (1).

Figure 4.

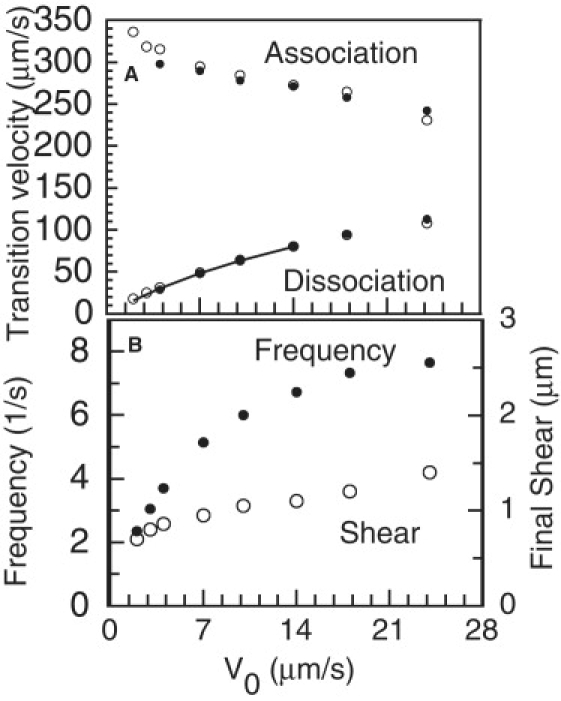
Effects of varying the unloaded sliding velocity, V₀, generated by the active sliding system. Except for variations in V₀, all other parameters are the same as given in Table 1 for example A. (A) Propagation velocities for the association (upper points) and dissociation (lower points) transition points. Solid circles are from simulations with the non(steady-state) dynein model; open circles used the steady-state dynein model. The line through the dissociation point velocities is the calculated relationship between dissociation velocity and sliding velocity obtained from experimental data, with K_m for dissociation velocity vs. [ATP] of 0.107 mM (1) and K_m for V₀ vs. [ATP] of 0.177 mM (17), assuming [ATP] = 0.5 mM for the standard conditions where V₀ = 14 μm s⁻¹. This line diverges only slightly from the linear relationship expected if K_m is the same for both variables, so that the dissociation rate is proportional to V₀. (B) Cycle frequency (solid circles) and final shear attained in the distal associated region, at the end of phase D (open circles). Note that the results for V₀ = 18 and 24 μm s⁻¹, at the right ends of the curves, are beyond the range accessible in the experiments (1).

The movement cycle has three distinct phases. Phase A (images 1–4 in Fig. 1, A and B) is the “Association phase” that begins after the complete dissociation of the doublets at their distal ends, which occurs between images 0 and 1. A combination of elastic straightening against the viscous resistance of the fluid environment and adhesive force that develops when the doublets are sufficiently close together then causes the doublets to move closer together and reassociate, beginning at the basal end. No sliding between the doublets occurs during phase A. Propagation of the association transition begins slowly and then accelerates to a more uniform velocity (Fig. 2). For comparison purposes, an average velocity of 272 μm s⁻¹ was obtained from linear fits of association point positions during the most constant part of phase 1 in example A, between 4 and 7 μm from the base. This is less than the value of about 400 μm s⁻¹ reported by Aoyama and Kamiya (1). In this example, phase A occupies 41% of the cycle period, or 0.061 s. In example B, the association transition propagates with an average velocity of 369 μm s⁻¹ and phase A occupies 33% of the cycle period, or 0.033 s.

Phase P is the “Propagation phase” that begins with a dynein-driven buckling event that creates a new separation region between 1–3 μm from the base (image 5 in Fig. 1, A and B). This new separation region has a nonpropagating association transition at its basal end and a propagating dissociation transition at its distal end. In example A, with doublet B straight, phase P begins when the associated region reaches a length of 8.2 μm. This is significantly greater than in the experimental example, where separation begins when the associated region appears to occupy less than half the length of the doublets. Introducing a fixed bend in doublet B, in example B, causes phase P to begin earlier, when the length of the associated region is 5.2 μm. This change, by itself, produces a small increase in cycle frequency. During most of phase P, the previous association transition and the new dissociation transition propagate with reasonably similar velocities, expanding the separation region and maintaining the intervening region of association, which is 4.8–5.4 μm long in example A and 2.5–3 μm long in example B. These propagation velocities are typically less than the velocity measured for the association transition in phase A, and this decrease in velocity can sometimes appear before the start of phase P (see Fig. 2 A). These details of association velocity changes were not revealed by the lower-resolution experimental data (1), which appear to show a near-constant association velocity over the full length of the doublets. In example A, as the association transition nears the distal end, it accelerates and progresses more rapidly to the end of the doublet to terminate phase P. Phase P occupies 7% of the cycle period, or 0.010 s, in example A, and 18% or 0.018 s in example B.

Phase D is the “Dissociation phase” in which the dissociation transition propagates to the distal end, with a gradually decreasing velocity. In example A, phase D, represented by images 6–10, occupies 52% of the cycle period (0.078 s). For comparisons, a velocity obtained from dissociation transition points between 7 and 10 μm was used. The average dissociation point velocity in this range is 80 μm s⁻¹ for example A and 83 μm s⁻¹ for example B. The dissociation phase of example A is not identical to the experimental results in Fig. 4 of Aoyama and Kamiya (1). The experimental results show a large increase in the propagation velocity of the dissociation transition during the latter part of phase D. This feature was introduced into example B by specifying that the adhesive elasticity constant, E_N, decreases linearly to 0 in the terminal 1.5 μm of doublet A. This specification decreases the duration of phase D to 0.049 s, or 49% of the cycle period, and causes a substantial increase in the cycle frequency. There is an additional frequency increase because the decreased duration of phase D reduces the separation amplitude, so that elastic straightening in phase A requires less time. However, this specification does not introduce the high degree of variability in propagation of the dissociation point seen in the experimental data (1), and only slightly decreases the acceleration of propagation of the association point during the latter part of phase P. During phase D, the amplitude of the separation increases as a result of sliding in the distal associated region. The final amplitude is best quantified by the total shear displacement accumulated at the distal end by the end of phase D. Plots of shear displacement during phase D for examples A and B are shown in Fig. 3. For example A, the final shear is 1.15 μm. For example B, the final shear is less (0.9 μm) because the duration of phase P is less. Fig. 3 shows sliding occurring at a nearly constant rate during phase P. However, this simply indicates that the force required to maintain the bend in the separated region is much less than the force required to initiate a separation, so the sliding velocity is very close to V₀, the velocity at 0 force. In these examples, the average velocity is 0.98 V₀. With the linear force model used here, the steady-state force density should be proportional to the difference between the observed sliding velocity and V₀, or 0.02 f₀. A more detailed examination of the difference between the observed sliding velocity and V₀ indicates that the force density is not perfectly constant, but does not change in a manner that would compensate for the decreasing length of the associated region, to maintain a constant total force.

Figure 3.

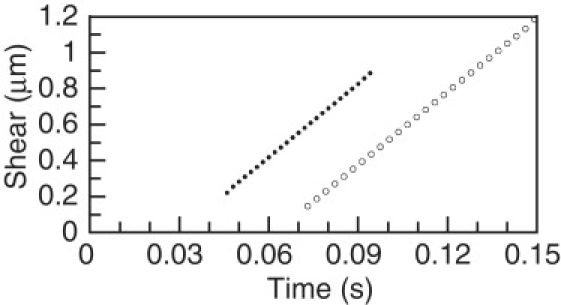
Shear displacement in segment 98 of 100, plotted against time, for typical cycles of examples A (open circles; cycle period 0.149 s) and B (solid circles; cycle period 0.98 s). For examples A and B, a least-squares linear fit gives a velocity of 13.53 μm s⁻¹ and 13.67 μm s⁻¹, respectively. Shear resulting from the fixed curvature of doublet B has been subtracted from the shear values for example B.

A length of 12 μm was used for these simulations based on measurements obtained with Chlamydomonas flagella (13). The doublets examined by Aoyama and Kamiya (1) appear to be at least 11 μm long, but the ends of the doublets are not resolved clearly enough to determine the exact length. The elastic bending resistance of the sea urchin sperm axoneme is 1 × 10⁸ pN nm² (14). For one doublet, a value of E_B = 0.1 × 10⁸ pN nm² was used. The active shear force density constant, f₀, of 0.11 pN nm⁻¹ corresponds to 11 pN for the repeating group of dyneins in a 96 nm length of axoneme. This value is equivalent to a value used in modeling flagellar movement (7). The value for the longitudinal viscous drag coefficient, C_L, in Table 1 is 1.5 times the value used in simulations of flagellar movement (7,8). Some factors, such as the small doublet diameter and higher temperature, suggest that a lower value might be appropriate. On the other hand, the shorter bend length and, more importantly, the small separation between doublets A and B suggest a higher value (15,16). The 1.5 factor was largely chosen to increase the relative duration of phase A, to better match the experimental results. Note that multiplying all of the first four parameters in Table 1 by a constant factor will not change any results. The values of C_L, V₀, and E_N were chosen for these examples to give a cycle frequency for example B similar to the experimental results (9 s⁻¹), with roughly similar separation amplitude and relative durations for the three phases. The sliding velocity parameter, V₀ = 14 μm s⁻¹, is somewhat less than the value of 18.5 μm s⁻¹ reported for sliding velocity during axonemal disintegration under similar conditions (17). Using V₀ = 18.5 μm s⁻¹, it was possible to obtain a frequency of 9 s⁻¹ for the bent doublet B case (as in example B) by increasing the relative value of external viscous resistance by 38%, but this caused the ratio of durations of phase A and phase D to increase to 1.4, compared to 0.7 for example B (see Fig. 2 B), which is closer to the experimental results.

Effects of changing the zero-force sliding velocity, V₀

Varying the value of V₀ in the range of 1–14 μm s⁻¹ changes the cycle frequency, as shown in Fig. 4 B, and the dissociation velocity measured during phase D, as shown in Fig. 4 A. There is a relatively small change in association velocity, which was not detected in the experiments (1). The change in dissociation velocity can be compared with changes caused by variations in ATP concentration, shown in Fig. 5 of Aoyama and Kamiya (1). Those authors reported a nonlinear Michaelis-Menten-type relationship between dissociation velocity and ATP concentration, with a K_m of 0.107 mM. Using this value and the value of K_m= 0.177 mM for V₀ reported from the same laboratory (17), the expected relationship between dissociation velocity and V₀ can be calculated, and is shown by the line through the dissociation velocity points in Fig. 4 A. This is not a very sensitive test because the difference between the two K_m values is small. The line and the data points are only slightly different from a linear proportionality between dissociation velocity and V₀. However, the difference indicates that dissociation velocity does not decrease as rapidly as V₀, which means that phase D allows more time for sliding to produce a larger final shear, so that the shear amplitude, shown in Fig. 4 B, does not decrease as rapidly as V₀.

Figure 5.

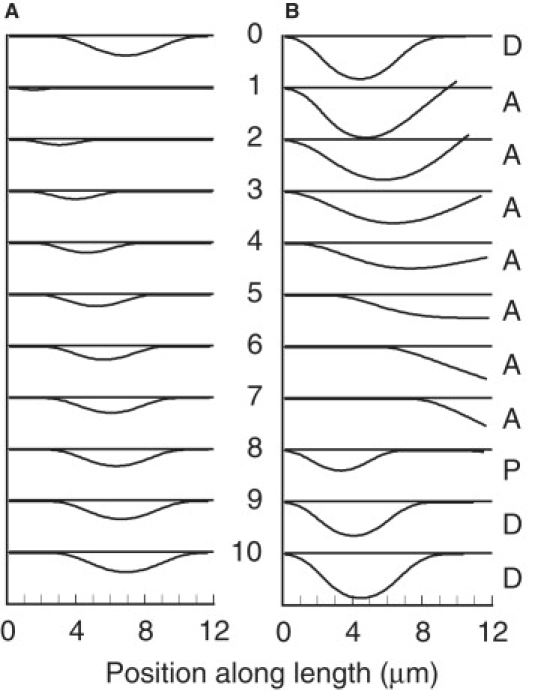
Panel A shows a sequence of images covering one cycle of oscillation of example A with V₀ reduced to 1.0 μm s⁻¹. The time interval between images is 38.5 ms and the frequency is 2.6 s⁻¹. Panel B shows a sequence of images covering one cycle of oscillation of example A with V₀ increased to 48 μm s⁻¹. Association, propagation, and dissociation phases are indicated by the letters A, P, and D, respectively. The time interval between images is 12.2 ms and the frequency is 8.2 s⁻¹.

The changes in shear amplitude, which produce changes in the amplitude of the separation, are also illustrated for extreme values of V₀ in Fig. 5. As V₀ is decreased, both the cycle frequency and the amplitude decrease, along with a relative decrease in the duration of phase P. When V₀ is ≤1 μm s⁻¹, a secondary bending pattern appears (Fig. 5 A), which does not divide into three phases as in the primary pattern. Instead, soon after the appearance of a new separation, the association transition at its basal end begins to propagate at a constant velocity, resulting in a cycle with a higher than expected frequency. This secondary pattern has a frequency that is highly dependent on the computational time step, Δt, and can only be consistently obtained with the steady-state force model. The secondary pattern might be dismissed as a computational artifact, except that this pattern of cycling occurs in the real world, as illustrated by the example shown in Fig. 6 and Movie S2 of Aoyama and Kamiya (1). For comparison, Movie S3 shows a simulation result for example B, with V₀ reduced to 1 μm s⁻¹ as in Fig. 5 A. Further exploration of this bending pattern will require a more realistic model for dynein force generation.

Figure 6.

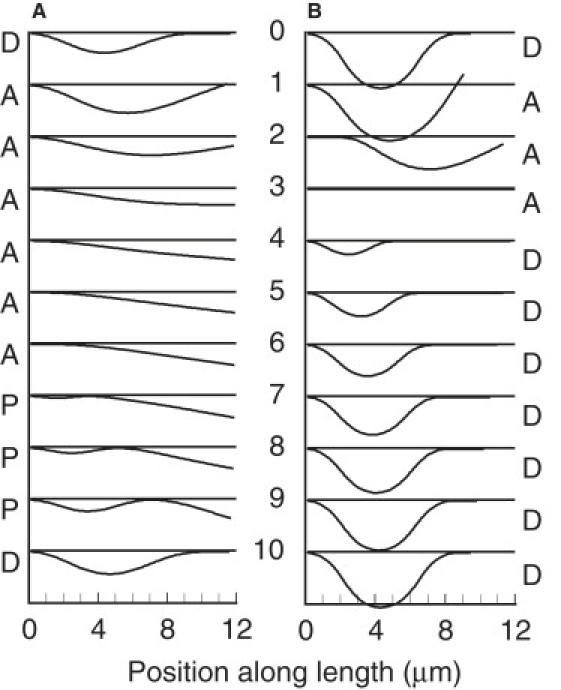
Panel A shows a sequence of images covering one cycle of oscillation of example A with E_N reduced to 2 × 10⁻⁶ pN nm⁻². Association, propagation, and dissociation phases are indicated by the letters A, P, and D, respectively. The time interval between images is 23.3 ms and the frequency is 4.3 s⁻¹. Panel B shows a sequence of images covering one cycle of oscillation of example A with E_N increased to 0.019 pN nm⁻². The time interval between images is 27.4 ms and the frequency is 3.65 s⁻¹.

With high values of V₀ (above the maximum V₀ of 19 μm s⁻¹ expected at saturating ATP concentration (17), if V₀ = 14 at 0.5 mM ATP), there is a large bend in the separation region (Fig. 5 B), and after complete separation (image 1), doublet A has to move a considerable distance against the fluid viscosity until reassociation can begin (images 4 and 5 in Fig. 5 B). Phase A includes images 1–7 in Fig. 5 B. Phase P is very short, and only its very end is captured in image 8. Phase D is reduced and is represented only by images 9 and 10.

Effects of changing the adhesive elasticity constant, E_N

The normal elastic resistance constant, E_N, is a new parameter that has not been used in previous modeling. The value of E_N = 0.005 pN nm⁻² was used for the examples in Fig. 1 to simulate the experimental result in Fig. 2 of Aoyama and Kamiya (1). Other values of E_N were explored, with C₄ adjusted to maintain E_N = 0.2 pN nm⁻² for the compression resistance at less than normal separations. With low values of E_N, a short associated region can initiate separation (see image 7 in Fig. 6 A), and the propagating associated region between the basal and distal separated regions is also very short (images 8 and 9 in Fig. 6 A). The cycle frequency increases to 8 cycles s⁻¹ when E_N = 0.001 to 0.0025 pN nm⁻², and then decreases to 4.3 cycles s⁻¹ with further reduction in E_N down to 2 × 10⁻⁷ pN nm⁻². Even when the adhesive force resulting from E_N is nearly eliminated, the elastic bending resistance is sufficient to bring the two doublets close together by straightening of doublet A, so that sliding force can be reactivated. This straightening will be sufficient for the special case in which doublet B is straight, and is also dependent on the boundary condition at the base of doublet A, which is rigidly clamped so that it is parallel to and at a constant distance from doublet B. Under these conditions, phase A is lengthened, as represented by images 1–6 in Fig. 6 A. The very brief phase D is represented by image 10 in Fig. 6 A.

Increased values of E_N increase the separation amplitude and decrease the cycle frequency. Increasing the value of E_N makes it more difficult for buckling to generate a new separation. With E_N = 0.019 pN nm⁻² (Fig. 6 B), a new separation does not appear until after reassociation is completed; there is no phase P. With E_N = 0.020 pN nm⁻², buckling is prevented and the doublets remain stably associated.

Requirements for initiation of separation between the doublets

If example A is started with the active force density constant, f₀, reduced from 0.11 to 0.062 pN nm⁻¹, the doublet pair remains straight for at least 10 cycle periods. With f₀ = 0.063, cyclic behavior is obtained, similar to that shown at high E_N in Fig. 6 B. The effect of reducing E_N was explored using a constant value of E_N = 0.2 pN nm⁻² for separations < 0. Decreasing E_N by 50% allows the critical f₀ to decrease to 0.046 pN nm⁻¹. A further decrease down to the low value of E_N = 2 × 10⁻⁶ pN nm⁻² used for the example in Fig. 6 A decreases the critical f₀ nonlinearly to 0.0028 pN nm⁻¹, but this is still well above the theoretical value of f₀ = 1.1 × 10⁻⁴ pN nm⁻¹ calculated using equations (18) for a self-loaded column in the absence of normal forces such as E_N. Other experiments have shown that the very low force produced by a single kinesin motor enzyme can cause buckling of a 6 μm length of microtubule (19). The critical value of f₀ can also be decreased by decreasing E_B, with a 50% decrease in E_B allowing f₀ to decrease to 0.043 pN nm⁻¹, which is a slightly greater decrease than that observed with a 50% decrease in E_N.

With bent doublets, as in example B, the minimum value of f₀ required for separation is reduced by 37%, to 0.0391 pN nm⁻¹. This is similar to the 37% decrease in the length of the associated region in example B, compared to example A, before separation begins. The reduced force requirement can be interpreted in terms of a transverse force, or t-force (10), that pushes the doublets apart. If some of the adhesive elastic force is required to balance the t-force, that reduces the amount of adhesive elasticity that is available to constrain separation. The t-force is equal to the product of curvature and the longitudinal force in the doublet. With a curvature of 0.05 rad μm⁻¹ and f₀ = 0.0391 pN nm⁻¹, the t-force increases linearly to 0.0235 pN at the base of the doublet. With E_N = 0.005 pN nm⁻² and C₂ = 8 nm, the maximum possible adhesive force will be 0.040 pN. After the t-force is balanced, only 41% of the adhesive force remains to constrain separation. Similarly, when the doublets are straight, as in example A, a 59% reduction in E_N reduces the required force density for separation by 32%.

Summary of comparisons with experimental data

In choosing the parameters listed in Table 1, it was important to make visual comparisons with Movie S1 and Fig. 2 of Aoyama and Kamiya (1) because there is no comprehensive quantitative description of the experimental movement. The best-determined result is the cycle frequency of 9 s⁻¹ for the experimental example in Fig. 2 of Aoyama and Kamiya (1); 10.1 s⁻¹ for model example B was considered to be adequately close. Inspection of their Fig. 2 shows that doublet separation has begun in images at times 20 and 130 ms, when the lengths of the associated region are between 4 and 5 μm. With example B, doublet separation began when the length of the associated region was 5.2 μm, and it then decreased to ≤3 μm. An inspection of Fig. 4 of Aoyama and Kamiya (1), which shows transition point propagation, as in Fig. 2 of this work, suggests that the duration of phase A is slightly less than the duration of phase B; however, the resolution of the plot is not sufficient to obtain a more precise value. In example B, the ratio of these phase durations is 0.7. Transition propagation velocities, shown in Fig. 5 of Aoyama and Kamiya (1) and Fig. 4 of this work, were determined differently. It may be coincidental that the association transition velocity of example B of 369 μm s⁻¹ is close to the value of about 400 μm s⁻¹ for an average of eight experiments (1). It is probably not significant that the dissociation transition velocity obtained for example B (83 μm s⁻¹) is smaller than the value of about 200 μm s⁻¹ obtained for an average of eight experiments (1), because the velocities for the model results were measured at a later time in the cycle. It is more significant that in both the model and the experiments, the dissociation transition velocity decreased when the siding velocity was reduced, with relatively little change in association transition velocity. The final shear amplitude was not reported for the experimental results, but an inspection of Fig. 2 of Aoyama and Kamiya (1) suggests a somewhat larger value than the value of 0.9 μm obtained with example B.

Discussion

Understanding the experiments

These simulations confirm the previous interpretation of the experimental observations of cyclic sliding, dissociation, reassociation, and sliding (1). The simulations make clear that the association phase (phase A) is an important rate-determining phase that depends on both the elastic return of doublet A to a position close to doublet B and an additional adhesive force, before any active sliding is resumed. The importance of the adhesive force can be seen by comparing the result in Fig. 6 A (with very little adhesive force) with the result in Fig. 1 A, which has a value of adhesive force chosen to reproduce the experimental results (1). With this value of E_N = 0.005 pN nm⁻², the peak force density normal to doublet A reached at a separation of 8 nm equals 0.04 pN nm⁻¹. This is considerably less than the peak active sliding force density of 0.11 pN nm⁻¹ used for these simulations. There does not seem to be any difficulty with the assumption that dyneins can provide adhesive forces comparable to those used in these simulations. The model presented here does not replicate all experimental observations, such as the details of the changes in association and dissociation transition velocities during the cycle. Further studies of the experimental situation may reveal other details that will be useful for improving the model for generation of dynein forces.

These simulations, which use only simplistic mathematical models for dynein force generation, establish a platform for further examination of detailed models for dynein function. Flagellar simulations have been performed successfully by including the kinetics of individual dynein motors (8,20). Incorporation of modeling of individual dyneins into the programming developed here will require specification of the adhesive forces produced by different states in the dynein mechanochemical cycle. Doing this in a manner that can produce results that more completely match the experimental observations on cyclic dissociation and association may place constraints on the dynein models that will help elucidate how dynein works.

Buckling and sliding initiation events

As previously recognized by Aoyama and Kamiya (1), the initiation of a new separation between doublets is the result of a buckling instability that occurs when the bending moment generated by the longitudinal force in doublet A exceeds the bending moment that can be overcome by bending resistances. The situation is similar to a vertical column loaded only by its own weight, which fails catastrophically near its base when a critical length is exceeded. However, the situation is not sufficiently similar to allow the use of standard equations for buckling criteria (18), because the normal elastic resistance, E_N, resists bending in a different manner than E_B. This makes the determination of the critical load force more complicated. Buckling is also a sliding initiation event. Sliding in the distal region reduces the longitudinal force, so that the situation is a controlled collapse rather than a catastrophic collapse. In the simulations, the controlled collapse during phase D involves sliding at a velocity close to the velocity for 0 force, and the system continues to collapse even though the force is only a small fraction of the force required to initiate buckling. The success in simulating the movement cycle seen in the experiments suggests that sliding during phase D of the experimental situation may have similar properties.

After the sliding initiation event, sliding is both constant in time and uniform throughout the length, and therefore strongly resembles what happens after a sliding initiation event in the bend cycle of cilia and flagella (21). This observation suggests that sliding initiation events in cilia and flagella may also be triggered by the removal of a resistance to sliding, allowing dyneins that are already in an active state to start producing sliding. This idea contrasts with the more common suggestion (20,22) that a sliding initiation event requires synchronous switching of dyneins from an inactive state to an active state throughout an extended length of an axoneme. No separate process that could cause such a propagated activation has been identified, although considerable attention has been given to the idea that sliding itself can regulate dynein activity (21). A buckling event that requires sliding might thus be able to activate a stronger sliding response. That does not appear to be happening in the situation considered here, where full dynein activation is required to produce the force that causes buckling, and no further activation of the force-producing system is required to continue the cycle. However, in a complete axoneme, it could be inhibition of dynein activity on one side of the axoneme resulting from backward sliding that is responsible for an apparent activation of sliding.

In previous studies (23,24), cytoplasmic kinesins that became attached to the microscope slide surface when axoplasm was extruded from squid nerve axons were observed to propel microtubules across the surface. Occasionally, a gliding microtubule encountered an obstacle that prevented forward movement. In such cases, the kinesin pushing on the microtubule caused the microtubule to bend and establish a pattern of cyclic bend initiation and propagation (23,24). Bend initiation in this situation, as seen in images 62–64 in Fig. 7 of Allen et al. (23) and images 42–45 in Fig. 5 of Weiss et al. (24), is probably similar to buckling, but is more complicated because it involves a regular reversal of curvature at the basal end. Although this movement has been successfully reproduced by computer simulations (6), a detailed analysis of buckling and bend initiation has not been performed. These observations also raise the question as to whether sliding initiation events in normal flagellar bend initiation, which also involve a reversal of curvature (21), should be interpreted as buckling events, and whether this interpretation would help us understand flagellar oscillation. There is a major difference: with the gliding microtubules, obstruction of the basal end was required, so that propagation of distal bends against viscous resistances produced compressive forces on the basal region. This is not necessary for flagella, where a shear resistance at the base is sufficient for generation of new bends even when the basal end is completely free. However, a situation in which compressive forces appeared to be significant for sliding initiation events was described by Woolley (25).

Relevance to flagellar oscillation and the “geometric clutch”

When shear forces are applied to a doublet, curvature of the doublet will cause the longitudinal force in the doublet to produce a bending moment. When a pair of doublets is bent into a curve, and the force on the outermost doublet is directed toward the basal shear resistance, these moments will cause the outer doublet to increase its curvature and move away from the inner doublet. This is the basis for the buckling separation described in this work. The separation of the doublets can also be considered to be the result of a transverse force or t-force that is the product of curvature and longitudinal force (10). As shown here, buckling can be prevented if the elastic resistance, E_N, is sufficient to produce a transverse “adhesive force” that exceeds the t-force. Recognition of the t-force led to the proposal of a “geometric clutch” model for regulation of flagellar oscillation and bend propagation (10,11). This model proposes that an imbalance between t-force and adhesive force will introduce a partial separation between flagellar doublets, which is normally limited by other interdoublet elements such that the doublet separation is sufficient to suppress dynein activity but not great enough to disrupt the structure of the axoneme. Computer simulations in which dynein activity is modulated by the t-force have been successful in generating realistic bending patterns for flagella and cilia (10,11). Obviously, the idea that dynein activity can be controlled by doublet separation is fully consistent with the observations on cyclic sliding, separation, and reassociation of doublet pairs. Development of programming for bending of both doublets of a pair will facilitate further exploration of the role of doublet separation in flagellar oscillation.

Supporting Material

Three movies, methods, and a reference are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01469-6.