Buckling, stiffening, and negative dissipation in the dynamics of a biopolymer in an active medium

Abstract

We present a generic theory for the dynamics of a stiff filament under tension, in an active medium with orientational correlations, such as a microtubule in contractile actin. In sharp contrast to the case of a passive medium, we find the filament can stiffen, and possibly oscillate or buckle, depending on both the contractile or tensile nature of the activity and the filament-medium anchoring interaction. We also demonstrate a strong violation of the fluctuation–dissipation (FD) relation in the effective dynamics of the filament, including a negative FD ratio. Our approach is also of relevance to the dynamics of axons, and our model equations bear a remarkable formal similarity to those in recent work [Martin P, Hudspeth AJ, Juelicher F (2001) Proc Natl Acad Sci USA 98:14380–14385] on auditory hair cells. Detailed tests of our predictions can be made by using a single filament in actomyosin extracts or bacterial suspensions.

The cytoskeleton (1) is a dense multicomponent meshwork of semiflexible polymers which interact sterically as well as through active (1 –3) processes. Although the blending of polymers industrially requires special effort, the active environment of the living cell provides a setting in which polymers that differ substantially in their stiffness are naturally mixed and interact. Moreover, active processes, such as polymerization and the working of molecular motors, lead to the generation of stresses without the external imposition of flow fields. These two mechanisms combine to yield a rich range of novel physical phenomena. The role of activity in cytoskeletal mechanics is receiving increasing attention, as seen from many recent theoretical and experimental studies of the rheology of cells and cell extracts (4 –6). It is clear in particular (7) that interactions between different species of filaments are crucial for cell motility, cell division, vesicular transport, and organelle positioning and integrity.

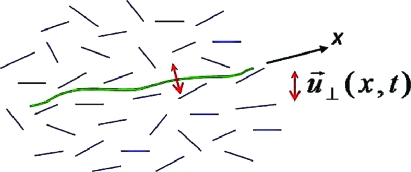
In this paper, we make a study of the effect of these interactions by modeling the dynamics of a stiff filament, which we will call a “microtubule”, immersed in an active medium (Fig. 1) with orientational degrees of freedom, which we will call “F-actin”. We emphasize here that the names microtubule and F-actin are introduced for convenience: We consider both contractile and tensile activity, although only the former applies to actomyosin. Our treatment applies more generally to semiflexible polymers under tension in a wide variety of active media. We describe the medium by the active generalization of liquid-crystal hydrodynamics (2, 3, 8–14). For the purposes of this paper, an active medium is one whose constituent particles possess the ability to extract energy from an ambient nutrient bath and dissipate it, executing some kind of systematic motion in the process. This activity endows each such particle with a permanent uniaxial stress. The other central ingredient of this work is anchoring, on which we now elaborate. In general, the interfacial energy of a liquid-crystalline medium at a wall depends on the relative orientation n of the molecules of the medium and the normal N to the wall. In the simplest cases, it is lowest for n parallel, or perpendicular, to N. This interaction is known as anchoring (15). In the present work, anchoring enters through the favored orientation of the F-actin when confronted with the surface of the microtubule (see, e.g., refs. 16 and 17). The interplay of the types of anchoring and activity—contractile or tensile—are fundamental to our theory. The filament in our study can be viewed as a spatially extended probe of the active medium, generalizing the microrheometry of (4 – 6, 18, 19) by simultaneous access to a wide range of scales. We make contact with earlier work on oscillatory filaments (20, 21) and suggest possible settings where our results could be tested.

Fig. 1.

A stiff filament (“microtubule”) embedded in an active isotropic medium consisting of oriented fiaments (“F-actin”). The conformations of the microtubule, aligned on an average along the x axis, are described by small transverse fluctuations u _⊥ (x,t). The active medium can either be contractile or tensile. The orientation of F-actin along the microtubule can either be parallel or normal to it.

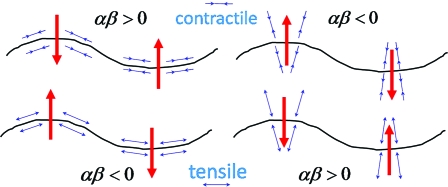
Here are our main results: (i) In the absence of activity, the microtubule will always buckle at large anchoring strength, regardless of the type of anchoring. (ii) An active medium, by contrast, can stiffen or buckle the filament, depending on the relative signs of activity and anchoring. A contractile active medium with parallel anchoring always stiffens the filament, as does a tensile active medium with normal anchoring, whereas a contractile (tensile) medium with normal (parallel) anchoring produces buckling if the strength W of the active stresses is large enough (see Fig. 2). When the nematic correlation length of the F-actin medium is large, compared with the linear dimension L of the sample transverse to the microtubule, the buckling wavelength decreases with L as $1∕\sqrt{WL}$ and $1∕\sqrt{W\log L}$ respectively in two and three dimensions. (iii) Activity leads to a breakdown of the fluctuation–dissipation (FD) relation: Most dramatically, in the regime of strong stiffening, we predict that the effective dissipation turns negative when the frequency crosses a threshold. This prediction is consistent with the observations of ref. 20 on auditory hair cells and ref. 21 on axons and suggests that a negative force–velocity relation at finite frequency should be a generic feature of actively stiffening systems. Indeed, the phenomenological model of ref. 20 emerges as a limiting case of our fundamental theory. (iv) In the SI Text, we speculate on a possible mechanism, arising from the results of this paper, whereby microtubules are able to target filopodia, the slender spikes that emerge from the leading edges of migrating cells.

Fig. 2.

A perturbation of a microtubule (black) leads, through anchoring, to a distortion of the F-actin medium and, hence, of the active stress profile. Depending on whether the actin is anchored parallel or normal to the microtubule and whether the active stresses (blue double-arrows) are contractile or tensile along the actin filaments, the resulting secondary flows (red arrows) either suppress or enhance the perturbation, leading to active stiffening or buckling.

A Filament in an Active Medium

Consider a stiff, locally inextensible filament of total contour length L, coinciding on average with the x axis (Fig. 1), with unit tangent vector t̂ = x̂ + δ t̂ ≃ (1+O(∂_x u _⊥)², ∥_x u _⊥(x,t)) where u _⊥(x,t) are small transverse fluctuations, and ⊥≡y,z, immersed in a d-dimensional active medium characterized by Q, is a symmetric traceless nematic order parameter (15). The effects of contractile or tensile active stresses enter the equations of motion

for u _⊥ and Q through the hydrodynamic velocity field v whose dynamics are governed by Eq. 3 below. The Gaussian, spatiotemporally white noises f _⊥, η in Eqs. 1 and 2 have strengths 2N ₁, 2N ₂, reducing respectively to 2k _B T/γ, 2k _B T/ζ for the equilibrium case. In Eqs. 1 and 2, u _⊥ and Q are coupled only through the free-energy functional F[u _⊥,Q] = F _f[u _⊥] + F _LD[Q] + F _anc[u _⊥,Q]. The filament free energy F _f[u _⊥] = ∫₀ ^L dx[(σ/2)(∂_x u _⊥)² + (κ/2)(∂_x ² u _⊥)²] contains bending energy with rigidity κ and an imposed tension σ (22, 23) to leading order in ∂_x u _⊥. The Landau–de Gennes free energy F _LD[Q] = ∫dx ∫d ² r _⊥[(a/2)Q ² + (K/2)(∇Q)²] describes incipient orientational ordering in the medium (15). We work here in the isotropic phase with correlation length $\sim \sqrt{K/a}$; a study of the nematic phase by generalizing ref. 24 to include activity will give rise to long-range elastic effects. The filament anchors the orientational degrees of freedom of the medium through

with negative and positive A corresponding, respectively, to parallel and normal anchoring. Note that Eq. 1 generalizes refs. 22 and 23 to include anchoring and hydrodynamic flow. In Eq. 2, we ignore flow-orientation coupling terms (15)*.

For thin-film samples at large F-actin concentration, as in the case of the lamellipodium of adhering cells, it is appropriate to treat the hydrodynamic velocity field in a local-friction approximation. We therefore write Γv _i(x,r _⊥,t) = −∇_jσ_ij, with Γ ∼ μ/ℓ² where μ is the cytoplasmic viscosity and the screening length (25) ℓ is no larger than the film thickness. We ignore pressure gradients on the assumption that the film thickness adjusts to accommodate them. The crucial piece of the stress σ_ij is the active contribution† σ_ij ^act ≃ Wc ₀ Q _ij(x,r _⊥,t) (2, 3, 8, 9, 11, 12), where W < 0 and W > 0 respectively correspond to contractile and tensile stresses, and c ₀ is the mean F-actin concentration. To leading order in gradients and linear order in filament undulations, the velocity transverse to the microtubule is

From Eqs. 1–3, the effective Fourier-transformed equation of motion for u _⊥(q _x,ω) is

where u _⊥ is coupled to Q only at r _⊥ = 0.

where G _qω ≡ (q _⊥ ² + q _ω ²)⁻¹, with q _ω ² ≡ −ζiω/K + a/K + q _x ², and ${\int }_{q_{\perp }}\equiv {\int }_0^{\Lambda }{d}^{d-1}(q_{\perp }/2\pi )$, with ultraviolet cutoff Λ ∼ (filament thickness)⁻¹. The signs of α ≡ (A/γ − Wc ₀/Γ) and β ≡ −A/ζ decide the fate of the filament (stiffening or buckling) in the following analysis. Because ${\int }_{q_{\perp }}{G}_{q\omega }\sim \ln ({\Lambda }^2/q_{\omega }^2)$ in 3D and π/(2q _ω) in 2D, we obtain the dispersion relations for u _⊥(q _x,ω) for the case of an unbounded medium:

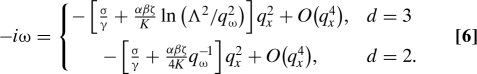The case of a confined medium is discussed in FD Ratio and Negative Dissipation.

Active Stiffening and Buckling

We are now in a position to investigate the (in)stability of the filament. At thermal equilibrium (W = 0) sgn [α] = −sgn [β]; indeed, αβ = −A ²/ζγ < 0 irrespective of the sign of A. This combination implies a buckling instability of the filament as the anchoring strength is increased, regardless of whether the anchoring is parallel or perpendicular. This prediction is consistent with observations (24) of buckling of filaments in isotropic solutions of fd virus (see figure 1 A of ref. 24). For strong anchoring, defining the anchoring length λ_anch ≡ k _B TK/A ² of the medium on the filament, and the persistence length ℓ_p ≡ κ/k _B T of the filament, and balancing (negative) effective tension and bending energies, we see that the buckling wavelength is $\sqrt{\kappa K/A^2}\sim \sqrt{{\lambda }_{anch}{\ell }_p}$, which can be much smaller than ℓ_p. When activity W is switched on, the signs of α and β become independent. For large enough |W|, α > 0 for contractile (W < 0) activity and α < 0 for tensile (W > 0) activity, whereas β is separately controlled by the nature of the anchoring (Fig. 2).

Defining the correlation length $\xi \equiv \sqrt{K/a}$ of the F-actin medium, we focus on two limiting cases: (i) deep in the isotropic phase; and (ii) close to the transition to a nematic phase. In (i), q _xξ ≪ 1, so Eq. 6 holds with $q_{\omega }=\sqrt{a/K}$ for small ω. Thus, for a filament in a strongly active medium, contractile (tensile) activity with parallel (normal) anchoring (αβ > 0) leads to enhanced tension, i.e., stiffening. On the other hand, for strong contractile (tensile) activity with normal (parallel) anchoring (αβ < 0), the filament becomes unstable to buckling. This set of possibilities is explained graphically in Fig. 2.

In case ii, q _xξ ≫ 1 (which should be accessible in F-actin; see ref. 26) so that a wide range of modes of Q contribute in Eq. 5. In dimension d = 3, Eq. 6 applies with q _ω ² ≃ q _x ² − ζiω/K, so that the dispersion relation differs from case i only by a logarithmic factor. In d = 2, however, solving the resulting cubic equation we find

where $Y=(-1/2\pm i\sqrt{3}/2)$ for αβ > 0 and 1 for αβ < 0. Thus, in 2D, close to the ordering transition of the F-actin, although stability is determined by the sign of αβ as before, the stable stiffening case αβ > 0, which can arise only for an active system, shows a damped oscillatory response, which should appear as dispersive propagating waves on the filament, with speed ∝q _x ^1/3. In the unstable case, the buckling wavelength can be found, by a balance between the negative tension q _x ² and bending elasticity q _x ⁴ terms in Eq. 6. For an F-actin medium of finite lateral extent L ≪ ξ, and for large destabilizing activity, the integrals leading to the q _ω-dependence in Eq. 6 are cut off by L, resulting in a buckling wavelength varying as $1/\sqrt{WL}$ (d = 2) and $1/\sqrt{W\log L}$ (d = 3), as claimed in the summary of results in the opening section of this paper.

In the SI Text, we discuss the possible realization of these ideas in a neuronal growth cone (Fig. S1) and speculate that active stiffening could offer a mechanism for guiding microtubules into filopodia. We note here that active buckling may have been seen in the experiments of Brangwynne et al. (8), who report significant bending fluctuations of microtubules in reconstituted networks (see figure 1 in ref. 8). Because actomyosin is contractile, our theory predicts that the contacts in a buckling system must be at near-normal alignment, and we look forward to independent tests of this. Moreover, our theory provides a fundamental theoretical explanation of the point-like normal force, which Brangwynne et al. (8) suggest buckles the system.

FD Ratio and Negative Dissipation

If χ(t) is the displacement of a degree of freedom of a system at time t in response to an impulsive force at time 0, and C(t) is the time-correlation of spontaneous fluctuations in that degree of freedom, the fluctuation-dissipation theorem (FDT) (27), which applies to systems at thermal equilibrium, says that C(t) = −k _B Tχ(t), where k _B is Boltzmann's constant and T is the temperature. This profound and universal connection can be understood in the familiar context of a particle undergoing Brownian motion in a fluid, where both the damping of an initially imposed velocity and the random motion of the particle, when no velocity is imposed, arise from the same microscopic collisions with molecules. For equilibrium systems, this relation allows one to obtain transport quantities, such as conductivity, without drawing a current. In systems far from equilibrium but where the bath producing the fluctuations is still thermal, a judicious definition of variables (28) can resurrect the FDT. For more general nonequilibrium systems too, a comparison of correlation and response can sometimes offer a useful notion (29) of an effective temperature. Our model system shows radical departures from such benign behavior.

We restrict attention to parameter ranges where there is no instability, so that a steady state exists. Let S(q _x,ω) ≡ ∫_x,t exp(iq _x x−iωt)〈u _⊥(x,t)·u _⊥(0,0)〉 be the correlation function and χ″(q _x,ω) the imaginary part of the response to an external force h(x,t) coupled to u _⊥ via a term −∫dx h · u _⊥ in the free-energy functional F in Eq. 1. The departure from unity of the FD ratio R(q _x,ω) ≡ (ω/2k _B T)S(q _x,ω)/χ″(q _x,ω) is a quantitative measure of nonequilibrium behavior. We find not only that R(q _x,ω) depends on its arguments but that it can turn negative for the stable stiffening case αβ > 0. The calculation, from Eqs. 4 and 5, is straightforward. We find

where D _qxω and $\Sigma (q_{\omega })={\int }_{q_{\perp }}{[{(q_{\perp }^2+a/K+q_x^2)}^2+{(\zeta \omega /K)}^2]}^{-1}$ are strictly positive and even in ω, and the FD ratio

At thermal equilibrium (W = 0) N ₁ = k _B T/γ, N ₂ = k _B T/ζ, α = A/γ, and β = −A/ζ, so that αN ₂/N ₁ = −β. Hence, the second term in the bracket in Eq. 9 vanishes and the FD ratio becomes unity as expected. With activity, the ratio becomes a strong function of frequency and wavenumber through the quantity Σ(q _ω). In the stiffening case αβ = (A/γ − Wc ₀/Γ)(−A/ζ) ∼ WA > 0, if the strength W of activity is large enough, as ω crosses a threshold that depends on q _x and W, we see from Eqs. 8 and 9 that, χ″ can pass through zero, and hence R _qxω can diverge. Past this threshold, both turn negative. Thus, one obtains a giant or even a negative FD ratio as a result of suppressed dissipation rather than enhanced noise. The FD ratio in Eq. 9 is sometimes referred to (20) as the ratio of an “effective temperature” T _eff to the thermodynamic temperature T, and a negative T _eff in this sense has been observed in experiments on hair cells (20). Our theory in Eqs. 1–3, rooted in the active-hydrodynamic approach of refs. 2, 3, 8, 9, 11, and 12, provides a fundamental basis for the model presented in (20) and suggests that the phenomenon of negative dissipation should be widely observed in active systems. To apply our treatment directly to axons (21) and hair cells (20), we consider a filament confined to a tube of radius L in the ⊥ directions and unbounded along x, and assume the correlation length $\xi \equiv \sqrt{K/a}$ of the active medium is of order L. The integrals over q _⊥ in Eq. 5 are replaced by sums dominated by a single mode with wavenumber of order 1/L. This analysis yields an effective equation of motion

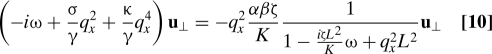plus noise. For strong, active stiffening, αβ large and positive, these dynamics lead to oscillatory modes with $\omega \simeq \pm \sqrt{\alpha \beta }{q}_x/L$. These modes correspond to the hair cell oscillations of ref. 20, generalized to allow a continuum of modes labeled by q _x.

Conclusion

We have presented a general theory for a single, long, semiflexible filament interacting with an active medium. The medium consists of orientable elements, endowed with built-in uniaxial stresses whose axes are correlated with those of their neighbors. The model thus describes, in particular, a single microtubule interacting with an actively contractile actomyosin environment but has broader applicability. Whereas the various components of the cytoskeleton are usually investigated separately, our paper lays the physical groundwork for a treatment of the interaction of these different elements, in particular the contractile actin, and microtubules as active transport highways. This framework is essential to an understanding of cell motility and active ribosomal transport.

The key ingredients of the model are anchoring—the preferred orientation imposed on the filaments of the medium when confronted with the surface of the long filament—and the contractile or tensile activity of the medium. The sign and strength of anchoring could possibly be tuned in cell extracts by modifications of the variety of proteins that link actin and microtubules (16, 17) or in conventional liquid-crystalline systems by varying temperature (30), for example. We find that the interplay between anchoring and activity radically affects the filament's dynamics, leading to a range of possible behaviors including active stiffening, negative dissipation, oscillations, and buckling.

The theory presented in this paper may also be applied to the dynamics of other diverse biological systems, such as axons and auditory hair cells, providing an important link between existing phenomenological models for these systems and the general framework of active matter. The stiffening and buckling behavior of a microtubule in a neuronal growth cone are in qualitative accord with the theory presented here. We look forward to quantitative experiments, for example on cell extracts or suspensions of swimming organisms, that will provide more stringent tests of our theory.