Abstract
Optical techniques enable portable, non-invasive functional neuroimaging. However, low lateral resolution and poor discrimination between brain hemodynamics and systemic contaminants have hampered the translation of near infrared spectroscopy from research instrument to widespread neuroscience tool. In this paper, we demonstrate that improvements in spatial resolution and signal-to-noise, afforded by recently developed high-density diffuse optical tomography approaches, now permit detailed phase-encoded mapping of the visual cortex's retinotopic organization. Due to its highly organized structure, the visual cortex has long served as a benchmark for judging neuroimaging techniques, including the original development of functional magnetic resonance imaging (fMRI) and positron emission tomography. Using phase-encoded visual stimuli that create traveling waves of cortical activations, we are able to discriminate the representations of multiple visual angles and eccentricities within an individual hemisphere, reproducing classic fMRI results. High contrast-to-noise and repeatable imaging allow the detection of inter-subject differences. These results represent a significant advancement in the level of detail that can be obtained from non-invasive optical imaging of functional brain responses. In addition, these phase-encoded paradigms and the maps they generate form a standardized model with which to judge new developments in optical algorithms and systems, such as new image reconstruction techniques and registration with anatomic imaging. With these advances in techniques and validation paradigms, optical neuroimaging can be extended into studies of higher order brain function and of clinical utility with greater performance and confidence.
Introduction
Functional near infrared spectroscopy (fNIRS) and diffuse optical tomography (DOT) have shown promise as tools for neuroimaging in populations ill-suited to functional magnetic resonance imaging (fMRI) and positron emission tomography (PET) due to a combination of the techniques' portability and comprehensive measurement of hemodynamics. While the potential impact is great, in order to become a widespread neuroscience tool, non-invasive optical imaging techniques need to be developed with the capability to map brain function with reasonably high resolution, repeatability, and sensitivity. Neuroimaging systems are expected to be able to not only identify cortical areas, but also discriminate features and borders within them. These challenges are not unique to emerging optical techniques, but were also faced by both PET and fMRI in their early development. fMRI and PET established their worth as brain mapping tools through their ability to map the highly organized structure of the visual cortex. In this paper, we demonstrate that high-density DOT is able to meet this same neuroimaging benchmark through mapping the visual field using traveling waves of neuronal activation and phase-encoded mapping procedures.
Invasive studies of animals have shown that the visual cortex is composed of many distinct processing areas, each with its own map of the visual field (or subset thereof) (Van Essen et al., 1992). These maps are retinotopic, meaning that adjacent areas in the visual field map to adjacent areas of the cortex. So, an easily controlled stimulus can be used to selectively activate these different cortical locations. Thus, the visual cortex provides an ideal test system for judging the reliability and resolution of new neuroimaging systems. Retinotopic mapping was used for the validation of both PET (Fox et al., 1987) and fMRI (Engel et al., 1994; DeYoe et al., 1994; Engel et al., 1997). The ability to conduct retinotopic mapping has further enabled neuroscience studies of processing in the visual cortex (Tootell et al., 1997; Tootell and Hadjikhani, 2001). In addition, the visual cortex continues to be used as a standard system by which to judge further improvements in image quality and algorithms, such as constructing a common atlas space for adults and children (Kang et al., 2003).
Visual responses have been studied with fNIRS using both the hemodynamic (Colier et al., 2001) and fast (Gratton et al., 1995) signals. However, the spatial resolution of the systems used in these optical studies was too low to distinguish the retinotopic organization within the visual cortex and were limited to differentiating the right and left hemispheres. However, even without access to high spatial resolution, the visual cortex has still served as a model system for advancing temporal fNIRS methods, including event-related algorithms (Schroeter et al., 2004; Plichta et al., 2006), multimodal imaging with fMRI (Toronov et al., 2007), extending optical methods to bedside neonatal measurements (Karen et al., 2008; Taga et al., 2003), and developing methods to simultaneously analyze multiple hemodynamic contrasts (Wylie et al., 2009).
Having developed a high-density diffuse optical tomography (HD-DOT) system as an advance on previous fNIRS technology, we have previously been able to discriminate two activations within the same visual quadrant using block-design paradigms (Zeff et al., 2007). We now address the task of mapping the visual field with higher spatial resolution to show that HD-DOT is able to reproduce classic neuroscience results. In this paper, rather than activating individual cortical regions in a block paradigm, we use stimuli that move periodically in the visual field, creating a traveling wave of activation in the visual cortex (Engel et al., 1994; DeYoe et al., 1994). Decoding the resulting periodic activations with Fourier analysis allows the construction of full retinotopic maps that relate each area of the visual field to locations in the cortex (Sereno et al., 1995; DeYoe et al., 1996; Tootell et al., 1998). Through these experiments, we are able to evaluate the ability of HD-DOT to contiguously map the entire visual field. Additionally, we can test our ability to construct high signal-to-noise maps in individual subjects, which is a crucial step for clinical neuroimaging. These results are intended to demonstrate increases in the fidelity of HD-DOT mapping, allowing the field to move forward more confidently into novel and clinical experiments.
Methods
HD-DOT imaging system
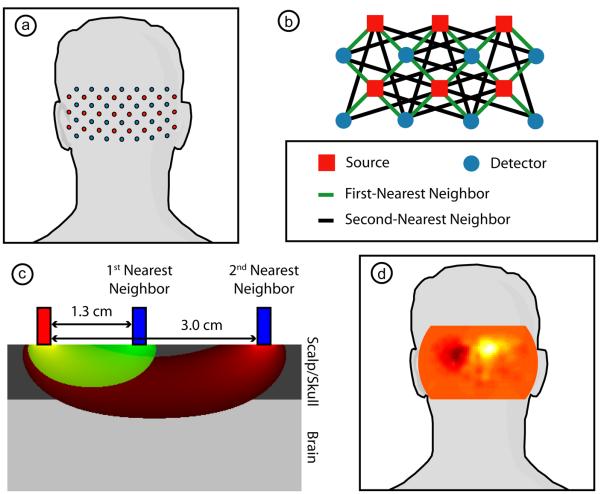
We have constructed a high-density DOT instrument with light-emitting diode (LED) sources and avalanche photo diode (APD, Hamamatsu C5460-01) detectors (Zeff et al., 2007). Since source encoding is controlled digitally with software and each detector has a dedicated 24-bit analog-to-digital converter (MOTU HD-192), the system is configurable for different imaging geometries. In this study, we used 24 source positions and 28 detector positions (collectively referred to as optodes) coupled with fiber optic bundles to a flexible imaging cap. This array is held on to the back of the head over the visual cortex with hook-and-loop strapping. Each source position consists of LEDs at 750 nm and 850 nm (750-03AU and OPE5T85, Roithner Lasertechnik) that were individually, digitally controlled to create an encoding pattern. Our standard encoding scheme uses spatial encoding (two distant sources are co-illuminated), temporal encoding (nearby sources are illuminated sequentially), and frequency encoding (the two wavelengths of illumination are modulated at different frequencies and demodulated with digital lock-in detection). After being digitized, the APD measurements were written directly to hard-disk at 96 kHz. With this configuration, the system worked in continuous wave mode with a frame rate of 10.78 Hz. The source and detector positions were arranged in a grid designed to cover the visual cortex, with a total size of 13.2 cm wide by 6.6 cm high (Fig. 1a). With the high sensitivity and dynamic range of the instrument, first- (13 mm) and second- (30 mm) source-detector pairs were sampled simultaneously with light levels well above the noise floor, for a total of 212 measurements (Fig. 1b shows a subset of the array with measurement definitions).
Figure 1. Our high-density diffuse optical tomography system.
(a) Schematic showing the placement of the array of 24 sources (red) and 28 detectors (blue) over the occipital cortex of an adult. (b) Schematic showing the arrangement of first-and second-nearest neighbors within a subset of this array. Due to the high dynamic range of our system, all of these measurements are used within the 3D reconstruction. (c) A cross-section through the analytic solution to the diffusion approximation for a first-nearest neighbor (sensitivity in green) and a second-nearest neighbor (sensitivity in red) within a semi-infinite, homogeneous geometry. The sensitivity functions have been truncated at a fluence of 5% of maximum. Optodes are modeled as exponentially decaying line sources and have been integrated across the 3 mm optode diameter. (Note that these sensitivity functions appear broader and with less of a peak under the source than would be obtained using the traditional point source model.) Measurement depth-of-penetration increases with increasing source-detection separation. Since first-nearest neighbor measurements contain only limited sensitivity to the cortex (shown here beginning at 8 mm depth), their average can be used as measurement of superficial and systemic hemodynamics. This nuisance regressor was then removed from all channels to improve the system's brain specificity. (d) A neuronal activation in the visual cortex due to a visual stimulus placed over a schematic of the head to show direction-of-view. All images are posterior coronal projections of a cortical shell, as if looking at the surface of the brain from behind the subject with the scalp and skull removed.
Stimulus paradigm
The study was approved by the Human Research Protection Office of the Washington University School of Medicine and informed consent was obtained from all participants prior to scanning. Fourteen healthy adult subjects (11 female, 3 male, age range 21-27) were recruited with no known neurological or psychiatric abnormalities. Subjects 1 to 5 were scanned three times each; the rest were scanned once. Thus, a total of 24 data sets were analyzed in the experiment. Subjects were seated in an adjustable chair in a sound-isolated room facing a 19-inch LCD screen at a viewing distance of 90 cm. The imaging pad was placed over the occipital cortex, and the optode tips were combed through the subject's hair. Hook-and-look strapping around the forehead held the array in place. The distance over the top of the head from the nasion to the top row of optodes was measured so as to establish repeatable cap placement.
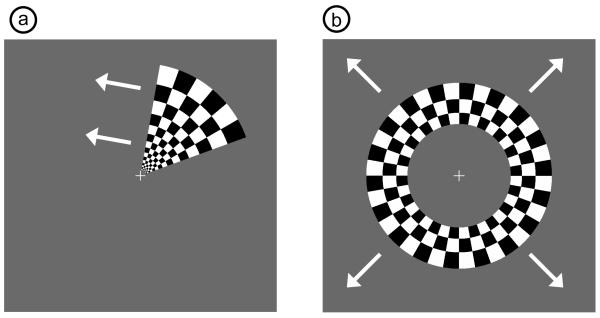
All stimuli were phase-encoded, black-and-white reversing logarithmic checkerboards (10 Hz contrast reversal) on a 50% gray background (Engel et al., 1994; DeYoe et al., 1994). Polar angle within the visual field was mapped using counterclockwise and clockwise rotating wedges: minimum radius 1°, maximum radius 8°, width 60°, and a rotation speed of 10°/s for a cycle of 36 s (Fig. 2a). This rotation frequency allows for each stimulated brain region to return to baseline before subsequent activations (Warnking et al., 2002). In fMRI retinotopic experiments, it is common to use two simultaneous rotating wedges. However, resolving the resulting ambiguity involves a priori knowledge of anatomy, allowing activations to be ascribed solely to the contralateral hemisphere (Warnking et al., 2002). In this study, we preferred not to use a priori knowledge of the functional architecture and instead decided to use a stimulus with a single rotating wedge to eliminate ambiguity. Eccentricity within the visual field was mapped with expanding and contracting rings: minimum radius 1°, maximum radius 8°, width 1.4° (3 checkerboard squares), and 18 positions with 2 s per position for a total cycle of 36 s (Fig. 2b). Subjects were instructed to fixate on a central crosshair for all experiments, and the four stimuli were presented in a pseudorandom order. All stimuli started with 5 s of a 50% gray screen, continued with ten cycles of the phase-encoded stimulus, and concluded with 15 s of a 50% gray screen.
Figure 2. Examples of phase-encoded visual stimuli.
(a) Still frame from wedge stimulus showing counter-clockwise direction of motion. (b) Still frame from ring stimulus showing expanding direction of motion. All four types of stimuli (counter-clockwise, clockwise, expanding, and contracting) have alternating contrast at 10 Hz and complete an entire cycle in 36 seconds.
HD-DOT processing and imaging
Raw detector light levels were decoded to source-detector pair (SD-pair) data (Vi(t)) and converted to log-ratio data (yi(t)=−log(Vi(t)/<V>). The data was then band-passed (0.02 Hz to 0.5 Hz) to remove long-term trends and pulse artifacts. Since every measurement results from sources and detectors outside the head, data are a mixture of hemodynamics occurring at different depths. However, due to our high dynamic range and high-density system, we are able to detect light from multiple source-detector distances, and measurements from short source-detector distances sample more superficially than those from longer distances (Fig. 1c). In our hemispherical head model, 3% of first-nearest neighbor sensitivity is from the brain, compared with 14% for the second-nearest neighbors; the full depth profiling of different source-detector separations in our array in both the forward and inverse models is detailed in Dehghani et al. (Dehghani et al., 2009). We, thus, averaged all of the signals from the first-nearest neighbor channels to create a measure of superficial hemodynamics. This nuisance signal was linearly regressed from all channels (Saager and Berger, 2005; Saager and Berger, 2008). In order to reject measurements with motion artifacts or poor optode coupling to the head, source-detector channels with high standard deviation (>7.5%) are excluded from further analysis. An average first-nearest neighbor had a standard deviation of 1.3% and an average second-nearest neighbor, 2.4% (with 1% of the latter being due to the desired activation); so, this three standard deviation threshold can exclude abnormally large variations while preserving normal physiology. Within a range, the reconstruction is relatively insensitive to the exact threshold chosen. Across all sessions, this procedure kept 97% of first-nearest neighbor signals and 92% of second-nearest neighbor signals.
In order to convert SD-pair data into a three-dimensional reconstruction, we first created a forward light model using finite-element modeling software (NIRFAST) and a two-layer hemispheric head model (radius 80 cm) (Dehghani et al., 2003; Zeff et al., 2007). Optode positions were determined in this geometry by centering the array over the apex of the hemisphere and conforming the two-dimensional array to the curved surface so as to preserve the angle and distance between each optode and the center of the array. The light model included the first- and second-nearest neighbor channels that passed the earlier signal-to-noise threshold. The mesh contained 22,731 nodes, and after light modeling the sensitivity matrix was interpolated to a 2 mm square voxel-grid. This sensitivity matrix was inverted once per subject per run (in order to account for the specific channels included), a process which takes 33 s. SD-pair data are then converted into images of differential absorption within the head using the inverted sensitivity matrix and a matrix multiplication (0.2 ms per frame per wavelength). We estimate the lateral resolution of this inversion process to be approximately 1 cm. Hemoglobin species concentrations were determined using their extinction coefficients.
As we were interested in hemodynamic responses within the cortex, we selected a cortical shell (1 cm thickness) from within our 3D data set and averaged across the thickness of the shell. While this shell is thicker than the actual layer of gray matter, the depth resolution of the system (~1 cm) means that the generated images are relatively insensitive to the thickness chosen as long as the shell excludes the superficial layer directly beneath the optodes and deep layers where the sensitivity of the measurements is low. All HD-DOT images displayed are posterior coronal projections of this cortical shell (i.e., we have averaged along the anterior-posterior axis), resulting in a point-of-view as if looking at the head from behind with the skin and skull removed (Fig. 1d). The field-of-view is 14 cm in width and 8 cm in height; each pixel is 2 mm by 2 mm. DOT simultaneously creates images of oxy- (ΔHbO2), deoxy- (ΔHbR), and total hemoglobin (ΔHbT). Since the purpose of this study was not to find differences between these different contrasts, for simplicity, all images shown are ΔHbO2. The images in the other contrasts are qualitatively similar.
Fourier analysis
The phase-encoded stimuli create a traveling wave of neuronal activity along the cortical surface as the stimuli move through the visual field. Relative to the stimulus onset, each cortical position will be periodically activated with a different delay. Since we know the position of the stimulus on the screen at each time, we can match each pixel's measured delay to the area of the visual field to which it corresponds (Sereno et al., 1995). In order to perform this analysis, the series of activations due to each stimulus was down-sampled to 1 Hz (36 time points per stimulus cycle). Since the data has already been low-pass filtered to 0.5 Hz, this step does not remove any information, but allows the convenience of having one activation frame per stimulus location. Recall that due to the earlier log-ratio step, each cortical location's time trace had been shifted (mean subtracted) so that the mean of each contrast was zero over the entire scan period. Every pixel's timecourse was Fourier transformed and the phase at the stimulation frequency (0.0278 Hz = 1/36 s) found. This phase then corresponds to the delay between stimulus onset and the pixel's activation.
However, we additionally need to correct for the finite neurovascular response time. Assuming that this lag time remains fixed at each cortical position, we can correct for this delay using counter-propagating stimuli (Sereno et al., 1995). Our convention is to define zero phase as the center of the visual field for the ring stimuli and as the lower vertical meridian for the wedge stimuli. The positive phase direction is defined as outwards for the ring stimuli and counter-clockwise for the wedge stimuli. The visual field is thus defined with a right-handed coordinate system (r,θ). (Note that while the end results are equivalent, this is the opposite visual angle phase definition from that used by Sereno et al. (Sereno et al., 1994; Sereno et al., 1995).) To find the corrected phase, we first inverted the phase found for clockwise and inwards stimuli by adding π and correcting for phase-wrapping. These phases, for each pixel, were then averaged with the phases from the counter-clockwise and outwards stimuli, respectively, to generate a corrected phase.
Using this phase analysis we find the average phase lag is approximately 1 radian. Given that an entire stimulus cycle is 36 seconds, this corresponds to a neurovascular lag of 5.7 s. This is longer than one might expect, however, it is a measure of the delay between of the time that the stimulus is centered over a cortical location until peak response rather than a measure of stimulus onset to response onset, which is how neurovascular lag is normally reported. While the phase images have this lag automatically removed by the above phase averaging, activations from a single stimulus still retain the lag. Thus, when presenting data from a single stimulus trial, we assume a 6 s lag.
After combining data from the two stimulus propagation directions, the wedge phase maps represented how every angle of the visual field is mapped to the cortex, and, similarly, the ring phase maps showed retinotopic eccentricity mapping (Sereno et al., 1994). Both before and after averaging, the phase maps were smoothed using a 3 pixel by 3 pixel moving box average.
Co-registration
Since DOT does not have concurrent anatomical information, as is obtained with MRI, it can be difficult to compare results taken over multiple imaging sessions. There are slight differences in where one subject places the pad day-to-day (~2 mm) and slightly larger differences in where the pad fits best on different subjects (~6 mm). While we measured the external position of the imaging pad relative to external anatomic landmarks, allowing us to be sure we were always imaging the visual cortex, the precision of this measurement was too low to serve as the sole co-registration method. We desired a method to locate the visual cortex that was relatively independent of the variables to be analyzed. Since the visual stimulus excites low-order visual cortex areas the most strongly, the magnitude of the Fourier component at the stimulation frequency measured at each cortical position creates an image that highlights the right and left visual cortices. All points with a magnitude greater than the half maximum were considered to be in either the right or left visual cortex (based on their position relative to the midline). The centroid of each region was then determined, and the midpoint between the two centroids was considered to be the center of the visual cortex. When combining or comparing data from multiple sessions and subjects, each imaging session was translated so that this center point was at the center of the image. It is important to note that co-registration was not used when analyzing data from a single imaging session. In all cases, we intend to judge the quality of the data based on its internal pattern and not on its location relative to unknown external landmarks.
Results
HD-DOT images from phase-encoded stimuli
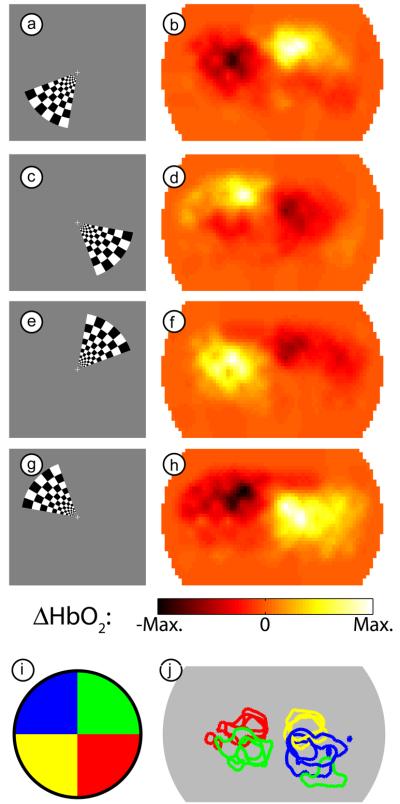
Our three-dimensional image reconstruction yields a 1 Hz series of images of cortical activations. In order to examine the contrast-to-noise of the responses to the visual stimuli, we block-averaged the data across the multiple cycles of the periodic stimuli, which resulted in a 36 frame movie (1 frame/second) for each stimulus. Four frames from a movie of the response to the counter-clockwise rotating wedge stimulus in one subject (subject 1, session 1) show that we can locate responses in all four visual quadrants (Fig. 3a-h). As expected from prior retinotopic studies, activations appear in the opposite cortical hemisphere from the area of the visual field where the stimulus was located. The full movie, showing how we are able to differentiate additional visual angles within the cortex is available as supplemental material (Supplemental Movie 1). Since every pixel has been independently mean-subtracted over the entire study, any pixel with activation necessarily has a time period where its value is negative. Thus, the regions with negative ΔHbO2 opposite the activation should not be confused with a true neuronal deactivation. This study was repeated in this subject in three sessions. In all three sessions, the activations appear in the same relative locations. This repeatability is demonstrated in Fig. 3i-j, where a contour has been drawn at half-maximum for each of the stimulus frames chosen above, corresponding roughly to the four visual quadrants.
Figure 3. Examples of activations due to a counter-clockwise rotating wedge stimulus.
(a) One frame of the counter-phase flickering checkerboard in the lower left visual field. (b) An activation in subject 1 (session 1) due to this stimulus. In order to match the stimulus and response for this figure, we have used our measured 6 second lag between stimulation and maximal response. Note the maximum response is in the upper right visual cortex. (c-h) Three additional frames from the rotating stimulus (spaced evenly) and the resulting responses (from the same session). Note that the hemodynamic response is always maximal in the opposite visual quadrant from the stimulus. (i) Legend showing the color-coding of different visual quadrants, each corresponding to one of the stimuli (a,c,e,g) chosen from the full movie. (j) An overlay of contours drawn at half-maximum contrast for each of four stimuli (roughly corresponding to the visual quadrants in (i)) in subject 1 over three separate imaging sessions. Note the repeatability of the localization of the measurements. (In one session the upper-right visual field caused a second activation in the ipsilateral cortex, which may be due to worse signal-to-noise on that day.)
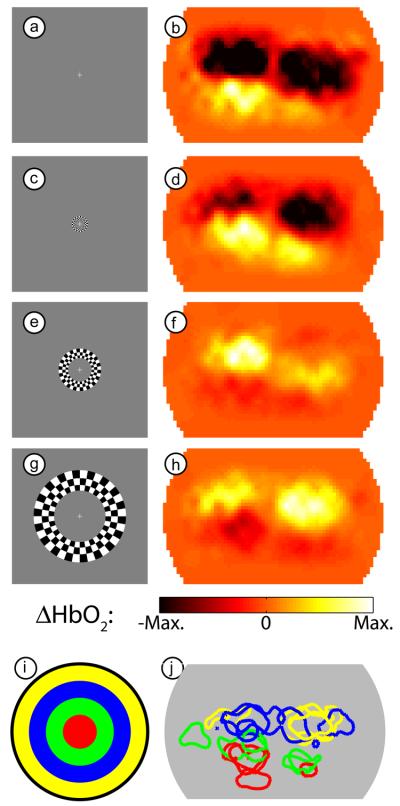
Similarly, four frames from a movie of the response to the expanding ring stimulus (subject 4, session 1) show that we can locate responses to multiple visual field eccentricities (Fig. 4a-h). Since this stimulus appears in both the right and left visual hemi-fields, we see activations corresponding to the left and right visual hemispheres. As the stimulus moves outward in the visual field, both activations move upward in our field-of-view. The full movie is also available as supplemental material (Supplemental Movie 2). The repeatability of our system is again demonstrated by overlaying contours at half-maximum for three separate sessions in this subject (Fig. 4i-j). While the eccentricity data is slightly noisier than the visual angle data shown above, the activations on subsequent days appear in the same area of the cortex.
Figure 4. Examples of activations due to an expanding ring stimulus.
(a) One frame of the expanding ring checkerboard in the central visual field. (b) An activation in subject 4 (session 1) due to this stimulus. In order to match the stimulus and response for this figure, we have used our measured 6 second lag between stimulation and maximal response. Note the maximal response is bilateral and in the lower visual cortex. (c-h) Three additional frames from the expanding stimulus (spaced evenly) and the resulting response (from the same session). Note that the hemodynamic response moves upward as the stimulus moves outward. (i) Legend showing the color-coding of different visual eccentricities, each corresponding to one of the stimuli (a,c,e,g) chosen from the full movie. (j) An overlay of contours drawn at half-maximum contrast for each of four stimuli (roughly corresponding to the eccentricities in (i)) in subject 4 over three separate imaging sessions. Note the repeatability of the localization of the measurements.
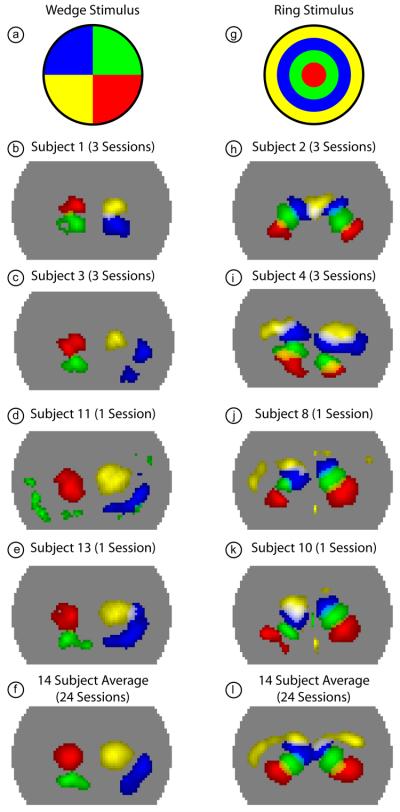
High contrast-to-noise data demonstrating the ability to discriminate multiple angles and eccentricities within the visual field was obtained from all 14 subjects analyzed. The robustness of the data is shown for selected data sets in Fig 5a-e for the wedge stimulus. The upper visual cortex (denoted with red and yellow) has the highest signal-to-noise in all subjects (both activations are placed in the correct hemisphere in all 14 subjects). The lower visual cortex (denoted with green and blue) is noisier (the lower left visual cortex is localized in 4 subjects, and the lower right visual cortex in 12 subjects). Similarly, Fig. 5g-k demonstrates the ability to robustly see multiple eccentricities within subjects with the ring stimulus. The central visual field (coded red and green) is seen in all 14 subjects, while the periphery (coded blue and yellow) is noisier and sometimes does not appear (the blue is localized in 13 subjects, yellow in 12). In addition, the system's sensitivity to the two hemispheres is not always equal. The average over all 24 sessions clearly shows clean discrimination of visual angles (Fig. 5f) and eccentricities (Fig. 5l), with all four selected frames having high signal-to-noise localized activations. Subject-averaged results without co-registration and with one session per subject still show the ability to distinguish multiple visual angles and eccentricities, although the data is slightly noisier (Supplemental Figure 1).
Figure 5. Activations due to phase-encoded retinotopic stimuli in multiple subjects.
(a) Legend showing the color-coding of different visual quadrants roughly corresponding to the four frames chosen from the full movie in Fig. 3. (b) Overlay of four activations (with a threshold at the half-maximum contrast of each frame) from subject 1 (all sessions averaged). Note the ability to clearly discriminate multiple visual angles within a single hemisphere. (c-e) Similar overlay images showing four visual quadrants in additional subjects. (f) Four visual quadrants shown in the average of all 24 sessions from 14 subjects. (g) Legend showing the color-coding of different visual eccentricities roughly corresponding to the four frames chosen from the full movie in Fig. 4. (h) Overlay of four activations (with a threshold at half-maximum contrast; due to uneven sensitivity to the two hemispheres, the right and left halves of the pad have different thresholds) from subject 2 (all sessions averaged). Note the ability to clearly discriminate multiple eccentricities within a single hemisphere. (i-k) Similar overlay images showing four eccentricities in additional subjects. Occasionally, the peripheral visual field (yellow) is seen only with low signal-to-noise. (f) Four visual eccentricities shown in the average of all 24 sessions from 14 subjects.
Retinotopic mapping using phase data
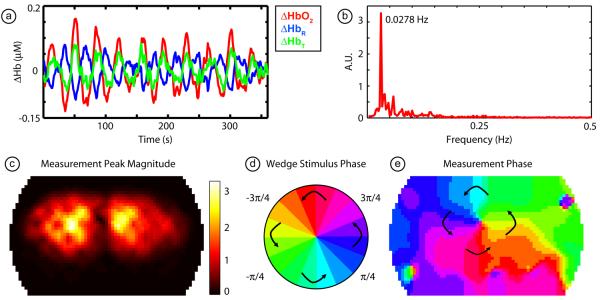
If we first examine a pixel chosen from one of the regions that responds strongly to the rotating wedge visual stimulus, we see that over the course of the entire stimulus presentation (10 cycles, subject 1, session 1) there is a strong hemodynamic response each time the stimulus passes (Fig. 6a), although since each contrast is mean subtracted, the traces don't return to a “baseline” in between stimulations. Note that the data has high signal-to-noise, which is reflected in this trace's (ΔHbO2) Fourier transform (Fig. 6b). Almost all of the power is concentrated in the stimulus frequency with little background noise. We then examine this Fourier transform at the rotation frequency (0.0278 Hz = 1/36 s). An image of the height of this peak indicates the areas that respond strongly to the stimulus, highlighting the two hemispheres of the visual cortex (Fig. 6c). The phase of this Fourier component relates each pixel to a visual angle within the visual field (Fig. 6d-e); in this image, we have used phases from the clockwise and counter-clockwise stimuli to remove the delay between the neuronal and vascular responses. In the middle of the field-of-view, we can see a clear “pinwheel” pattern that corresponds to a 180° rotation of the visual field.
Figure 6. Fourier processing of phase-encoded data.
(a) Time traces in all three contrasts (ΔHbO2, ΔHbR, and ΔHbT) from a single pixel (subject 1, session 1). Note the high signal-to-noise as we see ten activations due to the ten cycles of the stimulus. As each contrast trace has individually been mean-subtracted, the returns to baseline between the cycles appear as “deactivations”. (b) Magnitude of the Fourier transform of the ΔHbO2 signal in (a). Note the strong peak at the rotation frequency, with little background noise in the signal. (c) An image of the magnitude of the peak in the Fourier transform across the field-of-view of the pad. Bright areas correspond to pixels that respond most strongly to the stimulus. Two visual hemispheres are clearly visible. (d) A legend defining phases of visual angle within the visual field. (e) The phase of the Fourier transform of each pixel in the field-of-view. This phase corresponds to the delay between the start of the stimulus cycle and the activation of that region in the cortex and thus relates each location in the visual field to its cortical projections.
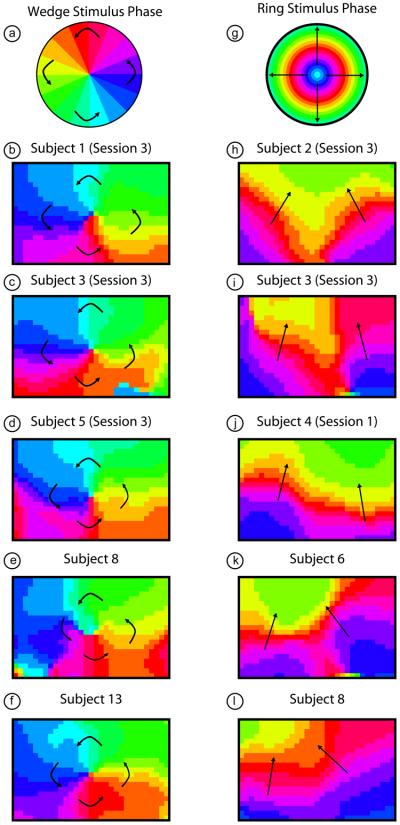
Examining the phase data from multiple subjects shows, as expected from the earlier quadrant data, that we see a similar pattern in all subjects (Fig. 7, here we are focused on a 6 cm by 4 cm subset of the imaging domain centered over the visual cortex). The lower visual field (phases color-coded light green through dark blue) is seen robustly in all subjects. However, the upper visual field (phases color-coded violet through yellow) is seen only in five subjects and is usually smaller in extent than the lower visual field representation. In eccentricity, we see the expanding rings as a stack of phases vertically and bilaterally in the two hemispheres. The most central areas of the visual field (lowest eccentricity, color-coded blue through red) are the most robustly visible (seen in all subjects). In twelve subjects, we are also able to see representations of the peripheral visual field (color-coded orange through green). The phase images shown were all constructed using oxyhemoglobin as a contrast, but maps constructed using deoxyhemoglobin and total hemoglobin are qualitatively similar (Supplemental Figure 2).
Figure 7. Retinotopic maps from phase-encoded stimuli in multiple subjects.
(a) A legend defining phases of visual angle within the visual field. (b-f) A retinotopic map of the organization of visual angle within the center of the visual cortex of four subjects. Note that in all subjects we see the same “pinwheel” pattern as in (a) and Fig. 3. Arrows are shown for orientation. (g) A legend defining phases of eccentricity within the visual field. (h-l) A retinotopic map of the organization of eccentricity within the center of the visual cortex of four subjects. Note that in all subjects we see the same stacked pattern as expected from the individual frame activation data (Fig. 4). Arrows are shown for orientation.
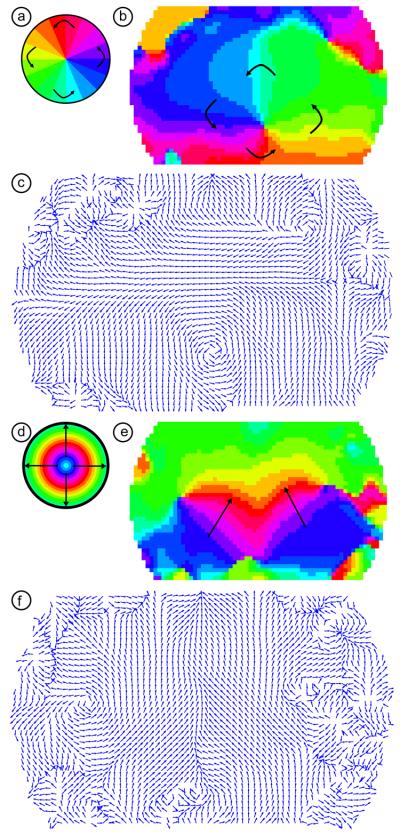
We also performed Fourier phase analysis using the co-registered, averaged data from all 24 scanning sessions. The phase from the wedge stimulus shows the “pinwheel” pattern around the center of the visual field (Fig. 8a,b). As with the individual subjects' data, the lower visual field (upper visual cortex) is more strongly represented in our field-of-view (in the figure, we see large areas with green through blue phases). The upper visual cortex (lower visual field, phases violet through yellow) is smaller, but can still be clearly seen. The phase from the ring stimulus shows the “stacked activations” pattern seen in the individual subjects' data (Fig. 8d,e). While the ability to see the peripheral visual field varied between subjects, here the periphery (phases colored orange through green) is clearly visible. Subject-averaged phase maps constructed without co-registration and multiple sessions per subject show similar patterns (Supplemental Figure 3).
Figure 8. Retinotopic maps from phase-encoded stimuli in the subject-averaged data.
(a) A legend defining phases of visual angle within the visual field. (b) A retinotopic map of the organization of visual angle within the center of the visual cortex. Note the same “pinwheel” pattern as in (a) and Fig. 7 in the center of the field-of-view. (c) The gradient of the phase map in (b). Each arrow's length is normalized to one and the direction shows the direction of steepest ascent (after compensating for phase-wrapping). The arrows thus show the direction of motion of the traveling wave of activity due to the counter-clockwise wedge stimulus on the visual cortex. Note the large area of rotation. There is additional structure visible in the periphery of the field-of-view. (d) A legend defining phases of eccentricity within the visual field. (e) A retinotopic map of the organization of eccentricity within the center of the visual cortex. Note the same stacked pattern as expected from Figs. 4 and 7. (f) The gradient of the phase map in (e). Each arrow's length is normalized to one and the direction shows the direction of steepest ascent (after compensating for phase-wrapping). The arrows thus show the direction of motion of the traveling wave of activity due to the expanding ring stimulus on the visual cortex. Note the large area of bilateral upward gradients.
The gradient of the phase images (steepest ascent in phase) shows the representation of the visual field unit vector within the visual cortex. The gradient of the wedge stimulus shows the angular unit vector, and the gradient of the ring stimulus shows the radial unit vector. The angular unit vector shows the direction of the cortical activation traveling wave associated with the counter-clockwise wedge stimulus, while that for the radial unit vector shows the direction of travel of the expanding ring activation. When we take the gradient of the group-average wedge stimulus phase map, we see that the unit vectors show a vortex around the center of the visual field (Fig. 8c). The gradient of the group-average ring activation phase map shows the upwards direction of movement that was clear in the earlier Supplemental Movie 2 (Fig. 8f). In both of the gradient images, the lengths of the vectors at each position have been normalized so that they contain information about the direction of the gradient but not its slope. These vector plots can also reveal areas of curl and divergence in the peripheral field-of-view that may be less apparent in the images of phase.
Discussion
Retinotopic mapping
In this paper, we performed a detailed spatial analysis of the visual cortex using our HD-DOT methods. Phase-encoded mapping of the visual cortex serves as an in vivo validation paradigm for many imaging questions. Here, our retinotopic mapping study highlights multiple advantages of the high-density diffuse optical tomography system. First, we are able to obtain high contrast-to-noise data from single subjects within a single session (for example, see Figs. 3 and 4 as well as the supplemental movies) instead of having to rely on multi-subject averages. Thus, we can reliably detect inter-subject differences, which is necessary for moving to future clinical paradigms. Second, our high spatial resolution allowed us to visualize features within the visual cortex, such as the multiple visual angles and eccentricity representations within a single hemisphere, that have previously been unobtainable with fNIRS. Third, we have used these traveling cortical activations to create cortical maps of the retinotopic organization of the visual cortex.
Determining the organization of how each area the visual field activates the cortex is difficult with fixed-position stimuli due to the nature of the visual cortex's organization. First, individual visual stimulations take up a finite amount of the visual field and, thus, naturally excite a large area of the visual cortex. In addition, a single visual stimulus can excite multiple visual processing areas. Second, the detected size of the activation is further increased by the spatial extent of the neurovascular response. And third, the measurement is further blurred by convolution with the point-response function of the imaging technique. While these points can be addressed through the use of a large number of stimuli, such a procedure would be inefficient. Alternatively, the phase-encoded mapping procedure followed here (and reviewed in depth by Warnking et al. (Warnking et al., 2002)) easily resolves these issues. The Fourier analysis can reveal subtle differences in phase allowing the maps to be determined with greater detail than that available from the broad response to individual visual stimuli (compare the spatial extend of an activation in Fig. 5 to an individual phase in Fig. 7). Furthermore, the dynamics of the traveling wave can be used to distinguish different visual cortex regions (see the discussion of future work, below), allowing more detailed studies of processing in the visual cortex (Wandell and Wade, 2003; Wandell et al., 2005).
High-density DOT
The retinotopic mapping techniques demonstrated in this paper are made possible by the image quality of high-density diffuse optical tomography systems. The majority of previous optical neuroimaging studies have been performed using solely time traces from source-detector measurements or images made with topographic back-projections. These techniques are usually referred to as functional near infrared spectroscopy (fNIRS) or diffuse optical imaging (DOI). Because such systems require source-detector separations of around 3 cm in order to sample the cortex, their spatial resolution is thus restricted. In addition, as all measurements are a mixture of hemodynamics in the scalp, skull, and brain, data is often obscured by superficial and systemic hemodynamic artifacts. Diffuse optical tomography addresses the limitations of fNIRS through a variety of methods. Time-resolved DOT systems rely on very high temporal resolution to gate the detected photons into groups that have traveled to different depths (Benaron et al., 2000; Steinbrink et al., 2001; Hebden et al., 2002; Selb et al., 2005). These systems require complex electronics and photomultiplier tubes, resulting in a particular set of trade-offs between measurement density, frame rate, and field-of-view.
An alternative DOT strategy is to use high-density grids of sources and detectors with each detector sensing light from many sources at different distances (Boas et al., 2004; Zeff et al., 2007; Bluestone et al., 2001). These measurements overlap laterally and in depth, allowing the construction of an inversion problem (Yodh and Boas, 2003), which enables higher resolution tomographic image reconstructions of brain activity (Zeff et al., 2007; Heiskala et al., 2009; Joseph et al., 2006). However, the light levels seen by a detector decrease exponentially with distance from the source. Thus, in order for light from multiple source-detector pairs to be measured, detectors must have very high dynamic range and low crosstalk. Our HD-DOT system relies on avalanche photodiodes with independent 24-bit analog-to-digital converters. This strategy yields the high dynamic range (>106) and low crosstalk (<10−6) necessary for using multiple source-detector distances (Zeff et al., 2007). In addition, the encoding pattern (the manner in which the sources are flashed) is digitally controlled in software, which allows more flexibility than having control fixed in hardware. As all source and detector channels are discrete, the system is easily reconfigurable and expandable.
The results of this paper show that HD-DOT is able to perform detailed studies of neural organization that are a step forward in the development of optical neuroimaging. It is likely that other DOT systems (both time-resolved and high-density systems developed by other groups) capable of the same resolution and signal-to-noise will be able to reproduce the brain mapping procedures demonstrated here. The additional advantage of high-density DOT is its relative simplicity and ease-ofuse, which should increase its potential for clinical and neuroscience applications.
Variability and cortical folding
The ability to make high contrast-to-noise images within a subject that are repeatable gives us the confidence to ascribe inter-subject variations to true response differences rather than to system noise. Within this study, we have been able to detect such inter-subject differences. While all subjects had responses that followed the expected retinotopic organization, not every area of the visible field was seen in all subjects. This is most likely due to differences in cortical folding. These differences are not unexpected; similar variations have been found in both previous invasive, anatomic studies (Stensaas et al., 1974) as well as in fMRI retinotopic studies (DeYoe et al., 1996; Dougherty et al., 2003). Due to DOT's low depth-of-penetration, the variations in the present experiment are more difficult to quantify. However, we can make some hypotheses about our observations. In some subjects, we fail to see the more peripheral areas of the visual field. Since the peripheral visual field in V1 is in the deepest (most anterior) area of the calcarine sulcus, we would expect this to be difficult to see with the current HD-DOT system. In those subjects in whom we do see more responses from stimulation in the peripheral visual field, we may be seeing representations in higher-order visual areas. The other area of the visual field that we sometimes fail to see is the upper visual field, which projects to the lower visual cortex. It may be that, in these subjects, the calcarine sulcus terminates inferiorly on the occipital pole, causing the lower visual cortex to be located deeper and behind the cerebellum.
In future studies, anatomic MRIs could be used to test these hypotheses. Photon propagation models could be generated using a more accurate tissue model. Localization of the pad would allow DOT image reconstructions to be inherently registered to the subject's anatomy, eliminating the need for post hoc co-registration. The position of activations relative to a segmented cortical surface would allow the calculated phases and gradients to be located on the known folded geometry. These advances would be aided by future improvements in dynamic range and signal-to-noise that allow increased depth sensitivity. For example, measurements up to fifth-nearest neighbor with SNR>100 would enable detection of activations in sulcal depths that are missed by current techniques (Dehghani et al., 2009).
The phase and vector plots can also reveal additional structure in the peripheral field-of-view. These features can be used to find the boundaries between different cortical processing regions (Sereno et al., 1994; Sereno et al., 1995). This extension would be important for taking the present HD-DOT results beyond a basic study of retinotopy towards studies of visual processing in populations not amenable to fMRI, such as development of the visual cortex in children and cortical plasticity after brain injury. However, this analysis requires interpolation that assumes the continuity of the retinotopic maps, including across cortical borders, while our current sampling is likely too superficial to separate gyral folds, at least in adults. This problem is especially acute in the subject-averaged results where data in the peripheral of the field-of-view might be from areas of the brain with more variable cortical folding, causing us to possibly average different cortical locations in each subject. With subject-specific anatomic modeling, the cortical folding could be made explicit, as it is with fMRI.
Conclusion
In this paper, we have shown the use of optical imaging to perform full retinotopic mapping of the visual cortex non-invasively in adult humans. Previous optical studies focused on activating small patches of cortex and had the limitations of fNIRS systems, such as low spatial resolution, poor depth discrimination, and restricted field-of-view. The higher spatial resolution, brain-specificity, and field-of-view of the high-density DOT system used herein enables us to map multiple visual angles and eccentricities within the same visual hemisphere. One of fMRI's original validations was its ability to reproduce retinotopic results that had been obtained through invasive animal experiments. This paper establishes that high-density DOT is also able to meet this benchmark. In addition, these phase-encoded paradigms and the maps they generate form a standardized model with which to judge new developments in optical algorithms and systems. With these advances in techniques and validation paradigms, the field of optical neuroimaging can move with more confidence into studies of higher order brain function and of clinical utility.
Supplementary Material
Subject-averaged activations due to phase-encoded retinotopic stimuli wihtout co-registration, using one session per subject (14 total sessions). (a) Legend showing the color-coding of different visual quadrants roughly corresponding to the four frames chosen from the full movie in Fig. 3. (b) The four visual quadrants are visible with the correct relative pattern. The activations from the upper-left visual field causes the most extended activation, possibly reflecting lower signal-to-noise. (c) Legend showing the color-coding of different visual eccentricities roughly corresponding to the four frames chosen from the full movie in Fig. 4. (d) The four selected visual eccentricities are all seen, with the lowest signal-to-noise occurring in the peripheral visual field.
Retinotopic maps from phase-encoded stimuli using multiple hemodynamic contrasts. (a) A legend defining phases of visual angle within the visual field. (b-d) Retinotopic maps of the organization of visual angle within the center of the visual cortex in subject 1, session 1 using all three hemodynamic contrasts. Note that in all contrasts we see the same “pinwheel” pattern as in (a) and Fig. 7. (e) A legend defining phases of eccentricity within the visual field. (f-h) Retinotopic maps of the organization of eccentricity within the center of the visual cortex in subject 2, session 3 using all three hemodynamic contrasts. Note that in all contrasts we see the same stacked pattern as expected from Fig. 7. Arrows are shown for orientation.
Retinotopic maps from phase-encoded stimuli in the subject-averaged data without co-registration and using one session per subject. (a) A legend defining phases of visual angle within the visual field. (b) A retinotopic map of the organization of visual angle within the center of the visual cortex. Note the same “pinwheel” pattern as in (a) and Fig. 8 in the center of the field-of-view, although the upper vertical meridian (red phase) is harder to see. (c) A legend defining phases of eccentricity within the visual field. (d) A retinotopic map of the organization of eccentricity within the center of the visual cortex. Note the same stacked pattern as expected from Fig. 8, although the peripheral visual field (green phase) is less localized.
Example of activations due to a counter-clockwise rotating wedge stimulus, shown at 10x actual speed. (Left Frame) The counter-clockwise rotating wedge checkerboard stimulus. For simplicity, the flickering is not shown. (Right Frame) Activations in subject 1 (session 1) due to this stimulus. In order to match the stimulus and response for this figure, we have user our measured 6 second lag between stimulation and maximal response. Note that the hemodynamic response is always in the maximal in the opposite visual quadrant from the stimulus.
Example of activations due to the expanding ring stimulus, shown at 10x actual speed. (Left Frame) The expanding ring checkerboard stimulus. For simplicity, the flickering is not shown. (Right Frame) Activations in subject 4 (session 1) due to this stimulus. In order to match the stimulus and response for this figure, we have assumed a 6 second lag between stimulation and maximal response. Note that the hemodynamic response moves bilaterally upward in the visual field as the stimulus moves outward.
Acknowledgements
We thank Benjamin Zeff, Gavin Perry, and Martin Olevitch for help with DOT instrumentation and software; Nicholas Gregg for help with some of the data acquisition and a thoughtful reading of the manuscript; and Abraham Snyder for help with data analysis and interpretation. This work was supported in part by NIH grants, R21-HD057512 (J.P.C.), R21-EB007924 (J.P.C.), K25-52273 (J.P.C.), and T90-DA022871 (B.R.W.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Benaron DA, Hintz SR, et al. Noninvasive functional imaging of human brain using light. J Cereb Blood Flow Metab. 2000;20:469–477. doi: 10.1097/00004647-200003000-00005. [DOI] [PubMed] [Google Scholar]
- Bluestone AY, Abdoulaev G, et al. Three-dimensional optical tomography of hemodynamics in the human head. Opt Express. 2001;9:272–286. doi: 10.1364/oe.9.000272. [DOI] [PubMed] [Google Scholar]
- Boas DA, Chen K, et al. Improving the diffuse optical imaging spatial resolution of the cerebral hemodynamic response to brain activation in humans. Opt Lett. 2004;29:1506–1508. doi: 10.1364/ol.29.001506. [DOI] [PubMed] [Google Scholar]
- Colier W, Quaresima V, et al. Simultaneous near-infrared spectroscopy monitoring of left and right occipital areas reveals contra-lateral hemodynamic changes upon hemi-field paradigm. Vision Res. 2001;41:97–102. doi: 10.1016/s0042-6989(00)00219-4. [DOI] [PubMed] [Google Scholar]
- Dehghani H, Pogue BW, et al. Multiwavelength three-dimensional near-infrared tomography of the breast: initial simulation, phantom, and clinical results. Appl Opt. 2003;42:135–145. doi: 10.1364/ao.42.000135. [DOI] [PubMed] [Google Scholar]
- Dehghani H, White BR, et al. Depth sensitivity and image reconstruction analysis of dense imaging arrays for mapping brain function with diffuse optical tomography. Appl Opt. 2009;48:D137–D143. doi: 10.1364/ao.48.00d137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeYoe EA, Bandettini P, et al. Functional magnetic resonance imaging (FMRI) of the human brain. J Neurosci Methods. 1994;54:171–187. doi: 10.1016/0165-0270(94)90191-0. [DOI] [PubMed] [Google Scholar]
- DeYoe EA, Carman GJ, et al. Mapping striate and extrastriate visual areas in human cerebral cortex. Proc Natl Acad Sci USA. 1996;93:2382–2386. doi: 10.1073/pnas.93.6.2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty RF, Koch VM, et al. Visual field representations and locations of visual areas V1/2/3 in human visual cortex. J Vision. 2003;3:586–598. doi: 10.1167/3.10.1. [DOI] [PubMed] [Google Scholar]
- Engel SA, Rumelhart DE, et al. fMRI of human visual cortex. Nature. 1994;369:525. doi: 10.1038/369525a0. [DOI] [PubMed] [Google Scholar]
- Engel SA, Glover GH, et al. Retinotopic Organization in Human Visual Cortex and the Spatial Precision of Function MRI. Cereb Cortex. 1997;7:181–192. doi: 10.1093/cercor/7.2.181. [DOI] [PubMed] [Google Scholar]
- Fox PT, Miezin FM, et al. Retinotopic organization of human visual cortex mapped with positron-emission tomography. J Neurosci. 1987;7:913–922. doi: 10.1523/JNEUROSCI.07-03-00913.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratton G, Corballis PM, et al. Shades of gray matter: noninvasive optical images of human brain responses during visual stimulation. Psychophysiology. 1995;32:505–9. doi: 10.1111/j.1469-8986.1995.tb02102.x. [DOI] [PubMed] [Google Scholar]
- Hebden JC, Gibson A, et al. Three-dimensional optical tomography of the premature infant brain. Phys Med Biol. 2002;47:4155–4166. doi: 10.1088/0031-9155/47/23/303. [DOI] [PubMed] [Google Scholar]
- Heiskala J, Hiltunen P, et al. Significance of background optical properties, time-resolved information and optode arrangement in diffuse optical imaging of term neonates. Phys Med Biol. 2009;54:535–554. doi: 10.1088/0031-9155/54/3/005. [DOI] [PubMed] [Google Scholar]
- Joseph DK, Huppert TJ, et al. Diffuse optical tomography system to image brain activation with improved spatial resolution and validation with functional magnetic resonance imaging. Appl Opt. 2006;45:8142–8151. doi: 10.1364/ao.45.008142. [DOI] [PubMed] [Google Scholar]
- Kang HC, Burgund ED, et al. Comparison of functional activation foci in children and adults using a common stereotactic space. Neuroimage. 2003;19:16–28. doi: 10.1016/s1053-8119(03)00038-7. [DOI] [PubMed] [Google Scholar]
- Karen T, Morren G, et al. Hemodynamic Response to Visual Stimulation in Newborn Infants Using Functional Near-Infrared Spectroscopy. Hum Brain Mapp. 2008;29:453–460. doi: 10.1002/hbm.20411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plichta MM, Herrmann MJ, et al. Event-related functional near-infrared spectroscopy (fNIRS): Are the measurements reliable? Neuroimage. 2006;31:116–124. doi: 10.1016/j.neuroimage.2005.12.008. [DOI] [PubMed] [Google Scholar]
- Saager R, Berger A. Measurement of layer-like hemodynamic trends in scalp and cortex: implications for physiological baseline suppression in functional near-infrared spectroscopy. J Biomed Opt. 2008;13:034017. doi: 10.1117/1.2940587. [DOI] [PubMed] [Google Scholar]
- Saager RB, Berger AJ. Direct characterization and removal of interfering absorption trends in two-layer turbid media. J Opt Soc Am A. 2005;22:1874–1882. doi: 10.1364/josaa.22.001874. [DOI] [PubMed] [Google Scholar]
- Schroeter ML, Bucheler MM, et al. Towards a standard analysis for functional near-infrared imaging. Neuroimage. 2004;21:283–290. doi: 10.1016/j.neuroimage.2003.09.054. [DOI] [PubMed] [Google Scholar]
- Selb J, Franceschini MA, et al. Improved sensitivity to cerebral hemodynamics during brain activation with a time-gated optical system: analytical model and experimental validation. J Biomed Opt. 2005;10 doi: 10.1117/1.1852553. [DOI] [PubMed] [Google Scholar]
- Sereno MI, McDonald CT, et al. Analysis of Retinotopic Maps in Extrastriate Cortex. Cereb Cortex. 1994;6:601–620. doi: 10.1093/cercor/4.6.601. [DOI] [PubMed] [Google Scholar]
- Sereno MI, Dale AM, et al. Borders of Multiple Visual Areas in Humans Revealed by Functional Magnetic-Resonance-Imaging. Science. 1995;268:889–893. doi: 10.1126/science.7754376. [DOI] [PubMed] [Google Scholar]
- Steinbrink J, Wabnitz H, et al. Determining changes in NIR absorption using a layered model of the human head. Phys Med Biol. 2001;46:879–896. doi: 10.1088/0031-9155/46/3/320. [DOI] [PubMed] [Google Scholar]
- Stensaas SS, Eddington DK, et al. The topography and variability of the primary visual cortex in man. J Neurosurg. 1974;40:747–755. doi: 10.3171/jns.1974.40.6.0747. [DOI] [PubMed] [Google Scholar]
- Taga G, Asakawa K, et al. Brain imaging in awake infants by near-infrared optical topography. Proc Natl Acad Sci USA. 2003;100:10722–10727. doi: 10.1073/pnas.1932552100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RBH, Mendola JD, et al. Functional Analysis of V3A and Related Areas in Human Visual Cortex. J Neurosci. 1997;17:7060–7078. doi: 10.1523/JNEUROSCI.17-18-07060.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RBH, Hadjikhani NK, et al. Functional analysis of primary visual cortex (V1) in humans. Proc Natl Acad Sci USA. 1998;95:811–817. doi: 10.1073/pnas.95.3.811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RBH, Hadjikhani NK. Where is 'Dorsal V4' in Human Visual Cortex? Retinotopic, Topographic and Functional Evidence. Cereb Cortex. 2001;11:298–311. doi: 10.1093/cercor/11.4.298. [DOI] [PubMed] [Google Scholar]
- Toronov VY, Zhang X, et al. A spatial and temporal comparison of hemodynamic signals measured using optical and functional magnetic resonance imaging during activation in the human primary visual cortex. Neuroimage. 2007;34:1136–1148. doi: 10.1016/j.neuroimage.2006.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Anderson CH, et al. Information Processing in the Primate Visual System: An Integrated Systems Perspective. Science. 1992;255:419–423. doi: 10.1126/science.1734518. [DOI] [PubMed] [Google Scholar]
- Wandell BA, Wade AR. Functional imaging of the visual pathways. Neurol Clin N Am. 2003;21:417–443. doi: 10.1016/s0733-8619(03)00003-3. [DOI] [PubMed] [Google Scholar]
- Wandell BA, Brewer AA, et al. Visual field map clusters in human cortex. Phil Trans R Soc B. 2005;360:693–707. doi: 10.1098/rstb.2005.1628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warnking J, Dojat M, et al. fMRI Retinotopic Mapping--Step by Step. Neuroimage. 2002;17:1665–1683. doi: 10.1006/nimg.2002.1304. [DOI] [PubMed] [Google Scholar]
- Wylie GR, Graber H, et al. Using Co-variation in the Hb Signal to Detect Visual Activation: A Near Infrared Spectroscopy Study. 2009 doi: 10.1016/j.neuroimage.2009.04.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yodh AG, Boas DA. Functional Imaging with Diffusing Light. In: Vo-Dinh T, editor. Biomedical Photonics. CRC Press; Boca Raton: 2003. pp. 21-1–21-45. [Google Scholar]
- Zeff BW, White BR, et al. Retinotopic mapping of adult human visual cortex with high-density diffuse optical tomography. Proc Natl Acad Sci USA. 2007;104:12169–12174. doi: 10.1073/pnas.0611266104. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Subject-averaged activations due to phase-encoded retinotopic stimuli wihtout co-registration, using one session per subject (14 total sessions). (a) Legend showing the color-coding of different visual quadrants roughly corresponding to the four frames chosen from the full movie in Fig. 3. (b) The four visual quadrants are visible with the correct relative pattern. The activations from the upper-left visual field causes the most extended activation, possibly reflecting lower signal-to-noise. (c) Legend showing the color-coding of different visual eccentricities roughly corresponding to the four frames chosen from the full movie in Fig. 4. (d) The four selected visual eccentricities are all seen, with the lowest signal-to-noise occurring in the peripheral visual field.
Retinotopic maps from phase-encoded stimuli using multiple hemodynamic contrasts. (a) A legend defining phases of visual angle within the visual field. (b-d) Retinotopic maps of the organization of visual angle within the center of the visual cortex in subject 1, session 1 using all three hemodynamic contrasts. Note that in all contrasts we see the same “pinwheel” pattern as in (a) and Fig. 7. (e) A legend defining phases of eccentricity within the visual field. (f-h) Retinotopic maps of the organization of eccentricity within the center of the visual cortex in subject 2, session 3 using all three hemodynamic contrasts. Note that in all contrasts we see the same stacked pattern as expected from Fig. 7. Arrows are shown for orientation.
Retinotopic maps from phase-encoded stimuli in the subject-averaged data without co-registration and using one session per subject. (a) A legend defining phases of visual angle within the visual field. (b) A retinotopic map of the organization of visual angle within the center of the visual cortex. Note the same “pinwheel” pattern as in (a) and Fig. 8 in the center of the field-of-view, although the upper vertical meridian (red phase) is harder to see. (c) A legend defining phases of eccentricity within the visual field. (d) A retinotopic map of the organization of eccentricity within the center of the visual cortex. Note the same stacked pattern as expected from Fig. 8, although the peripheral visual field (green phase) is less localized.
Example of activations due to a counter-clockwise rotating wedge stimulus, shown at 10x actual speed. (Left Frame) The counter-clockwise rotating wedge checkerboard stimulus. For simplicity, the flickering is not shown. (Right Frame) Activations in subject 1 (session 1) due to this stimulus. In order to match the stimulus and response for this figure, we have user our measured 6 second lag between stimulation and maximal response. Note that the hemodynamic response is always in the maximal in the opposite visual quadrant from the stimulus.
Example of activations due to the expanding ring stimulus, shown at 10x actual speed. (Left Frame) The expanding ring checkerboard stimulus. For simplicity, the flickering is not shown. (Right Frame) Activations in subject 4 (session 1) due to this stimulus. In order to match the stimulus and response for this figure, we have assumed a 6 second lag between stimulation and maximal response. Note that the hemodynamic response moves bilaterally upward in the visual field as the stimulus moves outward.