Database Analysis of Simulated and Recorded Electrophysiological Datasets with PANDORA's Toolbox

Abstract

Neuronal recordings and computer simulations produce ever growing amounts of data, impeding conventional analysis methods from keeping pace. Such large datasets can be automatically analyzed by taking advantage of the well-established relational database paradigm. Raw electrophysiology data can be entered into a database by extracting its interesting characteristics (e.g., firing rate). Compared to storing the raw data directly, this database representation is several orders of magnitude higher efficient in storage space and processing time. Using two large electrophysiology recording and simulation datasets, we demonstrate that the database can be queried, transformed and analyzed. This process is relatively simple and easy to learn because it takes place entirely in Matlab, using our database analysis toolbox, PANDORA. It is capable of acquiring data from common recording and simulation platforms and exchanging data with external database engines and other analysis toolboxes, which make analysis simpler and highly interoperable. PANDORA is available to be freely used and modified because it is open-source (http://software.incf.org/software/pandora/home).

Introduction

The amount of electrophysiological data is increasing as more channels can be sampled and recording quality improves, while rapid advances in computing speed and capacity (e.g., with grid computing) have enabled researchers to generate simulation data very quickly in massive amounts. Especially when diverse and customized sets of data analysis are used, proper handling of this data poses a neuroinformatics challenge (Bjaalie 2008).

Since more than 30 years, relational databases have been successfully used to manage large amounts of data (Chamberlin and Boyce 1974; Elmasri and Navathe 1994). In neuroscience, databases have been traditionally used to improve laboratory procedures, record keeping, and data sharing (Shepherd et al. 1998; Pittendrigh and Jacobs 2003; Hines et al. 2004; Morse 2007; Gardner et al. 2008), but only more recently they were found to be useful for storing and analyzing neural data (Prinz et al. 2003, 2004; Calin-Jageman et al. 2007), and being subjected to data mining (Lytton 2006; Taylor et al. 2006; Günay et al. 2008b). Constructing databases of neural analysis results addresses a bottleneck of neuroscience, which is analysis automation. In contrast, eyeballing or other semi-automatic analysis procedures would make it intractable to analyze the traces produced by the hundred thousands, or even millions, of neuron and network models (Prinz et al. 2003, 2004; Calin-Jageman et al. 2007; Günay et al. 2008a, b), or to analyze the continuous streams from dozens of electrodes (Nicolelis et al. 2003). Fully automatic analysis was demonstrated by Prinz et al. (2004) of intracellular data traces from 20 million neuronal network models, where the analysis results were saved in a custom database consisting of a collection of text files. Although reading text files is straightforward, understanding the organization of their contents requires specialized tools because of the lack of a querying capability. For instance, adding the output of a new analysis method into the text files would entail parsing and reconstructing thousands of files occupying a space of several hundred gigabytes. Using a more general database tool can provide the same functionality much more easily. Despite the need for database approaches to neural data analysis, almost no software tool have been developed to date for general use. Günay et al. (2008a) used such a tool to study the rat globus pallidus (GP) by comparing a database of recordings from 146 neurons to a database of 100,602 neuron models. In the current study, we illustrate the strengths of this database approach, specifically with the PANDORA tool-box (Günay 2008a, b) employed in the above study. The PANDORA database approach transforms the raw data into numerical matrices by collecting its important aspects (e.g., spike shape and firing rate characteristics), which enables the cross comparison between the model and recorded GP neuron databases efficiently. PANDORA works within the Matlab environment (Mathworks Inc., Natick, MA), which allows accessing other commonly used electrophysiological and statistical analysis toolboxes such as Chronux (Brown et al. 2004; Bokil et al. 2006), FIND (Meier et al. 2008), BSMART (Cui et al. 2008), and sigTOOL (Lidierth 2009). Interoperability with other analysis tools allows both: (1), improving reproducibility and cross validation of results; and (2), promoting to reuse existing analysis methods that helps the development of robust community toolboxes (Cannon et al. 2007; Günay et al. 2008c; Herz et al. 2008). Interoperability is achieved by using compatible input and output formats. PANDORA can import data from several different electrophysiological acquisition and simulation programs, and it constructs a self-describing database by keeping associated metadata in Matlab structures, that can be exported to several external spreadsheet and database formats. Here, we describe the specific advantages of using the PANDORA toolbox for electrophysiological data analysis, first in analyzing the above GP dataset (Günay et al. 2008a), and then by extending the database approach to study a network model dataset from the lobster stomatogastric ganglion (Prinz et al. 2004; Günay et al. 2008b) to show that the toolbox is capable of operating on different types of data.

Methods

The PANDORA toolbox defines a methodology to create searchable databases of electrophysiology data (see the user manual in Günay 2007, 2008a, b). It comes as an add-on toolbox to the Matlab computing and analysis environment (MathWorks Inc., Natick, MA). PANDORA is distributed free of charge with an open-source license (Academic Free License version 3.0; http://www.opensource.org/licenses/academic.php), organized with an object-oriented approach (see Supp. Methods A.1.1).

Overview of Database Analysis for Electrophysiological Data

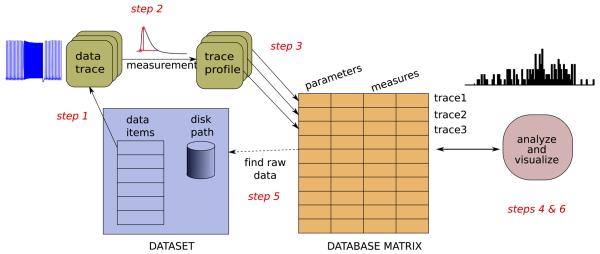
In PANDORA, database analysis consists of the following steps (Fig. 1):

1. Organizing raw data files in a dataset for performing automatic analysis;

2. Analyzing each raw electrophysiological data trace by measuring its electrophysiological characteristics (e.g., firing rate);

3. Inserting sets of measured characteristics from all items of a dataset into a database;

4. Analyzing databases by comparing, merging, joining, reducing dimensions, and calculating correlations, histograms, statistics, and component analyses;

5. Linking back to raw data traces associated with particular analysis values found; and

6. Visualizing raw or transformed results in a variety of graphical representations.

In this paper, we show application of this analysis approach first to a study of recordings and simulations from the globus pallidus (GP) of the rat (Günay et al. 2008a), and then to a study of the pyloric network of the lobster stomatogastric ganglion (Günay et al. 2008b). In the GP dataset, database analysis starts with identifying the sources from which to load the data.

Fig. 1.

Main components of PANDORA. Raw data traces are analyzed to create measurement profiles and then inserted into the database matrix along with metadata. See text for the details of the required steps

Organizing Data Files into a Dataset to Create a Database

The model GP neuron dataset contains 100,602 neurons modeled with nine Hodgkin and Huxley (1952) type ion channels with variable maximal conductance parameters (Günay et al. 2008a). Each of these models is simulated five times with different current stimulus magnitudes. The result was a dataset of more than 500,000 files. Especially with such large datasets, organizing and keeping track of data files scattered across many directories becomes challenging. The process of finding data files, loading the data with correct parameters, and inserting the measured characteristics into profile objects to create databases is automated by the dataset component in PANDORA (Fig. 1). These are achieved by keeping, in the dataset, the necessary information such as the location of raw data files; and the parameters used to load, preprocess and identify them (see Supp. Methods A.1.2 for details). Using this information, the dataset object creates the database structure after iterating through its data files.

The dataset can process any Matlab-readable data file. The supported data formats include the outputs of neural simulators, such as Genesis (Bower and Beeman 1998) and Neuron (Carnevale and Hines 2006), and outputs of data acquisition programs compatible with the NeuroShare initiative (http://neuroshare.sourceforge.net; see Supp. Methods. A.1.3 for a full list of formats). After the data are loaded into Matlab, they are analyzed to enter their salient characteristics into a database.

Measuring Electrophysiological Characteristics to be Entered into the Database

Interesting electrophysiological characteristics (e.g., firing rate) that deserve to be entered into the database must be extracted from loaded data files automatically. To achieve this, we programmed Matlab functions to extract a uniform set of characteristics from data trace files. As such functions for each data type need to extract different sets of salient characteristics, we group the functions into separate software components. For instance, functions for intracellular voltage traces of the GP dataset are grouped in the data trace component (Fig. 1). These functions extract the following characteristics:

• the voltage mean, minima and maxima;

• action potential (AP) peaks and troughs from voltage minima and maxima using a sliding-window approach;

• firing rate statistics from AP times: mean rate and inter-spike-intervals (ISIs), their standard deviation and ISI coefficient of variation (ISI-CV);

• the AP initiation point, using complex heuristics (Sekerli et al. 2004); and,

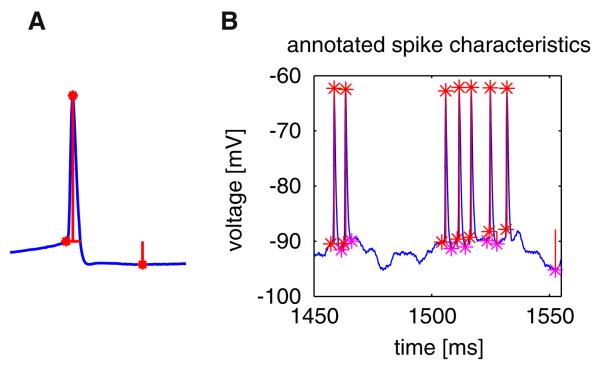
• using the initiation point, spike shape characteristics such as: the amplitude, rise and fall times, and the after-hyperpolarization (AHP) depth (Fig. 2a).

In the case when a stimulus is applied to the traces, additional characteristics must be measured.

Fig. 2.

PANDORA offers functions for automated measurement of electrophysiological characteristics from intracellular voltage traces. a Action potential (spike) shape characteristics of threshold, base width, amplitude and afterhyperpolarization (AHP) annotated on a single spike. b Automatically found spikes annotated on a recorded intracellular trace (PANDORA commands to obtain this plot are given in Supp. Matlab Code 1)

Measuring Responses to a Current Injection Stimulus

To test the input resistance of the neurons in the GP dataset and to find their firing rate as a function of input current (f/I curve), we used a current injection pulse (CIP) stimulus, which is commonly employed for current-clamp recordings and simulations. When there is a stimulus applied, the change in electrophysiological characteristics depending on the timing of the stimulus becomes interesting. With the use of the CIP stimulus protocol, the electrophysiological characteristics of the activity before, during and the recovery after the CIP period can be observed (Fig. 5c). Thus, the above measurements are replicated for each of these periods for CIP-applied data traces (cip_trace component in Supp. Mat. A.3). We also include additional measurements special to CIP-applied traces (described in Günay et al. 2008a), such as:

• the firing rates at the beginning and at the end of the CIP period corresponding to the initial response to current stimulus and the steady-state firing rate reached,

• the firing rate of the two halves of the recovery period corresponding to the initial recovery and steady-state rate reached,

• the ratio of the firing rates in periods before and after CIP,

• the voltage “sag” when a hyperpolarizing current is applied to measure the hyperpolarization-activated inward current (I_h), and

• the firing rate accommodation during the CIP period (ratio of last ISI to first ISI).

Once a comprehensive set of measurements are extracted from electrophysiology traces, they are used to represent the recorded or simulated neuron in the absence of the raw traces.

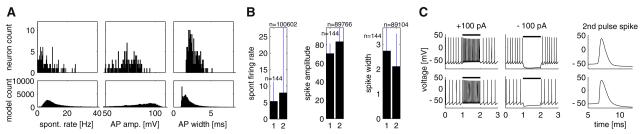
Fig. 5.

Extracted electrophysiological characteristics were adequate for comparing model and recorded GP neurons. a Spontaneous firing rate, action potential (AP) amplitude, and half-width characteristic distributions from the model neuron database were similar (symmetric KL divergence 6.19, 1.65, and 0.98 bits, respectively; see Supp. Methods A.1.6) and overlapped with distributions from the recorded neuron database. b Mean and standard deviation (STD) of the characteristics displayed in panel a (1: real, 2: model database). c Raw traces of matching real (top) and model (bottom) neurons

Creating a Database from Measured Dataset Files

A prerequisite to creating a database is having the measured characteristics uniform across dataset elements. During the creation, one function of the data trace component collects all of these characteristics and places them in a trace profile component object (Fig. 1). To form the database object, multiple profile objects are concatenated together into a matrix.

Since the measured characteristics and the parameters of the data files are all numeric, the PANDORA database object consists of a double-precision numerical matrix and its associated metadata. The metadata consists of parameters associated with the recording or simulation such as an identifying number, conductance values or drug concentrations. The dataset transfers the data and metadata from the files to create the database structures. To demonstrate this, a simple example shows how a database can be created from arbitrary data and metadata (Fig. 3). The metadata allows giving labels to the indices such as ‘firing_rate’, ‘spike_amplitude’, etc. The labels can be given to the rows, columns and pages (the third dimension) of the matrix, although the matrix can hold more dimensions. By convention, columns represent parameters and measurements, and rows represent independent observations (e.g., from a neuron, or from one of its traces with specific parameters). This convention allows specific types of analyses to be performed on this database.

Fig. 3.

A simple example of creating a database from a 2 × 2 arbitrary data matrix. tests_db is the name of the database component and it also represents the constructor function that generates such database objects. The function uses its arguments to generate the database object assigned to the db_obj variable. The function arguments consist of the matrix data, metadata to label column and row dimensions, and finally an identifying name for the database (see the Supp. Methods and the online PANDORA Manual in Günay 2007, 2008a, b for more details)

Database Analysis

Database analysis is performed by asking queries and applying transformations to a database and placing the results in new database objects (Supp. Methods A.1.4). Statistics, histogram, or cross-correlation functions that operate on a database produce their results in new specialized database objects. For instance, when the histogram of a database column is calculated, the histogram bins appear in a new histogram database object (histogram_db component in Supp. Mat. A.1.4) with the bin center and height as columns, which allows visualization and calculation of statistics such as the Kullback-Leibler (KL) divergence (Kullback and Leibler 1951; Johnson and Sinanović 2001; Sinanović and Johnson 2007, see Supp. Methods A.1.6). Similarly, a database can be subjected to statistics functions such as mean, mode, median, standard deviation, and standard error that generate a statistics database (stats_db component). In this database, the number of samples used for calculating the statistic is reported separately for each column for downstream analysis and plotting functions (e.g., see n values in bar plots of Figs. 5b and 8b) because it may be different due to missing values in the originating database. These missing values are represented by the not-a-number (NaN) symbol of Matlab, and treated specially by various PANDORA functions (e.g., averaging will skip NaNs). Since the statistics results are in databases, they can be queried to find an activity of interest (e.g., histogram peak, tail, outliers or specific ranges) and the query results can be used to query the original database to find the individual neurons that contributed to the desired activity.

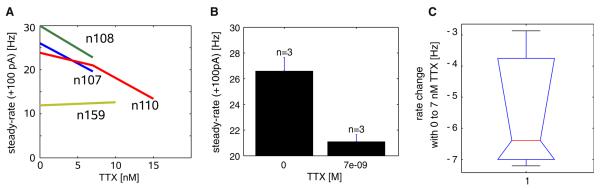
Fig. 8.

TTX block effects on steady-state firing rate (steady-rate) measured at the end of the CIP period. a Change in the firing rate with various TTX concentrations (n = 4). Different invariant parameter backgrounds were separated by the invarValues function (see “Methods” and Supp. Matlab Code 2 for an example program). The parameter backgrounds of each neuron (e.g., n107) annotated on the plot were taken from available NeuronIds of the example subset of the GP cell database (Table 4). b Mean and standard error of rate for 0 and 7 nM TTX (n = 3), obtained using the statsMeanSE function from the results of invarValues. c The change in rate from the control condition to application of 7 nM TTX (n = 3), displayed using a Matlab box-plot from the results of the diff2D function (see Supp. Methods A.1.8)

Querying the Database

The database contents can be searched by placing multiple constraints on the metadata and measured characteristics in database queries. In PANDORA, queries are expressed in the Matlab language syntax for addressing vector and matrix indices using parentheses, allowing the use of Matlab logical expressions (see Supp. Methods A.1.4 for examples). Returning matching database entries is only a simple application of queries, and they can be used to achieve more elaborate tasks. For example, queries were used to find unique parameter sets for automatically averaging repeated trials in the GP dataset.

Averaging Repeated Trials in the Database

Often experimental data from repeated trials with the same recording conditions need to be averaged. PANDORA's meanDuplicateParams function (see Supp. Section A.3) does this by collapsing all database rows that are equivalent in terms of chosen parameters (e.g., stimulus conditions) but, at the same time, distinguished by other parameters (e.g., neuron identifiers). The results of the function are the mean and the standard deviation (STD) of the measured characteristics corresponding to the repeated rows (see Supp. Matlab Code 2 for an example). After averaging repeated experimental conditions, we needed to find effects on characteristics between the changing parameter conditions.

Multivariate Parameter Analysis

In electrophysiology datasets, it is common to have multiple recording or simulation parameters. Across trials, parameters such as drug concentrations and stimuli magnitude vary. Especially in large datasets, unavoidable inconsistencies between values of these parameters makes it harder to find parameter effects on electrophysiological characteristics. For finding statistically significant effects, a sufficient number of consistent parameter values must be identified, which can be achieved with multivariate analysis methods. PANDORA has functions to identify consistent values, at the same time for several parameters, and calculate statistics from their effects on measured characteristics (see Supp. Methods A.1.8 for details and examples). Independent of the parameters, the uniform set of characteristics in the database also made it straightforward to compare neuron representations to one another.

Comparing Measured Characteristics of Two Neurons

Comparing neuron representations is especially useful to test whether a model neuron successfully simulates features of recorded neurons. The measured characteristics in the database represent a neuron in a vector format, making it easy to compare the characteristics across neurons (see Supp. Methods A.1.10 for PANDORA commands used). We use the normalized Euclidean distance method to calculate a distance between two vector neuron representations (see Supp. Methods A.1.9). Although these analysis methods are described above in the context of the GP dataset, they can be applied to the analysis of other types of data.

Database Analysis of a Neuron Activity Sensor Dataset

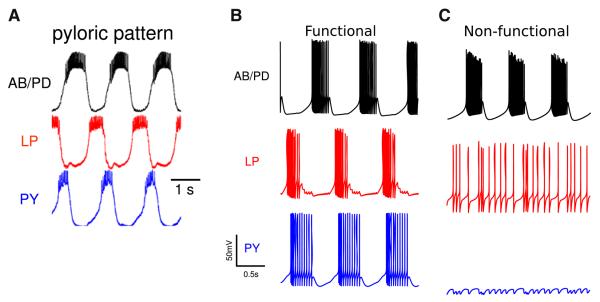
To show how to analyze data other than the GP intracellular voltage recordings in PANDORA (see Supp. Methods A.1.12), we applied the PANDORA methodology to a database of 20,250,000 models of the pyloric network in the stomatogastric ganglion (STG; Fig. 4a) of the lobster (Prinz et al. 2004). We used a new set of simulations of these models where the average values of calcium-dependent activity sensors (Liu et al. 1998) were saved from the model neurons in each network to create a sensor dataset (Günay et al. 2008b). In this dataset, average sensor readings from a single model network represented the raw data. From the raw sensor data, we measured the separation between functional and non-functional network models and saved them as characteristics in a database. These characteristics included a separation success rate obtained from an optimal linear classifier using sensor readings (see Supp. Methods A.1.13). From the characteristics in the database, this project aimed at identifying sensor parameters that can distinguish functional network activity patterns (Fig. 4b) from non-functional activity (Fig. 4c).

Fig. 4.

Electrophysiological activity of the real and model pyloric networks of the lobster stomatogastric ganglion. a Recorded functional network rhythms from the pyloric network. (b, c) Example functional (b) and non-functional (c) activity produced by the model pyloric networks

Out of the 20 million networks, we only used a 10 thousand-network subset that was chosen randomly. We chose this subset because it provides a good representation of the entire dataset, which is too large to analyze directly (Günay et al. 2008b).

Using External Storage for Large Databases

In the sensor database each network model has three model neurons with 366 sensors with different parameters, which makes the database especially large. Therefore, to store the bulk of the data we used an external MySQL (MySQL AB, Uppsala, Sweden) database. Manageable chunks of 10,000–250,000 networks from this database was transferred to PANDORA for analysis. Next, we describe the specific advantages of the PANDORA database analysis approach, starting with the analysis done on the GP dataset.

Results

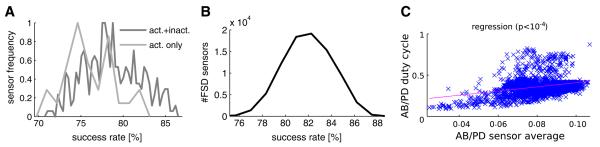
In Günay et al. (2008a), we considered a large model neuron database for matching the experimentally observed variability in rat globus pallidus (GP) neurons, and we showed that models matching recordings could be found efficiently by PANDORA (Fig. 5 shows that the distributions of model neuron characteristics, obtained only with conductance variations, are highly similar to that of recorded neurons). Here, we show in more detail the use of PANDORA in addressing this and similar problems that require database studies of electrophysiological recordings and simulations. In the subsequent sections, we show the advantage of constructing databases of extracted electrophysiological characteristics (such as spike times, spike shape information, and firing rates) rather than directly using the raw data traces from real and model GP neurons, and how these resulting databases of extracted characteristics can easily be queried to find interesting features of the neurons. Then, to establish the advantage of an automated technique over manual analysis of data, we demonstrate more practical uses of the database for routine maintenance of GP neural data such as averaging redundant recording trials. The database approach is useful for more complex parameter analysis that is often needed for understanding neural data. The following section describes the multivariate analysis performed in PANDORA to find the effects of pharmacological block experiments in GP recordings and matching model manipulations in the nine conductance parameters. Furthermore, our approach to extract the same characteristics from recorded and simulated neurons enabled their direct comparison, thus allowing us to better analyze parallels between model and real GP neurons. In the following section, we describe how to find models with different conductance densities that best match different recorded GP neurons and describe their natural variability. Finally, to show that the PANDORA analysis techniques can be applied to studies on datasets other than these GP neuron databases, we describe the database analysis to study a lobster stomatogastric ganglion neuronal network model in the final results section (Günay et al. 2008b). This study concerns 20 million instances of the network model and aims to find activity sensors that work best for separation of functional network activity patterns (Fig. 12 shows that activity sensors with inactivating variables performed better in these model networks).

Fig. 12.

Results of the lobster pyloric network sensor database analysis with PANDORA. a Success rate histogram of single inactivating and non-inactivating (DC) sensors, from a pool of 366 sensors, in distinguishing functional network patterns. b Success rate histogram of the 85,750 FSD sensor triplets in distinguishing functional network patterns showed up to 88% success. c Scatter plot of correlation between the sensor reading and the measured bursting duty cycle characteristic from the combined model of the anterior burster (AB) and pyloric dilator (PD) cells

Constructing a Database of Extracted Electrophysiological Characteristics was Efficient

Especially with large datasets (Prinz et al. 2003, 2004; Calin-Jageman et al. 2007; Günay et al. 2008a), it becomes difficult to store, search, and process the raw data quickly and efficiently for answering specific questions. Questions can be answered much faster if characteristics (such as firing rate) that pertain to the target questions are extracted and placed in a more compact database format. Once interesting entries are found among the characteristics in the database, the raw data can be consulted again for validation, visualization, and further analysis. To access the raw data associated with the results found, a database must also contain the recording or simulation parameters as metadata (e.g., an identifying label, current stimulation amplitude, physiological blocker concentration, etc.).

In Günay et al. (2008a), constructing such a database of extracted electrophysiological characteristics proved to be an efficient way to examine the overall distributions of electrophysiological data. The characteristics were extracted from 146 neurons recorded from the rat globus pallidus (GP) and from 100,602 model GP neurons. Characteristics, including for example firing rate, spike width and amplitude, and afterhyperpolarization depth before, during and after stimulation (see “Methods”), were extracted from voltage traces recorded in current-clamp mode (see “Methods”, Fig. 5c). The extracted databases improved the efficiency of the analysis by reducing the amount of data to be accessed: (1) the disk space occupied by the raw data was reduced from 2.4 gigabytes to 357 kilobytes for the recorded neuron database—a reduction of about four orders of magnitude; (2) and the simulation data was reduced from 6.8 gigabytes, in compressed form, to 109 megabytes in the database format. These databases of extracted characteristics were not intended to replace the raw data, but rather to complement it.

After constructing these two databases, we compared them to judge the quality of the model neurons in representing the recorded biological neurons (Fig. 5). Comparing the histograms representing the characteristic distributions of from both databases indicated that the varying conductance densities in the models can explain the natural variability found in GP neurons (Fig. 5a). Statistics of these characteristics offered a summary of comparison between the two databases (Fig. 5b). Highly similar recorded and model neurons could be found in the databases by using the querying capabilities of PANDORA (Fig. 5c).

The Database Can be Queried in Matlab for Finding Specific Neuronal Phenomena

An important advantage of using database-supported analysis is that we can query the data easily. For instance, in the GP recording database, the bias current applied to maintain recording quality was varied across trials from the same cell. To be consistent across trials, results from recordings with excessive bias currents had to be removed before interpreting the data. A single, simple PANDORA query composed of Matlab logical expressions allowed removing rows of characteristics extracted from such trials (see Supp. Methods A.1.4).

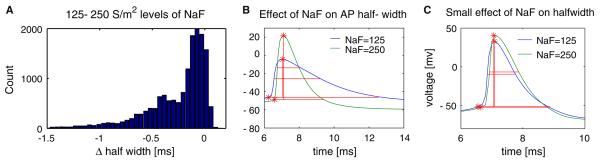
Querying is also useful to find traces or neurons from the histogram distributions which are outliers, or best represent an example of a desired activity pattern (Fig. 6). Together with sorting functions, querying allows finding maximal values from a database, such as the neuron with the fastest firing rate, with the shallowest afterhyperpolarization (AHP), or with the widest spike. Multiple queries can be nested or logically linked with Matlab logical operators, and additional functions can be used to form more complex queries (see Supp. Methods A.1.4).

Fig. 6.

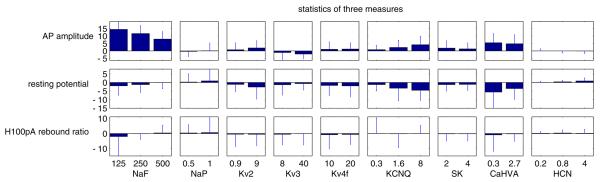
PANDORA's querying capability allows picking up models that exhibit characteristics in different regions of a distribution. a Histogram distribution of the effect of changing the fast sodium conductance (NaF) from 125 to 250 S/m² on the action potential (AP) half-width in the GP model neuron database. b At a fixed conductance background in two example model neurons show a large change in AP half-width with increasing NaF. c Another pair of models show a small change in AP half-width with increasing NaF

In PANDORA, a query filters a source database and produces a new database that can be subjected to further analyses (see Supp. Methods A.1.4). Since the database analysis depended on repetitive application of queries, we measured the speed of the querying operations and the calculation of the characteristics to estimate PANDORA's performance (Table 1). The first two rows in the table show the time it took to extract 202 electrophysiological characteristics from one recorded and one simulated trace, respectively. Since the time it takes to evaluate the querying operations varied according to parameters (e.g., number of rows and columns in a database), the rest of the time values are functions of these parameters (see Supp. Methods A.1.5). These numbers can be projected to estimate the elapsed time for PANDORA operations over large datasets such as the GP model database. On a single computer processor, extracting characteristics from the 100,602 model neurons took about 55 hours (row 2). It is also possible to extract them on multiple processors of a computing cluster by dividing the dataset into pieces, running separate Matlab processes and then reuniting the results. This reduces the time needed approximately linearly with the number of processors. Querying the resulting database for a single question took about 10 seconds (rows 3 and 10).

Table 1.

Time it took for PANDORA to perform key tasks related to extracting electrophysiological characteristics and to applying queries

	Task	n	m	Time [ms]
1	Extracting characteristics from a 3 s recording trace	1	–	1570
2	Extracting characteristics from a 2 s simulation trace	1	–	1420
3	Query: find a matching column value in a table of n rows (==)	1000	–	77
4	Query: match m column values in a table of n rows (anyRows)	1	1	7
5		1000	1	8
6		1000	100	14
7	Forming a query of m conjunctions (&) for a table of n rows	1	10	16.6
8		1000	10	38.9
9		1000	20	84.9
10	Apply query result to table of n rows and m columns	100	1	4.8
11		100	100	9.6

Time values were averaged after repeating operations for each n and m value for 100 or 1000 times

We also compared the time it takes to access, filter and index a database to show the overhead for using database tables rather than simple data matrices. Indexing to extract a part of a Matlab data matrix was about ten times faster than indexing the same data matrix as a part of a database table because of the function calls involved (Table 2, compare row 1 to 2). However, the overhead generated by the function calls happen once for each indexing operation since the duration did not significantly increase with more data items (compare different n and m values on row 2). Filtering the same portion of a database table to produce a new table was another four times slower because of the time needed to maintain the metadata (compare row 2 to 3). Because column names appear in the metadata, the time it took to create a new table was also proportional to the number of columns involved (row 3, compare m = 1 to m = 10), but a large number of rows can be indexed without penalty (compare n = 10 to n = 100). Using the overloaded parenthesis operators for indexing (see Supp. Methods A.1.5) only slightly increased processing time (compare row 3 to 4). A significant performance penalty appeared when using symbolic column names rather than numeric identifiers (rows 5 and 6), which again was independent of the number of rows indexed. These results show that some of the routine filtering, indexing and querying operations in PANDORA are slightly slower compared to similar operations in Matlab, but they take reasonable times considering the convenience of providing the metadata that allow using symbolic row and column names. When this convenience is unnecessary, one can operate on the data matrix of the database directly to gain speed (line 1; see Supp. Methods A.1.5 for commands involved).

Table 2.

Comparison of the time it took between data indexing operations in Matlab structures versus with PANDORA structures

	For n rows and m columns	Time [ms]
		n = 10	n = 100	n = 100
		m = 1	m = 1	m = 10
1	Numerically index a data matrix	0.017	0.019	0.022
2	Numerically index a DB's data matrix	0.136	0.141	0.141
3	Numerically index DB to create new DB	0.418	0.418	0.821
4	Overloaded numerically index DB to create new DB	0.472	0.473	0.879
5	Symbolically index DB to create new DB	1.652	1.657	11.251
6	Overloaded symbolically index DB to create new DB	1.717	1.717	11.333

For commands involved in these operations, see Supp. Methods A.1.5. Time values were averaged after repeating operations for each n and m value for 1000 times

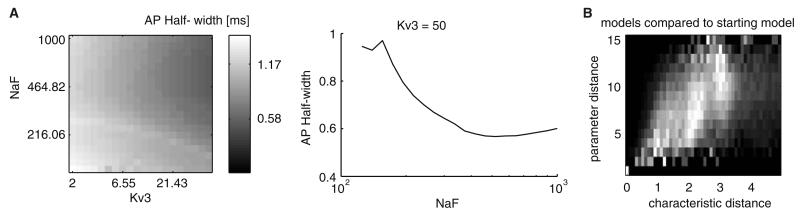
These queries were instrumental in more systematic analysis of the GP model neuron database, and allowed identification of conductance parameter subspaces in which models exhibited special behavior. For instance, we found a parameter subspace where the AP half-width showed a non-monotonic relation to the fast sodium conductance (NaF) level, which was modulated by the fast delayed rectifier potassium conductance (Kv3) level (Fig. 7a). The spike half-width initially decreased and then increased with increasing NaF values. As a second example, a complex query was required for finding candidate models that had maximal parameter distance (i.e., greatly differed in their conductance parameters), but minimal distance in terms of characteristics (i.e., most similar in activity patterns), compared to a chosen model. The density plot of database models in the parameter-characteristic distance plane showed how such a model could be found (Fig. 7b). This result from a multi-compartmental GP model neuron of the rat (Günay et al. 2008a) fortified previous findings from invertebrates showing that neuron models with disparate parameters can exhibit similar activity (Prinz et al. 2004). The database format also enabled automating routine maintenance operations on neural data.

Fig. 7.

Querying allowed systematic analysis of GP model neuron conductance parameter space. a Change of spike half-width in the two-parameter plane of NaF and Kv3 conductances (left) was displayed with a Matlab image plot, which was a useful method in depicting multivariate landscapes in the database. A cross-section of the plane showed the non-monotonic change in the half-width in the NaF dimension (right). b Density of models according of their distance in terms of parameters and measures from a chosen initial model. Each row was normalized to the maximal number of models found with a given parameter distance

Automatically Averaging Redundant Trials in the Database

Electrophysiological data sometimes needs to be analyzed at different levels of abstraction. On a fine scale, multiple traces collected from one neuron must be displayed and analyzed, and on a coarse scale, one must look at a summary information from each neuron to understand effects across neurons. PANDORA routines that allow us to sift, average and collapse parameter dimensions were essential in switching between these levels of abstraction. These routines worked on metadata that identify one trace or neuron from another. These metadata can be pharmacological treatments applied, stimulation parameters and identifying values for recordings, or model parameters and other similar identifying values for simulations.

In the above study comparing GP neurons to models, each row in the real neuron database contained results from one experimental trial with specific stimulus parameters, and therefore each neuron was represented by multiple rows. This initial database was informative to find ranges of activity characteristics, but it contained an unequal number of rows for each stimulus condition because of the varying number of redundant trials recorded (Table 3a). To have each stimulus condition represented once, we averaged results from different trials (Table 3b). Although this averaging operation may seem specific to the GP dataset, it can be generalized because the stimulus parameters were found by grouping database entries with matching parameters automatically in PANDORA (see Supp. Matlab Code 2 and “Methods”).

Table 3.

Before averaging, multiple characteristic rows existed in the database representing the same stimulation and recording conditions from a neuron

A						B
pAcip	0	0	100	100	100	pAcip	0	100
PicroTx	0.0001	0.0001	0.0001	0.0001	0.0001	PicroTx	0.0001	0.0001
KynAcid	0.001	0.001	0.001	0.001	0.001	KynAcid	0.001	0.001
TTX	0	0	0	0	0	TTX	0	0
Apamin	0	0	0	0	0	Apamin	0	0
drug 4AP	0	0	0	0	0	drug 4AP	0	0
NeuronId	107	107	107	107	107	NeuronId	107	107
TracesetIndex	109	109	109	109	109	TracesetIndex	109	109
steady rate	0	0	24.6975	26.4614	26.8358	NumDuplicates	2	3
						RowIndex	1	2
						steady rate	0	25.9982

The tables displayed were transposed to turn rows into columns for efficient display. a Example results of control recordings from one cell (NeuronId 107) is shown with several parameters and the steady-state firing rate (last row in table “steady rate”). Two entries existed where the current injection parameter, pAcip, was 0 pA and three entries existed where it was 100 pA. Notice that other drug application conditions stayed constant and the extracted rate value varied. b After averaging, the database was reduced to the two unique parameter conditions, the rate characteristic was averaged and a NumDuplicates parameter was added that represented the number of database rows that were averaged for each condition

Because many types of statistical analysis require that each neuron be treated as a single set of results (such as the histograms in Fig. 5a), we applied a similar transformation to the database to merge rows with different stimulus magnitudes into a single row for each neuron (see Supp. Methods A.1.7). This database allowed asking questions at the level of neurons, such as the effects of varying experimental parameters.

Multivariate Parameter Analysis to Find Effects on Activity Characteristics

PANDORA provides several functions to calculate parameter effects on electrophysiological activity characteristics. Calculating these effects starts with finding cases where only one parameter value changes at one time, and consistently, so that statistically significant effects can be identified in the experiments or simulations. For example, for finding the effects of the sodium channel blocker, tetrodotoxin (TTX), the experimenter must make sure that there are enough cells with control and TTX-applied conditions where all other treatment and stimulation parameters were constant. PANDORA offers functions to sort the data to identify traces meeting these conditions and to correctly treat the missing values (see “Methods”).

In the GP data mentioned above, experiments were done at different times and under different conditions yielding a database with several pharmacological treatments applied at concentrations sometimes inconsistent across cells, and with some of the control traces including different background treatments. Here, we demonstrate how PANDORA finds multiple measurements with consistent parameters from such complex datasets, in a small example subset of these data (Table 4). Based on neuron identifiers and other pharmacological treatments in this subset, we identified four background parameter conditions in which only the target TTX parameter is varying (Fig. 8a). By averaging results from different background conditions for two of the TTX parameter values (0 and 7 nM each have three data points), we found the average firing rate for different TTX concentrations across different neurons (Fig. 8b). Similarly, we can calculate the average rate change with increasing TTX from 0 to 7 nM, which we call its differential effect (Fig. 8c).

Table 4.

Pharmacological treatment parameters and one rate characteristic of four TTX-treated cells selected from a subset of the GP recording database

PicroTx	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
KynAcid	0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001	0.001
TTX	0	7e – 09	0	7e – 09	0	7e – 09	1.5e – 08	0	0	1e – 08
Apamin	0	0	0	0	0	0	0	0	0	0
drug 4AP	0	0	0	0	0	0	0	0	1e – 04	1e – 04
NeuronId	107	107	108	108	110	110	110	159	159	159
TracesetIndex	109	110	111	112	114	115	116	NaN	NaN	NaN
D100pA steady rate	25.9982	19.6056	29.9673	22.7628	23.8443	20.9744	13.3892	20.1947	11.8999	12.6017

Conditions applied to a cell can be distinguished by common NeuronId parameter values. Three different TTX concentrations 7, 10 and 15 nM were used variably in these experiments. Notice that the TTX effect on neuron n159 could only be discerned in parameter backgrounds where the potassium channel blocker, 4AP, was present

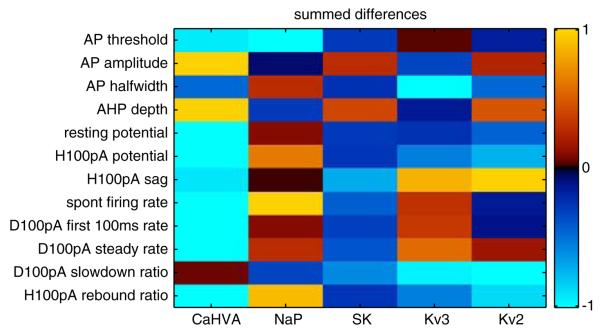
Multivariate parameter analysis was essential in methodically analyzing the large-scale GP simulation database which contained all combinations of nine conductance density parameters of the model GP neuron (Günay et al. 2008a). For each conductance, the distribution of its differential change on a characteristic described the possible outcomes of a conductance manipulation, such as in the effect of changing the NaF conductance between two values on the spike half-width (Fig. 6a). The average of this distribution gave a summary of such effects, which we applied to all the maximal conductance parameters by separately isolating each parameter level change (Fig. 9). By summing the average differential effects from all different levels of a conductance, we obtained a quantity that represents the general effect of a conductance on a measured characteristic. By repeating this calculation over all conductance and characteristic pairs, we found the general effect of changing each conductance on each characteristic in a comprehensive interaction matrix (Fig. 10). This should not be confused with a covariance matrix that finds average interactions between a conductance and characteristic across all parameter backgrounds because our interaction matrix precisely contains the differential effect of a conductance when all other conductances are constant. These modeling results not only gave a detailed prediction of ion channel interactions in affecting electrophysiological activity characteristics, but also allowed us to find parallels between the real and model GP databases in response to blocking ion channels (Günay et al. 2008a). Another way to compare the two databases is by finding individual models based on the activity characteristics that best match a real neuron.

Fig. 9.

Change in three characteristics for increasing values of several target maximal conductance parameters shows that each conductance affected multiple output characteristics in the model. The change was calculated as the difference in the characteristic for the displayed increase of a parameter value while other parameters were kept fixed. Bars show the mean and STD of this change for all combinations of the other background conductance density parameters

Fig. 10.

Interaction matrix between maximal conductance parameters and extracted characteristics in the model gave a comprehensive summary of conductance effects. This summary matrix was obtained by summing the mean change in characteristics (Fig. 9) between minimal to maximal values of each parameter

Cross Comparison Across Neuron Representations Allowed Finding Model Neurons Best Matching a Real Neuron

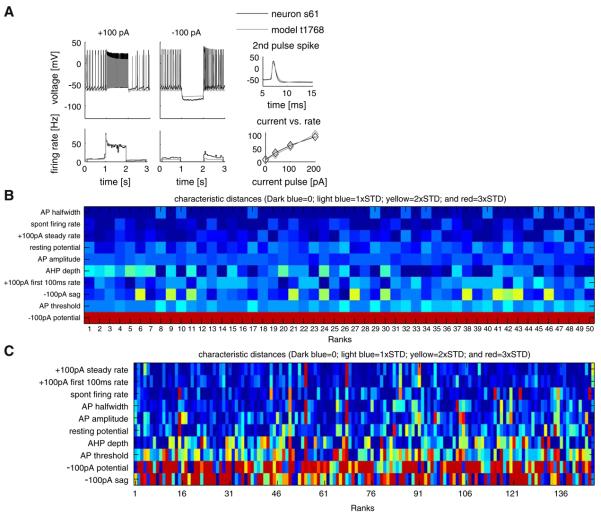
An advantage of extracting activity characteristics from voltage traces is that the same characteristics are obtained from both recorded and simulated neural output, allowing direct comparison. In particular, we were able to match models to each individual recorded neuron to quantify the biological heterogeneity found in the GP nucleus (example model-real neuron match in Fig. 11a and best matching models for all neurons in panel C). This is made possible by calculating a distance in terms of standard deviations (STDs) based on differences in characteristic profiles (see Table S3 in Supp. Methods A.1.10).

Fig. 11.

Models best-matching individual GP neurons can be found quantitatively. a A real neuron and the model that was found to match it most closely were compared by superimposing their raw voltage traces for ±100 pA CIP protocols aligned above their instantaneous firing rates (left), and the spike shape, and frequency-current (f-I) relationship plots (right). b The color-coded differences of individual characteristics of the top 50 matching models to the same real neuron, where the leftmost column represented the best matching model. Differences of characteristics were color-coded from dark blue (<1 STD) to red (>3 STDs). c Quality of the best matching models to each of the 146 real neurons visualized in the same way as panel b

The distance measure calculated allows more than finding a single match to a neuron; it allows ranking models in the database according to their match to real neurons (Table S3 and Fig. 11b). Some of the characteristics, such as the potential during the −100 pA current stimulus (−100 pA potential in the figure), is a bad match for all candidate models, so no improvement was seen even in the lower ranks. We repeated the procedure to find the model that best matched each recorded neuron to get a big picture of the variability in the GP (Fig. 11c). The distance used in matching models to neurons can also be used in parameter search algorithms to optimize the similarity of a model to a specific recorded neuron profile (see “Discussion”). Although the analysis of the GP real and model neuron databases are very specific, the database operations presented here can be applied to types of data and questions of other kinds.

Extending the Methodology to Custom Datasets: Analysis of a Model Network Database

We applied the above analysis methodology to the sensor database generated from lobster pyloric network model neurons (see “Methods”). We used this database to find if different sensor configurations in the network can perform better at distinguishing functional network activity patterns. The performance of the sensors is measured with a success rate characteristic (see Methods; Günay et al. 2008b). In the configuration with the same single sensor in each model neuron, we only considered a database of 366 sensors. In this database, we compared the success rates obtained with and without inactivating sensor types, and found that inactivating sensors were more successful (Fig. 12a). In the configuration with the same set of three sensors in each model neuron, we considered a larger database of characteristics from 85,750 sensor combinations. With three sensors, the success rate varied smoothly with changing sensor combinations in the database and reached up to 88% correct (Fig. 12b). The comparison between the two configurations indicated that having the three sensors is marginally better (88%) at separating functional networks than a single sensor (85%).

In addition to the sensor database used for distinguishing functional network activity, we constructed a second type of database to find correlations between sensor readings and activity characteristics from the networks' raw simulated electrophysiology data. From the voltage traces, we extracted burst characteristics such as burst duration, network rhythm period, and duty cycle to construct a database. In the database, we found that the sensor readings were most correlated with a cell's bursting duty cycle (Fig. 12c).

Discussion

We demonstrated the advantages of analyzing electrophysiology datasets by extracting interesting characteristics from the raw data and keeping them in a database format within the PANDORA framework. In the dataset of rat GP neuron recordings, the analysis of the database yielded several insights about the nature of the heterogeneity in these neurons. In the modeling dataset created to reflect the properties of these GP neurons, the database approach resulted in both finding important relationships between ion channel properties and intrinsic neuron activity, and finding parallels between the modeling and recording databases. In principle, the same approach can be applied to any type of dataset from which characteristic properties can be extracted.

The efficiency and advantages of using a characteristic database were especially apparent when analyzing such a large GP modeling database that resulted from a high-dimensional parameter search. This showed that other similar parameter search datasets with a large number of models can benefit from our database approach. The Matlab platform, that we employed for PANDORA, improved its interoperability with other acquisition and simulation programs, and standard data analysis tools by providing many input and output formats, and by providing a common computing environment. Finally, thanks to its object oriented software design (see Supp. Methods A.1.1), new features could be added to PANDORA and be part of the toolbox since it is open-source software. We start by discussing the specific approach taken to build databases in PANDORA.

Keeping Electrophysiological Features in a Relational Database Helps Analyze Experimental Data

Our database approach is based on the principle that raw data (e.g., membrane voltage traces) can be analyzed to extract a list of characteristics (see “Methods”, Fig. 2), which can then be related back to the recording conditions (e.g., recording channel, stimulus magnitude) or simulation parameters (e.g., ion channel densities, kinetics, compartment lengths) in a database table. Using such tables of parameters and associated characteristics allows the adoption of the well-established relational database paradigm (Codd 1970; Chamberlin and Boyce 1974), which has widespread industry support with robust theory and application (Elmasri and Navathe 1994). In particular, we map common operations necessary for analyzing electrophysiology datasets to relational database operations in PANDORA. We use histograms for finding distributions of interesting characteristics (Fig. 5), database queries for finding outliers (Fig. 6) and other interesting phenomena (Fig. 7), and custom database operations for averaging and combining recorded characteristics as necessary (Tables 3 and S1). PANDORA can find parameter effects on measured electrophysiological characteristics by automatically sorting the database for background stimulation and drug parameters where only the designated drug concentration varied (Table 4 and Fig. 8). We used this technique to find how GP neurons respond to drugs such as TTX, 4-AP and apamin, applied at low concentrations to partially block specific channel populations (Note that at a regular dose these currents provide a full block), for testing predictions from the model neuron database (Günay et al. 2008a).

Recorded and Simulated Data are Treated Similarly for Validating Model Results

PANDORA treats experimental and modeling data similarly, allowing the use of identical analysis routines for both data sets, which was not only economical, but most importantly allowed direct comparisons between simulation and physiological data using the measured characteristics (Fig. 5). This approach becomes particularly valuable to validate simulation results and guide model development because it is rare when a model can stand on its own without requiring experimental validation. Using a distance metric based on the set of measured characteristics, we compared the feature distributions in the model database to that of the recorded neuron database to assess the capacity of the models to represent the experimentally observed heterogeneity (Figs. 5, 11; Günay et al. 2008a).

Databases from Brute-force Parameter Exploration Allow Comprehensive Analysis

We built the database of 100,602 GP model neurons by exploring the parameter space for all possible combinations of the selected conductance density values (Günay et al. 2008a)—in brute-force fashion (Prinz et al. 2003, 2004). A brute-force database is special because the measured characteristics form a full multidimensional matrix indexed by model parameters. In contrast to the analysis of the recording database that allowed only finding effects on characteristics at few values from available drugs, this brute-force matrix permitted finding effects of changing conductance densities in all-to-all fashion (Figs. 9-10). This novel account of complete interaction in a mammalian neuron model fortifies earlier findings that electrophysiological characteristics, such as spike amplitude and afterhyperpolarization depth, are affected by multiple ion channels, and that each channel affects multiple characteristics (Bean 2007; Günay et al. 2008a).

Model Parameter Optimization Results can be Analyzed with PANDORA

On the downside, the brute-force approach to parameter exploration creates a problem of logistics and informatics due to the size and number of the files arising from the high dimensionality of the parameter space. Finding a unique solution in this space with an explicitly model-based approach is much more efficient because the problem is reduced to a linear search, which was shown to be possible under certain experimental conditions (Wood et al. 2004; Huys et al. 2006). However, if such an approach cannot be taken, a common alternative to brute-force exploration is to find model parameters by minimizing a goodness of fit value either by following its gradient (Vanier and Bower 1999; Weaver and Wearne 2006) or by using an evolutionary approach (Achard and Schutter 2006; Van Geit et al. 2007; Smolinski et al. 2008; Van Geit et al. 2008), which are both optimization algorithms. The PANDORA database approach applies to parameter optimization in two ways. First, by providing a platform for extracting characteristics, it allows defining fitness measures similar to our neuron comparison distances (see Supp. Methods A.1.9). Combining multiple separate characteristics in a fitness measure not only allows more precise control of which measures are more important for parameter optimization (Achard and Schutter 2006; Van Geit et al. 2007), but also enables employing a multi-objective approach that optimize models for each measure independently and choose best models later (Fonseca and Fleming 1993; Smolinski et al. 2008).

Second, during the parameter exploration of an optimization search, if the intermediate models and their characteristics are saved into a database, this database can be subjected to our analysis methodology to investigate how model behavior changes in various parts of the model parameter space. Although the optimization approach does not cover the parameter space equally, a similarly asymmetric GP recording dataset was subjected to the same analysis (Fig. 8 and Table S1). A similar impartial model database is obtained by starting at a known model parameter configuration and performing a local parameter exploration.

Analysis of Databases from Local Exploration of Few Parameters

The brute-force database allows querying for interesting local phenomena controlled by few parameters. For instance, it is interesting for the experimenter if a conductance modulates the effects of another conductance on a characteristic by reversing it. This reversing effect would contradict with the common view that blocking an ion channel results in a consistent effect that can be averaged across neurons without loss of information. We queried the GP model database for conductances that have reversing effects on the action potential (AP) half-width and we found that the parameters leading to this phenomenon were constrained to a local region of the fast sodium and fast delayed rectifier potassium conductances (Günay et al. 2008a). We generated a new parameter set that expanded this region with PANDORA to run new simulations. The results illustrated that reversing effects with these parameters in this region are dependent on the parameters of other ion-channels (Fig. 7a–b). In performing these analyses, PANDORA showed several advantages due to the approach we have chosen.

Advantages of a Native Matlab Database Approach

Using a relational database system, such as the Structured Query Language (SQL) (Chamberlin and Boyce 1974), to aid data analysis increases complexity because of the division of logic between the languages for data analysis and database operations. Furthermore, each piece of software requires additional knowledge and training, which makes the analysis programs harder to understand, maintain and troubleshoot (Baxter et al. 2006). In contrast, PANDORA allows expressing queries as Matlab commands, based on array indexing and logical operators (see “Methods” and Supp. Methods A.1.4). This empowers an experimenter, who is familiar with data analysis in Matlab, to manipulate the data without having to learn how to use a separate database application. More importantly, whereas commercial SQL database management systems do not provide easy access to common analysis routines for electrophysiological data (such as Oracle Database (Oracle, Inc., Redwood Shores, CA, USA), Microsoft SQL Server (Microsoft Corp., Redmond, WA, USA), or MySQL (MySQL AB, Uppsala, Sweden)), Matlab offers a suitable environment to conduct such analysis using its existing statistical, numerical, and visualization functions.

Despite the described need for database approaches to neural data analysis, almost no software systems have been developed to date for general use. Most of the large neuroscience database initiatives are targeted for building data and knowledge repositories for data sharing (Shepherd et al. 1998; Hines et al. 2004; Gardner et al. 2008; Bjaalie 2008). Few exceptions are OpenElectrophy (http://neuralensemble.org/trac/OpenElectrophy) and the Neural Query System (NQS) (Lytton 2006). The Open Electrophy project aims to simplify data analysis and sharing of intra- and extra-cellular recordings, but it is yet incomplete. NQS is a mature tool integrated into the Neuron simulator (Carnevale and Hines 2006) to manage simulations and record their results in a database. NQS allows accessing Neuron's specialized neural analysis routines (e.g., the multiple-run fitter) and easily tie simulations to databases. PANDORA can independently be used by users of either Neuron or Genesis, as well as other simulators. It is written completely with the object-oriented extensions of the Matlab scripting language (see Supp. Methods A.1.1), making it easily extensible (see Fig. 12) and cross-platform compatible (i.e., the same scripts work on PC, Macintosh and Windows operating systems in most cases).

The Matlab environment also offers visualization features that we integrated into the PANDORA components: raw data traces can be plotted, optionally annotated with their extracted characteristics (as in the AP shape in Fig. 2a); databases can be visualized as a text table, by exporting to external formats (such as a SQL database or Microsoft Excel; see Fig. S3), with scatter plots (Fig. 8), or with statistical error-bar plots (Fig. 9); and multiple database variables can be visualized with two- or three-dimensional image plots (Fig. 7). The plotting tools create a layer on top of the regular Matlab plotting system (see Supp. Methods A.1.11).

Interoperability with Other Electrophysiology Toolboxes and Supported Input Formats

Cross-checking of analysis results and subjecting them to further analyses are possible without completely switching to another platform only when the selected data analysis platform is compatible and interoperable with other programs. Data sharing and interoper-ability between tools are becoming essential with the advances in computing capabilities (Gardner et al. 2003; Cannon et al. 2007; Günay et al. 2008c; Bjaalie 2008). Using Matlab has the advantage of providing easy interoperability with existing tools. Thanks to the NeuroShare initiative's Matlab library (http://neuroshare.sourceforge.net), PANDORA can read the raw data from several data acquisition programs (see “Methods” and Supp. Mat. A.1.3). It can also read the Hierarchical Data Format (HDF5) files (http://www.hdfgroup.org). HDF5 was recently proposed as a standard for electrophysiological data (unpublished proceedings of the Interoperability Workshop at the Computational Neuroscience Conference, Portland, Oregon, July 2008; Herz et al. 2008). In addition, PANDORA supports reading outputs of various neural simulators (see “Methods”).

The Matlab environment allows passing data back and forth between PANDORA and other community toolboxes for analysis of electrophysiology data, such as:

• the Chronux Toolbox (Mitra Lab, Cold Spring Harbor Laboratory, NY) that allows frequency spectrum and coherence analyses for time-series data for both point and continuous processes (Brown et al. 2004; Bokil et al. 2006);

• the FIND toolbox that specializes for analyzing extracellular recordings (Meier et al. 2007, 2008; http://find.bccn.uni-freiburg.de);

• the BSMART software package that provides functions for multi electrode recordings (Cui et al. 2008); and

• the sigTOOL package which implements a range of waveform and spike-train analyses on neuroscience data (Lidierth 2009).

PANDORA differs from these toolboxes by providing database support and by its specific analysis routines for intracellular electrophysiology datasets.

Matlab also offers a Database Toolbox that can directly access an external database application without the need for PANDORA. It has the advantage of offering access to an optimized, industry-strength database, but brings with it the drawbacks of using an external database application as discussed above. PANDORA can use the Matlab Database Toolbox to import and export data between external databases (see the sql_portal component in Supp. Mat. A.3). In the analysis of the activity sensor network database, we used this feature of PANDORA to read data from an external MySQL database, which allowed accessing a large amount of data that would not fit into Matlab directly (see “Methods” and Fig. 12).

Limitations of the Approach

It should be mentioned that PANDORA has limitations due to the simplified approach that we have taken. The speed of querying operations depends on the number of rows in a table (i.e., it takes O(n) time) because no special effort was made to improve indexing (Table 1 and Supp. Methods A.1.4). Our approach of querying by overloading operators within the Matlab environment performs slower than directly accessing a matrix, but scales well with the number of rows and columns accessed (see Table 2 and Supp. Methods A.1.5). Across querying operations, the largest speed penalty occured in maintaining the metadata that holds the symbolic row and column names, which should be avoided for operations that need a large number of repetitive queries by directly accessing the database's data matrix (Supp. Methods A.1.5). In terms of working memory requirements, the database analysis needs to maintain one or more copies of the complete data matrix in memory, which limits the size of the analysis by the computer's physical memory. A simple workaround to the memory requirement is to perform analysis of large databases in several steps with smaller databases. Another solution is using PANDORA together with an external commercial database engine that supports large databases with the help of the Matlab Database Toolbox (see above).

Future Directions

Despite its advantages, Matlab is a commercial software which hinders the free use of PANDORA. However, a completely free version of PANDORA would need to be created from scratch because it is not straightforward to make PANDORA work with an alternative open-source scientific analysis platform that is Matlab-compatible. The best such alternative platform is GNU Octave (Eaton 2002), which uses a scripting language similar to that of Matlab, although its current version lacks Matlab's object-oriented programming features on which PANDORA heavily depends. If PANDORA needs to be rewritten, the Python language seems be a good choice because it offers efficient, open-source data analysis routines that were recently employed by several neural simulator and analysis tools available from the International Neuroinformatics Coordinating Facility (INCF) Software Center (http://software.incf.org; Bjaalie and Grillner 2007). NeuroTools is one of these toolsets written in Python to manage, store and analyze computational neuroscience simulations (http://neuralensemble.org/). The Java language is also appealing because it was employed by the neuroConstruct simulator tool (Gleeson et al. 2007). In an ambitious effort similar to ours, the G-node project proposes to convert the FIND Matlab Toolbox to a standalone, open-source program (Herz et al. 2008).

Information Sharing Statement

The software presented in this paper is freely available for download from http://software.incf.org/software/pandora/home.