Bidirectional membrane tube dynamics driven by nonprocessive motors

Abstract

In cells, membrane tubes are extracted by molecular motors. Although individual motors cannot provide enough force to pull a tube, clusters of such motors can. Here,weinvestigate, using a minimal in vitro model system, how the tube pulling process depends on fundamental properties of the motor species involved. Previously, it has been shown that processive motors can pull tubes by dynamic association at the tube tip. We demonstrate that, remarkably, nonprocessive motors can also cooperatively extract tubes. Moreover, the tubes pulled by nonprocessive motors exhibit rich dynamics as compared to those pulled by their processive counterparts. We report distinct phases of persistent growth, retraction, and an intermediate regime characterized by highly dynamic switching between the two. We interpret the different phases in the context of a single-species model. The model assumes only a simple motor clustering mechanism along the length of the entire tube and the presence of a length-dependent tube tension. The resulting dynamic distribution of motor clusters acts as both a velocity and distance regulator for the tube. We show the switching phase to be an attractor of the dynamics of this model, suggesting that the switching observed experimentally is a robust characteristic of nonprocessive motors. A similar system could regulate in vivo biological membrane networks.

Dynamic interactions between the cell's cytoskeletal components and the lipid membranes that compartmentalize the cell interior are critical for intracellular trafficking. Atrademark of these cytoskeletal-membrane interactions is the presence of continuously changing membrane tube networks. For example, in the endoplasmic reticulum in vivo (1,2) and in cell-free extracts (3,4,5–6), new membrane tubes are constantly formed as old ones disappear. Colocalization of these membrane tubes with the underlying cytoskeleton has led to the finding that cytoskeletal motor proteins can extract membrane tubes (6). Motors must work collectively to extract membrane tubes (7,8), because the force needed to form a tube, F_tube (9), is larger than the mechanical stall force of an individual motor (10).

Here, we investigate how the tube pulling process depends on fundamental properties of the motors involved. We use Ncd, a motor protein highly homologous to Kinesin, yet fundamentally different biophysically. Processive Kinesin motors take many steps toward the plus end (to the cell periphery) before unbinding from a microtubule (MT); they have a duty ratio of ≈1 (fraction of time spent bound to the MT) (11). Ncd, in contrast, is strictly nonprocessive: motors unbind after a single step (11) characterized by a duty ratio of 0.15 (12). The Ncd motor is unidirectional, moving towards the minus end (directed towards the nucleus) of MTs (13). Although Ncd is not involved in tube formation in vivo, we choose it as the model motor in our pulling experiments because of its nonprocessivity. We have studied Ncd in MT gliding assays where motors are rigidly bound to a glass substrate and show linear, motor-concentration dependent MT gliding speeds, up to a saturation of 120 nm/s [data shown in supporting information (SI) Figs. 4 and 5]. Due to their nonprocessivity, it is not a priori obvious that Ncd motors can cooperatively pull membrane tubes.

We use giant unilamellar vesicles (GUVs) as a substrate to study purified nonprocessive Ncd motors in vitro. Our key findings are, first, that Ncd motors readily extract tubes and, second, that the tubes display more complex dynamics than those pulled by processive motors. We report the emergence of a distinct switching behavior: the tube alternates between forward and backward movement with variable speeds, ranging from +120 nm/s to −220 nm/s. This bidirectional switching is a phenomenon entirely absent in membrane tubes extracted by processive Kinesin motors, which proceed at constant speeds ranging up to 400 nm/s.

Although the bidirectional tube behavior we observe could result from motors forced to walk backward under tension (14), thus far there is no experimental evidence to support this interpretation for unidirectional motors (15,16). Moreover, retraction speeds are much higher than the maximum speeds measured in Ncd gliding assays so that the reverse powerstroke would have to be much faster than the experimentally found speeds. We suggest a mechanism by which nonprocessive motors form clusters along the length of the entire tube, each of which is capable of withstanding the force due to tube tension. These clusters are dynamic entities that continuously fluctuate in motor number. The motors in the cluster at the tip of the membrane tube pull forward until the fluctuating cluster size falls below a critical value and the tip cluster can no longer support the tube. We implement this model mathematically and show that its necessary consequence is a distinct switching behavior in membrane tubes extracted at finite force. We analyze our experimental results in the context of this model and we predict the distribution of motor clusters all along the length of a membrane tube. The resulting dynamic distribution of motor clusters acts as both a velocity and distance regulator for the tube. Finally, we trace the evolution of the system through simulations and find the same behavior observed experimentally. In short, we show that not only can nonprocessive, unidirectional Ncd motors act cooperatively to extract membrane tubes, they do so in a highly dynamic, bidirectional switching fashion. Our findings suggest an alternative explanation for in vivo bidirectional tube dynamics, often credited to the presence of a mixture of plus and minus ended motors.

Results

Experimental Results

We investigate the influence of motor properties on membrane tube pulling with a minimal system where biotinylated motor proteins are linked directly via streptavidin to a fraction of biotinylated lipids in GUVs. Upon sedimentation to a MT-coated surface, and addition of ATP, motors extract membrane tubes from the GUVs. When we introduce nonprocessive Ncd motors to our system, we see networks of membrane tubes formed. Fig. 1a shows a fluorescence time series of mem- brane tubes pulled from a GUV by Ncd motors. The entire movie is provided as SI Movie 1. The tips of the membrane tubes formed by Ncd show remarkable variability. The arrow on the lower right corner of the image of Fig. 1a indicates a retracting membrane tube, and the remaining arrows show growing membrane tubes. In our experiments, we see not only tubes that persistently grow or retract, but also tubes that switch from periods of forward growth to retraction. We characterize these tube dynamics by tracing the tube tip location as it changes in time. Fig. 1b shows example traces of membrane tube tips in time: one of tube growth, one of retraction and two that exhibit a bidirectional movement. We verify that this bidirectional tube movement is unique to nonprocessive motors by comparing to membrane tubes pulled by processive motors. Under the same experimental conditions Kinesins produce only growing tubes (Fig. 1b Inset). In the rare cases of tube retraction with Kinesin, tubes snap back long distances at high speeds, at least 10 times faster than growth speeds. In these cases, it is likely that the motors pulling the tube have walked off the end of the underlying MT.

Fig. 1.

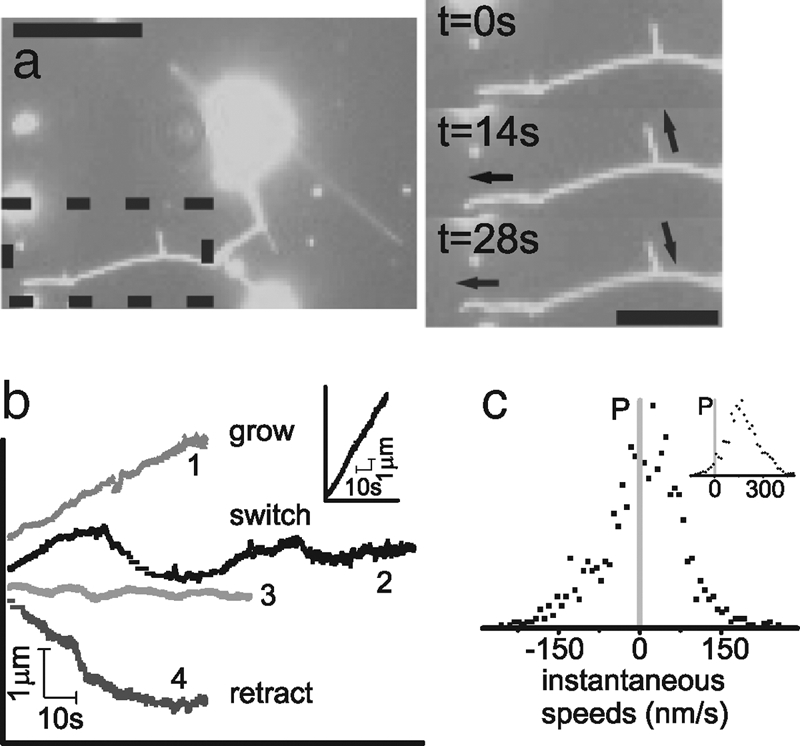
Membrane tubes formed by nonprocessive motors. (a) Fluorescence image of a membrane tube network extracted from GUVs by nonprocessive motors walking on MTs on the underlying surface. The time sequence images on the right show the detailed evolution of the network section within the dashed region on the left. The entire movie is provided as supplementary material. Arrows indicate direction of membrane tube movement: the left arrows indicate a growing tube and the right arrows show a tube that which is switching between growth and retraction (left scale bar, 10 μm; right scale bar, 5 μm). (b) Example traces of membrane tube tips formed by nonprocessive motors as they move in time. There are three distinct behaviors: tube growth (1), tube retraction (4), and switching between growth and retraction (2 and 3), a bidirectional behavior. The behavior is distinctly different for membrane tubes pulled by Kinesin (Inset) where tubes grow at steady high speeds. (c) The distribution of instantaneous tip speeds for membrane tubes pulled by Ncd is asymmetric and centers around zero, with both positive and negative speeds. Kinesin tubes move with only positive speeds (Inset).

We further quantify membrane tube dynamics by calculating instantaneous speeds for individual tip traces by subtracting endpoint positions of a window moving along the trace. As described in Materials and Methods, we use a window size of 1 s for the Ncd, and 2 s for the Kinesin membrane tube tip traces. Fig. 1c shows an example of the resulting distribution and frequency of tip speeds for a single dynamically switching membrane tube formed by Ncd (trace 3 from Fig. 1b). Fig. 1c Inset shows the speeds for a membrane tube pulled by Kinesin. The speed distributions for Kinesin and Ncd are distinctly different where Kinesin speeds are distributed around a high positive speed. From gliding assays, one expects that Kinesin would pull membrane tubes at a constant 500 nm/s. The Kinesin motors along the bulk of membrane tube are moving freely in a fluid lipid bilayer, do not feel any force, and may walk at maximum speed toward the membrane tube tip. However, the motors at the tip experience the load of the membrane tube and their speeds are damped (7,8,16). The Gaussian-like distribution of speeds we find for Kinesin elucidates the influence of load on the cluster of motors accumulating at the tip of the membrane tube. The distribution of speeds for Ncd is asymmetric and centered around zero with both positive and negative speeds. A simple damping of motor walking speed at the membrane tip, as in the case of Kinesin, does not provide an explanation for the distribution of negative membrane tube speeds found in the tubes pulled by Ncd. The unique tube pulling profile of the nonprocessive motors suggests that they provide a mechanism to mediate membrane retractions and hence, bidirectional tube dynamics.

Model

Koster et al. (7) show that membrane tubes can be formed as a result of motors dynamically associating at the tube tip. Collectively, the clustered motors can exert a force large enough to pull a tube. Evans et al. (17,18) find that this force scales as $F_{tube}\approx \sqrt{k\sigma }$, where κ is the membrane bending modulus and σ the surface tension. Koster et al. predict a stable tip cluster to pull a tube, which has been verified experimentally by Leduc et al. (8) and supported by a microscopic model by Campàs et al. (19).

Although accurate for membrane tubes produced by processive motors, the Kinesin model does not explain the bidirectionality in tubes formed by nonprocessive motors. There must be an additional regulatory mechanism for the tube retractions to explain the negative speed profiles seen in experiments with Ncd. We propose a mechanism to account for these retractions wherein dynamic clusters form along the entire length of the tube. In the case of Kinesin, motors walk faster than the speed at which the tube is pulled, and accumulate at the tip cluster (7,8). However, due to their low duty ratio, nonprocessive motors do not stay bound long enough to walk to the tip of the membrane tube. Compared to freely diffusing motors (D = 1 μm²/s; ref. 8), a MT-bound motor (bound for ≈0.1 s; refs. 12 and 20) is stationary. Consequently, there areMT-bound motors all along the length of the tube. Local density fluctuations lead to areas of higher concentration of bound motors, resulting in the formation of many motor clusters, not just a single cluster at the tube tip.

In both cases, the cluster present at the tip has to be large enough to overcome F_tube. Because an individual motor can provide a force up to ≈5 pN (10) and a typical F_tube is 25 pN (7), a cluster must consist of at least several motors to sustain tube pulling. Statistical fluctuations can make the tip cluster too small to overcome F_tube, resulting in a retraction event. In the case of Ncd, as soon as the retracting tip reaches one of the clusters in the bulk, the tube is caught, and the retraction stops. Growth can then resume, or another retraction event takes place. The process of clustering along the membrane tube, as illustrated in Fig. 2a, and the associated rescue mechanism are absent from the mechanism that describes Kinesin tube pulling.

Fig. 2.

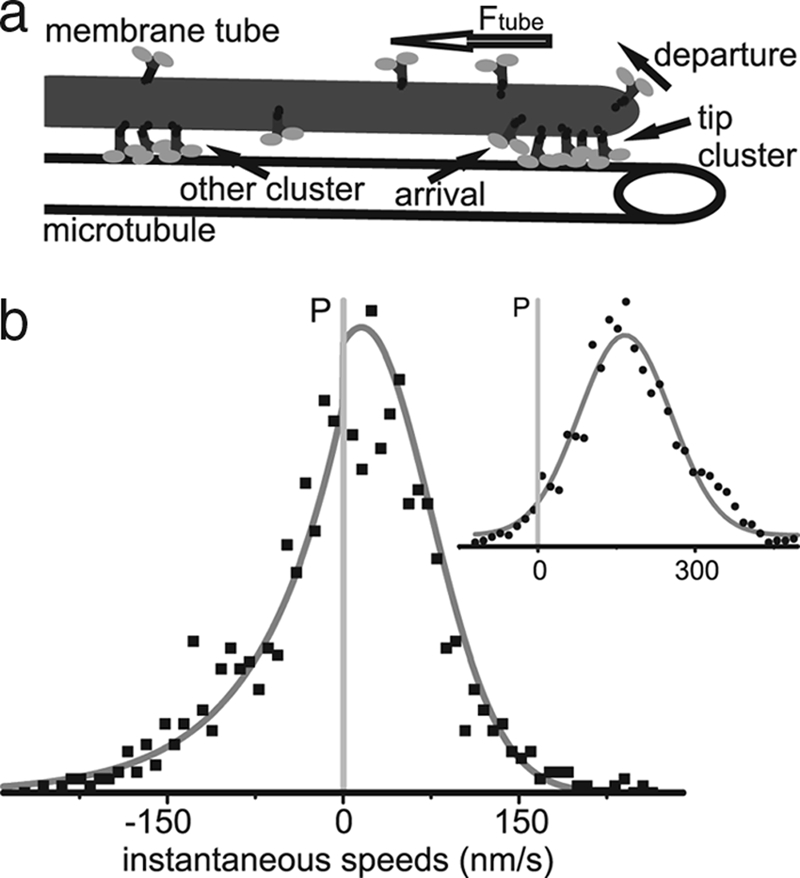
Model for membrane tube bidirectionality. (a) Sketch of nonprocessive motor clustering along a membrane tube. MT-bound nonprocessive motors are distributed along the entire length of the tube; local density fluctuations result in the formation of motor clusters. (b) Distribution of instantaneous speeds of a bidirectionally moving membrane tube (trace 2 in Fig. 1b). The speed distribution can be described as a combination of two different processes: pulling by nonprocessive motors and tube tension induced retraction. Therefore, the forward and backward speeds follow different distributions, as described by Eq. 1; the solid line shows the best fit of this distribution. (Inset) Tubes pulled by processive Kinesin motors follow a simple Gaussian speed distribution.

In our model, two different mechanisms drive forward and backward tube motion, so we expect two different types of characteristic motion profiles. Retraction is regulated by motor clusters that can form anywhere along the length of the tube: their locations are randomly taken from a uniform probability distribution. Consequently the distance between them follows an exponential distribution. The long steptime of MT-bound Ncd motors allows us to temporally resolve the effect of the disappearance of clusters from the tube tip: individual retraction events. Therefore, we expect to recover this exponential distribution in the retraction distances.

The forward velocity depends on the size of the cluster at the tube tip (11). Per experimental time step, there are many motors arriving at and departing from each cluster. Moreover, while taking a time trace, we observe pulling by several different clusters of motors. Because there are many clusters in an individual trace, we can employ the Central Limit Theorem to approximate the distribution of cluster sizes by a Gaussian. If the number of motors in the tip cluster is large enough to overcome the tube force, the speed at which the cluster pulls scales with the number of excess motors: v = A(n−c). Here, n is the number of motors, c is the critical cluster size, and A is the scaling constant that depends on the turnover rate, step size, and tube tension. The forward speed distribution will therefore inherit the Gaussian profile of the cluster size distribution, where the mean and spread of this distribution depend on the average tip cluster size. The probability density of the exponential distribution function depends on a single parameter λ, the mean retraction distance. The Gaussian distribution depends on both the mean 〈n〉 and the spread σn of the tip cluster.

The tube dynamics are described by the probability distribution of the tip displacement per unit time. From the individual probability densities for retraction and growth we find the combined density f (ΔL), the full probability density of advancing or retracting a distance ΔL:

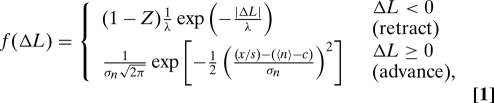where n is the size of the cluster at the tip, c is the minimal cluster size necessary to support the tube, and s is the step length, which is equal to the size of a MT subunit (8 nm) (11). The normalization constant Z depends on n̄ = 〈n〉 − c and σn and is given by $Z=\frac{1}{2}\left[1+\text{erf}(\frac{\overline{n}}{{\sigma }_n\sqrt{2}})\right]$.

Discussion

From the experimental data, we cannot determine 〈n〉 and c individually, but only speed profiles that scale with the difference n̄ = 〈n〉 − c, the number of excess motors present in the tip cluster that actually pull. To determine An̄, Aσ_n, and λ, we make use of the fact that Z is the fraction of forward motions, providing a relation between n̄ and σn. We then have a two-parameter fit for the entire speed distribution, or two single-parameter fits for the forward and backward parts of the total speed distribution.

We apply our model to experimental data and find that the different mechanisms for forward and backward motion accurately describe the experimental Ncd tip traces (Fig. 2b). As predicted, Kinesin motors only show forward pulling speeds, described by a Gaussian distribution (see Fig. 2b Inset). The marked contrast in speed profiles of processive and nonprocessive motors is a signature of different biophysical processes: for processive motors a single cluster remains at the tip ensuring a constant forward motion whereas tubes pulled by nonprocessive motors are subject to alternating growth and retraction phases.

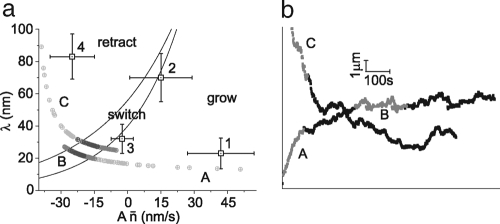
Growth and retraction are accounted for by the two different mechanisms in our model. Combined, they explain the three different types of observed behavior: growth, retraction, and switching between both. To unravel the relationship between the two mechanisms in describing membrane tube behavior, we plot the characteristic growth rate An̄ versus the characteristic retraction length λ. Because a trace exhibiting switching behavior should have an average displacement of zero, we can derive a “switching condition” from the probability distribution Eq. 1 by requiring the expectation value of ΔL to vanish. The line in the phase diagram where this switching condition is met by:

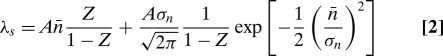where Z is the normalization constant from Eq. 1. In Fig. 3a, we plot the lines for which the switching condition holds for the range of values for Aσ_n we find in the experimental traces (50 nm/s ≤ Aσ_n ≤ 70 nm/s). We also plot the experimen- tally obtained values for An̄ and λ of the four traces given in Fig. 1b.We clearly see different regimes: growing tubes have large average cluster size and small distances between clusters, whereas retracting tubes show the inverse characteristics (small cluster size and large distance between clusters). The switching tubes are in between, in a relatively narrow region.

Fig. 3.

Membrane tube phase diagram and simulations. (a) Phase diagram showing mean retraction distance λ vs. effective growth speed An̄. Lines represent the switching condition described by Eq. 2 for Aσ_n = 50 nm/s and Aσ_n = 70 nm/s. Squares 1-4 correspond to traces 1-4 in Fig. 1b, where the errors are determined by the mean square difference between the data points and the fit of the distribution in Eq. 1. As expected qualitatively, retracting membrane tubes fall well into the retraction regime with large retraction distance and small cluster sizes, while growing membrane tubes have large cluster sizes and smaller distances between clusters. (b) Two simulated tube tip traces of a membrane tube pulled by nonprocessive motors. The time evolution of the parameters λ and An̄ for both traces is shown in the phase diagram (a), by circles getting darker in time. We see that both simulated tubes evolve towards a switching state. The highlighted sections of the simulated traces represent all possible characteristic behaviors of tubes pulled by nonprocessive motors.

Simulations

The switching regime covers only a small part of the total available parameter regime in the phase diagram (Fig. 3a). That we observe switching behavior in approximately 50% of the experimental traces indicates that these parameters are dynamic quantities that change over time. Our experimental observation times are too short to track these changes, but we can implement them in simulations. To introduce dynamics into our model, it is important to realize that the tube force F_tube is not independent of the tube length, an additional observation not yet integrated into the model. As tubes grow longer, the vesicle itself starts to deform. Consequently, the tube force increases with the tube length, an effect also observed experimentally (21).

As the tube force increases, larger tip clusters are required to continue pulling the tube. An immediate consequence of the force depending on the tube length is the emergence of a typical length scale, L_D. For a tube of length L_D, the forward force exerted by a an average motor cluster is balanced by F_tube. We can implement the force dependence in our model by introducing a Boltzmannlike factor that compares two energy scales: F_tube times the actual length of the tubeL(t) compared to the mean cluster forceFc times the typical length of the tube L_D. All constants are accounted for by L_D; we stress that choosing this form to incorporate a typical length scale is an assumption, but that the qualitative results do not depend on the exact functional form chosen.

Tubes are initially pulled from motor-rich regions on the GUV. As a tube grows longer, clusters are spread further apart and the average cluster size decreases. The average retraction distance increases with increasing tube length, L(t), and scales inversely with the total number of motors, N(t), on the tube: λ ≈ L(t)/N(t). Similarly, the average number of motors at the tip scales with the total number of motors N(t) and inversely with the tube length L(t) : 〈n〉 ≈ N(t)/L(t). Therefore, the total number of motors at the tip can now be expressed as:

where C is the average motor concentration on the GUV and R₀ is the tube radius. Combined, Eqs. 1 and 3 represent a system to describe the membrane tube dynamics caused by nonprocessive motors.

We perform simulations of membrane tubes extracted by nonprocessive motors using Eq. 3 with a given value for C, which is based on experimental values. We choose the simulation time step to match the experimental sampling rate of 25 Hz. In each time step, we add Gaussian noise to the position to account for the experimental noise (see Materials and Methods). In the simulations, we observe two kinds of behavior: tubes that grow and subsequently retract completely after relatively short times, and tubes that evolve to a switching state. When we perform control simulations with a cluster size that is independent of the tube length, we find either fully retracting or continuously growing membrane tubes, never switching. Fig. 3b shows two examples of simulated switching traces. We follow the average number of motors at the tip 〈n〉 and the retraction distance λ as they change in time. The simulated evolution from growth to a switching state can be seen in the phase diagram (Fig. 3a). In the switching state, the tube length and total number of motors on the tube are essentially constant, and Eq. 2 is satisfied.

The highlighted sections of the simulated traces shown in Fig. 3b represent all possible characteristic behaviors of tubes pulled by nonprocessive motors. The occurrence of all three types of behavior in a long simulated tube tip trace suggests that the experimental observations are snapshots of a single evolving process. The simulations indicate that all these processes eventually move to the switching regime. The switching state corresponds to a regulated tube length, determined by the GUV's motor concentration and surface tension.

Conclusion

We have shown that nonprocessive motors can extract membrane tubes. We find that at a given tension, these tubes exhibit bidirectionality of motion. We propose a model to explain our experimental findings wherein motors form clusters all along the length of the membrane tubes. The bidirectional membrane dynamics seen experimentally with nonprocessive motors can be accurately described by two different mechanisms for forward and backward motion. Future in vitro experiments will make use of single molecule fluorescence to directly quantify the locations of nonprocessive motors and motor clusters as they actively change in time. Our model predicts the emergence of motor clustering and an equilibrium tube length where tube bistability occurs. We propose that this mechanism with nonprocessive motors could also regulate tube dynamics in vivo and should be investigated.

Materials and Methods

GUVs

1,2,-Dioleoyl-sn-glycero-3-phosphocoline (DOPC), 1,2-dioleoyl-snglycero- 3-phosphoethanolamine-N-(cap biotinyl) (DOPE-Bio), and 1,2-dioleoyl- sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (DOPE-Rh) were purchased from Avanti Polar Lipids. Twenty microliters of lipids in 1:10 chloroform/methanol (2 mg/ml DOPC, 0.067 mg/ml DOPE-Rh, and 0.043 mg/ml DOPE-Bio) were dropped onto one of two indium tin oxidecoated glass slides (4 cm × 6 cm). The lipids were distributed on the glass by the “rock and roll” method (22) and dried for 1 hr under continuous nitrogen flow. A 1-ml volume chamber was constructed from the two glass plates, the dried lipids on the bottom glass, and a polydimethylsiloxane (PDMS) spacer. The chamber was filled with a solution of 200 mM sucrose and an AC voltage applied to the glass plates, forming GUVs by the electroformation method (22).

MTs and Motor Proteins

MTs were prepared from tubulin purchased from Cytoskeleton. Tubulin (10 mg/ml) in MRB40 (40 mM Pipes/4 mM MgCl2/1 mM EGTA, pH 6.8) with 1 mM GTP was incubated for 15 min at 37°C to polymerize. MTs were stabilized by mixing them 1:10 (vol/vol) with MRB40 containing 10 μM taxol (MRB40tax). The first 401 residues of the Kinesin-1 heavy-chain from Drosophila melanogaster, with a hemaglutinin tag and a biotin at the N terminus, were expressed in Escherichia coli and purified as described in ref. 23. Residues K195-K685 of the nonclaret disjunctional (Ncd) from D. melanogaster, with a 6x-His tag (20) and biotin, were expressed and purified in the same fashion, but with lower induction conditions: 10 μM isopropyl β-D-1-thiogalactopyranoside (IPTG)

Sample Preparation

Glass coverslips were soaked in chromosulfuric acid for 1 hr, rinsed with deionized H2O, and dried with nitrogen flow. The coverslips were soaked in poly(-L-lysine) 1:500 in ethanol for 5 min and dried with nitrogen flow. A circular area on the coverslip was defined with a circle of vacuum grease allowing for a 50-μl sample volume. MTs were dropped on to the sample area and incubated for 10 min to adhere. MTs that did not stick to the surface were removed by rinsing two times with MRB40tax. α-Casein (Sigma) was dropped on the surface (1 mg/ml) to coat the surface and minimize interaction of GUVs with exposed glass, incubated for 10 min, and rinsed with MRB40tax.

GUVs were mixed 1:1 in MRB40tax with 180 mM glucose to osmotically match the intravesicular osmolarity (Halbmikro Osmometer, Type M, Knauer, Germany). A total of 2.5 μl of 2 mg/ml streptavidin were added to 50 μl of the vesicle solution and incubated for 10 min. This quantity of streptavidin saturates all biotin binding sites on the vesicle. Next, 2 μl of motor (Kinesin or Ncd ≈650μg/ml) was added and incubated for 10 min. Forty microliters of the vesicle solution was dropped onto the sample area. Twenty microliters of MRB40tax with 180 mM glucose was dropped on top of the sample to help the vesicles to settle to the glass surface. Finally, 0.5 μl of Oxygen Scavenger (8 mM DTT/0.4 mg/ml catalase/0.8 mg/ml glucose oxidase) and 1 μl of 100 mM ATP were added to the sample followed by a placing on a top coverslip to seal the sample chamber.

Image Acquisition and Analysis

Images were acquired on an epifluorescence inverted microscope equipped with a CCD camera (Axiovert 40CFL, Carl Zeiss;WAT-902H ULTIMATE,Watec, Japan) at videorate. We developed a Matlab algorithm to trace the membrane tube growth dynamics by following the tip displacement as a function of time. The algorithm determines the intensity profile along a tube and extended beyond the tip. A sigmoidal curve fit to the profile determines the tip location with subpixel precision of 40 nm. We traced tip locations for seven individual Kinesin-pulled membrane tubes (all growing, a single one showing a rapid retraction event) and 15 Ncd tubes (five growing, three retracting, and seven switching). We calculate instantaneous speeds for individual tip traces by subtracting endpoint positions of a window moving along the trace. Initially we use a range of window sizes, from 0.5 to 12 s, to calculate instantaneous speeds from the tip traces. We find that, for the Ncd data, a window size of 1 s is large enough to average out experimental system noise (signal due to thermal noise, fluorophore bleaching and microscope stage drift) but small enough to preserve the unique bidirectional features we see in tube data. We find that 2- and 3-s windows begin to overaverage the data, and even larger window sizes smooth away the prevalent changes in speeds and directionality already qualitatively evident in the data. For Kinesin, however, the resulting speeds we find using a window size of 2 s (minimum size for the Kinesin data, the experimental signal is noisier than for the Ncd data) differ very little from the speeds using up to an 8-s window. Ultimately, we use small window sizes that are still large enough to average out experimental noise but preserve as much of the signal details as possible: 1 s for Ncd tip traces and 2 s for Kinesin traces, with steps of 0.04 s. We determined the noise in our system (signal due to thermal noise, fluorophore bleaching and microscope stage drift) by analyzing stationary membrane tubes with our tip-tracing algorithm and calculating instantaneous speeds in the same fashion as for active tube tips. The speeds from a noise trace showed a Gaussian profile centered around zero with a spread of 40 nm/s (data not shown).