A phenomenological model of the synapse between the inner hair cell and auditory nerve: Long-term adaptation with power-law dynamics

Abstract

There is growing evidence that the dynamics of biological systems that appear to be exponential over short time courses are in some cases better described over the long-term by power-law dynamics. A model of rate adaptation at the synapse between inner hair cells and auditory-nerve (AN) fibers that includes both exponential and power-law dynamics is presented here. Exponentially adapting components with rapid and short-term time constants, which are mainly responsible for shaping onset responses, are followed by two parallel paths with power-law adaptation that provide slowly and rapidly adapting responses. The slowly adapting power-law component significantly improves predictions of the recovery of the AN response after stimulus offset. The faster power-law adaptation is necessary to account for the “additivity” of rate in response to stimuli with amplitude increments. The proposed model is capable of accurately predicting several sets of AN data, including amplitude-modulation transfer functions, long-term adaptation, forward masking, and adaptation to increments and decrements in the amplitude of an ongoing stimulus.

INTRODUCTION

At the first synapse of the auditory pathway, the receptor potential of an inner hair cell (IHC) is converted into a discharge pattern on auditory-nerve (AN) fibers, where adaptation in discharge rate in response to a constant sound stimulus is observed. The IHC-AN synapse complex is believed to be mainly responsible for this adaptation. Although the mechanism that gives rise to synaptic adaptation is not completely understood, it could be caused either by the depletion of neurotransmitter from a readily releasable presynaptic pool of neurotransmitter (Moser and Beutner, 2000; Schnee et al., 2005; Goutman and Glowatzki, 2007) or by the desensitization of post-synaptic receptors (Raman et al., 1994).

Modeling the adaptation in the IHC-AN synapse has been a focus of extensive research over the last several decades. Early attempts employed a single-reservoir system with loss and replenishment of transmitter quanta (Schroeder and Hall, 1974; Oono and Sujaku, 1974, 1975), and later models added extra reservoirs (or sites) or more complex principles of transmitter flow control (Furukawa and Matsuura, 1978; Furukawa et al., 1982; Ross, 1982, 1996; Schwid and Geisler, 1982; Smith and Brachman, 1982; Cooke, 1986; Meddis, 1986, 1988; Westerman and Smith, 1988). In general, the transmitter in these models lies in reservoirs or sites close to the presynaptic membrane and diffuses between reservoirs within the cell and out of the cell to the synaptic cleft. Each diffusion step is controlled by a permeability parameter, and at least one of the permeabilities is dependent on the stimulus. Mathematically, low-pass filters with appropriate orders and cut-off frequencies can replicate the replenishment and diffusion mechanisms between different transmitter reservoirs. Depending on the interconnection of the reservoirs, the flow of transmitter for these models can be implemented using either a cascade of low-pass filters or parallel low-pass filters.

Adaptation in the IHC-AN synapse is very complex. Its characteristics depend on stimulus intensity, duration, previous stimulation history, and spontaneous rate (SR) (Rhode and Smith, 1985; Relkin and Doucet, 1991). The diversity and complexity of adaptation pose a great challenge for successful modeling of the dynamics of this synapse. Two models with different structures have been developed independently in a series of studies (Meddis, 1986, 1988; Westerman and Smith, 1988; Carney, 1993; Zhang et al., 2001; Sumner et al., 2002, 2003). However, the mathematical descriptions of these two models are essentially equivalent despite their structural differences (Zhang and Carney, 2005). Both of these models are successful to some extent in simulating the onset adaptation responses (characterized by two exponential time constants) of the AN fibers. They have the same double-exponential adaptation (rapid and short-term) in both onset and offset responses (Zhang and Carney, 2005). However, physiological data exhibit substantially different dynamics between the offset and onset responses; in particular, the discharge rate may drop below the spontaneous rate at stimulus offset, sometimes to the point where there is a cessation of firing (i.e., the discharge rate is zero), followed by a relatively slow recovery to the spontaneous rate. Also the magnitude and time course of the onset and offset adaptations of the physiological data scale with the duration of the stimulus (Kiang, 1965), providing one illustration of the long-term behavior of AN response dynamics. Synapse models based on exponential adaptation fail to account for the offset adaptation as well as these long-term response properties. For example, physiological forward-masking data cannot be explained by these models without changing the model parameters such that they are inconsistent for onset and offset adaptations, and the dynamics must also be adjusted for fibers with different spontaneous rates (Meddis and O’Mard, 2005). These models also produce inaccurate responses to amplitude-modulated (AM) signals (Nelson and Carney, 2004; Zhang and Carney, 2005) and to increments and decrements in the amplitude of ongoing stimuli (Hewitt and Meddis, 1991).

Zhang and Carney (2005) developed a strategy that effectively avoids the constraint on the time course of recovery in the offset imposed by the onset parameters. A simple shift in the upward and downward directions (by same amount) of the pre-and post-synaptic responses, respectively, results in a slower recovery with a cessation in the post-synaptic response immediately after stimulus offset. It was reported that an appropriate shift can produce a better modulation transfer function (i.e., strength of AN synchronization to the envelope of amplitude-modulated stimuli as a function of modulation frequency) (Fig. 11, Zhang and Carney, 2005). However, such a shift also results in a systematic variation in the average rate with modulation frequency, which is not observed in AN responses (Joris and Yin, 1992), and also produces unrealistic steady-state rates of low spontaneous-rate fibers to tones at high sound levels (Nelson and Carney, 2004).

Figure 11.

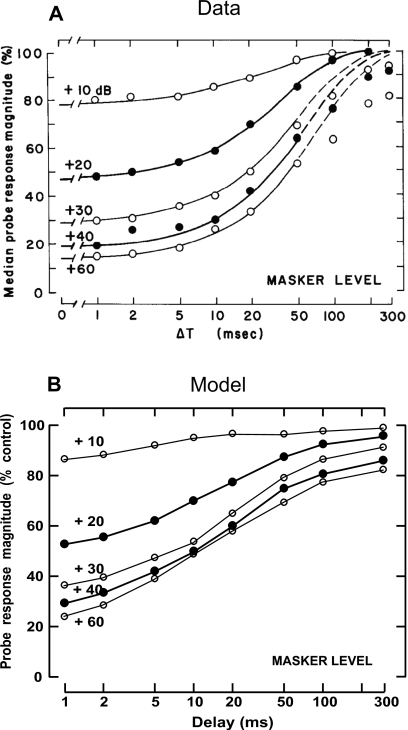
Forward-masking recovery functions for a population of fibers; masker level is the parameter. Masker stimuli were tones with frequency matched to CF, 100-ms duration. Probe stimuli were also tones at CF, +20 dB, 15-ms duration. (A) Actual median recovery functions from 37 fibers with CFs ranging from 0.5 to 16 kHz. From Harris and Dallos (1979, with permission). (B) Model average recovery functions from ten CFs (HSR and LSR) spaced logarithmically (range of 0.5–16 kHz).

Hewitt and Meddis (1991) compared the responses of eight different synapse models to a set of standard stimuli and found no single model that could satisfactorily explain all of the data in their target set of responses. Although addition of extra reservoirs or sites in the model (equivalent to adding more exponential processes) tends to address more response properties of the AN (e.g., Smith and Brachman, 1982; Payton, 1988), such a model becomes mathematically intractable, and thus finding a set of parameters that works well for a large set of AN response properties is difficult, if not impossible.

Recently, power-law adaptation (PLA) has drawn a lot of attention in describing the dynamics of biological systems at levels ranging from single ion channels up to human psychophysics (Wixted and Ebbesen, 1997; Toib et al. 1998; Fairhall et al., 2001; Leopold et al., 2003; Ulanovsky et al., 2004; Lundstrom et al., 2008). Power-law adaptation is characterized by an adaptation of discharge rate that follows a fractional power of time or frequency rather than an exponential decay (Chapman and Smith, 1963). In fact, power-law dynamics can be approximated by a combination of a large number of exponential processes with a range of time constants (Brown and Stein, 1966; Thorson and Biederman-Thorson, 1974; Drew and Abbott, 2006). It has been argued that on short timescales, underlying mechanisms represent the contribution of intrinsic nonlinearities (e.g., ion channel dynamics). However, adaptation often exhibits power-law-like dynamics over longer timescales, implying the coexistence of multiple timescales in a single adaptive process (Camera et al., 2006). In reality, multiple timescales exist in the multiplicity of channel dynamics present in a single neuron. To our knowledge, power-law dynamics has not yet been employed to explain adaptation at the level of the AN.

To illustrate a general model of power-law adaptation, suppose a stimulus s(t) produces a response r(t) that feeds back into an integrator I(t), such that the adapted response, r(t)=max[0,s(t)−I(t)], and

$$I\left(t\right)=\alpha {\int }_0^t\frac{r\left(t^{\prime }\right)}{t-t^{\prime }+\beta }d{t}^{\prime }=\alpha r\left(t\right)\ast f\left(t\right)\text{where}f\left(t\right)=1∕(t+\beta ),$$

where α is a dimensionless constant and β is a parameter with units of time (Drew and Abbott, 2006). The suppressive effects of the response, I(t), are accumulated with power-law memory that is intermediate between perfect (never forgotten) and exponential processes (Drew and Abbott, 2006). I(t) can be described as a convolution of a power-law kernel, f(t), with its prior responses, r(t).

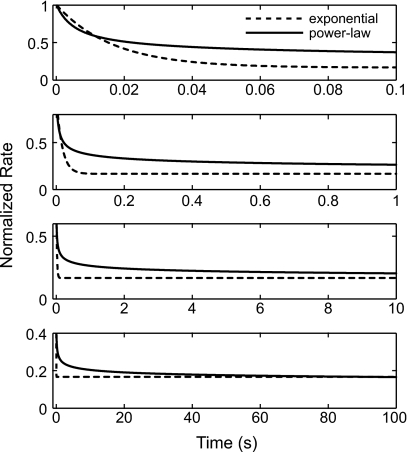
To compare the dynamics of adaptation between a power-law and a single exponential process, Fig. 1 illustrates power-law (solid) and exponential (dashed) adaptation in response to a unit step function [s(t)=1, t>0] over four different time scales. For exponential adaptation [i.e., $I\left(t\right)=1∕{\tau }_a{\int }_0^{t}r\left(t^{\prime }\right)\exp ((t^{\prime }-t)∕{\tau }_{\mathrm{ex}})d{t}^{\prime }$], the transient response decays exponentially to a steady-state value with a fixed time constant regardless of the stimulus time scale. Because the transition between the initial transient and the later sustained response occurs at a fixed time, exponential adaptation appears to have increasingly sharp transitions when observed over longer time scales. However, power-law adaptation has a similar shape for all four time scales, indicating the “scale-invariance” property of power-law adaptation. The responses appear qualitatively similar to exponential adaptation over any particular time period, and thus have no well-defined transient or sustained responses. Nevertheless, if a conventional time constant is evaluated from the responses of the power-law adaptation, its value depends on the duration of the responses being fit. This is illustrated by the power-law adaptation examples in Fig. 1, where the responses to the four different stimulus durations appear to have transient responses of different durations, even though they arise from the same power-law adaptation.

Figure 1.

Illustration of the dynamics of adaptation for exponential (dotted lines) and power-law (solid lines) models for four different time scales (0–0.1, 0–1, 0–10, and 0–100 s) in response to a unit step function. The parameters for the exponential adaptation are τ_a=0.2 s and τ_ex=0.1 s. The parameters for the power-law adaptation are α=5×10⁻⁵ and β=5×10⁻³ s. The solid curves retaining a similar shape across different time scales demonstrate the “scale-invariance” property of the power-law adaptation.

Mathematically, the dimensionless constant α controls the amount of adaptation and hence makes the power-law adaptation scale-invariant (Drew and Abbott, 2006). In contrast, in the case of exponential adaptation, the equivalent of α has units of frequency (1∕τ_a, where τ_a is the time constant in seconds); thus, the transition between transient and sustained responses is fixed in time (i.e., it is not scale-invariant) (Drew and Abbott, 2006). Moreover, the long tail of the power-law kernel provides a longer memory for past responses than does exponential adaptation. The hypothesis of this study was that inclusion of power-law adaptation in the IHC-AN synapse could account for offset responses as well as other long-term response properties of the AN.

This paper describes a model of rate adaptation at the IHC-AN synapse that was incorporated into a composite phenomenological model of AN responses (Zilany and Bruce, 2006, 2007). Model responses were compared to physiological data for several different stimulus paradigms. The proposed PLA synapse model that includes both exponential and power-law dynamics replaces the previous synapse model having only exponential adaptation. Westerman and Smith’s (1988) three-store diffusion model, which gives rise to exponential adaptation, is followed by two parallel power-law adapting paths that provide slowly and rapidly adapting responses, respectively. The parameters of the three-store diffusion model were adjusted to achieve desired onset responses with two time constants (rapid and short-term) and rate saturation at higher stimulus levels. It is worth mentioning that power-law adaptation alone does not result in rate saturation. The slowly adapting power-law component significantly improves the AN response at stimulus offset and also recovery after stimulus offset. The path with fast power-law dynamics contributes to the unsaturated onset response and to the “additivity” observed in AN rate responses to stimuli with amplitude increments. Several studies have confirmed that the process of short-term adaptation is additive in nature (Smith and Zwislocki, 1975; Smith, 1977; Abbas, 1979), meaning that the change in firing rate in response to an increment∕decrement in stimulus level does not greatly depend on the time between the onset and the subsequent change in level. Smith et al. (1985) showed that this property also holds if increment responses are analyzed with different window lengths that separate the portions of the response associated with rapid and short-term adaptation. In contrast, the small-window decrement response decreases with increasing time delay (i.e., decrement responses are not additive over a short time window following the decrement). With the inclusion of power-law dynamics in the synapse model, the AN model presented in this paper can successfully account for a wide range of response properties of the AN, including additivity.

Another “long-term” property of AN responses that was addressed in this study is the pattern of correlations in response rates over long time intervals. The discharge rate of a single AN fiber is positively correlated over long time scales, whereas its response is often negatively correlated over the short term (Teich, 1989; Kelly et al., 1996). Strong correlation of rate computed over widely separated analysis windows is referred to as “long-range-dependence” (LRD). Jackson and Carney (2005) investigated the implication of this effect of LRD in understanding SRs of AN fibers. They employed a fractional-Gaussian-noise-driven Poisson process to model LRD rates of AN fibers (Teich, 1989; Teich and Lowen, 1994). As LRD dramatically increases the variability of estimates of mean discharge rates (Jackson, 2003), they argued that the entire AN fiber population may be made up of neurons with only two or three true SRs. Incorporating appropriate LRD effects in their simulations, they successfully replicated the SR histograms of AN fibers. In order to model the distribution of SRs, the same approach was adopted in this study by adding a fractional Gaussian noise with appropriate parameters (Table 1) in the slow power-law adaptation path of the IHC-AN synapse model.

Table 1.

Parameter values.

Power-law adaptation
Dynamics	α (dimensionless)	β (s)
Slow	5×10−6	5×10−4
Fast	1×10−2	1×10−1
Fractional Gaussian noise
Spontaneous rate (spikes∕s)	Standard deviation (spikes∕s)
High (100)	200
Medium (5)	50
Low (0.1)	10

DESCRIPTION OF THE MODEL

Architecture of the PLA model

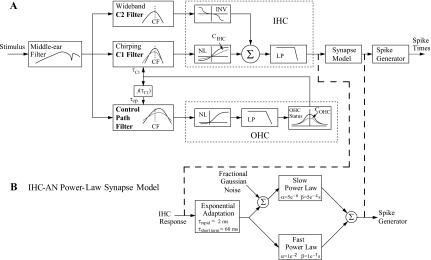
A schematic diagram of the PLA model for auditory-nerve responses is shown in Fig. 2. Each section of the model provides a phenomenological description of the major functional components of the auditory periphery, from the middle ear (ME) to the auditory nerve. The input to the ME is an instantaneous pressure waveform of the stimulus (in pascals) sampled at 100 kHz. The ME filter is followed by three parallel filter paths: the C1 and C2 filters in the signal path and the broad-band filter in the control-path. The feed-forward control-path regulates the gain and bandwidth of the C1 filter to account for several level-dependent properties in the cochlea (Zhang et al., 2001; Bruce et al., 2003). The parallel-path C2 filter is implemented based on Kiang’s two-factor cancellation hypothesis (Kiang, 1990). The combined response of the two transduction functions following the C1 and C2 filters provides the input to a seventh-order IHC low-pass filter (Zilany and Bruce, 2006, 2007). The IHC output drives the model for the IHC-AN synapse. In this study, a new model of the IHC-AN synapse replaced the previous synapse model. Finally the discharge times are produced by a renewal process that includes refractory effects (Carney, 1993). Detailed descriptions of the model stages are provided in Zilany and Bruce (2006, 2007); the model code is available at the following website: www.bme.rochester.edu∕carney.

Figure 2.

(A) Schematic diagram of the model for the auditory periphery. The input to the model is an instantaneous pressure waveform of the stimulus (in pascals) and the output is a series of AN spike times. The model includes a middle-ear filter, a feed-forward control-path, a signal-path (C1) filter and a parallel-path (C2) filter, the IHC section followed by the synapse model, and the discharge generator. Abbreviations: outer hair cell (OHC), low-pass (LP) filter, static nonlinearity (NL), characteristic frequency (CF), and inverting nonlinearity (INV). C_OHC and C_IHC are scaling constants that specify OHC and IHC status, respectively. From Zilany and Bruce (2006, with permission). (B) IHC-AN synapse model: exponential adaptation (three-store diffusion model by Westerman and Smith 1987, 1988) followed by parallel power-law adaptation models (slow and fast). Fractional Gaussian noise added at the input of the slow power-law adaptation model results in the desired distribution of spontaneous rates.

Modifications of the model from previous version

The model described and evaluated in this paper mainly differs from its predecessors (Zilany and Bruce, 2006, 2007) in the IHC-AN synapse section, which will be described in detail in the following sections. Another modification from the previous version of the AN model is that the cut-off frequency of the IHC low-pass filter was reduced from 3.8 to 3.0 kHz. The introduction of power-law adaptation in the synapse model significantly increases synchrony to pure tones, and thus the cut-off frequency was adjusted to match the maximum synchronized responses of AN fibers to pure tones as a function of characteristic frequency (CF) (Johnson, 1980).

It should be noted that in previous versions of the model, responses of the synapse were simulated for only one repetition of the stimulus. Because the discharge generator has relatively long-term dynamics that can span from one stimulus repetition to the next, a series of identical synapse output waveforms was concatenated according to the number of stimulus repetitions and the silent intervals between stimuli. In contrast, the PLA synaptic model presented here has power-law adaptation with memory that, in general, exceeds the duration of a single stimulus repetition. Thus, for the results described here, the responses of the IHC model (not synapse) output were simulated for one repetition of the stimulus, and then a series of identical IHC responses was concatenated and used as the input to the synapse model.

PLA model of the IHC-AN synapse

Although many biological systems exhibit power-law rather than exponential dependence on time, in some cases, power-law adaptation alone underestimates the amount of adaptation at short-times (Drew and Abbott, 2006). For example, the response of an electrosensory neuron in electric fish to a long duration (100-s) amplitude-modulated step stimulus (Xu et al., 1996) was well described by power-law adaptation from 20 ms to 100 s, but not from 0 to 20 ms [Fig. 2b, Drew and Abbott, 2006]. This observation led Drew and Abbott (2006) to argue for the presence of an additional exponential adaptation component with a small time constant. It is well-known that adaptation to sustained tones in mammalian AN fibers involves at least three time scales: rapid adaptation on the scale of milliseconds, short-term adaptation on the scale of several tens of milliseconds, and slow adaptation on the scale of seconds (Kiang, 1965). In order to include all of these time scales, the new IHC-AN synapse model has power-law adaptation following short-term exponential adaptation components.

The variation in adaptation characteristics across different AN fibers suggests that individualized sets of model parameters might be required to predict individual AN fiber responses accurately. However, the goal of this study was to determine a single parameter set that was satisfactory for a wide range of response properties of AN fibers.

Exponential adaptation

This part of the synapse model is exactly the same as in previous versions of the model (Zhang et al., 2001; Zilany and Bruce, 2006, 2007), which included a time-varying implementation of Westerman and Smith’s (1988) three-store diffusion model. The parameters were determined according to the derived equations (Appendix A of Westerman and Smith, 1988) based on the desired response characteristics for the onset and steady-state responses of the post-stimulus time histograms (PSTHs) to tones (Appendix in Zhang et al., 2001).

The onset response of the model AN fiber is governed by exponential adaptation with two time constants (2 and 60 ms). The other parameters of the three-store diffusion model in the exponential adaptation stage were set to produce spontaneous activity and rate saturation at higher stimulus levels (Zhang et al., 2001).

Power-law adaptation

In the PLA model, the output of the exponential process drives two parallel power-law adaptation paths, namely, slow and fast power-law adapting components. The inclusion of two power-law functions in the model was motivated by the fact that one power-law adaptation component alone cannot account for an important AN response property, additivity (see below), while retaining the onset adaptation dynamics set by the exponential processes. The selection of parameters for these two power-law functions is more challenging and was complicated by the fact that power-law adaptation has no well-defined transient or sustained responses (Fig. 1). So, rather than trying to fit individual data sets, parameters of the power-law functions were chosen in such a way that the model qualitatively addressed a range of AN response properties for a wide variety of stimulus conditions. The parameters were then kept fixed and were not optimized to fit individual AN responses.

The parameters of the slow power-law component were such that it closely followed the output of the exponential adaptation model for onset responses (i.e., slow power-law adaptation further adapts the signal, but with a time course that is similar to that of its input). Because the power-law has longer memory than the exponential function, the offset and other long-term response properties were significantly improved in the output of the slow power-law component. Thus, model predictions for forward-masking paradigms and for amplitude-modulated signals were also improved substantially by inclusion of the slow power-law adaptation component.

However, the desired property of AN additivity cannot be modeled with a power-law function that has the same time course of adaptation as the exponential adaptation (see below). To capture the phenomenon of additivity, a second power-law function with faster adaptation was therefore introduced in the model; this function adapts quickly and is very responsive to increments in amplitude of an ongoing stimulus. Thus the change in discharge rate in response to an increment remains almost the same irrespective of the delay between stimulus onset and presentation of the increment. However, in response to decrements, both power-law components turn off instantaneously and recover very slowly. As the fast power-law component is very sensitive to increments of the stimulus, it results in a highly synchronized response to the envelope of amplitude-modulated signals and also to pure tones at low frequencies (this synchrony is limited by the IHC low-pass filter).

As stated earlier, the parameters of the power-law functions were adjusted to qualitatively address a wide range of response properties of the AN. To determine the parameters of the slow power-law function, two particular data sets were used that require adaptation with longer memory and thus were relevant to the power-law dynamics. The first one was the offset responses to a pure tone stimulus across several sound levels (Kiang, 1965), and the other one was the responses to a probe in a forward-masking stimulus paradigm (Harris and Dallos, 1979). Once the parameters for the slow power-law component were set, the parameters of the fast power-law function were then chosen by qualitatively matching the model responses with the physiological data for the increment∕decrement paradigm (Smith et al., 1985). The parameters of both slow and fast power-law functions are provided in Table 1. After all parameters were set, the model was tested for a wide variety of AN response properties; the results are reported in Sec. 3.

Implementation of the power-law function

The computation of power-law functions is very expensive.1 As the duration of the signal increases, the corresponding computational time increases significantly because computation of each sample of the adapted response requires memory from the onset of the signal (i.e., onset of the first repetition in case of more than one repetition of the signal, which corresponds to time zero). As mentioned earlier, the power-law function can be expressed as the convolution of power-law kernel with its prior responses. When possible, for computational efficiency, power-law kernels of fast and slow power-law functions were approximated by sixth- and tenth-order infinite impulse response (IIR) filters, respectively. To ensure stability, these digital filters were implemented as a cascade of second-order systems. The responses of the model for actual and approximate implementations were almost the same for short duration stimuli (Fig. 5). However, for very long stimuli (as in Fig. 6), the actual implementation of the power-law functions was required to replicate the physiological data.2

Figure 5.

Effects of spontaneous rate on recovery in experimental [upper panels (A)] and model [lower panels (B)–(D): previous model, new PLA model with approximate and actual implementations, respectively] histograms of two AN fibers in response to 500-ms duration constant-amplitude stimuli. The stimuli were presented once a second. Each histogram represents 2 min of data collection. Left panels: CF = 1.82 kHz, HSR (unit 43 in data); right panels: CF = 10.34 kHz, LSR (unit 41 in data). (A) From Kiang (1965, with permission). (B) Model histograms of AN fibers at 25 dB SPL using the previous model (Zilany and Bruce, 2007) that has only exponential adaptation in the synapse model. (C) PLA model histograms at 25 dB SPL with approximate power-law implementation. (D) PLA model histograms at 25 dB SPL with actual power-law implementation.

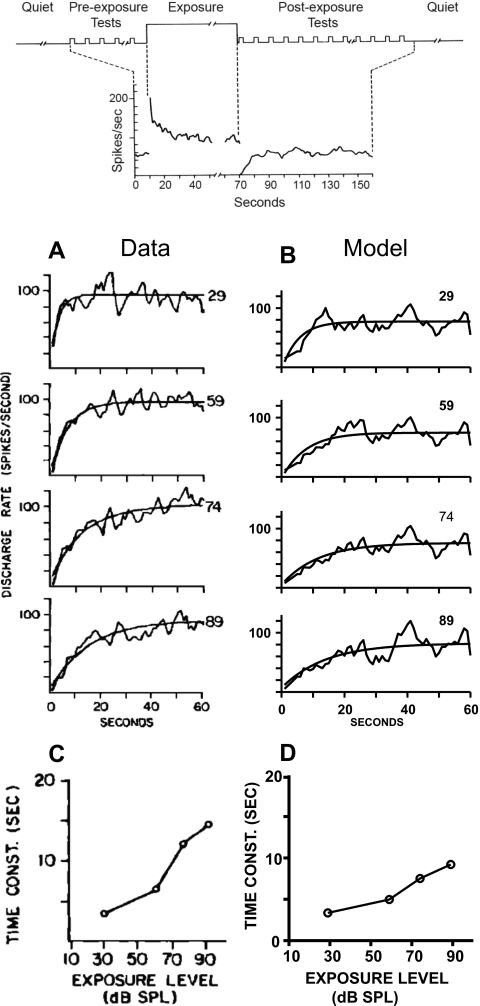
Figure 6.

Effect of exposure level on recovery for an AN fiber with CF = 2.15 kHz (HSR). The stimulus paradigm is illustrated at the top. Left panels [(A) and (C)] show the actual experimental responses, and the right panels [(B) and (D)] show the corresponding model responses. Duration of the exposure signal was 60 s, and the exposure levels were 29, 59, 74, and 89 dB SPLs (shown on the right∕above of each curve). The test signal (100-ms long applied once per second) was also at CF with level 19 dB SPL (fixed). However, the test signal level in the model responses was at 9 dB SPL to match with the level of the experimental fiber with respect to its threshold. Total durations of the pre- and post-exposure test signals were 10 and 60 s, respectively. Recoveries of the post-exposure responses (fitted to an exponential) are shown with their corresponding time constant values. [(A) and (C)] From Young and Sachs (1973, with permission). [(B) and (D)] Model responses of recovery employing the same experimental condition as in the data. Responses to ten repetitions of the same stimulus were averaged.

Implementation of SR

To model the distribution of SR, the fractional Gaussian noise (fGn) was added in the slow power-law adaptation path of the synapse model. The source of this noise within the auditory periphery is not known; it was introduced in the slow power-law path of the model for the following reasons. First, the parameters of the slow power-law path did not alter the dynamics of the noise significantly, whereas both exponential and fast power-law adaptation would have changed the noise dynamics substantially. That is, fGn maintains the spectral properties of 1∕f type noise with slightly altered magnitude after the slow power-law adaptation. Note that the fluctuation in the fGn also prevents the spontaneous rate from continuously adapting toward a value of zero (result not shown). Second, if the noise were added directly to the synapse output, the added noise would “fill in” the pause in the offset responses, and thus the dynamics of recovery would be obscured by the noise.

Three parameter sets were used in this study to generate fGn (with Hurst index H=0.9, which specifies the strength of the LRD) corresponding to three classes of SR (low, medium, and high). The rationale behind employing three true SRs rather than two (a possibility suggested by Jackson and Carney, 2005) will be examined in detail in Sec. 4. These parameters, provided in Table 1, were adjusted to simulate the distribution of AN SRs in cat (Liberman, 1978). Because the exponential adaptation model has a steady-state response that determines spontaneous rate, the added fGn has zero mean. It is worth noting that these parameters are different from those used in Jackson and Carney (2005) for two reasons. First, in Jackson and Carney (2005), refractory effects were not included in the Poisson process, whereas the discharge generator in the PLA model has refractory effects to simulate realistic responses of the AN. Second, the parameter values compensate for the slight alteration of the noise dynamics by the slow power-law adaptation.

RESULTS

In this section, the spontaneous activity as well as responses of the model to a wide variety of stimuli, including paradigms involving tones and noise, are compared to physiological data from the literature.

Spontaneous activity

The upper panel (A) in Fig. 3 is a histogram of SR estimates from 30-s recordings for 738 cat AN fibers (Liberman, 1978). The lower panel (B) is a histogram of model SR estimates, made using a paradigm that matched Liberman’s (1978). A total of 738 independent simulations was carried out, with the number of simulations for each SR class determined according to the proportions of different SR fibers reported in Liberman (1978) [high SR (∼61%), medium SR (∼23%), and low SR (∼16%)]. As described in Sec. 2, each SR type was simulated by choosing one of three possible parameter values for the fGn (Table 1). The model histogram matches the distribution of SRs reported for the physiological data.

Figure 3.

Histogram of actual (upper panel) and model (lower panel) SR estimates from 30-s recordings from 738 fibers in the auditory nerves of cats (binwidth of 1 spike∕s). (A) Actual AN SR histograms from Liberman (1978, with permission). (B) Model histogram of SR estimates using the same paradigm as in Liberman (1978) for 738 independent simulations. Three parameter sets for the fGn were used, applied to the proportions of different SR fibers reported in Liberman (1978). fGn parameters are provided in Table 1.

Responses to pure tones at CF

Recovery of spontaneous activity

At the offset of a tone pip, AN firing can be substantially reduced relative to spontaneous rate and is often characterized by a pause in the response followed by a slower recovery (on the order of several tens of milliseconds) to spontaneous activity (Harris and Dallos, 1979; Smith, 1977; Westerman, 1985). The amount of reduction in rate and the exact nature of recovery depend on the stimulus level (Yates et al., 1985) and also on the fiber’s spontaneous rate (Relkin and Doucet, 1991). Low spontaneous-rate (LSR) neurons take a longer time to recover from prior stimulation as compared to high spontaneous-rate (HSR) neurons (Relkin and Doucet, 1991).

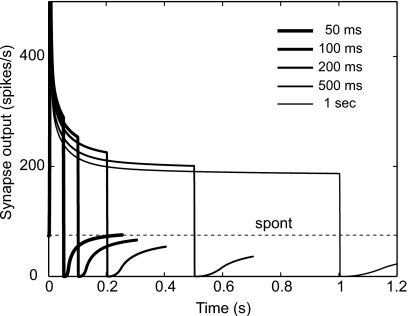
To demonstrate the scale-invariance property of the PLA model, the output of the synapse model is shown in Fig. 4 in response to a tone stimulus (tone at CF = 10 kHz, 12 dB above threshold) with different durations, but with a fixed inter-stimulus interval of 200 ms. The signal durations used were 50, 100, 200, 500, and 1000 ms. Responses to 50 repetitions of the stimulus were averaged. The dotted line indicates the (high) spontaneous rate of the fiber. To avoid fluctuations in the output and to emphasize the relevant response details for this simulation, fGn was not included in the model for this illustration. For short-duration signals (<∼200 ms), a 200-ms silent interval is adequate for full recovery to spontaneous rate, whereas longer signals require longer inter-stimulus intervals to completely recover to spontaneous rate. Since power-law adaptation has long memory for past responses, the dynamics of recovery after signal offset for the PLA model scales according to the duration of the signal. In contrast, the recovery to spontaneous rate in the exponential adaptation model (results not shown) would occur over a constant time period irrespective of the duration of the signal because the time constant of the exponential process is fixed. It should be noted that the relatively steady-state part of the PLA model response is noticeably reduced in response to longer duration signals because the responses do not fully recover to spontaneous rate during the inter-stimulus interval.

Figure 4.

Illustration of the “scale-invariance” property of the PLA model. Here the output of the synapse model is shown before the discharge generator. The fGn was not included in the model to avoid fluctuation in the output. The dotted line indicates the spontaneous rate of the fiber. The stimulus was a 10-kHz tone at CF, 12 dB above threshold. The duration of the signal varied from 100 ms to 1 s, but the inter-stimulus interval was fixed at 200 ms in all cases. Responses to 50 repetitions of the stimulus were averaged. The dynamics of recovery from the stimulus offset to spontaneous rate scales according to the duration of the signal.

Figure 5a shows PSTHs for a HSR AN fiber with CF = 1.82 kHz on the left and for a LSR AN fiber with CF = 10.34 kHz on the right (from Kiang, 1965). The stimulus was 120 repetitions of a 500-ms tone followed by a 500-ms silent period. Figure 5b shows corresponding responses of the previous AN model that had only exponential adaptation in the synapse model. In contrast to the physiological data, the responses of the previous model show no pause in the response after the stimulus offset and a very quick recovery to spontaneous activity. The two lower panels [Figs. 5c, 5d] show the PLA model responses for both the approximate and actual implementations of the power-law functions. In general, the PLA model responses closely resemble the physiological data. Also, as expected, the model response computed using the actual power-law implementation has a slightly slower recovery than the response computed with the approximation.

Long-term recovery

Young and Sachs (1973) measured the recovery of the discharge rate of single AN fibers to tone pips after exposure to 60-s long continuous tones. Both the exposure and test tones were at the fiber’s CF. The 100-ms test tones were presented once per second at 19 dB sound pressure level (SPL) either before or after the exposure. The total duration of pre- and post-exposure test signals were 10 and 60 s, respectively. Effects of exposure level on recovery were studied at four exposure SPLs (29, 59, 74, and 89 dB). The post-exposure test-tone response rates were fitted to an exponential to determine the time constant of recovery.

Figure 6 shows the recovery of post-exposure responses (to pre-exposure response rates) for a HSR AN fiber with CF = 2.15 kHz, using the stimulus paradigm described above. The left panels [(A)and (C)] show physiological responses from cat (Young and Sachs, 1973), and the right panels [(B) and (D)] show corresponding model responses. Recovery of the post-exposure response was fitted to an exponential, and the computed time constants are shown in the lower panels. The stimulus paradigm was the same for both actual and model fibers, except that the test signal used for the model was reduced to 9 dB SPL, to approximately match the level with respect to threshold to that of the cat AN fiber. Model responses to ten repetitions of the input stimulus were averaged, as was done for the experimental data.

Following exposure, the discharge rate to the test tone is transiently reduced, and the time constant of recovery increases as the exposure level increases, even though responses during the exposure saturate in response to higher-level exposure tones. Young and Sachs (1973) argued that there exists an additional suppression mechanism other than exposure evoked suppression to account for this phenomenon. The PLA model with two parallel power-law adaptation paths can qualitatively address this issue. Although the steady-state rate saturates at higher levels, model responses at onset have a much wider dynamic range (Smith, 1988). As the power-law function has a long memory (which extends back to the onset of the exposure stimulus), the reduction in the test signal responses continues to increase for higher-level exposure tones. In addition to the slow power-law component, the fast power-law component also plays a significant role in this case, as this component is very sensitive to level at the onset of the stimulus. For a good quantitative fit between model responses and actual data, the two parallel power-law adaptation paths could be driven by two separate inputs with a significant emphasis on the fast power-law component (results not shown). As the mechanism of these power-law functions is not known, and to keep the model structure simpler, both power-law functions of the PLA model are driven by the same input (i.e., the exponentially adapted IHC output). Note that since the recovery in the responses of the previous models (that have only exponential adaptation) does not scale with the duration of the stimulus, those models cannot account for these long time constants (on the order of several seconds) of recovery.

Effects of SR and inter-stimulus interval on adaptation at tone onset

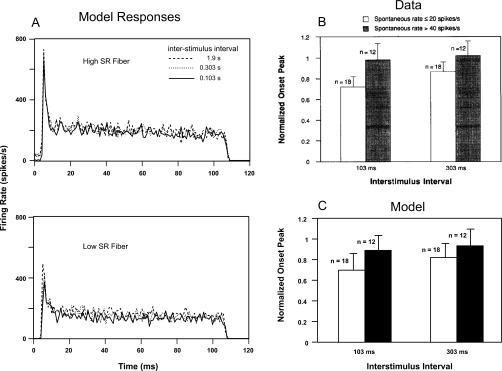
Rhode and Smith (1985) and Müller and Robertson (1991) investigated the effect of fiber types on adaptation after stimulus onset in cat and guinea-pig, respectively. They found that LSR fibers show no or very little adaptation, whereas HSR fibers show substantial adaptation. However, Relkin and Doucet (1991) pointed out that the inter-stimulus intervals used in these studies may have been too short to allow for full recovery from stimulation in previous repetitions, especially for LSR fibers. They reported that an inter-stimulus interval of 300 ms was long enough for a 100-ms duration signal (40 dB above threshold) to allow onset responses to fully recover in HSR fibers, but not in LSR fibers. The model was used to simulate their experiment using both HSR and LSR model fibers.

Left panels in Fig. 7a show the PST histograms of the PLA model for a HSR (upper) and a LSR (lower) fiber. The tone stimulus at CF (2 kHz) was 100 ms in duration with a level 40 dB above threshold and was presented 50 times with inter-stimulus intervals of 0.103, 0.303, and 1.9 s. For the LSR fiber, the peak at the stimulus onset was reduced to ∼74% with decreasing inter-stimulus interval from 1.9 to 0.103 s. In contrast, the peak onset of the HSR fiber was decreased to only ∼90% for the same condition. It should be noted that the spontaneous rate of the HSR fiber was significantly reduced for the 0.103-s inter-stimulus interval condition because the duration of the inter-stimulus interval was not sufficient to allow full recovery to spontaneous rate before the onset of each subsequent signal (see Fig. 4). For the results in the right panels, the onset spike rate was computed using the number of spikes in the most populated 1-ms bin of the response histogram after the onset of the stimulus. The onset peak for each AN fiber was normalized by the onset peak for that neuron when the inter-stimulus interval was 1.9 s. The right upper panel [Fig. 7b] shows the averaged responses from 12 HSR and 18 LSR AN fibers from chinchilla (Relkin and Doucet, 1991). Solid bars show the responses of HSR fibers, and open bars represent LSR fiber responses. Model responses shown in Fig. 7c were also averaged from AN fibers with CFs ranging from 1 to 20 kHz (logarithmically spaced) for both HSR and LSR fibers. Similar to the physiological data, the model HSR fibers were almost completely recovered when the inter-stimulus interval was 0.303 s, but the LSR fibers were ∼80% recovered by this time. This result is further supported by the observation of Young and Sachs (1973) that different SR classes have different time course of recovery at equal sound levels. However, their behavior was identical for SR classes when plotting the recovery of time constants vs driven rate instead of stimulus level. The PLA model responses are also consistent with the observation by Young and Sachs, 1973 (results not shown).

Figure 7.

Effect of inter-stimulus intervals on the responses of high and low SR fibers. (A) PST histograms of the PLA model in response to a 100-ms signal (tone at CF = 2 kHz), 40 dB above threshold for a HSR (upper panel) and a LSR (lower panel) fiber. The inter-stimulus intervals were 1.9, 0.303, and 0.103 s. With decreasing inter-stimulus interval, the peak of the onset was more reduced for the LSR fiber than for the corresponding HSR fiber. [(B) and (C)] Averaged value of normalized magnitude of the onset peak of PST histograms vs inter-stimulus intervals (0.103 and 0.303 s) for high (solid bar) and low (open bar) SR fibers is shown. The onset peak for each neuron was normalized by the onset peak of that neuron when the inter-stimulus interval was 1.9 s. The normalized values were averaged for all neurons within a group for different inter-stimulus intervals. (B) From Relkin and Doucet (1991, with permission). (C) Model responses from AN fibers with CFs ranging from 1 to 20 kHz for both high and low SRs.

Responses to tones with amplitude increments∕decrements

Conservation of energy

Westerman and Smith (1987) reported that the total transient response associated with an incremental stimulus paradigm shows a form of conservation. They computed the transient AN responses for two contiguous 300-ms tone bursts with the first tone (at CF) varying in level (5, 10, 15, and 20 dB above threshold) and the second tone (also at CF) fixed at a higher level (43 dB above threshold). Transient response components were obtained by fitting the histograms to a characteristic equation [having rapid, short-term, and sustained responses (Westerman and Smith, 1987)]. Then component integrals were calculated separately from the background (first tone) and increment portion of the response histogram. The integral of each component is the product of the component magnitude and the time constant and equals the number of spikes contributed by that component to the total transient response.

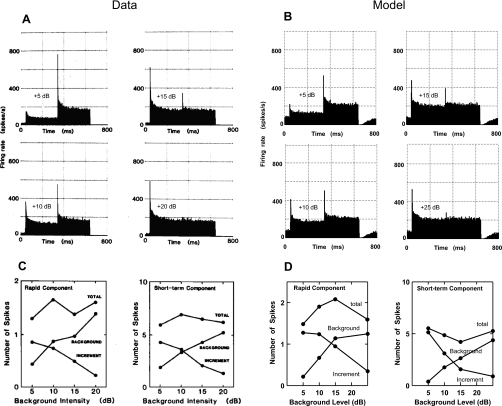
The upper panels [(A) and (B)] in Fig. 8 show the PST histograms of one AN fiber (CF = 5.99 kHz, HSR) in response to the above incremental stimulus paradigm. Panel (A) represents the physiological response from a gerbil AN fiber (Westerman and Smith, 1987), and panel (B) shows the corresponding model responses. As the level of the first (so-called “background”) tone increases, the amount of transient response associated with it also increases, whereas the transient activity in response to the second tone decreases.

Figure 8.

AN fiber histograms and conservation of adaptation in both rapid and short-term components for the amplitude increment response paradigm (binwidth of 2 ms). [(A) and (C)] Physiological responses from gerbil (Westerman and Smith, 1987). [(B) and (D)] PLA model responses. The stimulus was at CF (5.99 kHz, HSR) with duration of 600 ms. The initial levels of the tone were 5, 10, 15 and 20 dB above threshold (background). At 300 ms, the intensity was increased to 43 dB above threshold (increment) in all cases. (A) Actual AN fiber histograms from Mongolian gerbil: from Westerman and Smith (1987, with permission). (B) Model histograms using the same paradigm as above, except that the highest level of the background tone was 25 dB above threshold (because the model fiber shows a wider dynamic range than the corresponding AN fiber of the physiological data). (C) Mean values of rapid and short-term components from six fibers; from Westerman and Smith (1987, with permission). (D) Model transient responses (for one AN fiber) from the corresponding model histograms (one fiber) shown in (B) using the same method as employed in the data.

The rapid and short-term transient components were evaluated separately for both background and increment portions of the tone and are shown in the lower panels [(C) and (D)]. Panel (C) shows the average results for seven gerbil AN fibers (Westerman and Smith, 1987). Panel (D) represents the model’s rapid and short-term components determined from the model histograms shown in panel (B). The combined transient response associated with the two portions of the stimulus (background and post-increment) remains roughly constant (although slightly less for the rapid component) and thus exhibits conservation.

Increments∕decrements

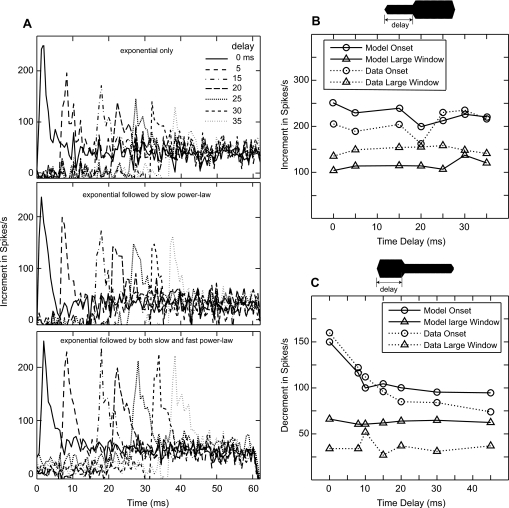
The effects of prior adaptation on responses in the increment∕decrement paradigm are illustrated in Fig. 9. Left panels (A) compare the increment responses of the model AN fiber with three different versions of the synapse model: one with only exponential adaptation (i.e., the previous model), one with exponential followed by slow power-law adaptation (middle panel), and one with exponential followed by both slow and fast power-law adaptations (lower panel). The stimulus was a 60-ms duration pedestal tone at CF (4.16 kHz), 13 dB above threshold, with a 6-dB increase in level occurring at various delays (up to 40 ms) after the onset of the pedestal. The increment responses were obtained by subtracting the response to the pedestal tone from the response to the tone with an increment in level. It is evident that the responses to the increment paradigm were not additive in the first two cases (especially for the short window at the onset of the increment), which justifies the inclusion of a fast power-law component in addition to a slow power-law adaptation component in the PLA model (as mentioned in Sec. 2C2). In Fig. 9b, the change in firing rate was analyzed over two windows: 0.64 ms (onset window, circles) and 10.2 ms (large window, upward triangles), both windows beginning at the time of the change in the response following the increment. Dotted lines show the physiological data from gerbil (Smith et al., 1985), and the solid lines represent the corresponding PLA model responses (of a HSR fiber) for the same stimulus paradigm. For both physiological data and model responses, the incremental change in discharge rate remains almost constant irrespective of the delay. As mentioned earlier, the fast power-law component in the PLA model adapts very quickly and is also very sensitive to increments of the stimulus. As a result, the change in discharge rate to an increment in stimulus level is almost the same, irrespective of the time delay at which the increment occurs. Thus, model responses exhibit additivity for both small and large analysis windows in response to increments in tone level.

Figure 9.

Effects of prior adaptation on increment and decrement responses. (A) Model increment responses as a function of time for three different conditions of the synapse model (with only exponential adaptation, exponential followed by slow power-law adaptation, and exponential followed by both slow and fast power-law adaptations). (B) Increment responses from both actual and PLA model responses. (C) Decrement responses. The stimulus was a 60-ms CF tone 13 dB above threshold, and subsequently levels were either increased or decreased by 6 dB at different delays from onset. The resulting increment∕decrement responses are obtained by subtracting the response to the constant-intensity tone (pedestal) from the response to the tone with an increment∕decrement in level. Changes in rate responses for both the onset window (first 0.64 ms, circles) and a larger window (first 10.2 ms, downward triangles) are shown. Dotted lines with symbols show the actual data (data points from Figs. 5 and 7 of Smith et al., 1985), and the solid lines with symbols represent the corresponding PLA model responses. (B) Increment responses. CF at 4.16 kHz (HSR). (C) Decrement responses. CF at 3.58 kHz (HSR).

Figure 9c shows the change in firing rates of an AN fiber (CF = 3.58 kHz, HSR) for decrements in level to an ongoing stimulus. The decrement stimulus paradigm is similar to the increment paradigm, except that the change in level is negative. Both small (0.64-ms) and large (10.2-ms) analysis windows were used (circles and upward triangles, respectively). Dotted lines show the physiological data from Smith et al. (1985), and solid lines indicate the corresponding PLA model responses. As in the physiological data, model responses after decrements are additive for the large window analysis, but onset window decrements are clearly not additive.

Forward masking

The responses of AN fibers to a probe stimulus are reduced immediately following stimulation by a masker. This reduction in response is presumed to be a function of adaptation and is likely to contribute to the psychophysical phenomenon of forward masking. Several physiological studies have been performed in different species to study the recovery of AN responses using forward-masking paradigms (e.g., Smith, 1977; Harris and Dallos, 1979; Westerman, 1985).

Figure 10 shows an example of the post-stimulus recovery function of a chinchilla AN fiber (CF = 2.75 kHz, HSR) in the left panels (Harris and Dallos, 1979), and the model responses with the same paradigm are shown in the right panels (B). The masking stimulus was 100 ms in duration, tone frequency was matched to CF (2.75 kHz), and tone level was 30 dB above threshold. The probe was 15 ms in duration, 20 dB above threshold, and its frequency was matched to CF. The probe responses are expressed as a percent of the control response (i.e., when there was no masker) and are shown as a function of probe delay, ranging from 1 to 150 ms. The histograms on the right show the responses that were used to compute the data points on the left. The PLA model responses agree with the physiological data; as the delay between masker offset and probe onset increases, the probe responses are less reduced as the AN fiber shows more recovery from adaptation. In contrast, the previous model shows significantly less reduction in rate than the physiological data, especially at short delays [shown by the dotted line, Fig. 10b]. In fact, the masked probe response of the previous model never fell below 50% of the control response, even at very small delays and high masker levels (result not shown).

Figure 10.

Actual [left panels (A)] and model [right panels (B)] post-stimulus recovery as a function of delay between masker offset and probe onset. Masker: 2.75-kHz tone (fiber’s CF, HSR), 30 dB above threshold (+30 dB), 100-ms duration. Probe stimulus: 2.75-kHz tone, +20 dB, 15-ms duration. Each data point represents the average number of spikes evoked by the probe as a percent of the control response (probe alone). The PST histograms on the right are the source for the data points on the left. (A) From Harris and Dallos (1979, with permission). (B) Model responses for the same paradigm as in the experiment. The solid line with filled circles represents the responses of the PLA model, and the dashed line with open circles indicates the responses of the previous model (Zilany and Bruce, 2007).

The influence of masker level on the post-stimulus recovery function is shown in Fig. 11. The same paradigm described above was used, except that the masker level varied from 10 to 60 dB above threshold. For both experimental and model paradigms, an inter-masker interval of 230 ms was used for the +10 and +20-dB maskers but was increased to 330 ms for higher masker levels to minimize the buildup of long-term effects. The upper panel (A) shows the median responses from 37 fibers with CFs ranging from 0.5 to 16 kHz from chinchilla (Harris and Dallos, 1979). Model responses shown in the lower panel (B) are averaged from ten fibers (six HSR and four LSR fibers) with CFs spaced logarithmically across the same range. Both the time course of recovery and the magnitude of forward masking increase with increasing masker level, and both tend to saturate at higher masker levels. Although PLA model responses qualitatively match with the chinchilla data, the recovery of model probe responses in the mid-delays (10–50 ms) is greater than the corresponding physiological responses; this difference could possibly be explained by differences between the spontaneous rates of the model and the data which are not specified in Harris and Dallos (1979). It should be noted that model LSR fibers show longer time courses of recovery and more reduction in probe response than the corresponding responses of HSR fibers.

Responses to amplitude-modulated tones

A systematic study of cat AN responses to sinusoidally amplitude-modulated (SAM) tones by Joris and Yin (1992) serves as an excellent template for a detailed evaluation of the PLA model in response to AM stimuli. The equation representing a SAM signal is given by

$$s\left(t\right)=[1+m\sin \left(2\pi f_{m}t\right)]\sin \left(2\pi f_{c}t\right),$$

where m is the modulation depth and f_m and f_c are modulation and carrier frequencies, respectively. Figure 12 illustrates the effect of increasing modulation depth (m) on PSTH shapes and the corresponding synchrony and modulation gain of an AN fiber with CF = 20.2 kHz (HSR fiber). The left panels [(A) and (C)] show the physiological responses from cat (Joris and Yin, 1992), and the right panels [(B) and (D)] show corresponding model responses with matched carrier frequency (at CF), modulation frequency (100 Hz), and other stimulus conditions. Modulation depths were varied from 0 to 0.99, and each response is accompanied by a half-wave rectified version of the respective input AM stimuli (i.e., a modulation gain of 0 dB) to the right (two cycles of the responses are shown). Model responses are simulated for a stimulus level 17 dB above the threshold of the model fiber. For both physiological data and model predictions, the modulation of the response increases with modulation depth and appears more modulated than the corresponding half-wave rectified input stimulus in almost all cases. Because the offset adaptation of the model response shows a pause with a very slow recovery to spontaneous activity, the model AN fiber is less responsive in the dip of the envelope, and thus shows enhanced phase-locking, with responses clustered near the peak of the envelope.

Figure 12.

Effect of increasing modulation depth (m) on synchrony for a HSR fiber with a CF of 20.2 kHz in response to amplitude-modulated tones with a carrier frequency matched to CF, modulation frequency (f_m)=100 Hz, and SPL = 49 dB (threshold = 32 dB SPL). Left panels [(A) and (C)] show the actual data and the right panels [(B) and (D)] represent the corresponding PLA model responses. Upper and lower panels show the period histograms, and their corresponding synchrony and gain, respectively, at different modulation depths. Modulation depths were varied from 0 to 0.99, and each histogram is flanked by a half-wave rectified version of the respective input AM stimulus to the right (two cycles of the responses are shown). [(A) and (C)] From Joris and Yin (1992, with permission). [(B) and (D)] Model period histograms and their corresponding synchrony and gain as a function of modulation depth using the same paradigm as employed in the experiment (the level of the stimulus is 17 dB above threshold). The dotted straight line represents 0-dB gain. Solid line with circles indicates the responses of the PLA model presented in this paper, and the dashed line with circles represents the responses of the previous model that had only exponential adaptation in the synapse model.

The lower panels [(C) and (D)] of Fig. 12 show the synchronization coefficient3 (R) and modulation gain [20 log(2R∕m), in decibels] derived from the corresponding histograms of the physiological data (A) and AN model responses (B) shown above. The dotted line shows the synchrony that would result if the response histogram perfectly followed the stimulus envelope. When the strength of synchrony for both model and physiological data is above the dotted line, the modulation gain is positive. Note that model responses show a higher synchronization coefficient than the corresponding data at higher modulation depths, which is due to the inclusion of fast power-law component in the model, as discussed further below. However, the previous AN model shows negative or near 0-dB gain (the model fiber in this case was substantially responsive in the dips of the AM stimulus and thus was not as well synchronized as the newer model responses).

Figure 13 illustrates the effects of modulation depth (m) and modulation frequency (f_m) on envelope synchrony as a function of AM stimulus level. The left panels [(A) and (C)] show physiological data from cat (Joris and Yin, 1992), and the corresponding model responses are shown in the right panels [(B) and (D)]. In this illustration of the effect of modulation depth [upper panels, (A) and (B)], the carrier frequency (set to the fiber’s CF) was 2 kHz for a HSR fiber. The general non-monotonic shape of the synchrony-level function remains unchanged as the modulation depth is varied, but the range of levels over which significant synchrony is observed increases with increasing depth. The effect of modulation frequency on the synchrony-level function [lower panels, (C) and (D)] was studied for a HSR fiber with CF = 20 kHz and m=0.99. As for the physiological data, model synchrony-level functions superimpose at low f_m, although unlike the data, the curves are slightly separated at levels higher than the best modulation level (BML) (the level at which the response is maximum). At high f_m in both data and model, the entire synchrony-level curve shifts downward. In the PLA model responses, the BML remains almost constant as f_m increases (Fig. 13, lower panels), similar to that observed in cat (Joris and Yin, 1992) [but note that an upward shift in BML with increasing f_m was observed in guinea pig AN responses by Yates (1987)].

Figure 13.

Effect of modulation depth (m) and frequency (f_m) on the actual [left panels: (A) and (C)] and PLA model [right panels: (B) and (D)] synchrony-level function. In the study of the effect of modulation depth (upper panels), CF is at 2 kHz (HSR fiber). For the effect of modulation frequency (lower panels) on synchrony-level function, CF is at 20 kHz (HSR fiber) with m=0.99. [(A) and (C)] From Joris and Yin (1992, with permission). [(B) and (D)] Model responses using the same paradigm as in the experiment.

Physiological and model AN modulation transfer functions (MTFs) of high-CF fibers (>10 kHz) are shown in Fig. 14. Model MTFs were determined for a population of fibers with CFs spaced logarithmically (ranging from 10 to 20 kHz) at a level 10 dB above threshold for high, medium, and low SR fibers. Responses of 24 AN fibers (according to the proportions of SRs in the AN population) were simulated. Both physiological and model MTFs are low-pass in shape with cutoffs between ∼600 and 1000 Hz. Each MTF is characterized by a shallow, slightly positive slope at f_m’s below BMF and by a sharp roll-off above BMF. Because the bandwidths of model AN fibers increase with CF, they are able to encode higher modulation frequencies; if this were the only factor limiting phase-locking to AM stimuli, the cut-off frequencies of the model MTFs would be expected to increase as a function of CF. However, as noted in Joris and Yin (1992), there exists an upper limit of f_m above which AN fibers cannot synchronize to the envelope because of low-pass filtering in the IHC, in addition to the progressive rejection of the sidebands by the sharp filtering in the cochlea, as discussed further below.

Figure 14.

MTFs of high CF (>10 kHz) fibers. Upper panel shows the actual MTFs from cat, and the lower panel represents PLA model responses. (A) From Joris and Yin (1992, with permission). (B) Model MTFs for a population of fibers with CFs spaced logarithmically (range of 10–20 kHz) at level 10 dB above threshold for high, medium, and low SR fibers. Responses for 24 AN fibers (according to the proportions of the distribution of SRs) are simulated. Solid lines show the responses of the PLA model presented in this paper, and the two dashed lines (CF at 10 and 20 kHz) indicate the responses of the previous model.

Figure 15 shows the relationship between AN fiber tuning-curve parameters (CF and bandwidth) and the MTF cut-off frequency. Left panels [(A) and (C)] show the physiological responses from cats (Joris and Yin, 1992), and the right panels [(B) and (D)] represent the corresponding model responses. Model responses were determined from a population of AN fibers (all operating at 10 dB above threshold) with CFs ranging from 250 Hz to 20 kHz (spaced logarithmically) for high (n=61), medium (n=23), and low (n=16) SR fibers. For better comparison to Joris and Yin (1992), medium SR fibers were included in the low SR group. Note that the abscissae in the lower panels differ because model responses had smaller bandwidths than the physiological data. This difference is explained by the fact that model responses were simulated using the 50th percentile of Q₁₀ (CF∕bandwidth) values (Zilany and Bruce, 2006) from Miller et al. (1997) which did not include the large range of bandwidths observed by Joris and Yin (1992). Because tuning bandwidth increases with CF, a positive correlation between the MTF cut-off frequency and CF is evident from both physiological data and model responses. However, MTF cut-off frequency saturates at higher CFs, which suggests that some mechanism in addition to peripheral bandpass filtering must exist to limit the response modulation. It is hypothesized here that the IHC low-pass filter is a candidate for this limitation, as discussed in detail in Sec. 4.

Figure 15.

MTF-3-dB cut-off frequencies vs CF and 10-dB bandwidth for high (plus) and low (down triangle) SR fibers. Left panels [(A) and (C)] show the actual responses from cat, and the right panels [(B) and (D)] represent the PLA model responses. (A) and (C) From Joris and Yin (1992, with permission). [(B) and (D)] Model responses for a population of fibers with CFs ranging from 250 Hz to 20 kHz (100 fibers spaced logarithmically) for high (61), medium (23), and low (16) SR fibers. Medium SR fibers are included in the low SR fibers, as treated in Joris and Yin (1992). Notice that the abscissae in the right panels (model responses) are different from those in the left panels (actual responses).

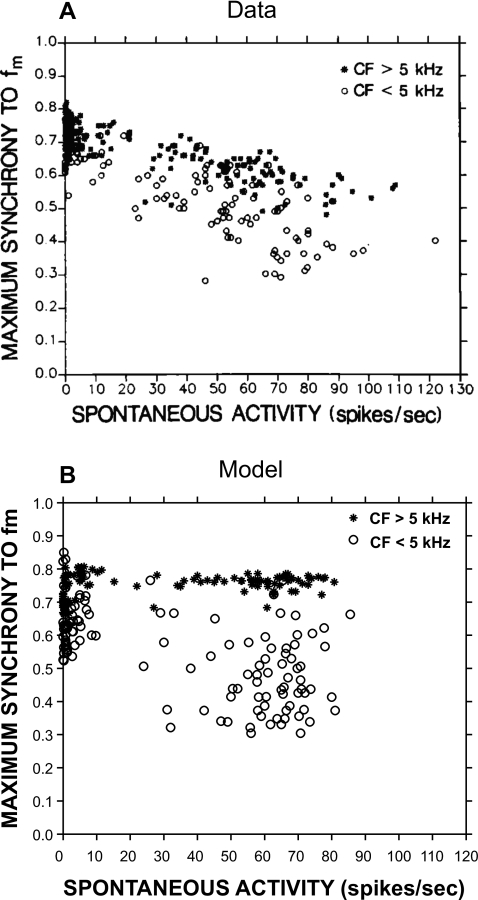
The effect of SR on maximum synchronization to f_m is shown in Fig. 16. The upper panel (A) shows physiological data from cats (Joris and Yin, 1992), and the lower panel (B) represents model responses. Model responses were determined from a population of AN fibers with CFs ranging from 250 Hz to 20 kHz, including high, medium, and low SR fibers. Stimuli were 10 dB above threshold for each model fiber, and the maximum synchrony was chosen from responses to a wide range of f_m’s (10 Hz–2 kHz). Both physiological data and model responses show that low-CF fibers tend to have lower maximum synchrony than high-CF fibers with similar SRs. However, model responses do not show an inverse relationship between maximum synchrony and SR for high-CF fibers, in contrast to the physiological data. This discrepancy could be due to the fact that the parallel fast power-law component provides significant synchronized responses to the envelope, irrespective of the model fiber’s SR.

Figure 16.

Effect of SR on maximum synchronization to f_m. Upper panel shows the actual data from cat, and the lower panel shows the PLA model responses. (A) From Joris and Yin (1992, with permission). (B) Model responses for a population of fibers with CFs ranging from 250 Hz to 20 kHz for high, medium, and low SR fibers. Each fiber operates at 10 dB above threshold, and the maximum synchrony is chosen from responses to a wide range of f_m (10 Hz–2 kHz).

Responses to noise stimuli

The shuffled autocorrelogram (SAC) and the cross-stimulus autocorrelogram (XAC) provide convenient and robust ways to quantify temporal information (discharge times) in response to wideband noise before and after polarity inversion (Joris, 2003; Louage et al., 2004). SACs reveal that AN fibers are more temporally consistent (i.e., tend to discharge at the same point in time on repeated presentations of the same stimulus) in response to stochastic noise stimuli than in response to periodic tones. The normalized SAC also reveals how spikes are constrained in their timing jointly by cochlear filtering and phase-locking to fine-structure and envelope. The maximum SAC value, referred to as the central peak, is always reached at a delay near 0 ms. Joris (2003) argued that the central peak of the SAC reflects synchronization to different waveform features for fibers with different CFs. Responses of low- and high-CF fibers reflect phase-locking to fine-structure and envelope, respectively. The central peak also shows large differences across different classes of SRs. The shapes of the SAC and XAC change with increasing CF: for CFs above the range of pure-tone phase-locking, the SAC and XAC become indistinguishable.

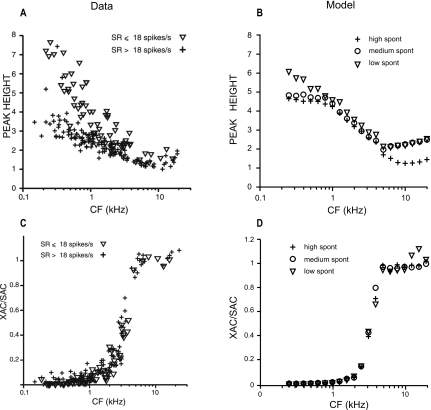
The upper panels in Fig. 17 show the central-peak height of normalized SAC to broadband noise (70-dB SPL) as a function of CF. Panel (A) shows the physiological responses from cats (Louage et al., 2004), and the right panel (B) represents corresponding PLA model responses. Each point represents the response from a single fiber. Model responses were determined for a population of fibers with CFs ranging from 250 Hz to 20 kHz (20 fibers logarithmically spaced) for high (plus), medium (circle), and low (downward triangle) SR fibers. In both physiological data and PLA model responses, the height of the central peak decreases with CF but asymptotes for CFs near the limit of pure-tone phase-locking (4–5 kHz), where it sometimes barely exceeds unity (a value of 1 in the normalized SAC corresponds to no temporal correlation). For fibers of similar CF, there is a considerable range of peak heights in the physiological data. Interestingly, the SR distribution within that range is bimodal: generally low∕medium-SR fibers have larger peak heights than high-SR fibers. This bimodality is not dependent on a particular choice of stimulus level and is also observed for responses obtained at a fixed suprathreshold level. Model responses are closest to the upper range of the peak heights in the physiological data, suggesting that discharge patterns in the model are more regular than in the data.

Figure 17.

Upper panels: central-peak height of normalized SAC to broadband noise (70-dB SPL) vs CF for a population of AN fibers. Lower panels: ratio of the value at delay 0 of XAC and SAC for a population of fibers. Left panels [(A) and (C)] show the actual responses from cat, and the right panels [(B) and (D)] represent the corresponding PLA model responses. Each point represents response from a single fiber. [(A) and (C)] From Louage et al. (2004, with permission). [(B) and (D)] Model responses for a population of fibers with CFs ranging from 250 Hz to 20 kHz (20 fibers logarithmically spaced) for high (plus), medium (circle), and low (downward triangle) SR fibers.

Figure 17c shows the ratio of XAC and SAC values at delay 0 for a population of AN fibers (Louage et al., 2004), and Fig. 17d shows the corresponding PLA model responses. Model responses were determined for a population of fibers with CFs ranging from 250 Hz to 20 kHz (20 fibers logarithmically spaced) for high (plus), medium (circle), and low (downward triangle) SR fibers. As in the physiological data, the ratio of XAC and SAC values in the model responses has a sigmoidal relationship as a function of CF which illustrates a transition from the fine-structure coding at low CFs to envelope coding at high CFs (Louage et al., 2004), and there is no apparent distinction across the SR groups.

DISCUSSION

Achievement with regard to previous models

The PLA model is successful in describing a range of response properties of AN fibers that were not adequately addressed by previous models. Models having only exponential adaptation produce responses that do not scale with the duration of the stimulus, which affects the recovery after stimulus offset as well as long-term response properties of these models. Power-law dynamics significantly improved the offset-recovery response, which in turn provided better responses to forward-masking and AM signals. The model also successfully replicated the histogram of AN SRs using only three true SRs with long-term fluctuations. Due to the addition of fGn to the input of the slow power-law adaptation path, the model responses are positively correlated over the long term and are negatively correlated over the short term (result not shown).

The IHC-AN synapse model presented in this study has two parallel paths with slow and fast power-law dynamics, following a stage with exponential adaptation. The model was thus capable of replicating additivity seen in AN responses to stimulus increment paradigm. Both the slow and fast power-law adaptation components contributed to higher synchronized responses to the envelope of AM signals and also to pure tones at low frequencies. It is worth mentioning that this model was also capable of producing strongly synchronized responses of high-CF fibers to low-frequency tones at high stimulus levels (Joris et al., 1994); for example, the synchronization coefficient of a model AN fiber with CF = 10 kHz to a 80 or 90 dB SPL, 800 Hz tone is ∼0.9, whereas the maximum synchronization coefficient of an 800-Hz model fiber to a tone at CF is ∼0.83 (Johnson, 1980).

One of the important achievements of the PLA model is that it can explain two seemingly contradictory aspects of forward-masking data reported by Harris and Dallos (1979) and Young and Sachs (1973). Harris and Dallos (1979) showed that the reduction in probe responses saturated at higher levels as the masker-evoked responses saturate at higher levels. However, Young and Sachs (1973) showed that the time course of recovery continues to increase with masker∕exposure level, even though the masker discharge rates saturate at higher levels. The duration of the forward masker (100 ms) in Harris and Dallos (1979) is much shorter than that of Young and Sachs (1973), which was 60 s. In response to a short duration masker and at small masker-probe delays, the fast power-law component of the PLA model remains almost shut off and contributes very little to the probe response at higher masker levels; it is the slow power-law adaptation component that contributes to the probe response at these higher levels. As the input to the slow power-law component (i.e., exponential output) saturates at higher levels, the reduction in probe response also nearly saturates in the output of the slow power-law adaptation. Therefore, the reduction in probe response at short masker-probe delays becomes nearly saturated at higher levels, as Harris and Dallos (1979) observed. This is also consistent with another observation by Smith (1977) that for shorter forward maskers, recovery depends on the discharge rate in response to the masker rather than on absolute masker intensity. However, when the duration of the masker and masker-probe delay is sufficiently long, both fast and slow power-law components contribute to the recovery and exhibit recovery time courses that increase with level, as explained in Sec. 3B2.

Source of power-law adaptation

Although power-law dynamics has been prevalent in descriptions of sensory adaptation, identification of their physical basis remains enigmatic. In some preparations, the site of power-law adaptation has been located in the conversion of the receptor potential into action potentials (French and Torkkeli, 2008). French (1984) observed no detectable adaptation in the receptor potential in cockroach tactile spine, whereas power-law adaptation exists in the action potential trains of the associated somatosensory neurons (Chapman and Smith, 1963). Even direct electrical stimulation of action potentials, which bypassed the mechanotransduction stage, produced the same power-law adaptation (French, 1984), suggesting that post-synaptic membrane dynamics could be responsible for the observed adaptation. In the visual system, studies of temporal contrast in mammalian (rabbit and guinea pig) retina by Smirnakis et al. (1997) showed that the timescale of adaptation varies as a function of the period between stimulus switches, indicating the presence of multiple timescales or power-law adaptation.

Recently, Zhang et al. (2007) observed spike-rate adaptation in AN fiber responses to stimulation by a cochlear implant using high-rate pulse trains (of 300-ms duration), which suggests that adaptation is not purely a synaptic phenomenon. They fitted the rate vs time functions (adaptation at the onset) with two-exponent models and reported time-constants (rapid 8 ms, and short-term 80 ms) which were slightly higher than those of similar acoustic studies. Although these time constants have little dependence on onset spike rate, they do show a strong relationship with input stimulus pulse rate. On the other hand, in simultaneous recordings from IHCs and AN fiber terminals, Goutman and Glowatzki (2007) observed that during a 1-s IHC depolarization, the synaptic response was depressed more than 90%, indicating that synaptic depression was the main source for adaptation in the AN. In their experimental data, the time course of transmitter release was fitted with three exponential transient components (with time constants of ∼2, ∼18, and ∼176 ms) in addition to a longer-term component that they described as being “robust” to adaptation. However, as the duration of their measurements was relatively short, it is not clear whether the adaptation in the release would scale with the duration of the stimulus (which would suggest the presence of power-law dynamics of adaptation).

In the above experiments, only responses at the onset were investigated. However, there exists a substantial body of experimental data describing adaptation to various acoustic stimulus features, such as responses to stimulus offset, forward masking, and increment∕decrement paradigms. Responses to similar stimulus paradigm are required in the above-mentioned experiments to elucidate the degree of contribution by synaptic and membrane mechanisms to the adaptation observed with acoustic excitation.

The strength of onset adaptation to acoustic stimuli seems more consistent across AN fibers, whereas the strength of suppression at offset seems to vary across fibers (even with similar SRs) (Kiang, 1965; Harris and Dallos, 1979). Similarly, Zhang et al. (2007) observed that some fibers were strong adapters and others showed weak adaptation in their electrical stimulation experiment, indicating that membrane dynamics might be responsible for the variable adaptation seen in the offset and long-term response properties of the AN. Also, in general, neural dynamics are more likely to give rise to power-law rather than exponential adaptation.

Factors influencing the MTF

MTFs at the level of the AN are characterized by low-pass filter shapes with sharp roll-offs and positive gains (ranging 0–5 dB) in the low-pass region. The offset adaptation properties of the IHC-AN synapse account for enhanced phase-locking to the stimulus envelope in AN fibers. As mentioned earlier, both the slow and fast power-law adaptation components of the model contributed to this synchronization and resulted in positive modulation gains in the model MTFs. However, the cut-off frequency (i.e., bandwidth) and the slope of the roll-off in model MTFs are slightly different than those of physiological MTFs (Fig. 14). At least two filtering actions by different mechanisms limit the frequency above which the AN fiber’s instantaneous discharge rate is no longer modulated at f_m: mechanical and temporal filtering (Greenwood and Joris, 1996). The local basilar partition motion driving the IHC is a mechanically bandpass-filtered version of the cochlear input. The Q₁₀ value, specified as a function of CF, sets the bandwidth of this filter in the model. Placing the carrier frequency at fiber CF, this filter progressively removes the sideband components of the AM stimulus in the local motion as f_m increases. The removal of sideband components effectively reduces the envelope amplitude variation and thus influences the MTF cut-off frequency. In model responses, higher Q10 values (i.e., lower bandwidths) at a particular CF produce MTFs with lower cut-off frequencies (results not shown). It is to be noted that the model Q₁₀ values are significantly higher at higher CFs than those in Joris and Yin (1992), and hence the cut-off frequencies of the model MTFs are lower.

The temporal filter resides in the stage between mechanical motion and AN spikes and acts as a low-pass filter that limits synchronization of AN responses to temporal variations in the IHC input. This added constraint on the bandpass-filtered signal further changes the magnitude of synchronization to envelope. A seventh-order low-pass filter with a cut-off frequency of 3.0 kHz was used in the model to represent this stage. However, both the order and the cut-off frequency of this low-pass filter influence the MTF shape (results not shown). A higher-order filter results in a MTF with a sharper roll-off, and a higher cut-off frequency of this temporal filter causes a higher cut-off frequency in the model MTF, unless it is already limited by the bandwidth of the basilar membrane (mechanical) filter (i.e., Q₁₀ value). Therefore, it is possible to accurately replicate individual physiological MTFs using appropriate model Q₁₀ values and the correct order and cut-off frequency of the IHC low-pass filter. This result illustrates that accurate modeling can identify or predict potential mechanisms of certain processes where direct physiological study is either very cumbersome or impossible.

Implementing SRs: Three rather than two true SRs

Jackson and Carney (2005) showed that a model with only two or three SRs with long-term fluctuations could describe the histogram of AN SRs in cat. In the case of two true SRs, instead of using an inhomogeneous Poisson process, they employed a Poisson-equivalent integrate-and-fire model in which negative values of the driving function (not rectified) have a negative effect on the output. In particular, the negative input values reduce the value of the running integral that accumulates toward threshold and thus delay the time of discharge occurrence. Although this property achieves the distribution of low SRs in the histogram, it produces AN responses that are inconsistent with physiological observations. For instance, in the PSTHs of low SR fibers in response to tones, the peak onset response strongly depends on the silent interval between stimulus offset and the next onset; shorter intervals reduce the onset responses because the fiber does not have enough time to recover, and on the other hand, sufficiently longer silent intervals produce sharp, large-magnitude peaks at the onset. However, in Jackson and Carney’s (2005) model with two true SRs, the negative input values for low SR fibers (which tend to have driving functions with more negative values) would result in the opposite pattern of response: longer silent intervals will accumulate more negative values, which will then result in greater reduction in the onset than for short intervals. In the three true SR model, negative inputs do not contribute to the running integral, and thus this unwanted result is not observed. This result suggests that the three true SR model better accounts for the observed AN responses as well as for the distribution of SRs. In the PLA model, the discharge generator (inhomogeneous Poisson process) section was implemented in such a way that the negative driving function has no effect on the output responses (i.e., equivalent to rectification of the driving signal). Three fGn parameter sets designed corresponding to three true SRs were able to describe the SR histogram of AN fibers, while maintaining other features of AN responses to a wide variety of stimuli.

Although fGn with appropriate parameters was added in the slow power-law adaptation path, the physiological correlate of this noise along the auditory-periphery is not clear. Kelly et al. (1996) reported that this noise is independent of CF and SR of the AN fiber. They argued that this fractal phenomenon originates either in the IHC or at the synaptic junction between IHC and AN fibers. Also, Teich and Lowen (1994) speculated on a number of possible origins of the observed fractal behavior, such as the slow decay of intracellular calcium in the hair-cell receptor or fractal ion-channel statistics.

Implications for complex sounds and psychophysics

In general, adaptation yields an efficient sensory code by removing redundant information inherent in the environmental cues. The natural acoustic environment is made up mostly of transients rather than constant stimuli. Adaptation helps to efficiently encode stimuli with statistics that vary in time (Delgutte, 1980). To encode efficiently, a neural system must change its coding strategy as the distribution of stimuli changes. Power-law dynamics, possessing no privileged timescales, is invariant with respect to changes in temporal scale, and such a system could therefore adjust its effective adaptation timescale to the environment. Recently, studies in the auditory midbrain (Dean et al., 2005) and cortex (Watkins and Barbour, 2008) show that neurons respond to recent stimulus history by adapting their response functions according to the statistics of the stimulus, alleviating the so-called “dynamic range problem.” However, the mechanism and origin of this adaptation along the auditory pathway remain unclear. An auditory-nerve model with appropriate long-term dynamics (power-law-like) in the IHC-AN synapse, such as that presented in this study, could successfully account for this adaptation, including the time course of adaptation. Further studies with this model will pursue this phenomenon.

Many psychophysical studies have mapped out the magnitude and time course of forward masking using a variety of stimulus paradigms (Hanna et al., 1982; Zwicker, 1984; Dau et al., 1996b). Several fundamental features of these data cannot be easily explained with the responses of single AN fibers (Relkin and Turner, 1988). Sub-cortical neural processing appears to have strong influence on perception in these tasks (Nelson et al., 2009), but specific mechanisms underlying the transformation of forward-masked stimuli have not been carefully tested with experiments or models. The phenomenological model described here provides a realistic front-end to test central models with an input that reasonably predicts several related sets of AN data.

Recently, Dau et al. (1996a) developed a model of signal processing in the auditory system to explain the psychophysical thresholds for various masking conditions (Dau et al., 1996b). They employed an adaptation stage in the peripheral system that has five feedback loops, connected in series, with five different time constants. In each loop, the output is the input signal divided by a low-pass-filtered version of the output, similar to a single-loop model proposed by Siebert and Gambardella (1968) to account for the effects of stimulus level and duration on adaptation in the discharge rates of AN fibers. Although these models can address rate adaptation to some extent, they do not have power-law dynamics because the time constants of the low-pass filters are fixed. The model by Dau et al. (1996a) explained the psychophysical data well, except for the forward-masked thresholds obtained with brief maskers, which were too high compared to the measured data. They pointed out that it was the adaptation stage in the model that was responsible for this behavior. As the time constants (ranging from 5 to 500 ms) of the low-pass filters in the adaptation-loop model are fixed irrespective of the masker duration, recovery in the masker offset does not scale appropriately with the duration of the masker. Thus, although the model explained the forward-masked thresholds for long maskers, it failed to address the thresholds for brief maskers. In this regard, the new AN model with power-law dynamics in the adaptation stage would be a better candidate to explain these monaural psychophysical data as well as other binaural masking data (Breebaart et al., 2001) that also employed the peripheral model of Dau et al.(1996a).

One of the most obvious features of a speech signal is amplitude modulation, and much of the information of speech appears to be carried in these changes rather than in the relatively stationary aspects of speech (Shannon et al., 1995). Recent psychophysical models of AM perception assume that a population of modulation-selective filters provides information about a signal’s temporal envelope to higher processing centers (e.g., Dau et al., 1997; Ewert et al., 2002). As the PLA model can reliably produce the MTFs of AN fibers, the output of this model can be used as front-end to models for higher auditory centers to test realistic neural-encoding hypotheses that may be used by the auditory system to encode envelope modulations.

Limitations

Despite its success in explaining a number of AN response features, there are a number of limitations in the PLA model that require further study. It was assumed that there is no adaptation in the voltage responses of the IHC, but recent studies suggest that there is indeed some adaptation at this level (Kros and Crawford, 1990; Zeddies and Siegel, 2004; Jia et al., 2007; Beurg et al., 2008). It would be important to explore the contribution of IHC adaptation to AN responses, especially at the onset and offset of tone bursts and in response to AM stimuli.

The PLA model does not capture the relationship between maximum synchrony to AM stimuli and SR, particularly for high-SR fibers. Physiological data show an inverse relationship between these metrics, whereas the model responses are nearly constant as a function of SR at a high value of synchrony. As mentioned in Sec. 3, the fast power-law adaptation component of the model yields highly synchronized responses to AM signals irrespective of SR, which explains the high maximum synchrony to modulation frequency. The ability of the model to relate SRs to different response properties is thus limited, and further exploration is needed in this regard.

The actual power-law adaptation is computationally very expensive. Although an approximation to the power-law was implemented by an IIR filter, the actual implementation was required to replicate the very long-term response properties (Fig. 6) with this model.

Although the PLA model captures a wide range of AN response properties, physiological correlates of the model architecture are not evident from existing studies. More experimental data are needed to build a more biophysically based model or to justify the proposed phenomenological model.

CONCLUSION

This paper presents a phenomenological model of the auditory periphery with a new IHC-AN synapse model that has adaptation at different time scales. Several important adaptation measures other than the onset response, such as recovery after offset (Harris and Dallos, 1979), responses to increments and decrements (Smith et al., 1985), and conservation (Westerman and Smith, 1987), were satisfactorily captured by this model. The PLA model is thus capable of accurately predicting several sets of AN data such as the amplitude-modulation transfer function and forward masking, which the exponential adaptation model clearly fails to address. The success of the power-law adaptation in describing a wide range of AN responses indicates a possible mechanism of adaptation, other than the classically described exponential adaptation, in the IHC-AN synapse and∕or in the AN membrane.