Significant speedup of database searches with HMMs by search space reduction with PSSM family models

Abstract

Motivation: Profile hidden Markov models (pHMMs) are currently the most popular modeling concept for protein families. They provide sensitive family descriptors, and sequence database searching with pHMMs has become a standard task in today's genome annotation pipelines. On the downside, searching with pHMMs is computationally expensive.

Results: We propose a new method for efficient protein family classification and for speeding up database searches with pHMMs as is necessary for large-scale analysis scenarios. We employ simpler models of protein families called position-specific scoring matrices family models (PSSM-FMs). For fast database search, we combine full-text indexing, efficient exact p-value computation of PSSM match scores and fast fragment chaining. The resulting method is well suited to prefilter the set of sequences to be searched for subsequent database searches with pHMMs. We achieved a classification performance only marginally inferior to hmmsearch, yet, results could be obtained in a fraction of runtime with a speedup of >64-fold. In experiments addressing the method's ability to prefilter the sequence space for subsequent database searches with pHMMs, our method reduces the number of sequences to be searched with hmmsearch to only 0.80% of all sequences. The filter is very fast and leads to a total speedup of factor 43 over the unfiltered search, while retaining >99.5% of the original results. In a lossless filter setup for hmmsearch on UniProtKB/Swiss-Prot, we observed a speedup of factor 92.

Availability: The presented algorithms are implemented in the program PoSSuMsearch2, available for download at http://bibiserv.techfak.uni-bielefeld.de/possumsearch2/.

Contact: beckstette@zbh.uni-hamburg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Profile hidden Markov models (pHMMs) are currently the most popular modeling concept for protein families. They provide very sensitive family descriptors, and sequence database searching with models from major pHMM collections (Finn et al., 2006; Haft et al., 2003) has become a standard task in sequence analysis. On the downside, database searching with pHMMs with well-known programs like hmmsearch or hmmpfam (Eddy, 1998) is computationally expensive. In particular, the long running times of pHMM-based methods and the time scaling behavior, which is linear in the length of the searched sequence, make them more and more demanding in today's sequence database search scenarios. This problem will become even more severe as the continuing exponential growth of sequence databases will certainly be amplified by the increasing dispersal of next-generation sequencing technologies (Shendure and Ji, 2008). Nevertheless, pHMM-based database searches are indispensable for today's genome annotation pipelines. For instance, the majority of member databases of the InterPro classification system (Hunter et al., 2009), a widely used system for protein annotation purposes, employ family information in form of pHMMs. The applied classification procedure InterProScan (Quevillon et al., 2005) includes searches with all pHMMs from the Pfam (Finn et al., 2006), TIGRFAM (Haft et al., 2003), Superfamily (Gough et al., 2001), PIRSF (Wu et al., 2004), Gene3D (Yeats et al., 2006), Smart (Letunic et al., 2006) and Panther (Mi et al., 2005) databases. These pHMM-based database searches render InterProScan a very compute intensive application whose employment on a large scale is challenging even on the largest cluster systems.

To solve this dilemma, much effort has been spent on improving the running time of pHMM-based database search tools. Some approaches for improvement use parallelism techniques and/or fast, extended, CPU-specific instructions sets, like SSE/SSE2 (Streaming Single Instruction/Multiple Data Extensions) (Walters et al., 2006). Hardware solutions implementing proprietary variants of hmmsearch on special field- programmable gate array (FPGA) boards are also available. Moreover, the application of machine learning techniques has been suggested (Lingner and Meinicke, 2008a, b). Very recently, Sun and Buhler (2009) described the design of patterns and profiles for speeding up hmmsearch using unordered sets of motifs in form of PROSITE-like patterns or position-specific scoring matrices (PSSMs) derived from a multiple alignment of a protein family. These motifs are then searched with standard regular expression matching and profile searching algorithms, respectively, to prefilter the search space for subsequent application of hmmsearch. The reported speedups over unfiltered search are in the range of 20-fold with almost 100% sensitivity and 30- to 40-fold with 90% sensitivity.

We propose a new software-based method well suited: (i) for efficient and reliable protein family classification, and (ii) to speedup database searches with hmmsearch. Our approach employs a simpler model of protein families based on PSSMs in combination with exact p-value computation using lazy evaluation and full text indexing with enhanced suffix arrays (Abouelhoda et al., 2004) to filter the search space for subsequent database searches with pHMMs corresponding to these families. The work is an extension of our PSSM search tool PoSSuMsearch (Beckstette et al., 2006), so we briefly describe previous work on index-based PSSM matching and efficient p-value computation for PSSM matchscores (Sections 2.2 and 2.3) before describing the new concepts and algorithms used in the new version of PoSSuMsearch (Sections 2.4–2.6), herein after referred to as PoSSuMsearch2.

2 METHODS

2.1 Preliminaries

Let S be a sequence of length n over finite alphabet 𝒜, and let S[i..j], 0≤i≤j≤n − 1, denote the substring of S of length j − i + 1 starting at position i and ending at (including) position j.

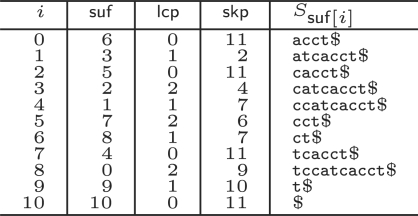
Let $ be a symbol in 𝒜, larger than all other symbols, which does not occur in S. The suffix array suf is a table of integers in the range 0–n that lists the starting positions of all n + 1 suffixes of S$ in lexicographical order (symbol $ must be appended to S to obtain a well-defined order on suffixes). That is, S_suf[0], S_suf[1],…, S_suf[n] is the sequence of suffixes of S$ in ascending lexicographic order, where S_i = S[i..n − 1]$ denotes the i-th non-empty suffix of the string S$, for i ∈[0, n]. lcp is a table in the range 0–n such that lcp[0]≔0 and lcp[i] is the length of the longest common prefix of S_suf[i−1] and S_suf[i], for i ∈[1, n]. skp is a table in the range 0–n such that skp[i]≔min({n+1}∪{j∈[i+1, n]∣lcp[i]>lcp[j]}). In terms of suffix trees, skp[i] denotes the lexicographically next leaf that does not occur in the subtree below the branching node corresponding to the longest common prefix of S_suf[i−1] and S_suf[i]. Tables lcp and skp can be computed as a by-product during the construction of suffix array suf, and enhance the basic suffix array. All three tables can be computed in linear time (Kärkkäinen and Sanders, 2003; Kasai et al., 2001). For a linear time construction algorithm for table skp, see Figure 1 in the Supplementary Material. We refer to the troika of tables suf, lcp and skp as enhanced suffix array. See Figure 1 for an example.

Fig. 1.

Enhanced suffix array for S = tccatcacct, consisting of the suffix array suf, and additional tables lcp and skp. The suffixes of S are sorted lexicographically (rightmost column).

A PSSM is an abstraction of a multiple alignment and is defined as a function M : {0,…, m − 1} × 𝒜→ℝ, where m is the length of M, also denoted with |M|, and 𝒜 is a finite alphabet. Usually function M is given by an m × |𝒜| matrix, where each row of the matrix reflects the frequency of occurrence of each amino acid or nucleotide at the corresponding position of the alignment. From now on, let M be a PSSM of length m and let w[i] denote the character of w at position i for 0≤i<m. The score range of a PSSM is the interval [sc_min(M), sc_max(M)] with sc_min(M) ≔ ∑_i=0^m−1 min{M(i, a)∣ a ∈ 𝒜} and sc_max(M) ≔ ∑_i=0^m−1 max{M(i, a) ∣ a ∈ 𝒜}. We define the match score for a segment w ∈ 𝒜^m of length m of the sequence w.r.t. M as sc(w,M)≔∑_i=0^m−1 M(i, w[i]). We also define pfxsc_d(w, M) ≔ ∑_h=0^d M(h, w[h]), max_d ≔ max{M(d, a) ∣ a ∈ 𝒜}, σ_d ≔ ∑_h=d+1^m−1 max_h and θ_d ≔ θ−σ_d for any d ∈[0, m−1]). pfxs_d(w, M) is the prefix score of depth d. σ_d is the maximal remainder score that can be achieved in the last m − d −1 positions of the PSSM and θ_d the intermediate threshold at position d. Given a score threshold θ, PSSM M is said to match string w with threshold θ if and only if sc(w, M)≥θ. Hence, the PSSM matching problem is to find all matching substrings of length m in some sequence S with their assigned match scores for a given threshold θ and PSSM M.

2.2 Fast database searching with single PSSMs

2.2.1 Algorithms for finding PSSM matches

A naive 𝒪(mn) time algorithm solving the PSSM matching problem moves a sliding window of size m over the text to be searched of length n and is implemented in many programs facilitating PSSMs (Henikoff et al., 2000; Kel et al., 2003; Quandt et al., 1995; Scordis et al., 1999). Considerable practical speedups can be obtained with the lookahead scoring technique of Wu et al. (2000). It uses the implication pfxsc_d(w, M) < θ_d⇒sc(w, M) < θ as an early stop criterion for the calculation of sc(w, M). However, lookahead scoring does not improve the theoretical worst case time complexity of the naive algorithm.

2.2.2 Index-based searching with PSSMs

For fast database searching with PSSMs, PoSSuMsearch2 employs the algorithm ESAsearch (Beckstette et al., 2006), which in turn makes use of enhanced suffix arrays. To use enhanced for fast database searching with PSSMs, one simulates a depth first traversal of the suffix tree (cf. Abouelhoda et al., 2004) by processing the arrays suf and lcp from left to right. To incorporate lookahead scoring, the search skips over certain ranges of suffixes in suf using the information from table skp. Algorithmic details are given in Beckstette et al. (2006).

The practical speedup of ESAsearch over methods that operate on the plain text is influenced by the choice of threshold θ. The larger the value of θ, the more likely it is to fall short of an intermediate threshold θ_d on average. This in turn means that the computation of the scores can be stopped earlier and more suffixes can be skipped by utilizing the information stored in tables lcp and skp. As shown in Beckstette et al. (2006), the expected runtime of ESAsearch is sublinear in the text length, whereas its worst case runtime is 𝒪(n + m) under the special condition that n≥|𝒜|^m + m − 1 holds, independent of the chosen threshold θ. The high speed of ESAsearch is the foundation for the speedup of database searches with pHMMs described in the sequel.

2.3 Efficient computation of score thresholds from p-values

To differentiate between match and mismatch, ESAsearch requires a score threshold parameter θ. However, PSSM scores are not equally distributed and thus scores of two different PSSMs are not comparable. This makes it difficult to choose a global score cutoff, meaningful for all PSSMs. Individual score cutoffs must be derived from p-values. This can be computed by dynamic programming (Rahmann, 2003; Staden, 1990; Wu et al., 2000), but is expensive as the complexity depends on the range of possible score values. For arbitrary floating point scores this problem is NP-hard (Touzet and Varré, 2007; Zhang et al., 2007). PoSSuMsearch2 uses the LazyDistrib algorithm (Beckstette et al., 2006) to speedup the computation of exact p-values for given PSSM scores. By lazily computing only the tail of the distribution function, LazyDistrib obtains a speedup of more than 300, compared with previous methods based on dynamic programming. For the special case of PSSMs employing floating point scores of several decimal digits, p-value computation could be further improved by more than a magnitude using the method of Touzet and Varré (2007), but this has not yet been integrated in the PoSSuMsearch software. Building on these techniques for fast searching of single PSSMs, we now proceed to their generalization to PSSM family models (PSSM-FMs).

2.4 PSSM-FMs

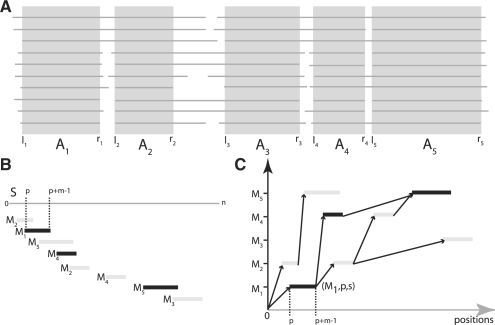
Let A=A₁, A₂,…, A_L be a sequence of non-overlapping alignment blocks. These alignment blocks are excised from a multiple alignment and the indexing from 1 to L reflects their order of occurrence in the alignment. See Figure 2A for an example. A PSSM-FM ℳ of length L is a sequence of L PSSMs ℳ=M₁, M₂, …, M_L where M_i denotes the PSSM derived from A_i, i∈[1, L]. The order ≪ of the PSSMs occurring in ℳ is imposed by the order of the corresponding alignment blocks. In practice, ℳ can be obtained from multiple alignments of related protein sequences (i.e. of a protein family). PSSMs can be computed from the blocks by several well-known methods (Gribskov et al., 1987; Henikoff and Henikoff, 1996; Tatusov et al., 1994). A match to ℳ is a non-overlapping sequence of matches for some or all of the PSSMs in ℳ in their specified order. We will now make this more precise.

Fig. 2.

(A) Non-overlapping alignment blocks, excised from ungapped regions of a multiple alignment. Since l_i≤r_i<l_j≤r_j for 1≤i≤j≤5, A=A₁, A₂, A₃, A₄, A₅ is an ordered sequence of non-overlapping alignment blocks suitable to construct a PSSM-FM ℳ=M₁, M₂, M₃, M₄, M₅. (B) Matches of M_i, i∈[1, 5], on sequence S, sorted in ascending order of their start position. (C) Graph-based representation of the matches of M_i, i ∈ [1, 5]. An optimal chain of collinear non-overlapping matches is determined, by computing an optimal path in the directed, acyclic graph. Observe that not all edges in the graph are shown in this example and that the optimal chain (indicated here by their black marked members) is not necessarily the longest possible chain.

Consider a PSSM-FM ℳ with total order ≪. Let MS be the set of all matches for all M∈ℳ in sequence S of length n. A match is represented by a triple (M, p, s) such that M matches at position p in S and s≔sc(S[p..p+m−1], M) is the corresponding match score.

We say that matches (M, p, s) and (M′, p′, s′) are collinear, written as (M, p, s) ≪ (M′, p′, s′) if M≪M′ and p+|M|≤p′. A chain 𝒞 for family model ℳ is a sequence of matches

all from MS, such that (M_i, p_i, s_i≪(M_i+1, p_i+1, s_i+1) for all i, 1≤i≤k−1.

To incorporate a measure of match quality into PSSM-FMs, we associate with (M, p, s) a p-value π(M, s) and a weight α(M, s) defined by

(1)

The chain score of a chain 𝒞 is defined by

(2)

The motivation for Equation (1) is as follows. π≔π(M, s) is the probability for the event that M matches a random string w of length m = |M| for score threshold s by chance, i.e. π = ℙ[sc (M, w)≥s]. Thus, (1 − π) is the probability for the complementary event that M does not match a random string of length m, and (1 − π)^n−m+1 is the probability that there is no match in n − m + 1 random strings. This corresponds to the number of different positions that M can actually match in a string of length n. Conversely, 1 − (1 − π)^n−m+1 is the probability for the event that there is at least one in n − m + 1 random strings that matches M with a score at least s. We take the logarithm to obtain additive weights and divide by ln(n) to account for sequence length.

The smaller the p-values of the matches in a chain (i.e. the more significant the matches of single PSSMs M are), the larger the fragment weights get, and hence the overall chain score. Consequently, chains that consist of a number of significant matches are assigned larger chain scores than those with fewer, or many less significant matches. Equation (2) implicitly assumes independence of random strings, which is certainly an invalid assumption in our case as the ‘random strings’ are overlapping substrings of some longer sequence. Yet, our experiments confirm our chain scoring to work well in practice; it is significantly better than a more straightforward strategy that simply computes the product of raw p-values, i.e. one that sets α(M, s)=−ln(π(M, s)) (see Fig. 2 in the Supplementary Material).

2.5 A specialized and improved PSSM chaining method

Thus far our description was based on a single sequence. However, the results described below are based on a large set of sequences S₁,…, S_k. To handle these, we concatenate the single sequences with separator symbols, and construct the enhanced suffix array for the concatenation. For a given PSSM-FM ℳ, all M_i, 1≤i≤L, are matched one after the other against the enhanced suffix array. This gives match sets MS(M_i) for PSSM M_i.

The PSSM chaining problem for a single sequence S_j can be considered a chaining problem for pairwise matches between sequence S_j and a virtual sequence V[1..L] such that a match for PSSM M_i is a match of length one at position i in V. The pairwise chaining problem can be solved in O(blogb) time using an algorithm described in Abouelhoda and Ohlebusch (2005), where b=|MS(S_j)| and MS(S_j) is the set of PSSM matches in S_j. This algorithm is called the general chaining algorithm. For the special case of the PSSM chaining problem, we have specialized and improved the general chaining algorithm to obtain a method with the following advantages:

• While the general chaining algorithm requires a dictionary data structure with insert, delete, predecessor and successor operations running in logarithmic time (e.g. an AVL-tree or a red-black tree), our approach only needs a linear list, which is much easier to implement and requires less space.

• While the general chaining algorithm requires an initial sorting step using O(b*logb*) time, our method only needs O(b*+∑_j=1^k∑_i=1^L b_j,ilogb_j,i) time for this step. Here, b* is the total size of all sets MS(M_i) and b_j,i=|MS(S_j, M_i)|, where MS(S_j, M_i) is the set of all PSSM matches of PSSM M_i in sequence S_j.

• While the general chaining algorithm solves the chaining problem for MS(S_j) in O(blogb) time, our method runs in O(b·L) time. If L is considered to be a constant, the running time becomes linear in b.

The details of the improved chaining method are described in the Supplementary Material.

2.6 Using PSSM-FMs for sequence classification

To employ PSSM-FMs for protein family classification, we combine the three algorithms sketched in Sections 2.2–2.5. Namely (i) ESAsearch for fast searching with single PSSMs; (ii) LazyDistrib for exact and efficient p-value computation; and (iii) chaining of single PSSM matches in the form of the chaining method sketched in Section 2.5. All three algorithms are implemented in PoSSuMsearch2 and, in combination provide, an efficient solution to the problem of protein family classification. In the first phase, PoSSuMsearch2 computes single PSSM matches for the PSSMs of a family model using algorithm ESAsearch. In the second phase, PSSM matches obtained in phase one and their ordering information are used to compute optimal chains of PSSM matches according to the order given in the family model.

When classifying an unknown protein sequence into a known family, a sequence is searched with several PSSM-FMs, representing different protein families. The classification into a certain family should be based on the quality of the best match of a sequence to the corresponding family model. Hence, the objective is to determine the best chain 𝒞^*_ℳ,S of PSSM matches in a sequence S for a given family model ℳ and their chain score

(3)

(4)

We call such a chain an optimal chain. With the definition of optimal chains and their chain scores, we introduce a quantifiable, rankable criterion of match quality to our PSSM-FM concept, making it applicable for sequence classification. More precisely, let S be a sequence and ℱ = {ℳ₁, ℳ₂,…, ℳ_T} be a collection of T PSSM-FMs, representing T distinct protein families. Further, let csc^*_ℱ,S≔max{csc^*_ℳi,S∣ℳ_i∈ℱ} be the maximal score of all optimal chains in S over all family models in ℱ. We classify S into the family represented by ℳ∈ℱ if and only if csc^*_ℱ,S=csc^*_ℳ,S. That is, we classify the sequence under consideration into the family whose family model generates the highest scoring optimal chain. In practice, it is often useful to employ a threshold constraint, like a minimal necessary chain length, as a lower boundary for classification. That is, sequences not satisfying this constraint are not classified.

PoSSuMsearch2 can be used in two modes of operation:

• Mode modsearch allows sequence classification based on a, typically small, library of PSSM-FMs. For each sequence the best matching chains for (up to) k different family models are reported.

• Mode seqclass allows sequence classification based on a, typically large, library of PSSM-FMs. For each model, the best matching chains in (up to) k different sequences are reported.

Hence, mode modsearch mimics the modus operandi of program hmmsearch, whereas mode seqclass is comparable with program hmmpfam.

3 RESULTS

3.1 PSSM-FMs for protein classification

Detection of protein families in large databases is one of the principal research objectives in structural and functional genomics. To evaluate the suitability of PoSSuMsearch2 employing PSSM-FMs for fast and accurate protein family classification, we rigorously tested and validated our method using the evaluation system Phase4 (Rehmsmeier, 2002). We evaluated the sensitivity and specificity, addressing different database search scenarios at different levels of difficulty. That is, we measured our method's ability to detect (A) very close, (B) close and (C) distant sequence relationships and compared the obtained results with those gained by the HMM-based hmmsearch from the HMMER package, which marks the state-of-the-art in this field. For the evaluation, separated training and test sets (i.e. the sets that define the true positives) were created from the SCOP database (Andreeva et al., 2008). SCOP contains protein sequences classified into families, superfamilies, folds and classes, depending on their structural relationships. To minimize the influence of redundancies on the results of our experiments, we used the non-redundant PDB90 subset of SCOP (Rel. 1.75), which contains sequences with pairwise homology of at most 90%. This subset consists of a total of 15 440 amino acid sequences classified into 3890 families and 1955 superfamilies.

3.1.1 Model construction and scoring

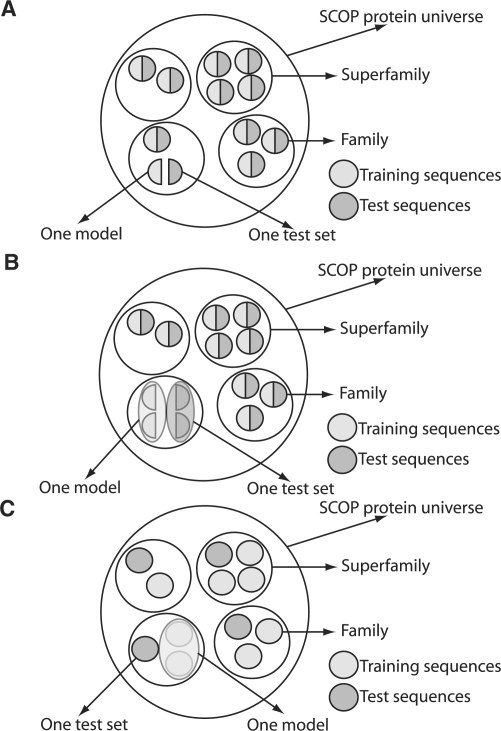
The three scenarios used for our evaluations differ in how training and test sets are constructed from SCOP data. Table 1 and Figure 3 give more details on the three scenarios. The task of the searching program in each case is to find, preferably, only protein sequences from the test sets in the whole SCOP database, while only providing the corresponding training sets to the searching program. That is, a perfect searching method would always find exactly the set of true positives, which is the test set.

Table 1.

Evaluation scenarios and number of models used in the experiments to assess method sensitivity and specificity

Scenario (#models)	Description
(A) Very close relationship (561)	For each superfamily: for each family, half of its sequences are chosen as test sequences, and the remaining ones are chosen as training sequences. The sequences of the surrounding superfamily are ignored in the evaluation.
(B) Close relationship (474)	For each superfamily, half of the sequences of each of its families are chosen as training sequences and the remaining ones are chosen as test sequences.
(C) Distant relationship (1221)	From a superfamily, each family in turn is chosen to provide the test sequences. The remaining families within that superfamily provide the training sequences.

Fig. 3.

Construction of training and test sets for (A) very close, (B) close and (C) distant relationships.

Since some superfamilies in SCOP contain only one family and some families are very small, we employed the following criteria to select superfamilies and families for evaluation. Only superfamilies comprised of at least two families were selected. From these superfamilies, families were chosen to be test families, if both, the family itself and the remainder of the superfamily contained at least five sequences. The resulting numbers of families employed in each evaluation scenario are given in Table 1. From each training set we constructed a PSSM-FM for use with PoSSuMsearch2 and a pHMM for hmmsearch, respectively. With these models, we subsequently searched the sequences in the corresponding test set. Both model types are derived from a multiple alignment, which we compute from each training set using CLUSTAL W (Higgins et al., 1994) with default parameters. To construct PSSM-FMs, we excised from the multiple alignments all blocks of width 6–12, favoring wider blocks and allowing at most 20% gaps per column inside a block. For this task, we used the BLOCKMAKER program from the BLIMPS distribution (Henikoff et al., 1995). We retained the block order and computed from the blocks log-odd score-based PSSMs with the method of Henikoff and Henikoff (1996). For this, we estimated residue probabilities of observing a certain residue in a column of the alignment block from relative frequencies. From the same multiple alignments, calibrated pHMMs for disposition with hmmsearch were computed using hmmbuild and hmmcalibrate (HMMER package version 2.3.1, using the programs' default parameters). Thus, the so computed PSSM-FMs and pHMMs are descriptors for their respective training sets and serve as input for a database search with PoSSuMsearch2 and hmmsearch, respectively. In these searches, thresholds were set in a very relaxed way (for hmmsearch E-value cutoff 10 and for PoSSuMsearch2 single PSSM p-value cutoff of 0.1) so that all sequences irrespective of their score are reported. Matches to a model were ranked by their method-specific scores in descending order, i.e. in case of PoSSuMsearch2 the best chain score csc^*_ℳ,S, and in case of hmmsearch the sequence classification score.

3.1.2 Assessment of sensitivity and specificity

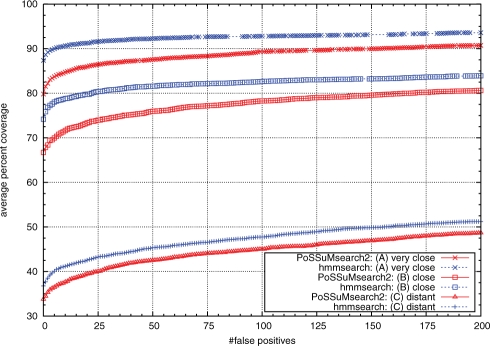
To assess the sensitivity and specificity of our PSSM-FM approach and to compare the classification accuracy with hmmsearch in the three different evaluation scenarios, we determined the percentage of true positives in all test sets (also called the coverage) that is achieved by the method when accepting different counts of false positives. We plotted the (accepted) false positive counts versus the average percent coverage. See Figure 4.

Fig. 4.

Classification performance of PoSSuMsearch2 using PSSM-FMs versus hmmsearch using pHMMs in the three evaluation scenarios. Shown are percentage true positives values averaged over all test families, called the average percent coverage value or just coverage for short (y-axis), for different numbers of accepted false positives (x-axis).

3.1.3 Comparison of runtime and scalability

All benchmark experiments described in this article were performed on a single Intel Xeon CPU running at 2.3 GHz. For runtime experiments, we took the first 100 protein families from the Pfam Rel. 23.0 database (Finn et al., 2008), and computed PSSM-FMs from the Pfam seed alignments by excising alignment blocks as described above, but of width 5–8. This resulted in 100 models, consisting of 2096 individual PSSMs. From the same alignments, we generated 100 calibrated pHMMs using hmmbuild/hmmcalibrate. We searched with these family descriptors in the UniProtKB/Swiss-Prot Rel. 57.5 database (Wu et al., 2006), containing 470 369 protein sequences in 167 MB. It took PoSSuMsearch2 ∼28.1 min to find all matches to the PSSM-FMs, using a p-value threshold of 10⁻⁴ for each PSSM. For hmmsearch, we chose an E-value of 10⁻⁵ in order to find roughly the same set of matches. It took hmmsearch ∼30 h to find matches to the pHMMs. This makes for a speedup factor of more than 64.8 for PoSSuMsearch2 over hmmsearch. Along with these results, PoSSuMsearch2 clearly showed sublinear time scaling when applied to subsets of UniProtKB/Swiss-Prot of different sizes, whereas hmmsearch showed linear scaling behavior due to the underlying Viterbi algorithm. For the results of this experiment, see Figure 3 in the Supplementary Material.

3.2 Acceleration of pHMM-based database searches

Here, we evaluate the performance of PoSSuMsearch2 when it is used as a filter to reduce the search space for hmmsearch. The combination of PoSSuMsearch2 and hmmsearch is called PSfamSearch. The intention is to speedup the database search while keeping the sensitivity of hmmsearch.

As a prerequisite for reliable filtering, we have to calibrate p-value cutoffs for the PSSM-FMs such that they match the corresponding pHMMs trusted cutoff (tc) and noise cutoff (nc). That is, our calibrated PSSM-FMs operate on the same level of sensitivity as hmmsearch employing the pHMM, but with possibly reduced specificity. Hence, the determination of a proper family-specific p-value cutoff is crucial for the sensitivity as well as overall speedup of PSfamSearch. A too stringent cutoff may reduce the search space too much and thus may have a negative effect on the sensitivity. On the other hand, a too relaxed cutoff may not sufficiently reduce the search space and lead to long running times. In the following, we evaluate two different strategies for cutoff calibration: cutoff calibration for lossless filtering and cutoff calibration based on training- and test-set separation.

3.2.1 Cutoff calibration for lossless filtering

We start by searching with a pHMM representing a protein family in a large protein database like UniProtKB/Swiss-Prot using hmmsearch with the model's trusted and noise cutoffs, respectively, and tabulate all matching sequences. From the seed alignment of the employed pHMM, we construct a PSSM-FM with a block width of 6–12 and use this family model to iteratively search UniProtKB/Swiss-Prot using PoSSuMsearch2. In each iteration, we relax the p-value cutoff until we find all the sequences also detected by hmmsearch using the model's trusted and noise cutoffs respectively. With this procedure, we determine p-value cutoffs denoted by π_tc and π_nc corresponding to the pHMM's trusted and noise cutoffs in terms of sensitivity. Observe that the set of matching sequences detected by PoSSuMsearch2 using cutoff π_tc or π_nc may be a super set of the set of sequences detected by hmmsearch employing the pHMM's trusted and noise cutoffs. However, since we are interested in using PSSM-FMs searched with PoSSuMsearch2 as a prefilter for search space reduction for hmmsearch, sensitivity is more important than specificity. Once π_tc and π_nc are computed on a large protein database, they are, together with the PSSM-FM, stored on file. That is, for further searches with hmmsearch using the model's trusted or noise cutoffs, we can use PoSSuMsearch2 using cutoff π_tc or π_nc as a filter and apply the compute intensive hmmsearch only on sequences that contain chains matching to the PSSM-FM. Sequences that contain no such chains are filtered out. Since sequences containing sufficiently long chains constitute only a small fraction of all sequences to be searched and since PoSSuMsearch2 is much faster than hmmsearch, we expect a reduced overall runtime. We tested this hypothesis with the following experiment.

We applied PSfamSearch to the first 200 out of 3603 pHMMs of the TIGRFAM database (Rel. 8.0) on the complete UniProtKB/Swiss-Prot database (Rel. 57.5, 471 472 sequences of total length ∼167 MB). We determined PoSSuMsearch2 p-value cutoffs corresponding to hmmsearch trusted as well as noise cutoffs with the iterative procedure described above. We measured the search space reduction (see Supplementary Fig. 4 for results for the first 20 TIGRFAM families) and the total runtimes of PSfamSearch and compared them with hmmsearch operating on the unfiltered dataset. PSSM-FM-based filtering reduces the search space and hence the overall runtime considerably. For example, for family TIGR00011 only five sequences remain after the filtering step and are handed over to hmmsearch. Filtering with p-value cutoffs corresponding to the less-stringent noise cutoffs reduced, in the worst case (TIGR00001), the search space by ∼80%. For all 200 tested families, the overall runtime is reduced from 4233 (4234) to only 46 (117) min when using trusted (noise) cutoffs. This is a speedup of factor 92 (36).

We emphasize that in this experimental setup, PSfamSearch and direct hmmsearch obtain exactly the same results on the full sequence set. Hence, PoSSuMsearch2 works as a perfect, lossless filter. This is not too surprising, since thresholds were trained/adjusted on the same set of sequences as were searched afterwards employing these thresholds. This raises the question, how well the calibrated p-value cutoffs generalize to sequences not included in the training set used for threshold determination. To test this, we performed additional experiments where p-value cutoffs are calibrated based on training- and test-set separation.

3.2.2 Cutoff calibration based on training- and test-set separation

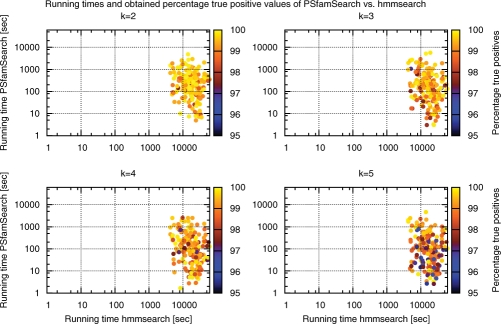
For the first 200 families listed in TIGRFAM, we built PSSM-FMs from the families' seed alignments with the procedure described in Section 3.1. We calibrated the p-value cutoffs and minimal chain lengths to match all sequences of training sets of different sizes. Training sets contain every k-th sequence returned by direct hmmsearch on UniProtKB/TrEMBL Rel. 40.3 (7 916 844 protein sequences with a total length of 2.58 GB) for k∈{2, 3, 4, 5} using the pHMMs' trusted and noise cutoffs (for k = 2 only), respectively. That is, we evaluated the classification performance of PSfamSearch using training sets that consist of 20%, 25%, 33% and 50% of the sequences matched by the pHMM. We employed these models and cutoffs in a database search with PSfamSearch on complete UniProtKB/TrEMBL and measured the overall running time and true positives coverage per family and compared the running time with the time needed by direct hmmsearch using trusted cutoffs. See Figure 5 and Supplementary Table 1 for the results of this experiment.

Fig. 5.

Comparison of running times (x- and y-axis) and achieved percentage true positive values (color coded) between PSfamSearch and hmmsearch, when searching with PSSM-FMs (pHMMs) representing the first 200 TIGRFAM families on UniProtKB/TrEMBL Rel. 40.3. Different values of k represent different training set sizes. For further details see text.

PSfamSearch returned >99.54% of the original results determined by hmmsearch, including their E-values and scores, when using half of the sequences matched by hmmsearch as training sets. Of 150 851, 523 matches (0.34%) were missed. With p-value cutoffs calibrated to match the sensitivity level of hmmsearch using noise cutoffs, PSfamSearch detected 99.4%, while missing 649 out of 180 263 sequences. See Figure 6 and Supplementary Tables 2 and 3 for more detailed results for the first 20 TIGRFAM families.

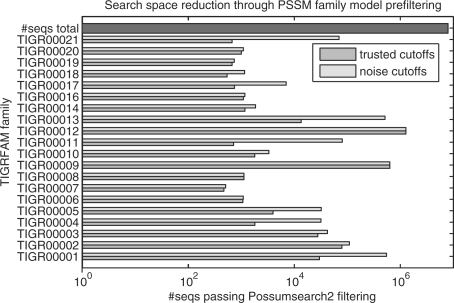
Fig. 6.

Reduction of UniProtKB/TrEMBL achieved by PSSM-FM filtering for the first 20 TIGRFAMs families. Dark (light) bars indicate the effective number of sequences to be searched with hmmsearch (x-axis) when using P-value cutoffs π_tc (π_nc). The bar on the top shows the total number of sequences in UniProtKB/TrEMBL Rel. 40.3 (7 916 844 protein sequences with a total length of ∼2.58 GB) needed to be searched by direct hmmsearch without filtering. Note that the x-axis has a logarithmic scale.

It took PSfamSearch ∼24.8 h to search with the first 200 TIGRFAM families, compared with >45 days for direct hmmsearch using the models' trusted cutoffs. That is, PSfamSearch achieves a speedup of factor 43.8 over direct hmmsearch, while retaining >99.5% of the original results. In this experiment, the set of sequences to be searched with hmmsearch was reduced to only 0.80% of all sequences. Using the less-stringent noise cutoffs, PSfamSearch reduces the search space to only 3.83% of the original search space size also with a sensitivity of 99.5% (see Supplementary Table 3 for more detailed results for the first 20 TIGRFAM families) and a speedup of factor ∼14 over direct hmmsearch.

3.2.3 Whole proteome annotation using PSfamSearch

In an additional experiment we searched with pHMMs and PSSM-FMs representing the first 500 protein families in the TIGRFAM database in 26 publicly available Escherichia coli proteomes (see Supplementary Table 4 for further details). These consist of 120 394 protein sequences with a total length of 37.3 MB. Cutoffs π_tc and π_nc for PSSM-FMs were adjusted based on UniProtKB/TrEMBL results as described above. In this experiment, hmmsearch detected 11 712 (12 516) matches to the 500 protein families when using trusted (noise) cutoffs and needed 2745 min for this task. Except for 1 (2) missed sequence(s), PSfamSearch returned exactly the same results at cutoff π_tc(π_nc), but it took only 93.3 (171.2) min; this makes for a speedup of 29.52 (16.01).

3.2.4 Comparison of PSfamSearch with other hmmsearch acceleration solutions

Another approach to accelerate hmmsearch is the HMMERHEAD program (Poster presentation at RECOMB2007).HMMERHEAD uses a filtration approach that employs four filtering stages with increasing computational costs to reduce the search space for the subsequent application of the hmmsearch engine. We applied HMMERHEAD to the same experimental setup as described in the former paragraph. That is, we searched with pHMMs representing the first 200 TIGRFAM families on the complete UniProtKB/TrEMBL database and measured the running time of HMMERHEAD and the coverage using the models' trusted (noise) cutoffs. In this experiment, HMMERHEAD was able to reduce the running time compared with direct hmmsearch from 1088.05 h to 626.08 h, while retaining 100% of the original results (for details, see Supplementary Fig. 5). This makes for a speedup of factor ∼1.7, with per model speedups in the range of 1.4–1.9.

rpsblast (Marchler-Bauer and Bryant, 2004) may be seen as an alternative to hmmsearch employing pHMMs. It uses psi-blast's (Altschul et al., 1997) checkpoint files which can be seen as models for protein families, much like pHMMs and our PSSM-FMs. rpsblast-compatible models representing TIGRFAM protein families are part of the CDD database (Marchler-Bauer et al., 2009). To test the ability of rpsblast to obtain the same results as hmmsearch and hence to offer an alternative to hmmsearch and PSfamSearch, respectively, we compared the classification performance of rpsblast with that of PSfamSearch employing PSSM-FMs for the first 200 TIGRFAM families with p-value cutoffs π_tc and π_nc, respectively. As a state of truth we use the results returned by hmmsearch using trusted (noise) cutoffs. In this experiment, rpsblast achieved an averaged coverage in the range of 85.6–98.6% (84.7–95.5%) compared with hmmsearch using trusted (noise) cutoffs. Using the same experimental setup, PSfamSearch achieved a uniform coverage of 99.54% (99.47%) when using cutoffs π_tc (π_nc). See Supplementary Figure 6 for further details on this experiment. It took PSfamSearch 1490 (4676) min using cutoffs π_tc (π_nc) to perform this task (Supplementary Table 1), while rpsblast needed only 1341.96 min. Hence, by application of rpsblast one obtains an additional speedup of factor 1.1 (3.4) at the price of reduced sensitivity.

Recently, Lingner and Meinicke (2008a) described an approach for search space reduction applicable to speedup database searches with pHMMs based on machine learning techniques. Although the described method and presented results seem to be promising, up to now only a prototype implemented in MATLAB and a web server for interactive usage (Meinicke, 2009) are available.

4 DISCUSSION AND CONCLUDING REMARKS

We have presented a new database search method based on PSSM-FMs. It is well suited for fast and reliable protein family classification. Moreover, it can serve as a filter to considerably speedup database searches with pHMMs, while retaining almost 100% sensitivity. Our method combines fast index-based searching of PSSMs, an efficient algorithm for exact p-value computation for PSSM score thresholds, and a fast fragment chaining algorithm. The methods described here are implemented in the robust and well-documented software tool PoSSuMsearch2.

We carefully evaluated the performance of PSSM-FMs in terms of sensitivity and specificity by using PoSSuMsearch2 in two different modes of operation, i.e. for direct sequence classification, and as a prefilter for hmmsearch. We have shown that PSSM-FMs are only marginally inferior to pHMMs when used for sequence classification. The FP50 value (the average coverage achieved when tolerating 50 false positives) for PSSM-FMs never dropped below the FP50 value for pHMMs by more than ∼6 percentage points in all of our three evaluation scenarios (Fig. 4). This renders PSSM-FMs a fast alternative to pHMMs: for example, we have observed that PoSSuMsearch2 is more than 64 times faster than hmmsearch for the same classification task.

We also demonstrated that PSSM-FMs are well suited for prefiltering sequence databases to be searched by hmmsearch. Using PSfamSearch (the combination of PoSSuMsearch2 and hmmsearch), we observed dramatic search space reductions for UniProtKB/TrEMBL to 0.80% and 3.83%, respectively, when filtering with 200 PSSM-FMs built from the TIGRFAM database using the pHMMs' trusted and noise cutoffs, respectively. The reduction of the sequence database resulted in speedups of ∼43.8 and 14 over original, unfiltered hmmsearch, respectively, while retaining 99.5% of the original results in both cases. Extrapolated to all 3603 families in TIGRFAM (Rel 8.0), we estimate a runtime of ∼18.6 days for PSfamSearch, and 2.23 years for direct hmmsearch using the models' trusted cutoffs. Notably, the observed speedups come from an algorithmic as well as a conceptual advancement: the speed of index-based PSSM searching, and the astonishing fact that pHMMs can be approximated well by the much simpler PSSM-FMs. This is also consistent with the finding that protein classification works well with word correlation matrices (Lingner and Meinicke, 2008b).

In our experiments, PSfamSearch also showed a >25-fold speedup over the program HMMERHEAD. Compared with the well-known rpsblast tool, PSfamSearch is slightly slower. PSfamSearch, however, achieved a significantly higher sensitivity in our experiment. In the experiment showing the ability of PSfamSearch for efficient annotation of E.coli proteomes, PSfamSearch returned >99.99% of the original hmmsearch results and showed a speedup over direct hmmsearch of ∼30.

PSfamSearch is twice as fast as the previously fastest software-based acceleration method for hmmsearch (Sun and Buhler, 2009). Note that Sun and Buhler (2009) focus on the problem of designing unordered sets of motifs with good filtering characteristics while searching them with straightforward algorithms, whereas our work focuses on efficient index-based searching in sublinear expected time while keeping the derivation of motifs rather simple. This raises the question whether a future combination of both approaches might lead to further improvements in software-based pHMM database search methods.