Abstract
The outer membrane protein OprP from Pseudomonas aeruginosa forms a phosphate selective pore. To understand the mechanism of phosphate permeation and selectivity, we used three simulation techniques [equilibrium molecular dynamics simulations, steered molecular dynamics, and calculation of a potential of mean force (PMF)]. The PMF for phosphate reveals a deep free energy well midway along the OprP channel. Two adjacent phosphate-binding sites (W1 and W2), each with a well depth of ≈8 kT, are identified close to the L3 loop in the most constricted region of the pore. A dissociation constant for phosphate of 6 μM is computed from the PMF, within the range of reported experimental values. The transfer of phosphate between sites W1 and W2 is correlated with changes in conformation of the sidechain of K121, which serves as a “charged brush” to facilitate phosphate passage between the two subsites. OprP also binds chloride, but less strongly than phosphate, as calculated from a Cl− PMF. The difference in affinity and hence selectivity is due to the “Lys-cluster” motif, the positive charges of which interact strongly with a partially dehydrated phosphate ion but are shielded from a Cl− by the hydration shell of the smaller ion. Our simulations suggest that OprP does not conform to the conventional picture of a channel with relatively flat energy landscape for permeant ions, but rather resembles a membrane-inserted binding protein with a high specificity that allows access to a centrally located binding site from both the extracellular and the periplasmic spaces.
Keywords: free energy profile, potential of mean force, anion selectivity, hydration, molecular dynamics simulation
The outer membrane of Gram-negative bacteria contains outer membrane proteins (OMPs) which perform diverse roles, including transport, recognition, and catalysis (1). Most OMPs are β-barrels. Porins are trimeric OMPs, each monomer a pore of nanometer dimensions across the outer membrane. Porins differ in their selectivity to the species that can pass through them. Some are relatively nonspecific (e.g., OmpF), whereas others are specific for small substrates such as sugars (LamB and ScrY) or phosphate ions (OprP). Thus, analysis of the relationship between structure and function of porins may reveal more general design principle for nanopores which could be exploitable from a technological perspective (2).
Under conditions of phosphate starvation, high-affinity uptake of inorganic phosphate (Pi) is required for bacterial growth. In the pathogen Pseudomonas aeruginosa, phosphate limitation leads to the induction of the protein OprP (3), an analogue of the PhoE porin of Escherichia coli. Although both OprP and PhoE form anion-selective channels whereby each monomer is formed by a 16-stranded β-barrel, they differ in the nature of their transmembrane pores. OprP has high affinity for Pi uptake via a strong phosphate-binding site (4–6). In contrast, PhoE is weakly anion-selective and does not contain a specific binding site for Pi, but rather is anion-selective due an overall excess of positively-charged residues along the pore surface (7).
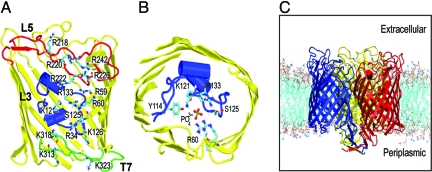
The X-ray structure of OprP (8) reveals three positively-charged loops (L3, L5, and T7) folded into the lumen (Fig. 1A). The arginine side chains of L3 and L5 and lysines of T7 form a “ladder” along the pore axis, which includes the phosphate-binding site of OprP (8). In vivo phosphate permeation by OprP is unidirectional, from the external environment to the cell interior, via an association of OprP with a periplasmic phosphate-binding protein (4, 9). OprP is selective for phosphate over other anions, as revealed by conductance studies (3–6), which indicate that phosphate permeation under conditions of phosphate starvation is ≈20-fold more efficient than Cl− transport (4). The primary contributing factor is a 100–500 times higher affinity of OprP for Pi than Cl− (4–6), which renders OprP one of the few known porins that not only selects anions over cations but also discriminates sensitively between different anions (10).
Fig. 1.
Outer membrane protein P (OprP) from Pseudomonas aeruginosa. (A) The structure of the OprP monomer showing the side chains of the arginine ladder and the lysines at the periplasmic mouth of the pore. The L3 and L5 loops are shown in blue and red, respectively, and the T7 turn in green. (B) The key residues in the constriction zone surrounding the central phosphate. (C) The OprP trimer in a DMPC bilayer. The three protein subunits are in red, blue and yellow. The lipid molecules are in cyan (tails) and red/blue/brown (headgroups). Water and counterions have been omitted for clarity.
Crystallographic (8) and mutational studies (11) have resulted in a plausible model for phosphate transport through OprP, stressing the role of the side chain of K121 (Fig. 1B) as a “molecular ratchet” (8). Here, we use a multitechnique molecular dynamics (MD) simulation approach to OprP embedded in a phospholipid bilayer (Fig. 1C) to explore the relationship between structure and function, and to evaluate and refine the proposed transport mechanism for Pi and for Cl−. MD simulations have been widely used to study channel and transport proteins (12, 13). In particular, calculations of the potential of mean force (PMF; i.e., the relative free energy profile) for permeant ions and solutes along the pores of K channels (14) and aquaporins (15–17) have been reported. In both of these cases the pore is relatively narrow (i.e., of comparable radius to a water molecule) and inflexible. In the current study, we present the PMF profile for phosphate and Cl− ions along the OprP pore. In contrast to previous simulation studies of pores and channels, we are analyzing a somewhat wider pore, lined by flexible basic side chains, that nevertheless exhibits significant specificity. Thus, our simulation results provide insights not only into the biology of OprP, but into more general aspects of the design principles of nanopores.
Results and Discussion
Three Types of Simulation.
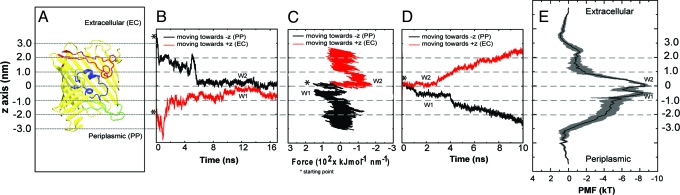
Three classes of simulation have been performed for the OprP trimer embedded in a phospholipid bilayer (Fig. 2): (i) equilibrium MD simulations (duration, ≈17 ns), in which a Pi anion is released at either mouth of the pore; (ii) constant-velocity steered (S)MD (18), in which a Pi is pulled through the pore on a timescale of 10 ns; and (iii) umbrella sampling calculations of the PMF of a Pi and of a Cl− ion as a function of their position along the pore axis. All three approaches provide evidence for an anion binding site at the center of the pore, close to the key K121 side chain. In the equilibrium simulations (Fig. 2B), a Pi ion released at either mouth of the pore diffuses to the central binding pocket within ≈10 ns where it remains for the remainder of the simulation. In the SMD simulations (duration, ≈10 ns; Fig. 2 C and D), the Pi ions were pulled in either direction from the central binding site. In each case the anion is slowly released from this site (>≈4 ns), interacting more weakly with other sites before exiting through either the extracellular or periplasmic mouth of the pore. The exact locations of the interaction sites within and at the mouths to the pore are revealed in the PMF (Fig. 2E).
Fig. 2.
Characterization of phosphate permeation through the OprP pore. (A) Cross section of the OprP monomer showing L3 (blue), L5 (red), and T7 (green) and defining the z axis coordinates used in other figures. (B) Phosphate trajectories from equilibrium MD simulations for an ion initially at the extracellular (black; −z) and periplasmic (red; +z) mouth of the pore. W1 and W2 represent the ion present at the two central energy wells. (C and D) Force profiles (C) and trajectories (D) from inward (black; −z) and outward (red; +z) constant-velocity SMD simulations of phosphate through the pore. Each phosphate was initially placed in the center of the pore. (E) PMF for a tribasic phosphate ion along the permeation pathway. The gray bars indicate one SD on the free energy as calculated from block averaging.
Energetics of the Phosphate Binding Sites.
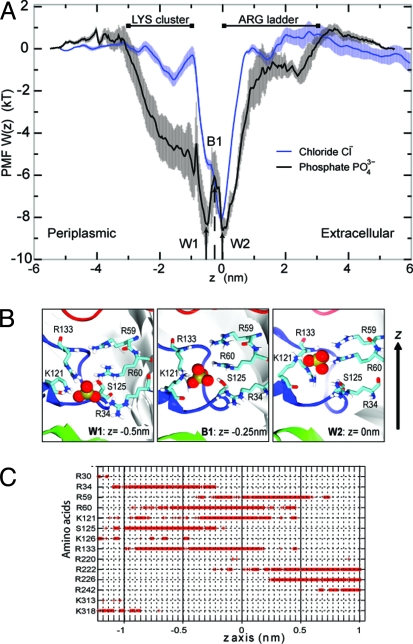
The PMF profile reveals no significant barrier to permeation anywhere along the pathway, both for PO43− and Cl−. This observation is in contrast with the corresponding profiles of narrower pores [e.g., KcsA (14) and aquaporins (15–17)], which show a complex energy landscapes composed of mixtures of wells and barriers. In the OprP phosphate profile, two adjacent energy wells (W1 and W2; Fig. 3A) are seen in the center of the pore in the vicinity of the L3 loop, forming the most favorable sites for Pi binding with a well depth of ≈−8 kT. These favorable Pi binding sites were also detected by equilibrium MD and SMD (see above). Thus, in SMD, pulling a Pi from the extracellular to a periplasmic side (−z in Fig. 2C) or in the reverse direction (+z) reveals a sudden increase in the force on the Pi of magnitude 150 kJ·mol−1·nm−1 at z values from −1 to 1 nm corresponding to the energy wells W1 and W2 found in the PMF. These two energy wells were thus observed in two independent SMD simulations and two equilibrium simulations. The SMD simulations also revealed two other minor phosphate-binding “sites,” which seem to correspond to shoulders/plateau regions in the PMF.
Fig. 3.
Interactions of phosphate with OprP. (A) Relative free energy profile (PMF) of anions along the OprP permeation pathway. Phosphate is stabilized in two wells (W1 and W2), separated by a small barrier (B1) in the constriction zone. A Cl− ion can bind in the W2 site. Error bars indicate one SD of the data as obtained from averaging over three blocks of 200 ps length. The approximate positions of clusters of basic residues along the pore axis are marked by extended lines. (B) Conformations of positively charged sidechains with Pi (in spacefilling format) at W1, B1, and W2. (C) Hydrogen bonds between Pi and the pore-lining amino acids as a function of position of the ion on the z axis.
We computed a dissociation constant Kd = 6 ± 1 μM for Pi from the PMF (see Methods). The predicted dissociation constant is within the range of reported experimental estimates of the Kd of Pi at neutral pH (0.15–310 μM) (4, 6, 10). A Kd of 6 μM corresponds to a standard free energy of binding ΔGo = −12.0 ± 0.2 kT. Such tight binding is also consistent with the presence of bound Pi in the X-ray structure of OprP (8).
Basic Side Chains form the Phosphate Binding Site.
The Pi binding site in the L3 region is unusual for a porin in that it binds the substrate tightly and selectively. The two subsites W1 and W2 are separated by only a small free energy barrier B1 of ≈2 kT (Fig. 3A). W1 and W2 are ≈0.5 nm apart. Analysis of the Pi-protein interactions indicates that the double-well structure of the binding site may be due to the movement of a single side chain, K121 (Fig. 3B). Hydrogen-bonding analysis (Fig. 3C) indicates that interactions with R59, R60, K121, and R133 are involved in the formation of the energy well at W2, whereas interactions with R34, R60, S125, and R133 form the second Pi binding site at W1. The free energy barrier at B1 appears to result from the loss of favorable electrostatic interactions. At the transition from W2 to W1, the hydrogen bond to S125 is being broken and the one to R59 is not yet formed, thus destabilizing the phosphate ion.
The side chain of K121 has a special role: It makes direct contact with the Pi during the whole transition from W2 to W1, which requires it to switch its rotameric state. Hydrogen bonds with R60 and R133 also form stable interactions with the Pi across the whole central binding site (i.e., W1, B1, and W2), thus contributing to the overall stabilization of the charged Pi at the center of the membrane. We find that interactions with other residues are localized at the edges of the free energy wells. K121 is thus a key residue that can interact with Pi across two regions; R60 and R133 can also facilitate Pi movement across the constriction site but to a lesser degree (Fig. S1).
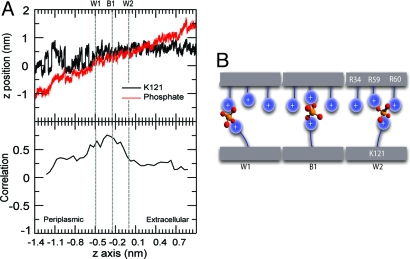
We observe a positive correlation between the z positions of K121 and the Pi (Fig. 4 A and B; Fig. S1B), indicating that the dynamics of K121 and Pi are coupled. This coupling in turn suggests a mechanism in which K121 plays a crucial role in directing a Pi ion from W2 to W1 by “sweeping” it along as a charged brush (Fig. 4C). Such a mechanism agrees with the suggestion from the crystallographic study that different conformations of K121 could enable the transfer of Pi to the constriction site (8). Site-directed mutagenesis showed that the K121E mutation both reduces Pi conductance and also the ability of Pi to inhibit Cl− conductance (11).
Fig. 4.
Translocation of phosphate through the central constriction. (A) Trajectories of the Nε atom of the side chain of K121 and a Pi in a constriction site from one OprP monomer extracted from the umbrella sampling simulations. The z position of the Nε atom or Pi ion is shown on the vertical axis as a function of the z coordinate of the center of the window (i.e., of the Pi ion restraint) on the horizontal axis. (B) Correlation coefficient between the z position of the K121 Nε and the center of mass of the Pi as a function of the z coordinate of the center of the umbrella window. (C) Schematic representation of the mechanism of positively-charged side chains acting as charged brushes to facilitate Pi transport along the pore.
Our simulations reveal that the Pi binding site is not rigid, but instead is flexible adapting its size to the presence of the solute. Analysis of the pore radius profile in the presence of trapped Pi at W1, W2, and B1 demonstrates that the change in conformation of the K121 side chain correlates with a change in the radius of the pore in the region of L3 (Fig. S2). The terminal amino group of the K121 side chain always points toward the narrowest region of the pore. We conclude that K121 is crucial for the formation of Pi-binding site and for dynamic changes at the narrowest region of the pore. Thus, the OprP permeation pathway may be thought of as a wide and relatively rigid tunnel provided by the β-barrel scaffold, which is lined by side chains protruding into the lumen that provide a flexible but highly specific binding site. In this picture, the pore may be thought of as resembling a polymer brush folded into a tube, forming a brush-like nanopore.
In addition to the dominant interaction network at the pore constriction site, the other interactions with residues lining the channel seen in the simulations support the arginine ladder mechanism proposed on the basis of the X-ray structure (8). Thus, the overlapping hydrogen bonds of R222 and R226 in the L3 and L5 region seem to be important in directing the phosphate to the constriction site (Fig. 3C). These major interactions found in L3 and L5 regions are also clearly seen in the SMD and equilibrium MD (Fig. S3).
Comparison of Phosphate and Chloride.
To elucidate the selectivity of OprP of Pi over Cl− ions we also computed the PMF for Cl− ions (Fig. 3A). The monovalent anion is stabilized in the W2 site to the same degree as the trivalent phosphate, with a free energy well depth of ≈8 kT. In contrast to Pi, W2 is the only binding site for a Cl− ion. A large portion of the periplasmic side of the pore that is lined by the “Lys-cluster” (3–5, 8, 11, 19) is also attractive for Pi but barely so for Cl−. The Kd as computed from the PMF is 44 ± 2 μM (equivalent to ΔGo = −10.0 ± 0.1 kT), which corresponds to a 7-fold stronger binding of Pi ions than Cl−. This number is smaller than an experimental estimate of the binding selectivity of ≈100–500-fold as derived from the measured Kd values (5, 6). Nevertheless, the calculation of the binding constants as integrals over pore volumes suggests that OprP is selective of Pi over Cl− because the total attractive pore volume is much larger for Pi than for Cl− (Fig. 3A).
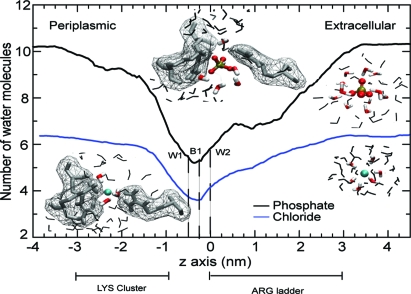
The mechanistic basis for selectivity between anions can then be traced to the differential hydration of the two ions (Fig. 5). The pore at the Lys-cluster is sufficiently wide to allow a Cl− ion to be fully solvated by a bulk-like hydration shell of approximately six water molecules (Fig. S4). Pi is larger and confinement strips approximately two waters from its hydration shell. Thus, the highly charged, partially desolvated Pi anion can interact strongly with the basic Lys residues, whereas the Cl− ion with its smaller charge is screened by its complete hydration shell. Partial desolvation is sufficient to establish direct interactions between the negative charges on the phosphate oxygen and the positive charge of the lysine ε-amino group.
Fig. 5.
Differential desolvation of permeant anions. The number of water molecules within an ion's first hydration shell was obtained from umbrella sampling simulations of Pi and Cl−. The approximate position of the “arginine ladder” and the Lys-cluster are shown along the permeation pathway. (Insets) Ion and water in CPK representation. Water molecules within the first hydration shell (water oxygen-anion distance <0.275 nm for Pi, <0.3 nm for Cl−) are shown in color, other nearby waters are gray. Pore-lining basic residues are shown as gray sticks together with their solvent accessible surface as a mesh. Images on the left hand side are from the binding site near K121, right hand side images are in bulk water.
Unlike the Lys-cluster, the Arg ladder motif does not appear to differentiate energetically between Pi and Cl− (Fig. 3A). Its role is rather to facilitate movement of the negatively charged particles toward the center of the low dielectric membrane through a narrowing pore. It facilitates gradual desolvation of the anions (which strips them of approximately half of their bulk hydration shell; Fig. 5) while stabilizing them through favorable electrostatic interactions.
Conclusions
Biological Function.
The use of a combination of simulation approaches has revealed the presence of two well defined and closely spaced energy wells (W1 and W2) along the permeation pathway of a Pi anion through the OprP pore. W1 corresponds to the Pi binding site in the X-ray structure. The transition from W2 to W1 is facilitated by K121. The highly-correlated Pi-K121 motion, the hydrogen-binding analysis, and the change in pore cavity due to the conformation change of K121 support the idea that K121 serves as a “charged brush” to facilitate Pi passage between the two subsites. From the PMF, we are able to compute a standard free energy of binding of phosphate to OprP (ΔGo = −12.0 ± 0.2 kT) equivalent to a dissociation constant of Kd = 6 ± 1 μM. In this sense, OprP is not a typical specific porin such as LamB with a dissociation constant only in the millimolar range (20). Such tight binding reflects the function of OprP under conditions of phosphate starvation when available phosphate must be scavenged from the extracellular environment at concentrations <200 μM (3). The OprP-bound phosphate is passed to a specific periplasmic binding protein at the periplasmic mouth of the pore to facilitate unidirectional phosphate uptake (4, 9).
OprP is also remarkable in that it discriminates between anions. The experimentally-observed stronger binding of tribasic phosphate over chloride ions could be qualitatively explained from the simulations and traced to the cluster of N-terminal lysine residues. The periplasmic mouth of the pore is sufficiently wide to admit a fully solvated Cl− ion but partially desolvates a Pi ion. Thus, the monovalent ion is screened from the positive charge of the lysine amino groups by its own hydration shell, whereas the unscreened Pi ion is stabilized by strong charge–charge interactions. Whereas the lysine-cluster is the selectivity filter for anions, the arginine ladder primarily facilitates the gradual dehydration of incoming anions from the extracellular side without discriminating between Cl− and Pi. Both Cl− and Pi are stabilized at the center of the pore to a similar degree, with approximately half of their hydration shells stripped; it is likely that the binding site itself also acts as a filter for anions over cations and a general size-exclusion filter.
PMFs of Biological Pores.
Free energy profiles (PMFs) have been calculated for a number of permeant species through biological pores, including, for example, K+ ions through the KcsA channel (14), water and glycerol through aquaporins and aquaglyceroporins (15–17), and ammonia through AmtB (21, 22). It is therefore useful to compare these pores with OprP.
Both the KcsA selectivity filter and the Aqp pore are (relatively) inflexible, narrow (≈0.2-nm radius), and are lined at least in part by backbone atoms. These pores present barriers to permeation of K+ ion (KcsA) or water (hAqp1) or glycerol (GlpF) of the order of 5 kT (14–17). In contrast, the pore of OprP which is flexible (especially at K121), relative wide (minimum radius >0.2 nm), and lined largely by side chains has an energy well of depth ≈8 kT, formed by positively-charged side chains as discussed above. Similar energetics have been observed for the ammonia channel AmtB, which has been estimated to present an interior energy well (formed largely by stabilizing interactions with His side chains) of overall depth ≈17 kT for ammonia molecules (22), although in the latter study, the authors comment on the structural invariance of the AmtB pore regardless of the location of the ammonia molecule. Thus, it would seem that the flexible, side-chain-lined pore constriction of OprP provides for a relatively high affinity binding site while allowing high permeation rates for phosphate and chloride anions (4). It is of particular interest that a side-chain-lined pore seems to be associated with formation of a well rather than a flatter energy landscape with one or more small barriers to permeation. Hence, OprP does not share the free energy landscape of permeation with “typical” channels or pores but it rather resembles a protein with a binding site with two openings that bridge the outer membrane. OprP can be understood as a brush-like nanopore, in which charged side chains provide a high local concentration of counter charge to stabilize a charged substrate, similar to highly simplified but successful models of sodium and calcium channels (23). In addition, it uses differential desolvation to probe different anions and can so discriminate between a chloride ion that “hides” under its hydration shell and a larger phosphate ion whose size forces it to make direct contact with the sensing charged brushes. This mechanism depends critically upon the degree of flexibility of the pore lining side chains. This blueprint may provide a new design principle, for example, derivatization of nanopores (24) to form ion selective biomimetic channels. Furthermore, an improved understanding may aid design of selective blockers of OprP to aid in fighting Pseudomonas infection.
Methods
System Preparation.
The OprP trimer (PDB 2O4V; resolution 1.94 Å) (8) was embedded in a preequilibrated dimyristoyl-phosphatidylcholine (DMPC; 290 lipids) bilayer using published methods (25). Water (simple point charge; SPC) molecules (47,092 waters) and counter ions (39 ions) were then added. Tribasic phosphate ions were placed at either mouth of the pore for the equilibrium MD simulations. Water molecules overlapping with phosphate ions were removed manually. Energy minimization (steepest descent algorithm) was run for 5,000 steps, followed by a 1-ns equilibration phase during which protein and phosphate were harmonically restrained with a force constant of 1,000 kJ mol−1 nm−2. Systems for umbrella sampling were prepared in the same manner except that no phosphate was added at this stage.
All simulations were carried out with GROMACS (26) version 3.3 (www.gromacs.org) with the extended united atom GROMOS96 forcefield (27). Long-range electrostatic interactions were treated using the particle mesh Ewald (PME) method (28) with a short range cutoff of 1 nm, a Fourier spacing of 0.12 nm, and fourth-order spline interpolation. All simulations were performed in the NPT ensemble at constant number of particles N, pressure, and temperature. The temperature of protein, DMPC, solvent, and ions were each coupled separately to a Berendsen thermostat (29) at 310 K with coupling constant τt = 0.1 ps. The pressure was coupled isotropically using the Berendsen algorithm at 1 bar with coupling constant τp = 1 ps. The time step for integration was 2 fs and all bonds were constrained with the LINCS algorithm (30). The two production runs of equilibrium MD were performed for 18 ns and 17 ns.
Constant-velocity SMD simulations were performed for 10 ns each to pull the phosphate in the ±z directions. Phosphate was initially at the center of the pore. An elastic spring with a force constant of 350 kJ·mol−1·nm−2 was attached to the center of mass of the phosphate and was moved in the direction parallel to the channel axis (z axis) at a rate of 0.25 nm/ns. Each SMD run was repeated twice.
Data were analyzed using GROMACS and locally written code. Molecular graphic images were prepared using visual molecular dynamics (VMD) (31).
Umbrella Sampling to Calculate Potential of Mean Force Profiles.
The starting system for the umbrella sampling simulations was obtained from a 1-ns equilibrium MD run. The 1D reaction pathway corresponds to the distance along the z axis between the centers of mass of each tribasic phosphate ion and each OprP monomer. The range of interest from −5.6 nm to + 5.6 nm was divided into 226 equidistant windows (each of width 0.05 nm). For each window simulation, a phosphate was placed into each of the three pores at a center of an umbrella window, with the xy-location of each phosphate determined by the pore radius profiles as calculated using HOLE (32). Water molecules that overlapped with a phosphate were removed. Each window was initially equilibrated for 0.5 ns with an isotropic harmonic restraint of 1,000 kJ·mol−1·nm−2 on the phosphate ions. Umbrella sampling calculations were carried out by applying a harmonic biasing potential on the center of each of the three phosphate ions relative to the center of mass of the corresponding monomer; the force constant was 1,000 kJ·mol−1·nm−2 and acted only along z. Data were collected for 1 ns and the last 600 ps of each run were used to construct the PMF. The unbiased PMF was computed with the weighted histogram analysis method (WHAM) (33), using Alan Grossfield's WHAM code (http://membrane.urmc.rochester.edu/Software/WHAM/WHAM.html). The final PMFs were obtained as the average of the PMFs for three ions, one for each pore of the OprP trimer. Errors were estimated from performing the above analysis in three trajectory blocks of length 200 ps and averaging the block-PMFs.
We calculated the dissociation constant (Kd) of phosphate and chloride ions from their PMFs. The standard free energy of binding, ΔGo, is related to Kd via Kd = V0exp(−ΔGo/RT), where V0 = 1.661 nm3 is the standard volume corresponding to a standard concentration of 1 M. ΔGo was computed from the 1D PMF, W(z), using the method of Doudou et al. (34) under the assumption that confinement of the three sampled ions in the bulk region is provided by the simulation cell (for details, see SI Methods).
Supplementary Material
Acknowledgments.
We thank Richard Henchman, Ranjit Vijayan, and Jayne Wallace for their help and comments, and the comments of two anonymous referees that lead to the hypothesis to explain anion selectivity in OprP by differential hydration. This work was supported by the Royal Thai Government, the European Commission under the FP7 EDICT Project Grant 201924, the Biotechnology and Biological Sciences Research (via the Oxford Centre for Integrative Systems Biology), and the Wellcome Trust.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0907315106/DCSupplemental.
References
- 1.Wimley WC. The versatile β-barrel membrane protein. Curr Opin Struct Biol. 2003;13:404–411. doi: 10.1016/s0959-440x(03)00099-x. [DOI] [PubMed] [Google Scholar]
- 2.Chen M, Khalid S, Sansom MSP, Bayley H. Outer membrane protein G: Engineering a quiet pore for biosensing. Proc Natl Acad Sci USA. 2008;105:6272–6277. doi: 10.1073/pnas.0711561105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hancock RE, Poole K, Benz R. Outer membrane protein P of Pseudomonas aeruginosa: Regulation by phosphate deficiency and formation of small anion-specific channels in lipid bilayer membranes. J Bacteriol. 1982;150:730–738. doi: 10.1128/jb.150.2.730-738.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Benz R, Egli C, Hancock RE. Anion transport through the phosphate-specific OprP-channel of the Pseudomonas aeruginosa outer membrane: Effects of phosphate, di- and tribasic anions and of negatively-charged lipids. Biochim Biophys Acta. 1993;1149:224–230. doi: 10.1016/0005-2736(93)90205-e. [DOI] [PubMed] [Google Scholar]
- 5.Benz R, Hancock RE. Mechanism of ion transport through the anion-selective channel of the Pseudomonas aeruginosa outer membrane. J Gen Physiol. 1987;89:275–295. doi: 10.1085/jgp.89.2.275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hancock RE, Benz R. Demonstration and chemical modification of a specific phosphate binding site in the phosphate-starvation-inducible outer membrane porin protein P of Pseudomonas aeruginosa. Biochim Biophys Acta. 1986;860:699–707. doi: 10.1016/0005-2736(86)90569-9. [DOI] [PubMed] [Google Scholar]
- 7.Bauer K, van der Ley P, Benz R, Tommassen J. The pho-controlled outer membrane porin PhoE does not contain specific binding sites for phosphate or polyphosphates. J Biol Chem. 1988;263:13046–13053. [PubMed] [Google Scholar]
- 8.Moraes TF, Bains M, Hancock RE, Strynadka NC. An arginine ladder in OprP mediates phosphate-specific transfer across the outer membrane. Nat Struct Mol Biol. 2007;14:85–87. doi: 10.1038/nsmb1189. [DOI] [PubMed] [Google Scholar]
- 9.Poole K, Hancock RE. Phosphate transport in Pseudomonas aeruginosa. Involvement of a periplasmic phosphate-binding protein. Eur J Biochem. 1984;144:607–612. doi: 10.1111/j.1432-1033.1984.tb08508.x. [DOI] [PubMed] [Google Scholar]
- 10.Hancock RE, Brinkman FS. Function of Pseudomonas porins in uptake and efflux. Annu Rev Microbiol. 2002;56:17–38. doi: 10.1146/annurev.micro.56.012302.160310. [DOI] [PubMed] [Google Scholar]
- 11.Sukhan A, Hancock RE. The role of specific lysine residues in the passage of anions through the Pseudomonas aeruginosa porin OprP. J Biol Chem. 1996;271:21239–21242. doi: 10.1074/jbc.271.35.21239. [DOI] [PubMed] [Google Scholar]
- 12.Roux B, Schulten K. Computational studies of membrane channels. Structure. 2004;12:1343–1351. doi: 10.1016/j.str.2004.06.013. [DOI] [PubMed] [Google Scholar]
- 13.Khalili-Araghi F, et al. Molecular dynamics simulations of membrane channels and transporters. Curr Opin Struct Biol. 2009;19:128–137. doi: 10.1016/j.sbi.2009.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bernèche S, Roux B. Energetics of ion conduction through the K+ channel. Nature. 2001;414:73–77. doi: 10.1038/35102067. [DOI] [PubMed] [Google Scholar]
- 15.Vidossich P, Cascella M, Carloni P. Dynamics and energetics of water permeation through the aquaporin channel. Proteins: Struct Func Bioinf. 2004;55:924–931. doi: 10.1002/prot.10642. [DOI] [PubMed] [Google Scholar]
- 16.Hub JS, de Groot BL. Mechanism of selectvity in aquaporins and aquaglyceroporins. Proc Natl Acad Sci USA. 2008;105:1198–1203. doi: 10.1073/pnas.0707662104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hénin J, Tajkhorshid E, Schulten K, Chipot C. Diffusion of glycerol through Escherichia coli aquaglyceroporin GlpF. Biophys J. 2008;94:832–839. doi: 10.1529/biophysj.107.115105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Isralewitz B, Gao M, Schulten K. Steered molecular dynamics and mechanical functions of proteins. Curr Opin Struct Biol. 2001;11:224–230. doi: 10.1016/s0959-440x(00)00194-9. [DOI] [PubMed] [Google Scholar]
- 19.Hancock RE, Schmidt A, Bauer K, Benz R. Role of lysines in ion selectivity of bacterial outer membrane porins. Biochim Biophys Acta. 1986;860:263–267. doi: 10.1016/0005-2736(86)90522-5. [DOI] [PubMed] [Google Scholar]
- 20.Klebba PE, Newton SM. Mechanisms of solute transport through outer membrane porins: Burning down the house. Curr Opin Microbiol. 1998;1:238–247. doi: 10.1016/s1369-5274(98)80017-9. [DOI] [PubMed] [Google Scholar]
- 21.Lin Y, Cao Z, Mo Y. Molecular dynamics simulations on the Escherichia coli ammonia channel protein AmtB: Mechanism of ammonia/ammnium transport. J Amer Chem Soc. 2006;128:10876–10884. doi: 10.1021/ja0631549. [DOI] [PubMed] [Google Scholar]
- 22.Bostick DL, Brooks CL. Deprotonation by dehydration: The origin of ammonium sensing in the AmtB channel. PLoS Comp Biol. 2007;3:0231–0246. doi: 10.1371/journal.pcbi.0030022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Boda D, et al. Steric selectivity in Na channels arising from protein polarization and mobile side chains. Biophys J. 2007;93:1960–1980. doi: 10.1529/biophysj.107.105478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu B, Li XY, Li BL, Xu BQ, Zhao YL. Carbon nanotube based artificial water channel protein: Membrane perturbation and water transportation. Nano Lett. 2009;9:1386–1394. doi: 10.1021/nl8030339. [DOI] [PubMed] [Google Scholar]
- 25.Faraldo-Gómez JD, Smith GR, Sansom MSP. Setup and optimisation of membrane protein simulations. Eur Biophys J. 2002;31:217–227. doi: 10.1007/s00249-002-0207-5. [DOI] [PubMed] [Google Scholar]
- 26.Van Der Spoel D, et al. GROMACS: Fast, flexible, and free. J Comput Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 27.van Gunsteren WF, et al. Biomolecular Simulation: The GROMOS96 Manual and User Guide. Zürich: Biomos and Hochschulverlag AG an der ETH Zürich; 1996. [Google Scholar]
- 28.Darden T, York D, Pedersen L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 29.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. [Google Scholar]
- 30.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. LINCS: A linear constraint solver for molecular simulations. J Comp Chem. 1997;18:1463–1472. [Google Scholar]
- 31.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 32.Smart OS, Neduvelil JG, Wang X, Wallace BA, Sansom MSP. HOLE: A program for the analysis of the pore dimensions of ion channel structural models. J Mol Graphics. 1996;14:354–360. doi: 10.1016/s0263-7855(97)00009-x. [DOI] [PubMed] [Google Scholar]
- 33.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J Comp Chem. 1992;13:1011–1021. [Google Scholar]
- 34.Doudou S, Neil A, Henchman RH. Standard free energy of binding from a one-dimensional potential of mean force. J Chem Theor Comput. 2009;5:909–918. doi: 10.1021/ct8002354. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.