Bandit solutions provide unified ethical models for randomized clinical trials and comparative effectiveness research

Abstract

As electronic medical records enable increasingly ambitious studies of treatment outcomes, ethical issues previously important only to limited clinical trials become relevant to unlimited whole populations. For randomized clinical trials, adaptive assignment strategies are known to expose substantially fewer patients to avoidable treatment failures than strategies with fixed assignments (e.g., equal sample sizes). An idealized adaptive case—the two-armed Bernoulli bandit problem—can be exactly optimized for a variety of ethically motivated cost functions that embody principles of duty-to-patient, but the solutions have been thought computationally infeasible when the numbers of patients in the study (the “horizon”) is large. We report numerical experiments that yield a heuristic approximation that applies even to very large horizons, and we propose a near-optimal strategy that remains valid even when the horizon is unknown or unbounded, thus applicable to comparative effectiveness studies on large populations or to standard-of-care recommendations. For the case in which the economic cost of treatment is a parameter, we give a heuristic, near-optimal strategy for determining the superior treatment (whether more or less costly) while minimizing resources wasted on any inferior, more expensive, treatment. Key features of our heuristics can be generalized to more complicated protocols.

Although randomized clinical trials are the gold standard for establishing the effectiveness of medical treatments, it is widely recognized that they raise nontrivial ethical issues. Although they seek to demonstrate an intervention's effectiveness at a high level of statistical significance, randomized trials will always assign some patients to an inferior treatment and they will often assign patients to a treatment for which there is already partial evidence of its inferiority. In this respect, clinical trials are allowed deviations from the physician's duty, “to do what is best for the patient” (1). That clinical trials are required to have independent data and safety monitoring boards (2) with the power to review partial data and recommend early termination of the trial is an indicator of inherent ethical discomfort. The lack of a uniform consensus on protocols governing early stopping also points to unsettled ethical issues, though there is no shortage of sensible recommendations (3–5).

After a clinical trial is over, the ethical nuances and the unrecorded discussions of its safety monitoring boards are forgotten with time. However, as health outcomes research enabled by electronic medical records becomes common (6), comparative effectiveness research (CER), which is logically, if not by name, a kind of clinical trial (7), will extend the duration of ethical questions, and the number of patients affected by such questions, almost without bound. It therefore seems worth revisiting these questions, with a view toward finding approaches that are ethically and statistically justified in the limit M _h (the “horizon,” or number of patients in a trial) → ∞.

Response-adaptive trials, often Bayesian in approach, have long been suggested as statistically more efficient and ethically better-grounded alternatives to standard experimental designs, such as equal allocations to experimental and control therapies (8–13). In response-adaptive trials, partial data inform not just “circuit-breaker” early stopping decisions, but also affect, by defined statistical protocols, such things as the assignment of patients to treatments, dosages, and so forth.

In this paper, we take as an idealized model the Bernoulli-outcome two-armed bandit problem. Multiarmed bandit problems, named after a metaphorical image of a slot machine with multiple handles, have been known for many decades (14–17). Bandit problems exemplify the tradeoff between the cost of gathering information and the benefit of exploiting information already gathered—the so-called “exploration versus exploitation dilemma”.

In the example used in this paper, there are two treatments, A and B, which have respective (unknown) success probabilities a and b with 0 ≤ a ≤ 1 and 0 ≤ b ≤ 1. In a clinical trial, patients are assigned in turn to one or the other treatment. The Bernoulli-valued outcomes for all previous patients, success or failure, are assumed to be known as each assignment is made. The questions are how best make the assignments, and, as the central issue for this paper, what should “best” mean in a context involving both ethical responsibilities and the limit M → ∞? Generalizations of this idealized model to more realistic cases (e.g., where the outcomes are not immediately known) and to cases where the cost of treatment is also a relevant variable, are discussed in Numerical Experiments and Heuristics and Discussion.

Methods

State Variables.

At any point in time, under the model assumptions, our total knowledge consists of four integers, the number of successes and failures for, respectively, treatments A and B, a lattice point in four dimensions,

Here, bars denotes failures. Our state of knowledge of the unknown success rates a and b at any time is captured by the (Bayesian) beta distributions

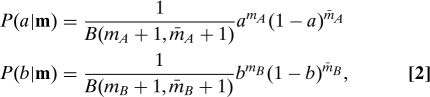where B is the beta function. Eq. 2 assumes uniform priors on a and b in the absence of any data. The number of patients M treated at any point is

where we have also defined totals M _A and M _B for each treatment. We may view M as the norm of m. Expressing our knowledge by means and variances,

(and correspondingly for B). Every point m has exactly four possible successor states, reached by the treatment of exactly one additional patient, and exactly four predecessor states. We denote these as m ^(i±) (see the SI Appendix). We write m ₀ ≺ m if m is a successor state of m ₀ (not necessarily an immediate successor), and similarly, m ₀ ≼ m.

Strategies.

A strategy tells us how to assign the next patient to treatment A or B given that our current state is m. It is thus a labeling of every lattice point by a value r,

Although we define r as a probability, it will in most cases turn out to be either 0 or 1 and thus deterministic. A more symmetric notation is

so that r = 0 or 1 corresponds respectively to s = −1 or +1. We refer to whole strategies as r ≡ {r _m} or s ≡ {s _m}.

Given a strategy r, and a starting point m ₀ [often (0,0,0,0) but not always], and a study size or horizon M _h, a distribution of paths through the lattice is defined. Namely, at each step along a path, the strategy r defines whether the next patient is assigned to A or B, and the probability a or b generates that patient's outcome. We proceed by incrementing M while M ≤ M _h, the horizon, then stop. An increasing path through the lattice is thus the history of a clinical trial on M _h patients. We denote the probability that a path that goes through m ₀ passes through a point m by p(m|a,b,r,m ₀).

Total and Patient-Specific Cost Functions.

For an optimal strategy to have meaning, we must have a cost function on strategies. We take this to be the expectation of the sum over patients of a cost function defined for each patient. We denote this patient-specific cost function by c(m|a,b,r). Also, we denote expectations over the product distribution P(a|m)P(b|m) by angle brackets, 〈 〉_m. Then the total cost C of a strategy r for a trial with starting point m ₀ and horizon M _h is

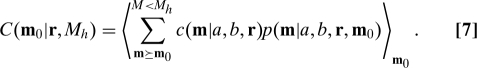Here the outer expectation brackets are necessary because the values of a and b are unknown, but at each m ₀ we can know expectations based on the current state. Already, Eq. 7 is an ethics-motivated choice, because it excludes the possibility of evaluating a strategy by anything except its effect on patients (summed and in expectation). We will say that this kind of cost function is utilitarian. (We nickname ethical principles in boldface, and specific cost models, below, in italics.)

Interestingly, it is straightforward, though not always computationally tractable, to find the optimal strategy r for any patient-specific cost function c(m|a,b,r), that is, the labeling r _m of the lattice that minimizes C(m ₀|r,M _h) (18), (see the SI Appendix). The solution, Eq. S7, has the form of backward recurrence for the cost C(m ₀|r,M _h) in terms of the four costs C(m ₀ ⁽ⁱ⁺⁾|r,M _h) with i = 1,2,3,4. This can be started at the horizon M _h with

If at each point we locally choose r _m to minimize C, then the recurrence guarantees that each point will acquire the globally smallest cost C to the horizon, so we get an optimal strategy r.

We do not need to start an optimal path at the zero-data origin (0,0,0,0). By its construction, the same strategy is optimal from any starting m ₀. So, we can have our choice of any prior states of knowledge that are adequately represented by Eq. 2 (Bayesian conjugate priors).

The computational workload implied by Eq. S7 grows in time and space as O(M _h ⁴), although parallelization and other optimizations are possible (19). However, for cases of interest, we will adduce from numerical experiment a fast heuristic that closely approximates the optimal solution for both moderate and very large horizon M _h. This strategy is in contrast to the previous literature, in which only the asymptotic behavior of proposed strategies, themselves not necessarily optimal, is at best rigorously bounded (20, 21).

Ethical Principles and Specific Models

The imposition of ethical constraints beyond utilitarian constrains possible choices for the patient-specific cost function c(m|a,b,r). One principle can be that the cost assigned to a patient should not depend explicitly on where they are in the study or on the assignments made for other patients. That is,

This principle excludes, e.g., cost functions that explicitly assign a lower cost to distant, later failures than to earlier ones and also cost functions that require explicitly greater sacrifices by earlier patients. We name this principle equality. Yet another interpretation of Eq. 9 is that it requires the cost function to be “ideal”, in the sense that it depends explicitly only on the true success probabilities a and b, even though these are unknown.

Discounting the future exponentially is incompatible with equality. The considerable body of literature that bears on that case, especially the Gittins Index and its extensions (14, 22, 23), is thus not directly applicable here (24).

A more subtle ethical principle is that the assignment probability r should enter c(a,b,r) only as an expectation over the decision between A and B. This principle then requires

where c _A and c _B (or their algebraic equivalents c _e and c _o, denoting “even” and “odd”, cf. Eq. 18, below) are still free for us to choose. (Recall that s ≡ 2r − 1.) The ethical meaning of this principle, here termed outcomes, is to require that the cost depend only on outcomes, as functions of the true values a and b, and not on some other explicit function of the strategy r.

Taken together, equality and outcomes imply

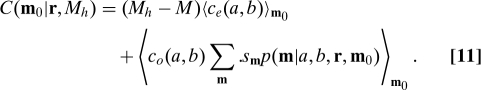Because only the second term depends on s, we see that the optimal strategy depends only on c _o(a,b), and not on c _e(a,b), an important simplification. Also, if Eq. 10 holds, then the recurrence Eq. S7 depends on r _m completely linearly, so the optimal strategy will always take the extreme values 0 or 1, so it will be deterministic.

Examples of Cost Functions.

We can express some standard cost functions (24), and others, in the context of Eq. 10. Expected failures (EF) are costed as 1 − a if A is assigned, or 1 − b if B is assigned, so

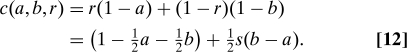Expected successes lost (ESL) are costed only as the difference in success rates and only when an inferior treatment is assigned. That is,

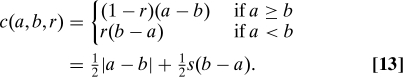Although ESL may seem a “fairer” strategy than EF, we can see immediately that the two are actually equivalent, because in both cases c _o(a,b) = $\frac{1}{2}$(b − a). This “natural” choice for c _o is the one that we model in more detail below. EF and ESL satisfy utilitarian, equality, and outcomes.

Other cost functions are possible: Discounting the future at some interest rate d was already mentioned. An example is discounted ESL,

which fails equality.

Expected inferior treatments (EIT) assigns a cost that depends only on the sign of a − b, not its magnitude,

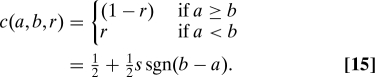We see that this cost function is not equivalent to ESL or EF but that it does satisfy equality and outcomes. It fails, however, a different desirable property, indifference, namely that c _o(a,b) should go to zero continuously as |a − b| → 0.

Dollar cost of failures (F$) is an example of a cost function that includes the direct economic cost of treatment. Here each treatment's failures are costed at respective prices D _A,B,

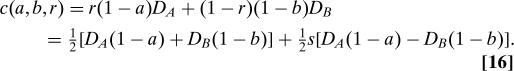This function illustrates two further principles by failing both. We can say that a cost function satisfies best treatment if

This principle says that assigning the better treatment should always yield the lower patient-specific cost. F$ also fails the level playing field principle that neither A nor B should be treated preferentially, that is, that interchanging the values a and b should yield a sign-flipped strategy,

Best treatment and level playing field are separable principles. For example, an interesting variant of Eq. 16 is the expected cost of treatment of lost successes (CTLS),

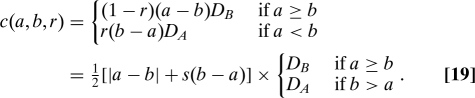This cost function assigns no cost to patients assigned to the superior treatment, or to successes of the inferior treatment; it assigns the (dollar) cost of the inferior treatment to that treatment's lost successes. CTLS satisfies best treatment, but it does not satisfy level playing field because it disfavors a treatment that is both inferior and more costly. We return to CTLS below in the context of comparative effectiveness research, for which it is a interesting model.

Numerical Experiments and Heuristics

Consider the case c _o(a,b) = $\frac{1}{2}$(b − a), which is shared by EF and ESL and which satisfies all of utilitarian, equality, outcomes, indifference, best treatment, and level playing field. Eq. S7 easily computes the optimal strategy on a desktop computer for M _h ≲ 300, and another order of magnitude or so is possible on a supercomputer (19). The solution for each value M _h labels the integer simplex (nonnegative lattice constrained by ≤ M _h) with r values 1 or 0 corresponding to patient assignments of A or B respectively. A crucial question is What is the topology of the solution? Are there regions with fine-grained patterns of interpenetrating 0's and 1's? Or are there large regions of 0's, separated from large regions of 1's by sharp boundaries? And, if the latter, how many such regions are there, and how sharp are their boundaries?

The Optimal Solution Has Sharp Boundaries.

The perhaps surprising answer from numerical experiment is that (except possibly for a set of small measure) the solution consists of a single four-dimensional region each of 0's and 1's, separated by a single sharp three-dimensional boundary surface. We have two lines of evidence for this claim. First, constructively, we actually find a simple, parameterized surface that very nearly separates the 0's and 1's. This surface is defined by just two variables (out of three possible, for fixed M)

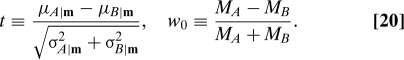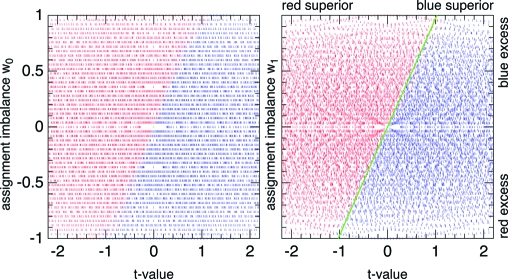
The salience of these variables is not unexpected: t is a t-value for a − b, viewed as a random variable, and measures the statistical significance with which a treatment is known to be superior; w ₀ is the relative imbalance in sample sizes. As an example, Fig. 1 shows all the optimal assignments for the values M = 50 and M _h = 100. Simply by trial and error, it is not hard to find a slight modification of w ₀, which even further sharpens the boundary and, as it happens, also makes it almost a straight line,

where μ′ ≡ $\frac{1}{2}$(μ_A + μ_B). This improved parameterization of the sharp boundary is also illustrated in Fig. 1, where the best-fitting straight-line boundary is shown in green. One could of course locate the true boundary more precisely, but Eqs. 20 and 21 are good enough for this paper.

Fig. 1.

Optimal EF or ESL assignments of patient M = 50 in a clinical trial with horizon M _h = 100 as a function of t and w ₀ (Left) or w ₁ (Right). The value t measures the certainty with which one treatment is known to be superior, whereas w ₀ or w ₁ parameterizes the imbalance of sample sizes. Blue indicates assignment to A, red to B. The rather sharp boundary in (t,w ₀) coordinates is even sharper, and more linear, in (t,w ₁) coordinates. A nearly optimal heuristic strategy is to assign the apparently superior treatment (by t-value) unless it is too overrepresented in the sample (by w ₁ value). The green line indicates the divide.

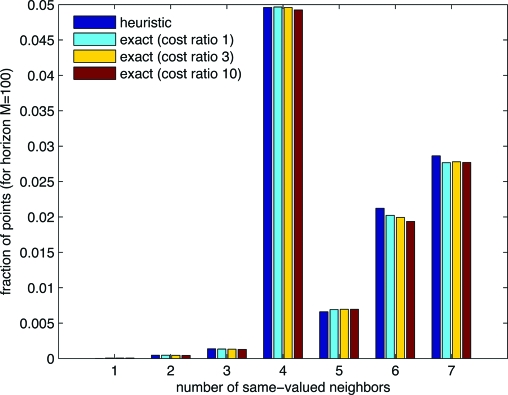
A second, quite different line of evidence that the boundary surface is sharp lies in neighbor statistics: for each point in the interior of the simplex, we ask how many of its Cartesian nearest neighbors have the same r value as it has. In four dimensions, a plane boundary allows only values 4, 5, 6, 7, and 8. Sharp, but slightly curved boundaries, can have smaller values, but only as rare perturbations from the plane value 4. However, interpenetrating 0's and 1's can also have values 3, 2, 1, or 0, generically. Fig. 2 shows the results for a sample case M _h = 100. The first bar in each group is for the heuristic linear relation between t and w ₁, by definition a sharp surface. The second bar is the exact solution. (The remaining bars are discussed later in this section.) No evidence of an excess of counts in the range 0–3 is seen, and the detailed statistics of the exact solution are indeed very close to that of the sharp-boundaried heuristic. Note that this test, for the range 1–7, is not biased by the decreasing surface-to-volume ratio as M _h → ∞.

Fig. 2.

A point can have 0–8 nearest neighbors sharing its strategy (of treatment A or B). The relative frequency of each value is indicative of whether the boundary between the two strategy regions is sharp or fuzzy. Comparing exact solutions with a heuristic with a known sharp boundary, one sees that the boundary for the exact solutions is apparently sharp.

Heuristic for the Optimal Solution.

We have glossed over the step of finding a fitting function for the slope of the (t,w ₁) line as a function of M and M _h, further described in the SI Appendix. For fixed M and increasing M _h, the dependence is very close to [ln(M _h/M)]^0.42 over a wide range of M and M _h. The remaining dependence on M is then empirically found to be very close to linear in ln(M), and hence extrapolatable with some confidence to values of M and M _h much larger than the values used for the fit.

The result of these empirical fits to a sharp boundary is a heuristic (that is to say, empirically justified) approximation to the optimal strategy:

where

(Note that t and t _crit can each be of either sign.)

To gauge how good is the heuristic approximation, we can compare it with the optimal strategy in the latter's computationally accessible region. Simply counting correct vs. incorrect values on the lattice, one finds that Eq. 22 is correct 99.43% of the time at M _h = 60, rising slightly to 99.66% at M _h = 280 (which has about 2.6 × 10⁸ lattice points). A more meaningful comparison is to compute, by Monte Carlo trials, the mean cost of various strategies from various starting points (priors m ₀). Table 1 shows results for ESL costs with horizon sizes M _h = 100 and 200 and for three priors. One sees that the exact and heuristic strategies are within a few hundredths of each other. Because the units are lost successes over the entire trial, approximation errors of this magnitude seem genuinely negligible.

Table 1.

ESL costs for various strategies

Starting point m0 =	(0, 0, 0, 0)	(0,0,10,5)	(10,5,10,5)
Horizon Mh = 100
Exact	1.75	1.48	1.64
Heuristic	1.76	1.50	1.65
Scaled horizon	1.84	1.55	1.69
Local Bayes	2.76	2.67	2.52
Play-the-winner	7.69	6.73	3.24
MA = MB ≡ 50	16.6	14.2	6.37
Horizon Mh = 200
Exact	2.24	2.05	2.65
Heuristic	2.28	2.10	2.67
Scaled horizon	2.44	2.31	2.79
Local Bayes	3.53	3.40	4.19
Play-the-winner	15.3	14.6	7.82
MA = MB ≡ 100	33.3	28.4	12.7

Table 1 also shows comparable ESL costs for the traditional strategy of dividing the M _h patients into equal samples M _A = M _B = M _h/2. When one or both treatments have initially unknown efficacy, the lost successes are an order of magnitude larger than for an adaptive strategy that is anything close to optimal. Also shown in the table is a popular “local” strategy, play-the-winner, which assigns the same or different treatment as the immediate predecessor depending on whether it was a success or failure; it is seen to be far from optimal. (The entries labeled “scaled horizon” and “local Bayes” are discussed in the following subsection.)

Infinite Horizon Problem and Scaled-Horizon Strategy.

Apart from solving (if in heuristic approximation) a long-outstanding computational problem (19), the purpose of Eq. 22 is to allow us to think quantitatively about the infinite horizon problem. Formally, if we fix m (and thus M) and let M _h → ∞, then t _crit (Eq. 23) also → ∞, though only very slowly as a small power of a logarithm. The optimal strategy r _m thus formally converges to assigning whichever treatment is underrepresented, that is, to the traditional strategy of equal sample sizes for A and B. Although this technically satisfies our ethical principles thus far, it is not a useful answer, because all beneficial exploitation of information has been pushed to the infinite future. There is no escaping this, except to forbid it by an additional ethical principle, one that must slightly modify how we interpret equality.

Consider this principle: Patient number M's assignment to A or B should be no less beneficial to her than as if the horizon were 2M − 1 rather than ∞. We can call this past-future parity. The ethical justification is that patient M has benefitted from M − 1 predecessors, so she should in turn benefit M − 1 successors, but not be obligated for more. We can apply this principle by the horizon-independent strategy of assigning to patient M the value r(m|2M − 1); we refer to this as a scaled-horizon strategy. In Eq. 23, we replace the factor containing M _h by (ln 2)^0.42 ≈ 0.857.

The scaled-horizon strategy is not the exact optimization of any simply stated total cost function. However, given a current state of knowledge, it assigns to each patient M the treatment that would have been assigned if the strategy were an optimal equality strategy for horizon 2M − 1. Whether one chooses to say that a scaled-horizon strategy “satisfies” equality, or “modifies” it, the relevant quantitative question is how much cost is actually added by the scaled-horizon strategy, which is horizon-independent, as compared with optimal strategies for horizon values M _h known in advance. Table 1 gives examples for horizon values M _h = 100 and 200. One sees that the added cost is at most the order of tenths of a lost success in this parameter range, and it should increase only very slowly with M _h. These numerical results suggest that scaled-horizon strategies can be statistically and ethically justifiable approaches for M _h → ∞, that is, for arbitrarily large clinical or comparative-effectiveness trials whose size is not known in advance, or indeed for standard-of-care recommendations in a large population.

For comparison with the scaled-horizon strategy, Table 1 also gives results for a “local Bayes” strategy (called “TAB” in ref. 25). This strategy assigns a patient to A with probability Prob(a > b | m). Because the horizon M _h does not enter, it is by definition horizonless. However, its performance is inferior to the scaled horizon (see the SI Appendix).

Worth noting is that expected (i.e., mean) costs, as shown in Table 1, may not be the only quantities of interest. All of the strategies listed in Table 1 produce heavy-tailed distributions, so that the cost of any one trial may be several times the mean. See the SI Appendix for more details of the distributions.

Cost of Treatment as a Variable.

How should the economic cost of treatment enter the equation? There is little dispute that comparative effectiveness research should seek to find interventions that are cheaper and more effective than alternatives. Controversy arises in considering how to approach treatments that may be slightly more effective but significantly more expensive (26, 27). Then, fears about access to treatment and tension between the benefit to the patient and the economic cost to society are unavoidable.

Here we consider only the limited, but ethically less perilous, case where the costs of treatments A and B are known, but their effectiveness is not known or only imperfectly known. The goal is to learn which treatment is superior and then to assign the superior treatment independent of cost. However, we want to expend a minimum economic cost in gaining the required comparative knowledge. In other words, we don't want to waste resources on a more expensive treatment that also turns out to be inferior. CTLS, Eq. 19, was constructed exactly for this situation. CTLS assigns no cost to patients assigned to the superior treatment, or to successes of the inferior treatment; it assigns the dollar cost of the inferior treatment to that treatment's lost successes. Like EF and ESL, CTLS satisfies utilitarian, equality, outcomes, indifference, and best treatment; it thus deserves serious consideration as an ethical approach to incorporating the economic cost of treatment into a strategy for clinical trials or comparative effectiveness studies.

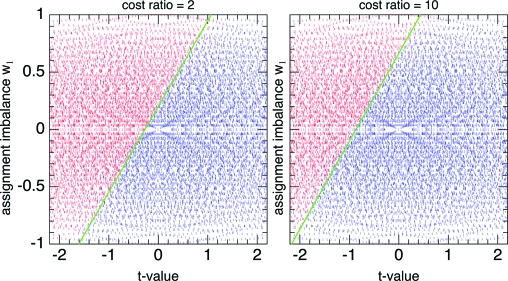
As above, but with the CTLS patient-specific cost function, we can easily compute exactly optimal strategies up to M _h ∼ 300. There is one new parameter, namely the cost-of-treatment ratio D _B/D _A ≥ 1. (As a convention, we take B to be the more expensive treatment.) Also as above, we can ask whether the boundaries of the optimal strategy are sharp. Again, the evidence is that they are, as shown in Fig. 3 and the yellow and red bars in Fig. 2. One sees in Fig. 3 that the effect of a cost ratio different from 1 is to shift the (still quite straight) boundary to the left, so that the more expensive treatment is allocated only when the t-value more strongly indicates its superiority.

Fig. 3.

Optimal CTLS assignments of patient M = 50 in a clinical trial with horizon M _h = 200 as a function of t and w ₁, for cost ratios D _B/D _A = 2 (Left) and 10 (Right). The more expensive treatment (red) requires a more convincing t-value to justify its assignment.

Numerical experiments indicate that the slope of the boundaries in Figs. 1 and 3 vary only very slightly with cost ratio and that the dependence on D _B/D _A is close to logarithmic. A generalization of heuristic Eq. 23 is then

This is not as good an approximation to the exact solution as was Eq. 23, but it is good enough for understanding the nature of the solution. A better fit could be found, as needed.

Discussion

For specificity we have focused on finding, by numerical experiment, near-optimal heuristic solutions to a specific two-armed bandit problem. This problem models only a very idealized clinical trial: exactly two treatments, exactly two outcomes, previous outcomes known as each patient is assigned. However, the solutions that we found have striking properties that suggest immediate generalizations to more complicated cases.

In brief, the heuristic solutions have this form: (i) Compute a t-value that measures the certainty with which a treatment is known to be superior. (ii) Assign that treatment if the t-value exceeds some threshold value t _crit. (iii) t _crit increases monotonically (something like linearly) with the imbalance of previous assignments; that is, an overrepresented treatment requires a somewhat higher standard of proof. (iv) t _crit increases slowly (something like logarithmically) with patient number M, and even more slowly (as something like the square root of a logarithm) with horizon size M _h. These increases ensure that new information will be gathered, when it is needed, even at late times as M → ∞. (v) If cost of treatment is a relevant variable, then t _crit is additively increased by a slowly increasing function of the unfavorable cost ratio (something like logarithmically), so that expensive treatments require more proof of effectiveness.

For cases more complicated than those considered here, one could readily search for optimal strategies only within the above restricted framework, that is, for an optimal or near-optimal formula for t _crit. This is a much easier problem than the optimization over a general strategy, and susceptible to direct optimization techniques. One might also try strategies that leverage off the approximations in this paper. For example, for a clinical trial with block assignments of N new patients at a time, with the outcomes of previous blocks available as each new block is assigned, one might compute (e.g., by Monte Carlo using Eqs. 23 or 24) the expected number of assignments to each treatment for the next N patients from any point m. Although the resulting strategy is not an exact optimization, it should be close to one.

This paper's specific model also suggests a general utility for scaled-horizon strategies which allow the horizon M _h to be unknown or unbounded. Although not exactly optimal, scaled-horizon strategies are close enough to optimal to be ethically desirable: They impose much lower expected costs on patients than fixed allocation strategies like equal sample size, or nonoptimal adaptive strategies like play-the-winner. The scaled-horizon strategy is not the same as exponentially discounting the future, but the two strategies each have a kind of scale invariance. It seems possible that there could be approaches analogous to the Gittins Index (14, 22, 23) for scaled-horizon strategies.

Finally, we think that the exact role of economic cost of treatment should be mathematically explicit in clinical trials, comparative effectiveness studies, and clinical recommendations. We have given an example of a cost function, CTLS, that completely avoids the ethical issue of whether an inferior, but less costly, treatment should be assigned, but which nevertheless minimizes resources wasted on costly, inferior treatments. Combining CTLS with a scaled-horizon strategy gives a methodology for choosing among treatments that is unified and applicable from early clinical trials through to standard-of-care clinical recommendations affecting potentially unlimited numbers of patients. This methodology optimizes resources in a definably ethical way. In particular, a proposed new treatment that is more expensive but no better than an existing treatment becomes quickly disfavored under the CTLS cost function.