Homologous pairing in stretched supercoiled DNA

Abstract

By using elastic measurements on single DNA molecules, we show that stretching a negatively supercoiled DNA activates homologous pairing in physiological conditions. These experiments indicate that a stretched unwound DNA locally denatures to alleviate the force-driven increase in torsional stress. This is detected by hybridization with 1 kb of homologous single-stranded DNA probes. The stretching force involved (≈2 pN) is small compared with those typically developed by molecular motors, suggesting that this process may be relevant to DNA processing in vivo. We used this technique to monitor the progressive denaturation of DNA as it is unwound and found that distinct, stable denaturation bubbles formed, beginning in A+T-rich regions.

Many cellular processes involving DNA–DNA and DNA–protein interactions (replication, homologous recombination, transcription etc.) are affected by the superhelicity of the DNA (1–3). A plausible explanation is that the torsional energy of a negatively supercoiled molecule helps lower the barrier to local denaturation of the double helix (4–8). In support of this notion, experiments have shown that large-scale pairing between negatively supercoiled DNA and homologous single-stranded DNA could be achieved by heating the DNA (9) or in the presence of the recA protein (10–12). In this study, we used DNA micromanipulation techniques to show that homologous pairing also can be regulated by varying the stretching force applied to a negatively supercoiled duplex. Stretching the DNA prevents it from relaxing its torsional stress by writhing, and its only alternative is to locally denature (13, 14). Previous mechanical measurements of the energetics of the denatured phase indicate that the molecule is strand-separated locally (15). Here, the denaturation is detected by monitoring the pairing of homologous single-stranded DNA probes with the exposed regions of a single mechanically constrained DNA molecule (see Fig. 1). We found that, in physiological conditions of ionicity, temperature, and supercoiling, a 2-pN force is sufficient to provoke large-scale denaturation of the DNA. This force is small in comparison to those generated by molecular motors; forces of up to 14 pN (16) have been measured on transcribing Escherichia coli RNA polymerase. This suggests that force-driven denaturation may occur in vivo during the course of DNA transcription or replication.

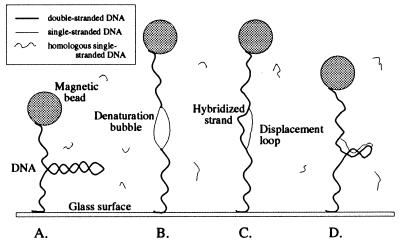
Figure 1.

An overview of the experiment, which takes place in four steps: (A) We apply a low stretching force (F < F_c) to the DNA and measure its extension as a function of supercoiling. In these conditions, a negatively supercoiled DNA forms writhed structures known as plectonemic supercoils (or plectonemes) and its extension decreases. (B) The negatively supercoiled DNA then is stretched with a force F > F_c. This disrupts plectonemes and locally denatures the molecule. (C) Single-stranded, 1-kb DNA fragments complementary to the sequence in the denaturation bubble thus can hybridize onto the exposed bases of the duplex. A double helix is formed on one strand of the denaturation bubble, and the other single strand is displaced. (D) We relax the stretching force. The hybridized exogenous strand now prevents the bubble from closing. The bubble absorbs a part of the negative supercoiling of the DNA, and as a result, fewer plectonemes are present in the molecule. This is detected when we measure the low force extension vs. supercoiling curve.

Topological Formalism.

The topology of DNA is described by two parameters: the molecule’s writhe Wr and its twist Tw. The twist is the number of times the constituent strands of the molecule wrap around each other (equal to the number of helical steps in the molecule), and the writhe counts the number of times the axis of the molecule crosses itself in interwound structures. White’s theorem (17) states that the sum of these two terms is the linking number of the DNA, Lk = Tw + Wr, which is constant when the ends of the molecule are prevented from rotating freely. Assuming that a torsionally relaxed DNA lacks the spontaneous curvature needed to form loops (Wr₀ = 0), Lk₀ = Tw₀ = L/h where L is the contour length of the molecule and h ≈ 3.5 nm its helical pitch. Thus, ΔLk = Lk − Lk₀ = ΔTw + Wr, which means that the excess or deficit in linking number can be stored by modifying the helical pitch of the molecule (ΔTw = Tw − Tw₀) and by forming interwound structures (Wr). The degree of supercoiling σ = ΔLk/Lk₀ is the normalized measure of the number of turns, or links, added to or removed from the molecule. The DNA is negatively supercoiled when σ < 0 and positively supercoiled when σ > 0. The DNA of organisms living at or around 37°C is estimated to have a degree of supercoiling σ ≈ −0.06 (18).

METHODS

Experimental Setup.

Our experimental set-up has been described previously (15, 19). We work with λ-DNA (48, 502 bp), which was modified by ligating to one end a 1.3 kbp DNA fragment labeled with biotin groups and to the other end a 0.9-kbp fragment labeled with digoxigenin groups. The final construction is 50,702 bp (16.9 μm) long. The construction is anchored at multiple sites at one end to a treated glass surface coated with anti-digoxigenin and at the other end to a Dynal M280 superparamagnetic bead coated with streptavidin (Fig. 1A). A magnetic field gradient is used to pull on the tethered bead, and rotating the magnetic field causes the bead to rotate and coil the DNA. An unnicked molecule can thus be under- (over-) wound to a fixed negative (positive) number of turns n relative to its torsionally relaxed state n = 0. Thus, in our system σ = n/Lk₀. By placing the glass surface in thermal contact with Pelletier modules, we can regulate the temperature at which the experiments are performed from 15 to 65°C (the limits actually are set by the thermal stresses on the optics). The glass surface rests atop an inverted microscope that relays video images of the bead’s Brownian motion to a PC. The DNA’s extension l can be measured to within <100 nm by determining the mean position of the bead relative to the surface, and computer analysis of the bead’s fluctuations is used to determine the magnitude of the vertical force F applied to the molecule (15, 19). Indeed, the DNA bead system behaves like a simple pendulum whose tranverse fluctuations Δx² satisfy the equipartition theorem: ½ 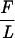 Δx² = ½ k_BT. Thus, the three mechanical parameters in our experiments are the degree of supercoiling σ of the DNA, the applied stretching force F, and the resulting extension l of the molecule. We measure either force vs. extension curves (at constant supercoiling) or extension vs. supercoiling curves (at constant force).

Preparation of Single-Stranded DNA Probes.

For the purposes of the hybridization reactions, three double-stranded, 1-kb DNA fragments were generated by using standard PCR techniques based on a λ-DNA template (see Fig. 2). They were selected based on their position and A+T content. The primers were 30 bp long, and one of the primers in each pair was 5′ end-labeled with biotin. The PCR products were purified by using the QiaQuick PCR purification kit and were quantified by gel electrophoresis techniques. Biotin-labeled DNA probe (10 μg) then was incubated for 1 h with 1 mg of streptavidin-coated DYNAL Dynabeads in a 20-μl volume of Tris 10 mM/EDTA 1 mM containing 1 M NaCl. The quantity of unbound DNA was evaluated by gel electrophoresis to determine the total mass of DNA bound to the beads. The bead–DNA mixture then was washed with the standard experimental solution (all of the experiments were performed in a buffer consisting of 10 mM phosphate buffer, pH 8/150 mM NaCl/0.01% Tween-20/3 mM NaN₃) and brought to a final concentration of 0.02–0.03 mg/ml DNA. The solution then was heated 5 min at 94°C to denature the DNA, and the beads carrying the biotin-labeled single-strands were isolated magnetically and eliminated to prevent re-annealing of the 1-kb single-stranded probe. The single-stranded DNA fragments, referred to hereafter as AT₁, AT₂, and GC₁ (see Fig. 2) then usually were sonicated to yield smaller fragments (≈100 bp) that hybridized better with the stretched, coiled DNA.

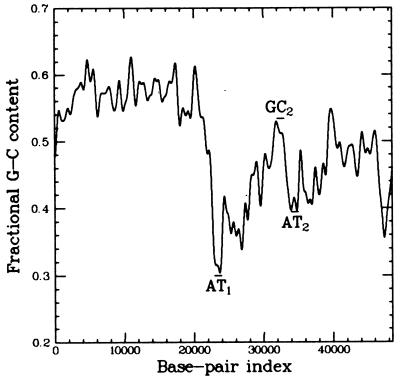
Figure 2.

The fractional GC content of λ-DNA averaged over a few hundred base pairs (on shorter length scales, this value fluctuates more). This map was used to test for the localization of denaturation bubbles: 1-kb probe AT₁ (consisting of a ssDNA fragment spanning base pairs 22,942–23,942) was selected for its high AT content (70%). AT₂ (60% A+T) probed base pairs 34,000 to 35,000, and GC₁ (50% A+T) covered base pairs 32,000 to 33,000. Probes AT₂ and GC₁ were selected because they have significantly different AT contents yet are physically very close to one another. All probes were prepared homologous to the same strand of λ-DNA.

RESULTS

Characterization of a Single Supercoiled DNA Molecule.

We began our work by selecting a dsDNA molecule in our sample whose extension was sensitive to the degree of supercoiling (molecules with a nick in their phospho-diester backbone are insensitive to supercoiling). Indeed, our experiments relied on stretching and twisting to both perform diagnostic tests on the DNA and drive the hybridization reactions. Consider a normal supercoiled molecule at 27°C: its extension vs. supercoiling curve obtained at low constant force (F = 0.1 pN; see open circles in Fig. 3A) is symmetric with respect to the sign of coiling (15, 19, 20). As one over- or underwinds the molecule, interwound structures known as “plectonemes” begin to form (generating writhe), and the extension of the molecule diminishes. The molecule’s σ is equal to zero when its extension is maximal. Such a curve obtained at low force serves to characterize the initial topology of the DNA and serves as a reference data set. Then, by measuring the molecule’s force vs. extension behavior at σ = 0 and fitting the data to the worm-like chain model of elasticity (21, 22), we determined the persistence length ξ and contour length L of the molecule.

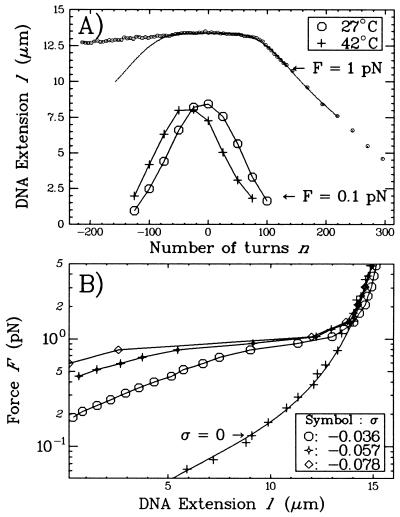
Figure 3.

(A) Extension vs. supercoiling curves for a single DNA molecule in the standard solution. The DNA measured 16 μm as determined by a worm-like chain fit (21, 22) to its torsion-free force vs. extension curve (data not shown). The low force curve (F = 0.1 pN) obtained at 42°C is translated by −27 turns relative to the one obtained at 27°C. The high force curve (F = 1 pN and T = 27°C) is interesting in that the molecule contracts differently for n > 0 than for n < 0. In particular, the symmetry between overwinding and underwinding is broken at about n_c ≈ −70 turns (where the experimental curve separates from the symmetrical continuous curve, obtained by reflecting the data for σ > 0 about σ = 0). (B) Force vs. extension curves obtained at 27°C. The σ = 0 data set was fit by the worm-like chain model with L = 16 μm and ξ = 45 nm. Note that the rigidity of the molecule is a sensitive function of the degree of supercoiling. In these conditions, the molecule undergoes an abrupt transition to an extended state at the critical force F_c ≈ 1 pN.

To clarify how extension vs. supercoiling curves may be used to characterize the topology of the molecule, consider the following example. Previous studies have shown that the twist angle between base pairs is a function of several environmental parameters such as temperature and cation concentration. In particular, the rotation angle of DNA has the following temperature dependence: −0.011° °C⁻¹bp⁻¹ (23, 24). According to this formula, the natural twist Tw₀ of a 48.5-kbp DNA will decrease by 22 turns if it is heated from 27 to 42°C. This effect is visible in Fig. 3A, where the extension vs. supercoiling curve for such a DNA at 42°C is translated by −27 turns relative to the curve measured at 27°C. This system thus constitutes a highly sensitive means for studying changes in DNA topology.

When we increase the stretching force (F = 1 pN), the molecule no longer behaves similarly under positive or negative supercoiling (see Fig. 3A). As one begins to overwind the molecule, its extension changes little as its twisting starts to increase. We assume that the torque Γ acting on the DNA increases linearly (5, 13, 14): Γ ≈ k_BT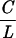 2πn where k_B is Boltzmann’s constant and T the temperature, C the DNA twist elasticity (of the order of 80 nm), L the contour length of the molecule, and n the number of turns by which the molecule is twisted. At n ≈ 80 turns, the molecule undergoes a buckling instability (similar to that observed in twisted ropes) (25, 26), and stable plectonemes begin to form, thus shortening the molecule. When the molecule is unwound at F = 1 pN, one notes that its extension is much less sensitive to supercoiling. Such a behavior suggests that no plectonemes form as one progressively unwinds the molecule. We presume that, as the molecule is negatively twisted, its torque increases linearly until it reaches a critical torque Γ_c, at which point the molecule locally denatures. This occurs for n = n_c ≈ −70 turns (σ_c ≈ −0.015; see Fig. 3A), beyond which the extension of the molecule is no longer symmetric with respect to the sign of the coiling. We thus estimate that Γ_c ≈ 2k_BT and propose that, as the molecule continues to be underwound, the energy supplied to the system goes toward enlarging the bubble and the torque of the molecule remains at or near Γ_c.

The force vs. extension curves obtained for negatively supercoiled DNA at 27°C (Fig. 3B) complete this picture. As one stretches the molecule, it begins to lengthen as its plectonemes are removed. The stretching thus drives an increase in the twist and in the torque acting on the molecule, which reaches Γ_c at the critical force F_c ≈ 1 pN. At this point, the molecule locally denatures, destroying its remaining plectonemes and abruptly lengthening. An analysis of these force curves (15) shows that the denatured regions have a free energy per base pair equal to the energy of denaturation E_d of AT base pairs, implying that these regions are strand separated. Another estimate also gives E_d = Γ_c2π/10.4 ≈ 1.2k_BT/bp. Note that, by increasing the temperature from 27 to 42°C, the critical force F_c decreases from 1 pN to ≈0.7 pN (see Fig. 4). These curves characterize the elasticity of negatively supercoiled DNA and also can serve as topological references.

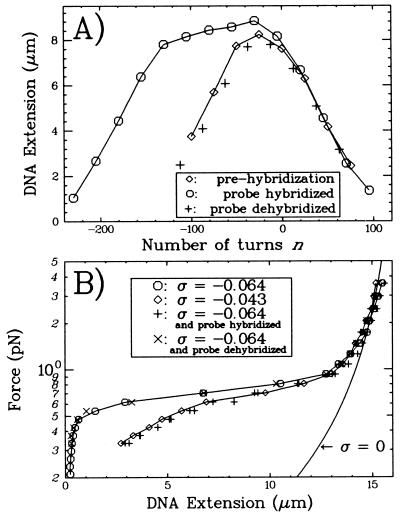
Figure 4.

(A) Extension vs. supercoiling curves for a DNA molecule during the course of the hybridization experiment (T = 42°C). The low force curve obtained before hybridization (⋄) is symmetric and serves as the reference data set. After hybridization has occurred (at n = −500 and F = 2 pN), the curve obtained at low force (○) is no longer symmetric but is “broadened” by ≈100 turns relative to the prehybridization curve. +, After dehybridization is performed (see text), the molecule recovers its initial extension vs. supercoiling behavior. (B) Force vs. extension curves for a single DNA molecule (T = 42°C). Plain curve: worm-like chain model (22) for a torsionally relaxed (σ = 0) DNA with a persistence length ξ ≈ 50 nm and contour length L ≈ 16 μm. (○): DNA unwound by n = −300 turns (σ = −0.064). ⋄, DNA unwound by n = −200 turns (σ = −0.043). Note that at T = 42°C F_c = 0.7 pN. +, DNA unwound by n = −300 turns and containing a region hybridized to a 1-kb homologous single-stranded DNA. The elastic properties of the DNA are now similar to those for a DNA unwound by n = −200 turns. ×, After dehybridizing the probe, the duplex recovers its initial behavior.

Hybridization§ and Dehybridization of Probe AT₁.

As just described, we began by obtaining reference data sets for the DNA’s extension vs. supercoiling and force vs. extension behaviors (see Fig. 4). Then, to initiate full hybridization with probe AT₁, we unwound the molecule by n = −500(σ = −0.107), applied a force (F = 2pN > F_c) to open a denaturation bubble, and added homologous probe AT₁ to the solution. The probe was left to incubate for 1 h (typical hybridizations were complete after 1 h, when the probe was at a concentration of 10–20 μg/ml). To check that hybridization had occurred, we reduced n to −300 and F to 0.1 pN and measured either a force vs. extension or an extension vs. supercoiling curve for comparison with the reference data sets. In the former case (Fig. 4B), we observed that the curve now matches the force-extension diagram obtained at n = −200 before addition of probe AT₁. In the latter (Fig. 4A), the extension vs. supercoiling curve shows that, as one increases n, the molecule’s extension is no longer symmetric with respect to n = 0. Instead, the curve obtained is “broadened” by ≈100 turns relative to the initial curve. This new behavior is due to specific homologous pairing with probe AT₁; no such changes occur if nonhomologous, single-stranded DNA is used (19). Thus, the hybridization of a 1-kbp probe to a negatively supercoiled DNA “resorbs” ≈100 plectonemic supercoils.

Once hybridization has occurred, the exogenous DNA remains in place until it is forced out by rewinding the molecule to n > −100. Indeed, the force vs. extension and extension vs. supercoiling curves are reversible as long as n < −100 (data not shown). Full dehybridization could be achieved within minutes by overwinding the DNA to n = 200 and stretching it with a 4-pN force. The initial behavior of the duplex is fully recovered once dehybridization is complete (see Fig. 4), and the whole process may be repeated.

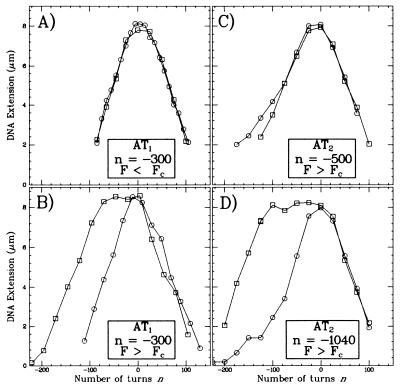
Next, we tested the hybridization of probe AT₁ onto DNA at a more physiological degree of supercoiling (n = −300, σ = −0.064) (see Fig. 5 A and B). These experiments indicate that partial (80%) hybridization can be obtained only if F > F_c. No hybridization was detected at F < F_c. We conclude that, at the critical force F_c, a negatively supercoiled DNA alleviates its torsionnal stress by forming a denaturation bubble in an A+T-rich region.

Figure 5.

Extension vs. supercoiling curves measured at low force (F ≈ 0.1 pN) for DNA incubated with (□) or without (○) a 1-kb hybridization probe. The labels indicate the conditions of incubation: the probe tested, the degree of unwinding of the DNA, and the stretching force applied. (A and B) Experiments performed with probe AT₁. (C and D) Experiments peformed with probe AT₂. (A) No hybridization takes place in these conditions, as F < F_c does not generate a denaturation bubble. (B) Because F > F_c can generate a denaturation bubble, hybridization has occurred as evidenced by the broadening between the two curves. (C) The stretching force is large enough to generate a denaturation bubble in the DNA, but this bubble does not encompass the region spanned by probe AT₂. (D) With this degree of unwinding, a denaturation bubble has formed in the region spanned by AT₂, allowing for hybridization.

Finally, it is interesting to note that these hybridization reactions also could be performed at a lower temperature (27°C) or by using intact 1-kb probes (data not shown). For instance, hybridization of sonicated AT₁ probe at 27°C on DNA unwound and stretched (n = −500, F > F_c) yielded the same results as observed at 42°C. In the case in which intact AT₁ probe was used for hybridization at 42°C, we only observed partial hybridization.

Hybridization of Probes AT₂ and GC₁.

The hybridization reactions performed at F > F_c with the three probes differed only in the degree to which the target λ-DNA must be unwound before hybridization can occur. The various curves obtained after hybridizing and dehybridizing the probes all presented the same characteristics as those described for AT₁. Thus, full hybridization of AT₁ was obtained for duplex unwindings of >−500 turns. Fragment AT₂ only would hybridize onto DNA unwound by a minimum of 1,100 turns (see Fig. 5 C and D). No hybridization with fragment GC₁ was detected for DNA unwinding ranging from −1,300 to −2,900, and only partial hybridization was obtained for an unwinding of −2,930 (data not shown). AT₁ and AT₂ may hybridize onto DNA unwound by −1,200 turns but not GC₁, so we conclude that at least two static and distinct denaturation bubbles are formed in stretched DNA unwound by n = −1,200.

DISCUSSION

The experimental results described above can be explained by considering the topology of the DNA under the combined effects of stretching and twisting. As mentioned previously, negatively supercoiled DNA stores its linking number deficit by reducing its twist and by forming negative writhe. This is typically the case for negatively supercoiled plasmids that are not subject to a constant external force: Wr/ΔTw ≈ 3 (18). When the negatively supercoiled DNA is stretched, however, its writhing is repressed (Wr→0) and, according to White’s theorem, the magnitude of its twist must increase (ΔTw becomes more negative). The consequent increase in torque results in the molecule locally unravelling, i.e., concentrating its twist deficit in local denatured regions. Because unpaired strands have zero twist, a 1-kbp denaturation bubble maintains a linking number deficit of nearly −100 turns (1,000 bp divided by 10.4 bp/turn). Our force vs. extension data for negatively supercoiled DNA shows this process to be reversible; relaxing the force allows the strands to reanneal and restores plectonemes.

Now consider the case in which a 1-kb single-strand DNA has hybridized to one side of a stress-induced denaturation bubble. Our experiments show that relaxing the force does not eject the hybridized strand. The bubble is stabilized by hybridization and even at low force absorbs a twist deficit of −100 turns. The force vs. extension curves are thus similar to the ones observed for unhybridized molecules with smaller values of  σ . Similary, the extension vs. n curves (Figs. 4A and 5) show that, to generate the same number of plectonemes (i.e., the same extension), one has to unwind the hybridized molecule by an extra number of turns (Δn ≈ −100), roughly equal to those absorbed by the stabilized bubble.

These curves also show that, for −100 < n < 0, the extension of the hybridized system is maximal and does not change noticeably with supercoiling, confirming that, in this regime, Wr remains near zero. Thus, as one winds the hybridized system from n = −100 to n = 0, the two strands of the denaturation bubble wind back around each other, displacing and eventually ejecting the exogenous probe. It is interesting to note that reactions using unsonicated probes always yielded incomplete hybridization, indicating that entanglement may occur between the probe and the strands of the bubble.

Our findings relative to probe AT₁ indicate that, at F < F_c = 0.7 pN in physiological conditions of unwinding, temperature and ionic strength A+T-rich regions do not denature massively. In support of this, nuclease hypersensitivity experiments (6) on unwound plasmids have only evidenced small-scale helix destabilization, and this in the presence of low concentrations of stabilizing cations (10 mM Tris HCl/1 mM Na₂EDTA). However, applying a slight stretching force F = 2 pN > F_c results in the denaturation of at least 1.6% of the molecule at σ = −0.064. Thus, as one unwinds a stretched DNA molecule, it starts to denature, beginning at regions with the highest A+T content and continuing to those with the lowest A+T content. The hierarchical nature of denaturation is evidenced by the fact that hybridizing GC-rich probes requires higher degrees of unwinding than AT-rich probes. We find that multiple, static bubbles form, as GC-rich barriers can halt the progression of a bubble. Although these experiments probed regions on the kilobase scale, it is possible that smaller bubbles may form according to their (sequence-dependent) energy of nucleation. The signals we observe nonetheless indicate that this technique has the potential to detect hybridization of fragments as small as 30 bp.

Finally, it is interesting to note that the denaturation generated by stretching negatively supercoiled DNA requires a lower stretching force than that needed for direct unzipping of the molecule (27). To unzip 10.4 bp requires separating the two strands of DNA over a ≈10-nm distance using a ≈15-pN force. In our system, we estimate (15) that adding one plectonemic supercoil reduces the extension of the DNA by ≈0.1 μm. These plectonemes act as a sort of lever arm; pulling the molecule with a 1 pN force over ≈0.1 μm removes one plectonemic turn, also denaturing 10.4 bp.

This lever arm property of our setup also might be useful in measuring the topological effects of motor proteins (such as topoisomerases and condensins) in real time. Indeed, if a topoisomerase II acts on the DNA by adding or removing two supercoils at each catalytic step, one can hope to observe directly the extension of the molecule changing by increments of ≈0.2 μm.

CONCLUSION

By using a DNA micromanipulation technique, we have shown that, in physiological conditions, a negatively supercoiled DNA stably unwinds over large distances if it is stretched. The unwinding is detected by measuring the hybridization of single homologous single-strand DNA molecules to the duplex. We conclude that the supression of writhing in negatively supercoiled DNA causes denaturation and promotes homologous pairing. In vivo, DNA writhing may be supressed as a result of the anchoring of the molecule to the nuclear matrix and the subsequent crowding by neighboring loops (28) or scaffold proteins. Also, because the stretching force required to unwind negatively supercoiled DNA is an order of magnitude smaller than those achievable by molecular motors [such as transcribing RNA polymerase (16)], our results suggest that this type of denaturation may occur in vivo in transcribed regions where the supercoiling is unrestrained (29, 30).