On The Use of Dynamic Bayesian Networks in Reconstructing Functional Neuronal Networks from Spike Train Ensembles

Abstract

Coordination among cortical neurons is believed to be key element in mediating many high level cortical processes such as perception, attention, learning and memory formation. Inferring the topology of the neural circuitry underlying this coordination is important to characterize the highly non-linear, time-varying interactions between cortical neurons in the presence of complex stimuli. In this work, we investigate the applicability of Dynamic Bayesian Networks (DBNs) in inferring the effective connectivity between spiking cortical neurons from their observed spike trains. We demonstrate that DBNs can infer the underlying non-linear and time-varying causal interactions between these neurons and can discriminate between mono and polysynaptic links between them under certain constraints governing their putative connectivity. We analyzed conditionally-Poisson spike train data mimicking spiking activity of cortical networks of small and moderately-large sizes. The performance was assessed and compared to other methods under systematic variations of the network structure to mimic a wide range of responses typically observed in the cortex. Results demonstrate the utility of DBN in inferring the effective connectivity in cortical networks.

1 Introduction

Brain networks are of fundamental interest in systems neuroscience. An essential step towards understanding how the brain orchestrates information processing in these networks is to simultaneously observe the activity of their neuronal constituents that mediate perception, learning and motor processing. Numerous functional neuroimaging studies suggest that cortical regions selectively couple to one another (Greicius, Krasnow, Reiss et al. 2003; Koshino, Carpenter, Minshew et al. 2005; Winder, Cortes, Reggia et al. 2007), for example, during complex visual stimulus presentations (Hasson, Yang, Vallines et al. 2008; Tsao, Schweers, Moeller et al. 2008; Bell, Hadj-Bouziane, Frihauf et al. 2009), during motor prehension and execution in visuomotor tasks (Lotze, Montoya, Erb et al. 1999; Verhagen, Dijkerman, Grol et al. 2008), or in working memory and auditory-related tasks (d'Esposito, Aguirre, Zarahn et al. 1998; Caclin and Fonlupt 2006). Despite these significant findings, understanding the highly-distributed nature of cortical information processing mechanisms remains elusive. It is widely believed that the temporal and spatial resolution of current neuroimaging techniques do not enable the investigation of the brain's functional dynamics at the single cell level, nor do they enable the identification of causal relationships between multi-units across distant cortical regions.

Implantable high-density microelectrode arrays (Normann, Maynard, Rousche et al. 1999; Wise, Anderson, Hetke et al. 2004) have enabled scrutinizing activity from cortical neurons at an unprecedented scale, and greatly accelerated our ability to monitor functional alterations of cortical networks in awake, behaving subjects beyond what fMRI studies have revealed. Consequently, the development of analysis tools that can infer the functional connectivity in these networks can yield more insight into how these networks form in response to dynamic complex stimuli, or to signify movement intention and execution through causal interactions between the observed neurons, often referred to as effective connectivity (Aertsen, Gerstein, Habib et al. 1989). Such tools can reveal more evidence in support of modern views suggesting that multisensory integration occurs early in the neocortex (Kayser and Logothetis 2009), as opposed to the more traditional cognitive models of the sensory brain that contends higher level integration of unisensory processing (Ghazanfar and Schroeder 2006). They can also be useful in identifying plastic changes in cortical circuitry during learning and memory (Mehta, Quirk and Wilson 2000; Brown, Nguyen, Frank et al. 2001; Martin and Morris 2002), or post traumatic brain injury (Girgis, Merrett, Kirkland et al. 2007; Jurkiewicz, Mikulis, McIlroy et al. 2007).

Graph theory, widely used in mathematics and machine learning applications, is increasingly becoming popular in the analysis of large scale neural data (Sporns 2002; Denise, David, Richard et al. 2007). In particular, Dynamic Bayesian Network (DBN) is one potential graphical method for identifying causal relationships between simultaneously observed random variables. It was introduced as a probabilistic model of dynamic systems in which temporal dependency governs the statistical relationship between the system elements (Murphy and Mian 1999; Murphy 2002). DBN has also been recently used in inferring transcriptional regulatory networks from gene expression data (Bernard and Hartemink 2005; Dojer, Gambin, Mizera et al. 2006; Geier, Timmer and Fleck 2007). For brain connectivity, DBN has been coarsely applied to infer effective connectivity between multiple brain areas from fMRI data (Zhang, Samaras, Alia-Klein et al. 2006; Rajapakse and Zhou 2007) and, at a more refined resolution, from multi-unit activity recorded throughout the songbird auditory pathway (Smith, Yu, Smulders et al. 2006). Nevertheless, the use of DBNs to characterize cortical networks at the single neuron and the ensemble level has not been fully explored.

In this work, we investigate the application of DBNs to determine the effective connectivity in spiking neuronal networks from the observed spike trains. We assess DBN performance in identifying networks with excitatory, inhibitory, and mixed mono and polysynaptic connectivity patterns with various characteristics using metrics from graph theory. We compare their performance to two multivariate statistical measures, namely, Generalized Linear Models (Dobson 2002) and Partial Directed Coherence (PDC) (Baccalá and Sameshima 2001). Both have been used in studying coarse neural interaction in EEG (Astolfi, Cincotti, Mattia et al. 2006) and fMRI signals (Roebroeck, Formisano and Goebel 2005) as well as spike trains (Sameshima and Baccala 1999; Okatan, Wilson and Brown 2005). We demonstrate the superiority of DBN over these methods for inferring the connectivity of small and moderately large size networks.

2 Theory

2.1 Bayesian Networks

A Bayesian Network (BN) is a graphical representation of statistical relationships between random variables, widely used for statistical inference and machine learning (Pearl 1988; Heckerman 1995). A BN is denoted by B =< G, P >, where G is a directed acyclic graph (DAG) and P is a set of conditional probabilities. Each graph G consists of a set of nodes V and edges E, and is usually written as G =< V, E >. Each node in V, denoted by v_i, corresponds to a random variable x_i. Each directed edge in E, denoted by v_i → v_j, indicates that node v_i (i.e., random variable x_i) is a parent of node v_j (i.e., random variable x_j). Conditional probabilities in P are used to capture the statistical dependence between child nodes and parent nodes. In particular, given a random variable x_i in the graph, we denote by x_π(i) the set of random variables that are parents of x_i. The statistical dependence between x_i and its parent nodes x_π(i) is captured by the conditional probabilities Pr(x_i|x_π(i)). More precisely, the value of random variable x_i is decided by the values of its parents via the conditional probabilities Pr(x_i|x_π(i)), and is independent from the values of other random variables in the graph given the value of x_π(i). Thus, the joint probability distribution of the random variables x_i can be expressed given the conditional dependence on the parents using the chain rule

$$\mathrm{Pr}(x_1,x_2,...,x_N)=\prod _{i=1}^N\mathrm{Pr}\left(x_i\mid {\mathbf{X}}_{\pi \left(i\right)}\right).$$ (1)

Figure 1a shows an example of a Bayesian Network, in which we have three binary random variables: random variable R indicates “if it rains” or not, W indicates “if the grass is wet” or not, and U indicates “if people bring umbrella” or not. The arc from R to W indicates that “the grass being wet” is decided by “if it rains”. Similarly, the arc from R to U indicates that “whether or not people bring umbrella” is decided by “if it rains”. The conditional probabilities Pr(U|R) and Pr(W|R) are summarized in Table 1. According to the chain rule described before, the joint probability Pr(R, U, W) is written as

$$\mathrm{Pr}(U,R,W)=\mathrm{Pr}\left(R\right)\mathrm{Pr}(U\mid R)\mathrm{Pr}(W\mid R).$$ (2)

Figure 1.

(a) An example of a Bayesian Network. Random variable R indicates if it rains or not, W indicates if the grass is wet or not, and U indicates if people bring umbrella or not.

(b) An example of a Dynamic Bayesian Network. Each morning an automatic sprinkler randomly decides whether it should water the lawn or not conditioned on whether it watered the day before and whether there was rain the day before.

Table 1.

Conditional probabilities Pr(W|R) and Pr(U|R).

Pr(W|R)	R = true	R = false	Pr(U|R)	R = true	R = false
W = true	0.7	0.4	U = true	0.9	0.2
W = false	0.3	0.6	U = false	0.1	0.8

2.2 Dynamic Bayesian Network

A Dynamic Bayesian Network (DBN) is an extension of BN to handle time-series or sequential data (Murphy 2002) and, therefore, are much more suitable to analyze nonstationary random processes. In a DBN, the status of a node (variable) at time t₀ is conditionally-dependent on its parents' state in history. Specifically, given a random variable x_i at time T = t + 1, denoted by $x_i^{(t+1)}$, and its parents x_π(i), the value of $x_i^{(t+1)}$ is decided by the values of its parents x_π(i) observed during the interval T = 1 to T = t, denoted by ${\mathbf{x}}_{\pi \left(i\right)}^{(1:t)}$. Note that T here is assumed to be a discrete variable. Similar to Bayesian networks, the statistical dependence between $x_i^{(t+1)}$ and ${\mathbf{x}}_{\pi \left(i\right)}^{(1:t)}$ is captured by conditional probabilities $\mathrm{Pr}(x_i^{(t+1)}\mid {\mathbf{x}}_{\pi \left(i\right)}^{(1:t)})$, and the joint probability $\mathrm{Pr}(x_1^{(t+1)},\dots ,x_N^{(t+1)})$ is computed as

$$\mathrm{Pr}\left(x_1^{(t+1)},x_2^{(t+1)},...,x_N^{(t+1)}\right)=\prod _{i=1}^N\mathrm{Pr}\left(x_i^{(t+1)}\mid {\mathbf{X}}_{\pi \left(i\right)}^{(1:t)}\right).$$ (3)

In many cases, and for the sake of simplicity, it is often assumed that $x_i^{(t+1)}$ is only dependent on the value of its parents observed at time T = t, which simplifies the conditional probabilities $\mathrm{Pr}\left(x_i^{(t+1)}\mid {\mathbf{x}}_{\pi \left(i\right)}^{(1:t)}\right)$ to $\mathrm{Pr}\left(x_i^{(t+1)}\mid {\mathbf{x}}_{\pi \left(i\right)}^{\left(t\right)}\right)$. This is known as the Markov assumption with Markov lag equal to 1. A special case of DBN is the well-known Hidden Markov Model (HMM) (Rabiner 1989). This simplification to the Markov assumption can be extended to include multiple Markov lags. For instance, a DBN with maximum Markov lag equals 3 implies that $x_i^{(t+1)}$ is decided by the value of its parents observed at time T = t, t – 1, t – 2, or $\mathrm{Pr}\left(x_i^{(t+1)}\mid {\mathbf{x}}_{\pi \left(i\right)}^{(t-2:t)}\right)$. Figure 1b is an example of a DBN. Each morning, an automatic sprinkler decides whether to water a lawn. The sprinkler makes a probabilistic decision based on 1) whether it watered the lawn the day before and 2) whether there was rain the day before. The conditional probability distribution table of Pr(S^t+1= true| S^t, R^t) is listed in Table 2. Note that in this example, the variable S is also one of its parents.

Table 2.

Conditional probabilities Pr(S^t+1| S^t,R^t).

Pr(St+1= true| St, Rt)	St	Rt
0.8	false	false
0.3	true	false
0.3	false	true
0.1	true	true

2.3 Learning Bayesian Networks

Learning a Bayesian network from data involves two tasks: learning the structure of the network and learning the parameters of the conditional probability distributions. Structure learning of Bayesian networks is much more difficult compared to parameter learning because once the structure is known, it is easy to learn the parameters of the conditional probability distributions using existing algorithms such as Maximum Likelihood Estimation (MLE).

Learning the structure of the network can be formulated as searching for a network structure G* that best fits the observed data D. Formally, this is expressed as

$$\begin{array}{cc}\hfill G^{\ast }& =\underset{G}{\arg \max }\left(\log \mathrm{Pr}\left(G\mid D\right)\right)\hfill \\ \hfill & =\underset{G}{\arg \max }\left(\log \mathrm{Pr}\left(D\mid G\right)+\log \mathrm{Pr}\left(G\right)\right),\hfill \end{array}$$ (4)

where Pr(D|G) is the likelihood of the data D given the structure G and Pr(G) is the prior probability of G. In our experiments, we assumed a uniform distribution for Pr(G).

There are many structure learning algorithms, and the most popular among them are the score-based approaches (Heckerman 1995; Friedman, Nachaman and Peer 1999; Hartemink, Gifford, Jaakkola et al. 2001). Figure 2 outlines the steps of the DBN structure search algorithm. A scoring function is first defined to estimate the likelihood Pr(D|G) by which a given Bayesian network structure is evaluated on a given dataset, and then a search is performed through the space of all possible structures to find the one with the highest score. Score-based approaches are typically based on well-established statistical principles such as Minimum Description Length (MDL) (Lam and Bacchus 1994), Bayesian Dirichlet equivalent (BDe) score (Heckerman, Geiger and Chickering 1995) or Bayesian Information Criterion (BIC) (Schwarz 1978). In our analysis, we used the BDe score. Let θ_G denote the parameters for the conditional probability distribution for structure G. To evaluate the posterior Pr(D|G), one needs to consider all possible parameter assignments of θ_G, namely

$$\log \mathrm{Pr}\left(D\mid G\right)=\log \int \mathrm{Pr}(D\mid G,{\theta }_G)\mathrm{Pr}({\theta }_G\mid G)d{\theta }_G,$$ (5)

where Pr(D|G,θ_G) is the probability of the data given the network structure and the parameters and Pr(θ_G|G) is the prior probability of the parameters which penalizes complex structures. Under the assumption that the distribution of each node in the network can be learned independently of all other distributions in the network and assuming Dirichlet priors, the BDe score can be expressed in a closed form of (5) as (Cooper and Herskovits 1992; Heckerman 1995)

$$\log \mathrm{Pr}(D\mid G)=\sum _{i,k}\left(\log \frac{\Gamma \left(Z_{ik}^{\prime }\right)}{\Gamma (Z_{ik}^{\prime }+Z_{ik})}+\sum _j\log \frac{\Gamma (Z_{ijk}^{\prime }+Z_{ijk})}{\Gamma \left(Z_{ijk}^{\prime }\right)}\right)$$ (6)

where $\Gamma \left(x\right)=\underset{0}{\overset{\infty }{\int }}{t}^{x-1}{e}^{-t}$ dt is the Gamma function satisfying Γ(x+1)=xΓ(x) and $\Gamma \left(1\right)=1,Z_{ik}=\underset{j}{\Sigma }{Z}_{ijk},Z_{ijk}$ is the number of times random variable $x_i^{\left(t\right)}=j$ and ${\mathbf{x}}_{\pi \left(i\right)}^{(1:t)}=k,Z_{ik}^{\prime }=\underset{j}{\Sigma }{Z}_{ijk}^{\prime }$ and $Z_{ijk}^{\prime }=\mathit{a}Pr(x_i^{\left(t\right)}=j,{\mathbf{x}}_{\pi \left(i\right)}^{(1:t)}=k\mid G_0)$, where a is the equivalent sample size and G₀ is a prior structure.

Figure 2.

Schematic of the DBN structure search algorithm.

The associated optimization of this approach, however, is intractable (Chickering, Meek and Heckerman 2003). Commonly used methods to alleviate this problem include: 1) using some preprocessing methods like conditional independence test to infer the Markov blanket for each node, and thus limiting the candidate structure space; 2) using heuristics, like greedy search or simulated annealing, to find the sub-optimal structures. Herein, we use a score-based approach with simulated annealing search. Simulated annealing search avoids falling in local maxima by choosing certain modifications to the structure that do not necessarily increase the score. Specifically, if for a given modification the score increases, then this modification is accepted, while if the score decreases, then this modification is accepted with probability exp(Δe/T₀) where Δe is the change in the score, which is negative in this case, and T₀ is the system `temperature'. The search starts with a very high T₀ so that almost every structure modification is accepted, and then decays gradually as the search process progresses (Kirkpatrick, Gelatt and Vecchi 1983).

3 DBN and Spike Trains

In the context of spiking cortical networks, we model each neuron in the data by a set of nodes where each node corresponds to the neuron's firing state (`0' or `1') at a given Markov lag. A directed edge between two nodes represents a causal relationship between them that is detected at the associated Markov lag. Figure 3 illustrates an example of a causal network and the corresponding DBN. Consider for example the connection between neurons 3 and 4 with a synaptic latency of 2 bins. This connection is represented in the DBN as a directed edge from one node representing neuron 3 firing state at a Markov lag of 2 to another node representing the current firing state of neuron 4. Modeling time dependency allows DBN to model cycles or feedback loops as illustrated by the loop involving neurons 1, 2 and 3 (represented by a DAG in the DBN). Moreover, this makes DBN capable of capturing relationships that appear at different time lags. This is particularly useful considering that many unobserved neurons, e.g. interneurons, may exist in the pathway between observed efferent and afferent neurons. This may contribute considerable latency between causal events as a result of the aggregate synaptic delay.

Figure 3.

(a) A simple causal network where nodes represent neurons and edges represent connections. l_ij indicates the synaptic latency associated with each connection.

(b) Corresponding DBN where black nodes represent the neuron firing state at a specific Markov lag while white nodes represent the present state.

Existing directed and undirected techniques for identifying neuronal connectivity such as cross-correlograms, partial correlation and partial directed coherence (Sameshima and Baccala 1999; Eichler, Dahlhaus and Sandkuhler 2003) mainly rely on pair-wise correlations assessed over a very fine time scale (typically 0–5 milliseconds). While these techniques may be feasible to implement for a small number of neurons, they become computationally prohibitive for large number of cells and inadequate to collectively assess casual relationships in networks with polysynaptic connectivity in which interaction occurs over broader time scales (10's-100's of milliseconds). DBN, on the other hand, does not rely on pair-wise relationships. It rather takes into account the activity of the entire observed ensemble when searching for relationships between the neurons as expressed in equations (1) and (3). This enables DBN to identify only direct, and not indirect, relationships between observed neurons. This is particularly important when dealing with cortical networks with complex connectivity patterns that are likely to span broader temporal and spatial scales. In such a case, simple pair-wise measures may erroneously lead to classify indirect relationships as direct, or entirely miss certain connections.

An added advantage is that DBN has a unique ability to detect nonlinear relationships that other techniques for inferring effective connectivity (such as Granger causality (Granger 1969)) cannot detect. Nonlinear neuronal response to stimuli has been consistently found in auditory neurons performing coincidence detection of their dendritic inputs in several regions of the auditory system (Agmon-Snir, Carr and Rinzel 1998; Peña, Viete, Funabiki et al. 2001), and in gain modulatory neurons in posterior parietal cortex in response to visual stimuli (Salinas and Their 2000; Cohen and Andersen 2002). Thus, using DBN in analyzing neuronal spike trains might facilitate revealing how the underlying cortical circuits are reconfigured in response to complex, nonlinear stimuli features. Moreover, they can be used to explain the observed correlation in cortical network states beyond what 2^nd order maximum entropy models can reveal, given their sensitivity to variations in temporal dependence (Shlens, Field, Gauthier et al. 2006; Tang, Jackson, Hobbs et al. 2008).

4 Population Model

To examine the performance of DBN in reconstructing a spiking neuronal network, it was essential to use a model to simulate the spike train data in which the “ground truth” was known. We found that multivariate point process models (Brillinger 1975; Brillinger 1976; Brown 2005) are by far the most widely used in recent literature to fit statistics of spiking cortical neurons in a wide variety of brain structures. In our simulations, we used a variant of the generalized linear model (GLM) proposed by (Truccolo, Eden, Fellow et al. 2005). In this model, the spike train S_i of neuron i is expressed as a conditionally-Poisson point process with mean intensity functionλ_i (t|H_i(t)), where H_i(t) denotes the firing history of all the processes that affect the firing probability of neuron i up to time t (e.g. stimulus feature, other neurons' interaction, the neuron's own firing history, etc…). Herein, we do not consider an explicit external stimulus to drive the network, albeit this can be included as an object in the graphical representation in the stationary case or as a set of objects with known transitions in the nonstationary case. We focus on two main variants contributing to λ_i (t|H_i(t)): a) the neuron's background level of activity; and b) the spiking history of the neuron itself and that of other neurons connected to it. Mathematically, the firing probability f(S_i(t) of postsynaptic neuron i at time t can be expressed as

$$f(S_i\left(t\right)=1)\cong {\lambda }_i(t\mid H_i\left(t\right))\Delta =\left(\exp \left({\beta }_i+\sum _{j\in \pi \left(i\right)}\sum _{m=0}^{M_{ij}}{\alpha }_{ij}\left(m\Delta \right)S_j(t-m\Delta )\right)\right)\Delta ,$$ (7)

where Δ is a very small bin width, β_i is the log of the background rate of neuron i, π(i) is the set of pre-synaptic neurons of neuron i (this set includes neuron i itself to model self-inhibition), M_ij is the number of history bins that relate the firing probability of neuron i to activity from presynaptic neuron j, α_ij models the connection between neuron i and neuron j (excitatory or inhibitory), and S_j(t − mΔ) is the state of neuron j in bin m (takes the value of 0 or 1). Unlike the model in (Truccolo, Eden, Fellow, Donoghue and Brown 2005), the length of the history interval of interaction between neurons i and j (equals M_ij × Δ) was not fixed for all neuron pairs, consistent with the notion of cell assemblies (Hebb 1949). To mimic the influence of excitatory post-synaptic potential (EPSP) and inhibitory post-synaptic potential (IPSP), we used the following decaying exponential functions for synaptic coupling (Kuhlmann, Burkitt, Paolini et al. 2002; Zhang and Carney 2005; Sprekeler, Michaelis and Wiskott 2007)

$${\alpha }_{ij}^{\pm }\left(t\right)=\{\begin{array}{cc}0\hfill & ,\mathrm{if}t<l_{\mathit{ij}}\Delta \hfill \\ \pm A_{\mathit{ij}}\exp (-3000(t-l_{\mathit{ij}}\Delta )∕M_{\mathit{ij}})\hfill & ,\mathrm{if}t\ge l_{\mathit{ij}}\Delta \hfill \end{array}\phantom{\}}$$ (8)

where t is the time (in seconds), +/− indicate excitatory/inhibitory interactions, A_ij models the strength of the connection, and l_ij models the synaptic latency (in bins) associated with that connection. Similar to the effects of EPSP and IPSP, the decaying exponential in these expressions implies that a spike from a pre-synaptic neuron occurring towards the end of the history interval has a smaller influence on the firing of the post-synaptic neuron than if it were to occur at a closer time. Figure 4 illustrates α⁺_ij(t) showing that α⁺_ij(t) attains its peak value at l_ijΔ and that the time constant of the decaying exponential is M_ij/3000.

Figure 4.

An illustrative graph of α_ij⁺ (t) where l_ijΔ is the synaptic latency, A_ij models the connectivity strength, M_ij/3000 is the time constant of the decaying exponential where M_ij denotes the number of history bins, and M_ijΔ is the history interval.

5 Results

We tested the algorithm on multiple network structures simulated using the point process model in (7). For each parameter setting in the results that will follow, we generated 100 networks of different structures, each containing 10 randomly connected neurons, where for each post-synaptic neuron, the indices of pre-synaptic neurons were drawn from a uniform distribution to avoid biasing the algorithm to a specific model. In addition, each neuron had a self-inhibitory connection to model post-firing refractoriness and recovery effects. The duration of the generated spike trains was set to 1 minute with a bin width of 3 ms that included the refractory period.

In our experiments, we used the Bayesian Network Inference with Java Objects (BANJO) toolbox (Smith, Yu, Smulders, Hartemink and Jarvis 2006). We used the simulated annealing search algorithm in all the analyses (Kirkpatrick, Gelatt and Vecchi 1983). The search time was set to 1 minute in all the analyses except for Section 5.6, where the performance was examined as the search time was increased for large populations. All the analyses were performed on a Dual Intel Xeon machine (2.33 GHz, 64 bit) with 8 GB of memory. We used the F-measure to quantify the inference accuracy (Rijsbergen 1979). This measure is the harmonic mean of two quantities: the recall R and the precision P, defined by

$$\begin{array}{cc}\hfill & R=\frac{C}{C+M},P=\frac{C}{C+W}\hfill \\ \hfill & F=\frac{2\mathit{RP}}{R+P}=\frac{2C}{2C+M+W},\hfill \end{array}$$ (9)

where C is the number of correctly inferred connections, M is the number of missed connections and W is the number of erroneously inferred spurious connections. Thus, F will be `0' if and only if none of the true connections are inferred (C = 0) and will be `1' if and only if all the true connections are inferred (M = 0) and no spurious connections are inferred (W = 0). Note that we are interested here in comparing the connections inferred by the DBN to the true connections regardless of the Markov lag they appear at or the strength of the actual connections. For example, if a true connection has a synaptic latency of 1 bin, it should be inferred at a Markov lag of 1. If it were to be inferred at a Markov lag of 2, it will still be considered as correct when computing F.

5.1 Networks with Fixed Synaptic Latency

We thoroughly investigated the performance of DBN by varying the model parameters in (7) and (8) while keeping the synaptic latency for all neurons fixed at 3 ms. This mimics direct connectivity that may exist in a local population rather than diffuse connections that may be observed across different parts of the cortex. Figure 5 shows the performance of DBN for different settings of the model parameters when the DBN Markov lag was set to match the synaptic latencies. Each point represents the mean and standard deviation of the inference accuracy for 100 different network structures.

Figure 5.

(a) DBN performance vs. number of excitatory pre-synaptic connections. Inset: Connection strengths A_ij for each choice of that number.

(b) DBN performance vs. firing history interval length. Inset: Connection strengths A_ij for each choice of this length.

(c) DBN performance (solid) vs. ratio of inhibitory to excitatory synaptic strength (I/E Ratio). The accuracy gets closer to unity as inhibition strength surpasses excitation strength (I/E ratio increases above 1). Partial Directed Coherence (PDC) (dashed) and Generalized Linear Model (GLM) fit (dotted) performance shown for comparison.

(d) Coefficient of variation for the data analyzed in (c).

(e) DBN performance vs. background rate.

We initially examined the performance as the number of pre-synaptic neurons was varied between 1 and 6 while fixing all other parameters. All the connections here were excitatory with a history interval of 180 ms. We decreased the strength of the connections A_ij in (7) as shown in the inset in Figure 5a as the number of pre-synaptic neurons increased in order to keep the mean firing rate in the range of 20 to 25 spikes/sec and prevent unstable network dynamics while the background rate of each neuron was set to 10 spikes/sec. The results in Figure 5a suggest that DBN achieves 100% accuracy with a slight decline above 4 pre-synaptic connections. This decline can be attributed to the decrease in the synaptic strength A_ij, thereby reducing the influence a pre-synaptic spike has on the firing probability of the post-synaptic neuron.

We then varied the history interval of the interaction by varying M_ij and examined the performance. Each neuron received two excitatory connections of equal weight from two neurons. The weights were adjusted in order to keep the mean firing rate in the same regime for different settings of M_ij as illustrated in the inset of Figure 5b. Given that the synaptic latency was fixed among all neurons and matched the DBN Markov lag used, we expected the performance to be invariant to changes in the history interval length. Figure 5b illustrates that this is indeed the case and that the DBN performance is almost steady regardless of the length of the history interval.

When inhibitory connections exist, the inference task becomes more complicated, particularly for hypoexcitable neurons, due to the fact that the neuron's spiking pattern becomes very sparse. As a result, observing a spike event may contain a lot more information about causal effects than not observing one. We further investigated the performance in the presence of inhibitory connections with variable degrees of strength. Each neuron received two pre-synaptic connections, one excitatory and one inhibitory. The excitatory synaptic strengths in (8) were fixed at 2.5, while those of the inhibitory connections were varied. We defined I/E ratio as the ratio of the cross-inhibitory to cross-excitatory synaptic strength and tested ratios of 0.25, 0.5, 1, 2, and 4, respectively. All other parameters were set as previously described. Taking the self-inhibition mechanism inherent in our model into account (A_ii = −2.5), an I/E ratio of 4 would correspond to a post-synaptic neuron with equal degree of inhibition and excitation. Such neuron should display homogeneous – Poisson like - characteristics reminiscent of independent firing. Figure 5c illustrates the inference accuracy as a function of the I/E ratio. For ratios below 1, a neuron is more affected by the excitatory connection than the cross-inhibitory one. Therefore, the drop in performance observed suggests that DBN is unable to detect the presence of weak inhibition in the presence of a strong excitation. This can be attributed to the relatively insignificant effect of weak inhibitory input on the firing characteristics of post-synaptic neurons conditioned on receiving a strong excitation. When the I/E ratio increases above 1, the accuracy rapidly gets closer to unity and does not deteriorate even when the inhibitory connections are 4 times stronger than the excitatory connections.

To interpret these results, we used the coefficient of variation (CV) of the inter-spike interval (ISI) histograms (CV = std(ISI)/mean(ISI)) to quantify the variability in the firing characteristics of post-synaptic neurons for variable I/E ratios. We hypothesized that if weak inhibitory connections do not significantly influence the firing of these neurons, then the CV should be close to those receiving pure excitation. Moreover, one would not expect to see a sharp transition in CV characteristics for I/E values adjacent to purely-excitatory connections. Figure 5d demonstrates that this is indeed the case. The average CV for I/E ratios of 0.25 is not significantly different from that of purely-excitatory connections. This suggests that weak cross-inhibition did not result in large effects on the post-synaptic neurons' firing characteristics, making it more difficult for DBN to detect this type of connectivity. The CV monotonically increases as the I/E ratio increases, reaching an average of 1 (similar to that of an independent Poisson neuron) when cross-inhibition, on average, is 4 times stronger than excitation (I/E ratio = 4).

We compared DBN performance to a related measure of connectivity - Partial Directed Coherence (PDC) – that has been proposed to study causal relationships between signal sources at coarser resolution in EEG and fMRI data (Sameshima and Baccala 1999). PDC is the frequency domain equivalent of Granger causality that is based on vector autoregressive models of certain order. A connection is inferred between a given pair of neurons if the PDC at any frequency exceeded a threshold of 0.1. For each network, PDC was applied using models of orders 1 to 30. The accuracy shown by the dashed plot in Figure 5c represents the maximum accuracy achieved across all model orders. As can be seen, DBN outperformed PDC over the entire range of the I/E ratio, while exhibits similar performance around an I/E ratio of 0.25. Closer examination of the networks inferred using PDC for I/E ratios greater than 0.25 revealed that the deterioration in the PDC performance compared to the DBN was due to its inability to detect most of the inhibitory connections, consistent with previous findings with spectral coherence as well as Granger causality (Dahlhaus, Eichler and Sandkuhler 1997; Cadotte, DeMarse, He et al. 2008).

We also compared DBN performance to that obtained using a Generalized Linear Model (GLM) fit (Truccolo, Eden, Fellow, Donoghue and Brown 2005; Czanner, Eden, Wirth et al. 2008). Ideally, GLM fit should yield the best result for our data since this is the generative model we used in (7). A maximum likelihood estimate of the coupling function α_ij in (8) for each neuron i is computed in terms of the spiking history of all other neurons j within a certain window of length W_GLM. Since our goal is to identify the existence of connections and not to estimate the coupling function, we post-processed the estimated coupling functions such that a connection was inferred if the estimated coupling function was larger/lower than a given threshold for excitatory/inhibitory connections, respectively, for 3 consecutive bins while their p-values were significant. The spiking history considered for fitting W_GLM was set to 20 bins (60 ms). The threshold was varied between 0 and ±1.5 and the p-value between 0.1 and 0.0001. The dotted plot in Figure 5c shows the maximum accuracy obtained across all thresholds and p-values. Superior performance of the GLM can be seen compared to DBN at I/E ratios below 1, while comparable if not slightly inferior for I/E ratios above 1. We note, however, that the GLM approach has a number of limitations: First, the performance is highly dependent on the choice of the fitting spiking history interval W_GLM. Second, the inference threshold and the p-values have to be carefully set to identify the connections. Finally, the GLM method search time was approximately 20 times that needed by the DBN to estimate the coupling functions for each 10-neuron population.

Finally, we examined the performance as a function of the background rate in (7). This may mimic variations in the afferent input current to the neuron, and increments in this input when there is not coupling to other neurons are known to impact estimates of correlation between their output spike trains (Rocha, Doiron, Shea-Brown et al. 2007). This is because correlation between a neuron pair cannot be orthogonally separated from their firing rates, thereby potentially leading to spurious connectivity inference (Amari 2009). Here, we had 2 pre-synaptic connections per neuron, one excitatory and one inhibitory having the same strength. Figure 5e illustrates that the inference accuracy was above 96% for background rates higher than 5 spikes/sec. Most remarkable is the ability of DBN to infer roughly 70% of the connections at background rates around 2 spikes/sec, despite that at this low rate, neurons are “silent” most of the time.

5.2 Mismatch between Actual Synaptic Latency and DBN Markov Lag

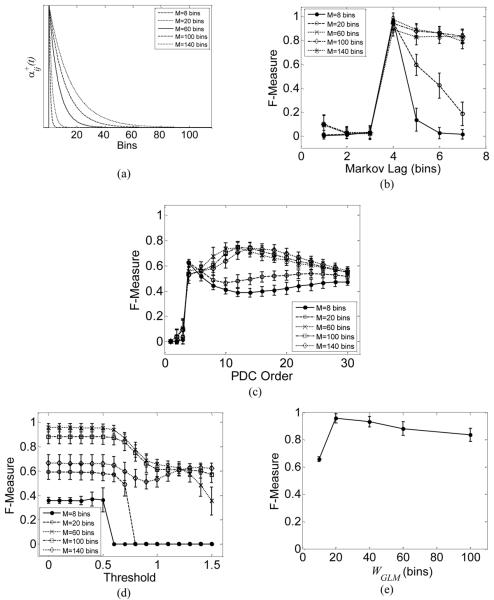
In practice, the synaptic latency between any two observed neurons is unknown and it is more likely that synaptic latencies between network elements to be heterogeneous, reflecting the highly distributed nature of cortical processing. For example, the synaptic weight functions expressing the EPSP and IPSP characteristics in Figure 6a for different choices of M illustrate that for relatively longer history intervals, the effect of a pre-synaptic spike on the firing probability of a post-synaptic neuron should last longer. This should enable the DBN to infer these connections even if the Markov lag is chosen to be larger than the true synaptic latency. On the other hand, the influence of a pre-synaptic spike on the post-synaptic neuron firing for a short history interval should behave in a similar fashion.

Figure 6.

(a) Coupling function α_ij⁺ (t) for different history intervals M.

(b) DBN performance vs. Markov lag for variable history intervals and fixed synaptic latency (4 bins).

(c) PDC performance vs. model order for the data analyzed in (a).

(d) GLM fit performance vs. detection threshold for the data analyzed in (b).

(e) GLM fit performance vs. GLM parameter W_GLM when the model parameter M was set to 60 bins.

Figure 6b demonstrates the performance of the DBN when there is a mismatch between the DBN Markov lag and the synaptic latency in the model. In this experiment, we generated 100 different networks, 10 neurons each, in which each neuron had two pre-synaptic connections, one excitatory and one inhibitory of the same strength. The synaptic latency was fixed for all neurons at 4 bins. As can be seen, when the Markov lag was set to a value smaller than the populations' true average synaptic latency, almost none of the connections was inferred. On the other hand, when the Markov lag was set to be larger than the true synaptic latency, the inference accuracy deteriorated only slightly for relatively long history intervals, while deteriorated significantly for shorter history intervals. To interpret this result, let's first denote by l_ij the synaptic latency between neurons j and i. The firing of neuron i at time bin m is only affected by the firing of neuron j in the range [m−M_ij, m−l_ij], where M_ij is the number of bins in the history interval. Thus, setting the Markov lag to a value less than l_ij (for example, trying to relate the firing of neuron i at time bin m to that of neuron j at time bin m − l_ij + 1) did not help to detect the presence of the connection between the neuron pair. Not surprisingly, DBN attained accuracy close to unity when the Markov lag matched the synaptic latency, consistent with the results previously shown in Figure 5b.

For the sake of comparison, Figure 6c and Figure 6d show the performance of PDC and GLM-fit, respectively. For PDC, almost none of the true connections were inferred when the model order was less than the synaptic latency. The performance improved when the model order was set greater than or equal to the synaptic latency, but the accuracy never exceeded 0.8 across the entire range of history intervals considered in the model. The drop in performance was again due to the inability of PDC to infer inhibitory connections. For the GLM fit shown in Figure 6d, the spiking history interval W_GLM considered in the fitting procedure was kept fixed at 20 bins (60 ms) for all the examined populations. As can be seen, the GLM fit highly depends on the threshold used to detect the existence of connections.

To demonstrate GLM fit dependency on the choice of W_GLM, we examined its performance in Figure 6e when the history M_ij in the model was fixed to 60 bins. Peak performance was obtained when W_GLM was set to 20 bins. For this choice of M_ij (60 bins), the weight function α_ij (t) in (8) falls to roughly 95% of its peak value after 20 bins (Figure 6a). Therefore, a choice of W_GLM that does not match the GLM model order may result in over or under fitting.

5.3 Networks with Variable Synaptic Latencies

As stated before, a functional cortical network is more likely to have heterogeneous synaptic latencies. Typically, synaptic latencies can range from a few milliseconds for monosynaptic connections (Kandel, Schwartz and Jessell 2000; Debanne 2004) to a few tens of milliseconds for polysynaptic connections (Molnar, Olah, Komlosi et al. 2008; Toni, Laplagne, Zhao et al. 2008). In addition, the limited sample size precludes the ability to record all the neurons that are directly connected in a given population. It is therefore much more realistic for our model to have variable synaptic latencies in order to test the applicability of the method to data from real cortical networks.

We investigated the performance when multiple synaptic latencies exist within the population. We defined a heterogeneity index (HI) as the number of distinct synaptic latencies that exist in the network as illustrated by the simple network in Figure 7a. Figure 7b demonstrates the accuracy for networks of 10 neurons with different HIs where HI=1 implies that all neurons had the same synaptic latency while 5 implies that every 20% of the neurons in the network had similar synaptic latency. Each neuron received 2 random connections, one excitatory and one inhibitory. In order to identify connections at different synaptic latencies, we applied DBN with a range of Markov lags such that the maximum lag matched the maximum synaptic latency in the population while the minimum lag was set to 1. In this case, DBN considers those lags simultaneously and tries to identify the best lag at which each connection is most prominent. Surprisingly, Figure 7b demonstrates that the accuracy was not significantly impacted at high HI. In addition, the DBN performance was superior to that of the GLM-fit and PDC for the same populations.

Figure 7.

(a) A simple network illustrating the dependence on the synaptic heterogeneity index (HI). The subpopulation inside the dashed circle has a HI of 3 while the entire population (neurons 1 to 6) has a HI of 5. The firing history was fixed at 60 bins (180 ms).

(b) DBN, PDC and GLM-fit performance vs. HI.

5.4 Identifying Monosynaptic Connectivity

One important feature of using DBN in structure learning is its ability to detect causal relationships between the children nodes and their immediate monosynaptic parents and not the higher-order polysynaptic parents. Figure 8a shows a simple network consisting of a 3-neuron chain where a directed information flow characterizes the connectivity such that neuron A excites neuron B, while in turn neuron B excites neuron C. The synaptic latency of both connections was set to 1 bin. In this case, neurons A and B are considered monosynaptic parents of neurons B and C, respectively. On the other hand, neuron A is considered a 2^nd order polysynaptic parent (ancestor) of neuron C. It is expected that the connections between neurons B and C and their monosynaptic parents can be best detected using a DBN with a single bin Markov lag, while a spurious monosynaptic relationship between neuron A and neuron C (2^nd order connection) might be detected with a 2-bin Markov lag as a result of the polysynaptic pathway between the two neurons. The complexity in discriminating between these two types of connections would be most pronounced in the absence of prior knowledge of the best Markov lag to use, particularly when analyzing a heterogeneous network such as the ones analyzed in Figure 7. Herein, we demonstrate the ability of DBN to restrict its inference to only direct causal relationships despite using a non-optimal Markov lag.

Figure 8.

(a) Example 3-neuron chain, where solid arrows represent true connections while the dotted one represents a spurious connection, l indicates the synaptic latency associated with each connection.

(b) Average number of spurious connections inferred per chain.

We investigated the performance using 100 different network structures with a history interval fixed to 60 bins (180 ms), a fixed synaptic latency of 1 bin, and 1 excitatory and 1 inhibitory pre-synaptic connections per neuron. Each of the 100 networks examined had a total of 40 chains with 3 neurons each similar to the one in Figure 8a. A successful DBN inference should yield two connections matching the true monosynaptic connections and no 2^nd order connections per chain. Figure 8b shows the number of erroneously inferred 2^nd order connections per chain versus Markov lag. It can be seen that when a Markov lag of 1 bin was used, DBN did not infer any of the spurious 2^nd order connections as expected since the lag is shorter than the superposition of two synaptic latencies. When a Markov lag of only 2 bins was used, DBN surprisingly had a very low error rate despite that true monosynaptic connections should be inferred in addition to the spurious 2^nd order connection in each chain as shown in Figure 8b. We attributed this superior performance to two factors: first, the effect of the pre-synaptic neuron on the probability of firing of the post-synaptic neuron lasts for a period of time governed by the synaptic coupling function given in (8). Given the exponential decay form of this coupling, it is expected that the probability of a post-synaptic neuron firing at times beyond those governed by the synaptic latency will be influenced by the time constant of that exponential function. Consider the example in Figure 8a, when the synaptic latency is 3 ms (1 bin) and given the firing of neuron A at time t, equation (8) yields a probability of firing for neuron B at time t + 3 ms of 0.25, while that at time t + 6 ms (i.e. after 2 bins of neuron A firing) to be 0.2. Thus, the probability of firing at t + 6 ms has only declined by 20% of its maximum attained at t + 3 ms. Therefore, the connection A→B can still appear at a Markov lag of 2. The same applies to the connection B→C. Second, as the DBN tends to find the network structure with the least number of edges to explain the data, the connection A→C is a redundant one given the presence of the connections A→B and B→C.

Figure 8b also shows that a Markov lag of 3 results in a slight increase in the number of spurious 2^nd order connections. This can also be attributed to the effect of the time constant of the synaptic coupling. As the lag increases, the effect of the pre-synaptic spike on the post-synaptic neuron firing decreases, making it relatively harder to detect true monosynaptic connections, while increasing the probability of detecting only spurious 2^nd order connections. Finally, at a Markov lag range of 1 and 2 in which connections at both lags should be simultaneously identified, no 2^nd order connections were inferred since in this case DBN finds the best lag (or a combination of lags) that best explains the data. These results indicate that even if the Markov lag is not correctly set, DBN can still succeed in identifying only true monosynaptic connections provided that the lag range is chosen equal to or more than the maximum anticipated synaptic latency in the population.

5.5 Networks with Unobserved and Independent Neurons

Cortical neurons are known to receive common excitatory and inhibitory inputs from other regions (Turker and Powers 2001; Turker and Powers 2002; Keen and Fuglevand 2004; Yoshimura, Dantzker and Callaway 2005). These common inputs are a major source of complexity in inferring causal relationships since they cannot be distinguished from actual coupling caused by true synaptic links. We investigated DBN performance when unobserved common inputs exist in the form of synaptic coupling from unobserved neurons. Figure 9a shows a sample structure of the network examined in which unobserved neurons in the top row simultaneously excite pairs of observable neurons in the bottom row. The dashed connections in the figure indicate the connections that are expected to be inferred by DBN when the synaptic latency is fixed. These bidirectional connections indicate that each pair of neurons receives the same input at the same time, and therefore there should be no causal, time-dependent relationship between them.

Figure 9.

(a) Network structure examined where black nodes 1–5 in the dashed rectangle represent unobserved neurons. Solid arrows indicate real connections while dashed ones indicate the expected connections to be inferred by DBN.

(b) DBN performance vs. difference between the synaptic latency of the connections to odd numbered neurons and even numbered neurons (l_o − l_e) where l_e is fixed at 1 bin.

(c) A network of 20 neurons, where white nodes indicate observed neurons while black nodes indicate unobserved neurons.

(d) A network with 15 observed neurons; neurons 1–10 (inside the dashed circle) receive connections while neurons 11–15 are not connected to any neurons. The history interval was set to 60 bins (180ms) and the synaptic latency was fixed to 1 bin (3 ms) for all connections.

We studied the performance of DBN in inferring connectivity between the observed neurons (indexed 6 to 15). The synaptic latency of connections to even numbered neurons l_e was kept fixed at 1 bin (3 ms) while that to odd numbered neurons l_o was varied. Figure 9b demonstrates the inference accuracy plotted as a function of the difference l_o-l_e. We considered a bidirectional connection as an indicator of a common input. The Markov lag of the DBN was set to 1 bin (3ms). As can be seen, the inference accuracy peaks when the synaptic latency of the connections to both odd and even numbered neurons was the same (i.e. the difference in synaptic latency l_o – l_e is 0). As the difference in synaptic latency increases, the accuracy decreases. This may be interpreted as follows: when there is a difference between the synaptic latencies of the common input, an indirect relationship between the neurons receiving that common input emerges. For example, consider the common input from neuron 1 to neurons 6 and 7 shown in Figure 9a when the synaptic latency of the connection 1→ 6 is 1 bin (3 ms) while that of 1→7 is 2 bins (6 ms) . In this case, the influence of an event from the common input (neuron 1) on neuron 7 probability of firing has a latency of 1 bin relative to its influence on neuron 6. Thus, not observing the common input coupled with a difference in synaptic latency between that input and the observed neurons results in a spurious connection between the observed neurons directed from the shorter latency neuron to the longer latency one. On the other hand, an inferred bidirectional connection between two observed neurons might indicate a common input simultaneously received by both neurons. Nevertheless, it can still be indicative of a pair of unidirectional physical connection between the two neurons rather than a common input. Discrimination between the two cases can be achieved if prior knowledge about the anatomy of the brain area and the duration of the synaptic latencies are available.

We further examined the performance in the case of unobserved neurons within the population. We were interested in assessing whether this would hinder our ability to detect functional relationships between the actual observed neurons. We randomly selected 6 neurons to be unobserved from 20-neuron populations as shown in Figure 9c. DBN was applied to the spike trains of the remaining 14 neurons. The synaptic latency of all the neurons was set to 1 bin (3 ms) and the Markov lag was also set to 1 bin to match the synaptic latency. The inference accuracy achieved by examining 100 different networks was 0.96±0.03. When computing the accuracy, all the connections that involved the unobserved neurons in the simulated networks were not considered.

We also examined the performance when some of the observed neurons are not elements of the functional network. These can be typically thought of as task-independent neurons. Identifying these neurons can be useful in the context of decoding spike trains. In such a case, the performance of a decoder should improve if the posterior probability of the stimulus is expressed in terms of the conditional probabilities of the task-dependent neurons, while excluding the task-independent ones from the computation of the joint prior distribution (Aghagolzadeh, Eldawlatly and Oweiss 2009). Figure 9d shows a sample network of 15 neurons in which neurons 1–10 receive 2 pre-synaptic connections each (1 excitatory and 1 inhibitory), while neurons 11–15 are not connected to any other neurons. The Markov lag was set at 1 bin. The inference accuracy obtained by applying the DBN to 100 networks was 0.98±0.07. The number of spurious connections inferred per network between any of the connected neurons (i.e. neurons 1–10) and the unconnected ones (i.e. neurons 11–15) was 0.1±0.3, and occurred in 10 out of 100 networks. The number of connections inferred per network among unconnected neurons (i.e. neurons 11–15) was 0.05±0.2 and occurred in only 5 out of 100 networks. To compare this number with what would be expected by chance, we simulated 100 different networks with 10 unconnected neurons each. The number of connections inferred per network was 0.02±0.14, and occurred in 2 out of 100 networks.

5.6 Identifying Connectivity in Large Populations

All the analyses shown so far were carried out on relatively small populations of 10 to 15 neurons each. Given that simultaneous recording of multiple single units in excess of these numbers is expected, we were interested to investigate how the method scales as a function of the number of neurons in the population. We simulated 10 different populations, 120 neurons each. Each population consisted of 12 clusters, 10 neurons each, in which each neuron received 3 excitatory connections from neurons belonging only to its own cluster. The history interval was set to 60 bins (180 ms) and the synaptic latency to 1 bin (3 ms).

Figure 10a shows the inference accuracy when DBN was applied to the entire population with a Markov lag set to 1 bin (3 ms) for different search times. For a search time of 1 min, it is clearly seen that DBN was unable to infer the network structure (only 15% accuracy). To improve the accuracy, two different approaches were examined. First, when allowing the DBN more search time (2 hours), an inference accuracy of 100% was attained for the 120 neuron population. Second, one can try to break down the large population into smaller, functionally-interdependent subpopulations if prior knowledge of any clusters in the neural space is available. When this is the case, we found that applying DBN to subpopulations when keeping the search interval fixed at 1 min significantly improved the performance. Specifically, we divided each of the 120 neuron populations into 2 subpopulations with 60 neurons each (i.e. clusters 1–6 in one subpopulation and clusters 7–12 in the other). The performance increased in this case by more than two fold as indicated in Figure 10a. When subsequent division is carried out into 3, 4, 6 and 12 subpopulations, with 40, 30, 20, and 10 neurons each, respectively, accuracy of 100% was achieved on populations of sizes 10 to 20 neurons each. In this realm, the functional connectivity algorithm reported in (Eldawlatly, Jin and Oweiss 2009) was applied prior to DBN analysis. In summary, for large populations, a two-stage framework is suggested in which the neural space is first clustered to identify any potential statistical dependence between neuronal elements. This is then followed by DBN analysis to identify the effective connectivity structure within each cluster. Figure 10b illustrates the minimum search time needed to achieve 100% accuracy for each subpopulation size. It can be seen that the computational complexity increases exponentially with the population size. Finally, we investigated the performance when no clusters are present. As can be seen in Figure 10c, when more search time is allowed (in this case by 2 fold), the underlying network was correctly inferred.

Figure 10.

(a) DBN performance vs. number of neurons/subpopulation for different search intervals. 10 different populations of 120 neurons each were simulated.

(b) Search time required by DBN to achieve 100% accuracy (F-Measure=1) vs. number of neurons/subpopulation.

(c) DBN performance vs. search time for 120 neuron populations with no clusters.

5.7 Estimating the Markov Lag of Maximum Accuracy

We have demonstrated how the DBN performance is highly dependent on the selection of the Markov lag and that the accuracy is maximized when the Markov lag is equal to or slightly greater than the population true average synaptic latency. When dealing with real neural data, prior knowledge of this synaptic latency may be unavailable, and therefore some measure is needed to devise the best Markov lag to use for a given population. For that purpose, we computed the mean influence score (IS), defined as the average absolute value of the influence score for each inferred connection. The influence score IS(i, j) measures the degree to which neuron j influences neuron i's firing, independent of the output of the other parents of neuron i (Yu, Smith, Wang et al. 2004). Its computation is based on the same conditional probabilities used in inferring the network structure. IS can be either positive or negative depending on whether the connection is excitatory or inhibitory, respectively. Since IS measures the degree of influence of the pre-synaptic neuron on the post-synaptic neuron for a given inferred connection, it is expected that the mean of the absolute value of the IS of all the inferred connections for a given network structure will be maximum if the inferred structure matches the true one.

Figure 11a shows the mean IS at different Markov lags for the data sets previously analyzed in Figure 6 in which the heterogeneity index (HI) was 0. Comparing the results in Figure 11a with those in Figure 6, it can be seen that for each choice of history interval length M, the mean IS profile matches the F-measure profile obtained when exact knowledge of the network structures was available. Thus, the mean IS can be used to quantify the degree of confidence in the inferred network and to potentially estimate the best Markov lag that explains the data. Figure 11b shows the inference accuracy for more complex networks with HI = 3 at different ranges of Markov lags. The inference accuracy peaks when the maximum Markov lag matches the maximum synaptic latency in the population. Figure 11c shows similar result using the mean IS. It is clearly seen that, similar to the fixed synaptic latency case (HI = 0), the mean IS behaves similar to the F-measure. This confirms the utility of the mean IS as a metric for determining which network best explains the data when information about the anticipated synaptic latency is unavailable.

Figure 11.

(a) Mean influence score (IS) vs. Markov lag for variable history intervals for the same data analyzed in Figure 6a. Note that the mean IS has similar profile to the accuracy.

(b) DBN performance vs. Markov lag for networks with HI equals 3. Maximum accuracy is attained when the maximum Markov lag matches the maximum synaptic latency in the population.

(c) Mean influence score vs. Markov lag for networks with HI equals 3.

6 Conclusion

Identifying the effective connectivity between cortical neurons is a fundamental goal in systems neuroscience. In this work, we demonstrated the utility of Dynamic Bayesian Networks (DBN) in inferring this connectivity from the observed spike trains under a wide variety of conditions. Our main conclusion is that DBN is a useful tool for analyzing spike trains, and is capable of identifying causal relationships between distinct neuronal elements in small and moderately-large populations of neurons, particularly when nonlinear interaction between these neurons is present.

We have applied the method to probabilistic neuronal network models. These models are increasingly being used in the neuroscience community because they are highly non-linear, stochastic, and faithfully model the dynamic discharge patterns of many cortical neurons. DBN outperformed Partial Directed Coherence (PDC), particularly when temporal dependence was variable among the population elements. The diminished PDC performance was mainly attributed to its inability to detect inhibitory connections. Compared to GLM fit, DBN performance was comparable overall, and occasionally superior in highly heterogeneous network structures. The GLM performance was not surprising, given that it was tested on data simulated using the same generative model, while the DBN did not assume any specific generative model. Therefore, we expect DBN to have more powerful generalization capability compared to GLM fit, although not tested here. Some disadvantages of the GLM method are the need to specify a detection threshold (with associated p-values) due to the dependence of the neuron's firing on the spiking history of other neurons that is likely to be variable across neuron pairs. In addition, the orders of magnitude difference in computational time, in favor of the DBN, makes the inference task more daunting for the GLM.

Two issues deserved detailed investigations in the proposed approach. The first is the dependence of the DBN performance on the Markov lag, which can be regarded as playing the same role as the model order in the GLM fit. Nevertheless, choosing the Markov lag to be exactly matching the synaptic latencies is not necessary, as long as it is not smaller than the maximum synaptic latency expected in the population. Information about synaptic latency may be available if knowledge of the anatomical structure of the sampled cortical regions is available. In such a case, running the DBN using different Markov lags and finding the Markov lag(s) at which the mean influence score is maximized should yield the best accuracy. The structure obtained would be the most likely network structure that best explains the data.

The second issue is the complexity of the search in the high-dimensional neural space that is directly proportional to the number of the neurons in the population. We found that the computational complexity increases exponentially with the population size. However, we found that when clusters of functionally interdependent neurons do exist, the computational complexity can be reduced. This is important, given the plethora of studies suggesting that neuronal interaction across multiple time scales may underlie multisensory neuronal integration in naturalistic behavior, perception, and cognition. The results suggest that a two-step framework may be best suited for large-scale analysis, whereby populations are first clustered to discover any inherent statistical dependency between their elements. These clusters are subsequently analyzed by DBN to infer their underlying structures. The clustering step, however, can be eliminated without affecting the DBN performance if longer search time is permitted.

Though not included in this paper, the proposed approach can also be useful in quantifying synaptic plasticity that is strongly believed to underlie learning and memory formation. In such case, graphical approaches such as DBNs can reveal potential plastic changes reminiscent of cortical re-organization during learning or recovery from injury. It can also be used to identify task-dependent neurons when neural decoding is sought to reconstruct a sensory stimulus or predict an intended motor behavior in a wide range of neuroprosthetic applications. Our most recent results demonstrate that DBN inference can be very useful in optimizing the decoder structure during motor learning (Aghagolzadeh, Eldawlatly and Oweiss 2009).