Abstract
This study presents the results of a de novo approach modeling possible conformational dynamics of the extracellular (EC) loops in G-protein-coupled receptors (GPCRs), specifically in bovine rhodopsin (bRh), squid rhodopsin (sRh), human β-2 adrenergic receptor (β2AR), turkey β-1 adrenergic receptor (β1AR) and human A2 adenosine receptor (A2AR). The approach deliberately sacrificed a detailed description of any particular 3D structure of the loops in GPCRs in favor of a less precise description of many possible structures. Despite this, the approach found ensembles of the low-energy conformers of the EC loops that contained structures close to the available X-ray snapshots. For the smaller EC1 and EC3 loops (6-11 residues), our results were comparable with the best recent results obtained by other authors employing much more sophisticated techniques. For the larger EC2 loops (25-34 residues), our results consistently yielded structures significantly closer to the X-ray snapshots than the results of the other authors for loops of similar size. The results suggested possible large-scale movements of the EC loops in GPCRs that might determine their conformational dynamics. The approach was also validated by accurately reproducing the docking poses for low-molecular weight ligands in β2AR, β1AR and A2AR demonstrating the possible influence of the conformations of the EC loops on the binding sites of ligands. The approach correctly predicted the system of disulfide bridges between the EC loops in A2AR and elucidated the probable pathways for forming this system.
Keywords: GPCR, protein loops, molecular modeling
Introduction
G-protein coupled receptors (GPCRs) constitute a protein family involved in a vast array of physiological functions. GPCRs are transmembrane proteins that include seven-helical transmembrane segments (TM helices, TMs), the N- and C-terminal fragments and the extra- (EC) and intracellular (IC) loops connecting the TM helices. Knowledge of the detailed 3D structures of GPCRs is relevant to wide areas of biochemistry, biophysics and medicinal chemistry, since it has been estimated that ca. 400 GPCRs are potential drug targets1; also, almost 50% of the therapeutic compounds in use act via GPCRs2.
The 3D structures of the EC loops are of special interest as they are factors in determining specificity of GPCRs, especially those interacting with high-molecular weight peptide ligands. Site-directed mutagenesis experiments demonstrated that residues of the EC loops are also involved in interactions with low-molecular weight ligands such as biogenic amines, adenosines, lipids, prostanoids, purines, etc. The numerous examples of functionally important mutations in the EC2 loop (connecting TM4 and TM5) were briefly discussed in several recent publications3-6. The recent data on mutations in the EC1 loop (connecting TM2 and TM3)7 and the EC3 loop (connecting TM6 and TM7)8 are also available. It was also shown that constraining of the EC2 loop movement by inserting additional disulfide bridges significantly changed GPCR functionality3,9. The special role of the long EC2 loop in GPCR activation was also demonstrated for various GPCRs10-13; very recently, the movement of EC2 in the activated (MII) state of rhodopsin was captured by the solid-state NMR14.
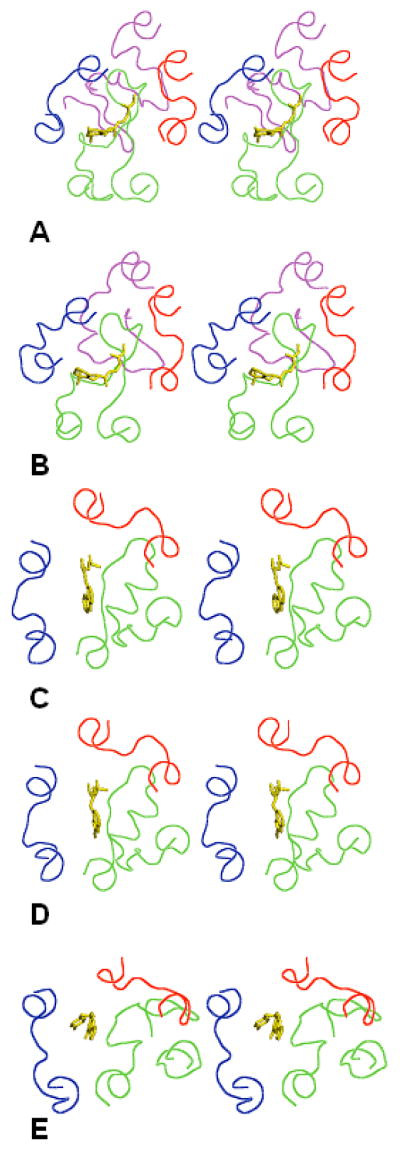
According to a recent minireview15, 17 crystal structures of six GPCRs are now available in the PDB. The crystallizing conditions varied as did several post-translational modifications for five GPCRS, which were bovine rhodopsin, bRh; squid rhodopsin, sRh; bovine opsin (the ligand-free rhodopsin), Ops; human β-2 adrenergic receptor, β2AR; turkey β-1 adrenergic receptor, β1AR; and human A2 adenosine receptor, A2AR. All these structures are remarkably similar in their TM regions15, but show significant dissimilarities in the 3D structures of the IC and EC loops. By structural features of the EC loops, the available X-ray structures of GPCRs can be grouped together as photoreceptors (rhodopsins and opsin), β-adrenoreceptors and A2-adenosine receptors. This is exemplified by Figure 1 that shows 3D structures of bRh (the PDB entry 1F8816), sRh (2Z7317), β2AR (2RH118), β1AR (2VT419) and A2AR (3EML20). (Note that 2RH1 was used to phase the X-ray crystal structure of β1AR, 2VT419.) Figure 1 also shows the ligands co-crystallized with the receptors, namely retinal for rhodopsin, carazol for β2AR, cyanopindolol for β1AR and the ZMA ligand for A2AR. In all cases, some residues of the EC loops are located in close proximity of the ligands confirming involvement of the EC loops in interactions with low-molecular weight compounds.
Figure 1.
Stereoviews of the X-ray structures of the EC loops in five GPCRs shown as lines in red (EC1), green (EC2), blue (EC3) and magenta (the N-terminal tail). Ligands crystallized with the GPCRs are shown as sticks in yellow. A) bRh; B) sRh; C) β2AR; D) β1AR; E) A2AR. The view is from the extracellular space normal to the membrane plane.
The X-ray structures of the EC loops shown in Figure 1 present only a single “frozen” snapshot of the set of possible conformations of the highly flexible loops in GPCRs. At the same time, molecular mechanisms of the GPCR–ligand interactions and of GPCR activation would likely involve conformational re-arrangements of the EC loops (see, e.g., the recent discussion on the concept of target flexibility in drug discovery and design21). The solid state NMR data on EC2 in bRh presented direct structural evidence of the re-arrangement in the activation process; however, they also are limited with only one conformational snapshot of EC214. On the other hand, these molecular motions would be difficult to follow by spectroscopic techniques in solution as NMR which produce only “averaged” 3D structures. In this regard, computational molecular modeling, which yields energetically and sterically feasible conformations of the EC loops in GPCRs, has become of special importance (see, e.g., the recent studies22-24).
Current approaches to molecular modeling of the protein loops use either de novo restoration of the loops connecting the fixed atomic points or homology modeling of the loops. Both techniques successfully restore 3D structures of the loops with lengths up to 12 residues (see recent studies22,25-32; most modeling studies prior to 2006 were referenced earlier33). The latest de novo studies reproduced 3D structures for 13-membered loops34,35, and homology modeling was applied to 14-membered loops36. However, the average length of the EC2 loop in GPCRs is ca. 20-35 residues37, which precludes efficient homology modeling and severely limits opportunities for de novo modeling. In this case homology modeling is not viable because it is difficult to find templates with sufficient sequence homology; while de novo modeling is restricted by the enormous amounts of computer resources needed to efficiently sample larger loops and to account for the heterogeneous membrane environment. Thus far, only the Rosetta approach attempted de novo modeling of several 24- to 34-membered “structurally variable regions”38,39, while homology modeling of the EC2 loop in bRh and in the dopamine D2R receptor40, as well as in three other GPCRs5, was performed based on the rhodopsin 3D template.
In view of the above problems and limitations, we employed a de novo approach that deliberately sacrificed a detailed description of any particular 3D structure of the loops in GPCRs in favor of a less precise description of many possible conformations. The major differences among the sets of predicted loop structures can then be resolved by experimental procedures33. This approach successfully restored the 3D structures of the EC and IC loops in bRh, the only GPCR with a known X-ray structure available at the time. In the present study, we developed this approach further and applied it to determine the possible 3D structures of the EC loops in bRh, sRh, β2AR, β1AR and A2AR. The obtained results showed consistency with the X-ray structures of the EC loops and were used to examine the docking of the ligands co-crystallized with β2AR, β1AR and A2AR. The computational models also offered insights regarding the system of the four disulfide bridges connecting the EC loops of A2AR. Importantly, our approach outlined experimentally testable possibilities for large-scale conformational transitions in the EC loops of GPCRs.
Computational Methods
Computational techniques for loop restoration used in this study were similar to those employed earlier33; therefore, we will focus mostly on novel elements introduced in the approach. As earlier, loop restoration involved two main steps, 1) geometrical sampling of the space between the fixed points in the GPCR (the 4-residue stems of TM helices) to select possible loop-closing backbone conformations, and, 2) energy calculations for all selected conformations of the individual EC loops and, then, of the selected EC1+EC2+EC3 “packages” of the loops. Computational procedures employed to dock ligands to the restored EC loops are described in more detail.
EC loops selected for modeling
The EC loop boundaries were determined by sequential alignment of the five GPCRs with the Clustal-W procedure. Table I lists the sequences, lengths and sequential numbering of the EC loops restored in this study for five GPCRs. Sequences of the four-residue TM helical stems (in italics) flanking the loops together with the sequence numbers of the first residue of the starting TM stem and of the last residue of the end TM stem are also listed. Loops were mounted on the 3D structures of the fixed TM helical stems deduced from the X-ray crystal structures of bRh (the PDB entry 1F88, chain A), sRh (2Z73, chain A), β2AR (2RH1), β1AR (2VT4, chain A) and A2AR (3EML).
Table I.
Sequences of the EC loops selected for modeling
| Loop | GPCR | TM stem | Loop sequence (length, sequential numbering) | TM stem |
|---|---|---|---|---|
| EC1 | bRh | 96 YTSL | HGYFVFGP (8, 100-107) | TGCN 111 |
| sRh | 94 ISCF | LKKWIFGF (8, 98-105) | AACK 109 | |
| β2AR | 92 AHIL | MKMWTFGN (8, 96-105) | FWCE 107 | |
| β1AR | 100 TLVV | RGTWLWGS (8, 104-111) | FLCE 115 | |
| A2AR | 65 TIST | GFCAAC (6, 69-74) | HGCL 78 | |
| EC2 | bRh | 169 APAL | VGWSRYIPEGMQCSCGIDYYTPHEETN (27, 173-199) | NESF 203 |
| sRh | 168 IGAI | FGWGAYTLEGVLCNCSFDYISRDST (25, 172-196) | TRSN 200 | |
| β2AR | 167 LPIQ | MHWYRATHQEAINCYANETCCDFFTNQ (27, 171-197) | AYAI 201 | |
| β1AR | 175 LPIM | MHWWRDEDPQALKCYQDPGCCDFVTNR (27, 179-205) | AYAI 209 | |
| A2AR | 138 TPML | GWNNCGQPKEGKNHSQGCGEGQVACLFEDVVPMN (34, 142-175) | YMVY 179 | |
| EC3 | bRh | 274 YIFT | HQGSDFGP (8, 278-285) | IFMT 289 |
| sRh | 281 ALLA | QFGPLEWVTP (10, 285-294) | YAAQ 298 | |
| β2AR | 294 IVHV | IQDNLIRKE (9, 298-306) | VYIL 310 | |
| β1AR | 311 IVNV | FNRDLVPDW (9, 315-323) | LFVF 327 | |
| A2AR | 254 CFTF | FCPDCSHAPLW (11, 258-268) | LMYL 272 |
Geometrical sampling of the loops
Geometrical sampling of the conformations for a given loop consisted of stepwise elongation (“growing”) of the peptide backbone of the loop starting from the last residue of the starting TM stem (the starting residue, residue 1) in the frame of the existing TM regions (the X-ray structures without the EC loops). The target point of the growing loop was the first residue of the end TM stem (the target residue, residue M). The backbone dihedral angles of the starting and target residues were fixed. At each step of the elongation procedure, all possible conformations of the peptide backbone for the loop fragment 1 – i (from the starting residue to the last residue of the growing fragment, residue i) were considered. The conformations were selected from the set of the local minima of the Ramachandran map including the following φ,ψ points: -140°, 140°; -75°, 140°; -75°, 80°; -60°, -60°; and 60°, 60° (i.e., all combinations of β, pII, γ', αR and αL minima). For the Gly residues, the minimum pII' (φ,ψ = -140°, 80°) and all minima symmetrical to β, pII, γ' and pII' were added; totally, there were 10 local minima for Gly. For Pro, the φ,ψ points were −75°, 140°; -75°, 80°; and −75°, -60°.
Out of all conformational possibilities for the growing backbone chain of the loop, potentially loop-closing conformations were selected at each elongation step as those satisfying the following limitations. First, the loop fragment 1 – i was required to be self-avoided, i.e., the corresponding Cα-Cα distances within the loop should not be less than the predefined distance Inp (usually 4.0 Å). Second, the fragment had to avoid steric clashes with the existing TM region, i.e., the corresponding Cα-Cα distances between the loop and the TM region should not be less than the distance Out, usually 6.0 – 8.0 Å. Third, spatial positions of the last residue of the growing fragment, residue i, should not be too far both from the starting residue, 1, and from the target residue, M. For this, the Cα-Cα distances between the current end residue of a growing chain and residues 1 and M were restricted by the upper limit, which was 3.5 Å if Δ = i−1 or Δ= M−i equal 1; 5.8 Å if Δ = 2; 7.8 Å if Δ = 3; 3Δ Å if 4 ≤ Δ ≤ 8; 24 Å if 9 ≤ Δ ≤ 25; and 20 Å if Δ ≥ 26 (this empirical dependence was deduced from our analysis of protein loops in the PDB; data not shown). Sometimes, this last constraint was applied with some “tolerance” distance, Del, so the corresponding limitations were actually the Cα-Cα distances determined as above ±Del. Generally, the exact values of the distances Inp, Out and Del, which were used as parameters of the geometrical sampling procedure were slightly varied at each elongation step to ensure the numbers of selected conformers were not less than tens and not exceeding millions (see Results and Discussion).
For the smaller EC1 and EC3 loops, the elongation procedure was performed in one step considering a single fragment 1 – M. For the larger EC2 loops, sampling was performed in several steps, where each next step utilized the potentially loop-closing conformations selected at the previous step. Elongation on some intermediate steps also made use of combinations of the low-energy backbone conformations of the fragments selected by separate energy calculations (see Results and Discussion). Also, it was assumed that the highly conserved disulfide bridge between the cysteine residues Cys3.25 (according to the universal nomenclature41) in the TM3 helical stem and Cys45.50 in EC2 (both shown in bold in Table 1) is always present in the 3D structure; therefore, the stepwise elongation proceeded first from the last residue of the starting TM3 stem to Cys45.50, and then from Cys45.50 to the first residue of the end TM5 stem. For this, it was assumed that the position of the Cα-atom of Cys45.50 (not known during the procedure) was the same as that of Cys3.25.
Energy calculations for the loops
All selected loop-closing conformations for each individual loop (with all side chains) were subjected to energy minimization employing the ECEPP/2 force field42,43 with rigid-valence geometry and planar trans-peptide groups (for prolines, the ω angles were allow to vary); the dielectric constant was chosen equal to 80 to mimic, to some extent, the water environment of the protruded loops. Two flanking TM stems were added to each selected loop structure; the stem residues were replaced by alanines (except for prolines and glycines) and the backbone dihedral angles were fixed. The side chains of the loops were repacked according to a previously developed algorithm44 for each backbone structure that was subjected to energy minimization. The total energy also included the sum of parabolic potentials (harmonic restraint potentials) between the Cα-atoms in the stems (U0 = 10 kcal/mol*Å2) to keep the stem residues in the relative spatial positions they occupied in the X-ray template structures. Energy calculations for the EC2 loops also included the additional parabolic potentials between the Cα-atoms of the stem residues and the Cα-atom of residue Cys45.50 to place the latter in a spatial position occupied by the Cα-atom of Cys3.25. Since the ECEPP force field parameters do not tolerate two sequential proline residues in a helix (as in the X-ray structure of the TM5 helical stem of bRh, fragment 169-172, APPL), the non-conserved P171 residue was replaced by alanine (shown in bold italics in Table I). After energy minimization, low-energy conformers were selected as those with relative energies less than the assumed energy cut-offs ΔEs, which were typically of 1 kcal/mol per residue45; see Results and Discussion for the actual values.
The low-energy conformers selected by results of energy calculations for individual loops were then combined into the EC1+EC2+EC3 “packages” to account for the inter-loop interactions. Typically, energy calculations for the individual loops yielded a fairly large number of low-energy conformations for each loop, from tens to hundreds (see Results and Discussion), which makes it impractical to perform energy calculations for all their combinations. Therefore, the sets of low-energy conformers for the smaller EC1 and EC3 loops were divided into clusters by the rms values from 2 Å to 3 Å, and only the lowest-energy conformers in each cluster were selected as representatives for further consideration in the EC1+EC2+EC3 packages. Each package involved six TM stems (all side chains present); in this case, the backbone dihedral angles of the residues directly flanking the loop were not fixed and allowed to rotate. Total energy included the additional parabolic potentials (U0 = 10 kcal/mol*Å2) between the Cα-atoms of the starting and end residues of the TM helical stems to keep them in the relative spatial positions close to those in the TM templates (36 constraints) as well as the parabolic potentials to ensure formation of the disulfide bonds (the Cys3.25 – Cys45.50 bond and possible others, see Results and Discussion). Again, optimization of the spatial positions of side chains44 was performed along with energy minimization. In 10 – 20% cases, the changes in the structures of the packages after final energy minimization resulted in newly emerged contacts that are too close (the Cα-Cα distances less than 4 Å) to the template TM regions, i.e., the loops may be “inserted” into the membrane; conformers of this type were discarded from the final results (specifically, see Table IV). The structures with the values of the parabolic potentials larger than 30 kcal/mol (i.e, those with discrepancies in the restored spatial positions of the TM stems) were also omitted; see Table IV.
Table IV.
Modeling results for the EC1+EC2+EC3 packages
| GPCR | ||||||
|---|---|---|---|---|---|---|
| bRh | sRh | β2AR | β1AR | A2AR | ||
| Number of initial structures | 8604 | 8760 | 1032 | 5264 | 3060 | |
| Selection criteria | ΔE < 50 kcal/mol | 1076 | 531 | 95 | 352 | 228 |
| Ecl < 30 kcal/mol | 1040 | 497 | 95 | 352 | 170 | |
| No clashes with TM | 884 | 378 | 95 | 261 | 149 | |
| Number of clusters | 78 | 65 | 12 | 32 | 36 | |
| Best rms values, Å | EC1+EC2+EC3 | 4.4 | 4.6 | 3.6 | 4.4 | 5.2 |
| EC1 | 2.5 | 1.4 | 1.7 | 2.0 | 1.7 | |
| EC2 | 4.7 | 4.8 | 3.8 | 4.3 | 5.9 | |
| EC3 | 1.3 | 2.8 | 2.0 | 2.0 | 1.8 | |
| EC1+EC2+EC3 (starting from X-ray) |
3.0 | 3.0 | 2.6 | 1.8 | - | |
Docking procedures
The RosettaLigand program46 was used to dock the ligands to β2AR, β1AR and A2AR. The structures of the EC1+EC2+EC3 packages that resulted from the modeling calculations were spliced with the TM regions of 2RH1, 2VT4 and 3EML, respectively; then all hydrogens were added to the resulting fragments and 100 cycles of energy minimization with the standard Tripos force field were performed employing the Sybyl 7.3 package. To prepare the X-ray receptor structures from the Protein Databank, hydrogen atoms were added and the energies of the structures were minimized using the standard Tripos force field in Sybyl 7.3. Further, the X-ray crystal structures of the receptors were also run without the EC loop regions present; specifically, the following regions were used in the calculations: β2AR (V34-H93, E107-I169, A200-L230, K263-V295, Y308-L342), β1AR (W40-V102, K114-H180, I209-I238, R284-I311, W323-A358) and A2AR (I3-I106, Y119-L141, Y176-R206, E228-F257, L269-A289). The X-ray crystal conformations of the various ligands were used in the calculations (carazol, (2S)-1-(9H-carbazol-4-yloxy)-3-(isopropylamino)propan-2-ol for β2AR; cyanopindolol, 4-{[(2S)-3-(tert-butylamino)-2-hydroxypropyl]oxy}- 3H-indole-2-carbonitrile for β1AR, and ZMA, 4-{2-[(7-amino-2-furan-2-yl[1,2,4]triazolo[1,5-a][1,3,5]triazin-5-yl)amino]ethyl}phenol for A2AR). The ligand for A2AR was modeled as charged and all the other ligands as neutral. Hydrogens were added to the X-ray crystal conformation of the ligands in Sybyl 7.3, and then energies of the structures were minimized using the Tripos force field. The X-ray crystal structure conformation of the ligands was held rigid during docking calculations.
Before running the RosettaLigand calculation, the model receptors and the X-ray crystal structure receptors were superimposed in the Macromodel package such that the calculations started with the ligand in the same position seen in the crystal structure. The ligand conformation was run through RosettaLigand, essentially as described in the original publication46. Ligand poses were sampled within a 6 Å × 16 Å × 16Å box centered on the center of mass of the input ligand's coordinates. The ligand was allowed to rotate with an 8° standard deviation from the position observed in the crystal structure. Optimization of the pose included one cycle of gradient rigid-body energy minimization of the receptor-ligand energy, followed by side-chain repacking. A total of 2000 ligand poses were calculated for each receptor structure. The lowest-energy pose was taken from the calculation and the corresponding rms value was noted. In some cases, the ligand docked outside the binding pocket around the TM domains; only poses within the GPCR receptor pocket were considered.
Results and Discussion
EC1 and EC3 loops
Geometrical sampling for the smaller EC1 and EC3 loops was performed in one single step covering all combinations of the local minima in the Ramachandran maps for each individual residue in the loop (see Computational methods). Results of both geometrical sampling and energy calculations are described in Table II. Table II lists all parameters employed for sampling (Inp, Out, Del and the numbers of selected conformers) and for energy calculations (the energy cut-offs ΔE and the numbers of selected low-energy conformers) as well as the numbers of clusters of low-energy conformers grouped by the corresponding rms values. Note that the rms values throughout this paper were calculated between the heavy atoms of the loop backbones with the TM stems overlapped (the method commonly used to compare the calculation results with crystal structures, see corresponding references below). Table II lists also the lowest rms values (the “best” values) obtained by comparison of the low-energy structures of the EC1 and EC3 loops with the corresponding X-ray structures, namely 1F88 for bRh, 2Z73 for sRh, 2RH1 for β2AR, 2VT4 for β1AR and 3EML for A2AR.
Table II.
Procedure and modeling results for the smaller loops EC1 and EC3
| GPCR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Procedure | Sampling parameters | bRh | sRh | β2AR | β1AR | A2AR | |||||
| EC1 | EC3 | EC1 | EC3 | EC1 | EC3 | EC1 | EC3 | EC1 | EC3 | ||
| Geometry sampling | Inp | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 |
| Out | 7.0 | 7.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | |
| Del | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Selected | 87 | 414 | 126 | 892 | 323 | 840 | 272 | 683 | 40 | 3,867 | |
| Energy sampling | ΔE, kcal/mol | 10 | 10 | 10 | 12 | 10 | 10 | 10 | 10 | 6 | 10 |
| Selected | 17 | 55 | 36 | 75 | 90 | 50 | 88 | 32 | 7 | 102 | |
| Best rms, Å | 1.4 | 1.0 | 1.2 | 2.7 | 1.6 | 1.9 | 1.9 | 2.3 | 1.9 | 1.6 | |
| Clusters | Rms, Å | 2.0 | 2.0 | 3.0 | 2.5 | 2.0 | 2.0 | 3.0 | 2.0 | 2.0 | 2.0 |
| Number | 3 | 6 | 5 | 6 | 4 | 2 | 2 | 7 | 2 | 6 | |
EC2 loops
Table III describes the procedure of restoring the larger EC2 loops, the most challenging part of this study. The EC2 loops are less “stretched” and much more flexible than the EC1 and EC3 loops: while the “flexibility ratios” (calculated as defined elsewhere51) for the EC1 and EC3 loops were 1.24 – 1.79 (the “full stretch” value is ca. 1), for the EC2 loops they were 4.82 – 7.41. Table III contains the values of all parameters employed at each step and numbers of the conformers selected at the each step. Geometry sampling was performed first from the beginning of the loop to the Cys45.50 residue (residue 187 in bRh; 186 in sRh; 191 in β2AR; 199 in β1AR; and 166 in A2AR, see Table I), and then further to the end of the loop. To reach the Cys45.50 residues, all combinations of the set of local minima on the Ramachandran map for the first sampled fragments were explored; after that, the selected conformations were successively elongated in two additional steps with low-energy structures of the two fragments, namely 179-182 and 183-187 for bRh; 178-182 and 183-186 for sRh; 179-183 and 184-191 for β2AR; 186-191 and 192-199 for β1AR; and 146-159 and 160-166 for A2AR (see Table III). Energy calculations and selection of the low-energy structures for these fragments were performed separately according to the established procedure45.
Table III.
Procedure and modeling results for the larger loops EC2
| GPCR | Procedure | Procedure outline | ||||||
|---|---|---|---|---|---|---|---|---|
| bRh | Geometry sampling | Fragment | 172-178 | 172-182 | 172-187 | 172-192 | 172-195 | 172-200 |
| Inp | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | ||
| Out | 6.0 | 6.0 | 6.0 | 2.9 | 6.0 | 6.0 | ||
| Del | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Selected | 15,345 | 358,343 | 6,656 | 20,912 | 69,755 | 119,309 | ||
| Energy calculation | Fragment | 179-182 | 183-187 | 188-192 | 169-203 | |||
| ΔE, kcal/mol | 6 | 7 | 7 | 20 | ||||
| Selected | 270 | 143 | 85 | 478 | ||||
| sRh | Geometry sampling | Fragment | 171-177 | 171-182 | 171-186 | 171-191 | 171-194 | 171-197 |
| Inp | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | ||
| Out | 6.0 | 6.0 | 6.0 | 4.0 | 6.0 | 6.0 | ||
| Del | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Selected | 30,360 | 1,228,400 | 30,476 | 165,916 | 446,435 | 158,643 | ||
| Energy calculation | Fragment | 178-182 | 183-186 | 187-191 | 168-200 | |||
| ΔE, kcal/mol | 10 | 10 | 10 | 20 | ||||
| Selected | 493 | 226 | 156 | 292 | ||||
| β2AR | Geometry sampling | Fragment | 170-178 | 170-183 | 170-191 | 170-194 | 170-198 | |
| Inp | 4.0 | 4.0 | 4.0 | 3.5 | 4.0 | |||
| Out | 7.5 | 8.0 | 6.0 | 3.5 | 6.0 | |||
| Del | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | |||
| Selected | 110,710 | 565,652 | 23,805 | 12,690 | 9,818 | |||
| Energy calculation | Fragment | 179-183 | 184-191 | 167-201 | ||||
| ΔE, kcal/mol | 6 | 10 | 20 | |||||
| Selected | 22 | 315 | 129 | |||||
| β1AR | Geometry sampling | Fragment | 178-185 | 178-191 | 178-199 | 178-202 | 178-206 | |
| Inp | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | |||
| Out | 8.0 | 8.0 | 6.0 | 3.5 | 6.0 | |||
| Del | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | |||
| Selected | 14,305 | 597,932 | 35,079 | 22,930 | 18,969 | |||
| Energy calculation | Fragment | 186-191 | 192-199 | 175-209 | ||||
| ΔE, kcal/mol | 6 | 8 | 20 | |||||
| Selected | 115 | 1,570 | 376 | |||||
| A2AR | Geometry sampling | Fragment | 141-145 | 141-159 | 141-166 | 141-170 | 141-176 | |
| Inp | 4.0 | 4.0 | 4.0 | 3.5 | 4.0 | |||
| Out | 6.0 | 8.0 | 6.0 | 3.5 | 6.0 | |||
| Del | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | |||
| Selected | 680 | 82,016 | 7,402 | 49,128 | 56,783 | |||
| Energy calculation | Fragment | 146-159 | 160-166 | 138-179 | ||||
| ΔE, kcal/mol | 12 | 8 | 20 | |||||
| Selected | 2,162 | 1,877 | 255 | |||||
Elongation beyond the Cys45.50 residues to the end of the loops was achieved in three successive steps for bRh and sRh and in two steps for β2AR, β1AR and A2AR. The additional steps for bRh and sRh involved low-energy structures of the fragments 188-192 and 187-191, respectively (see Table III); all other steps utilized sampling with all combinations of the set of local minima on the Ramachandran map. The step of elongation from Cys45.50 further used the smaller values of the Int and Out parameters for all GPCRs; otherwise this step recovered too few conformations for the next steps. Finally, energy calculations were performed for the selected conformations of the loops flanked by the fixed backbones of the TM stems (as in the above case of the EC1 and EC3 loops) and low-energy structures were selected by the energy cut-off of 20 kcal/mol.
Final EC1+EC2+EC3 packages
Energy calculations for the EC1+EC2+EC3 packages were performed for all combinations of the obtained low-energy conformations of the individual EC2 loops and the representative structures from the clusters of low-energy conformations for the EC1 and EC3 loops. Final low-energy structures of the packages were selected in three steps as described in Table IV. First, conformers within the energy cut-off of 50 kcal/mol were selected; then, conformers with high values for the sum energy of the parabolic constraint potentials (37 potentials, see Computational Methods) were excluded; and, finally, only conformers without steric clashes with the TM templates were selected. The remaining conformers were clustered together by the rms value of 4.0 Å calculated for all loop residues included in the EC1+EC2+EC3 packages.
Table IV contains the best rms values obtained for the EC1+EC2+EC3 packages of each GPCR, as well as the rms values calculated for each EC loop in the packages. Generally, the latter values were slightly higher than the same values for the EC1 and EC3 loops in Table II, since the initial structures of EC1 and EC3 included in the packages were representatives of the clusters of their low-energy conformations and not the structures producing the best rms values of Table II.
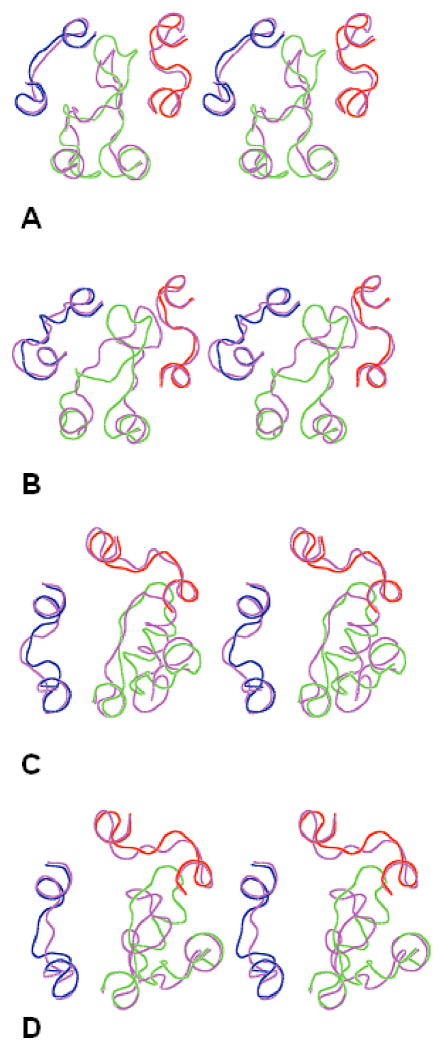
According to Table IV, our calculations more accurately reproduced the X-ray snapshots for adrenoreceptors β2AR and β1AR, than for photoreceptors bRh and sRh; the least accurate reproduction was obtained for the A2AR structure. One reason may be suggested based on Figure 2 depicting the predicted 3D structures of the EC loops corresponding to the best rms values listed in Table IV and the actual X-ray structures for the extracellular regions for each GPCR. The N-terminal tail region was not represented in the X-ray structures of adrenoreceptors (as well as of A2AR) since it was truncated in β1AR19 and, most likely, disordered in the crystal β2AR structure18. In contrast, the N-terminal tail was well resolved in the X-ray structures of photoreceptors bRh16 and sRh17 (compare Figures 2A and 2B with Figures 2C and 2D). Our calculations did not consider the N-terminal tail in the EC1+EC2+EC3 packages, and, therefore, did not account for possible interactions between the N-terminal tail and the EC loops, which might be important in the specific X-ray snapshots of the photoreceptors. Indeed, Figures 2A and 2B show possible steric clashes between the N-terminal tail of the X-ray snapshot and the calculated EC2 and EC3 loops. On the other hand, the long N-terminal tails in photoreceptors are flexible enough to adopt quite different conformations in the X-ray structures of bRh and sRh (compare Figures 2A and 2B); other conformations of N-terminal segments not interacting with the EC loops may occur depending on specific experimental conditions of crystallization.
Figure 2.
Stereoviews of the X-ray structures of the EC loops shown as lines in red (EC1), green (EC2) and blue (EC3) and the 3D structures of the calculated EC loops shown as lines in magenta. A) sRh; B) sRh; C) β2AR; D) β1AR. The view is from the extracellular space normal to the membrane plane.
Additional disulfide bridges in the EC loops
Our de novo modeling assumed that the highly conserved disulfide bridge, Cys3.25 in the TM3 helical stem and Cys45.50 in EC2, was present in the EC1+EC2+EC3 packages for all GPCRs. However, additional possibilities for forming disulfide bridges that were observed in some X-ray structures were also considered. For instance, there is the disulfide bridge between Cys45.43 and Cys45.49 in the EC2 of β2AR and β1AR. No other additional cysteines are present in the EC loops of β2AR and β1AR (see Table I), but there are several cysteines in the EC loops of A2AR that form three additional disulfide bridges in the X-ray structure, namely C71-C159 and C74-C146 between EC1 and EC2 and C259-C262 within EC3.
To account for the possible additional disulfide bridge in β2AR and β1AR, the modeling procedure for the EC2 loops of β2AR and β1AR was repeated as outlined in Table III, but considered elongations at steps 170-191 (β2AR) and 178-199 (β1AR) employing low-energy conformations of the fragments 184-191 (or 192-199) that included the disulfide bridges C184-C190 and C192-197, respectively. The resulting low-energy structures of EC2 (192 and 89 conformers, respectively) were then included in the EC1+EC2+EC3 packages yielding 260 low-energy structures for β2AR and 285 low-energy structures for β1AR. When compared to the X-ray snapshots, insertion of the additional disulfide bridges in the EC2 loops did not result in significant changes in both cases indicating that formation of the additional disulfide bridges in the EC2 loops of β2AR and β1AR occurred in strict agreement with the entire system of residue-residue interactions. The best rms values calculated for EC1, EC2, EC3 and EC1+EC2+EC3 (reported in Table V) were only slightly better than the corresponding values listed in Table IV.
Table V.
Modeling results for insertion of additional disulfide bridges in the EC loops
| GPCR | β2AR | β1AR | A2AR | |||
|---|---|---|---|---|---|---|
| Additional disulfide bridges | C259- | C259- | ||||
| C184- | C192- | C259- | C262; | C262; | ||
| C190 | C198 | C262 | C74- | C74- | ||
| C146 | C146; | |||||
| C71- | ||||||
| C159 | ||||||
| Low-energy conformers | 260 | 285 | 46 | 27 | 12 | |
| Rms, Å | EC1+EC2+EC3 | 3.4 | 4.0 | 4.6 | 4.7 | 4.1 |
| EC1 | 1.4 | 2.1 | 1.7 | 1.8 | 1.9 | |
| EC2 | 3.7 | 4.1 | 5.7 | 5.5 | 4.8 | |
| EC3 | 1.9 | 2.3 | 1.8 | 1.6 | 1.6 | |
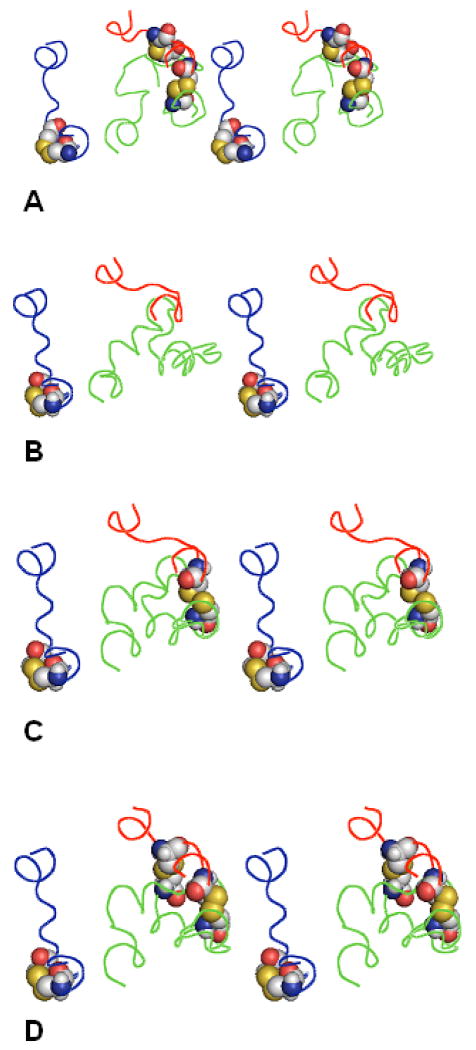
For A2AR, on the contrary, the additional disulfide bridges between the EC loops significantly altered the low-energy structures of the EC loops. A2AR contains C71 and C74 in EC1; C146 and C159 in EC2; and C259 and C262 in EC3 (see Table I). Potentially, there are three options to form additional bridges within each of the loops (C71-C74, C146-C159 and C259-C262), four options for bridges between EC1 and EC2 (C71-C146, C71-159, C74-C146 and C74-C159) and four options for bridges between EC2 and EC3 (C146-C259, C146-C262, C159-C259 and C159-C262). Evaluation of the Cβ-Cβ distances between all pairs of cysteines for the low-energy conformations of the EC1+EC2+EC3 packages showed that distances were less than 8 Å between 71-74 in 62% of conformers; between 146-159 in 9% of conformers; and between 259-262 in 49% of conformers. If one reasonably assumes that disulfide bridges formed first within the loops rather than between them, then the distance evaluation suggests that there are three likely options for this first step of forming the system of the disulfide bridges in the EC loops of A2AR, namely, forming either C71-C74 in EC1, or C259-C262 in EC3, or both.
All three options were explored by the modeling procedure for the EC1+EC2+EC3 packages. In each option, the procedure included representatives from the clusters of low-energy conformers obtained by additional calculations of the EC1 and EC3 loops of A2AR with insertion of the C71-74 or C259-C262 disulfide bridges, respectively. The option featuring both the C71-C74 and C259-C262 disulfide bridges yielded 14 low-energy conformations; in this case, obviously, no disulfide bridge between the loops was possible. The option with the C71-C74 disulfide bridge yielded 48 low-energy conformers of the EC1+EC2+EC3 package; according to distance evaluations, the only possibilities for introducing an additional disulfide bridge between EC2 and EC3 in this case were either C146-C259 or C146-C262. The former possibility led to 23 low-energy structures of the EC1+EC2+EC3 package with two disulfide bridges, C71-C74 and C146-C259, and the latter yielded 6 low-energy structures with the C71-C74 and C146-C262 disulfide bridges.
The remaining option (the C259-C262 bridge in EC3) resulted in 46 low-energy structures of the EC1+EC2+EC3 package, where evaluation of the Cβ-Cβ distances between cysteines generated only one additional disulfide bridge between EC1 and EC2, that of C74-C146. Insertion of this constraint yielded 27 low-energy structures of the EC1+EC2+EC3 package with the two additional disulfide bridges; distance evaluation in these structures determined one more possible contact between C71 and C159. Energy calculations for the EC1+EC2+EC3 package with all three disulfide bridges, C259-C262, C74-C146 and C71-C159 led to 12 low-energy structures with the same system of the additional disulfide bridges as presented in the X-ray structure of A2AR.
These results demonstrate that modeling was able not only to identify the correct system of the additional disulfide bridges in the EC loops of A2AR (along with several other possible systems), but also to outline probable pathways for forming such system, namely from the C259-C262 bridge in EC3 to the C74-C146 bridge and then to C71-C159 bridge. Figure 3 presents sketches of the EC1+EC2+EC3 low-energy structures corresponding to the best rms values obtained at each step of the pathway along with the X-ray structure of the EC loops of A2AR; the best rms values are listed in Table V. The data in Figure 3 and Table V suggested that, unlike in photoreceptors and adrenoreceptors, the 3D structures of the EC loops in A2AR are strongly influenced by the constraints from the system of the disulfide bridges between them.
Figure 3.
Forming the system of additional disulfide bridges between the EC loops in A2AR. The EC loops are shown as lines in red (EC1), green (EC2) and blue (EC3). Residues C71, C74, C146, C159, C259 and C262 are shown as space-filled models. A) the X-ray structure; B) calculated structure with the best rms values,C259-C262 bridge added; C) calculated structure with the best rms values, C74-C146 bridge added; D) calculated structure with the best rms values, C71-C159 bridge added. The view is from the extracellular space normal to the membrane plane.
Comparison of our results with the data of the other authors
Since our modeling procedure employs an unsophisticated force field, a rather rough sampling grid and deliberately sacrifices detailed description of the system (no membrane lipids, no water molecules, etc.) in favor of rapid determination of sterically and energetically reasonable conformers of the loops, it would be unrealistic to expect that the closest spatial similarity to the X-ray structures would be achieved by the lowest-energy conformation. On the other hand, the X-ray structures themselves are only specific snapshots frozen out of many possible conformations of the EC loops. Therefore, in our view, the best rms values as defined above can be considered an adequate measure of agreement between the available experimental data and the results of our calculations.
Our results are also quite comparable to the best rms values obtained by recent predictions of the various protein loops of the same size by other modeling procedures. Table VI lists the best rms values and the rms values corresponding to the lowest-energy structures in our calculations and in the modeling studies by other authors25-27,34,36,38,49. In almost all cases, the rms values were calculated for all heavy backbone atoms (as in our rms values); in some studies, the rms value were calculated for only Cα atoms27,49, or for Cα, C and N atoms26. The rms values by the other authors were extracted either from the Tables26,27,38,49, or estimated from the Figures25,34,36. Only one rms value is shown in Table VI for the data obtained by knowledge-based approaches (no energy was calculated)36. Also, the study using the most recent de novo modeling procedure did not present the final best rms values34; they were estimated from the data shown for the 50 best-scoring structures preceding the final refinement. In most cases, the rms values in Table VI obtained by the other authors refer to the average (median) values over the specific benchmark sets of the loops from the soluble global proteins; note that the methods for predictions of the loops in soluble proteins are currently more developed than those for the membrane proteins.
Table VI.
Comparison of our data with the data of the other authors (rmsB – the best rms values; rmsL – the rms values corresponding to the lowest-energy conformation; in Å)
| Loop length | Loop | Our data | Data of other authors for the loops of the same size | Reference, specific Table/Figure, prediction method cited | ||
|---|---|---|---|---|---|---|
| rmsB | rmsL | rmsB | rmsL | |||
| 6 | EC1 (A2AR) | 1.9 | 2.1 | 0.2 | 0.5 | Ref. 27, Table IV |
| 0.3 | 0.5 | Ref. 27, Table V | ||||
| 0.2 | 0.4 | Ref. 25, Fig. 1K, Prime | ||||
| 1.1 | - | Ref. 36, Fig. 4B; MolLoop | ||||
| 1.1 | 3.0 | Ref. 25, Fig. 1K, Modeler | ||||
| 1.2 | 2.2 | Ref. 25, Fig. 1K, ICM | ||||
| 1.3 | - | Ref. 36, Fig. 4B | ||||
| 1.7 | 2.0 | Ref. 25, Fig. 1K, Sybyl | ||||
| 8 | EC3 (bRh) | 1.0 | 2.8 | 0.7 | 1.4 | Ref. 38, Table II |
| EC1 (sRh) | 1.2 | 4.3 | 0.9 | 1.3 | Ref. 34, Fig. 2, Table V | |
| EC1 (bRh) | 1.4 | 5.2 | 1.0 | 1.2 | Ref. 25, Fig. 1K, Prime | |
| EC1 (β2AR) | 1.6 | 5.2 | 1.1 | 1.3 | Ref. 27, Table VI | |
| EC1 (β1AR) | 1.9 | 2.7 | 1.6 | 3.3 | Ref. 26, Table 2 | |
| 2.3 | 3.7 | Ref. 25, Fig. 1K, ICM | ||||
| 2.5 | - | Ref. 36, Fig. 4B; MolLoop | ||||
| 2.7 | 3.9 | Ref. 25, Fig. 1K, Sybyl | ||||
| 2.8 | 4.0 | Ref. 25, Fig. 1K, Modeler | ||||
| 3.4 | - | Ref. 36, Fig. 4B | ||||
| 9 | EC3 (β2AR) | 1.9 | 3.4 | 1.4 | 1.9 | Ref. 34, Fig. 2, Table V |
| EC3 (β1AR) | 2.3 | 3.3 | 2.0 | 2.6 | Ref. 25, Fig. 1K, Prime | |
| 2.8 | 4.2 | Ref. 25, Fig. 1K, ICM | ||||
| 3.0 | 4.7 | Ref. 25, Fig. 1K, Modeler | ||||
| 3.0 | 5.0 | Ref. 25, Fig. 1K, Sybyl | ||||
| 3.3 | - | Ref. 36, Fig. 4B; MolLoop | ||||
| 4.5 | - | Ref. 36, Fig. 4B | ||||
| 10 | EC3 (sRh) | 2.7 | 2.9 | 1.1 | 1.9 | Ref. 34, Fig. 2, Table V |
| 2.5 | 3.0 | Ref. 25, Fig. 1K, Prime | ||||
| 2.8 | 3.7 | Ref. 25, Fig. 1K, Sybyl | ||||
| 2.9 | 4.5 | Ref. 25, Fig. 1K, ICM | ||||
| 3.0 | 6.4 | Ref. 25, Fig. 1K, Modeler | ||||
| 3.7 | - | Ref. 36, Fig. 4B; MolLoop | ||||
| 4.8 | - | Ref. 36, Fig. 4B | ||||
| 11 | EC3 (A2AR) | 1.6 | 2.3 | 1.6 | 2.5 | Ref. 34, Fig. 2, Table V |
| 2.5 | 3.7 | Ref. 25, Fig. 1K, Prime | ||||
| 3.3 | 5.0 | Ref. 25, Fig. 1K, Modeler | ||||
| 3.5 | 5.6 | Ref. 25, Fig. 1K, ICM | ||||
| 4.3 | 6.6 | Ref. 25, Fig. 1K, Sybyl | ||||
| 4.6 | - | Ref. 36, Fig. 4B; MolLoop | ||||
| 5.6 | - | Ref. 36, Fig. 4B | ||||
| 25 | EC2 (sRh) | 4.8 | 12.4 | |||
| 27 | EC2 (β2AR) | 3.8 | 7.4 | - | 5.4 | Ref. 38, Table VII |
| EC2 (β1AR) | 4.3 | 6.4 | ||||
| EC2 (bRh) | 4.7 | 8.4 | ||||
| 34 (27) | EC2 (A2AR) | 5.9 | 10.2 | |||
| 34 (23) | EC2 (A2AR) | 6.4 | 10.9 | - | 7.1 – 12.7 | Ref. 49, Table 1 |
| 34 (27) | EC2 (A2AR) | 4.8 | 4.8 | |||
Table VI shows that the best rms values for smaller EC1 and EC3 loops (8 to 11 residues) obtained by our procedure are, on the average, as good as the rms values by the other authors. Invariably, our best rms values for the EC1 and EC3 loops were closer to the smallest rms values obtained for the loops of the same size in the most recent de novo modeling procedure34 that was based on very thorough sampling of conformational space47 combined with sophisticated energy-based scoring function48, than to the largest values obtained by the knowledge-based homology modeling36. Interestingly, it seems that the larger the loop, the more accurately our results reproduced the native loop structures compared with the data of the other authors. Indeed, our best rms value for the 6-membered loop was 1.9 Å, whereas the other author's values ranged from 0.25 Å to 1.7 Å. At the same time, our best rms value for the 11-membered loop was 1.6 Å compared to 1.6 Å – 5.6 Å obtained by the other authors. The same tendency is observed in the rms values corresponding to the lowest-energy structures: while our values are clearly worse than the best of the other authors for the 6- to 10-membered loops, they became practically the same for the 11-membered loop. However, as noted above, employing simplified force field and environment model precludes using the rms values corresponding to the lowest-energy structures as reliable validation parameter.
The best rms values for the EC2 loops ranged from 3.8 Å to 5.9 Å, the smallest loop being of 25 residues and the largest having 34 residues (see Table I). (For A2AR, however, calculation of the rms values did not involve the fragment EC2 149-155 missing in the 3EML X-ray structure, therefore only 27 residues were involved as shown in brackets in Table VI.) The loops (“structurally variable regions”) of that size were modeled recently only by the Rosetta approach for predictions of protein structures within the CASP-5 competition38. The obtained rms values were of 19.0 Å for 26 residues; of 5.4 Å for 27; of 4.3 Å, 4.6 Å and 7.1 Å for 28; 12.8 Å for 31; and 20.4 Å for 34 residues38; in comparison, our predictions of the large EC loops in GPCRs were of higher accuracy and consistence. Also, the very recent community-wide blind prediction of the 3D structure of A2AR (206 models by 29 group of authors) yielded rms values of 7.1 Å – 12.7 Å for EC2 (23 residues from 143 to 172, without missing fragment 149-155); again, our results were clearly superior. The last row of Table VI lists the rms values obtained for EC2 in A2AR with all additional disulfide bonds in the EC loops inserted; in this case, not only the best rms value improved, but the lowest-energy structure was the same as that with the best rms value. On the other hand, we have also performed additional energy minimizations starting from the corresponding X-ray structures of the EC1+EC2+EC3 packages that resulted in the rms values ranged from 1.8 Å to 3.0 Å. Obviously, these results represent the best agreement with the experimental X-ray structures that could be obtained by our procedure of energy calculations (see the last row in Table IV; for A2AR, where the EC2 149-155 fragment was missing in the X-ray structure, energy calculations were not performed).
Conformational dynamics of the loops
Our modeling procedure deliberately used simple assumptions regarding molecular environment of the loops and simple energy functions, essentially scoring functions. Therefore, it would be inaccurate to arrange the obtained low-energy loop structures according to the calculated energy values; instead, all structures possessing energies within the accepted cut-off (ΔE = 50 kcal/mol) should be considered as equally probable in the entire ensembles of possible structures. In this regard, the sets of low-energy structures of the EC1+EC2+EC3 packages obtained by energy calculations may be used for studying conformational possibilities of the EC loops in GPCRs.
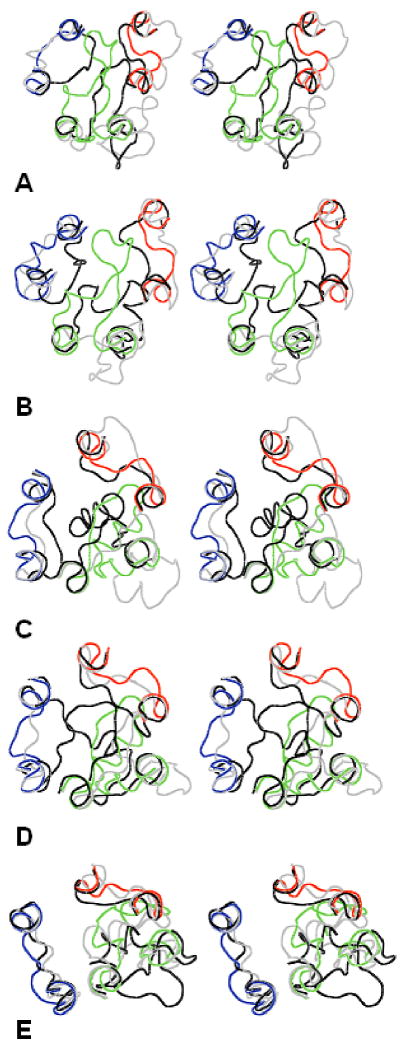
Figure 4 presents the X-ray structures of the EC loops for GPCRs in question together with the “most open” and “most closed” structures of the EC1+EC2+EC3 packages singled out by the largest and smallest Cα-Cα distances among residues at the “tips” of EC1, EC2 and EC3, which were selected as F103, T193 and S281 for bRh; W101, I191 and E290 for sRh; W99, E180 and L302 for β2AR; W107, Q188 and L319 for β1AR; and A72, K153 and S263 for A2AR. It is clearly seen that, in all cases, the most open structures provide ample space for a ligand to enter the TM cavity and the most closed structures almost fully isolate the TM cavity from solvent (compare Figures 4 and 1). According to these results, conformational dynamics of the EC loops may involve large molecular movements; the largest movements between the most opened and most closed structures being estimated as ca. 25 Å for bRh (the difference in Cα-Cα distances between F103 and S281), 20 Å for sRh (W101 – E290), 18 Å for β2AR (W99 – E180), 17 Å for β1AR (Q188 – L319), and 8 Å for A2AR (K153 – S263). This estimates are much larger than, for instance, movement of the EC2 loop in bRh upon activation found by the very recent solid state NMR experiment14, but an ensemble of possible conformations of EC2 obtained by modeling calculations includes also a range of smaller movements. On the other hand, the solid state NMR experiment captures just one conformational state of the EC loops. Note that the movements of this scale could be found only by the ultra-long (up to microseconds) MD simulations.50
Figure 4.
Stereoviews of the X-ray structures of the EC loops shown as lines in red (EC1), green (EC2) and blue (EC3) overlapped with the most open (gray lines) and most closed (black lines) calculated structures. A) bRh; B) sRh; C) b2AR; D) b1AR; E) A2AR. The view is from the extracellular space normal to the membrane plane.
Docking ligands to GPCR models
Our modeling procedure reproduced the X-ray structures of the EC1+EC2+EC3 packages for five GPCRs with the best rms values ranged from 3.4 – 3.6 Å for β2AR to 4.6 Å for sRh (see Tables IV and V). One more element of validation for the predicted structures of the EC loops would be to reproduce the binding pose for the low-molecular weight ligands crystallized together with GPCRs (namely, carazol for β2AR, cyanopindolol for β1AR and ZMA for A2AR) within the binding pocket that makes contacts with loop residues.
In this regard, the above ligands were docked to the corresponding receptors using the RosettaLigand program as described in Computational Methods to determine possible differences between the docking poses in the crystal structures and in the predicted loop structures of the receptors. The docking procedure started from the actual spatial positions of the ligands whose conformations were constrained as in the crystal structures. For each GPCR, the docking procedure was run independently for the two options of the crystal structure, with and without the EC loops, and for receptors with the predicted structure of the EC loops corresponding to the best rms values from Tables IV and V (see also structures in Figures 2C, 2D and 2D). Also, two other options of the EC loops with the “average” and “worst” (largest) rms values relative to the X-ray structures were considered to determine the importance of specific conformations of the loops for accurate docking. (The specific average and worst rms values for the EC1+EC2+EC3 packages were 6.3 Å and 8.2 Å for β2AR; 6.2 Å and 10.4 Å for β1AR; and 6.2 Å and 8.4 Å for A2AR; the corresponding structures are not shown.) The lowest-energy docking pose was selected from each run, and the rms values calculated for the ligand structures in the selected poses and the X-ray crystal structures of the ligands are listed in Table VII.
Table VII.
Rms values for the ligands docked to GPCRs (in Å)
| Receptor | X-ray structure | Predicted loops with rms values: | |||
|---|---|---|---|---|---|
| without loops | with loops | best | average | worst | |
| β2AR | 0.96 | 3.40 | 0.89 | 1.12 | 1.30 |
| β1AR | 0.58 | 2.30 | 0.59 | 1.06 | 1.10 |
| A2AR | 2.89 | 3.54 | 3.56 | 6.56 | ≫10 |
The results in Table VII demonstrate, first of all, that the docking procedure using the predicted EC structures with the best rms values indeed was able to accurately reproduce the docking poses found in the crystal structures of GPCRs. Also, in all cases, the structures with the average and the largest rms values yielded docking poses least similar to the crystal structures, though still rather close to those observed in β2AR and β1AR. For A2AR, the loop conformations seem more important. With the loop conformations corresponding to the largest rms value, the ligand did not dock near the binding site. Also, the conformations with the average rms value did not yield accurate docking in the case of A2AR. However, when the loop conformations with the best rms values were used, the ligand docked with accuracy similar to the accuracy seen when docking to the crystal structure. In general, the docking accuracy in the case of A2AR appears to be significantly less accurate than for β1AR and β2AR. One explanation for this may be the high B-factors of the ligand found in 3EML, particularly around the phenyl group, which could be indicative of some disorder in that region20. To try to improve accuracy, RosettaLigand was also run with a Monte Carlo minimization, which involves 50 cycles of side chain repacking, followed by gradient rigid-body energy minimization of the ligand-receptor structure. The standard Metropolis criterion was used to accept or reject the move that results from each cycle. This procedure yielded results similar to side chain repacking followed by one round of gradient rigid-body energy minimization of the ligand-receptor structure. Interestingly, other authors that re-docked the ZMA ligand to the 3EML crystal structure in the native-like docking pose employing the ICM package yielded the ligand rms < 3.0 Å49, close to our data in Table VII.
The accuracy of docking the ligands to the crystal structures without loops was higher than for the crystal structures with loops. In fact the accuracy of docking to the predicted structures of the loops in β2AR and β1AR was higher than that for docking to the crystal-based loops. This may be due to insufficient repacking of the side chains in the binding pocket of the X-ray structures used by the docking procedure or due to the rotamer approximation used by the docking program; the side chains of the calculated structures were repeatedly repacked at all stages of our modeling procedure (see above). On the other hand, a similar tendency was noted in virtual screening of a large database of low-molecular weight ligands against the modeled structures of three rhodopsin-like GPCRs, where the loopless models showed quite accurate predictions for two out of three GPCR receptors5.
Concluding Remarks
The main goal of this study was to restore long (20-30 residue) protein loops and to study the conformational dynamics of the EC loops in GPCRs. We applied our modeling approach to recently solved structures of different GPCRs complementing the experimental techniques of X-ray crystallography and NMR spectroscopy. Our specific aims included the determination of possible low-energy conformations of the loops without employing extensive computational resources, which could then be validated by available X-ray structures of GPCRs. We did not focus on a single possible conformation of the 3D structure of EC loops, but on producing a variety of energetically and sterically consistent options testable by rationally planned experiments.
Despite simplifications (no membrane lipids, no water molecules and ions, simple force field, etc.), our modeling resulted in ensembles of the low-energy conformers of the EC loops that contained structures similar to the X-ray snapshots. For the smaller EC1 and EC3 loops, our results were at least as good as those obtained by other authors employing much more sophisticated approaches. For the larger EC2 loops, our results consistently yielded structures significantly closer to the X-ray snapshots than the results of the other authors for loops of similar size.
Our modeling pointed out possibilities for large scale movements of the EC loops in GPCRs that may determine their conformational dynamics. It was validated also by reproducing the docking poses for low-molecular weight ligands in β2AR, β1AR and A2AR demonstrating the possible influence of the structures of the EC loops on spatial binding positions of the ligands. Our modeling correctly predicted the system of disulfide bridges between the EC loops in A2AR and elucidated probable pathways for forming of disulfides. It suggested that this simplified approach could be useful for rational design of specific mutations leading to insertion of an additional disulfide bridges constraining conformational flexibility of the EC loops of GPCRs and, therefore, influencing ligand binding and functional activity. The approach could be also used for rationalizing available data on the site-directed mutagenesis in the EC loops from a structural standpoint.
Our current approach to modeling the structure of GPCRs can be further developed. For instance, we noted that in some cases interactions with the N-terminal tail may change the structures of the EC loops. Also, introducing the solvent and/or membrane lipids into energy calculations may limit large-scale movements of the loops. While the rather rough “grid” of the dihedral angle values employed in geometrical sampling proved satisfactory for the smaller EC loops, larger loops may require application of a finer grid. However, even in the present state, the approach successfully generated ensembles of energetically and sterically acceptable 3D structures for the EC loops in five GPCRs validated by comparisons with available X-ray structures. One obvious application for the approach is predicting possible ensembles of the 3D structures of the large flexible loops in soluble proteins, a challenging problem for protein modeling.
Acknowledgments
Grant sponsor: NIH; Grant numbers GM 71634 and GM63720, Fellowship F32GM082200
References
- 1.Kroeze WK, Sheffler DJ, Roth BL. G-protein-coupled receptors at a glance. Journal of Cell Science. 2003;116(Pt 24):4867–4869. doi: 10.1242/jcs.00902. [DOI] [PubMed] [Google Scholar]
- 2.Drews J. Drug discovery: A historical perspective. Science. 2000;287:1960–1964. doi: 10.1126/science.287.5460.1960. [DOI] [PubMed] [Google Scholar]
- 3.Avlani VA, Gregory KJ, Morton CJ, Parker MW, Sexton PM, Christopoulos A. Critical role for the second extracellular loop in the binding of both orthosteric and allosteric G protein-coupled receptor ligands. Journal of Biological Chemistry. 2007;282(35):25677–25686. doi: 10.1074/jbc.M702311200. [DOI] [PubMed] [Google Scholar]
- 4.Wacker JL, Feller DB, Tang XB, Defino MC, Namkung Y, Lyssand JS, Mhyre AJ, Tan X, Jensen JB, Hague C. Disease-causing mutation in GPR54 reveals the importance of the second intracellular loop for class A G-protein-coupled receptor function. Journal of Biological Chemistry. 2008;283(45):31068–31078. doi: 10.1074/jbc.M805251200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.de Graaf C, Foata N, Engkvist O, Rognan D. Molecular modeling of the second extracellular loop of G-protein coupled receptors and its implication on structure-based virtual screening. Proteins. 2008;71(2):599–620. doi: 10.1002/prot.21724. [DOI] [PubMed] [Google Scholar]
- 6.Gkounteilas K, Tselios T, Venihaki M, Deraos G, Lazaridis I, Rassouli O, Gravanis A, Liapakis G. Alanine scanning mutagenesis of the second extracellular loop of type 1 corticotropin releasing factor receptor revealed residues critical for peptide binding. Molecular Pharmacology. 2009 doi: 10.1124/mol.108.052423. 10.1124/mol.108.052423. [DOI] [PubMed] [Google Scholar]
- 7.Sura-Trueba S, Aumas C, Carre A, Durif S, Leger J, Polak M, de Roux N. An Inactivating Mutation within the First Extracellular Loop of the Thyrotropin Receptor Impedes Normal Posttranslational Maturation of the Extracellular Domain. Endocrinology. 2009;150:1043–1050. doi: 10.1210/en.2008-1145. [DOI] [PubMed] [Google Scholar]
- 8.Chee MJ, Morl K, Lindner D, Merten N, Zamponi GW, Light PE, Beck-Sickinger AG, Colmers WF. The third intracellular loop stabilizes the inactive state of the neuropeptide Y1 receptor. Journal of Biological Chemistry. 2008;283(48):33337–33346. doi: 10.1074/jbc.M804671200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Storjohann L, Holst B, Schwartz TW. A second disulfide bridge from the N-terminal domain to extracellular loop 2 dampens receptor activity in GPR39. Biochemistry. 2008;47(35):9198–9207. doi: 10.1021/bi8005016. [DOI] [PubMed] [Google Scholar]
- 10.Klco JM, Wiegand CB, Narzinski K, Baranski TJ. Essential role for the second extracellular loop in C5a receptor activation. Nature Struct Mol Biol. 2005;12:320–326. doi: 10.1038/nsmb913. [DOI] [PubMed] [Google Scholar]
- 11.Samson M, LaRosa G, Libert F, Paindavoine P, Detheux M, Vassart G, Parmentier M. The second extracellular loop of CCR5 is the major determinant of ligand specificity. Journal of Biological Chemistry. 1997;272(40):24934–24941. doi: 10.1074/jbc.272.40.24934. [DOI] [PubMed] [Google Scholar]
- 12.Shi L, Javitch JA. The second extracellular loop of the dopamine D2 receptor lines the binding-site crevice. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(2):440–445. doi: 10.1073/pnas.2237265100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Scarselli M, Li B, Kim SK, Wess J. Multiple residues in the second extracellular loop are critical for M3 muscarinic acetylcholine receptor activation. Journal of Biological Chemistry. 2007;282(10):7385–7396. doi: 10.1074/jbc.M610394200. [DOI] [PubMed] [Google Scholar]
- 14.Ahuja S, Hornak V, Yan EC, Syrett N, Goncalves JA, Hirshfeld A, Ziliox M, Sakmar TP, Sheves M, Reeves PJ, Smith SO, Eilers M. Helix movement is coupled to displacement of the second extracellular loop in rhodopsin activation. Nature Structural & Molecular Biology. 2009;16(2):168–175. doi: 10.1038/nsmb.1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mustafi D, Palczewski K. Topology of class A G protein-coupled receptors: insights gained from crystal structures of rhodopsins, adrenergic and adenosine receptors. Molecular Pharmacology. 2009;75(1):1–12. doi: 10.1124/mol.108.051938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Palczewski K, Kumasaka T, Hori T, Behnke CA, Motoshima H, Fox BA, Le Trong I, Teller DC, Okada T, Stenkamp RE, Yamamoto M, Miyano M. Crystal structure of rhodopsin: A G protein-coupled receptor. Science. 2000;289(5480):739–745. doi: 10.1126/science.289.5480.739. [DOI] [PubMed] [Google Scholar]
- 17.Murakami M, Kouyama T. Crystal structure of squid rhodopsin. Nature. 2008;453:363–367. doi: 10.1038/nature06925. [DOI] [PubMed] [Google Scholar]
- 18.Cherezov V, Rosenbaum DM, Hanson MA, Rasmussen SG, Thian FS, Kobilka TS, Choi HJ, Kuhn P, Weis WI, Kobilka BK, Stevens RC. High-resolution crystal structure of an engineered human beta2-adrenergic G protein-coupled receptor. Science. 2007;318(5854):1258–1265. doi: 10.1126/science.1150577. see comment. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Warne T, Serrano-Vega MJ, Baker JG, Moukhametzianov R, Edwards PC, Henderson R, Leslie AG, Tate CG, Schertler GF. Structure of a beta1-adrenergic G-protein-coupled receptor. Nature. 2008;454(7203):486–491. doi: 10.1038/nature07101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jaakola VP, Griffith MT, Hanson MA, Cherezov V, Chien EY, Lane JR, Ijzerman AP, Stevens RC. The 2.6 angstrom crystal structure of a human A2A adenosine receptor bound to an antagonist. Science. 2008;322(5905):1211–1217. doi: 10.1126/science.1164772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cozzini P, Kellogg GE, Spyrakis F, Abraham DJ, Costantino G, Emerson A, Fanelli F, Gohlke H, Kuhn LA, Morris GM, Orozco M, Pertinhez TA, Rizzi M, Sotriffer CA. Target flexibility: an emerging consideration in drug discovery and design. Journal of Medicinal Chemistry. 2008;51(20):6237–6255. doi: 10.1021/jm800562d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sellers BD, Zhu K, Zhao S, Friesner RA, Jacobson MP. Toward better refinement of comparative models: predicting loops in inexact environments. Proteins. 2008;72(3):959–971. doi: 10.1002/prot.21990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Groban ES, Narayanan A, Jacobson MP. Conformational changes in protein loops and helices induced by post-translational phosphorylation. PLoS Computational Biology. 2006;2(4):e32. doi: 10.1371/journal.pcbi.0020032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nikiforovich GV, Marshall GR, Baranski TJ. Modeling Molecular Mechanisms of Binding of the Anaphylotoxin C5a to the C5a Receptor. Biochemistry. 2008;47:3117–3130. doi: 10.1021/bi702321a. [DOI] [PubMed] [Google Scholar]
- 25.Rossi KA, Weigelt CA, Nayeem A, Krystek SR., Jr Loopholes and missing links in protein modeling. Protein Science. 2007;16(9):1999–2012. doi: 10.1110/ps.072887807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Olson MA, Feig M, Brooks CL., 3rd Prediction of protein loop conformations using multiscale modeling methods with physical energy scoring functions. Journal of Computational Chemistry. 2008;29(5):820–831. doi: 10.1002/jcc.20827. [DOI] [PubMed] [Google Scholar]
- 27.Mehler EL, Hassan SA, Kortagere S, Weinstein H. Ab initio computational modeling of loops in G-protein-coupled receptors: lessons from the crystal structure of rhodopsin. Proteins. 2006;64(3):673–690. doi: 10.1002/prot.21022. [DOI] [PubMed] [Google Scholar]
- 28.Spassov VZ, Flook PK, Yan L. LOOPER: a molecular mechanics-based algorithm for protein loop prediction. Protein Engineering, Design & Selection. 2008;21(2):91–100. doi: 10.1093/protein/gzm083. [DOI] [PubMed] [Google Scholar]
- 29.Lee DS, Seok C. Protein Loop Modeling Using Fragment Assembly. Journal of the Korean Physical Society. 2008;52:1137–1142. [Google Scholar]
- 30.Lin MS, Head-Gordon T. Improved Energy Selection of Nativelike Protein Loops from Loop Decoys. Journal of Chemical Theory and Computation. 2008;4:515–521. doi: 10.1021/ct700292u. [DOI] [PubMed] [Google Scholar]
- 31.Cui M, Mezei M, Osman R. Prediction of protein loop structures using a local move Monte Carlo approach and a grid-based force field. Protein Engineering, Design & Selection. 2008;21(12):729–735. doi: 10.1093/protein/gzn056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hu X, Wang H, Ke H, Kuhlman B. High-resolution design of a protein loop. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(45):17668–17673. doi: 10.1073/pnas.0707977104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nikiforovich GV, Marshall GR. Modeling Flexible Loops in the Dark-Adapted and Activated States of Rhodopsin, a Prototypical G-Protein-Coupled Receptor. Biophys J. 2005;89:3780–3789. doi: 10.1529/biophysj.105.070722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Soto CS, Fasnacht M, Zhu J, Forrest L, Honig B. Loop modeling: Sampling, filtering, and scoring. Proteins. 2008;70(3):834–843. doi: 10.1002/prot.21612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Felts AK, Gallicchio E, Chekmarev D, Paris KA, Friesner RA, Levy RM. Predictiion of Protein Loop Conformations Using the AGBNP Implicit Solvent Model and Torsional Angle Sampling. Journal of Chemical Theory and Computation. 2008;4:855–868. doi: 10.1021/ct800051k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fernandez-Fuentes N, Oliva B, Fiser A. A supersecondary structure library and search algorithm for modeling loops in protein structures. Nucleic Acids Research. 2006;34(7):2085–2097. doi: 10.1093/nar/gkl156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mirzadegan T, Benko G, Filipek S, Palczewski K. Sequence Analyses of G-Protein Coupled Receptors: Similarities to Rhodopsin. Biochemistry. 2003;42:2769–2767. doi: 10.1021/bi027224+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rohl CA, Strauss CE, Chivian D, Baker D. Modeling structurally variable regions in homologous proteins with rosetta. Proteins. 2004;55(3):656–677. doi: 10.1002/prot.10629. [DOI] [PubMed] [Google Scholar]
- 39.Wang C, Bradley P, Baker D. Proten-Protein Docking with Backbone Flexibility. Journal of Molecular Biology. 2007;373:503–519. doi: 10.1016/j.jmb.2007.07.050. [DOI] [PubMed] [Google Scholar]
- 40.Kortagere S, Roy A, Mehler EL. Ab initio computational modeling of long loops in G-protein coupled receptors. Journal of Computer-Aided Molecular Design. 2006;20(7-8):427–436. doi: 10.1007/s10822-006-9056-0. [DOI] [PubMed] [Google Scholar]
- 41.Ballesteros JA, Shi L, Javitch JA. Structural mimicry in G protein-coupled receptors: implications of the high-resolution structure of rhodopsin for structure-function analysis of rhodopsin-like receptors. Mol Pharmacol. 2001;60(1):1–19. [PubMed] [Google Scholar]
- 42.Dunfield LG, Burgess AW, Scheraga HA. Energy Parameters in Polypeptides. 8. Empirical Potential Energy Algorithm for the Conformational Analysis of Large Molecules. J Phys Chem. 1978;82:2609–2616. [Google Scholar]
- 43.Nemethy G, Pottle MS, Scheraga HA. Energy Parameters in Polypeptides. 9. Updating of Geometrical Parameters, Nonbonded Interactions, and Hydrogen Bond Interactions for the Naturally Occuring Amino Acids. J Phys Chem. 1983;87:1883–1887. [Google Scholar]
- 44.Nikiforovich GV, Hruby VJ, Prakash O, Gehrig CA. Topographical Requirements for Delta-Selective Opioid Peptides. Biopolymers. 1991;31(8):941–955. doi: 10.1002/bip.360310804. [DOI] [PubMed] [Google Scholar]
- 45.Nikiforovich GV. Computational molecular modeling in peptide design. Int J Peptide Protein Res. 1994;44:513–531. doi: 10.1111/j.1399-3011.1994.tb01140.x. [DOI] [PubMed] [Google Scholar]
- 46.Meiler J, Baker D. ROSETTALIGAND: protein-small molecule docking with full side-chain flexibility. Proteins. 2006;65(3):538–548. doi: 10.1002/prot.21086. [DOI] [PubMed] [Google Scholar]
- 47.Zhu K, Pincus DL, Zhao S, Friesner RA. Long loop prediction using the protein local optimization program. Proteins. 2006;65(2):438–452. doi: 10.1002/prot.21040. [DOI] [PubMed] [Google Scholar]
- 48.Zhang G, Liu S, Zhou Y. Accurate and efficient loop selections by the DFIRE-based all-atom statistical potential. Protein Science. 2004;13:391–399. doi: 10.1110/ps.03411904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Michino M, Abola E, GPCR Dock 2008 participants. Brooks CL, 3rd, Dixon JS, Moult J, Stevens RC. Community-wide blind assessment of methods for GPCR structure modeling and docking. Nature Reviews Drug Discovery. 2009 doi: 10.1038/nrd2877. 10.1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dror RO, Arlow DH, Borhani DW, Jensen MO, Piana S, Shaw DE. Identification of two distinct inactive conformations of the β2-adrenergic receptor reconciles structural and biochemical observations. Proceedings of the National Academy of Sciences of the United States of America. 2009 doi: 10.1073/pnas.0811065106. 10.1073/pnas.0811065106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tastan O, Klein-Seetharaman J, Meirovitch H. The Effect of Loops on the Structural Organization of α-Helical Membrane Proteins. Biophys J. 2009;96:2299–2312. doi: 10.1016/j.bpj.2008.12.3894. [DOI] [PMC free article] [PubMed] [Google Scholar]