Apo and Nickel-bound Forms of the Pyrococcus Horikoshii Species of the Metalloregulatory Protein: NikR Characterized by Molecular Dynamics Simulations

Abstract

NikR is a homotetrameric nickel regulatory protein whose binding to free Ni2+ increases its binding affinity for a gene that codes for a nickel transporter protein. It is comprised of a tetrameric nickel-binding domain, flanked by two dimeric DNA-binding domains. Though x-ray crystallography data for various species (Escherichia coli, Heliobacter pylori, and Pyrococcus horikoshii) of NikR reveal large conformational differences between Nickel-bound, DNA-bound, and unbound forms, transitions between them have never been observed. We have run all-atom molecular dynamics simulations of three forms of the Pyrococcus horikoshii species of NikR including two apo-forms and one nickel-bound form. Though all 552 residues of this species occur naturally, quantum-mechanics-based force-field parameterization was required to accurately represent the four nickel-centers in the nickel-bound form. Global conformational analysis of the three 100-ns-long simulations indicates slow conformational kinetics and independent DNA binding domain motion. Correlation and flexibility analysis revealed regions of high structural and dynamical importance. A striking relationship was observed between regions with high levels of structural importance and regions with known biological importance. Mutation of key regions of P. horikoshii and analogous regions in both E. coli and H. pylori are suggested that might inhibit DNA-binding activity while not affecting nickel-binding.

The understanding of metal ion homeostasis at the molecular-level is critical to our understanding of how toxic metal ions are delivered safely and specifically to the appropriate location within cells.^1–3 There is a significant structural, biochemical and medical literature on the homeostasis of Cu, for example, due to its role in several neurodegenerative disorders (Alzheimer’s and amyotrophic lateral sclerosis (Lou Gehrig’ disease), for example).^{1, 2, 4–8} Despite its inherent toxicity, many microorganisms require cellular nickel as an enzyme co-factor.^{9, 10} Escherichia coli and Heliobacter pylori, for example, utilize nickel for [NiFe]-hydrogenases and urease, which are important for microbial energy metabolism and creation of ammonia as nitrogen source, respectively.^{10, 11} NikR is a DNA-binding metalloregulatory protein that utilizes nickel-responsive allostery to modulate cellular nickel concentrations in various ways.^{3, 12, 13} In E. coli, NikR detects cellular nickel levels and selectively binds and represses the operon which encodes NikABCDE, an ABC-type membrane transporter^{12, 14} effectively reducing nickel import. In H. pylori, NikR, activated by high nickel levels, represses expression of nickel-dependent proteins, such as the HoxN type permease (NixA) which imports nickel, while stimulating activation of other proteins.¹⁵ Hence, NikR senses intracellular levels of Ni and shuts downs the production of the transporter when the level of Ni is appropriate for the cell to function.¹²

Allosteric mechanism

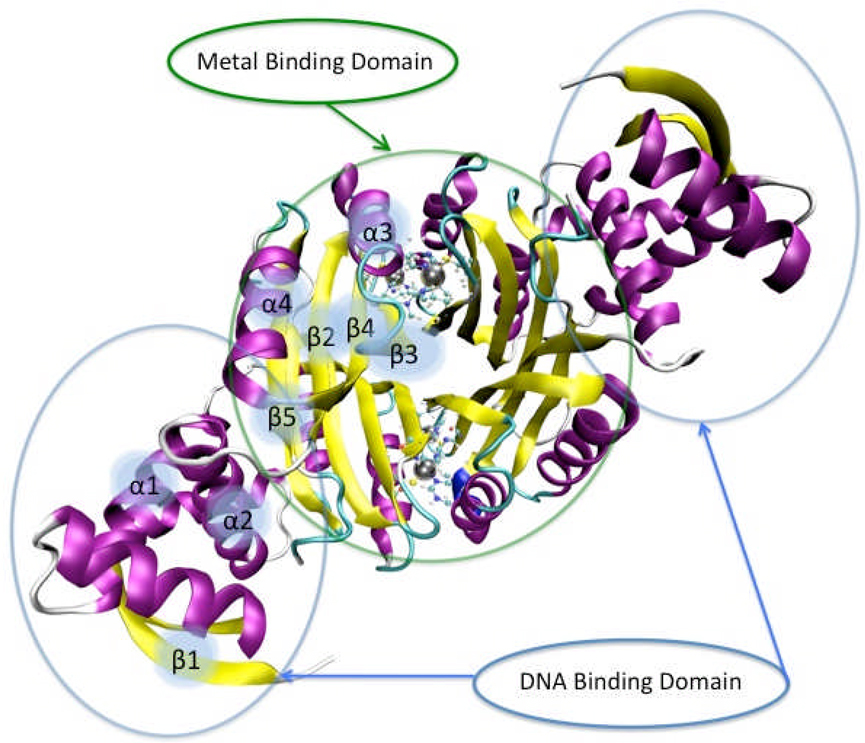
It has been found that NikR’s affinity for DNA is dependent on nickel concentration.^{16, 17} NikR contains both low (30 nM) and high-affinity (20 pM) nickel-binding sites; when the high (low) affinity nickel sites become occupied, DNA affinity increases to nanomolar (picomolar) levels.¹⁷ Carrington et al. found that nickel binds to the high affinity sites in a unique square-planar geometry, but changes to 6-coordinate when bound to DNA.¹⁸ Several species of NikR have been crystallized in various forms by Drennan and co-workers (E. coli NikR – EcNikR)^{19, 20} Terradot and co-workers (H. pylori NikR - HpNikR)²¹ and Chivers and Tahirov (Pyrococcus horikoshii NikR - PhNikR).²² The overall structure consistently shows NikR to have a central tetrameric metal-binding domain (MBD) constructed of a βαββαβ ferredoxin-like fold binding nickel in square-planar geometry flanked by two dimeric ribbon-helix-helix (βαα) DNA binding domains (DBDs) (see Figure 1).

Figure 1.

A rendering of PhNikR. The DNA binding domains (βαα) surround the central metal binding domain (βαββαβ). Metallic spheres represent bound nickels.

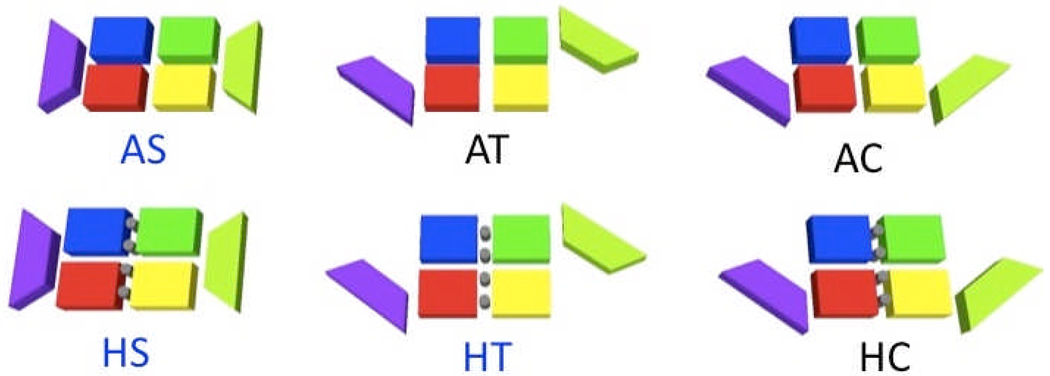
There are, however, some unique characteristics between different species’ crystal structures. The relatively stable MBD of NikR and two rotatable DBDs of NikR can adapt roughly three different main conformations (straight, trans or cis) whose stability seems to be related to both nickel and DNA binding. We will refer to the different forms by the presence of nickel, A (apo) for nickel-free, H (holo) for nickel-bound, and the global conformation, T for trans-like, C for cis-like, and S for straight. Figure 2 shows sketches of various forms of NikR. Schreiter et al. crystallized EcNikR in AS, HS and HC (DNA-bound) forms.^{19, 20, 23} They found that only the nickel-bound forms had a well-ordered α3 helix (a helix containing one of the four nickel-binding residues). This lead to the proposition that the stabilization of the α3 helix assists in DNA binding, a hypothesis supported by comparative metal binding studies.²⁴ Chivers and Tahirov crystallized five forms of P. horikoshii including AS, HS, and three forms of HT: one with the four high affinity nickel-binding sites occupied and PhNikRs unique additional four auxiliary high affinity sites bound, one with all high and low sites bound, and one with all sites bound in the presence of free phosphate ions (to simulate DNA).²² The AS form, similar to EcNikR, was found to have a highly mobile and disordered α3-helix. Interestingly, the form with phosphate ions is oriented in a trans-form that should not fit into the corresponding DNA operon assuming that the DNA binding is similar to that of EcNikR which binds in a cis-form. As Chivers and Tahirov noted, this form can be converted into a cis-form if one half (any two chains that share a DBD) is rotated by 180 degrees about the center axis (turning it from a trans to a cis).²² The crystal forms found by Dian et al. of HpNikR were the most unique set of the three species crystallized.²¹ They found a unique AT structure, which roughly resembles the HT form of PhNikR but lacks dimeric symmetry. Also, HpNikR was never found with all four high-affinity nickel-binding sites occupied, but rather with a single high-affinity nickel site bound per dimer, an intermediate site, or an external site. It is possible that this peculiarity could have been caused by the low pH conditions of the crystallization,²¹ as noted by Zambelli et al.²⁵

Figure 2.

Sketch of various possible forms of NikR. Rectangles represent metal binding domains (each color represents a different chain, purple and lime represent intertwined chains). Trapezoids represent the DNA binding domains (each has contributions from two chains). Grey circles represent primary nickel binding sites. Only the three with names written in blue were found experimentally in the absence of DNA. In the cis form, NikRs DBDs snugly fit into the major groove of DNA.

These various permutations of conformations and nickel and DNA bound states both provide insight and raise questions about NikR’s allosteric mechanism. What role does nickel binding have in the structural preference of NikR? Does nickel-binding preferentially stabilize one conformation over another otherwise in preexisting equilibrium?²⁶ What residues are important in promoting these conformational changes?

To elucidate the role of nickel binding on conformational states and dynamics of NikR we simulated various forms using all-atom molecular dynamics (MD) simulations. MD simulations of biological molecules have often been utilized to elucidate biological mechanisms.²⁷ Few computational studies of any species of NikR have been reported. Cui and Merz utilized a course-grained Gaussian-network-model to find natural global fluctuations in PhNikR.²⁸ They found that natural fluctuations lead to transitions between the major conformational states found in NikR crystal structures (between straight, trans, and cis). This coarse-grained study supports the pre-existing equilibrium hypothesis – that all the available conformational states are available to each bound state.²⁶ Bradley et al. utilized²⁹ an 80 ns all-atom explicit solvent simulation of EcNikR starting from the AT state (PDB code 1Q5V). In that work, a potential interaction network between the metal-binding and DNA binding residues was highlighted using a novel correlation-matrix-based residue clustering technique.²⁹ However, the metal binding states we not examined. During the preparation of this manuscript, a computational study by Phillips et al. was published regarding NikR metal binding specificity based on free energy simulations.³⁰ This study utilized relatively stable, DNA-bound states of EcNikR for Poisson-Boltzmann Thermodynamic Integration calculation of free energy differences between different bound ions.

Herein, we examine the dynamics of three 100 ns simulations beginning from three forms of PhNikR in solution. The Ph species was chosen because the crystal structures available had the least amount of missing atoms. We chose the AS, HT (with only four nickels bound) and AT forms (PDB codes: 2BJ3, 2BJ7 (with 4 primary nickel ions), 2BJ7 (without nickel ions)). Our goal is to highlight the features of the dynamics of each form to compare and contrast any apparent differences between them. The analyses reported herein include: RMSD analysis to look at conformational changes of various regions of interest, center-of-mass angular analysis to measure global conformational change, correlation analysis to examine inter-residue communication, and flexibility analysis to identify residues necessary for hinge-motion.

Materials and Methods

Simulation details

We chose to simulate three forms of PhNikR²²: the apo-straight form, taken from PDB ID 2BJ3 (PhNikR-AS), the holo-trans form with only four nickels simulated, taken from PDB ID 2BJ7 (PhNikR-HT), and an apo-trans from where all nickels were stripped from the original pdb structure 2BJ7 (PhNikR-AT). An implicit generalized Born solvation model (GB(OBC))³¹ was chosen to reduce the system size as well as the solvent viscosity to allow for faster kinetics.³² Recently, Hornak et al. successfully utilized implicit solvation to witness flap-motion in a simulation of HIV-1 protease.^33,34 In our simulations, each form was taken from the appropriate PDB structure with missing residues built by the TLEAP program, which is part of the AMBER suite.³⁵ The PhNikR-HT form required additional modeling in order to properly represent the nickel centers (see the “Force Field Parameters” section). The proteins were simulated in AMBER using the ff99SB parameter set.³⁶ Hydrogen vibrations were restrained using the SHAKE algorithm allowing a 2 fs timestep. Each form was minimized in AMBER10 using the SANDER module, then relaxed at 100K for 10 ps. The production runs were 100 ns long at 300K for each form using the PMEMD module. Temperature was regulated by utilization of Langevin dynamics using a 1.0 ps⁻¹ solvent coupling constant. Successive restart runs utilized different pseudorandom seeds as recommended by Sindhikara et al.³⁷ Analysis of the trajectories was performed using the PTRAJ module.

Force field parameters

All 138×4 of the amino acid residues in Ph apo-NikR occur naturally and thus force field parameters are available in various parameter sets (ff99SB in our case³⁶). For the apo forms, all histidine protonation states were chosen to agree with the most likely protonation state at the experimental pH of 7.5 and are thus delta-protonated. Since in the apo form no histidines are hydrogen bound any other residues, the difference between the delta and epsilon (the second most likely state) protonation will have a limited impact, if at all, to global dynamics.

For the nickel-bound form, there are several approaches to metal modeling that we could have chosen. These approaches can roughly be classified into three categories: quantum mechanical, non-bonded, and bonded. Quantum mechanical treatment or a mixed QM/MM treatment of metals has the most potential for accuracy, but its huge computational cost deters usage for large systems. A non-bonded approach would treat the nickel as a free ion whose interaction with the protein is strictly through van der Waals and Coulomb forces. This is the approach Phillips et al. in their metal preference study.³⁰ This approach is delicate to parameterize, does not enforce a particular geometry, and may ignore any covalent bond characteristics.^38–42 Finally, a bonded approach utilizes all terms in the typical all-atom force field to treat the metal ion. Parameterization of this approach can be done by combination of experimental and quantum mechanical methods. This method is the most restrictive geometrically, but is useful when modeling stable metal sites. We chose the bonded approach since NikR is too large to treat quantum mechanically, and we know precisely what the Ni coordination state is in NikR.

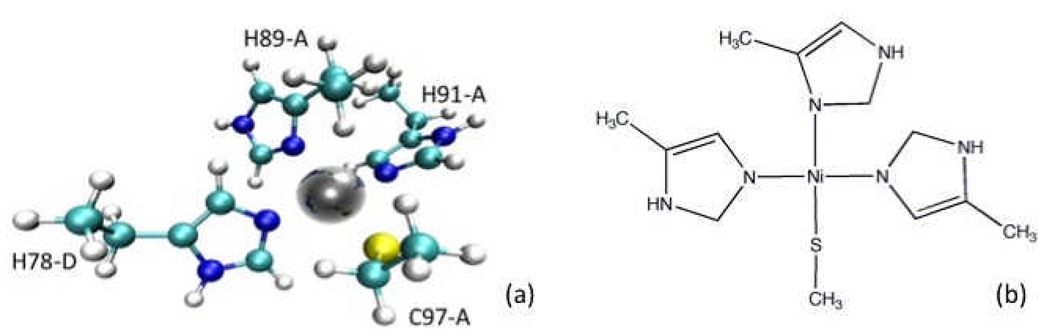
New force field parameters were created and used for both the bound nickel ions, and the ligating residues. The MTK++ package was used to expedite the force field parameterization process.⁴³ First, a single copy of one of the nickels plus the four ligating sidechains were isolated from the holo structure (pdb code: 2BJ7) then capped with CH3 groups (in the position of the original ). Figures 3a and b show representations of this “small” metal-cluster model.

Figure 3.

Representations of the “small” metal cluster. Atoms included in this model were used to obtain force constants via DFT calculations. a) A ball-and-stick representation. Labels indicate residue identity and chain ID b) A 2D representation.

The histidine protonation states were taken from experiment: H91-A and H78-D are epsilon-protonated, and H89-A is delta-protonated with the remaining sites occupied by the Nickel ion. The resultant cluster was then minimized using the TPSSTPSS/TZVP level of DFT theory with Gaussian 03.⁴⁴ This method and basis has been shown to model nickel compounds well.⁴⁵ The minimization did not alter the square-planar geometry (though use of smaller basis sets did, data not shown). Following the minimization, force constant calculations were performed using the same methods.

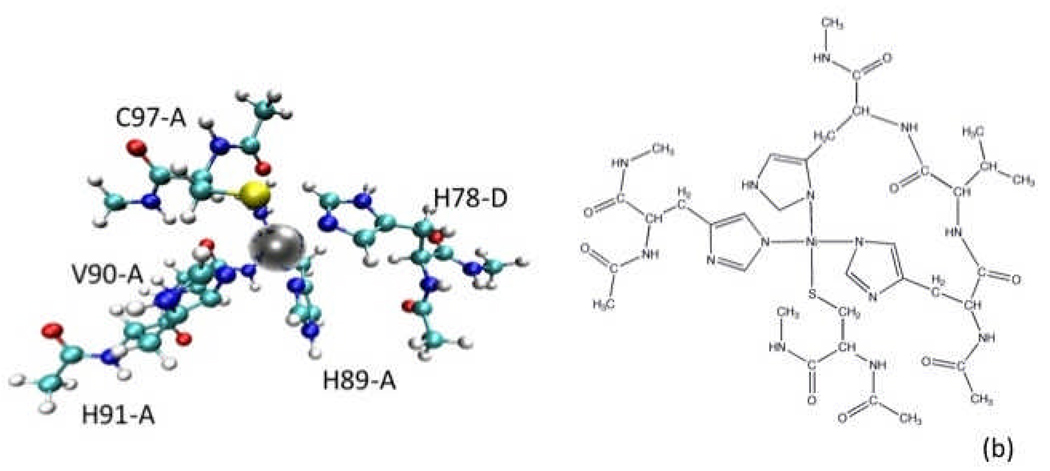
To obtain the partial charges on all the atoms, a larger cluster was selected from the pdb file, this time including backbone atoms, but capped with Acetyl and N-Methyl groups in appropriate positions. Figures 4a and b show representations of this “large” cluster.

Figure 4.

Representations of the “large” metal cluster. Atoms included in this model were used to obtain partial atomic charges via DFT. a) A ball-and-stick representation. b) A 2D representation.

Charges were obtained using the RESP algorithm^46–53 on this model cluster. van der Waals parameters were not adjusted for the ligating residues. For the Nickel, thermodynamic-integration simulations were performed for Ni2+ + 2Cl- + nH2O → nH2O for various ε and r values for nickel. The combination of r and ε that most closely resulted in the experimental free energy of hydration was used for nickel.⁵⁴ The new set of parameters for the nickel ions and ligating residues were then mapped to the four primary nickel-binding sites in the holo form of NikR. The ff99SB parameter set³⁶ was used for all other residues. Note that although no restraints were used to maintain the planarity of the nickel center the planarity was maintained throughout the course of the simulations described below (data not shown).

Table 1 shows the partial charges of the nickel center along with those of the nickel-bound atoms. For the nickel ion, we used a van der Waals radius of 1.10Å and a well-depth of 0.013 kcal/mol in all instances. All additional parameters are available in the supporting information.

Table 1.

Classification of structure based on angles between centers of mass of different domains.

	Angle(DBDAB,MBDAB,MBDCD)	Angle(MBDAB,MBDCD,DBDCD)	Dihedral(DBDAB,MBDAB,MBDCD,DBDCD)
Straight	≈180°	≈180°	any
Cis	<180°, > 90°	<180°, > 90°	≈0°
Trans	<180°, > 90°	<180°, > 90°	≈180°

Results and Discussion

Simulation stability

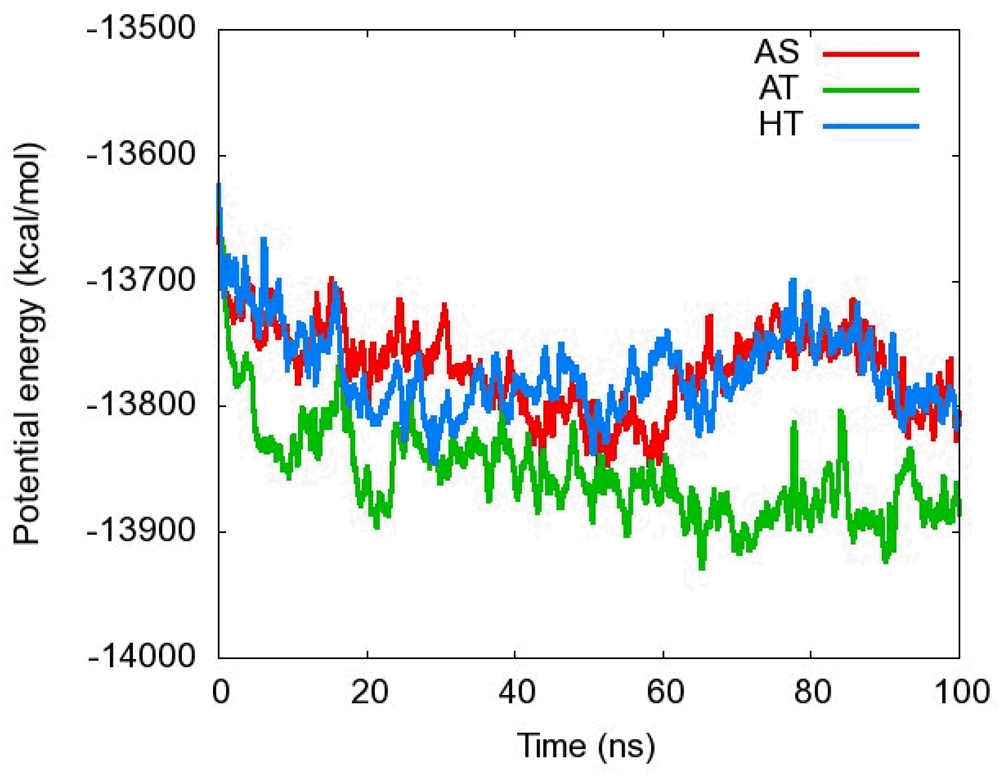
To evaluate the energetic relaxation of the simulations, the potential energy of each system was examined. Figure 5 shows a block-averaged time-series of the potential energy. AS refers to the straight nickel-free structure (pdb ID 2BJ3), AT the trans nickel-free structure (pdb ID 2BJ7), and HT is the nickel-bound trans structure (pdb ID 2BJ7).

Figure 5.

Averaged potential energy time series for three simulations of NikR. The smoothing window size is 50 ps.

The potential energy for all simulations had standard deviations below 80 kcal/mol for the last 90% of the simulation. This is consistent with the fluctuation in the simulation by Bradley et al.²⁹ whose potential energy fluctuated by about 200 kcal/mol. It should be noted, however, that these systems potential landscapes are quite different considering the different solvent representations. The potential energy drops off slightly for the first 10 ns. After that, all three simulations fluctuate about each of their respective averages. Thus for the final 90 ns, each simulation is likely in thermal equilibrium.

Global conformational dynamics

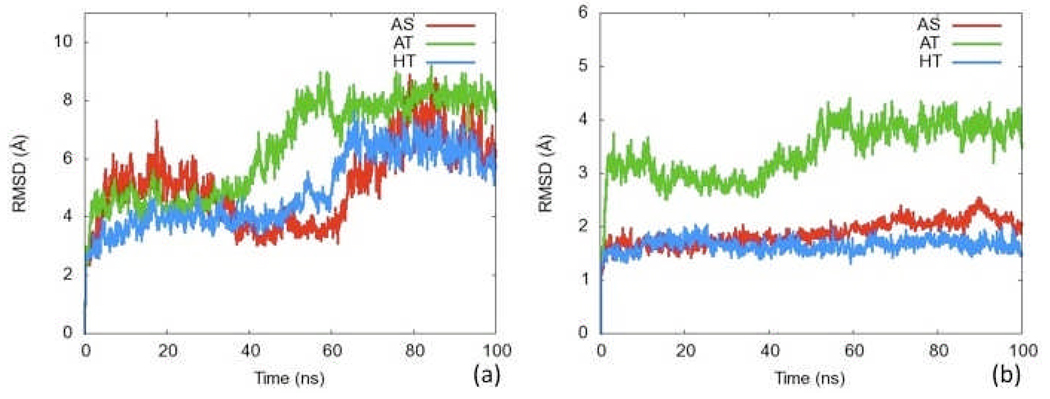
Observing the global RMSD vs. time can give a first glimpse as to whether major conformational changes occurred during the simulation. A relatively static RMSD compared to the initial structure suggests a stable conformation while a dynamic RMSD suggests significant motion (thought it gives little insight to the specifics of that motion). Figures 6a–b show the RMSD of Cα atoms for key subsets of the NikR structure. Figure 6a shows the Cα RMSD against the initial structure versus time for all three simulations (AS, AT, and HT). All three simulations deviate more than 2Å within the first nanosecond. Though none of the simulations are stable over the entire 100 ns of simulation, they each maintain a steady RMSD between transitions. Both of the simulations whose initial structures came from forms found via crystallography (AS and HT) maintain states for nearly 60 ns. The AT simulation only stays steady for ~40 ns and experiences the highest RMSD change. The magnitude of fluctuations is similar to that of the 80 ns explicit solvent E. Coli simulation of Bradley et al.²⁹ whose backbone RMSD, after relaxation, fluctuated between 2.5 and 5Å. The greater fluctuation observed in the simulations herein is likely due to the lack of explicit solvent molecules in the GB simulation. This inhomogeneous behavior suggests that none of the three systems have attained conformational equilibrium within the limit of the 100 ns timescale used in our simulations. Thus, we conclude that our analyses of the resultant trajectories only provide qualitative insights into these fascinating systems.

Figure 6.

RMSD plots for Cα atoms of selected regions of NikR. a) Cα RMSD for entire protein in the AS, AT and HS simulations b) Cα RMSD for the metal binding domain for all three simulations.

The x-ray structures available for NikR suggest that the central MBD and two flanking DBDs may act similarly to rigid bodies. If each of these domains were rigid, the Cα RMSD would be relatively low and stable throughout the simulation. Figure 4b shows the Cα RMSD against the first frame for only the MBD of the protein (Residues 57 to 131 of each chain). Both the AS and HT simulations jump initially and stay in a steady state between 1.5 and 2Å from the initial structure. Thus, for these two forms, the central MBD is relatively rigid throughout the simulation. For the AS and HT forms, the large conformational change around 60 ns indicated by the full protein RMSD in Figure 6a must not be directly due to changes within the MBD. The AT simulation jumps initially to 3Å then rises to 4Å between the 40th and 60th ns. This larger jump may be due to the instability of the initial nickel-free AT structure and may be the source of the global conformational change indicated in Figure 6a. Since the MBD is relatively stable for both the AS and HT simulations, the conformational changes must come from the DBD motion. RMSD plots for DBDs can be found in the SI.

To observe the rigid body motion of the DBDs relative to the MBD, motion was observed in the context of the transition between the straight, trans, and cis forms referred to in Figure 2. Consider the centers of mass (COMs) of the four major domains: DBD from chains A and B (DBDAB), MBD from AB (MBDAB), MBD from CD (MBDCD), and DBD from CD (DBDCD). We can classify the shape of the protein based on these four points as in Table 2.

Table 2.

Partial charges for the nickel center along with each ligating atom. Partial charges for each atom in the ligating residues are provided in the supporting information.

Ni2+	Cys 97 S	H89 NE (HID)	H91 ND (HIE)	H78D NE (HID)
0.66275	−0.52432	−0.66101	0.00690	−0.16857

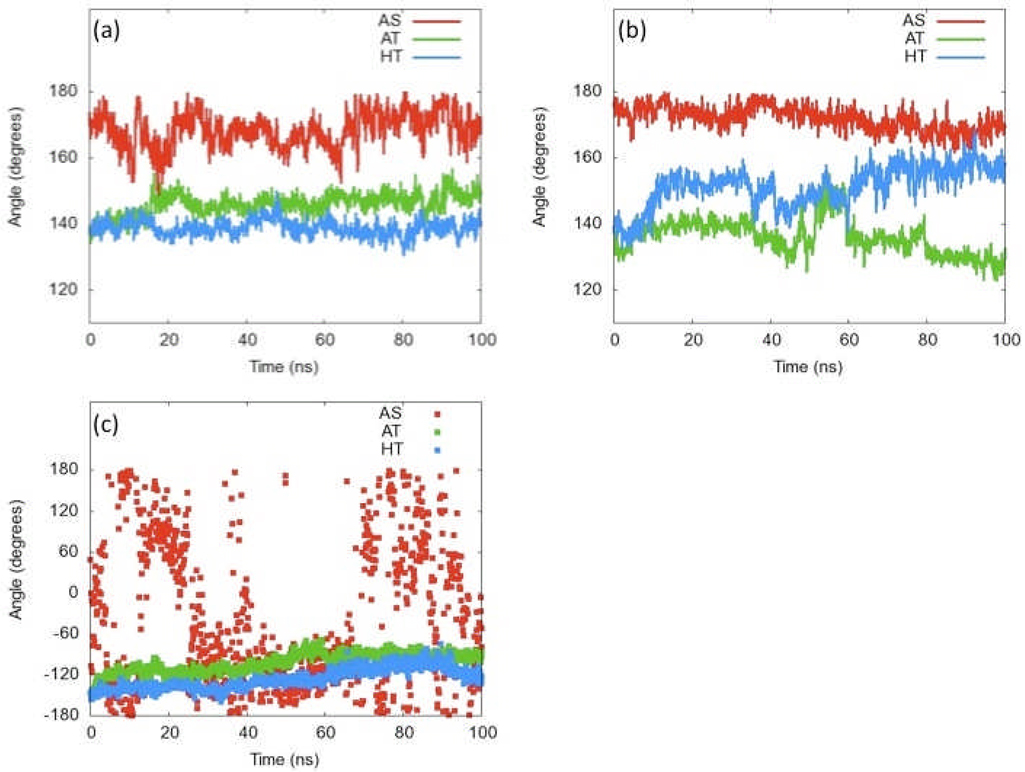
Figures 7a and b show the angles between both (DBDAB, MBDAB, and MBDCD) and (MBDAB, MBDCD, and DBDCD) for all three forms. The AS form, clearly maintains angles near 180 degrees, indicating that the COMs of the four domains are roughly linear. Conversely, the AT and HT forms maintain an angle of 150 degrees or less -- indicating a bend in the structure. While fluctuations do exist, no major conformational changes are evident from this analysis other than the HT CD DBD, which drifts near 160 degrees. This could indicate that this DBD is “straightening out”. Interestingly, the flapping motion seems to be independent, suggesting that the global conformational rearrangement may act in a step-wise fashion, rather than in concert.

Figure 7.

Angles between centers of mass of adjacent domains vs time. a) Angle made by DBDAB, MBDAB, and MBDCD. b) Angle made by MBDAB, MBDCD, and DBDCD. c) Dihedral angle between DBDAB, MBDAB, MBDCD, and DBDCD.

Figure 7c shows the dihedral angle between these four points for each simulation. Unsurprisingly, the AS domain-COM dihedral angle fluctuates wildly across all angles since it is nearly linear and thus small motions can cause large angular changes. Conversely, the AT and HT, both starting at less than − 150 degrees, slowly drift up throughout the simulation. This could be simply relaxation, or more significantly, a slow conformational change to the cis form.

These Cα RMSD and domain COM angular analyses indicate significant conformational motion, but no complete transitions between the major states observed in the crystallographic experiments. However, the CD DBD of the HT simulation begins to straighten out within the timescale of the simulation. This motion suggests that conformational transitions may be observable within an order of magnitude longer simulation (~1 µs).

Features of key structural segments

Though the relative motion of the large domains reflects global conformational changes, the behavior of the segments that comprise and connect these regions can reflect the communication between them. We identified structural segments with key functionalities by analyzing both residue-level distance correlation and flexibility.

(A) Residue Correlation

To elucidate inter-residue dynamical relationships, distance correlation analysis was performed on all Cα atoms for each simulation with the PTRAJ module from AMBER10 (see Equation 1)

$$C(i,j)=\frac{\langle \mathrm{\Delta }{x}_i(t_k)\cdot \mathrm{\Delta }{x}_i(t_k)\rangle }{{\langle \mathrm{\Delta }{x}_i{(t_k)}^2\rangle }^{1/2}{\langle \mathrm{\Delta }{x}_j{(t_k)}^2\rangle }^{1/2}}$$ (1)

The correlation matrices for each simulation (found in SM) contain much information but are difficult to parse visually. Bradley et al. reported visually similar correlation plots for their EcNikR simulation. In order to quantify the relevance of specific residues, we summed the absolute value of the correlation matrix along either a row or column for each residue summed over the four chains as in Equation 2

$${\mathit{\text{cREL}}}_i={\displaystyle \sum _{\mathit{\text{chains}}}{\displaystyle \sum _{j=1}^M\left|c_{i,j}\right|}}$$ (2)

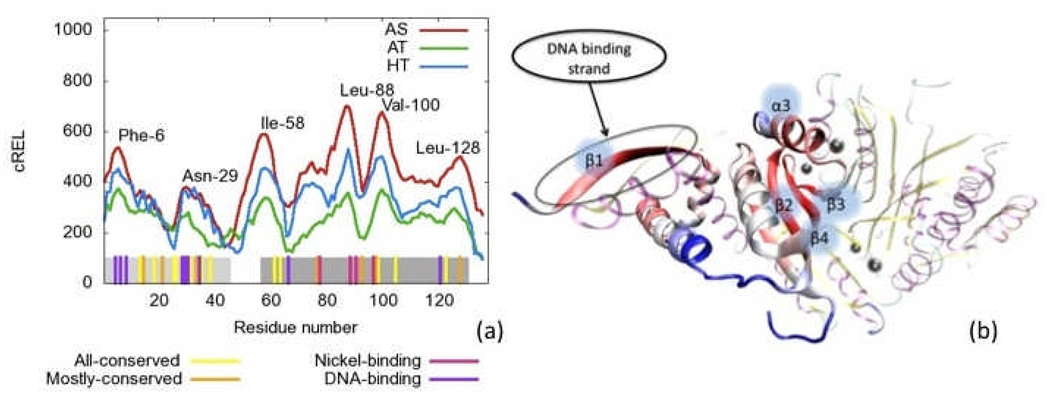
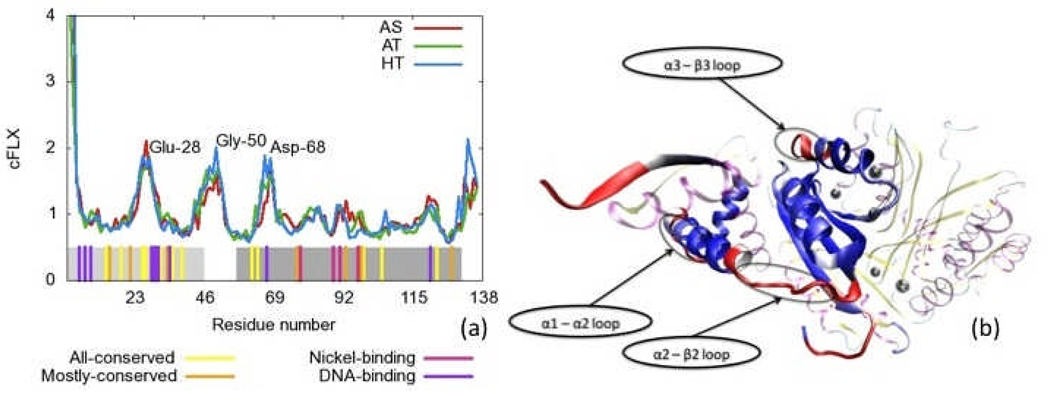
Here M is the number of residues per chain. Figure 8a shows this correlation relevance summed over chains (cREL). The colored area just above the x-axis indicates biological information including binding residues and highly conserved residues across 12 selected species of NikR.^55–65 We chose to use the same 12 species examined in the original PhNikR crystal structure paper by Chivers et al.²² The DNA binding residues include those involved in nonspecific contacts. The graphs suggest that each form exhibits similar behavior, residue-to-residue, and that the residues of AS and HT forms are much more coupled. Interestingly, for most of the DBD (approximately first 38 residues) for these two forms, the chain-independent correlation relevance values are nearly identical. In the MBD, the AS is more correlated than the HT form (and even more so than the AT). Additionally, the graph suggests that residues with known biological function tend to have higher correlation relevance with the exception of Gly-67, which may require more flexibility.

Figure 8.

Correlation relevance summed over chains (cREL) for all three simulations. a) cREL vs residue number. Residue identities are labeled at peak values. Bottom bars indicate residues with high conservation across species, or with either nickel or DNA binding function as labeled. Light and dark grey regions represent the DBD and MBD respectively. b) Correlation relevance summed over chains (cREL) for the HT simulation applied to a color scheme (red is the highest, blue is the lowest) on a single chain the initial structure of the HT form of NikR. The rest of the protein is present but deemphasized and uses the same color scheme as Figure 1. The figure suggests strong influence on the rest of the protein by the secondary structure segments involved in both DNA and nickel binding.

Figure 8b shows the values cREL of the HT simulation (though all simulations are qualitatively similar in this respect) applied to a color scheme (red is the highest, blue is the lowest). Remarkably, both the segments of secondary structure involved in nickel-binding (α3 and β3) and those involved in DNA-binding (β1) have the highest value of cREL. This suggests that these regions are the most important structural regions since they coordinate motion the strongest with other residues. Mutation of the residues that would disrupt the structural stability of these segments would likely inhibit DNA-binding. Previously performed mutation studies of some of the residues for various species in these segments have already shown the importance of these segments in DNA and nickel-binding.^{13, 18, 21} However, the DNA binding characteristics of each species is unique; thus, mutation studies should be performed on different but analogous residues. Additional correlation analysis can be found in the SM. We note that Bradley et al. utilized a different correlation-based measure to determine interaction groups rather than individual residue relevance as shown here.²⁹

(B) Residue Flexibility

Flexibility can be a necessary attribute in key regions of a protein to allow it to not only fold but also undergo functional conformational changes. For example, flexibility in hinge regions is advantageous.^66–68 To identify regions of high flexibility in NikR, each residue was characterized by the standard deviation of the distance between the Cα atoms of its nearest neighbors summed over chains (see Equation 3)

$${\mathit{\text{cFLX}}}_i={\displaystyle \sum _{\mathit{\text{chains}}}}\sigma (|{\stackrel{╵}{x}}_{i-1}-{\stackrel{╵}{x}}_{i+1}|)$$ (3)

Here x̍_i represents the position of the Cα atom of the i^th residue. Figure 9a shows cFLX for each simulation. The flexibility seems to be almost identical for all three simulations suggesting the form has little effect on the residue-level motion. High flexibility is seen at the two termini as well as in three regions centered on Glu-28, Gly-50, and Asp-68 as labeled. It is unsurprising that the correlation relevance, cREL, and flexibility, cFLX, do not correlate with each other. cREL corresponds more to structural stability while cFLX corresponds to instability. We note that there is no correlation between the X-ray B-factor and this measure of flexibility (data not shown). This loop flexibility may play a key role in allowing the allosteric conformational change required for NikR’s function. A mutation to a residue within a region of high flexibility to increase stability should decrease the biological function.

Figure 9.

Residue flexibility, cFLX, for all three simulations. a) cFLX vs. residue number. Residue identities are labeled at peak values. Bottom bars indicate residues with high conservation across species, or with either nickel or DNA binding function as labeled. Light and dark grey regions represent the DBD and MBD respectively. b) Flexibility summed over chains (cFLX) for the HT simulation applied to a color scheme (red is the highest, blue is the lowest) on a single chain the initial structure of the HT form of NikR. The rest of the protein is present but deemphasized and uses the same color scheme as Figure 1. Highly flexible regions may be key for functional conformational changes.

Figure 9b shows the values cFLX of the HT simulation in the same manner as in 8b applied to a color scheme (red is the highest, blue is the lowest). The figure shows that the highest flexibility regions are in only a few of the loop regions, particularly the α1-α2, α2-β2, and α3-β3 loops (these correspond to the three peaks in Figure 9a. The analogous flexible loops for E. coli are Gly-24 to Asn-27, Gln-47 to Gln-51 and Glu-70 to Asp-73, and for H. pylori are Gly-33 to Ser-36, Glu-56 to Asn-60, and His-72 to Glu-85. While all three of these loop regions may have a distinct biological function, the α2-β2 loop is the most interesting in the context of the global conformational changes NikR undergoes since it lies at the interface between the DBD and MBD regions. The hinge-motion of this loop is key for the switching between the cis, trans, and straight conformations. Interestingly, the sequence conservation in this region is low.^55–65 This may indicate that these residues are necessary in DNA-binding specificity.

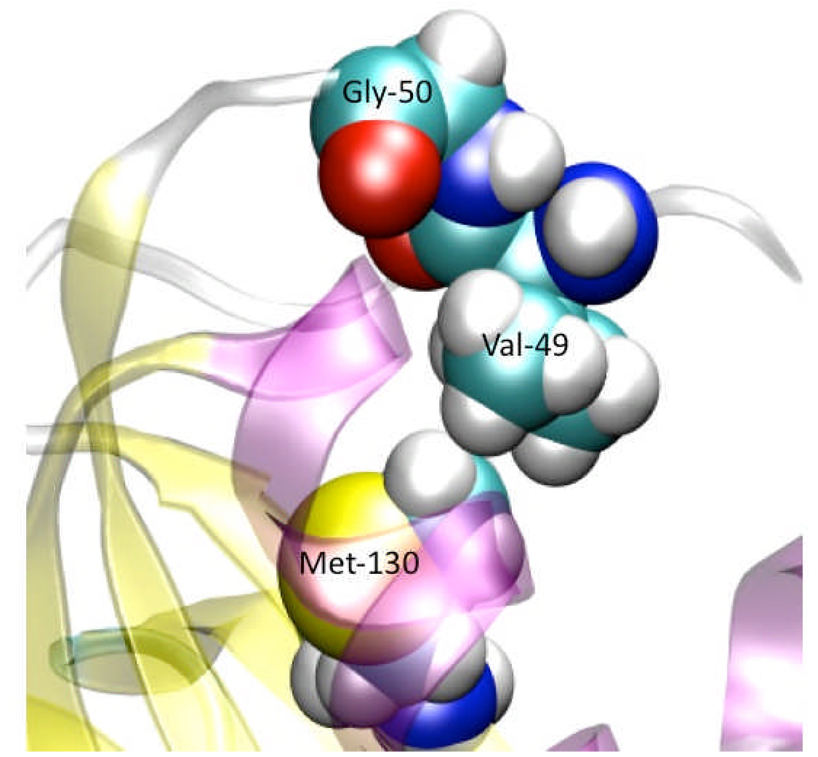
Since the α2-β2 loop is a hinge that allows the global conformational change required for NikR to bind to DNA (converting to the cis-form), and in the wild type it is highly flexible, mutations to this region that restrict motion should inhibit DNA binding activity. Two key features of this loop are highlighted in Figure 10. The first is the Gly-50 residue that most known species of NikR contain (it is absent in the α2-β2 loop of H. pylori).^55–65 The mutation of this glycine to a conformationally less flexible residue such as a proline might reduce NikRs ability to change conformation to accommodate DNA binding. Secondly, there is a hydrophobic interaction between Val-49 in the α2-β2 loop and Met-1 in the β5 strand. The reduction of the length of either of these sidechains could reduce the flexibility as well. For example, mutation of the Met-1 to a Val or Val-49 to Ala would keep the hydrophobic interaction but would tie-down the loop to restrict motion. Similar mutations on other species of NikR would likely produce the same effect. For example, in HpNikR, this interaction is coulombic rather than hydrophobic (Lys-31 with Glu-56) as the crystal structure (PDBID: 2CA9) suggests. For E. coli, the interactions is not obvious from the crystal structure (PDBID: 2HZA), however, the study by Bradley et al. did indeed recognize a non-covalent interaction in this general region (in that a unified cluster was recognized containing both sides of this region).

Figure 10.

Close-up of α2-β2 loop. Key residues are represented by VDW volume spheres and labeled appropriately. Gly-50 provides flexibility. Shortening the sidechains while keeping the hydrophobic interaction can reduce the Cα-Cα distance between residues 49 and 130.

Conclusions

NikR regulates cellular nickel concentration by responding to high nickel concentrations by suppressing nickel transport protein expression. Experimental data gives clues to its mechanism but without conclusive detail. We have performed three simulations to help elucidate the dynamics of NikR. The modeling of this system required special parameterization to accurately represent the nickel and its ligating residues. Our analyses of these simulations provide additional insight into the dynamical preference that different initial conformations and nickel-binding states have on the protein. While not observing global conformational changes on the computational time-scale available, several distinct features of NikR were observed. The flanking DBDs move independently of each other. Analysis of biologically relevant residues tend to influence motion across domains much more strongly than others residues.

The secondary structure segments directly pertaining to binding of either DNA or nickel were found to be structurally important by correlation analysis even in the absence of both of these ligands. Additionally, key flexible regions were highlighted especially the α2-β2 loop whose hinge-like motion allows functional global conformational change. Regions with either high correlation relevance or flexibility seem to be correlated with biologically important regions. We suggested some specific mutations to these residues for the P. horikoshii species and also identified analogous regions in E. coli and H. pylori species of NikR that we expect to have similar character.

With current computational capacity, simulating a global conformational change in a system like NikR is a significant challenge. Beyond brute force simulations, it is possible that advanced sampling algorithms could be applied to not only establish a meaningful reaction coordinate between NikR states, but also to calculate the free-energy change between states.