Proposed mechanism for stability of proteins to evolutionary mutations

Abstract

It is shown that the sequence-ordering tendencies induced by design into different fast-folding, thermally stable native structures interfere. This interference results in a type of quasiorthogonality between optimal native structures, which divides sequence space into fast-folding, thermally stable families surrounded by slow-folding, low stability shells. A concrete example of this effect is provided by using a simple α carbon type model in which a complete correspondence is established between sequence and structure. It is speculated that gaps can occur in the space of protein-like sequences separating the sequence families and resulting in a mechanism for stability and diversity of protein sequence information.

According to energy landscape principles (1–11), proteins are distinguished from nonfolding amino acid sequences by having a rugged but funnel-like configurational energy landscape. In the simplest possible picture, this landscape is locally rugged with barriers among many local minima, whereas globally the landscape has an overall energy gradient that guides the chain toward its native configuration. When this gradient is dominant, the landscape is a deep funnel that allows the protein to fold on physiological timescales.

To design sequences with funnel-like landscapes focused on a particular target structure, it is therefore necessary to stabilize the target energetically against the ensemble of misfolded configurations (12–20). However, when a sequence has been designed into a predetermined structure, there is no guarantee that by slightly altering this structure and redesigning the sequence, one may arrive at a new sequence with better properties. Thus, to obtain the most optimal sequence–structure combinations, it is necessary to anneal sequence and structure together (17–21). This results in sequence–structure combinations that could be called the modes of design for a polymer with the 20 letter amino acid code, and ideally, proteins correspond to such combinations.

To be more precise, a mode of design corresponds to a compact native structure for which, once a sequence has been optimally designed into it, one cannot obtain a less frustrated sequence by changing a small part of the structure and redesigning the sequence. Thus, when a mutation is applied to a minimally frustrated sequence, it always increases frustration, although in most cases it does not substantially change the folded structure. This results in a picture of sequence space as being populated by families, each folding to a particular coarse grained structure and each surrounded by a shell of increasingly frustrated sequences.

One of the goals of this paper is to explain how this situation occurs. We show that to achieve minimal frustration, the modes are driven apart, or “orthogonalized,” very much like the orthogonalization of memories in a neural network (22–24). Specifically, because the fastest-folding, most stable sequences are those that minimize the energy of one highly connected compact structure against all the others, the energy of a minimally frustrated sequence placed into the folded structure of the wrong sequence family will have one of the worst possible energies. Hence, the sequences and structures of the minimally frustrated modes tend to be mutually dissimilar.

We demonstrate the emergence of this orthogonality property in a simple α carbon-type model of proteins (20) (Fig. 1), in which we have previously established a complete correspondence between sequence and structure (Fig. 2) and have determined both the folding times and folding temperatures of the sequences. The model is quite convenient to illustrate how structure information is stored in proteins, and the simple hydropathic interaction rule (26–29) is already sufficient to produce two minimally frustrated sequence families.

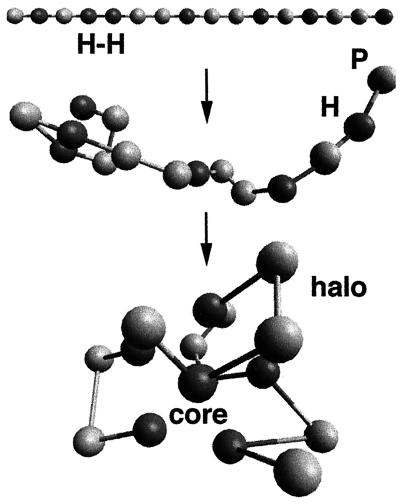
Figure 1.

Illustration of the folding process for a sequence of hydrophobic (H) and polar (P) beads that has one nearest neighbor H—H chain bond (Top) out of a possible six. All sequences in this model contain seven H (dark beads) and nine P (light beads) “residues.” Nearest neighbor residues along the chain are connected by freely jointed string bonds of finite minimum and maximum extension (i.e., a square well potential). Cross chain contacts between pairs of H residues are strongly attractive unless the residues are nearest neighbors in sequence. All other (non-nearest neighbor) pairs of residues interact as hard beads, and all nearest neighbors in sequence interact according to the string potential. The sequences fold into structures with an ordered hydrophobic core surrounded by a liquid-like halo of P residues.

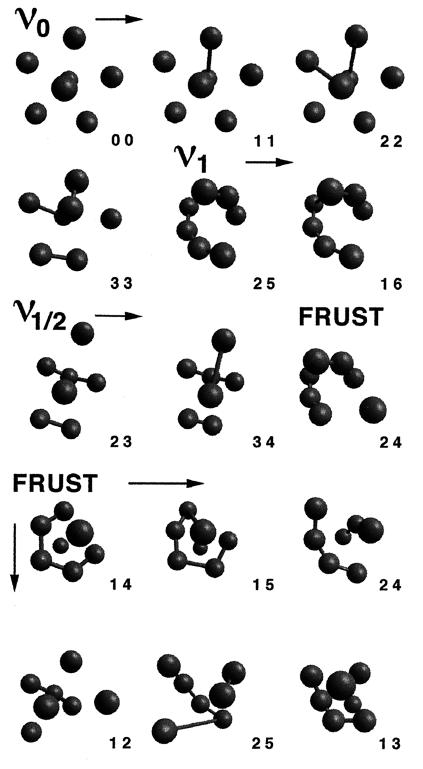
Figure 2.

The 15 ground-state core structures that emerge from all of the 11,440 HP sequences of the type described in Fig. 1. Only H residues and H—H string bonds are shown. The pair of numbers at the lower right of each structure are (respectively) the number of sequential H-segments and the number of H—H string bonds contained in the sequence folding to the structure. The symmetry of the core is abbreviated by the terms ν₀ ν₁, ν_1/2, and FRUST (i.e., frustrated). The ground-state core geometry of any sequence is uniquely determined by set of internally clamped sequential H-segments along its length (e.g., the geometry ν₀ 3 3 corresponds to all permutations of the four fragments (H—H … H—H … H—H … H). The number of sequences folding to a particular geometry is given by the total number of permutations, which do not break, create, or extend the length of the sequential H-segments.

We parameterize the level of fast folding and stability of a sequence by the degree of frustration minimization (6, 7, 31) as measured by the ratio of folding to glass temperatures (6–8)

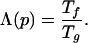1

The negative of this parameter, −Λ(p), can be used to define a landscape in sequence space, and we show that this landscape has pronounced valleys or frustration minima, each containing a family of sequences and each family folding to a different coarse grained compact structure. Once again, these are structures for which, once a sequence has been optimally designed into them, one cannot obtain a less frustrated sequence by altering a small part of the structure and redesigning the sequence. Each optimal target structure is associated with a famility of sequences that fold to it, and each family is characterized by a different tendency for ordering the residues. Because the optimal structures are substantially different, the ordering tendencies of different families must oppose, or contrast each other in the way that residues are patterned within a sequence. This results in a matrix of similarity parameters x^μν(p), which defines the degree of sequence ordering toward one minimally frustrated sequence class (μ) and against another (ν). Large values of x^μν(p) are associated with class μ, and large values of x^νμ(p) are correspond to occupying class ν. For intermediate values of this parameter, cancellation occurs between the ordering tendencies μ and ν, in the sense that the sequences corresponding to such regions of sequence space are highly frustrated. This produces a frustration barrier, e.g., a region of frustrated sequences between each pair of minimally frustrated families. Any stepwise mutational path between one minimally frustrated sequence family and another (32) must then visit a region of slow or nonfolding sequences. This property will be clearly demonstrated for the example presented in this paper.

In the case of real proteins, the sequences in these high frustration regions are much less likely to meet physiological requirements on foldability (of course, real physiological requirements can be much more extensive than this; refs. 32–34). If the sequences in these regions do not meet the physiological criteria, then they cannot participate in biochemical processes, which means that they will be physiologically excluded. If the requirement is sufficient, the region between two families will be completely excluded, which cuts sequence space into separate fast-folding, stable parts. This provides a mechanism for partitioning protein sequence information into evolutionarily stable (31, 33), biochemically useful (foldable) subsets.

Stability to Mutations.

Implicit in the concept of sequence design is the idea that proteins must exceed a certain level of fast folding and stability to function in biochemical processes. The frustration function Λ(p) (which measures this ability) separates sequences, independent of length, into two distinct regimes (6–8). In the frustrated regime, Λ̃ < 1, the energy gap ΔE between native and non-native (misfolded) configurations cannot be distinguished from the characteristic energy barriers δE between misfolded structures (5). This means that below the collapse (coil-globule) temperature, the chain exists in a superposition of long-lived, misfolded traps. For a frustrated sequence, the misfolded structures are substantially different from the native state, and because the energy bias ΔE is weak, any small rearrangement of the sequence can drastically alter its native structure. In the low frustration regime, Λ is substantially greater than 1, and the energy gap between native and misfolded states is larger than the characteristic energy barriers between them. Furthermore, the configuration space of the chain is energetically correlated with the native structure (2, 9) so it is much less likely for a random mutation to cause any significant damage to the energy funnel (5, 20).

According to this “evolutionary” selection principle, a threshold value Λ₀ can be introduced to describe the physiological criteria needed to be met for sequences to be biochemically useful, such that for physiologically allowed proteins

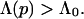2

A crude calculation shows that Λ₀ should be somewhere around Λ₀∼1.5 for single folding domain proteins (45, 46). Of course, this in itself does not stabilize any structure because it does not eliminate the possibility to evolve from one native structure into another along a pathway on which every sequence meets the requirement. Stability appears when we consider that single folding domain proteins correspond to valleys (local minima) in the landscape −Λ(p), and because the folded structures corresponding to separate valleys are substantially different, the sequence-ordering tendencies induced by design into these structures must oppose each other, so that every stepwise mutational path between one sequence family and another must encounter a region where the sequence-ordering tendencies counteract and the criteria Λ(p) > Λ₀ may not be met.

To be more precise, consider two native configurations ν₀ and ν₁ of sequences p₀ and p₁ with nearly equal degrees of frustration

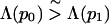3

but with low structural similarity, such that

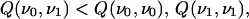4

where Q(ν₀,ν₁) is the number of cross chain contacts common to ν₀ and ν₁. Furthermore, assume that p₀ and p₁ are the least frustrated sequences folding to ν₀ and ν₁ respectively. We can then define a sequence similarity parameter x(p) to measure the degree of ordering toward p₁ and away from p₀. For simplicity, we define x(p₀) = 0 and x(p₁) = 1. The similarity parameter allows us to prescribe a minimal frustration path p(x) in sequence space, such that p(x) is the least frustrated sequence having the similarity parameter value x [hence p(0) = p₀ and p(1) = p₁]. For example, in the α carbon model discussed below, there are two sequence ordering tendencies, characterized by the sequences 1 0 0 1 0 1 0 1 0 1 0 0 1 0 0 1 and 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 (where 1 and 0 stand respectively for H and P residues). In this situation, the similarity parameter x corresponds to the degree of clustering of the H residues. More generally, x(p) is a matrix x^μν(p), but for two families x⁰¹ = x, x¹⁰ = 1 − x, and x^νν = 1.

To complete this picture, we can interpret functions of x in terms of the minimal frustration path p(x), for example

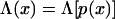5

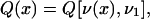6

where

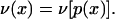7

It is clear now, that if we attempt to evolve p₀ into p₁, the most optimal trajectory from the standpoint of equation (2) is along the minimal frustration path. Nevertheless, even along this path, a region of frustrated sequences will be encountered at some x = x_m where the sequence-ordering tendencies completely counteract, and hence lose the capacity to fold sequences efficiently. Thus, because p(x) is the best path, a gap will occur, completely separating the sequence families, when the requirement Λ₀ exceeds Λ(x_m).

Protein Model.

In the following sections, we present a simple concrete example of this effect in the α carbon model of proteins described in Figs. 1 and 2. The model is essentially a continuum version of the HP model (26); however, the residues also are allowed to approach each other more closely when they are nearest neighbors in sequence (i.e., along the chain) than through contacts across the chain. Thus, there are two types of interaction potentials present in the chain. The cross chain (nonlocal) interactions between hydrophobic residues are determined by a short range Morse potential (similar to the Van der Walls potential). All cross chain interactions between other pairs of species (HP, PP) are determined by the hard core of this potential. The chain-bonded (local) interactions are defined by a “square well” potential. The effect of this potential is similar to having hard beads tethered together by string. The string bond minimum approach radius is one-half the cross chain hard core radius, which results in two structural mechanisms for maximizing the number of favorable energetic connections in the core. The first mechanism is dominated by the local interactions, and the second by nonlocal interactions. These correspond to the core structures ν1 and ν0 shown in Fig. 2. More explicit details of the model are described in a recent article (20).

The basic effect of protein folding captured by this model is that, as the chain folds, it is forced to have a clearly defined inside (core) and outside (surface) determined by the twofold identity of its residues. The hydrophobicity of small, single folding domain proteins is peaked around one-half so that roughly one-half the residues are forced into the core. Lower hydrophobicity results in nonfolding sequences, whereas higher hydrophobicity leads to aggregation. We thus use a fraction of 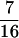hydrophobic residues consistent with these observations (30). This level of representation of proteins is similar in spirit to many other minimalist models (3, 5, 26, 31, 35–44).

An important feature of this model is that the ground-state core geometry and energy of a sequence is determined uniquely by the set of internally clamped sequential H-segments along its length (such as, H—H … H—H—H … H … H) and not by permutations of the segments within a sequence. For example, the sequence H—H—H … H … H … H—H folds into exactly the same hydrophobic core geometry as H—H … H—H—H … H … H.† For sequences that fold to the same core geometry, this is roughly true for both the folding temperature T_f and the folding time τ_f. Because the P residue chain segments can always access a significant number of configurations when the H residues are clamped in the ground-state, changing the length of these P-segments should contribute mainly to the very early stages of folding and has been seen only in the fastest folding sequences. In testing different mutations of these fast-folding sequences, we find only a small spread in T_f and τ_f within sequence families. Hence, we take the folding parameters to be essentially invariant of permutations that do not break, create, or extend the length of the H-segments, and we only calculate the folding temperature T_f and the folding time τ_f for one sequence folding to each of the 15 core structures.

For convenience we represent the degree of frustration minimization by the following function

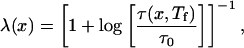8

where τ₀ = min[τ(p,T_f)] is the minimum folding time for all 15 representative sequences, and τ(p,T_f) is the folding time measured at the folding temperature. The function in the denominator of this expression T_f log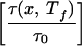is roughly the difference between the typical energy barrier encountered in folding the sequence and the typical energy barrier for the fastest folding sequence.‡ λ(x) therefore is strongly correlated with the ratio of folding to glass temperatures Λ(x), but the functional form of this equation causes the degree of frustration minimization λ(p) to vary between the limits 0 and 1 [rather than 0 and ∞ as with Λ(x)].

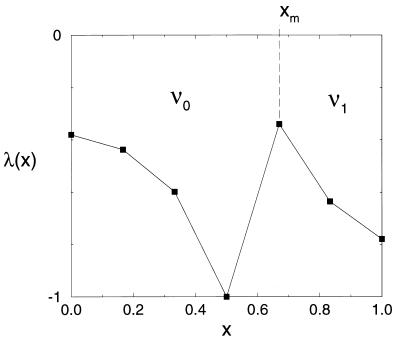
λ(x) is plotted in terms of the similarity parameter x in Fig. 3. As expected, all three functions λ(x), T_f(x), and τ(x,T_f) exhibit two regions of minimal frustration (large λ, T_f, and τ_f⁻¹) between 0 ≤ x ≤ ½ (small sequence clustering) and 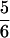≤ x ≤1 (large sequence clustering). The minimally frustrated sequences in these two frustration valley regions fold to the ν₀ and ν₁ structures. The valley regions are separated by a “barrier” or saddle region at x ≡ x_m = 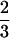. The least frustrated sequences from this barrier region fold to the FRUST geometry 2 4 (Fig. 2).

Figure 3.

Plot of the function −λ(x). The frustration maximum occurs at x ≡ x_m = 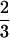, and all of the data points correspond to the minimally frustrated sequences p(x) with similarity parameter value x. The fastest folding sequence at x_m folds ∼10 times slower than sequences in the ν₀ and ν₁ regions of this plot—for typical sequences at x_m the situation is much worse. If “physiological” sequences are required to have −λ̃ < −λ(x_m) (dotted line) to be considered biochemically useful, a “nonfolding” gap opens up in sequence space between the two sequence families folding to the ν₀ and ν₁ core geometries.

Stable Modes of the Model.

The two minimally frustrated sequence families in this model fold to structures that favor either the local (chain bonded) or nonlocal (cross chain) interactions. The first family occurs due to the fact that the mutual cross chain exposure of H residues can be maximized by minimizing the number of sequential H—H bonds. According to the interaction rule, H residues can interact across the chain only when they are not nearest neighbors in sequence. Thus, sequences like

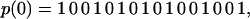9

(where 1 (0) stand for H (P) residues) maximize the number of available energetic cross chain contacts between H residues. As discussed above, the similarity parameter x(p) is the fraction of possible H—H bonds. The ground state core symmetry for these small x sequences is the ν₀ structure. This symmetry is stable even when some of the H residues are joined together into sequential segments. However, when three or more sequential H residues occur within a sequence, interference is introduced between the local and nonlocal interactions, and the ground-state symmetry is broken (see Fig. 2, FRUST 1 2).

As we increase x, so that H residues are steadily bonded together into segments, a new mode develops to maximize energetic connectivity. This second mode occurs due to the fact that residues connected by nearest neighbor (string) bonds can approach each other more closely along the chain (the string bond hard core radius is 0.4) than across the chain (cross-chain hard core radius ∼ 0.75), and therefore the core is able to compact itself into a smaller globule to increase cross chain contacts. This second mechanism operates in sequences with a nearly homogeneous grouping of H residues,

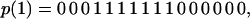10

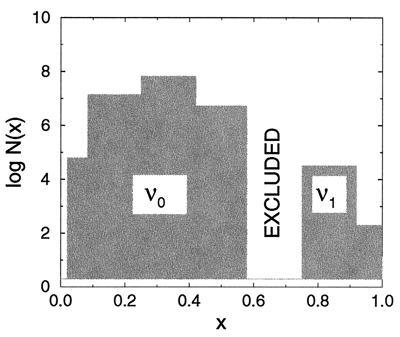
which fold to the ν₁ core structure. Although this sequence family corresponds to a frustration minima, it is very small, leading to a much lower sequence entropy (logarithm of the number of sequences) (ref. 19) (Fig. 4).

Figure 4.

Bar graph schematic of the model sequence space. The shaded areas correspond to sequence families folding to the ν₀ and ν₁ core geometries. The height of each shaded bar is the logarithm of the number of sequences log N(x) folding to the structure type at x. The unshaded (excluded) region contains only frustrated FRUST sequences. When λ₀ passes below the frustration maxima in Fig. 3, this unshaded region is physiologically excluded. A spontaneous double or triple exchange mutation is required to mutate across the gap.

Again, because the two minimal frustration sequence families are dissimilar in the way that H residues are distributed in sequence, a substantial number of exchange mutations (two to three) are required to change a sequence folding to ν₀ into a sequence folding to ν₁. If we take a stepwise mutational trajectory between ν₀ and ν₁ along the least frustrated path, we must pass through a region where the sequences fold ∼10 times slower, whereas if we do not take this path, the situation is much worse. If sequences are required to fold faster, and be more stable than those at the cusp λ(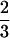) in the frustration function, i.e., if λ₀, exceeds λ(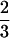), then all the sequences between the two families folding to ν₀ and ν₁ are excluded (Fig. 4). If these were real proteins, this would mean that the sequences could not continuously evolve from one structure into the other, i.e., we would always encounter a region of sequences that do not fold on the order of physiological timescales.

DISCUSSION

The results of this model suggest that the sequence space of single folding domain proteins is split into mutually dissimilar, low frustration families folding to mutually dissimilar native structures. The principle by which this situation emerges is the design requirement of minimal frustration, which allows efficient folding of sequences into their functional (native) structures. Each family is characterized by a particular tendency for ordering the residues, which results naturally in a matrix of similarity parameters, x^μ≠ν to describe the geometry of sequence space (ref. 48). Minimal frustration is expressed in the sense that one of these parameters can be large, whereas the rest are small, in other words, in a type of orthogonality (dissimilarity) property. At intermediate values of the parameters, the sequence-ordering tendencies of pairs of families counteract each other, resulting in saddle regions of frustrated sequences. If the physiological requirement on folding ability exceeds the folding ability of sequences in these frustrated regions, all the sequences within them will be excluded from biochemical processes, resulting in a mechanism for evolutionarily stable partitioning of sequence information into biochemically useful subsets.

Although we have focused on a highly simplified model, we have taken into account a fundamental ingredient of the protein self interactions—the coupling between local and nonlocal interactions—which allows for two different mechanisms for maximizing energetic connectivity. It is certain that much more elaborate effects exist in proteins due to the complex interactions between different amino acids. However, the fact that this model is capable of capturing a clear mechanism for evolutionary stability lends credit to its comparison with proteins. Finally, it is important to point out that, although the minimal frustration path between sequence families is the most optimal path from the standpoint of equation (2), real population dynamics will explore a much wider region of sequence space.