Abstract
We describe and test a Markov chain model of microsatellite evolution that can explain the different distributions of microsatellite lengths across different organisms and repeat motifs. Two key features of this model are the dependence of mutation rates on microsatellite length and a mutation process that includes both strand slippage and point mutation events. We compute the stationary distribution of allele lengths under this model and use it to fit DNA data for di-, tri-, and tetranucleotide repeats in humans, mice, fruit flies, and yeast. The best fit results lead to slippage rate estimates that are highest in mice, followed by humans, then yeast, and then fruit flies. Within each organism, the estimates are highest in di-, then tri-, and then tetranucleotide repeats. Our estimates are consistent with experimentally determined mutation rates from other studies. The results suggest that the different length distributions among organisms and repeat motifs can be explained by a simple difference in slippage rates and that selective constraints on length need not be imposed.
Microsatellites are tandem repeats of short units of DNA that occur with high frequency throughout the genomes of many organisms (1). Microsatellite loci have a high degree of variability that is caused by a high rate of mutations that alter microsatellite length. There are several major reasons for interest in microsatellite loci. First, the abundance and high level of allelic variation at microsatellite loci in the genomes of many organisms has made them popular genetic markers (2). Also, genetic distance measures based on microsatellites can be used to answer questions concerning population structure and divergence (3–5). Finally, expansion of one type of microsatellite (triplet repeats) leads to several human genetic disorders such as fragile X syndrome (6) and myotonic dystrophy (7).
The primary mutational mechanism leading to changes in microsatellite length is polymerase template slippage (8, 9). During replication of a repetitive region, DNA strands may dissociate and then reassociate incorrectly. Renewed replication in this misaligned state leads to insertion or deletion of repeat units, thus altering allele length. At the triplet repeat loci associated with various genetic disorders, there is also some possibility of very rapid growth in allele size. Biological explanations for this phenomenon are provided in ref. 10, and a mathematical model for rapid growth is discussed in ref. 11. We restrict our attention to loci that do not undergo such rapid growth. In microsatellite loci where rapid growth does not occur, most of the observed changes in length are by ±1 repeat unit. For this reason, the stepwise mutation model (SMM) (12) has often been used to model microsatellite evolution (3, 13–15).
Following the SMM, the length of a microsatellite varies at a fixed rate independent of length, according to a symmetric random walk on the positive integers. The problem with this model for the study of microsatellite length evolution is that a symmetric random walk does not converge to a stationary distribution, and it is expected to attain arbitrarily high values. Moran (16) noted that the SMM would not predict a stationary distribution of lengths but that the variance in allele length within a population of fixed size would stabilize. This observation has led most works to analyze the difference in microsatellite length between individuals (5, 13, 15). This approach is useful for estimating the time of divergence of populations (4), but it fails to explain why individual alleles do not grow to arbitrarily large lengths.
Some variants of the SMM address this problem by considering length constraint on microsatellites (17–19). An upper bound on the number of repeat units in microsatellites greatly simplifies computations and is based on the observation that very long alleles are rare (20). Although the presence of an upper bound leads to a stationary distribution of lengths, it is not clear why a strict upper bound should exist, and what its value should be.
An alternate explanation for the absence of very long alleles is that point mutations within a repeat unit interrupt the microsatellite repeat region, creating two shorter repeat regions (21). Bell and Jurka (17) were the first to incorporate this idea into a model of microsatellite evolution. However, their study differs from ours in two important respects. First, because they kept track of both parts of a repeat split by a point mutation, their model was analytically intractable and could be studied only by simulation. Second, they imposed an artificial upper bound of 30 repeat units to ensure the existence of a stationary distribution. The fact that our stationary distribution can be computed explicitly allows us to estimate slippage rates by fitting the model to data. More importantly, the absence of a selective constraint in our model allows us to conclude that the equilibrium distribution of microsatellite repeat lengths can result from a balance between slippage events and point mutations.
The Model.
Our model is a continuous time Markov chain that incorporates length dependent slippage events that may lead to small changes in microsatellite length and incorporates point mutations within a microsatellite that may greatly reduce length (i.e., the number of consecutive repeat units). The states of the chain are the positive integers, 1, 2, 3 … , each of which corresponds to the number of tandem repeat units at a microsatellite locus. In formulating our chain, we are thinking of the experiment in which we randomly select adjacent nucleotides as a possible starting point for a microsatellite and count the number of tandem repeats, starting with the chosen pair and scanning to the right in the sequence.
For each generation, three types of transitions may occur.
1. The number of repeat units may change by ± 1 unit due to polymerase slippage. Slippage events at a microsatellite consisting of k repeat units occur at rate (k−1)*b, where b is the per repeat unit slippage rate. This choice is motivated by the idea that a longer allele will present more opportunities for a slippage event during replication.
2. A point mutation may occur within a repeat, thus cutting the perfect microsatellite repeat into two smaller repeats. Because we are tracking the evolution of one perfect repeat, only the portion of the microsatellite to the left of the point mutation is retained in the counting scheme of the model. This allows us to monitor the evolution of one microsatellite and study its stationary length distribution, without introducing complications associated with keeping track of both portions (17), that would make analytic computations impossible. A microsatellite consisting of k repeat units will move to any of the states, 1, 2, … k −1 at point mutation rate a.
3. A transition from one to two repeat units due to specific base substitutions occurs at some small rate c. This transition provides a way for microsatellite lengths to leave state one, thus preventing length one from being an absorbing state.
Although this model imposes no artificial upper bounds on microsatellite length, we have shown that a stationary distribution exists. For details see ref. 22. A formal proof involves some knowledge of Markov chain theory, but the intuition behind it is clear. Suppose that slippage events can only increase microsatellite length. The microsatellite will increase in length due to slippage at a rate proportional to the number of repeat units. Point mutations, which also occur at a rate proportional to the length, decrease the length of the perfect repeat by a factor of two on average. Because dividing by two reduces the number of repeat units much faster than addition can increase them, microsatellite length will not grow without bound, and an equilibrium distribution will become established. The existence of a stationary distribution in this worst case implies that a stationary distribution will also exist if slippage events can either increase or decrease length.
DNA Sequence Analyses.
DNA sequences from humans, mice, fruit flies, and yeast were used to test the model. The data collected for each organism is a concatenation of 15–20 BAC, PAC, and P1 clones down-loaded from the web home pages of Lawrence Berkeley Labs (http://www.lbl.gov; August 1997), the Genome Sequencing Center (http://genome.wustl.edu/gsc/yeast/yeast.html; August 1997), and the Whitehead Institute (http://www-seq.wi.mit.edu; August 1997). A serious problem with this type of data collection is the possibility of overlap among the contigs, which would lead to double counting of certain regions. To avoid this problem, the blast software package was used to align all of the sequences (23), and overlapping regions were removed. After this step, the remaining data consisted of ≈1 million bp of nonoverlapping DNA from each organism.
Each sequence was scanned for di-, tri-, and tetranucleotide repeats. Different repeat types were considered separately because there is evidence that mutation rates at microsatellite loci vary depending on the length of a repeat unit (24–26). Repeats such as (A)n were classified as mononucleotide repeats and were not counted. Dinucleotide repeats were not counted when examining tetranucleotide repeats. A microsatellite was defined as a sequence consisting of five or more tandemly repeated units. Shorter sequences were not considered because we aim to compare our findings with experimental results in which shorter sequences are usually ignored.
A counting scheme consistent with the stochastic model was chosen to tabulate the data. We described the method used for counting dinucleotide repeats. The case of tri- and tetranucleotides was completely analogous. We processed the data by examining each successive pair of nucleotides and then counting the number of times that the pair occurs to the right in the sequence. This scheme has the property that a repeat of n units also will generate repeats of length n−1, … , 5. The counting scheme was consistent with our viewpoint of picking a random starting point for a microsatellite and scanning the sequence to the right. The counts collected by this scheme were the appropriate data for fitting our model. In the next section, we related our results to the more typical scheme of counting each microsatellite once.
As explained in ref. 22, the stationary distribution of the Markov chain, π(i), i ≥ 1 can be computed by solving the following equations:
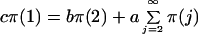 |
1 |
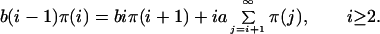 |
2 |
This distribution is a function of the parameters a, b, and c, described in the previous section. Because we define microsatellites to be a sequence of five or more repeat units, we need to consider the stationary distribution conditioned on length ≥5 to compare our results with data. The parameter c controls the relative frequency of length one repeats to the frequency of other repeats. For this reason, the actual value of c is not relevant given that we consider the conditional distribution. Furthermore, one can see from Eq. 2 that the stationary distribution only depends on a and b through their ratio. It follows that the only true parameter needed to compute the stationary distribution is b/a, the ratio of slippage rate to point mutation rate. For the purpose of obtaining numerical values of b that could be compared across organisms and with experimental results, we fixed the point mutation rate at a = 1 × 10−8 per nucleotide per generation (27). We then fit the empirical distribution of microsatellite repeats with values of the stationary distribution computed for various values of the slippage rate.
RESULTS AND DISCUSSION
The number of microsatellites of different lengths are shown in Tables 1, 2, 3. In this presentation of the data, each microsatellite is counted once, and allele length is given in number of repeat units. The mouse has a higher density of microsatellites per megabase of sequence than the other organisms. Humans and fruit flies have a comparable density of dinucleotide repeats, but the distributions of repeat lengths vary in that humans have far more long repeats than fruit flies. Finally, there are almost no tetranucleotide repeats of length ≥5 in the yeast and fruit fly data.
Table 1.
Dinucleotide repeat counts in 1 Mb of sequence data
| Length | Human | Mouse | Fruit fly | Yeast |
|---|---|---|---|---|
| 5 | 88 | 111 | 95 | 30 |
| 6 | 31 | 75 | 38 | 10 |
| 7 | 23 | 34 | 16 | 12 |
| 8 | 9 | 23 | 13 | 6 |
| 9 | 3 | 19 | 11 | 2 |
| 10 | 5 | 10 | 4 | 5 |
| 11 | 5 | 8 | 5 | 3 |
| 12 | 4 | 15 | 1 | 1 |
| 13 | 3 | 5 | 1 | 2 |
| 14 | 5 | 15 | 0 | 1 |
| 15 | 0 | 21 | 0 | 1 |
| 16 | 5 | 7 | 0 | 1 |
| 17 | 3 | 9 | 0 | 0 |
| 18 | 4 | 13 | 0 | 1 |
| 19 | 3 | 7 | 1 | 0 |
| 20 | 5 | 10 | 0 | 0 |
| 21 | 2 | 11 | 0 | 0 |
| 22 | 2 | 2 | 0 | 0 |
| 23 | 1 | 8 | 0 | 0 |
| 24 | 2 | 7 | 0 | 0 |
| 25 | 1 | 2 | 1 | 0 |
| 26 | 0 | 4 | 0 | 0 |
| 27 | 0 | 3 | 0 | 0 |
| 28 | 0 | 5 | 0 | 0 |
| 29 | 0 | 1 | 0 | 0 |
| 30 | 1 | 0 | 0 | 0 |
| 31 | 0 | 2 | 0 | 0 |
| 32 | 0 | 1 | 0 | 1 |
| 33 | 0 | 1 | 0 | 0 |
| 34 | 0 | 1 | 0 | 0 |
| Total | 205 | 430 | 186 | 76 |
Table 2.
Trinucleotide repeat counts in 1 Mb of sequence data
| Length | Human | Mouse | Fruit fly | Yeast |
|---|---|---|---|---|
| 5 | 19 | 16 | 26 | 23 |
| 6 | 4 | 15 | 14 | 10 |
| 7 | 5 | 4 | 2 | 3 |
| 8 | 1 | 4 | 2 | 4 |
| 9 | 0 | 5 | 2 | 3 |
| 10 | 1 | 0 | 0 | 1 |
| 11 | 0 | 1 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 |
| 13 | 1 | 0 | 0 | 0 |
| 14 | 0 | 1 | 0 | 0 |
| 15 | 3 | 0 | 0 | 0 |
| 16 | 0 | 1 | 0 | 0 |
| 19 | 0 | 2 | 0 | 0 |
| 20 | 0 | 1 | 0 | 0 |
| 26 | 0 | 2 | 0 | 0 |
| Total | 34 | 52 | 46 | 44 |
Table 3.
Tetranucleotide repeat counts in 1 Mb of sequence data
| Length | Human | Mouse | Fruit fly |
|---|---|---|---|
| 5 | 23 | 33 | 3 |
| 6 | 7 | 18 | 0 |
| 7 | 1 | 12 | 0 |
| 8 | 0 | 8 | 0 |
| 9 | 0 | 7 | 0 |
| 10 | 4 | 1 | 0 |
| 11 | 3 | 4 | 0 |
| 12 | 0 | 8 | 0 |
| 13 | 0 | 1 | 0 |
| 14 | 0 | 2 | 0 |
| 15 | 1 | 0 | 0 |
| 18 | 0 | 1 | 0 |
| Total | 39 | 95 | 3 |
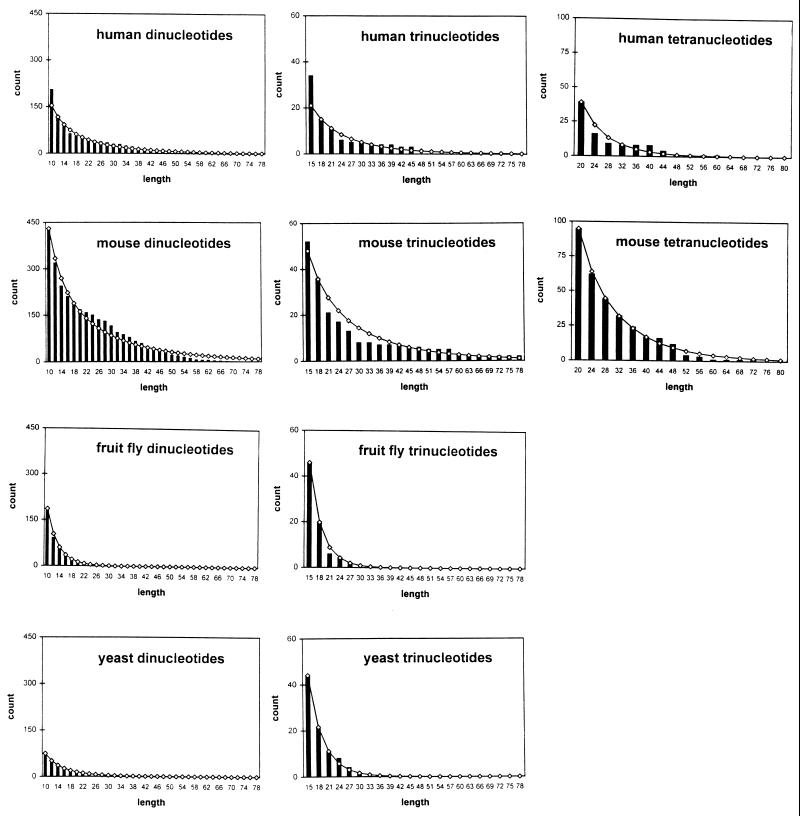
Fig. 1 shows the best fit results for the four organisms. The histogram provides the observed counts, whereas the line graph is the stationary distribution multiplied by a scaling factor, K. The scaling factor corresponds to looking at the distribution conditional on length ≥5 and converting conditional probabilities to expected counts. For each length i ≥ 5, the line graph gives a value Kπ(i). Because each microsatellite of length n generates exactly 1 microsatellite of length n− 1, … , 5, π(i) can be interpreted as the frequency of microsatellites of length i or greater. Note that p(i), the frequency of a microsatellite of length i, is simply given by p(i) = π(i) − π(i + 1). Hence π(n), n ≥ 5, is the scaled tail of the stationary distribution of lengths.
Figure 1.
The best fit results of the model across organisms and repeat motifs. Observed counts of di-, tri-, and tetranucleotide repeats from 1 Mb of sequence in each organism are given by the histogram. Expected counts based on the model are given by the line graph. The counts are presented according to the counting scheme described in the text, and the lengths are given in number of nucleotides.
Our fits are based on the one-step, symmetric slippage model. The final fit was chosen based on the slippage rate that minimized the sum of absolute differences between the observed and expected length distributions. This criterion worked better than minimizing squared error because using squared error led to fits that were insensitive to the tail of the empirical distribution. We considered variants that allowed slippage by two repeat units and asymmetry in the slippage rates (i.e., slippage rate up ≠ slippage rate down). Slippage by two repeat units led to slight improvements in the fit but greatly increased computational complexity. The best fit results suggested that slippage by two repeat units occurred at a rate that was two orders of magnitude lower than the one-step slippage rate. The asymmetric model gave similar quality fits to the symmetric model. In general, the results were robust to small variations in the model.
For each organism, we fit the one-step, symmetric model to the data by choosing an appropriate value for the slippage rate. Higher values of slippage rate led to a heavier tail in the stationary length distribution. Table 4 shows the different best fit slippage rates per dinucleotide microsatellite per generation. The results indicate that slippage rates are highest in mice, followed by humans, then yeast, and then fruit flies. To compare the per repeat unit slippage rates given by the best fits with experimentally determined per locus rates, it is necessary to multiply the rates by (l − 1), where l is the average microsatellite length in the experimental study. For example, mutation rates in dinucleotide repeats in fruit flies were estimated to be 9.3 × 10−6 per locus per generation (M.D.S., C. Hutter, K. Wetterstrand, M. Gaudette, T. Mackay, and C.F.A., unpublished results). The per repeat unit slippage rate from the best fit of the model to dinucleotide data was 2.3 × 10−7, and the average number of repeat units per microsatellite in the study was 13.1, so our per locus slippage rate estimate is (2.3 × 10−7)(12.1) = 2.8 × 10−6. The other entries in Table 4 were computed in the same way.
Table 4.
A comparison of dinucleotide slippage rates per locus
| Predicted rates
|
Experimental rates
|
||||
|---|---|---|---|---|---|
| Per repeat unit | Mean locus length | Per locus | Per locus | Reference | |
| Human | 4.8 × 10−6 | 24.7 | 1.1 × 10−4 | 4.5 × 10−4 | 28 |
| 4.8 × 10−6 | 28 | 1.3 × 10−4 | 2.3 × 10−4 | 29 | |
| Mouse | 1.0 × 10−5 | 20 | 1.9 × 10−4 | 4.6 × 10−5 | 30 |
| 1.0 × 10−5 | — | — | 4.7 × 10−4 | 31 | |
| Fruit fly | 2.3 × 10−7 | 13.1 | 2.8 × 10−6 | 9.3 × 10−6 | † |
| Yeast | 9.3 × 10−7 | 14 | 1.2 × 10−5 | 3.0 × 10−5 | 32 |
A comparison between our predicted dinucleotide repeat slippage rates and experimentally determined rates. Per locus rates are obtained by multiplying the per repeat unit rates from the best fit of the model by (l − 1), where l is the locus length of the corresponding experimental study. Locus length was not available for one mouse microsatellite study (—). The locus length of 20 in Ref. 30 is an approximation based on the authors statement that only microsatellites of length 10 or more repeat units were considered, and 85% of microsatellites were longer than 15 repeat units.
M.D.S., C. Hutter, K. Wetterstrand, M. Gaudette, T. Mackay, and C.F.A., unpublished result.
Weber and Wong (26) presented data showing that tetranucleotide repeats in humans are more mutable than di- or trinucleotide repeats. However, most subsequent studies (14, 24, 33) indicate that dinucleotides have the highest mutation rate, on average, followed by tri- and tetranucleotide repeats. Our results support this latter view. Chakraborty et al. (24) explain that Weber and Wong (26) may have over-estimated average tetranucleotide mutation rates and performed a two-way ANOVA to determine that dinucleotide repeats in humans have a per locus mutation rate that is higher than the trinucleotide rate by a factor of 1.22–1.97 and higher than the tetranucleotide rate by a factor of 1.48–2.16. Because average allele lengths are not reported, we cannot give comparable per locus estimates. However, our per repeat unit estimates for di-, tri-, and tetranucleotides (4.8 × 10−6, 2.2 × 10−6, and 5.2 × 10−7, respectively) suggest that dinucleotide repeats in humans have a dinucleotide slippage rate that is higher than the trinucleotide rate by a factor of 2.2 and higher than the tetranucleotide rate by a factor of 9.2.
An analysis of population variation (M.D.S., C. Hutter, K. Wetterstrand, M. Gaudette, T. Mackay, and C.F.A., unpublished results) in fruit flies, using Chakraborty’s approach, showed that per locus dinucleotide mutation rates in fruit flies are 6.4 times higher than trinucleotide mutation rates and 8.4 times higher than tetranucleotide mutation rates. The average number of repeat units per microsatellite was 13.1, 6.5, and 5.75 for di-, tri-, and tetranucleotides, respectively. Given these locus lengths and per repeat unit slippage rates of 2.3 × 10−7 and 1.3 × 10−7 for di- and trinucleotide repeats respectively, our per locus estimates would indicate that dinucleotides are a factor of 3.6 times more mutable than trinucleotide repeats. We had insufficient data to estimate tetranucleotide mutation rates. The same trends were evident in mouse and yeast data. The per repeat unit slippage rates in di-, tri-, and tetranucleotide repeats in mouse were 1.0 × 10−5, 4.4 × 10−6, and 1.5 × 10−6, respectively. The per repeat unit dinucleotide slippage rate in yeast was 9.3 × 10−7, and the trinucleotide rate was 2.0 × 10−7.
Our results are consistent with the trends evident in experimental findings and are in approximate agreement with experimentally determined slippage rates. There are several reasons for expecting some differences between our estimates and those found in the literature. Most importantly, our model does not include all of the biological complexities of microsatellite evolution and can only be expected to provide rough estimates. For example, we do not account for unequal crossing over or the possibility of selective constraint. Furthermore, we make the rough estimate that the point mutation rate a is fixed at 1 × 10−8 per nucleotide per generation across organisms and repeat motifs. Because our true parameter is b/a, the ratio of slippage and point mutation rate, one may conjecture that differences in length distributions are caused by differences in the value of a. However, this seems unlikely because significantly different values of b/a were found in di-, tri-, and tetranucleotide repeats within the same species. Because per basepair substitution rates should be the same in this situation, the different ratios are likely caused by different values of slippage rate.
An alternate reason for the discrepancies between our rate estimates and experimental estimates may be the uncertainty involved in the experimental studies. Because mutation events are rare, most experimental estimates are based on finding a small number of mutant alleles. For example, the estimates in humans were based on finding one and two mutations, respectively (28, 29), and one of the estimates in mouse is based on four mutations (31). As a consequence, the estimates are highly variable. In all cases, our predictions fall within the 95% confidence interval of mutation rates for all four organisms.
CONCLUSIONS
We have introduced a Markov chain model that can explain the differences in the distributions of lengths of microsatellite lengths in various organisms and repeat motifs. We have computed the stationary distribution of this Markov chain as a function of the ratio of slippage rate and point mutation rate and used it to fit observed microsatellite data. The data we have presented and used are a compilation of di-, tri-, and tetranucleotide repeats from approximately 1 million bp of sequence data from humans, mice, fruit flies, and yeast. By fixing point mutation rate and varying the rate of polymerase slippage, we were able to fit the data in all four organisms and to obtain slippage rate estimates that are consistent with experimental findings. The per repeat unit estimates can be compared with per locus estimates of any study by multiplying our rates by the average length of the microsatellite of interest. This type of estimation can be carried out in any organism in which sufficient sequence data is available. The results suggest that a simple difference in slippage rates can explain the variation in length distribution of microsatellites across different organisms and repeat motifs. In our estimates, and in experimental findings, slippage rates are highest in mice, followed by humans, then yeast, and then fruit flies. Furthermore, slippage rates are highest in di-, followed by tri-, and then tetranucleotide repeats. These results raise the testable hypothesis that slippage rates vary taxonomically.
Acknowledgments
S.K. was supported by the Department of Defense National Graduate Fellowship. R.T.D. was supported by a grant from the National Science Foundation. M.D.S. and C.F.A. are supported by grants from the National Institutes of Health.
ABBREVIATION
- SMM
stepwise mutation model
References
- 1.Weber J L. Genomics. 1990;7:524–530. doi: 10.1016/0888-7543(90)90195-z. [DOI] [PubMed] [Google Scholar]
- 2.Weissenbach J, Gyapay G, Dib C, Vignal A, Morissette J, Millasseau P, Vaysseix G, Lathrop M. Nature (London) 1992;359:794–801. doi: 10.1038/359794a0. [DOI] [PubMed] [Google Scholar]
- 3.DiRienzo A, Peterson A C, Garza J C, Valdes A M, Slatkin M B, Freimer N. Proc Natl Acad Sci USA. 1994;91:3166–3170. doi: 10.1073/pnas.91.8.3166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goldstein D B, Linares A R, Cavalli-Sforza L L, Feldman M W. Proc Natl Acad Sci USA. 1995;92:6723–6727. doi: 10.1073/pnas.92.15.6723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pritchard J K, Feldman M W. Theor Popul Biol. 1996;50:325–344. doi: 10.1006/tpbi.1996.0034. [DOI] [PubMed] [Google Scholar]
- 6.Fu Y H, Kuhl D P A, Pizzuti A, Pieretti M, Sutcliffe J S, Richards S, Verberk A J M H, Holden J J A, Fenwick R G, Jr, Warren S T, et al. Cell. 1991;67:1047–1058. doi: 10.1016/0092-8674(91)90283-5. [DOI] [PubMed] [Google Scholar]
- 7.Brook J D, McCurrach M E, Harley H G, Buckler A J, Church D, Aburatani H, Hunter K, Stanton V P, Thirion J P, Hudson T, et al. Cell. 1992;68:799–808. doi: 10.1016/0092-8674(92)90154-5. [DOI] [PubMed] [Google Scholar]
- 8.Schlotterer C, Tautz D. Nucleic Acids Res. 1992;20:211–216. doi: 10.1093/nar/20.2.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Strand M, Prolla T A, Liskay R M, Petes T M. Nature (London) 1993;365:274–276. doi: 10.1038/365274a0. [DOI] [PubMed] [Google Scholar]
- 10.McMurray C T. Chromosoma. 1995;104:2–13. doi: 10.1007/BF00352220. [DOI] [PubMed] [Google Scholar]
- 11.Gawel B, Kimmel M. J Appl Prob. 1996;33:949–959. [Google Scholar]
- 12.Ohta T, Kimura M. Genet Res. 1973;22:201–204. doi: 10.1017/s0016672300012994. [DOI] [PubMed] [Google Scholar]
- 13.Kimmel M, Chakraborty R. Theor Popul Biol. 1996;50:345–367. doi: 10.1006/tpbi.1996.0035. [DOI] [PubMed] [Google Scholar]
- 14.Valdes A M, Slatkin M, Freimer N B. Genetics. 1993;133:737–749. doi: 10.1093/genetics/133.3.737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhivotovsky L A, Feldman M W. Proc Natl Acad Sci USA. 1995;92:11549–11552. doi: 10.1073/pnas.92.25.11549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Moran P A P. Theor Popul Biol. 1975;8:318–330. doi: 10.1016/0040-5809(75)90049-0. [DOI] [PubMed] [Google Scholar]
- 17.Bell G I, Jurka J. J Mol Evol. 1997;44:414–421. doi: 10.1007/pl00006161. [DOI] [PubMed] [Google Scholar]
- 18.Feldman M W, Bergman A, Pollock D D, Goldstein D B. Genetics. 1997;145:207–216. doi: 10.1093/genetics/145.1.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Garza J C, Slatkin M, Freimer N B. Mol Biol Evol. 1995;12:594–603. doi: 10.1093/oxfordjournals.molbev.a040239. [DOI] [PubMed] [Google Scholar]
- 20.Goldstein D B, Pollock D D. J Hered. 1997;88:335–342. doi: 10.1093/oxfordjournals.jhered.a023114. [DOI] [PubMed] [Google Scholar]
- 21.Schug M D, Wetterstrand K A, Gaudette M S, Lim R H, Hutter C H, Aquadro C F. Mol Ecol. 1998;7:57–69. doi: 10.1046/j.1365-294x.1998.00304.x. [DOI] [PubMed] [Google Scholar]
- 22.Kruglyak, S. & Durrett, R. (1998) J. Appl. Prob., in press.
- 23.Altschul S F, Gish W, Miller W, Meyers E W, Lipman D J. J Mol Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- 24.Chakraborty R, Kimmel M, Stivers D N, Davison L J, Deka R. Proc Natl Acad Sci USA. 1997;94:1041–1046. doi: 10.1073/pnas.94.3.1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schug M D, MacKay T F, Aquadro C F. Nat Genet. 1997;15:99–102. doi: 10.1038/ng0197-99. [DOI] [PubMed] [Google Scholar]
- 26.Weber J L, Wong C. Hum Mol Genet. 1993;2:1123–1128. doi: 10.1093/hmg/2.8.1123. [DOI] [PubMed] [Google Scholar]
- 27.Li W H. Molecular Evolution. Sunderland, MA: Sinauer; 1997. pp. 177–236. [Google Scholar]
- 28.Kwiatowski D J, Henske E P, Weimer K, Ozelius L, Gusella J F, Haines J. Genomics. 1992;12:229–240. doi: 10.1016/0888-7543(92)90370-8. [DOI] [PubMed] [Google Scholar]
- 29.Petrukhin K E, Speer M C, Cayanis E, DeFatima Bonaldo M, Tantravahi U, Soares M B, Fischer S G, Warburton D, Gilliam T C, Ott J. Genomics. 1993;15:76–85. doi: 10.1006/geno.1993.1012. [DOI] [PubMed] [Google Scholar]
- 30.Dietrich W, Katz H, Lincoln S E, Shin H S, Friedman J, Dracopoli N C, Lander E S. Genetics. 1992;131:423–447. doi: 10.1093/genetics/131.2.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dallas J F. Mamm Genome. 1992;3:452–456. doi: 10.1007/BF00356155. [DOI] [PubMed] [Google Scholar]
- 32.Henderson S T, Petes T D. Mol Cell Biol. 1992;12:2749–2757. doi: 10.1128/mcb.12.6.2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Edwards A, Hammond H A, Jin L, Caskey C T, Chakraborty R. Genomics. 1992;12:241–253. doi: 10.1016/0888-7543(92)90371-x. [DOI] [PubMed] [Google Scholar]