Predictive Computational Models of Substrate Binding by a Nucleoside Transporter

Abstract

Transporters play a vital role in both the resistance mechanisms of existing drugs and effective targeting of their replacements. Melarsoprol and diamidine compounds similar to pentamidine and furamidine are primarily taken up by trypanosomes of the genus Trypanosoma brucei through the P2 aminopurine transporter. In standardized competition experiments with [³H]adenosine, P2 transporter inhibition constants (K_i) have been determined for a diverse dataset of adenosine analogs, diamidines, Food and Drug Administration-approved compounds and analogs thereof, and custom-designed trypanocidal compounds. Computational biology has been employed to investigate compound structure diversity in relation to P2 transporter interaction. These explorations have led to models for inhibition predictions of known and novel compounds to obtain information about the molecular basis for P2 transporter inhibition. A common pharmacophore for P2 transporter inhibition has been identified along with other key structural characteristics. Our model provides insight into P2 transporter interactions with known compounds and contributes to strategies for the design of novel antiparasitic compounds. This approach offers a quantitative and predictive tool for molecular recognition by specific transporters without the need for structural or even primary sequence information of the transport protein.

Introduction

Trypanosoma brucei are unicellular trypanosomal parasites that cause African sleeping sickness in humans and nagana in livestock. These trypanosomes are auxotrophic for purines and thus rely entirely on purine supplies salvaged from the host environment. As such, T. brucei brucei expresses a multitude of purine nucleoside and nucleobase transporters (1). One of these, the T. brucei aminopurine P2 transporter, is unusual as a genuine nucleoside-nucleobase transporter in that it equally transports the nucleoside adenosine and the nucleobase adenine but has virtually no affinity for any other natural purines or pyrimidines (1–3). Yet, despite this apparent high level of selectivity, it has been shown that P2 also mediates cellular uptake of the Food and Drug Administration-approved drugs melarsoprol and pentamidine (2, 4, 5), the main veterinary trypanocides diminazene aceturate (6) and possibly isometamidium (7), and various nucleoside drugs (8).

The unusual nature of this transporter has led to efforts to exploit it as an efficient conduit for novel trypanocides (9, 10), but this requires the identification of the exact pharmacophore as well as the physical limitations on size and charge distribution of the extracellular binding site of the transporter. From the structural similarities between known P2 substrates, it could be concluded early on that the so-called amidine motif of adenine, i.e. N(1)=C(6)-NH₂ (see Fig. 1), was very likely to play a major role in the high affinity interaction with the transporter (3, 11). However, quantitative information or three-dimensional models explaining the high affinity binding, by one transporter, of such diverse molecules as adenosine (Fig. 1A) (2, 3), stilbamidine (Fig. 1C) (12), melarsoprol (Fig. 1F) (2, 3), and even isometamidium (Fig. 1G) (7), have not been available. The apparent broad selectivity has been all the more intriguing for the highly similar transport efficiencies of P2 for adenosine and adenine, a most unusual feature for nucleoside transporters (1).

FIGURE 1.

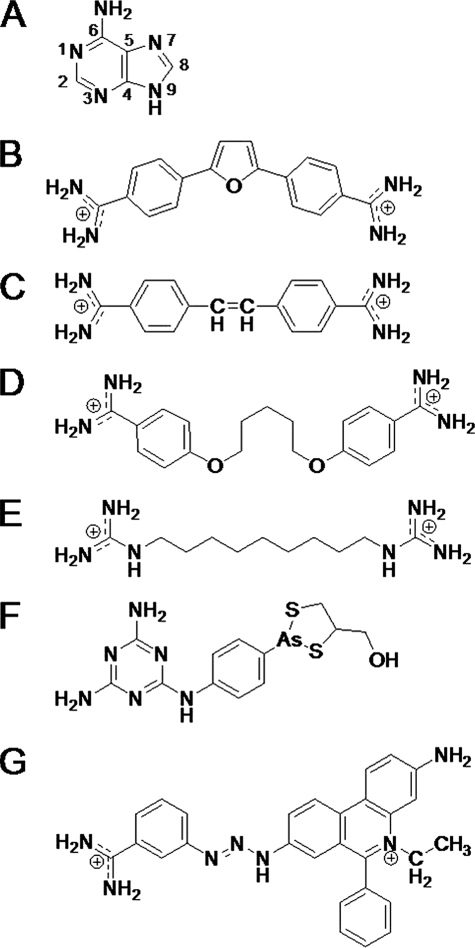
Scaffolds for initial alignment: A, adenine; B, furamidine; C, stilbamidine; D, pentamidine; E, 1,1′-(nonane-1,9-diyl)diguanidine; F, melarsoprol; G, isometamidium. All 112 compounds could be aligned to one of these scaffolds. Most compounds were in A–D.

To construct a predictive and quantitative model of P2-substrate interactions, we determined the K_i values of a large number of highly diverse potential inhibitors, with affinities ranging over several orders of magnitude, through competition experiments with radiolabeled adenosine. These values and structures were then employed for a computational modeling approach to gain more information about the molecular basis for P2 transporter inhibition. The resulting model can be used to evaluate the affinity of the P2 transporter for existing and novel compounds in silico, potentially aiding in the development of novel and selectively targeted trypanocides. More important yet, this strategy allows robust three-dimensional insights into transporter-ligand binding while not requiring knowledge of the structure, or indeed the sequence, of a transporter and can be applied to any solute transport mechanism for which uptake or binding experiments can be routinely performed.

EXPERIMENTAL PROCEDURES

Transport of [³H]Adenosine by Bloodstream Forms of T. brucei

Bloodstream forms of T. brucei brucei strain 427 were taken from stocks in liquid nitrogen and injected in adult female Wistar rats, from which they were harvested by exsanguination by cardiac puncture at peak parasitemia. Parasites were isolated from the blood by elution over a DE52 column (Whatman) (13) and washed twice in assay buffer (AB: 33 mm HEPES, 98 mm NaCl, 4.6 mm KCl, 0.3 mm CaCl₂, 0.07 mm MgSO₄, 5.8 mm NaH₂PO₄, and 14 mm glucose, pH 7.3). Cells were resuspended in this buffer at ∼10⁸ cells/ml prior to use in transport experiments. Cell counts were performed using a hemocytometer. Transport of [³H]adenosine (20–40 Ci/mmol; Amersham Biosciences) was performed exactly as described previously (14), in the presence of 250 μm inosine to block the P1 adenosine uptake system (2). Briefly, 100 μl of 50 nm [³H]adenosine, mixed with various concentrations of nonradiolabeled test compounds, was added to 100 μl of AB containing 10⁷ trypanosomes and incubated at room temperature for 30 s, within the linear phase of uptake (3). Uptake was terminated by the addition of 1 ml of ice-cold assay buffer containing 1 mm adenosine followed by immediate centrifugation through an oil layer to separate cells from external radiolabel. The amount of radiolabeled adenosine inside the cell was then determined using a scintillation counter and corrected for externally associated label as described previously (14). A plot of inhibitor concentration versus adenosine uptake rate (expressed as pmol(10⁷ cells⁻¹ s⁻¹)) yielded sigmoidal curves with Hill coefficients of approximately −1, consistent with monophasic competitive inhibition (Prism 4.0, GraphPad). Inhibition constants were calculated from the EC₅₀ values, using the Cheng-Prusoff equation as described previously (12).

Inhibitor Dataset

Compounds were acquired from several academic laboratories as well as purchased from various commercial sources. Their respective in vitro transport activities along with the compound names and sources are shown in supplemental Table 1. Employing the formula pK_i = −log(K_i), the K_i micromolar values for the 112 compounds were converted to corresponding pK_i values. The pK_i values for this training set span more than 4 log units.

Software

All 112 compounds were constructed in silico with the SYBYL 8.1 software package on a Fedora Core 5 Linux workstation. Compound structures were minimized to convergence using a conjugate gradient of 0.01 kcal/(mol Å) and a maximum of 10⁴ iterations employing the Tripos force field with Gasteiger-Hückel charges. A three-dimensional cubic lattice with 2-Å grid spacing in all directions was created to analyze compounds that were aligned as described below. No improvement was seen in the models when the grid spacing was reduced to 1 Å (15).

Initial Alignment

Through the implementation of the SYBYL software alignment modules, the compounds were three-dimensionally arranged by an initial analysis of structurally and chemically related atoms. Algorithm-generated alignment was performed using the align data base command, whereas the atom-to-atom alignment implemented the match feature of the alignment tools. The algorithm alignment took place first by employing similar backbone structures so that the majority of similar compounds was overlaid in the same molecular space. Structurally related aligned compounds were then moved into separate data bases. The compounds that belonged to the same structural classes, but which varied in atom types or had slight structural differences, were placed into respective data bases and aligned to the most structurally related compound using atom-to-atom alignment. Seven optimum data bases of compounds resulted from initial alignment.

When more rigid compound structures, consisting of a larger number of atoms, were selected as scaffolds for alignments, a greater number of data bases were created. These data bases lacked the variation necessary to form comparative molecular field analysis (CoMFA)² and comparative molecular similarity indices analysis (CoMSIA) models for predictability. Also, when the data bases were aligned by less rigid scaffolds, consisting of a smaller number of atoms, fewer models resulted, and the models produced were not statistically significant in terms of q²_cv (16). The best models were obtained when compounds were aligned by the carbons of common compound backbones. These scaffolds for alignment were obtained from the compounds displayed in Fig. 1: dataset A, adenine; dataset B, furamidine; dataset C, stilbamidine; dataset D, pentamidine; dataset E, 1,1′-(nonane-1,9-diyl)diguanidine; dataset F, melarsoprol; and dataset G, isometamidium. Datasets E–G are composed of four, seven, and four compounds, respectively. The alignment for these last three datasets can be viewed in supplemental Fig. 1. These data bases together consist of less than 8% of the total compounds. Because the purpose of the initial alignment was to determine the pharmacophore for the final alignment, only initial datasets A–D were evaluated through statistics and contour maps. All 112 compounds were included in the final pharmacophore models.

Multiple Regression Analysis

CoMFA and CoMSIA quantitative structure-activity relationship models were generated for molecular data bases through a partial least squares (PLS) multiple regression analysis with molecular descriptors as independent variables and the pK_i values as dependent variables. Statistical significance in the form of q²_cv was assessed through the leave-one-out cross-validation method. The number of components was determined by the smallest predicted error sum of squares, a value that does not always correspond to the highest q²_cv value. Further statistical significance assessment was performed for the final model using 10-fold cross-validation. The values obtained from the 10-fold cross-validation assessment are averages of 10 trials implementing random compound selection. Column filtering did not improve the signal-to-noise ratio (16).

Molecular Descriptors

There are two CoMFA molecular descriptors. The steric van der Waals interaction and the electrostatic Coulombic interaction descriptors were calculated at each lattice intersection using a probe, an sp3 carbon atom with a formal +1 charge. Standard scaling and default energy cutoffs were employed. There are five CoMSIA molecular descriptors. Steric, electrostatic, hydrophobic, hydrogen bond donor, and hydrogen bond acceptor descriptors were calculated using a standard probe as follows: +1 charge, 1 Å radius and +1 hydrophobicity, +1 hydrogen bond donor, and +1 hydrogen bond acceptor. Steric descriptors are related to the third power of the atomic radii. Electrostatic descriptors are derived from partial atomic charges. Hydrophobic descriptors are derived from atom-based parameters. Hydrogen bond donor and acceptor atoms are derived from experimental values.

Three-dimensional Contour Analysis

The interactions of CoMFA and CoMSIA descriptors were visualized through mapping of the product standard deviation with respect to molecular descriptor values and coefficients (S.D.*Coeff.) at each lattice point. For the initial models, the default levels of contour by contribution were employed as follows: 80% for a favored region and 20% for a disfavored region. Data were analyzed, and a common pharmacophore was identified. The compounds of the final pharmacophore model were further analyzed through a contour by actual analysis, where the software output assisted in the determination of proper ranges for assigned values of favored and disfavored contour regions.

Pharmacophore Model

Common contours for the initial quantitative structure-activity relationship models were identified through the analysis of favored and disfavored contour regions. The alignment of such contours aided in the identification of a final pharmacophore. All compounds were realigned, and the final models were constructed.

RESULTS

As seen in supplemental Table 1, this study employs 112 compounds acquired from several academic and industry locations. These compound all exhibit some level of inhibitory activity for the T. brucei brucei P2 transporter. For large datasets of compounds with known activity values, it is possible to employ computational biology to investigate the molecular basis of their activity in terms of structural contributions to K_i values. Predictive models can then be constructed, and important interactions can be identified. Because a large number of diverse compounds are in our data base, a two-step procedure was used to establish a final model.

Initial Quantitative Structure-Activity Relationship Models

As a first step, compounds were obtained in their minimal energy conformation by using standard molecular mechanics energy minimization methods with the Tripos force field. Compound alignment by similar atoms of backbone structures initially separated the 112 compounds into seven data bases, although the majority of the compounds resided in four of the sets. The datasets with the majority of compounds were used for initial PLS modeling. Table 1 displays the total number of compounds in each dataset, the number of components (n) used in PLS, and the statistics for each model as follows: the cross-validated correlation coefficient (q²), the standard error of estimate (SEE), the coefficient of determination (r²), and the F statistic. When q² is greater than 0.5, a model is said to have predictability better than chance (16); however, it is also important that the r² value is near 1, the SEE is small, and the F statistic is large. The r² is a positive value between zero and one; with one being the best correlation and zero being no correlation. The SEE is a measure of the accuracy of the predictions. The F statistic is used in comparing the variance between the experimental and predicted values; a larger value indicates a more statistically significant model.

TABLE 1.

CoMFA and CoMSIA model statistics for the datasets A–D of Fig. 2

	A	B	C	D
CoMFA
Total Compounds	36	29	16	16
n	7	4	5	2
q2cv	0.65	0.55	0.57	0.79
SEE	0.29	0.32	0.17	0.12
r2	0.93	0.89	0.98	0.99
F statistic	55.9	50.5	74.4	311
CoMSIA
Total compounds	36	29	16	16
n	5	3	3	2
q2cv	0.50	0.55	0.65	0.61
SEE	0.32	0.34	0.26	0.11
r2	0.91	0.86	0.93	0.99
F statistic	62.5	51.5	47.4	358

The average statistics for the initial four models with CoMFA molecular descriptors are as follows: q²_cv equal to 0.64; SEE equal to 0.23; r² equal to 0.95; and F statistic equal to 123. Similarly, the average statistics for the four models with CoMSIA molecular descriptors were as follows: q²_cv equal to 0.58; SEE equal to 0.26; r² equal to 0.92; and F statistic equal to 130. Although the models with CoMFA and CoMSIA molecular descriptors were comparable, the ones with CoMFA molecular descriptors display better overall potential for analysis of molecular descriptor contribution by contour maps. This is primarily due to the simplicity of two versus five molecular descriptors.

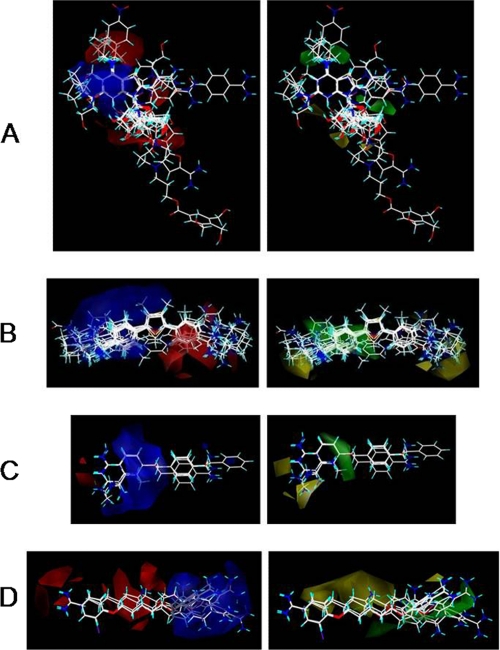
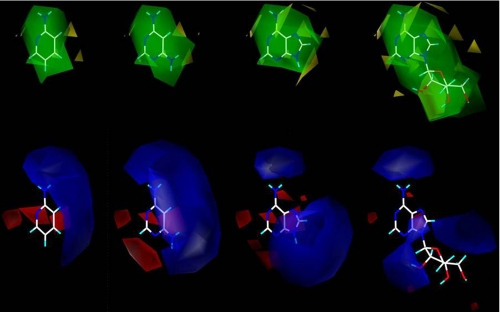
Contour maps of CoMFA molecular descriptor contributions were generated for each model (Fig. 2). The electrostatic interactions are shown as red and blue contours, and the steric interactions are displayed as green and yellow contours. Increasing partial positive charge is favored in blue regions, and increasing partial negative charge is favored in red regions, whereas increasing bulk in substituents are favored in green regions and disfavored in yellow regions.

FIGURE 2.

First alignment processes produced seven different data bases for the 112 compounds. The compounds of the larger datasets, A–D, were employed for quantitative structure-activity relationship CoMFA and CoMSIA studies. Resulting three-dimensional CoMFA molecular surfaces are shown for datasets A–D, which are labeled A–D, respectively. Steric contributions are shown in green (favors bulky substituents) and yellow (bulky substituents impact negatively on binding), and the electrostatic contributions are displayed in blue (favoring a positive charge) and red (favoring a negative charge).

The red, blue, yellow, and green regions were then analyzed to find common alignment features of structures that are of importance for the final, combined pharmacophore alignment. Red regions of dataset A are in the areas above C6, below N9, and beside the imidazole ring of adenine, whereas those of datasets B–D were localized to a single location most often than not on the backbone structure. The red contours of datasets A–D can be aligned in several ways to one another; thus, this descriptor alone is not enough to find the final pharmacophore for alignment. The blue regions were most commonly found in areas of N(R₁)=C(R₂)-NH(R₃), where R₃ is usually H. The alignment was much improved with the inclusion of both the red and blue regions and further enhanced by the addition of the yellow and green regions. Yellow contour regions can be reduced by realignment of compounds into green regions. The yellow regions for dataset A are small in relation to all other contours, and reside near the 2′- and 3′-hydroxy groups of the ribose moiety. Dataset B exhibited yellow contours on both ends of the furamidine backbone, whereas dataset C displayed a yellow contour only at one end of the stilbamidine backbone. The areas of yellow contour appear most at regions that consist of several compounds with substituents that are not precisely aligned, either because they differ largely in structure or because the backbone allows for deviations in the alignment. Dataset D consisted of yellow regions in the areas consisting of compounds that were longer than pentamidine and/or that did not align fully to the pentamidine backbone. Green regions of dataset A were shown above C6 and next to bond C8/N9 of the adenine backbone, whereas the green contours of dataset B appear near and encompassing the phenyl with the most precise alignment. Datasets C consists of green contour near the most precise alignment of the compounds. For dataset D, green contours were located in areas that were not precisely aligned to the pentamidine structure. The green and yellow contours of dataset D both reside in areas of structural deviation; however, the green appears nearest the aromatic linking oxygen and the unaligned amidines.

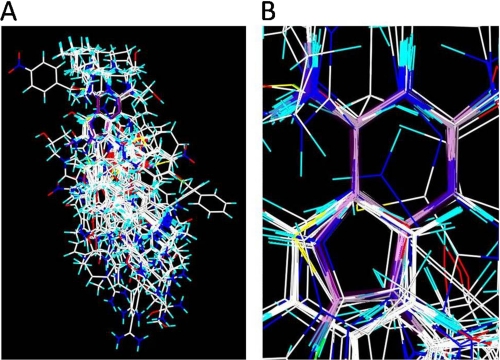
The identification of important structural features, described above, made it possible to realign all 112 compounds, primarily by the common N(R₁)=C(R₂)-NH(R₃) structure found in the blue contour regions and secondarily by the other contour regions. The red regions of the four main datasets overlapped strongly, whereas the yellow regions of datasets B–D can be aligned to green regions of dataset A. The large compounds of dataset A also had to be realigned. Fig. 3A displays the alignment of all 112 compounds with adenine displayed in purple, and Fig. 3B zooms in on the location of the adenine now with the purple displayed as transparent, and this clearly shows the pharmacophore alignment.

FIGURE 3.

Final alignment of 112 compounds, with adenine displayed in purple.

Final Pharmacophore Model

Aligned by the N(R₁)=C(R₂)-NH(R₃) structure with respect to contour regions, as described above, compounds were then employed for PLS modeling. As before, CoMFA and CoMSIA models were generated and examined for statistical significance. The two models each consisted of 112 compounds but use different molecular descriptors and a different number of components. Although the q²_cv values are similar, the remaining statistics are not; the model with CoMFA molecular descriptors achieved a higher level of confidence than the model with CoMSIA molecular descriptors (Table 2). To further validate these models, 10-fold cross-validation was performed. The q²_10-fold values for the models with CoMFA and CoMSIA molecular descriptors were 0.56 and 0.54, respectively. These values, along with the rest of the statistics, indicate statistical significance within each model.

TABLE 2.

CoMFA and CoMSIA model statistics for the 112 compound data base

	CoMFA	CoMSIA
Total compounds	112	112
n	11	6
q2cv	0.55	0.54
q210-fold	0.56	0.54
SEE	0.22	0.37
r2	0.95	0.86
F statistic	190	109

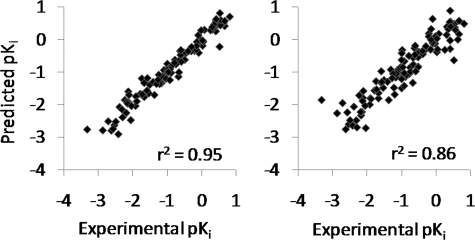
The calculated predictions of the models formed from the dataset with 112 compounds exhibit linear relationships with the experimental K_i values (Fig. 4). Predictions from the model with CoMSIA molecular descriptors are somewhat scattered, especially at high affinity, whereas the model with CoMFA molecular descriptors produces more linear pK_i predictions, especially for compounds with high affinity for the P2 adenosine transporter (Fig. 4). The r² values for the linear relationships are 0.95 for the model with CoMFA molecular descriptors and 0.86 for the model with CoMSIA molecular descriptors.

FIGURE 4.

Actual versus predicted results from PLS models employing CoMFA (left) and CoMSIA (right) molecular descriptors.

These models can be further evaluated through examination of the final contour maps. Although it is useful to analyze models as a whole to gain information about a possible pharmacophore, once a pharmacophore model is obtained, much more information can be gathered by evaluating the contour regions of individual compounds within the model. Because the model with CoMFA molecular descriptors is outperforming the model with CoMSIA molecular descriptors, the focus of this analysis will remain on the contours of the model with CoMFA molecular descriptors. As before, the steric contributions are displayed in yellow and green, and the electrostatic contributions are shown in red and blue.

The overall contour regions from the initial model have changed significantly with realignment and incorporation of all 112 compounds. These changes appear most dramatic when looking at individual compounds. In the initial models, each compound contributed roughly 2.8–6.3%. This was due to similar compounds being aligned by a common backbone scaffold and their being only 16–36 compounds in each dataset; 1 in 36 is ∼2.8%, and 1 in 16 is about 6.3%. This percent of contribution is much larger than the final model, where 1 in 112 compounds is roughly 0.89%. It is also important to note that a larger quantity of compounds with similar backbones will have a significant effect on the contribution. Hence, based on initial models, the compounds with the adenosine scaffold structure should contribute the most. There are 36 of these compounds. Those with the pentamidine and stilbamidine scaffolds are similar and align to one another well within the final model. There are 32 of these compounds, whereas there are 29 compounds related to furamidine.

From close observations of compound structure relationships in the form of contour maps, it is possible to determine where partial charge addition or subtraction to substituents could improve compound interactions with the P2 adenosine transporter. The evolutionary process by which this model calculates predictions can be viewed through the evaluation of contour regions and experimentally determined K_i values (Fig. 5). The K_i of 2-aminopyridine is 14 μm. When an amino group is added into the favorable steric and positive electrostatic contour regions to form 4,6-diaminopyrimidine, the K_i becomes 3.2 μm. Note that the amino group has a partial positive charge. This amino group addition thus results in improved affinity. When the additional groups, which reside in even more favorable contour regions, are added to the compound structure, the K_i value becomes even smaller. Adenine is an example of a compound with groups residing in favorable contour regions. This compound has a K_i of 0.30 μm. When a compound interacts with both positive and negative contour regions, the K_i increases; the K_i value for adenosine, for example, increases 3-fold relative to adenine as a result of the bulky ribose group. The evolutional process taken when using these potentials to design compounds for synthesis is quite similar to the progression shown in Fig. 5. It is important to make small changes and evaluate how the designed compound will fit within the steric and electrostatic potentials assigned by the model.

FIGURE 5.

Calculated three-dimensional molecular surfaces for analyses of compound structural relationships with P2 transporter inhibition. From left to right, the compounds shown above are 2-aminopyridine, 4,6-diaminopyrimidine, adenine, and adenosine. Colors are as in Fig. 2.

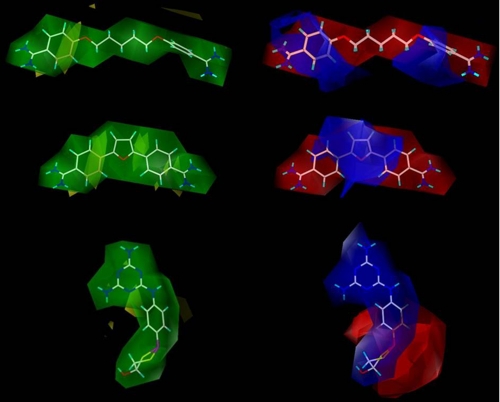
Other important compounds to evaluate with this model are the pentamidine-, furamidine-, and melarsoprol-like compounds (Fig. 6). Pentamidine, furamidine, and melarsoprol all have good affinity for the P2 transporter with respective K_i values of 0.37, 1.19, and 0.54 μm. Contour regions of pentamidine, furamidine, and melarsoprol are displayed in Fig. 6. These regions display several areas where some steric bulk and partial positive charge can be added to improve affinity for the P2 adenosine transporter. A loss of affinity will occur if bulky substituents interact with the unfavorable yellow contour regions and/or if positive charge interacts with the red contour regions.

FIGURE 6.

Three-dimensional molecular surfaces for pentamidine (top), furamidine (middle), and melarsoprol (bottom). Colors are as in Fig. 2.

With pentamidine, which is a very flexible compound, the final pharmacophore model yellow contours display most central atoms to be suitable for substituent addition; however, the area nearest the pharmacophore should not be modified. Melarsoprol is a more rigid structure, although rotation can occur throughout the compound. There can be rotation between the melamine ring and the phenyl and between the phenyl and the dithiarsolan ring. For this compound, the yellow contours reside near the melamine and the phenyl. This suggests that a loss of affinity may result from substituent addition to the atoms in these regions. Furamidine is a much more rigid and curved structure. For this structure, the yellow contours are much more abundant near the phenyls and yet away from the furan and the amidines. This is even clearer when the compound and its contour are viewed in three-dimensional space. The areas where yellow contours do not exist are optimum for substituent modification.

The red contours encompass both pentamidine and furamidine, whereas blue contours surround melarsoprol. The blue contours appear to be based on the partial charge distribution. For the diamidine compounds the partial charge distribution is strongly localized at the amidines. This appears beneficial for binding to the transporter; however, it is evident that more charge to an amidine location will not improve binding. Instead, a partial charge distribution that is shared within a ring structure appears to be more advantageous. This is seen in the melamine-like structure of melarsoprol. Findings suggest that additional charge, which is less localized, may be able to improve binding of diamidine compounds.

DISCUSSION

The efficacy of many drugs is determined to a large extent by the processes that govern their uptake into the cell or into the cellular compartment that is the site of action (7, 17–19). These processes obviously include transporters for water-soluble drugs but even rates of diffusion for lipophilic drugs. An example of the latter is chloroquine, which as a weak base diffuses across several membranes before it reaches the Plasmodium falciparum food vacuole where it is trapped by protonation and fatally inhibits heme polymerization (20, 21). Equally, efflux systems such as ATP-binding cassette transporters (22) and the P. falciparum CRT1 channel-like protein (23) have been implicated in resistance to drugs ranging from antibiotics and antiparasitics to antineoplastic drugs. As such, detailed insights into the processes that determine drug flux across the (plasma) membranes of target cells are vital for the rational optimization of drug activity and both the prevention and bypassing of drug resistance.

It is of pivotal importance that we gain insight into the molecular mechanisms by which transporters bind and thus select their substrates as this would allow us to construct models with predictive value, which would allow us to optimize substrate design. Although in silico screening of virtual libraries and predictions of substrate affinity are now possible for proteins with known or computable structure (24–26), this is not ordinarily possible for transporters as very few structures have been obtained, and the protein structures, with usually 10–12 transmembrane domains, are highly complex and extremely difficult to crystallize, although there have recently been some notable successes, mostly with prokaryotic membrane proteins (27–29). One approach is to use the few known transporter structures as scaffolds for other transporters, by a computational process called fold recognition or threading. We recently obtained a model for the T. brucei brucei nucleobase transporter NBT1 by this process and validated it by site-directed and random mutagenesis (30). The creation of a structural model of the closely related Leishmania donovani LdNT1.1 nucleoside transporter by ab initio calculation was also very recently reported (31). Although these approaches did produce approximate models for the overall structure of the transporters and identified key amino acid residues, they allow at best limited prediction of substrate selection, and only if the amino acids involved in binding have been separately identified. Thus, with the current technologies, it is exceedingly difficult to obtain the required functional insights with the protein structure as starting point.

A radically different approach was pioneered some time ago to study purine transport in T. brucei brucei by systematically altering the substrate and calculating inhibition constants, K_i, and from there binding energy ΔG⁰ (1, 17). This method was used to explain substrate preferences of purine and pyrimidine transporters in T. brucei brucei (32), Leishmania major (33, 34), Toxoplasma gondii (35), Leishmania mexicana (36), and the human NBT1 nucleobase transporter (14), human concentrative nucleoside transporters (37), and human equilibrative nucleoside transporters (38) with semi-quantitative models of substrate binding that did not require any structural or genetic information about the transport protein. However, this method still did not allow genuinely quantitative or three-dimensional predictions nor was it suitable for screening of virtual libraries.

In this study, we have adapted the method to address the above issues; energy-minimized three-dimensional structures of 112 compounds with experimentally obtained binding affinities for the TbAT1/P2 transporter were employed through the use of CoMFA and CoMSIA molecular descriptors for PLS model regression construction and analysis. The various molecules were preliminarily aligned by their common structural and chemical features, resulting in four datasets of compounds, Fig. 2, A–D, large enough for individual model formation and analysis. This was followed by optimized alignment of all 112 compounds using four molecular descriptor contour potentials, negative and positive steric and electrostatic, as a guide. This has generated an in silico computational model into which new molecules can be entered to arrive at a reliable estimate of binding energy. This constitutes a first computational approach to the design of novel ligands for the TbAT1/P2 transporter and allows for in silico evaluation of large numbers of known and novel compounds as substrates. The computational analysis was validated to be statistically significant using leave-one-out cross-validation and 10-fold cross-validation, as well as by other statistics and the internal predictability of this model, as displayed in Fig. 4.

The contour profiles of steric and electrostatic factors also allow fundamental insights into how various ligands interact with the transporter binding pocket. The P2 transporter, with its highly unusual substrate profile and involvement in drug transport and resistance (2–5, 11, 39), was chosen for this study to gain insight into how a transporter that is on the one hand completely selective for adenine and adenosine only (out of all nucleosides and nucleobases) can also bind molecules as diverse as isometamidium, melarsoprol, and furamidine with similar affinity. Previous studies (3, 11) already identified the “amidine” motif formed by R₁-N1=C6(R₂)-NH₂ of adenine as the main motif responsible for P2 binding, and it was further argued that the positive charge on N9 of adenine and adenosine, as well as the aromaticity of the purine, also makes important contributions to the high substrate affinity (3, 17).

The calculated substrate-transporter interaction contours for adenine and adenosine in Fig. 5 now allow us to evaluate these earlier conclusions against the advanced modeling approach employed in this study. Fig. 5 identifies four substrates that have a partial positive charge on the position of the amino group of 2-aminopyridine/adenine/adenosine as essential for optimal binding. Similarly, a partial negative charge is strongly favored at position 1, along with a positive charge at positions 8 and 9, whereas there is no clear electrostatic preference at positions 3 and 7 or most of the ribose moiety, except perhaps a preference for a positive charge at the 2′-position. Large substitutions are indicated as unfavorable in positions 1, 2, 8, and 2′, and at the 6-amino group of adenosine (Fig. 5, yellow indicators), but the position of the ribose group does not appear to be restricted with respect to further expansion/elongation, in line with the positioning and high affinity of the long diamidines.

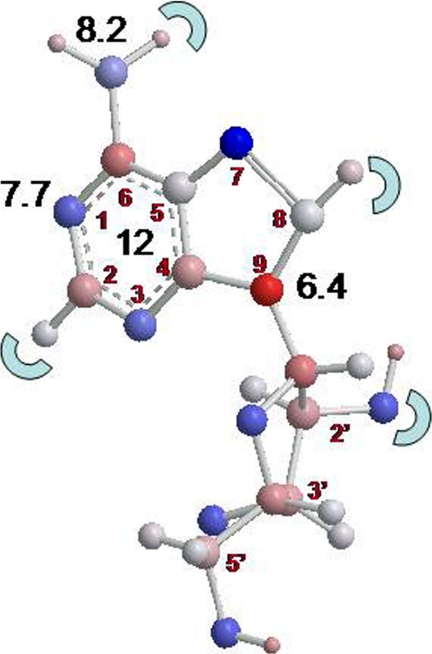
The above interpretation of the CoMFA and CoMSIA models is entirely consistent with the experimentally obtained ΔG⁰ values listed in supplemental Table 1. For instance the importance of the partial negative charge on position 1, presumably as hydrogen bond acceptor, is demonstrated by the reduced affinity of 1-deazaadenosine versus adenosine (δ(ΔG⁰) = 9.7 kJ/mol) and of 1-deazapurine versus purine (δ(ΔG⁰) = 5.7 kJ/mol). Similarly, the positive charge provided by the 6-position amine is quantified by comparison of purine riboside with adenosine (δ(ΔG⁰) = 7.3 kJ/mol), purine with adenine (δ(ΔG⁰) = 10.2 kJ/mol), and 6-chloropurine riboside with adenosine (δ(ΔG⁰) = 7.0 kJ/mol). As shown in Fig. 7, this gives estimates of contributions of 7.7 and 8.2 kJ/mol for the N1 and 6-amino groups, respectively. The loss of both these groups should thus result in a loss of binding energy of ∼16 kJ/mol, and this was demonstrated by comparing 2′-deoxyinosine with 2′-deoxyadenosine (δ(ΔG⁰) = 16.3 kJ/mol) and 1-deazapurine with adenine (δ(ΔG⁰) = 15.8 kJ/mol). The strong contribution from N9 likewise follows from comparing 9-deazaadenosine with adenosine and 4,6-diaminopyrimindine with 2-aminopyridine (δ(ΔG⁰) = 6.4 and 5.7 kJ/mol, respectively). The relative unimportance of positions N3 and N7 was demonstrated using 3-deazaadenosine and 7-deazaadenosine, respectively, as cataloged in supplemental Table 2, which also lists relative affinities for compounds with substitutions at positions 2 and 8.

FIGURE 7.

Model of adenosine, giving estimates of the contributions to the total binding energy of 34 kJ/mol in the black numbers, with the red numbers indicating the position on the purine or ribose rings. The half-circles indicate positions where substitutions reduced the adenosine binding affinity. The aromatic rings are estimated to contribute ∼12 kJ/mol to the binding energy, although this could not be verified directly, as a nonaromatic adenosine analog would have a completely different three-dimensional structure. However, comparisons between aromatic diamidines and nonaromatic diamidines (supplemental Table 2) are consistent with this estimate.

Finally, a substantial contribution to binding is made through interactions between the aromatic purine or benzamidine moieties, and amino acids in the transporter binding pocket, through π-π stacking with aromatic residues, cation-π bonding, or amino-aromatic interactions (40). Although this cannot be directly demonstrated by the use of “nonaromatic purines,” which would have a completely different three-dimensional structure, uniquely for P2 this can be shown and quantified comparing aromatic and nonaromatic diamidines (supplemental Table 2). The diagram in Fig. 7 summarizes these data in the form of an interaction diagram between the P2 transporter and adenosine. This figure, gained from experimental data and using a previously validated approach (1, 17), is in close agreement with data presented in Fig. 5 based on the predictive PLS regression model. It is important, however, to be clear that both modeling approaches (Figs. 5 and 7) are predictive with respect to substrate binding rather than translocation, i.e. do not predict transport efficiency for any individual substrate. This limitation is not inherent to the computational approach, rather it is the result of using K_i values (transport inhibition through extracellular binding) instead of Michaelis-Menten constants (K_m and V_max values, determined from measurement of transport) as input for the models. A similar approach as followed here could predict transport, but it would have required radiolabeled analogs of all the compounds used in the study, and this was not feasible. We also would not wish to suggest that efficient uptake by a pathogen is sufficient to ensure efficacy of a potential therapeutic agent, as this requires optimal interaction with the intended intracellular target as well. In summary, we have developed and validated a novel computational approach to analyze, explain, and predict the interactions between transporters and their substrates that does not require prior knowledge of transporter structure or indeed primary sequence.