Factorial Invariance and The Specification of Second-Order Latent Growth Models

Abstract

Latent growth modeling has been a topic of intense interest during the past two decades. Most theoretical and applied work has employed first-order growth models, in which a single manifest variable serves as indicator of trait level at each time of measurement. In the current paper, we concentrate on issues regarding second-order growth models, which have multiple indicators at each time of measurement. With multiple indicators, tests of factorial invariance of parameters across times of measurement can be tested. We conduct such tests using two sets of data, which differ in the extent to which factorial invariance holds, and evaluate longitudinal confirmatory factor, latent growth curve, and latent difference score models. We demonstrate that, if factorial invariance fails to hold, choice of indicator used to identify the latent variable can have substantial influences on the characterization of patterns of growth, strong enough to alter conclusions about growth. We also discuss matters related to the scaling of growth factors and conclude with recommendations for practice and for future research.

The use of Latent Growth Models (LGMs) is a typical approach in longitudinal studies for investigating change across time in a latent construct that is measured by a set of manifest variables. Often, each manifest variable is constructed as the sum or average of a set of items collected at a particular point in time to create a single composite or index variable for that time of measurement, and the resulting manifest variables are used in the specification of a first-order latent growth model. In this method, the model is fit directly to the vector of means and the matrix of covariances among the newly created manifest scores or to the matrix of raw scores on manifest variables, which consist of one score per person at each measurement occasion. Such an approach, however, does not capitalize on the benefits inherent in modeling the relations between the multiple indicators comprising the manifest variable and the manifest composite variable itself (Sayer & Cumsille, 2001). In addition to ignoring important information about the psychometric properties of the indicators, this procedure incorporates specific variance and measurement errors of the indicators into the manifest composite score and assumes that the same latent construct is measured at all times.

A more appropriate way to model change when multiple indicators are available at each time of measurement is a second-order growth model. In this approach, the observed variables are used as indicators of a construct or latent variable (i.e., first-order factor) at each measurement occasion. Then, a growth model is used to structure the covariation among these first-order latent factors. Thus, change is modeled through the repeated latent factors, rather than through the manifest variables.

Latent Growth Curve Models

First-order Latent Growth Curve Model

Suppose the presence of a set of manifest indicators X, W, …, and Y, and the sum of these manifest indicators is a manifest variable V, which is computed as the sum of variables X through Y, or V = X + W + … + Y. A first-order latent growth curve model, or 1LGC model, could then be specified as:

$$V_{(t)n}=f_{0n}+{\mathrm{\beta }}_{(t)}{f}_{\mathrm{s}n}+e_{(t)n},$$ (1)

where V represents the score on the manifest variable for person n at time t, f_0n and f_sn are the intercept and slope latent variable scores, respectively, for person n, β represents the set of basis coefficients that determine the shape of the curve, and e represents residual term for person n on the manifest variable at time t unexplained by the intercept and slope latent variables.

Because the model is simple to specify, virtually all applications of growth curve modeling in the field of psychology have utilized the 1LGC model. The ease and directness of fitting the model are important strengths of this approach. However, a most important shortcoming of the 1LGC model is the inability to test whether the same latent variable is assessed at each time of measurement. Because only a single indicator is available at each time of measurement, standard approaches to investigating factorial invariance cannot be pursued, so researchers must assume, and cannot test, that the manifest variable reflects variation on an invariant latent dimension at each time of measurement.

Second-order Latent Growth Curve Model

A 2^nd-order Latent Growth Curve (2LGC) model is an approach to modeling change at the latent level over time. This modeling procedure was proposed by McArdle (1988) as a “curve of factors (CUFF) model” as well as by Tisak and Meredith (1990) as a “latent variable longitudinal curve model,” and is related to the invariant factors models of McDonald (1985). This approach has also been used by Duncan and Duncan (Duncan et al., 1999) and by McArdle and colleagues (McArdle & Woodcock, 1997; McArdle et al., 2002).

The 2LGC model is a multivariate extension of the first-order LGM. One major advantage of this approach is the opportunity for the researcher to investigate the factorial invariance of model parameters across times of measurement. If factorial invariance constraints hold, then the investigator has greater confidence that the same latent dimension is assessed or measured at each time of measurement. Having demonstrated factorial invariance one can then model the growth in the factors through an intercept and a slope. For example, for a system of three variables, X, Y, and W, this model can be written as

$$\begin{array}{c}{X}_{(t)n}={\mathrm{\tau }}_{\mathrm{x}}+{\mathrm{\lambda }}_{\mathrm{x}}{f}_{(t)n}+e_{x(t)n},\hfill \\ W_{(t)n}={\mathrm{\tau }}_{\mathrm{w}}+{\mathrm{\lambda }}_{\mathrm{w}}{f}_{(t)n}+e_{w(t)n},\text{and}\hfill \\ Y_{(t)n}={\mathrm{\tau }}_{\mathrm{y}}+{\mathrm{\lambda }}_{\mathrm{y}}{f}_{(t)n}+e_{y(t)n},\text{with}\hfill \\ f_{(t)n}=f_{0n}+{\mathrm{\beta }}_{(t)}{f}_{\mathrm{s}n}+z_{(t)n},\hfill \end{array}$$ (2)

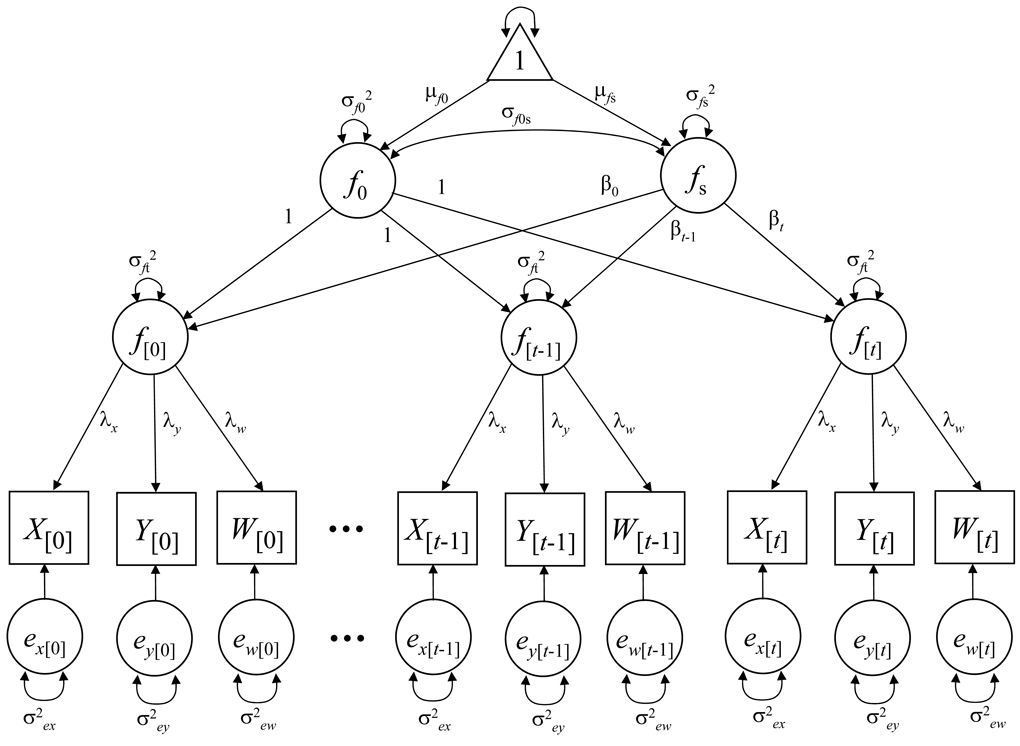
where X, W, and Y, represent manifest variables for person n at a time t, τ represents the intercept, λ represents the factor loading, or linear slope relating the factor f to the indicator, e represents the unique factor score, f_0n and f_s are the intercept and slope of the factor f for person n, respectively, β represents the set of basis coefficients that determine the shape of the curve, and z_(t) represents a disturbance term for the factor f at time t. Figure 1 is a path diagram of this model. This figure represents the three variables, X, Y, and W measured over t occasions. For each occasion, the three variables comprise a latent factor f_t. The growth in such factors is then modeled through a second-order level and slope (f₀ and f_s).

Figure 1.

Path diagram of a second-order latent growth model. Manifest variables are represented by squares. Latent variables are represented by circles. The triangle represents a constant to estimate the means and intercepts. Although not depicted in this figure, the intercepts of the manifest variables are estimated. Also not depicted in this figure are the covariances among same manifest variables at adjacent time points. Factor loadings and unique variances are represented as invariant over time.

Although second-order growth modeling has been available for almost twenty years, it has not been used to any great extent. Therefore, the advantages of such models over the first-order latent growth models have remained unfamiliar to many researchers. Some recent papers have illustrated the 2LGC approach and discussed a number of related methodological issues (e.g., Hancock, Kuo, & Lawrence, 2001; Oort, 2001; Sayer & Cumsille, 2001; Stoel, van den Wittenboer, & Hox, 2004), but much remains to be done to understand all aspects of the fitting and the interpretation of these models.

The 2LGC model has important advantages over the first-order model. First, it allows separating observed score variance into reliable construct variance, reliable specific variance, and random occasion-specific, or error, variance. In a first-order model, the unique variance associated with each indicator is confounded with time-specific variance (i.e., variance dependent on time), but in the second-order model the error score can be interpreted as unique variance or measurement uniqueness in the factor-analytic sense (i.e., a mixture of non-random specific item variance that is not attributable to the common factor and random measurement error; Sayer & Cumsille, 2001). Because measurement error is removed from the construct over time, the regression coefficients representing relations among the growth parameters and other covariates should be disattenuated and the standard errors smaller, which allows for more precise estimates of the relation between change and its correlates. In sum, a 2LGC model has the advantage of creating a theoretically error-free construct for growth modeling rather than using error-laden manifest variables or composites. Second, because the measurement structure of the indicators is modeled directly, the second-order model can provide information about the characteristics of the individual manifest variables. Third, by comparing the goodness of fit of nested models, a second-order model allows for testing different kinds of factorial invariance of the composites over time. This last aspect is one of the most important advantages of a second-order latent growth model approach when investigating change in observed indicators that compose an underlying latent construct. We examine it in more detail in following sections.

Latent Difference Score Models

First-order Latent Difference Score Model

A newer model for longitudinal data, proposed first by McArdle (2001; McArdle & Hamagami, 2001), is a first-order latent difference score (1LDS) model. The 1LDS model begins with the conception of the observed score Y for person n at time t, or Y_(t)n, as a combination of, or sum of, true status at time n plus error at time n, or Y_(t)n = y_(t)n + e_(t)n. Then, the difference in true status between two adjacent times of measurement can be written as Δy_(t)n = y_(t)n – y_(t−1)n. Once the difference score is defined in this fashion, then the difference scores can be modeled as:

$$\mathrm{\Delta }{y}_{(t)n}=\alpha ·f_{sn}+\beta ·y_{(t-1)n}+z_{\mathrm{\Delta }(t)n},$$ (3)

where Δy represents the change in true status on variable y at time t, α is a parameter that expresses the influence of the factor slope f_s on the changes, β is a coefficient representing the effect of true status on variable y at the previous state on the change, and z_Δ(t)n is the residual of the latent changes.

Second-order Latent Difference Score Model

The 2^nd-order Latent Difference Score (2LDS) model is a newer – and less widely used – approach to model change in latent factors over time than the 2LGC model. This extension was proposed by McArdle (2001; McArdle & Hamagami, 2001) and has been used by Ferrer and McArdle in several investigations (2003, 2004; Ferrer et al., 2006).

As it was the case with the 2LGC, the 2LDS model is a multivariate extension of the 1LDS. It also presents advantages over the 1LDS, especially related to factorial invariance, and with regard to the possibility of examining dynamic evidence of a common factor underlying the changes in the manifest variables. Similar to the 2LGC model, for a system of three variables, X, Y, and W, the 2LDS model can be written as

$$\begin{array}{c}{X}_{(t)n}={\mathrm{\tau }}_{\mathrm{x}}+{\mathrm{\lambda }}_{\mathrm{x}}{f}_{(t)n}+e_{x(t)n},\hfill \\ Y_{(t)n}={\mathrm{\tau }}_{\mathrm{y}}+{\mathrm{\lambda }}_{\mathrm{y}}{f}_{(t)n}+e_{y(t)n},\text{and}\hfill \\ W_{(t)n}={\mathrm{\tau }}_{\mathrm{w}}+{\mathrm{\lambda }}_{\mathrm{w}}{f}_{(t)n}+e_{w(t)n},\text{with}\hfill \\ \mathrm{\Delta }{f}_{(t)n}=\alpha ·f_{sn}+\beta ·f_{(t-1)n}+z_{\mathrm{\Delta }(t)n},\text{and}\hfill \end{array}$$ (4)

where Δf represents change in factor f at time t, α is a parameter that expresses the influence of the factor slope f_s on change, β is a coefficient representing the effect of the factor at the previous state on the change, and z_Δ(t)n is the residual of latent change. Thus, the trajectory of the latent factor f at any given time t can be written as a function of its initial state plus all the changes accumulated up to time t, as

$$f_{(t)n}=f_{\mathit{0}n}+({\displaystyle \sum _{i=1}^t\mathrm{\Delta }{f}_{(i)n}}).$$ (5)

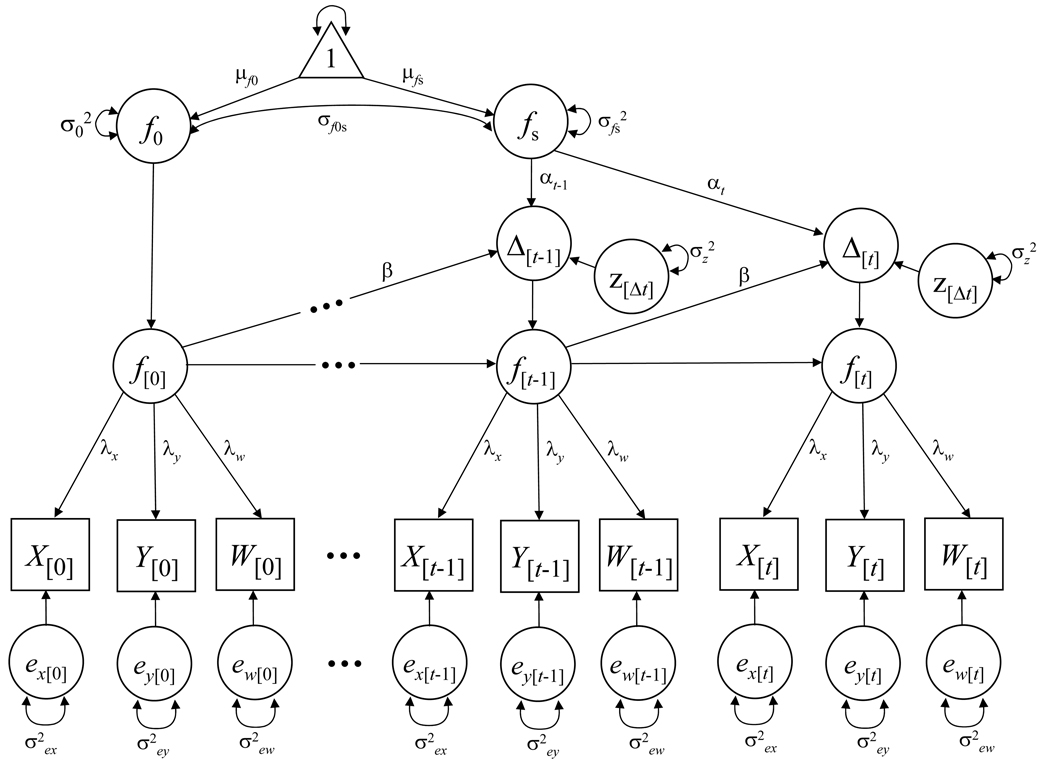
Figure 2 is a path diagram of the 2LDS model. As was the case for the 2LGC model, this figure represents three variables, X, Y, and W measured over t occasions. For each occasion, the three variables comprise a latent factor f. Further, for each repeated assessment, a new latent variable Δ_t is created that represents a latent change between the two occasions. The growth in the factors over time can now be modeled through these latent changes. The specification and identification constraints for this model are explained below.

Figure 2.

Path diagram of a second-order latent difference score model. Manifest variables are represented by squares. Latent variables are represented by circles. The triangle represents a constant to estimate the means and intercepts. Although not depicted in this figure, the intercepts of the manifest variables are estimated. Also not depicted in this figure are the covariances among same manifest variables at adjacent time points. Factor loadings and unique variances are represented as invariant over time.

Measurement Invariance When Investigating Change in Multiple Manifest Indicators Of a Latent Construct Across Time

Longitudinal measurement invariance, or measurement invariance across time, refers to the situation in which the numerical values across measurement occasions are obtained on the same measurement scale (Drasgow, 1987; Meredith, 1993). Measurement invariance ensures an equal definition of a latent construct over time; that is, each indicator with the same surface characteristics (i.e., identical scaling and wording) must relate to the underlying construct in the same fashion over time (Hancock et al., 2001; Sayer & Cumsille, 2001).

The concept of factorial invariance (Meredith, 1964, 1993) is often used to investigate measurement invariance in reference to the common factor model (Stoel et al., 2004). Building on prior work by Horn, McArdle, and Mason (1983) and Meredith (1993), Widaman and Reise (1997) distinguished between nonmetric (configural) and metric factorial invariance, with metric factorial invariance composed of three hierarchical levels: weak, strong, and strict factorial invariance. Configural invariance means that the same indicators of the latent construct are specified at each occasion, regardless of the numerical values of the parameter estimates. Weak factorial invariance requires the factor loading of each indicator to be invariant (i.e., to take the same numerical value) over time. Strong factorial invariance adds to weak factorial invariance the requirement that the measurement intercept for each indicator is invariant across time. Strict factorial invariance requires, in addition to the factor loading and intercept, that the unique variance for each manifest variable be equal over time. Some researchers (e.g., Sayer & Cumsille, 2001) have argued that strict factorial invariance is unlikely to hold due to the fact that heterogeneous variance across time is often observed when modeling change and because the random error component of uniqueness may vary in magnitude with the level of the manifest variable. In addition to the preceding distinctions, the terms “weak factorial invariance,” “strong factorial invariance,” and “strict factorial invariance” are used in reference to models in which all relevant parameters exhibit invariance. But, if the qualifier “partial” is used, this indicates that some of the relevant parameters of the model are not invariant. Thus, strong factorial invariance implies that all factor loadings and intercepts are invariant, whereas partial strong factorial invariance would refer to a model in which at least one of the factor loadings or intercepts failed to exhibit metric invariance.

In growth modeling, it is important to ensure that change happens at the level of the construct or latent variable rather than at the level of the observed variables used to measure such a construct. If only a single composite is used as the indicator of the construct at each time of measurement, as occurs when first-order models are specified, a researcher must assume that the manifest variables satisfy the requirements of measurement invariance because invariance constraints cannot be tested or evaluated. Because virtually all published studies employing any kind of growth modeling have used first-order models, this is potentially important, given the inability to verify measurement invariance of the indicators. When the same multiple indicators are used to measure change over time, researchers often assume that indicators display measurement invariance, but this assumption is seldom tested in practice. Modeling multiple indicators in a longitudinal setting requires a test of factorial invariance to ensure that the same latent variable is assessed at each time of measurement, and this can only be achieved by means of a second-order model.

Furthermore, several important problems arise if factorial invariance of manifest variables fails to hold. First, if factor loadings and intercepts vary freely, there is no guarantee that the same latent construct is being measured over time. Thus, any changes across time might represent shifts in the nature of the construct over time rather than quantitative growth in the construct. Second, under partial factorial invariance, selection of a different reference indicator for the scaling of the latent variable may change substantially model fit and growth model parameter estimates. This scaling choice, however, does not occur under full strong or strict factorial invariance, if other model assumptions are satisfied (Stoel et al., 2004). Full measurement invariance may, therefore, be a necessary condition for a valid interpretation of change in latent constructs with multiple indicators for models that scale the latent variable structure using reference indicators.

Issues related to factorial invariance, on the one hand, and to latent growth modeling, on the other, have been widely studied but few attempts have been made to integrate both. In this paper, we illustrate both by dealing with the implications of factorial invariance for specification of latent growth models and for interpretation of results obtained in modeling change over time. We use longitudinal confirmatory factor analysis models and 2LGC and 2LDS models to investigate change across time in a set of manifest indicators that compose an underlying latent construct when the assumption of factorial invariance is met and when it is violated. We use two samples to evaluate parameter estimates and model fit under different conditions of invariance and to investigate the consequences of violating invariance assumptions on the modeling of change across time.

Method

Participants

Two data sets are used for the analyses in this study. The first data set is from the “Motivation in High School Project” (MHS), a study initiated by E. Ferrer and aimed at examining determinants of motivation among high school students. In this project, adolescent students were contacted as they entered high school and followed through their first semester. The sample comprised 261 volunteer participants (149 males and 112 females) ranging from 14 to 17 years of age (M = 14.4, SD = .57). The participants described themselves as White (68.8%), African-American (18.8%), Asian (1.3%), Hispanic (2.7%), Native American (0.4%), or Other (0.7%). At four occasions (during the first week in class and at succeeding six-week intervals) students completed a questionnaire during physical education classes. The questionnaire covered a wide array of measures to assess the students’ self-perceptions and motivation in their classes. Of the 261 participants, 144 completed all the measures at four occasions. Students with complete data reported slightly higher levels of motivation at the first and fourth occasions than students with incomplete data did. No other differences were detectable.

The second data set is described by Sayer and Cumsille (2001) to illustrate second-order growth modeling. These data were originally from the Adolescent Alcohol Prevention Trial (AAPT), a longitudinal investigation of children enrolled in school-based prevention programs (see Hansen & Graham, 1991). The AAPT study was designed to assess the relative impact of four different school-based alcohol-prevention curricula for young adolescents in Southern California. The data set included four panels of data, each one corresponding to a sample of children followed for several years. Following Sayer and Cumsille (2001), we used a subsample drawn from panel 1, which followed children from fifth through 10th grades (except for eighth grade). This sample included 610 children who were measured for the first time in 1986–1987 and then assessed annually for six years (except for the fourth year of the study). The distribution of boys and girls was approximately equal at each time of measurement. The ethnic distribution of the sample in fifth grade was approximately 51% White, 28% Latino, 9% Asian, and 4% African American, and it remained relatively unchanged over time.

Measures

The variables from the first (MHS) data set represent perceived competence in the physical domain. Perceived physical competence was measured using the athletic competence subscale of the Self-Perception Profile for Adolescents (Harter, 1988). This scale contains five items and measures the adolescent’s perceived ability in physical activities. One sample item is: “Some teenagers do very well at all kinds of physical education activities BUT Other teenagers don’t feel that they are very good when it comes to physical education”. This scale uses a structured alternative response format with scores ranging from 1 (low) to 4 (high). Perceived competence in this study was computed by averaging the scores of four of the five original items. One of the five items was deleted to reduce the overall number of items in the questionnaire and ease the burden of responding. This decision was implemented after pilot data and previous work by the authors with this scale, ensuring that the deletion of one item did not distort the properties of the original scale. The alpha reliabilities for this variable were computed as .83, .83, .86, and .86, for the four occasions, respectively.

The children included in the second (AAPT) sample were administered a survey containing questions on alcohol beliefs at Grades 5, 6, 7, 9 and 10. Positive alcohol expectancy was assessed with three items tapping the social consequences of drinking alcohol. They include “Does drinking alcohol make it easier to be part of a group?” (GROUP), “Does drinking alcohol make parties more fun?” (PARTIES), and “Does drinking make it easier to have a good time with friends?” (GOODTIME). Adolescents had to indicate the extent of their agreement with each item using a 4-point Likert Format, with anchors at 1 (strongly disagree) and 4 (strongly agree). Sayer and Willett (1998) had previously summed these items within grades using principal-components analysis to form a composite score. Thus, positive alcohol expectancy is represented as a linear composite of the three expectancy items at each occasion of measurement.

Tables 1a and 1b list the means, standard deviations, and correlations for the composite scores from the two samples. Apparent from these tables is the larger variability as well as correlations among the scores in the MHS sample. In addition, whereas for the MHS sample there are approximately equal increments in the scores across all the occasions, this is not true for the AAPT sample. Here, the unequal increment from the third to fourth occasion may be due to the unequal intervals in the data collection (grades 5, 6, 7, 9, and 10) and to the transition from elementary to junior high and then to high school.

Table 1.

Table 1a Descriptive Statistics for MHS Sample (N = 261)
	PC[t1]	PC[t2]	PC[t3]	PC[t4]
Means	2.756	2.850	2.914	2.946
SD	.935	.873	.897	.899
PC[t1]	1.000
PC[t2]	.764	1.000
PC[t3]	.766	.783	1.000
PC[t4]	.748	.699	.834	1.000

Table 1b Descriptive Statistics for AAPT Sample (N = 610)
	EXP[t1]	EXP[t2]	EXP[t3]	EXP[t4]	EXP [t5]
Means	1.217	1.221	1.304	1.638	1.747
SD	.454	.587	.569	.761	.761
EXP[t1]	1.000
EXP[t2]	.256	1.000
EXP[t3]	.106	.345	1.000
EXP[t4]	.107	.195	.296	1.000
EXP[t5]	.146	.132	.191	.545	1.000

Note. PC = perceived competence. t = measurement occasion.

Note. EXP = positive alcohol expectancy. t = measurement occasion.

Analytic Models

We considered two sets of structural models for the changes over time and applied them to the MHS and AAPT samples data (see Table 2). The first set of models included longitudinal confirmatory factor analysis models that specified a relation between each indicator and its underlying construct, with the constructs allowed to freely covary among themselves. Our aim in these analyses was to examine the factor structure at each measurement occasion. The second set of models included second-order latent growth models and the aim was to structure the covariation among the constructs through second-order growth factors (i.e., level and slope).

Table 2.

Description of Analytic Models

Model	Description
CFA1	Initial confirmatory factor analysis
CFA2a	Adding unique factor covariances among adjacent times
CFA2b	CFA2 (reference indicator = item2)
CFA2c	CFA2 (reference indicator = item3)
CFA2d	CFA2 (reference indicator = item4)
CFA3	Weak factorial invariance (λ=)
CFA4	Strong factorial invariance (λ= + τ=)
CFA5	Strict factorial invariance (λ= + τ= + Θ=)
CFA6	Strict factorial invariance (λ= + τ= + Θ=, and covariances of unique factors)
2LGC2a	2nd-order growth model (based on CFA2)
2LGC2b	2LGC1 (reference indicator = item2)
2LGC2c	2LGC1 (reference indicator = item3)
2LGC2d	2LGC1 (reference indicator = item4)
2LGC3	2LGC1 with weak factorial invariance (λ=)
2LGC4	Strong factorial invariance (λ= + τ=)
2LGC5	Strict factorial invariance (λ= + τ= + Θ=)
2LGC6	Strict factorial invariance (λ= + τ= + Θ=, and covariances of unique factors)

In the first set of analyses, we began with a minimally restricted longitudinal confirmatory factor analysis model (CFA₁) in which the first item was used as reference indicator at each time of measurement (i.e., its factor loading was fixed to unity) and continued with a similar model in which we added covariances between unique factors of the same item at adjacent points (CFA_2a). In the next three models, we altered the item used to set the metric of the factor by fixing its factor loading to unity (CFA_2b, CFA_2c, CFA_2d, when using the second, third, and fourth item, respectively). Because the AAPT data set had only three items, only three CFA models in this series (CFA_2a, CFA_2b, CFA_2c) were possible. The next model (CFA₃) was a test of weak factorial invariance and constrained the factor loadings to be invariant across time. The next model (CFA₄) was a test of strong factorial invariance and added constraints on the intercepts by fixing them to be invariant over time. The last two models tested strict factorial invariance by setting the unique variances to be invariant over time (CFA₅) and then additionally by constraining to invariance the first-order covariances between unique variances of similar items (CFA₆).

In the second set of analyses, we followed a similar logic. We started with a second-order latent growth curve model (2LGC_2a) based on CFA_2a (i.e., structuring the covariances among the factors through a level and slope). To identify this model and scale the latent variables, we set the factor loading and intercept of a manifest variable to unity and zero, respectively. As was the case for the CFA models, in the next three models (2LGC_2b, 2LGC_2c, and 2LGC_2d) we changed the reference indicator to scale the latent factor; again, the AAPT data had only three of these four models because only three manifest indicators were available. The final four models in the series (2LGC₃, 2LGC₄, 2LGC_5, and 2LGC₆) were specified to test factorial invariance following the same steps as before. To be consistent with Sayer and Cumsille’s analyses (2001) with the AAPT data, we specified two slope latent variables in addition to the level latent variable. The first slope latent variable was a linear slope across the entire range of grades that was centered at grade 7; the second slope latent variable was the change in the linear slope that occurred after grade 7. Therefore, the first slope latent variable had fixed coefficients of −2, −1, 0, 2, and 3 for grades 5, 6, 7, 9, and 10, respectively, and the second slope latent variable had fixed coefficients of 0, 0, 0, 2, and 3 for the preceding grades, respectively. We also fitted a third set of 2^nd-order LDS models with specification and order similar than those of the 2LGC models.

As discussed above, we expected the same estimates and overall model fit to emerge when changing the reference indicator to scale the latent variable structure in the longitudinal CFA models regardless of any measurement invariance assumption. In the 2^nd-order growth models, however, we hypothesized that the choice of reference indicator could lead to differences in both model fit and parameter estimates when measurement invariance was not met. To illustrate this issue we use one data set with construct stable measurement properties over time (MHS) and another sample for which measurement invariance is violated (AAPT).

Results

All analyses were conducted using the Mplus program (Muthén & Muthén, 2005). In testing each of the hypothesized models, goodness of fit was evaluated using the χ² statistic, the root mean square error of approximation (RMSEA; Browne & Cudeck, 1993), the comparative fit index (CFI; Bentler, 1990), the Tucker-Lewis index (TLI; Tucker & Lewis, 1973), and the Bayesian Information Criterion (BIC; Schwarz, 1978).

2^nd-order Latent Growth Curve Models

Information about fit from all tested models is reported in Tables 3a and 3b for the MHS and AAPT samples, respectively. For the MHS sample, the first model (CFA₁), yielded a good fit to these data. In the second model (CFA_2a), freeing the lag-1 covariances among unique factors (i.e., 12 parameters) led to a significant improvement in fit (Δχ²/Δdf = 67/12, p < .001). The model fit of the next three models (CFA_2b, CFA_2c, and CFA_2d) remained exactly the same, indicating that changing the reference indicator to scale the latent variable had no effect on model fit. The sixth model (CFA₃) restricted the factor loadings to be invariant over time; and this led to a model that was more restricted by nine degrees of freedom, but these restrictions did not worsen the fit significantly (Δχ²/Δdf = 13/9, p > .05). The seventh model (CFA₄) restricted the intercepts to invariance over time also leading to an additional nine restrictions; once again, model fit was not altered significantly (Δχ²/Δdf = 11/9, p > .05). The results from these two models indicate that weak and strong factorial invariance are both met in these data. Models CFA₅ and CFA₆ imposed additional constraints consistent with strict factorial invariance, and the results indicated decreases in fit according to a chi-square test (Δχ²/Δdf = 57/12, p < .001 and Δχ²/Δdf = 26/8, p < .001), but improvements in fit according to the BIC. These two models show that strict factorial invariance is a restrictive hypothesis that is possibly tenable in this sample.

Table 3.

Table 3a Goodness-of-fit Indices of the Models (MHS Sample)
Model	χ2	df	RMSEA	(90% CI)	CFI	TLI	BIC	Δχ2 / Δdf
CFA1	234	98	.07	(.06 - .08)	.94	.92	6897	---
CFA2a	167	86	.06	(.05 - .07)	.96	.95	6897	67 / 12
CFA2b	167	86	.06	(.05 - .07)	.96	.95	6897	---
CFA2c	167	86	.06	(.05 - .07)	.96	.95	6897	---
CFA2d	167	86	.06	(.05 - .07)	.96	.95	6897	---
CFA3	180	95	.06	(.05 - .07)	.96	.95	6859	13 / 9
CFA4	191	104	.06	(.04 - .07)	.96	.95	6821	11 / 9
CFA5	248	116	.07	(.06 - .08)	.94	.94	6811	57 / 12
CFA6	274	124	.07	(.06 - .08)	.93	.93	6792	26 / 8
2LGC2a	182	91	.06	(.05 - .07)	.96	.94	6884	---
2LGC2b	185	91	.06	(.05 - .08)	.96	.94	6887	---
2LGC2c	181	91	.06	(.05 - .07)	.96	.94	6882	---
2LGC2d	183	91	.06	(.05 - .08)	.96	.94	6884	---
2LGC3	192	100	.06	(.05 - .07)	.96	.95	6844	10 / 9
2LGC4	204	109	.06	(.05 - .07)	.96	.95	6806	12 / 9
2LGC5	261	121	.07	(.06 - .08)	.93	.94	6796	57 / 12
2LGC6	286	129	.07	(.06 - .08)	.93	.93	6777	25 / 8

Table 3b Goodness-of-fit Indices of the Models (AAPT Sample)
Model	χ2	df	RMSEA	(90% CI)	CFI	TLI	BIC	Δχ2 / Δdf
CFA1	210	80	.05	(.04 - .06)	.95	.93	18427	---
CFA2a	117	68	.03	(.02 - .04)	.98	.97	18411	93 / 12
CFA2b	117	68	.03	(.02 - .04)	.98	.97	18411	---
CFA2c	117	68	.03	(.02 - .04)	.98	.97	18411	---
CFA3	187	76	.05	(.04 - .06)	.95	.94	18430	70 / 8
CFA4	245	84	.06	(.05 - .06)	.93	.92	18436	58 / 8
CFA5	461	96	.08	(.07 - .09)	.85	.84	18575	216 / 12
CFA6	508	105	.08	(.07 - .09)	.83	.82	18571	47 / 9
2LGC2a	138	74	.04	(.03 - .05)	.97	.96	18393	---
2LGC2b	126	74	.03	(.02 - .04)	.98	.97	18381	12 / 0
2LGC2c	138	74	.04	(.03 - .05)	.97	.96	18394	12 / 0
2LGC3	209	82	.05	(.04 - .06)	.95	.93	18414	71 / 8
2LGC4	255	90	.05	(.04 - .06)	.93	.92	18408	46 / 8
2LGC5	472	102	.08	(.07 - .09)	.85	.84	18548	217 / 12
2LGC6	518	110	.08	(.07 - .09)	.83	.84	18543	46 / 8

The results from the 2LGC models reveal a similar pattern. The first model (2LGC_2a) fit the data well. The next three models (2LGC_2b, 2LGC_2c, and 2LGC_2d) changed the reference indicator to scale the latent variable. Contrasting with results with the preceding CFA models, these four 2LGC models – which differed only in choice of which item was the lead indicator (with loading fixed at unity) – did not have identical fit to the data, although the variations across models were quite small and therefore did not have any substantive consequences for model fit. The results obtained in the fifth and sixth models (2LGC₃ and 2LGC₄) indicated that both factor loadings and intercepts are invariant over time (Δχ²/Δdf = 10/9, p > .05 and Δχ²/Δdf = 12/9, p > .05, respectively), thus satisfying both weak and strong factorial invariance. As was the case with the CFA models, the last two 2LGC models (2LGC₅ and 2LGC₆) imposed additional constraints on the unique variances and first-order unique covariances. Each of these models resulted in a substantial decrease in fit according to a chi-square test (Δχ²/Δdf = 57/12, p < .001 and Δχ²/Δdf = 25/8, p < .001, respectively), but also improvements in fit according to the BIC. Although not shown in Table 3a we fitted a series of models based on strong factorial invariance (2LGC₄) but changing the reference indicator. These models yielded identical fit indices.

Table 3b reports the fit of all the models fit to the AAPT sample. For this sample, factorial invariance fails to hold at any level. That is, a model imposing restrictions over time in either the factor loadings, intercepts, or unique variances and covariances (CFA_3–6) results in a significant worsening of fit (Δχ²/Δdf = 70/8, 58/8, 216/12, and 47/9, p < .001 for all models). For the second set of analysis, the important information refers to the changes in fit as a function of the reference indicator used to scale the latent variables. Models 2LGC_2a and 2LGC_2c yielded the exact same fit but model 2LGC_2b yielded a better fit, with the same number of parameter estimates and degrees of freedom. As was the case for the CFA models, factorial invariance does not hold at any level for the 2LGC models (Δχ²/Δdf = 71/8, 46/8, 217/12, and 46/8, p < .001 for all models, for loadings, intercepts, unique variances, and unique covariances, respectively).

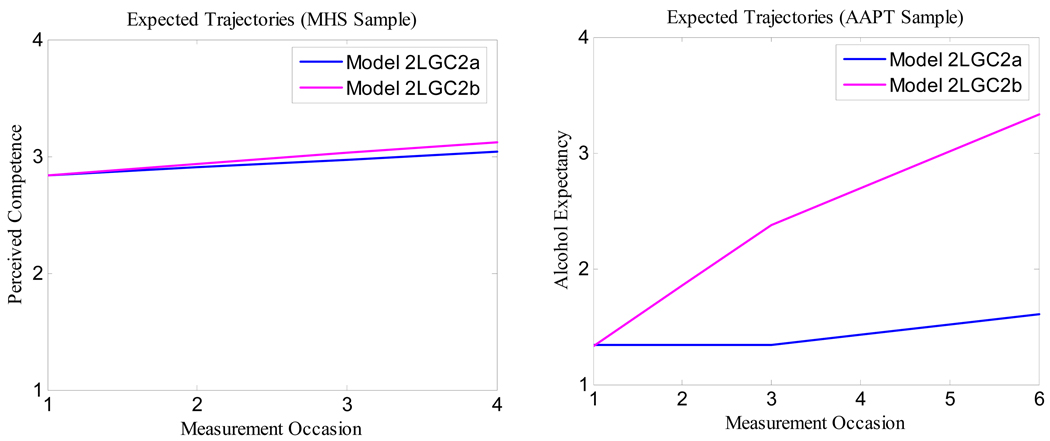
To illustrate the consequences of failing to meet invariance assumptions on the parameter estimates of second-order latent growth curve models, we examined such estimates in 2LGC_2a and 2LGC_2b models for both samples. As explained before, the only difference between the two models was the indicator used as reference to scale the latent variable. The results from these comparisons are displayed in Table 4. For the MHS sample, for which factorial invariance holds, the values of the estimates are approximately equal for the level (µ₀ = 2.835 and 2.836, for 2LGC_2a and 2LGC_2b, respectively), slope (µ_s = .069 and .095), variance of the level (σ²₀ = .413 and .419), variance of the slope (σ²_s = .005 and .004), and level-slope covariance (σ_0s = −.012 and −.009). The only difference across models is that the standard error for the slope in model 2LGC_2b is larger and the slope estimate is therefore not significant. For the AAPT sample, for which invariance cannot be assumed, the pattern of results is very different depending on the reference indicator used to scale the latent variable. The estimates from these models are: for the level (µ₀ = 1.343 and 2.378, for 2LGC_2a and 2LGC_2b, respectively), linear slope (µ_s = .003, p > .05 and .525, p < .01), increment slope (µ_I = .085, p < .01, and −.206, p > .05), variance of the level (σ²₀ = .110 and .297), variance of the linear slope (σ²_s = .037 and .083), and variance of the increment (σ²_I = .083 and .211). Whereas for the MHS sample the estimates from these two models lead to approximately equal trajectories, this is not true for the AAPT sample. Such trajectories are displayed in Figure 3a and 3b (for the MHS and AAPT samples, respectively). For the AAPT sample, model 2LGC_2a leads to trajectories with almost no change, whereas model 2LGC_2b generates highly increasing trajectories. These results illustrate that parameter estimates in 2LGC models are sensitive, at times extremely sensitive, to the choice of reference indicator when measurement invariance cannot be assumed.

Table 4.

Parameter Estimates for Models 2LGC_2a and 2LGC_2b fitted to MHS and AAPT Data

	MHS Sample		AAPT Sample
Model	2LGC2a	2LGC2b	2LGC2a	2LGC2b
Fixed effects
µ0 Level	2.835 (.054)	2.836 (.233)	1.343 (.029)	2.378 (.226)
µs Slope	.069 (.018)	.095 (.123)ns	.003 (.023)ns	.525 (.179)
µI Increment			.085 (.033)	−.206 (.268)ns
Random Effects
σ02 Level	.413 (.063)	.419 (.065)	.110 (.018)	.297 (.039)
σS2 Slope	.005 (.005)	.004 (.005)	.037 (.008)	.083 (.014)
σI2 Increment			.083 (.016)	.211 (.032)
σ0S Level-Slope	−.012 (.015)	−.009 (.016)	.044 (.010)	.130 (.020)
σ0I Level-Increment			−.067 (.015)	−.178 (.032)
σSI Slope-Increment			−.050 (.011)	−.113 (.020)

Note. Values in parentheses indicate standard errors. All values are maximum likelihood estimates from Mplus. For the MHS sample, the basis coefficients were fixed to β_t = [0, 1, 2, 3]. For the AAPT sample, the coefficients for the slope were fixed to β_t = [−2, −1, 0, 2, 3] and for the increment to β_t = [0, 0, 0, 2, 3]. “ns” indicates a parameter whose 95% confidence interval includes zero.

Figure 3.

Expected trajectories for 2LGC models as a function of scale indicator for both samples.

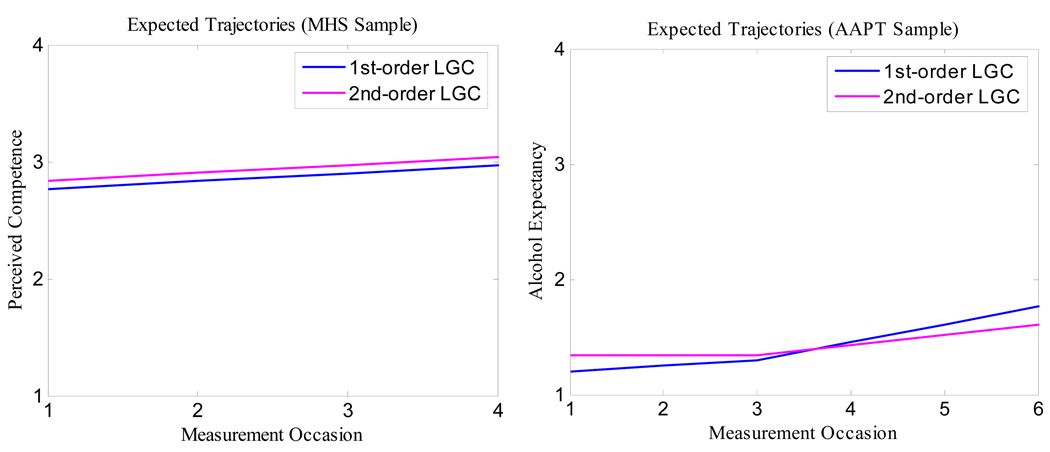
To further illustrate the issue of invariance, we compared the results from a 2LGC model (i.e., 2LGC_2a) with those from a first-order LGC model using composites as manifest variables. These results are reported in Table 5. For the MHS sample, the estimates are very similar, with only a small difference in the estimate of the level. This estimate appears to be slightly larger for the 2LGC model than for the first-order LGC model. The expected values from these two models are displayed in Figure4a and lead to parallel trajectories with a very small separation. For the AAPT sample, however, the results between the 1LGC and 2LGC models present some differences. For example, the level for the 1LGC is smaller than that for the 2LGC, indicating differences in the intercept at the third measurement occasion. Such differences are also true for the slope, which is a substantially larger value for the 1LGC than for the 2LGC (for the latter value the slope is not different from zero), and for the increment, which is larger for the 1LGC than for the 2LGC. The estimates from these two models lead to rather different trajectories (see Figure4b). The trajectory from the first model shows increases during both segments, before and after the third assessment, although with a faster rate for the latter segment. The trajectory from the second model, in contrast, is flat across the first three measurement occasions with a subsequent small linear increase.

Table 5.

Parameter Estimates for Models 1LGM and 2LGC_2a fitted to MHS and AAPT Data

	MHS Sample		AAPT Sample
Model	1LGC	2LGC2a	1LGC	2LGC2a
Fixed effects
µ0 Level	2.771 (.046)	2.835 (.054)	1.299 (.022)	1.343 (.029)
µs Slope	.061 (.012)	.069 (.018)	.048 (.014)	.003 (.023)ns
µI Increment			.108 (.022)	.085 (.033)
Random Effects
σ02 Level	.460 (.048)	.413 (.063)	.137 (.018)	.110 (.018)
σS2 Slope	.011 (.003)	.005 (.005)	.022 (.008)	.037 (.008)
σI2 Increment			.073 (.018)	.083 (.016)
σ0S Level-Slope	−.024 (.009)	−.012 (.015)	.051 (.010)	.044 (.010)
σ0I Level-Increment			−.062 (.016)	−.067 (.015)
σSI Slope-Increment			−.028 (.011)	−.050 (.011)

Note. Values in parentheses indicate standard errors. All values are maximum likelihood estimates from Mplus. For the MHS sample, the basis coefficients were fixed to β_t = [0, 1, 2, 3]. For the AAPT sample, the coefficients for the slope were fixed to β_t = [−2, −1, 0, 2, 3] and for the increment to β_t = [0, 0, 0, 2, 3]. “ns” indicates a parameter whose 95% confidence interval includes zero.

Figure 4.

Expected trajectories for 1^st and 2^nd-order LGC models for both samples.

2^nd-order Latent Difference Score Models

In the last set of analyses, we fitted a set of 2^nd-order LDS models with similar specification (including the increment slope) and order than those used with the 2LGC models. The results from these analyses are displayed in Table 6. For the MHS data (displayed in the first section of Table 6), the results resemble the findings from the 2LGC models. First, changing the indicator used to scale the latent variable (Models 2LDS_2a-2LDS_2d) did not make a substantial difference in model fit. Second, imposing restrictions of factorial invariance (2LDS₃-2LDS₆) indicated unequivocal strong invariance and a less clear strict invariance. This latter hypothesis was tenable using some fit criteria (BIC) but was less reasonable with other criteria (χ²/df).

Table 6.

Goodness-of-fit Indices of 2LDS Models (MHS and AAPT Samples)

Model	χ2	df	RMSEA	(90% CI)	CFI	TLI	BIC	Δχ2 / Δdf
MHS
2LDS2a	185	93	.06	(.05 - .07)	.96	.94	6876	---
2LDS2b	180	93	.06	(.05 - .07)	.96	.95	6871	---
2LDS2c	178	93	.06	(.05 - .07)	.96	.95	6868	---
2LDS2d	178	93	.06	(.05 - .07)	.96	.95	6869	---
2LDS3	194	102	.06	(.05 - .07)	.96	.95	6835	9 / 9
2LDS4	203	111	.06	(.04 - .07)	.96	.95	6794	9 / 9
2LDS5	261	123	.07	(.05 - .08)	.94	.94	6785	58 / 12
2LDS6	290	131	.07	(.06 - .08)	.93	.93	6769	29 / 8
AAPT
2LDS2a	147	77	.04	(.03 - .05)	.97	.96	18384	---
2LDS2b	144	77	.04	(.03 - .05)	.97	.96	18380	---
2LDS2c	198	77	.05	(.04 - .06)	.95	.93	18434	---
2LDS3	262	85	.06	(.05 - .07)	.93	.91	18446	64 / 8
2LDS4	313	93	.06	(.06 - .07)	.91	.90	18447	51 / 8
2LDS5	563	105	.08	(.08 - .09)	.81	.81	18620	258 / 12
2LDS6	614	113	.09	(.08 - .09)	.80	.81	18620	51 / 8

For the AAPT sample (displayed in the second section of Table 6), the results from the 2LDS models also resemble those from the 2LGC models. Selecting a particular indicator as the marker to scale the latent variable (Models 2LDS_2a-2LDS_2c) resulted in large differences in model fit (Δχ² ranging from 3 to 54). Similarly, each increasingly restrictive hypothesis of invariance led to a clear worsening in fit, indicating that factorial invariance does not hold for these data.

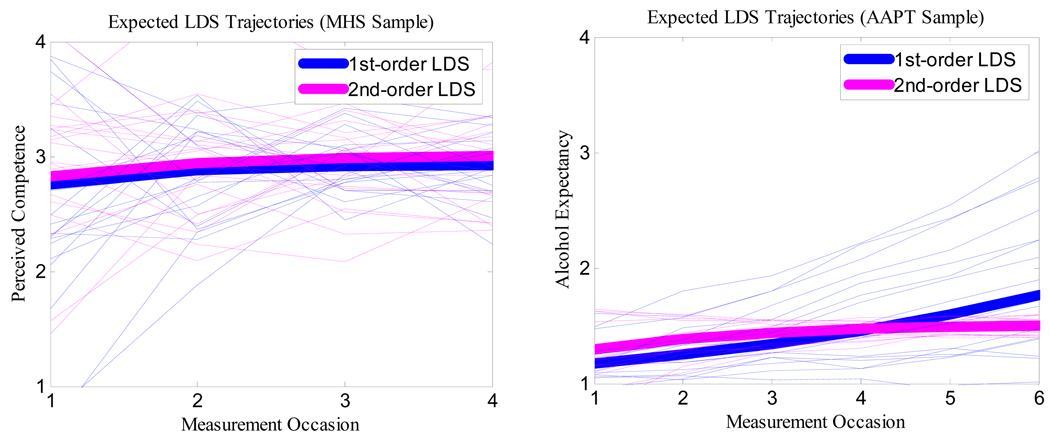
To illustrate possible differences between 1^st-order and 2^nd-order LDS models, we compared the results from a 2LDS model (i.e., 2LGC_2a) with those from a first-order LDS model using composites as manifest variables. These results are reported in Table 7. As it was the case for the LGC models, all the estimates for the MHS sample are very similar. For the AAPT sample, however, the results show important differences between both models in almost all parameter estimates. Figure 5a and 5b display the expected trajectories generated from these models for both samples. In these figures, the thick line represents the average trajectory whereas the thin lines represented individual trajectories. For the MHS data, the trajectories generated from the 1LDS and 2LDS models are very similar. For the AAPT data, the trajectories from the 1LDS model are steeper and with more variability than those from the 2LDS model.

Table 7.

Parameter Estimates for Models 1LDS and 2LDS₂ fitted to MHS and AAPT Data

	MHS Sample		AAPT Sample
Model	1LDS	2LDS1(2a)	1LDS	2LDS1(2a)
Means
µ0 Level	2.755 (.050)	2.825 (.052)	1.201 (.018)	1.356 (.036)
µs Slope	2.049 (.725)	1.976 (.447)	.347 (.186)ns	.762 (.165)
µI Increment			.068 (.022)	.068 (.015)
By Auto-proportion	−.699 (.255)	−.657 (.153)	−.232 (.156)ns	−.571 (.127)
Variances/Covariances
σ02 Level	.584 (.128)	.531 (.063)	.075 (.022)	.135 (.036)
σS2 Slope	.164 (.132)ns	.151 (.081)ns	.003 (.011)ns	.015 (.012)ns
σI2 Increment			.006 (.004)ns	.003 (.003)ns
σ0S Level-Slope	.270 (.116)	.259 (.077)	−.013 (.009)ns	−.002 (.010)ns
σ0I Level-Increment			.013 (.005)	.009 (.004)ns
σSI Slope-Increment			.001 (.006)ns	−.001 (.003)ns

Note. Values in parentheses indicate standard errors. All values are maximum likelihood estimates from Mplus. For the MHS sample, the basis coefficients were fixed to β_t = [0, 1, 2, 3]. For the AAPT sample, the coefficients for the slope were fixed to β_t = [−2, −1, 0, 2, 3] and for the increment to β_t = [0, 0, 0, 2, 3]. “ns” indicates a parameter whose 95% confidence interval includes zero.

Figure 5.

Expected trajectories for 1^st and 2^nd-order LDS models for both samples.

Scaling of Latent Variables

One additional concern in growth modeling is the interpretation of results after an optimal model has been obtained. In much applied work with growth models, researchers emphasize only whether parameter estimates are statistically significant and, if significant, the sign of the parameter estimate, without offering detailed interpretations of the magnitudes of the parameter estimates. Under such an approach, statistical significance leads to presumed theoretical significance, even if the magnitude of a key parameter estimate is miniscule. The problem is compounded by the use of raw score metrics of various sorts for manifest variables and the tendency to identify the latent variables with a factor loading fixed to unity. This leads to manifest and latent variables that can have unusual metrics, impeding detailed evaluation except by the methodological expert.

One step in the direction of easing the interpretive burden for the investigator is to scale the latent variables in a metric that enables an easier and more direct interpretation. Consider Model 2LGC₄, the second-order latent growth model with strong factorial invariance constraints. One standard way to identify this model is to fix the factor loading of the first manifest variable to unity and the intercept for this indicator to zero at each time of measurement (cf. Hancock et al., 2001). Strong factorial invariance requires that all remaining factor loadings and intercepts are invariant across times of measurement. Under this method of identification, the latent variables at each time of measurement are scaled relative to the first indicator. Furthermore, under a linear growth specification, the basis coefficients for the slope latent variable are often fixed at values of 0, 1, 2, …, (t − 1) for equally-spaced times of measurement 1, 2, 3, …, t, respectively, regardless of the magnitude of the time gap between measurement occasions (e.g., one week, one month, one year). There is nothing inherently wrong with this specification. Indeed, one important advantage of this approach is that routine use of the method can help ensure that substantive researchers who are not expert in structural equation modeling will specify models correctly. However, if the manifest variables have rather unusual metrics (e.g., very large or very small variances), the resulting latent variables may have metrics that impede interpretation.

One alternative approach to model specification is to establish a precisely standardized metric, or an approximately standardized metric, for the latent variables with reference to a given time of measurement. One common standardized metric is a metric in which a variable has a mean of zero and a standard deviation of unity. We imposed such a metric directly in the longitudinal confirmatory factor model for the MHS data for Model CFA₄ by fixing the variance of the latent variable at unity at the first occasion of measurement, fixing the mean of the latent variable at zero at this time point, estimating all factor loadings and intercepts, and constraining factor loadings and intercepts to invariance across the remaining times of measurement. Under this specification, the latent variable has a mean of 0 and SD of unity at Time 1, and varying means and SDs at the remaining times of measurement, but scaled relative to the “mean 0, SD 1” at Time 1. When we specified the model in this fashion, the estimated factor loading for the first item was .706 (SE = .044). We then used this value to fix the factor loading for the first item in a 2LGM re-specification.

This approach to fixing the scale of the latent variables ensured that the variance of the first-order latent variable at Time 1 was approximately unity. By fixing the mean of the second-order Intercept latent variable at zero, the first-order latent variable at Time 1 was in an approximate z-score metric, having mean of zero and SD of about 1.0. Under this re-specification, the mean of the Slope was 0.091 (SE = .017), which is the estimated change from one time of measurement to the next. From the first to fourth times of measurement, this would translate into a mean change of 3 × 0.09 or 0.27 units. Because the first-order latent variable at Time 1 had a mean of zero and SD of unity, this represents a change of just over one-quarter of a SD-unit, or a change of 0.27 units in a Cohen’s d metric. Because measurement occasions 1 and 4 differed by 6 months, mean growth of this magnitude would then translate into an annual growth rate of 0.54 units in Cohen’s d metric, or a change of over one-half SD units, a nontrivial, moderate level of change.

Discussion

In this study we examined the issue of factorial invariance in growth models as related to model fit and estimates of growth parameters. We used 1^st- and 2^nd- order latent growth curve models as well as 1^st- and 2^nd- order latent difference score models to investigate change across time in a set of manifest indicators that compose an underlying latent construct when the assumption of factorial invariance is met and when it is violated. In general, the results suggest that several important problems arise if factorial invariance does not hold.

One finding from our analysis concerns the parameter estimates. Our results indicate that when the hypothesis of factorial invariance over time is tenable in the data, the estimates from a 1^st-order latent model and a 2^nd- order latent model lead to roughly equal expected trajectories. When such an assumption is not reasonable, however, the estimates can lead to very different estimated trajectories. These results apply to both latent growth curve models and latent difference score models. Given the inability to formally test measurement invariance of the indicators when a 1^st-order latent growth model is fitted to the data, measuring the same latent construct over time cannot be guaranteed.

Furthermore, we illustrated that 2^nd-order growth models, a strategy available for almost two decades (McArdle, 1988) but rarely used in contemporary research, provide a useful tool for investigating different forms of factorial invariance. The results obtained when fitting 2^nd-order growth models to the two data sets used in this study show that, when measurement invariance cannot be assumed, the selection of a different reference indicator for the scaling of the latent variable can substantially change both model fit and parameter estimates. Under conditions of strong or strict factorial invariance, on the other hand, this scaling choice does not affect either aspect of the model. This finding supports previous work in the area (Stoel et al., 2004) and has implications for the interpretation of change in latent constructs measured by a set of manifest variables.

Some alternatives have been proposed to deal with lack of factorial invariance. One such alternative consists on identifying the covariance and mean structure of the model setting constraints on the latent variable structure instead of constraining the measurement (i.e. the factor loadings and intercepts) part of the model (Chan, 1988; Dolan & Molenaar, 1994; Horn & McArdle, 1992; Stoel et al., 2004). We recognized, however, that this strategy may make for a difficult interpretation of some parameters if a latent growth structure is imposed on the first-order factors. Although not addressed in our analyses, this is an important area of research for future studies.

With regard to rescaling issues, we illustrated that rescaling can be used to make a much more clear interpretation about the magnitude of growth trajectories without altering any of the psychometric or statistical features of the raw scores. After our rescaling, we found that change could be expressed directly in a Cohen’s d metric, which facilitates interpretation of the numerical value and the practical magnitude of mean change. Given the results obtained in our study, we encourage researchers to rescaling latent variables into a metric that allows them to make the most informative interpretations of their data.

The primary aim of our study was to examine issues of factorial invariance in the context of state-of-the-art latent growth models. Because of this objective, we did not focus on issues of comparing alternative models of growth. For this, extensions to the models examined here – together with different models altogether – certainly can be considered. Some logical extensions include models that consider external predictors, when such covariates exist in the data, or nonlinear forms of the latent difference score models (Ferrer et al., 2006). But, regardless of the model used, formally testing factorial invariance assumptions is important when using multiple manifest variables for examining change in a construct over time.