Abstract
Plant development is genetically determined but it is also plastic, a fundamental duality that can be investigated provided large number of measurements can be made in various conditions. Plasticity of gravitropism in wild-type Arabidopsis (Arabidopsis thaliana) seedling roots was investigated using automated image acquisition and analysis. A bank of computer-controlled charge-coupled device cameras acquired images with high spatiotemporal resolution. Custom image analysis algorithms extracted time course measurements of tip angle and growth rate. Twenty-two discrete conditions defined by seedling age (2, 3, or 4 d), seed size (extra small, small, medium, or large), and growth medium composition (simple or rich) formed the condition space sampled with 1,216 trials. Computational analyses including dimension reduction by principal components analysis, classification by k-means clustering, and differentiation by wavelet convolution showed distinct response patterns within the condition space, i.e. response plasticity. For example, 2-d-old roots (regardless of seed size) displayed a response time course similar to those of roots from large seeds (regardless of age). Enriching the growth medium with nutrients suppressed response plasticity along the seed size and age axes, possibly by ameliorating a mineral deficiency, although analysis of seeds did not identify any elements with low levels on a per weight basis. Characterizing relationships between growth rate and tip swing rate as a function of condition cast gravitropism in a multidimensional response space that provides new mechanistic insights as well as conceptually setting the stage for mutational analysis of plasticity in general and root gravitropism in particular.
Plant development is genetically determined, but also importantly shaped and molded by influences both external and internal, and even from the previous generation's life history (Roach and Wulff, 1987; Donohue, 2009). Variation in development due to local conditions, or plasticity, may be especially important to plants due to their sessile nature (Schlichting, 1986). Understanding the consequences of external factors on growth and development is important for basic and practical reasons (Sultan, 2004). Studying one standard condition will not produce a satisfactory basic understanding of how plants grow and develop in a variable environment. On the practical side is the design of screens for discovery of gene function through mutant analysis. A mutant phenotype is often the single most important source of information about the altered gene's function, but without knowledge of what contributes to the wild-type range of responses or behaviors (plasticity) a mutant phenotype may go undetected or misunderstood.
The conditional nature of plant development is often dealt with by controlling conditions as best as possible to isolate the particular relationship under study. In cases where the experimental method allows, the influences of multiple conditions may be examined to create a richer description of the response, and a fuller assessment of a mutant phenotype. Automation makes this form of description more feasible. Automated acquisition and computational analysis of digital images could enable studies of plant growth and development that are both broad and rich in detail. This study uses such a machine vision-based approach to create a multicondition, high-resolution description of root gravitropism in Arabidopsis (Arabidopsis thaliana) seedlings, resulting in what might be termed a behavioral space.
Gravity is a constant, pervasive environmental influence that significantly shapes plant form above and below ground. Much of what is known about gravity sensing and signal transduction in plants has been learned from studies of gravitropism of the seedling primary root. Root gravitropism has many attributes of a model stimulus-response system, being easy to initiate, fast to react, and quantifiable with a straightforward measurement of root tip angle (Boonsirichai et al., 2002). Genetic screens have isolated several mutants defective in the process (Harrison et al., 2008). Their study with the full range of modern biological tools has produced a satisfyingly rich molecular and physiological view of the process. Upon reorientation, statoliths in the central columella cells of the root cap sediment to the new lower side of the cell (Blancaflor et al., 1998; Kiss, 2000). Rapid ionic fluxes are triggered within seconds, resulting in proton and possibly other ion concentration changes (Scott and Allen, 1999; Fasano et al., 2001; Hou et al., 2004) that result in redistribution of auxin efflux facilitator proteins, resulting in redistribution of auxin across the root (Friml et al., 2002; Lewis et al., 2007; Harrison and Masson, 2008), causing cells along the lower flank to expand more slowly than those on the upper flank (Mullen et al., 1998). Curvature is generated (Miller et al., 2007), resulting in downward bending of the tip.
While some aspects of the gravitropism mechanism are understood in considerable detail other important aspects such as dependence of the response on developmental age or environmental conditions are unknown and perhaps not readily addressable by standard methods. Yet, the range and plasticity of the underlying, causal mechanisms must be learned if what governs the natural response is to be understood. This multifactorial study was designed to identify and quantify the strengths of different dependencies and influences of conditions on gravitropism to generate a more comprehensive characterization of this model stimulus-response couple. The largely automated, computational approach may prove useful for the study of plant development in general.
RESULTS
Automated Image Acquisition and Analysis for Gravitropism Studies
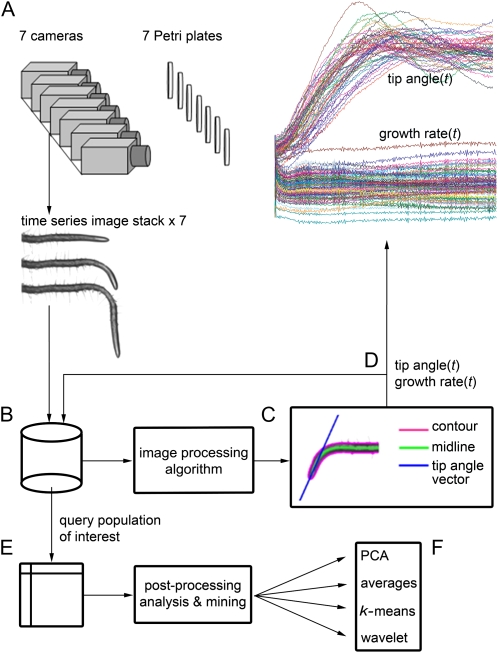
A machine vision acquisition and analysis platform capable of high spatiotemporal resolution measurements of root gravitropism was established to characterize the extent and causes of variability in this model stimulus-response process. Figure 1 shows a schema of the image acquisition, image processing, and post-processing analysis workflow. A bank of seven computer-controlled CCD cameras acquired electronic grayscale images of roots, one per camera, at 2 min intervals over a period of 10 h (Fig. 1A). A movie made from the 301 high-resolution images of a root undergoing gravitropism is presented in Supplemental Movie S1. Acquired image files automatically streamed to a data server (Fig. 1B). A custom image-processing algorithm, essentially the same as that reported by Miller et al. (2007), automatically computed the midline (medial axis) of the root in each image (Fig. 1C) from which root growth rate and tip angle could be computed (Fig. 1D). The individual midlines were returned to the dataserver and linked to the experimental metadata via a relational database. With this workflow, 1,216 gravitropism trials consisting of 366,016 separate images were algorithmically and automatically condensed down to sets of midline coordinates and their associated metadata. These processed data sets were mined by querying the database (Fig. 1E) and performing analyses such as principal components analysis (PCA) to reduce 301-point time courses to the fewest information-rich dimensions, simple averaging, classification by k-means clustering, or differentiation by wavelet analysis (Fig. 1F).
Figure 1.
A schema of the automated image acquisition, analysis, and data-mining workflow. A, Seven CCD cameras acquired electronic images of seedlings growing along the surface of agar-filled petri plates maintained vertically, then rotated 90° to induce gravitropism. B, Images acquired at 2-min intervals streamed from the cameras to storage discs and database. C, Custom image-processing algorithms extracted the root midline. D, Analysis of the midlines returned tip angle and growth rate as a function of time. A relational database stored the extracted results with the metadata. E, Post acquisition, the database was queried with analysis algorithms designed to identify patterns and quantify relationships between key parameters of the gravitropic response. F, The analyses involved standard statistics, classification, and signal processing.
Root Gravitropism within a Condition Space
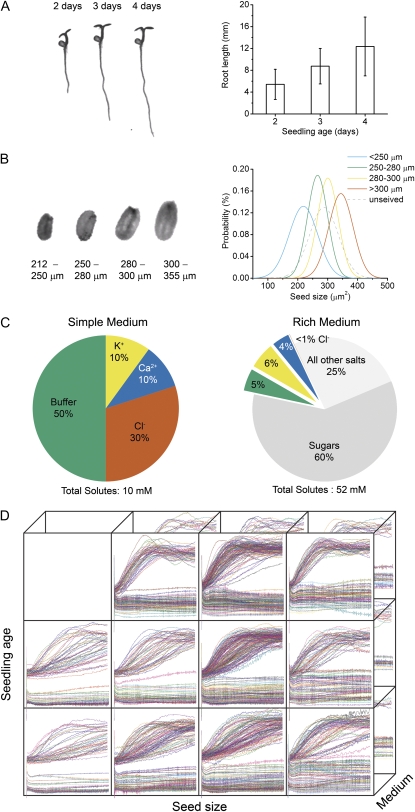
The automated workflow (Fig. 1) made it possible to investigate multiple experimental conditions in a study of condition-dependent response or plasticity. Seedling age was one of the chosen variables because initial pilot studies indicated that a 24-h difference in age was enough to affect the gravitropic response. Seedlings were systematically grown for 2, 3, or 4 d before gravitropism was induced and the root response recorded. Seedlings representative of these age classes and the mean lengths of their roots are shown in Figure 2A. A previous study had shown that the size of the seed from which a seedling emerges influences the behavior of the root, and surprisingly more aspects of development (T.L. Durham Brooks, unpublished data), so seed size was chosen as a variable. Seeds representative of the size classes used here are shown in Figure 2B along with a quantitative description of each class. The third axis of the condition space is growth medium composition. A simple medium consisting of two salts and a buffer, and a rich medium including Suc and all essential minerals (Fig. 2C) were the conditions employed along the growth medium axis. Altogether, high-resolution assays of gravitropism were conducted in 22 discrete combinations of seedling age (a developmental variable), seed size (an intrinsic variable), and medium composition (an extrinsic variable). The resulting set of growth rate and tip angle versus time plots is shown in Figure 2D.
Figure 2.
The three axes of the condition space. A, Seedling age formed one axis of the condition space. The root of a seedling between 2, 3, and 4 d (left) doubled in length (right) on average. B, The size of the seed formed another axis. Mechanical sieving separated seeds (left) into subpopulations with different mean sizes and distributions (right) quantified by image analysis. C, Composition of the agar growth medium (either a simple mix of KCl and CaCl2 or a rich mixture of all essential elements). D, The complete set of tip angle and growth rate versus time data acquired in 22 different condition combinations.
Response Trends throughout the Condition Space
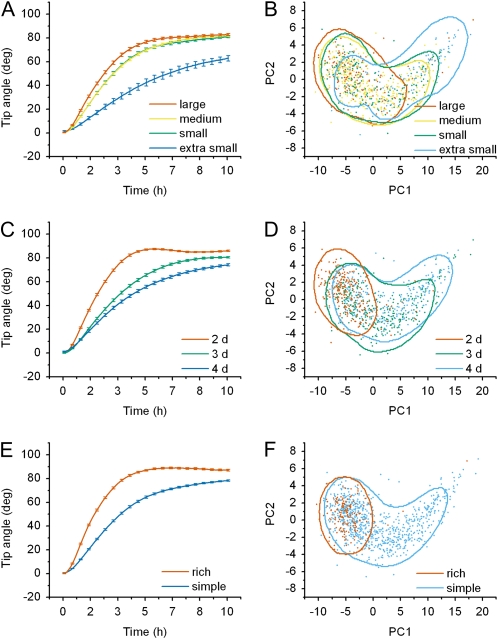
Figure 2D shows a large amount of variation in tip angle realignment and growth rate between discrete conditions. In some conditions, nearly agravitropic individuals were observed while robust responses that overshot their set-point angle and then autocorrected during the recorded 10 h were common in other conditions. One way to characterize the dependence of tip angle response on position within the condition space is to average the separate trials along a condition axis. Figure 3A shows the average tip angle (response) development of the different seed size classes, irrespective of age or growth medium. Seedlings from extra-small seeds responded slowest, not reaching their steady-state tip angle by the end of 10 h, while seedlings from large seeds responded faster and completely. Each of the traces consists of 301 time points; therefore, each individual response can be treated as a vector in 301 dimensional space. PCA was employed to reduce the 301 dimensions down to two that could best discriminate individual responses from each other. The first principal component (PC1) described 85% of the variation in the data set. Addition of the second principal component (PC2) increased the description to 99%. Determinations of these two coefficients for each individual in the data set allowed any individual tip angle response to be discerned from another individual 99% of the time. An alternative representation of the results in Figure 3A is a plot of PC2 versus PC1 coefficients for each individual in the data set. The points are colored to represent the seed size class they belonged to (Fig. 3B). Colored boundaries containing 75% of the data for each population were estimated with a Parzen window method employing a Gaussian kernel having a bandwidth of 1.75 to aid visualizing trends in the distributions, namely that increasing seed size was associated with a more homogenous response pattern (less spread in the PC2 versus PC1 points). Together, sections A and B of Figure 3 indicate that roots from large seeds respond more robustly and with less variability than do roots from small seeds.
Figure 3.
Tip angle development throughout the conditional space. A, Average tip angle development for each seed size class. B, Principal components coefficients of the entire root data set colored according to seed size class. C, Average tip angle development across developmental time. D, Principal components coefficients colored according to developmental age. E, Average tip angle development of seedlings grown on either rich or simple medium. F, Principal components coefficients of all individuals colored according to media condition. The contours in each principle components plot outline where 75% of the data for each population should lie.
Averaging all trials along the seedling age axis regardless of seed size or growth medium (Fig. 3C), and circumscribing distributions of principal components coefficients (Fig. 3D) showed that younger roots responded with rapid initial bending like roots from large seeds, while older roots responded at a steadier, slower rate like those from small seeds. On average, only 2-d-old seedlings overshot the ultimate angle. The response pattern (time course) displayed by root tips of the three age classes differed much more than the angle finally achieved within the 10-h assay period. As can be seen from Figure 3D, the response of 2-d-old seedlings was less variable than that of older roots. In addition, the PC coefficients of 3-d-old roots were similar to that of roots from small and medium seeds.
Growth medium composition also had a large effect on root gravitropism. Seedlings grown on a nutrient-rich medium responded like young seedlings from large seeds based on the mean response curves (Fig. 3E) and the PC2 versus PC1 distributions (Fig. 3F). One possible interpretation of the seed size effect is that large seeds contain more resources than small seeds, that resources become depleted between day 2 and day 4, and that enriching the medium counteracts this resource limitation. Levels of 19 elements in the seeds were measured by inductively coupled plasma-mass spectrometry (Lahner et al., 2003) in two separate generations of seeds. The results are presented in Supplemental Tables S1 and S2. On a tissue weight basis (Supplemental Table S1), none of the 19 elements was less abundant in small seeds than large seeds. In fact, small seeds contained more sodium (Na), potassium, rubidium, magnesium, cadmium, nickel, and molybdenum than large seeds on a tissue weight basis, though only the Na difference exceeded 2-fold. This result argues against the effect of medium enrichment on gravitropism being due to amelioration of an embryonic mineral deficiency. Per individual seed (Supplemental Table S2), sulfur, calcium, phosphorus, magnesium, zinc, manganese, iron, and copper were less abundant in small seeds than large seeds by amounts roughly proportional to the difference in seed size. No element was less abundant in small seeds compared to large seeds on a per weight basis. If expressing levels on a per seed basis better describes the environment within which seeds germinate then the seed size effect on root growth observed here could be due to a deficiency in small seeds of one or more of these elements. Again, Na was more abundant in small seeds than large seeds when the results were expressed per seed. Whether the higher levels of some elements in small seeds, particularly Na, relates to the different behavior of the seedlings they produce is worthy of further study.
Classifying Patterns in the Pooled Data
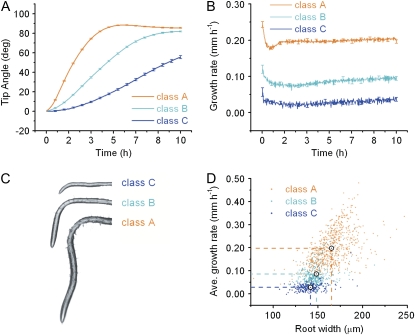
The large, all-trials-pooled data set was subjected to classification by a k-means clustering algorithm, which iteratively segmented the population of results into a prechosen number of classes until within-class variance was minimized. Selecting three as the number of classes to create followed by averaging all the trials ascribed to a particular class produced the average response curves shown in Figure 4A. Class A roots responded vigorously to gravistimulation and overshot the final angle. The class B response was less vigorous, but on average achieved the same final angle as class A. Class C roots displayed a longer lag and did not reach a steady state during the 10-h assay period. The average growth rate within each of the three classes is shown in Figure 4B. Roots of class A individuals grew approximately twice as fast as class B roots, raising the possibility that overshooting is mechanistically linked to growth rate. Class A, B, and C roots make up 56%, 27%, and 17% of the population. Shown in Figure 4C are representative roots of each class after 10 h of gravistimulation.
Figure 4.
k-means clustering of tip angle responses into three distinct classes. A, Average tip angle development of each k-means defined class. B, Average growth rates of the k-means defined tip angle responses. C, Representative roots at 10 h after gravistimulation from each of the classes. In addition to showing differences in final root length and tip angle between the classes, there is an apparent difference in root width. D, Average growth rate plotted against root width at 10 h of gravistimulation. The data are colored according to k-means class.
In addition to obvious differences in root length, root width also differed (Fig. 4C). Class A roots were 165 μm on average, approximately 15 μm wider than class B and C roots. The widths of class B and C roots were similar, averaging 148 and 142 μm, respectively. Width was plotted versus average growth rate for each individual root in Figure 4D, with classes indicated by color and the class mean by a bull's eye point and dotted lines. The large scatter of the points precludes growth rate predictions based on root width, but the more distinct upper edge of the distribution indicates that width may constrain growth rate. For example, a 150 μm-wide root can apparently elongate at any rate up to 0.25 mm h−1 and this upper limit increases linearly with width.
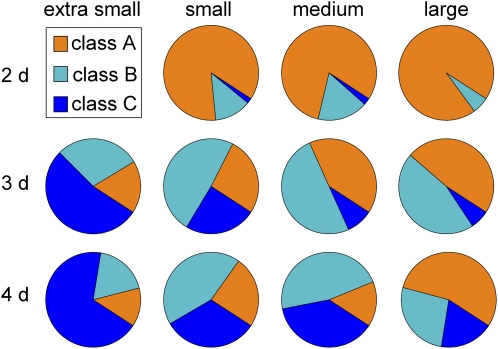
Figure 5 presents class frequencies according to position with the condition space. The proportion of class A roots increased with seed size and decreased with seedling age, while the proportion of class C roots showed the complementary pattern. No class C individuals were found in the population of 2-d-old seedlings coming from large seeds. Thus, the likelihood of a particular response pattern being displayed by a root varied greatly across the condition space. Figure 5 can be viewed as a graphical representation of a gravitropism behavioral space containing information about response plasticity. Only results obtained on the simple growth medium are shown in Figure 5 because enriching the medium eliminated much of the response heterogeneity. Nearly all 2- and 3-d seedlings independent of seed size were class A on the rich medium (data not shown).
Figure 5.
Distribution of class A, B, and C roots throughout the condition space. Percentage of roots falling into each class was determined by k-means clustering for plants on simple medium only. Class A roots increased with seed size and decreased with age.
Relationships between Growth Rate and Tip Angle throughout the Condition Space
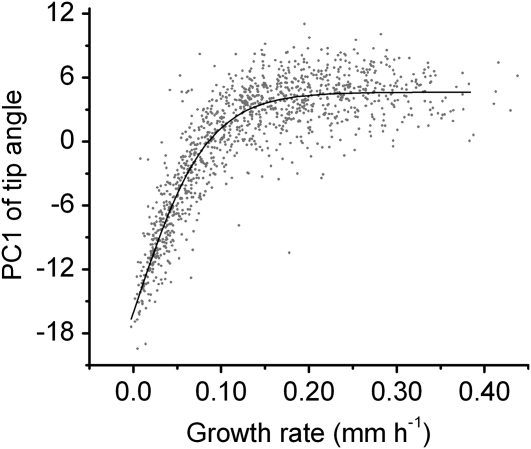
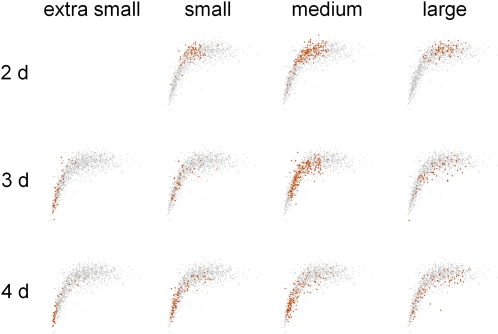
The variability of response parameters observed across the condition space provided an opportunity to test relationships between parameters, such as growth rate and tip angle. Figure 6 shows a plot of PC1, which correlates well with magnitude of the tip angle response (data not shown), versus the average rate at which that root elongated for each separate trial. This plot of all 1,216 trials shows that growth rate and response magnitude were strongly correlated until growth rate exceeded 0.1 mm h−1, after which no relationship was apparent. Forty-one percent of the responses lay within the linear range. Thus, for more than half of the individuals, growth rate and tip angle were not correlated. Perhaps different gravitropism mechanisms with different growth rate dependencies pertain in different conditions. Evidence of this may be seen in Figure 7, which shows the same information as Figure 6 except that the points obtained in each discrete condition (simple media only) are colored. Older seedlings or those from smaller seeds tended to operate in the growth rate-dependent mode whereas younger seedlings or those from larger seeds responded in a growth rate-independent mode. Responses of 4-d seedlings from large seeds mapped fairly uniformly across the population.
Figure 6.
Relationship between tip angle and average growth rate throughout the condition space. PCA was performed on the entire population of tip angle responses. Plotted is PC1 of the tip angle versus the average growth rate of the same individual for each individual in the data set. Growth rates below 0.10 mm h−1 reasonably predict tip angle development of an individual. Growth rate is not a good predictor of tip angle when the root grows faster than 0.10 mm h−1. The line is a Boltzman equation fit to the data.
Figure 7.
The relationship between tip angle and growth rate varies throughout the conditional space. Shown in gray in each figure are the PC1 coefficients and average growth rate for all 1,216 individuals in the data set, as was shown in Figure 6. In vermillion are the PC1 coefficients and average growth rates for the individuals at each developmental age and seed size on simple media.
Rate of Tip Angle Change throughout the Condition Space
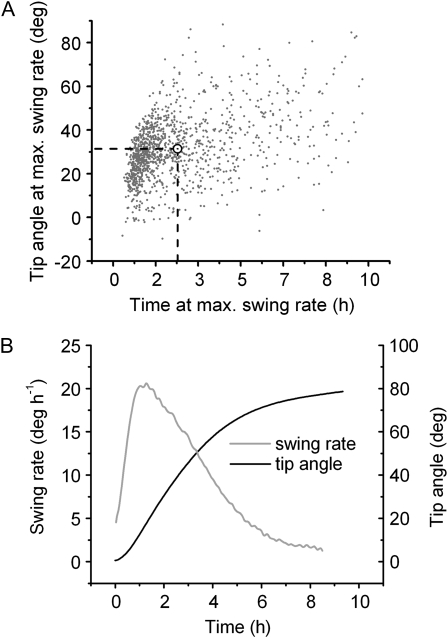
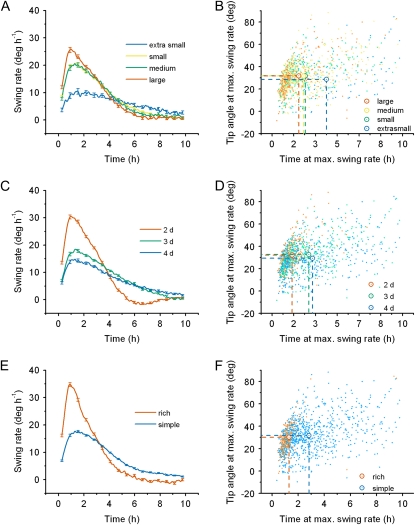
To take advantage of the temporal information provided by capturing images at 2-min intervals, the rate of root tip realignment was estimated by convolving each separate tip angle time course with a first-order Gaussian derivative wavelet. The resulting tip swing rate, also called tropic speed (Chavarría-Krauser, 2006), was plotted versus time for each trial and then all trials in the entire data set were averaged and plotted along with the average tip angle response (also entire data set) in Figure 8A. The average swing rate plot shows a rapid initial acceleration phase followed by a longer decelerating phase as the tip approaches its steady-state angle. From each trial in the full data set, the time point at which swing rate peaked and the tip angle accrued at that time were extracted and plotted against each other in Figure 8B. The points were broadly distributed, though a large percentage of them clustered within the 15° to 40° and 1- to 2.5-h range. The green circle and dotted lines of Figure 4B show the average of the population, approximately 30°, 2.5 h. Thus, sections A and B of Figure 8 together demonstrate that swing rate peaks when the response is approximately 40% complete.
Figure 8.
Relationship between swing rate and tip angle. A, The tip angle at the time of maximum swing rate versus the time when swing rate was maximal. The dashed lines show that the average maximum swing rate of the data set occurred when the tip angle was 30° on average, and 2.5 h after gravistimulation, on average. B, The average swing rate (gray) and the average tip angle (black) response of the entire data set.
Swing rate also varied along the condition space axes, with maxima ranging from approximately 10° h−1 (extra-small seeds) to more than 30° h−1 (rich growth medium). Shown in Figure 9A is the large dependence of maximum swing rate on seed size. Figure 9B, which is a seed size coded version of Figure 8B, shows that the fastest-bending roots came from the larger seed classes while slower-responding roots were much more likely to come from smaller seeds. The white circles and dashed lines indicate group means. The time it took for a root tip to swing at its maximal rate varied considerably, but the tip angle at that time point was a remarkably consistent 30°. Seedling age also had a large effect on swing rate magnitude and time course, with the youngest roots showing the most rapid and dynamic response. As seen for tip angle (Fig. 3, C and E), enriching the growth medium shifted the swing rate profile from a response similar to that of a 4-d seedling to something like a 2-d seedling, with comparable peaks in excess of 30° h−1 (Fig. 9, C and E). Much more clearly than the tip angle plots of Figure 3, this derivative analysis shows how the response builds up and slows down as the objective angle is achieved. Large swing rate maxima in fast-swinging groups are followed by minima that dip below even the slowest phases of the slow-swinging groups. Also, analysis of peaks in the derivative (Fig. 9, D and F) shows again how remarkably consistent root tip angle is at the time of its maximal swing rate. Conservation of this feature in the face of large plasticity in tip angle development across the conditional space (e.g. Figs. 2D and 5) is striking and perhaps mechanistically meaningful.
Figure 9.
Patterns in swing rate and time to reach maximum swing rate throughout the condition space. A, Average swing rates of roots coming from each seed size class. B, Tip angle and time to maximum swing rate by seed size class for each individual root. C, Average swing rates of roots over developmental time. D, Tip angle and time at the maximum swing rate grouped by developmental age. E, Average swing rates of roots grown on simple or rich medium. F, Tip angle and time at the maximum swing rate grouped by growth medium. The enlarged points within these plots indicate the population means for each condition.
Curvature Distribution throughout the Condition Space
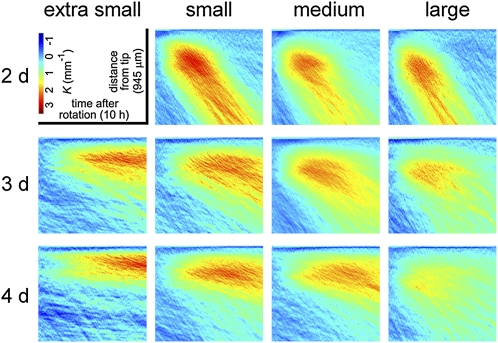
In the previous figures, root tip angle was the sole measure of the gravitropic response. However, for any given tip angle curvature may be concentrated toward the base, toward the tip, or evenly distributed along the root axis. Local curvature measurements give more information than angle measurements about the dynamics of a tropic response and its kinematic basis (Silk and Erickson, 1978; Chavarría-Krauser et al., 2008; Moulia and Fournier, 2009). Therefore, curvature at each point along each midline at each time point was determined essentially as in Miller et al. (2007). In Figure 10, the y axis marks position along a constant-sized portion of root midline with the apex at the top, the x axis represents time, and curvature (K) is represented by a color scale. The results show when, to what extent, and where along the root curvature develops, on average, in each condition. The roots were initially straight; blue representing low curvature dominates the early midlines. The curved portion of the root (red) spreads over time more in some conditions than others (e.g. compare 3- to 4-d seedlings from small seeds) but the most obvious feature in this display is the difference in slope of the curved region between the top and bottom rows (2- and 4-d seedlings). An explanation of this difference can be found in the growth rate and classification analyses in Figures 4D and 5. The top row of the grid (2-d seedlings) is predominantly populated by class A root behavior (Fig. 5), which correlates with above-average growth rate (Fig. 4D). Therefore, the larger blue area above the curvature patch in 2-d seedlings (Fig. 10, top row) reflects the greater speed with which the tips of these roots reorient and are displaced by growth from the curved region.
Figure 10.
Distribution of curvature along the root axis during gravitropism throughout the condition space. Color-coded curvature (K in units of mm−1) is shown at each point along the midline of the root apex (y axis) beginning 60 μm from the tip (top edge of each section) and extending back 945 μm at each time point (x axis) over the 10-h experiment. The plots, which are the averages of at least 40 roots per condition, show where along the root midline, when, and to what extent curvature developed after reorientation, at each position in the condition space.
DISCUSSION
The original motivation for understanding variability in gravitropism displayed by genetically identical, homozygous wild-type plants was to facilitate detection of subtle mutant phenotypes. Machine vision tools and a computational workflow made it feasible to study this variability, which is a reflection of genome function with evolutionary and ecological consequences (Tonsor et al., 2005). The thousands of measurements made from the image sets cast the gravitropic response as a multidimensional behavior space coordinated by the condition axes.
The intention was to frame the condition space with three orthogonal or qualitatively different axes: intrinsic (seed size), extrinsic (medium composition), and early developmental time (seedling age). But it is probably more realistic to recognize some interdependence between the axes. The intrinsic property of seed size includes elements of life history and influences of the previous generation. The effects of maternal environment can be large and may have important ecological and evolutionary consequences (Roach and Wulff, 1987; Schmitt et al., 1992). Indeed, a recent study showed a heavy maternal condition influence on seed size affected seedling development and even aspects of adult plant development (T.L. Durham Brooks, unpublished data). The seed size effect described here was largely suppressed by enriching the growth medium. The rich medium may have exerted its influence less directly than by rescuing a particular mineral deficiency, because evidence of a deficiency could not be found (Supplemental Tables S1 and S2). Instead, perhaps synthesis of a hormone or regulatory metabolite was influenced by the medium composition and this affected seedling root behavior. The seed size effect is potentially related to disproportionately higher Na levels in small seeds (Supplemental Tables S1 and S2). Deleterious effects of Na+ can be ameliorated by enrichment with K+ (Spalding et al., 1999; Qi and Spalding, 2004). Other possible mechanisms underlying the seed size effect include epigenetic regulation (Nakabayashi et al., 2005) or differences in the levels of signaling components such as hormones that could affect subsequent seedling development (Ali-Rachedi et al., 2004). The data presented here and by T.L. Durham Brooks (unpublished data) together make the case that parental environment can have a significant effect on the gravitropic response in seedling roots by influencing seed size.
Growth medium composition was selected as an extrinsic environmental variable though, as Schlichting and Smith (2002) point out, a change outside usually exerts its effect by causing a change inside. Distinctions between extrinsic and intrinsic may be less useful when the intrinsic parameter (seed size) can be influenced by maternal environment (an extrinsic parameter) and the extrinsic parameter (growth medium) can be expected to affect the ionic milieu of the cell. Therefore, it may be fair to view seed size and growth medium as parameters on different environmental axes. Regardless of these perspectives, when developmental time is admitted via the third axis, a condition space with discriminating power was constructed. By virtue of being embedded in this condition space, the results acquire extra relevance to physiology, genetics, development, and the nature of variability.
Phenotypic plasticity refers to a change in phenotype as a function of an extrinsic variable (Schlichting and Pigliucci, 1998; Pigliucci, 2005). It is a quantitative trait such that changes in phenotype vary in size as shifts are made along an extrinsic variable axis such as growth medium composition. Plasticity in gravitropism is displayed graphically in Figure 3F as the large effect of growth medium on the distributions of the principal component values of tip angle versus time data, and in Figure 3E by differences as large as 30° between mean tip angles on simple and rich media. Also, the maximum swing rate on rich medium was nearly twice that of roots grown on the simple medium (Fig. 9E). These various observations indicate that the gravitropic response is highly plastic in the most widely used sense of the term. The concept of developmental stability (Schlichting and Pigliucci, 1998) provides an alternate but related view. Developmental stability has been invoked to explain the observation that a process may be very stable or canalized despite changes in condition until at the margins of the condition space stability breaks down and variability increases (Schlichting and Pigliucci, 1998; Schlichting, 2008). Hsp90 has been identified as a gene that mediates canalization in multiple organisms, including Arabidopsis (Sangster et al., 2008). In this case, the simple growth medium may be functioning as such a marginal condition, also with natural relevance. The simple medium used here, while unnatural in its chemical details, is more like a soil solution in terms of total solutes (10 mm) than a rich medium with some minerals and sugars at levels never found in soils. The range of responses expressed here on simple medium (e.g. Fig. 5 or 7) may be expected in natural conditions. Therefore, natural conditions may produce the variable gravitropism shown in the above-mentioned figures rather than the nonplastic, canalized type of response observed on the rich medium.
Projection of the behaviors onto the early developmental time axis characterizes response ontogeny (Pigliucci and Schlichting, 1995). Variation apparent in this projection is usually considered development rather than phenotypic plasticity (Pigliucci and Schlichting, 1995). Here, an ontogenetic trajectory or developmental progression is obvious in the age-dependent shifts of the principle components distributions in Figure 3D. Not only do the distributions shift, they become distinctly broader with age, indicative of more variability. Young roots, like those in rich medium, displayed more uniform (and similar) behavior. Thus, seedling age, like growth medium composition, may contribute to developmental stability. The greater developmental stability of young roots is also seen in the age-dependent shifts in the response classes defined by k means (Fig. 5). The limited developmental stability of older roots or those on simple medium may have adaptive value, promoting more variable or exploratory behaviors at the edges of the condition space.
With respect to the original goal of improved mutant phenotype detection, systematic sampling within the condition space may be expected to help in cases where the altered gene's function is conditional. A phenotype could be manifested, for example, as a change in distribution of the class frequency plots in Figure 5. Such a mutation that alters behavior within a condition space may provide key information about the gene's primary function. For example, weak gravitropism in a mutant could be a symptom of an ontogenetic shift along the seedling-age axis (see the effects 48 h has on the response as quantified in Figs. 3, C and D, 5, 7, and 9, C and D). To label the affected gene as a component of the gravitropism response when in fact the mutant is aging more quickly would be to miss the larger point. Such refinement of explanations is an anticipated premium derived from characterizing a process within the context of a condition space.
Also regarding phenotype detection, this work highlights the importance of growth medium. Rich medium reduced the response plasticity such that responses regardless of condition resembled those of young seedlings from large seeds. The equivalent of Figure 5 for rich medium was so uniform that it was not shown. This equalizing effect of medium indicates that the common practice of screening for mutant phenotypes on a rich medium such as 0.5× Murashige and Skoog may minimize phenotype expression.
The wild-type condition space characterized here may serve as a reference for future genetic comparisons but it also provides independent insights into plant growth and development. For example, on the simple growth medium, root tip reorientation was most rapidly achieved at the minimum possible growth rate by 2-d roots, regardless of seed size (Figs. 3, C and D, and 7). This may reflect a principal role of gravity sensing by the seedling primary root in nature, namely reorientation of the tip upon germination even as it emerges from the randomly oriented seed. Two days later, an overriding gravity response may be less advantageous as guidance responses to various soil factors such as obstacle avoidance (Massa and Gilroy, 2003) must be accommodated.
Other dimensions could be added to the behavior space, such as extending the age range studied, or potentially even from further analysis of the original image set. Also, the cellular basis of gravitropic bending could be explored by kinematic assays (Silk, 1984) that may show informative patterns in local growth rates, cell production rates, and cell displacements relative to the tip throughout the condition space (Walter et al., 2009). A next step in the systems-level direction would be to add root gene expression profiles at different positions in the condition space such that the molecular underpinnings of the different behaviors could be inferred.
MATERIALS AND METHODS
Seeds, Solutions, and Plant Culture
Seven separately raised lots of Arabidopsis (Arabidopsis thaliana; Columbia ecotype) seeds harvested over a 12-month period were used here. After harvesting, seeds were passed through a series of U.S. standard brass test sieves (Fisher Scientific Co.; http://www.fishersci.com) with grading sizes of 212, 250, 280, 300, or 355 μm. Morphological characteristics of the resulting four seed populations were determined by collecting images of approximately 1,000 seeds spread over the bottom of a dish with a high-resolution flatbed scanner. An image analysis algorithm used thresholding and blob detection routines to quantify the area of each seed. The recorded seed areas were used to construct the distributions in Figure 2B. For each gravitropism experiment, two seeds were sown on either simple or rich medium in petri plates and then stratified at 4°C for 2 to 6 d to synchronize germination. The simple medium consisted of 1 mm KCl, 1 mm CaCl2, 5 mm MES, and 1% agar adjusted to pH 5.7 with BisTris propane. The rich medium consisted of 3 mm KNO3, 2 mm Ca(NO3)2·4H2O, 0.5 mm MgSO4·7H2O, 1 mm (NH4)H2PO4, 0.56 mm myoinositol, 2.3 mm MES, 10 g/L Suc, micronutrients, and 1% agar and was adjusted to pH 5.7 with KOH or HCl. The micronutrients consisted of 25 μm KCl, 17.5 μm H3BO3, 1 μm MnSO4·H2O, 1 μm ZnSO4·7H2O, 0.25 μm CuSO4·5H2O, 0.25 μm (NH4)6Mo7O24·4H2O, and 25 μm (ethylene-dinitrilo)tetraacetic acid (Fe-Na EDTA). After stratification, plates were placed vertically under continuous white fluorescent light at a photon fluence rate of 50 μmol m−2 s−1 in a room used only for these experiments maintained at approximately 25°C.
Image Acquisition
A Marlin F146B CCD camera (Allied Vision Technologies; http://www.alliedvisiontec.com) outfitted with a macro-zoom lens (model NT59-157; Edmund Optics; http://www.edmundoptics.com) and an infrared-passing filter (UV/Vis-Cut R-72; Edmund Optics Inc.; http://www.edmundoptics.com) formed the basis of an imaging station. The petri plate with seedling to be imaged was held vertically and transverse to the optical axis of the camera in a fixture mounted on an x,y,z positioning device. An hour after the plates with seedlings were placed in front of the cameras, the plate was rotated clockwise until the tip of the root being imaged was aligned by eye with the camera horizon. An infrared backlight with peak output at 880 nm (model NT55-819; Edmund Optics Inc.) behind the sample formed the captured image while white fluorescent light provided illumination for the seedlings. More details of the custom image acquisition system are presented here: http://phytomorph.wisc.edu/parts_list.htm. Seven identical stations were closely spaced to reduce any microenvironmental differences in the room. A single computer acquired images every 2 min for 10 h from each of the seven cameras. The resulting 8-bit grayscale tagged image format files each consisted of 1,392 × 1,040 pixels. The combination of lens and CCD sensor gave a spatial resolution of 8 μm pixel−1. Typically, two 10-h experiments employing the bank of seven cameras were performed each day. The systematized workflow made it possible to control seedling age (2, 3, or 4 d after removal from stratification) within a range that did not exceed 4 h. Each discrete condition is represented by at least 40 independent trials.
Image Analysis
The root midline or medial axis was extracted from each image using the distance transform-based method described by Miller et al. (2007). The direction of the root tip in each image was determined by determining the first principal component of the last 10 midline points. Tip angle was taken as the angle formed between the first principal component and the camera's horizon. Growth rate was calculated as the derivative of the midline length over time. Tip angle and root length measurements were indexed into a database containing the metadata related to each experiment. Access to the entire database is available on request. To measure root width, a region from 100 μm back from the root tip was isolated from the final image of each trial. The average distance from the midline to the nearest root contour point within this isolated region was found and then multiplied by 2 to estimate the root width. The curvature distributions were determined as previously described (Miller et al., 2007) except that instead of extending the analysis window over time at a rate equal to the average growth rate, a fixed-length section of midline anchored at the tip was analyzed over time. The color curvature plots in Figure 10 cover this portion of the root except for the apical-most 60 microns because curve fitting required for curvature determination was not reliable at the terminus and this portion of the root does not undergo differential growth.
Data Analysis
All image processing and post-processing analyses were performed by algorithms custom coded in the MATLAB programming language (Mathworks Inc.; http://www.mathworks.com). Eigenvector decomposition, k-means clustering, and wavelet analysis were performed using built-in MATLAB functions. For k-means clustering, each trial was treated as a point in 301-dimensional space and the entire population of trials was optimally separated into three groups without respect to condition. Three was chosen as the number of classes for k-means classification because inspection of the results by eye showed under benders, normal benders, and overshooters were natural, useful categories. Also, three categories displayed the informative trends shown in Figure 5 while useful, integrative trends were not obvious when larger numbers of classes were tried. After classification was performed, each trial was parsed out by position in the conditional space to which it belonged to create Figure 5. PCA was also performed on the covariance matrix, with column vectors as tip angle observations at a particular time. PC1 and PC2 of each response were then categorized according to position within the conditional space. Wavelet analysis was performed on each individual tip angle response using the derivative of the Gaussian as the transforming function. A window size of 3 was used, which resulted in some smoothing of the resulting curve.
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Table S1. Elemental content of small and large seeds expressed per microgram of tissue.
Supplemental Table S2. Elemental content of small and large seeds expressed per seed.
Supplemental Movie S1. Example movie of an Arabidopsis root undergoing gravitropism.
Supplementary Material
Acknowledgments
We thank David Salt, Purdue University, for performing the elemental analysis on seeds.
This work was supported by the National Science Foundation Plant Genome Research Program (grant no. DBI–0621702) and by the Department of Energy (grant no. DE–FG02–04ER15527).
The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (www.plantphysiol.org) is: Edgar P. Spalding (spalding@wisc.edu).
The online version of this article contains Web-only data.
Open Access articles can be viewed online without a subscription.
References
- Ali-Rachedi S, Bouinot D, Wagner M, Bonnet M, Sotta B, Grappin P, Jullien M (2004) Changes in endogenous abscisic acid levels during dormancy release and maintenance of mature seeds: studies with the Cape Verde Islands ecotype, the dormant model of Arabidopsis thaliana. Planta 219 479–488 [DOI] [PubMed] [Google Scholar]
- Blancaflor EB, Fasano JM, Gilroy S (1998) Mapping the functional roles of cap cells in the response of Arabidopsis primary roots to gravity. Plant Physiol 116 213–222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boonsirichai K, Guan C, Chen R, Masson PH (2002) Root gravitropism: an experimental tool to investigate basic cellular and molecular processes underlying mechanosensing and signal transmission in plants. Annu Rev Plant Biol 53 421–447 [DOI] [PubMed] [Google Scholar]
- Chavarría-Krauser A (2006) Quantification of curvature production in cylindrical organs, such as roots and hypocotyls. New Phytol 171 633–641 [DOI] [PubMed] [Google Scholar]
- Chavarría-Krauser A, Nagel KA, Palme K, Schurr U, Walter A, Scharr H (2008) Spatio-temporal quantification of differential processes in root growth zones based on a novel combination of image sequence processing and refined concepts describing curvature production. New Phytol 177 811–821 [DOI] [PubMed] [Google Scholar]
- Donohue K (2009) Completing the cycle: maternal effects as the missing link in plant life histories. Philos Trans R Soc Lond B Biol Sci 364 1059–1074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fasano JM, Swanson SJ, Blancaflor EB, Dowd PE, Kao T, Gilroy S (2001) Changes in root cap pH are required for the gravity response of the Arabidopsis root. Plant Cell 13 907–922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friml J, Wisniewska J, Benková E, Mendgen K, Palme K (2002) Lateral relocation of auxin efflux regulator PIN3 mediates tropism in Arabidopsis. Nature 415 806–809 [DOI] [PubMed] [Google Scholar]
- Harrison B, Morita M, Masson P, Tasaka M (2008) Chapter 2: Signal transduction in gravitropism. In S Gilroy, P Masson, eds, Plant Tropisms. Blackwell Publishing, Ames, IA, pp 21–45
- Harrison BR, Masson PH (2008) ARL2, ARG1 and PIN3 define a gravity signal transduction pathway in root statocytes. Plant J 53 380–392 [DOI] [PubMed] [Google Scholar]
- Hou G, Kramer VL, Wang YS, Chen R, Perbal G, Gilroy S, Blancaflor EB (2004) The promotion of gravitropism in Arabidopsis roots upon actin disruption is coupled with the extended alkalinization of the columella cytoplasm and a persistent lateral auxin gradient. Plant J 39 113–125 [DOI] [PubMed] [Google Scholar]
- Kiss JZ (2000) Mechanisms of the early phases of plant gravitropism. CRC Crit Rev Plant Sci 19 551–573 [DOI] [PubMed] [Google Scholar]
- Lahner B, Gong J, Mahmoudian M, Smith EL, Abid KB, Rogers EE, Guerinot ML, Harper JF, Ward JM, McIntyre L, et al (2003) Genomic scale profiling of nutrient and trace elements in Arabidopsis thaliana. Nat Biotechnol 21 1215–1221 [DOI] [PubMed] [Google Scholar]
- Lewis DR, Miller ND, Splitt BL, Wu G, Spalding EP (2007) Separating the roles of acropetal and basipetal auxin transport on gravitropism with mutations in two Arabidopsis Multidrug Resistance-like ABC transporter genes. Plant Cell 19 1838–1850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massa GD, Gilroy S (2003) Touch modulates gravity sensing to regulate the growth of primary roots of Arabidopsis thaliana. Plant J 33 435–445 [DOI] [PubMed] [Google Scholar]
- Miller ND, Parks BM, Spalding EP (2007) Computer-vision analysis of seedling responses to light and gravity. Plant J 52 374–381 [DOI] [PubMed] [Google Scholar]
- Moulia B, Fournier M (2009) The power and control of gravitropic movements in plants: a biomechanical and systems biology view. J Exp Bot 60 461–486 [DOI] [PubMed] [Google Scholar]
- Mullen JL, Ishikawa H, Evans ML (1998) Analysis of changes in relative elemental growth rate patterns in the elongation zone of Arabidopsis roots upon gravistimulation. Planta 206 598–603 [DOI] [PubMed] [Google Scholar]
- Nakabayashi K, Okamoto M, Koshiba T, Kamiya Y, Nambara E (2005) Genome-wide profiling of stored mRNA in Arabidopsis thaliana seed germination: epigenetic and genetic regulation of transcription in seed. Plant J 41 697–709 [DOI] [PubMed] [Google Scholar]
- Pigliucci M (2005) Evolution of phenotypic plasticity: where are we going now? Trends Ecol Evol 20 481–486 [DOI] [PubMed] [Google Scholar]
- Pigliucci M, Schlichting CD (1995) Ontogenetic reaction norms in Lobelia siphilitica (Lobeliaceae): response to shading. Ecology 76 2134–2144 [Google Scholar]
- Qi Z, Spalding EP (2004) Protection of plasma membrane K+ transport by the salt overly sensitive1 Na+-H+ antiporter during salinity stress. Plant Physiol 136 2548–2555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roach DA, Wulff RD (1987) Maternal effects in plants. Annu Rev Ecol Syst 18 209–235 [Google Scholar]
- Sangster TA, Salathia N, Undurraga S, Milo R, Schellenberg K, Lindquist S, Queitsch C (2008) HSP90 affects the expression of genetic variation and developmental stability in quantitative traits. Proc Natl Acad Sci USA 105 2963–2968 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlichting CD (1986) The evolution of phenotypic plasticity in plants. Annu Rev Ecol Syst 17 667–693 [Google Scholar]
- Schlichting CD (2008) Hidden reaction norms, cryptic genetic variation, and evolvability. Ann N Y Acad Sci 1133 187–203 [DOI] [PubMed] [Google Scholar]
- Schlichting CD, Pigliucci M (1998) Phenotypic Evolution: A Reaction Norm Perspective. Sinauer, Sunderland, MA
- Schlichting CD, Smith H (2002) Phenotypic plasticity: linking molecular mechanisms with evolutionary outcomes. Evol Ecol 16 189–211 [Google Scholar]
- Schmitt J, Niles J, Wulff RD (1992) Norms of reaction of seed traits to maternal environments in Plantago lanceolata. Am Nat 139 451–466 [Google Scholar]
- Scott AC, Allen NS (1999) Changes in cytosolic pH within Arabidopsis root columella cells play a key role in the early signaling pathway for root gravitropism. Plant Physiol 121 1291–1298 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silk WK (1984) Quantitative descriptions of development. Annu Rev Plant Physiol 35 479–518 [Google Scholar]
- Silk WK, Erickson RO (1978) Kinematics of hypocotyl curvature. Am J Bot 65 310–319 [Google Scholar]
- Spalding EP, Hirsch RE, Lewis DR, Qi Z, Sussman MR, Lewis BD (1999) Potassium uptake supporting plant growth in the absence of AKT1 channel activity: inhibition by ammonium and stimulation by sodium. J Gen Physiol 113 909–918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sultan SE (2004) Promising directions in plant phenotypic plasticity. Perspect Plant Ecol Evol Syst 6 227–233 [Google Scholar]
- Tonsor SJ, Alonso-Blanco C, Koornneef M (2005) Gene function beyond the single trait: natural variation, gene effects, and evolutionary ecology in Arabidopsis thaliana. Plant Cell Environ 28 2–20 [Google Scholar]
- Walter A, Silk WK, Schurr U (2009) Environmental effects on spatial and temporal patterns of leaf and root growth. Annu Rev Plant Biol 60 279–304 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.