Distributions of observed death tolls govern sensitivity to human fatalities

Abstract

How we react to humanitarian crises, epidemics, and other tragic events involving the loss of human lives depends largely on the extent to which we are moved by the size of their associated death tolls. Many studies have demonstrated that people generally exhibit a diminishing sensitivity to the number of human fatalities and, equivalently, a preference for risky (vs. sure) alternatives in decisions under risk involving human losses. However, the reason for this tendency remains unknown. Here we show that the distributions of event-related death tolls that people observe govern their evaluations of, and risk preferences concerning, human fatalities. In particular, we show that our diminishing sensitivity to human fatalities follows from the fact that these death tolls are approximately power-law distributed. We further show that, by manipulating the distribution of mortality-related events that people observe, we can alter their risk preferences in decisions involving fatalities. Finally, we show that the tendency to be risk-seeking in mortality-related decisions is lower in countries in which high-mortality events are more frequently observed. Our results support a model of magnitude evaluation based on memory sampling and relative judgment. This model departs from the utility-based approaches typically encountered in psychology and economics in that it does not rely on stable, underlying value representations to explain valuation and choice, or on choice behavior to derive value functions. Instead, preferences concerning human fatalities emerge spontaneously from the distributions of sampled events and the relative nature of the evaluation process.

Every year, millions of human lives are lost to accidents, disasters, armed conflicts, and other deadly causes. Our reactions to these tragic events—including our willingness to provide aid and demand that our governments intervene—depend largely on the extent to which we are moved by the size of their associated death tolls (1). Research in psychology (1–4) and economics (5–7) has demonstrated that people tend to show a diminishing sensitivity to the number of human fatalities and, equivalently, a preference for risky (vs. sure) alternatives in decisions under risk involving human losses. As a result, policy makers charged with responding to humanitarian crises or preventing unnecessary deaths may inadvertently fail to maximize the number of lives saved (1). Although well documented, and despite its grave implications, the reason for this tendency is not well understood.

The standard way of explaining valuation and choice, even for human fatalities, has been to assume the existence of underlying utility functions (i.e., stable representations of value) that drive observed preferences (8). Although utility-based approaches have provided important constraints on the set of possible theories that can describe people's preferences, they are nonetheless limited in several ways. Most importantly, utility functions do not really explain preferences but merely redescribe them in mathematical terms (unless one assumes that such functions are directly represented in our mental architecture, which seems computationally implausible). Our understanding of valuation and choice concerning human fatalities would therefore greatly benefit from a process-level theory, which moves past the limitations of utility-based theories while still being able to accurately predict people's preferences.

In this article, we provide such an account and report empirical evidence to support it. Our account capitalizes on parallels between perception and decision-making (2, 9, 10). In particular, sensitivity to changes in a perceptual stimulus (e.g., brightness) or decision outcome (e.g., wealth) generally diminishes as the stimulus's initial magnitude increases (2, 9). This diminishing sensitivity implies that, in perception and decision-making alike, the relationship between objective magnitude and subjective evaluation is often a concave function that is monotonically increasing but marginally decreasing. As we noted earlier, a number of studies have shown that this psychophysical relationship even extends to evaluations of human fatalities: as an event's death toll increases, our sensitivity to the loss of life decreases, so that each additional death has a diminishing affective impact (1, 3, 4). Other studies have shown a general preference for risky alternatives in decisions under risk involving human losses (2), which also implies a concave disutility function for human fatalities (2, 8, 9).

Model Description.

The model we describe builds on a recently developed theoretical framework (11–13) that uses fundamental psychological principles to explain how we evaluate relatively abstract magnitudes such as money (11, 12), time (11), probability (11, 12), color (14), and luminance (15). According to this framework, the evaluation process is governed by a few simple cognitive operations (11, 12): To evaluate the death toll associated with a specific target event (or “event-associated death-toll”; EADT), people first draw upon a sample of comparable events from their memory. Specifically, they sample from a mixture of previously observed events (i.e., long-term memory sampling) and events in their recent or immediate context (i.e., short-term memory or working memory sampling) to obtain a set of comparison death tolls. Then they compare the target EADT with all those in the sampled set. For example, a person might compare a target EADT with other EADTs that he or she has recently learned about from watching the news, reading a newspaper, or conversing with family, friends, or colleagues. The disutility or “shock” associated with a target EADT is simply the proportion of pair-wise comparisons in which it dominates or ties, which is its percentile rank among the sampled events (i.e., the proportion of sampled EADTs that are smaller than or equal to the target). (A formal description of the model is provided in the SI Text.) Thus, a target EADT is considered large if it ranks above most sampled EADTs (and small if it ranks below most of them) regardless of its absolute magnitude. The sampling process is psychologically plausible given evidence that humans and other animals efficiently encode and recall frequencies (16). And the relative nature of the evaluation process is supported by extensive evidence that people are much better able to provide relative, rather than absolute, judgments (17, 18). For our current purposes, this model can remain agnostic about whether the memory sampling and pair-wise comparison operations are fast, unconscious, and automatic or slow, conscious, and deliberate processes (future research will be needed to answer this question). For simplicity, we start by assuming that the sampling process is uniformly random, so that every EADT in memory is equally likely to be selected for comparison.

This model implies that the disutility associated with a target EADT will be determined by the distribution of comparison EADTs from which a person can draw, which will be a function of his or her accumulated experiences and the recent or immediate context surrounding the evaluation. This allows the model to parsimoniously explain individual and contextual differences in reactions to human fatalities. Specifically, as an EADT's disutility is equal to the probability that it is larger than or equal to another randomly sampled EADT, the psychophysical (or disutility) function relating human fatalities to their associated shock values is equivalent to the cumulative probability distribution of EADTs that one has observed (see SI Text). And because risk preferences follow from these disutility functions (2, 8, 9, 19) (see SI Text), the model should be able to predict people's choices in decisions under risk involving human losses, as long as the distribution of sampled EADTs is approximately known.

This led us to make three predictions. First, diminishing sensitivity to human fatalities and risk-seeking preferences in the domain of human losses should be reflected in the distribution of EADTs that people generally observe. Specifically, for the model to explain existing results, the cumulative probability distribution of observed EADTs must be concave. In addition, the model makes two unique predictions: (i) that altering the distribution of observed EADTs will lead to predictable changes in people's risk-preferences and (ii) that risk preferences will vary between countries with different EADT distributions. We tested these predictions in three separate studies.

Study 1.

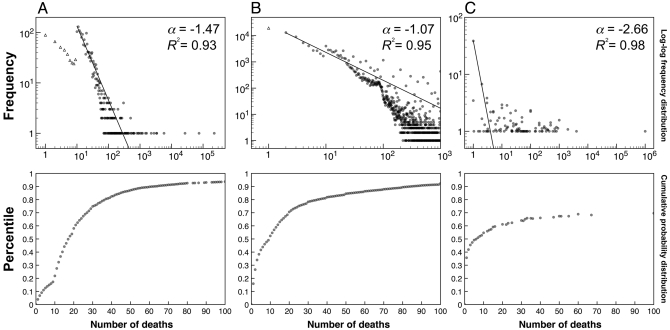
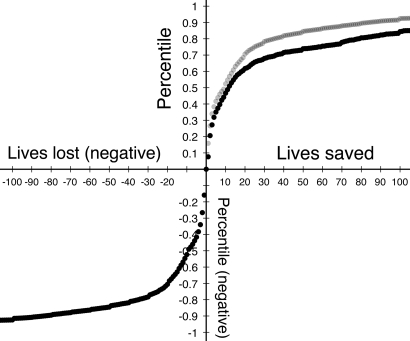
First, we hypothesized that the cumulative probability distribution of EADTs that people typically observe is concave. To test this prediction, we analyzed data from three sources: (i) a global survey of disasters and their associated death tolls (Study 1A), (ii) a measure of the frequency with which EADTs are mentioned in the media (Study 1B), and (iii) the examples provided by a sample of respondents who were asked to recall EADTs from memory (Study 1C). This first prediction is well supported: all three cumulative probability distributions are monotonically increasing and marginally decreasing (Fig. 1 A–C). This concavity is a direct result of the fact that EADT frequencies are reasonably well approximated by a power-law distribution (Fig. 1 A–C). Power-laws are characterized by a number of interesting properties, such as scale invariance (20, 21), and may provide important clues about the underlying generation process (22, 23). With regard to the psychophysics of human life valuation, they have one particularly useful property: integrating over them yields cumulative probability functions that are equivalent to the constant relative risk aversion (CRRA) utility functions often used in economics to describe preferences (19, 24) (see SI Text). In fact, one result of the model we describe is that the best-fitting power-law parameter provides a reasonably good measure of disutility curvature, which quantifies both the rate at which sensitivity to human life decreases and the resulting level of risk preference (see SI Text). The best fitting estimate of the power-law parameter for each dataset is negative (Fig. 1 A–C) and therefore implies a concave disutility function and a preference for risky alternatives (see SI Text). Furthermore, an examination of media attention to the number of human lives that are saved (rather than lost) reveals that the cumulative distribution of human “gains” is also concave but less steep than the cumulative distribution of lives lost (Fig. 2). We would therefore predict that the utility associated with lives saved is concave, leading to risk-averse choices (2, 9), and that human losses receive more weight than equivalent gains (9). In fact, both predictions are empirically supported (2, 25, 26).

Fig. 1.

Log-log plots of EADT frequency distributions (Top) and their corresponding cumulative probability distributions shown up to 100 deaths (Bottom). Solid lines (Top) are best-fitting power-functions of the frequency data, with the associated power parameter estimate (α) and model fit (R²) displayed (Top Right). (A) Fatalities from natural and industrial disasters occurring in 2003 through 2007. The power-law function is fitted to events involving 10 or more deaths (dots) because frequencies are underestimated for events involving fewer than 10 deaths (triangles; see SI Text). The cumulative probability distribution plot is based on all of the data (triangles and dots). (B) Media attention (in 2000–2007) to mortality-related events. The power-law function is fitted to events involving two or more deaths (dots) because media attention to events involving a single death (triangle) is likely underestimated (see SI Text). The cumulative probability distribution plot is based on all the data (triangle and dots), as well as estimated frequencies for events involving more than 1,000 deaths (see SI Text). (C) Mean recalled EADTs occurring in a person's lifetime. Mean frequencies and mean percentile-ranks were obtained by repeatedly and randomly sampling the events that respondents recalled (see SI Text).

Fig. 2.

Black dots represent the cumulative probability distributions of media attention (in 2000–2007) to events involving human lives saved (Top Right) and lives lost (Bottom Left). The gray dots (Top Right) represent a 180° rotation of the data for lives lost (Bottom Left) obtained by multiplying the coordinates by −1, and show that the curve is steeper for lives lost than for lives saved.

Study 2.

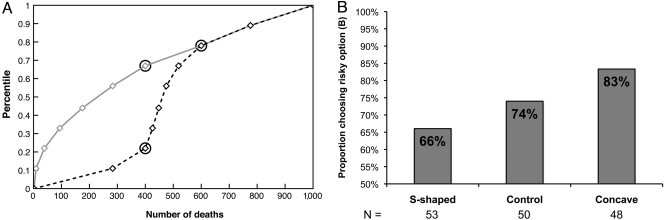
Second, we hypothesized that altering the distribution of EADTs that people observe would lead to predictable changes in their risk preferences. Although we have assumed, for simplification, that comparison EADTs are uniformly sampled from memory, a more realistic assumption is that recently observed EADTs are sampled with higher likelihood (27). This would allow them to have a nonnegligible impact on risk preferences even though they represent a tiny fraction of all of the EADTs in memory. We therefore predicted that exposing decision-makers to a highly concave cumulative distribution of EADTs would increase the appeal of risky options whereas exposing them to an S-shaped cumulative distribution of EADTs would have the opposite effect (see Methods). To test this prediction, we conducted an experiment in which we had some human participants read about a set of EADTs and rate how negatively they felt about each one. These EADTs were selected to form either a concave or S-shaped cumulative distribution (Fig. 3A). Following this subtle manipulation, participants were asked to choose between a risky option and a sure option in a hypothetical decision scenario involving human lives at risk (2). The rating task had a significant impact on participants' risk preferences (Fig. 3B). Participants who first rated a concave cumulative distribution of EADTs were subsequently more likely to choose the risky alternative than those who first rated an S-shaped cumulative distribution of EADTs [n = 101, χ²(1) = 3.94, P = 0.047, φ = 0.20].

Fig. 3.

Experimental manipulation and results for Study 2. (A) Cumulative probability distributions of EADTs (diamonds) obtained by ranking the EADTs that participants rated and the decision scenario's two target EADTs (circled). The S-shaped distribution curve (dashed black line) is superimposed on the concave distribution curve (gray line). (B) The proportion of participants in each condition who chose the risky option (program B). Numbers below the bars are sample sizes.

Study 3.

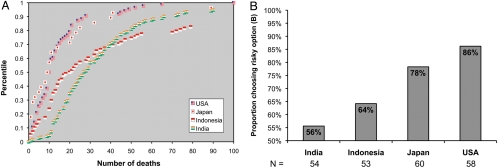
Finally, we hypothesized that risk preferences would vary between countries with different EADT distributions (we assume that people are especially likely to observe and sample EADTs occurring in their own country). In particular, we predicted that a preference for risky options would be more prevalent in countries in which the cumulative distribution of EADTs is highly concave than in countries in which it is less concave. To test this prediction, we measured risk preferences in four countries that differ substantially in terms of their EADT distributions: Japan, the United States, India, and Indonesia. High-magnitude EADTs are relatively rare in Japan and the United States, but much more frequent in India and Indonesia [Emergency Events Database (EM-DAT); see www.em-dat.net]. As a result, the cumulative distributions of EADTs are more concave for the former two countries than for the latter two (Fig. 4A). We therefore predicted that a large majority of American and Japanese respondents would prefer the riskier option in a decision under risk involving human fatalities, but that Indian and Indonesian respondents would be less inclined to choose it. To test this prediction, we gave respondents in each country a hypothetical decision scenario similar to the one we used in our previous experiment and measured the proportion of risky option choices (Fig. 4B). The tendency to select the risky alternative differed across countries [n = 225, χ²(3) = 15.69, P = 0.0013, φ = 0.26]. Specifically, Indian respondents were less likely to prefer the risky option than American respondents [n = 112, χ²(1) = 12.87, P = 0.00033, φ = 0.34] and Japanese respondents [n = 114, χ²(1) = 6.73, P = 0.0095, φ = 0.24]. Similarly, Indonesian respondents were less likely to choose the risky option than American respondents [n = 111, χ²(1) = 7.32, P = 0.0068, φ = 0.26] and Japanese respondents [n = 113, χ²(1) = 2.79, 1-tailed P = 0.047, φ = 0.16]. By contrast, Indian and Indonesian respondents did not significantly differ in terms of their risk preferences [n = 107, χ²(1) = 0.82, P = 0.36], nor did American and Japanese respondents [n = 118, χ²(1) = 1.25, P = 0.26]. In line with our prediction, we found that Indian and Indonesian respondents were less likely to choose the risky alternative than Japanese and American respondents (Fig. 4B). In fact, the relative prevalence of risk-seeking choices across countries (Fig. 4B) is perfectly predicted by the relative size of their EADT frequency distribution power parameter estimates (Fig. 4A; also see SI Text), which further supports the model we are testing. The possibility that these results reflect a domain-general tendency for Indian and Indonesian respondents to be less risk-seeking (or more risk-neutral) than American and Japanese respondents seems unlikely in light of evidence that Indian and American respondents have comparable risk preferences in the financial domain (24, 28), that risk preferences are highly domain-specific (29), and that the existence of cross-national differences in risk preferences is domain-dependent (30).

Fig. 4.

Cross-national disaster deaths and risk preferences in Study 3. (A) Cumulative probability distributions of disaster-related fatalities in 2003 through 2007 (shown up to 100 deaths) experienced by India (best-fitting power parameter for ≥10 deaths, α = −0.59, R² = 0.33), Indonesia (α = −3.07, R² = 0.78), Japan (α = −4.56, R² = 0.91), and the United States (α = −6.64, R² = 0.78). (B) The proportion of respondents in each country who chose the risky option (program B). Numbers below the bars are sample sizes.

Discussion

In summary, we find support for a model of human life valuation based on memory sampling and relative judgment (11–13). This model departs from the utility-based approaches typically encountered in psychology (8) and economics (19) in that it does not rely on stable, underlying value representations to explain valuation and choice, or on choice behavior to derive value functions. Instead, preferences concerning human fatalities emerge spontaneously from the distributions of sampled events and the relative nature of the evaluation process. The model successfully explains a variety of findings in the existing literature (Study 1) and makes unique predictions that were also supported (Studies 2 and 3). Our results suggest that reactions to fatalities are fundamentally relative and dependent on personal history and context. These studies also provide support for the general idea that the distributional properties of our environment are reflected in our cognitive system (31–34), and that some apparent cross-cultural differences may actually reflect cross-national variations in these distributions (35).

The diminishing sensitivity we show to losses of human life could have a number of functional purposes. For example, if our capacity to distinguish EADTs is limited, it might make sense for this ability to be concentrated (i.e., sharpest) around high-frequency, low-death toll events, as these tend to be packed together in time and in magnitude, making them otherwise very difficult to distinguish. Unfortunately, this comes at the cost of blurring our ability to distinguish low-frequency, high-death toll events. Alternatively, and given evidence that people have limited resources for coping with negative events (36), a diminishing sensitivity to increasing fatalities may protect us from being emotionally overwhelmed by large death tolls. The notion that there is an upper bound on the disutility (or shock) experienced by a person who observes a tragic event is captured in our theoretical account by the asymptotic nature of cumulative probability functions.

Regardless of its possible functions, understanding the factors responsible for our diminishing sensitivity to human fatalities has the potential to save many lives by increasing public reactions to distant disasters, epidemics, and genocides, while also helping policy makers correctly prioritize their efforts to prevent and respond to these humanitarian crises and other deadly risks.

Methods

Study 1A: Centre for Research on the Epidemiology of Disasters/EM-DAT Data.

Data on the occurrence of disasters and their associated death tolls were obtained from the EM-DAT (www.em-dat.net) maintained by the Centre for Research on the Epidemiology of Disasters (CRED) at Université Catholique de Louvain in Brussels, Belgium. The EM-DAT is the only publicly available global database on the occurrences and impacts of natural and industrial disasters. The EM-DAT data were also used to produce the country-specific disaster-mortality distributions in Study 3 (see Fig. 4A). See SI Text for details of Study 1A data collection.

Study 1B: Google News Archive Data.

Data on media attention to events involving human deaths (i.e., EADTs) were obtained by iterative search of the Google News Archives (GNA; see http://news.google.com/archivesearch) for news articles whose titles contained keywords related to losses (e.g., “10 people died”) or “gains” (e.g., “10 people survived”) in human lives. For each search, the number of relevant articles returned (i.e., the number of “hits”) was recorded, thus providing a measure of the total media attention allocated to events associated with a given loss (or gain) in human lives. See SI Text for details of Study 1B data collection.

Study 1C: Recalled EADTs.

Data on recalled EADTs were obtained by administering a survey that asked respondents to recall events involving human deaths. We then repeatedly sampled these events to estimate the average frequency and cumulative probability distribution of recalled EADTs. See SI Text for details of Study 1C data collection.

This study and all future studies reported in this paper were approved by Princeton University's Institutional Review Panel for Human Subjects and/or the University of Oregon's Office for Protection of Human Subjects (in Study 3, we also obtained approval from the overseas institutions where we administered surveys). Written or oral consent was also obtained from all our participants.

Study 2: Experimental Manipulation of Observed EADTs.

Participants were 157 adults (56% female; age range, 18–77 y) recruited from a large shopping mall in the northeastern United States, who were paid for their participation.

The entire experiment was conducted using a paper questionnaire that participants read and completed on their own. The questionnaire's cover page contained written instructions and the final page asked participants to report various demographic characteristics. The manipulation and the decision scenario were presented on separate pages (with the former directly preceding the latter).

To manipulate the distribution of comparison EADTs from which they would sample, participants were alternately assigned to one of three conditions (concave distribution, S-shaped distribution, and control). Participants in the two treatment groups were first presented with eight randomly ordered single-sentence descriptions of disasters and accidents whose death tolls ranged from two to 1,000 (see Table S2). The top of the page containing the manipulation explained that these events represented a random sample of all of the natural and industrial disasters that had occurred in the past year (in reality, these events were all fictional). Participants were instructed to first read all the event descriptions carefully, and then to indicate how each event made them feel, using a 10-point rating scale that ranged from “neutral” to “very negative.” The purpose of this exercise was to provide a subtle channel through which participants would encode these EADTs. The two distributions of EADTs were selected so that, if sampled, they would either increase or decrease the distance (relative to baseline), in percentile-ranks, between the two key magnitudes that participants had to evaluate in the subsequent decision scenario (400 deaths and 600 deaths; as discussed later).

Participants in the concave distribution condition were presented with eight EADTs that, if used as comparison magnitudes, would decrease the distance between the percentile-ranks of the two options presented in the subsequent decision scenario, thereby making the risky option more appealing (according to the model we are testing). Specifically, these EADTs were all selected to be either less than 400 or greater than 600, thus reducing the difference in ranks between the two target EADTs (Fig. 3A). Participants in the S-shaped distribution condition were presented with eight EADTs that, if used as comparison magnitudes, would increase the distance between the percentile-ranks of the two options presented in the subsequent decision scenario, thereby reducing the appeal of the risky option (according to the model we are testing). Specifically, these EADTs were selected so that many of them fell between 400 and 600, thus increasing the difference in ranks between the two target EADTs (Fig. 3A).

Following this manipulation, participants in both treatment conditions advanced to the decision scenario, which was presented on the next page of the questionnaire. To establish a baseline, a third, control group of participants was not exposed to either distribution manipulation and instead advanced directly to the decision scenario.

The decision scenario used to measure risk preferences was a modification of the “loss frame” version of the “Asian disease” problem (2, 8), which asks respondents to imagine a choice between two programs for combating the outbreak of a disease that is expected to kill 600 people. One program (the sure option) leads to 400 deaths with certainty, whereas the other (the risky option) offers a one-third chance that no one will die, but a two-thirds chance that all 600 will die. Our scenario referred to a real disease (the West Nile virus) rather than an imaginary “Asian disease,” but this was the only notable modification. One respondent did not provide a response to the disease scenario and was therefore excluded from the analysis. We also excluded data from five respondents who recognized the disease scenario (all five were university students). The exact scenario is presented in Fig. S1.

Although both programs have the same expected value (both lead to 400 deaths, on average), previous research (2) found that the majority (78%) of respondents preferred the risky option when these choices were framed in terms of lives lost, implying a diminishing sensitivity (i.e., marginally diminishing disutility) for the loss of human lives (a result that we replicated with our control group; see Fig. 3B). In particular, people seem to perceive the disutility associated with a sure loss of 400 lives to be greater than the expected disutility associated with a two-thirds probability of 600 deaths. In other words, for most respondents, the subjective shock produced by the knowledge that 400 people will die (or have died) seems to be greater than two thirds of the subjective shock associated with 600 deaths.

However, we expected that the share of respondents preferring the risky option in this scenario would decrease as the subjective distance (in terms of psychological shock) between 400 deaths and 600 deaths increased. Similarly, the share of respondents preferring the risky option was expected to increase as this subjective distance decreased. According to the model we are testing, participants assigned to the concave distribution condition would therefore be more likely to choose the risky alternative than participants assigned to the S-shaped distribution condition, which is what we found (Fig. 3B).

We should note that, strictly speaking, our manipulation varied not only the relative ranks of the target EADTs within the distributions that participants were exposed to, but also the means of these distributions. One might therefore attribute our results to a difference in means rather than ranks. This alternative explanation, however, is unlikely for at least three reasons. First, it seems implausible that participants calculated the means of these EADT distributions, let alone used this information to inform their subsequent choices. Second, research shows that rank-based accounts are better able to explain the effects of observed distributions on people's attitudes and preferences compared with mean-based accounts (37). Finally, an account based on differences between means fails to explain the results of Study 3 as, for example, Indonesia experienced a much higher mean EADT (1,813 deaths, on average, between 2003 and 2007) than the other three countries (including India, which was second with an average of 153 deaths), yet Indonesian respondents were neither the least, nor the most, likely to choose the risky alternative.

Study 3: Cross-National Differences in Risk-Preferences.

Data on EADT frequencies in each country were obtained from the EM-DAT (www.em-dat.net), as described earlier (Study 1A in Methods). Responses to the risky-decision scenario were collected from 249 university students in four countries. The Indian sample consisted of students at the University of Delhi (n = 60; 55% female). The Indonesian sample consisted of students at Pelita Harapan University and Ciputra University (n = 56; 73% female). The Japanese sample consisted of students at Rissyo University (n = 62; 65% female). The American sample consisted of students at the University of Oregon (n = 71; 61% female).

The procedure was similar across countries: paper questionnaires containing the decision scenario were administered to respondents who were recruited in their classrooms (some American respondents instead completed a Web-based version of the questionnaire in exchange for course credit). The questionnaire's cover page contained written instructions and the final page asked participants to report various demographic characteristics, including whether they had lived their entire life in the country where they were recruited. Those respondents who reported having lived outside the country in which the data were collected (n = 24) were excluded from the analysis.

The decision scenario was similar to the one used in Study 2 except for three modifications: First, the disease in question was not a specific epidemic but was simply described as “an unusual disease.” Second, the disease was specifically described as affecting the country in which the data were collected (this was the only feature that differed across countries). Third, the outbreak in the scenario was expected to kill 40 people, and the sure option led to 20 deaths with certainty whereas the risky option offered a 50% probability that all 40 would die and a 50% chance that none would die. These numbers were chosen because they represented values for which the four countries differed strongly in terms of EADT percentile-ranks (Fig. 4A) and because a 50% probability is easier to understand and compute than the one-third and two-thirds probabilities used in the original scenario. A 50% probability can, for example, be conceptualized as equivalent to flipping a fair coin to determine the outcome of the risky option. As before, the expected value, in terms of lives lost, was the same for both programs (20 deaths on average). English, Indonesian, and Japanese versions of the scenario are presented in Figs. S2–S4.

The survey was written in English for the American and Indian samples and translated for the Japanese and Indonesian samples. Two steps were taken to ensure that translations were as similar as possible in terms of the information conveyed: First, the survey was translated into Japanese and Indonesian by one pair of translators, then back-translated into English by a separate pair of translators. This was done to identify any meaningful distortions produced by the translation process. In addition, the three versions (English, Japanese, and Indonesian) of the survey were iteratively modified to accommodate each language's unique constraints until they converged on a shared meaning. These steps were repeated until we were satisfied that the three versions were as semantically similar as possible, and that they properly communicated the scenario.