Hierarchical computation in the canonical auditory cortical circuit

Abstract

Sensory cortical anatomy has identified a canonical microcircuit underlying computations between and within layers. This feed-forward circuit processes information serially from granular to supragranular and to infragranular layers. How this substrate correlates with an auditory cortical processing hierarchy is unclear. We recorded simultaneously from all layers in cat primary auditory cortex (AI) and estimated spectrotemporal receptive fields (STRFs) and associated nonlinearities. Spike-triggered averaged STRFs revealed that temporal precision, spectrotemporal separability, and feature selectivity varied with layer according to a hierarchical processing model. STRFs from maximally informative dimension (MID) analysis confirmed hierarchical processing. Of two cooperative MIDs identified for each neuron, the first comprised the majority of stimulus information in granular layers. Second MID contributions and nonlinear cooperativity increased in supragranular and infragranular layers. The AI microcircuit provides a valid template for three independent hierarchical computation principles. Increases in processing complexity, STRF cooperativity, and nonlinearity correlate with the synaptic distance from granular layers.

Sensory cortical processing is achieved through a basic anatomical and functional microcircuit that appears to be repeated across modalities with only minor modifications. It represents a hierarchy of connection patterns, with information proceeding to elements of the circuit in a largely sequential manner. In the main excitatory feed-forward pathway, thalamus sends projections to granular cortical layers. Information proceeds, largely serially, to supragranular and infragranular layers, where it is distributed to cortical and subcortical targets (1, 2). The basic structure of this microcircuit is present in auditory cortex (3), although despite our anatomical knowledge, little is known about whether and how processing principles differ between layers (4).

In primary auditory cortex (AI), the organization of each layer is complex, and much like a nucleus, has specific sources, targets, and local projection patterns, in addition to intralaminar and interlaminar connections (5). Further, the ascending and descending outputs originating from each layer likely serve different purposes, because each targets different regions of the auditory system (6). Because of this complexity, general rules that capture how stimulus representations change between layers remain unclear. To date, only a few parameters have been identified that remain relatively constant across cortical depth, including preferred frequency (7) and aurality (8–11). However, even for those parameters, deviations from uniformity have been observed (12, 13).

The complexity of auditory cortical anatomy leads to two main schemes. The first is that no general processing rules exist, because it has been speculated that microcircuits are too diverse to generate universal processing patterns (14). Alternatively, how stimuli are processed, such as the degree to which responses are nonlinear, may be stereotyped within and between layers. This would align the design of the cortical microcircuit with predictable algorithms and functional consequences.

Past work has produced ambiguous results when these schemes were explored. Some aspects of cortical response preferences are inherited from subcortical stations and typically show no major changes across layers (7–11). Other stimulus-related aspects undergo substantial transformations between auditory thalamus and cortex, in particular the sensitivity and selectivity for spectral and temporal envelope modulations (15). The shaping of these modulation preferences is predominantly accomplished through intracortical networks and can be captured by properties of spectrotemporal receptive fields (STRFs). Further transformations of spectrotemporal processing may occur in AI; thus, we need to examine how local circuits may transform stimulus information and express processing principles across cortical layers.

Because the connection patterns in cortical circuits are precise and relatively stereotyped, we can study the transformation of receptive field properties at different positions in the auditory microcircuit, paralleling approaches in the primary visual cortex (16). Here, we tested the hypothesis that properties of spectrotemporal receptive fields, and, in particular, how neurons process acoustic stimuli, follow an ordinal functional progression from granular to supragranular and then to infragranular layers, respectively, in accordance with the standard model of the dominant interlaminar circuit (1).

Results

We used multichannel electrode arrays to simultaneously record from several single neurons across all laminae in cat AI. Dynamic moving ripple noise stimuli were presented that contained temporal and spectral modulations known to drive cortical cells (15, 17). Modulation parameters were randomly varied, and STRFs were calculated from the responses. Two methods were used to obtain STRFs. In the first, we calculated the spike-triggered average (STA) (18, 19), which represents the average time-frequency stimulus envelope preceding a cortical action potential. A second approach to determine STRFs is based on maximizing the mutual information (MI) between the stimulus and the evoked spike train of a neuron. In this case, two parametrically independent but jointly operating STRFs are iteratively adjusted until the MI is maximized, resulting in two maximally informative dimensions (MIDs), and their associated nonlinearities (20). Earlier, we demonstrated that the concurrent operation of these two MIDs can capture a substantially larger proportion of the MI of cortical neurons than the STA or a single MID alone (21). In a previous report (46), we focused on the layer-specific temporal and spectral modulation content. However, neuronal stimulus preferences change widely across the tonotopic array, e.g., stimulus binaurality, bandwidth, or intensity, complicating a population analysis of general processing aspects (9, 10, 34). Here, we focus on layer-dependent auditory processing principles (“how”) that are largely independent from the stimulus content (“what”) (22).

Laminar Differences for STAs.

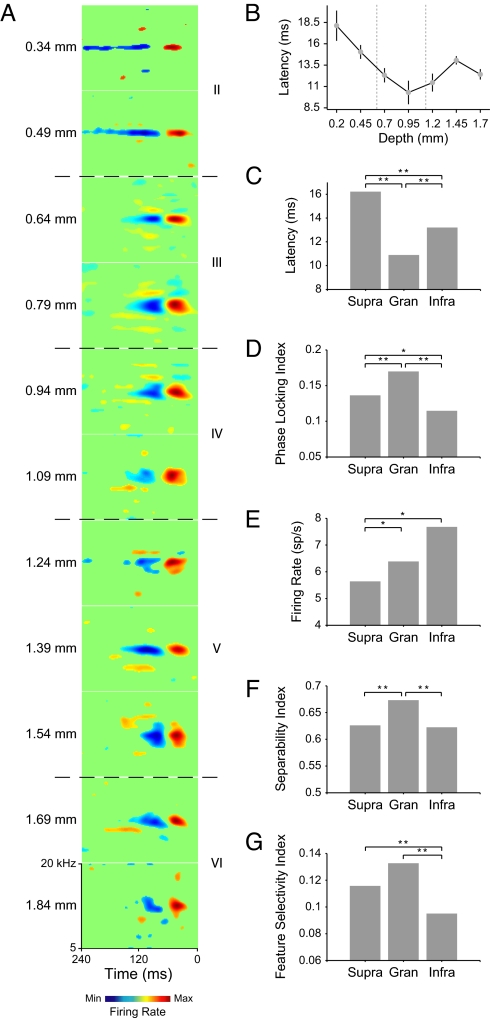
Across cortical depth, the main excitatory and inhibitory subfields of STAs were quite congruent for spectral position and shape (Fig. 1A). Usually, a main excitatory subfield (Fig. 1A, red) was followed by an inhibitory one (Fig. 1A, blue) at a consistent spectral position throughout the cortical depth. In contrast, other spectrotemporal characteristics clearly varied with layer. Excitatory latency was shortest at intermediate depths (Fig. 1A; 0.79 and 0.94 mm), and longest in supragranular layers (0.34 mm). The duration of the inhibitory subfields was often longest at more superficial locations (0.34 and 0.49 mm). At intermediate cortical depths, excitatory and inhibitory subfields for higher or lower frequencies were often temporally aligned (Fig. 1A; 0.79 and 0.94 mm). The spectrotemporal constellation of excitatory and inhibitory subfields often took more complex shapes at greater depths (Fig. 1A; 1.54 and 1.84 mm). Combined, many spectrotemporal features of STAs were not constant across cortical laminae.

Fig. 1.

Laminar distribution of STRF response properties. (A) STAs at different cortical depths. Red indicates increasing responsiveness, and blue indicates decreasing responsiveness. Depth is indicated to the left of the STAs, and layer is indicated to the right (II/IIIa: supragranular; IIIb/IV: granular; V/VI: infragranular). Value ranges are the same for all STAs. (B) Latency depth profile for all neurons (mean/SEM in nonoverlapping 0.25-mm bins). Dashed vertical lines indicate laminar boundaries. (C) Latency in supragranular, granular, and infragranular layers. (D) Phase-locking precision. (E) firing rate. (F) Spectrotemporal separability of STAs. (G) Feature selectivity. (t test with Bonferroni correction, *, P < 0.05; **, P < 0.01).

Several timing- and firing rate-related receptive field characteristics, estimated from the STAs, showed significant layer specificity. For population analysis, layers were differentiated according to recording depth measurements of the linear multielectrode array: supragranular (0–0.6 mm), granular (0.7–1.1 mm), and infragranular (1.2–1.85 mm) (see Materials and Methods and SI Text). For population data, STA latency was shortest in granular layers, which are known to receive early lemniscal thalamic inputs (Fig. 1 B and C). Time-locked responses to the ripple stimulus were most precise in granular layers, with progressively decreasing precision in supragranular and infragranular layers (Fig. 1D), compatible with the standard model of serial columnar information transfer.

Overall firing rate varied significantly with depth, with the highest rates in infragranular layers, and the lowest in supragranular layers, perhaps reflecting differences in dominant cell types and a greater diversity in converging inputs in lower layers (Fig. 1E) (23). These layer-dependent changes in firing rate do not correlate with the standard model of serial columnar information transfer alone, because the change in rate does not vary monotonically with position in the vertical cortical microcircuit.

Further layer-dependent differences emerged for the complexity of STA structure and the neural selectivity for stimulus features. One aspect of STRF/STA complexity is the independence of spectral and temporal processing. A low degree of separability indicates interdependence of temporal and spectral STRF aspects. STAs were most separable in granular layers, processing time and frequency more independently. Supragranular and infragranular layer STAs were significantly less separable (Fig. 1F), reflecting an increased spectrotemporal interdependence beyond that in lemniscal thalamic inputs.

Laminar differences were also evident in the degree of feature selectivity, which expresses how similar a stimulus has to be to the averaged preevent ensemble to produce an action potential (17). Neurons were most feature selective in granular layers, i.e., deviations between stimulus and STA pattern are not well tolerated (Fig. 1G). In infragranular layers, the feature selectivity was the lowest, and neurons were responsive to a less strict match between STA and stimulus. The STA analysis shows that major processing aspects captured by the STRF change with cortical layer. Neurons in granular layers appear to have a shorter response latency, higher timing precision, more separable STRFs, and higher feature selectivity than those in supragranular and infragranular layers. Thus, compared with thalamocortical input layers, the dominant cortical output layers have more complex STRF compositions, increased spectrotemporal interactions, and lower degrees of precision in response timing and feature specificity.

Laminar Differences for MIDs.

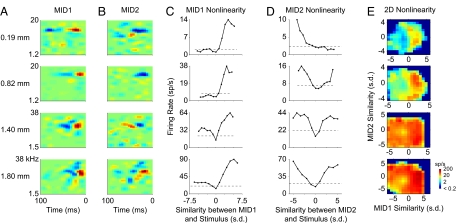
MIDs provide an expanded characterization of neuronal processing by revealing contributions of more than one STRF (or multicomponent stimulus dimension) in shaping a neuron's response properties (20, 21, 24). MIDs fall under linear–nonlinear models (25, 26) that combine linear spectrotemporal stimulus features with a static, but neuron-specific, nonlinearity to compactly represent neural processing (27). We estimated two MIDs, where the first (MID1) accounted for the most information between the stimulus and the response, and the second (MID2) further maximized the information (Fig. 2 A and B), and the nonlinearity associated with each MID (Fig. 2 C and D). Additionally, because both MIDs process stimuli concurrently, we estimated a 2D joint nonlinearity for the combined processing of the MIDs (Fig. 2E). The nonlinearities describe the relationship between stimulus features and neural response, representing a rule that quantifies the likelihood of a response given a stimulus (28).

Fig. 2.

MIDs and their nonlinearities. (A and B) First (MID1, A) and second (MID2, B) MIDs at different depths. Each row represents a neuron. (C) MID1 1D nonlinearities. Ordinate: spike rate; abscissa: similarity between the MID and stimulus. Dashed line indicates average firing rate. (D) MID2 1D nonlinearities. (E) 2D MID nonlinearities. Abscissas of C, D, and E and the ordinate of E are in units of standard deviations.

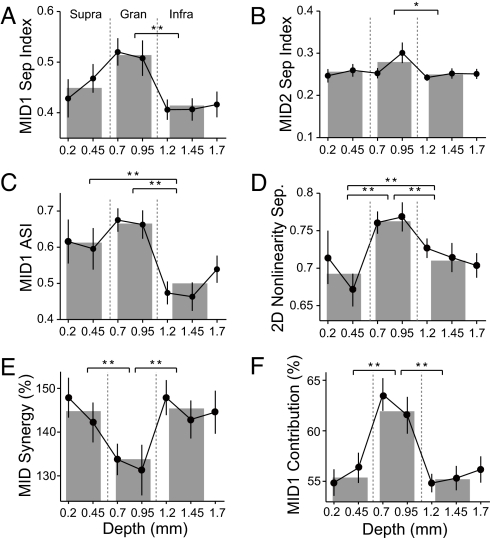
The two MIDs, and their nonlinearities, differed in shape (21) and showed different properties with laminar position. The spectrotemporal separability of MID1s mirrored that of STAs (21). MID1s were most separable in granular layers (Fig. 3A). Also, in granular layers, the MID1 nonlinearities were most asymmetric, i.e., responses are greatest for stimuli that are highly matched to the MID (Figs. 2C and 3C). On average, supragranular MID1 nonlinearities showed the same degree of asymmetry as granular MID1s (Fig. 3C). Infragranular neurons, however, had a clearly reduced asymmetry (Fig. 3C), suggestive of a processing strategy less sensitive to the phase, or polarity, of the spectrotemporal envelope. MID2s were relatively inseparable and with little layer specificity. Their time and frequency aspects may be less easily dissociated (Figs. 2B and 3B).

Fig. 3.

Population analysis of MIDs and nonlinearity structure across cortical depth. Data were binned according to cortical depths (filled circles; mean and SEM) and divided into supragranular, granular, and infragranular regions (gray bars). t test with Bonferroni correction, *, P < 0.05; **, P < 0.01. (A and B) Spectrotemporal separability of MID1 (A) and MID2 (B). (C) Asymmetry index of MID1 nonlinearity. (D) Separability of 2D nonlinearities. (E) Synergy of MID information. (F) Contribution of MID1 information relative to the joint MID1 and MID2 information.

The shape of the MID2 nonlinearity was highly symmetric, and this property was maintained across all depths (Fig. 2D), i.e., stimuli positively or negatively correlated with MID2 led to increased firing probabilities. The least asymmetric MID1 nonlinearities in infragranular layers were still significantly more asymmetric than the MID2 nonlinearities in any layer (Fig. 3C; ANOVA, P < 0.01). The structure of the joint 2D nonlinearities reflects the degree and nature of cooperativity between the two MIDs (see Fig. 2E). Absence of cooperativity would result in a joint nonlinearity nearly equal to the product of the two 1D nonlinearities, i.e., the 2D firing-probability distribution would be fully separable into two independent components. All neurons exhibited some degree of inseparability of their 2D nonlinearity, i.e., the two MIDs cooperated (Fig. 3D). The most separable nonlinearities were in granular layers, with significantly lower separability and increased cooperativity in supragranular and infragranular layers (Fig. 3D). Thus, the rule that governs the joint, two-MID processing is not a simple product of two 1D nonlinearities and implies that information processing becomes more nonlinear and complex as the synaptic distance from granular layers increases.

The degree of cooperativity of the two STRFs can be quantified by the synergy of the MIDs. Synergy is the MI captured by the jointly applied STRFs divided by the sum of the MI of each individual STRF. Synergy thus compares the joint processing to the independent processing of the MIDs. The average synergy in granular layers was significantly >100%, i.e., the cooperating STRFs captured more information than when considered in isolation (Fig. 3E). Furthermore, the synergy in supragranular and infragranular layers exceeded that in granular layers, suggesting an increasing impact of cooperativity within the hierarchy of the columnar microcircuit.

The laminar-dependent changes in synergy covaried with the relative contribution of the first and second MID. The information for a reduced model, consisting of only the first MID and its nonlinearity, relative to the information for both MIDs, the first MID contribution, clearly differed across the three laminar regions (Fig. 3F). In granular layers the first MID provides the greatest contribution. The second MID attains increasing importance at supragranular and infragranular locations, closely following the laminar-dependent changes in synergy. It implies that an increasing contribution of MID2 enhances the synergy.

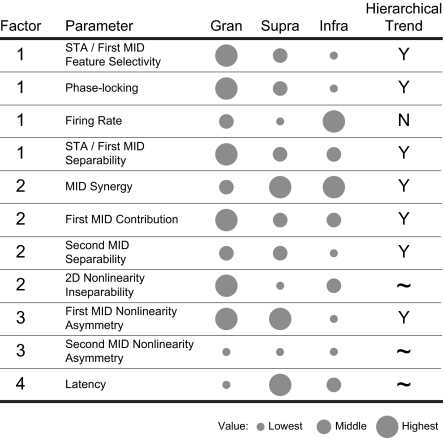
Previously, we have shown that parameters that describe the stimulus-based content of receptive fields (e.g., characteristic frequency, excitatory bandwidth, envelope modulation preferences) are relatively independent of parameters that describe how the processing is accomplished (e.g., receptive field separability, feature selectivity, nonlinearity structure) (22). A factor analysis revealed potential interdependences among variables that characterize how spectrotemporal stimuli are processed. We recovered four factors from the 11 variables (eigenvalues: 3.35, 2.33, 1.42, and 1.07; accounting for 74.3% of the data variance; Table S1). Factor 1 had major contributions from firing rate, phase locking, and MID1 separability and feature selectivity; factor 2 comprised MID1 contribution, MID synergy, MID2 separability, and, less specifically, the inseparability of the 2D MID nonlinearity; factor 3 reflected covariations in the asymmetry of the two nonlinearities; and factor 4 captured response latency, which was the weakest factor and describes the time to response. Thus, in addition to a timing sequence, the parameters express three main independent principles of auditory cortical processing. The first connects spectrotemporal structure of the STA/MID1 to response strength and timing precision. The second determines how multiple features cooperate to influence neural sensitivity. The third factor reveals an interaction between the shape of the two nonlinearities. All four aspects vary with cortical layer.

The various processing changes between the three layer groups appear compatible with a sequential process that follows the connection patterns in the canonical columnar circuit (Fig. 4). Across-layer comparisons (ANOVA, P < 0.05) of the receptive field parameters revealed that all of them showed layer differences, and 7 of the 11 parameters changed monotonically from granular, to supragranular, and then to infragranular regions (Fig. 4). Some of the processing characteristics showed nonmonotonic changes from granular to infragranular laminae, which points to contributions of nonsequential, perhaps lamina-specific, aspects. In general, however, the principal processing sequence in AI is consistent with a progressive laminar hierarchy of auditory cortical computations.

Fig. 4.

Hierarchical trend analysis of laminar receptive field organization. Columns indicate granular (Gran), supragranular (Supra), and infragranular (Infra) layers. The circle size represents the relative magnitude of each parameter. Circles of different sizes represent significantly different values. A parameter was consistent (Y) with a laminar hierarchical trend if it changed monotonically from granular, to supragranular, to infragranular layers (∼ = inconclusive, implying a nonmonotonic granular to nongranular layer change; N = not consistent).

Discussion

Three main results point to substantial differences in how auditory stimuli are processed in different cortical layers. First, by focusing on the strategy of processing, we uncovered three independent factors that describe how stimulus information is processed. A fourth factor, dominated by response latency, illuminated the columnar processing sequence. The receptive field characteristics from the first three factors dealt less with stimulus preferences (such as temporal or spectral modulations) and more with how STRFs and their nonlinearities are structured and interact. Second, different positions in the AI microcircuit correlate with differences in the main neural response factors and with changes in the interactions between the two STRFs of a neuron. Finally, the laminar processing progression is largely compatible with a sequential receptive field modification from granular to supragranular to infragranular layers. Overall, how stimuli are processed along the columnar microcircuit becomes more complex in structure, less linear in interaction and response generation, and potentially more abstract and variation tolerant (29).

Key in this study was the simultaneous recording from neurons across all layers and the analysis of multiple information-bearing STRFs and their nonlinearities. The first aspect substantially reduced variability introduced by the large parametric range of cortical neurons in the thalamocortical input layers and by changes in physiological state in sequential recordings along electrode tracks (4, 22). The second aspect used a new window on neuronal processing, the MIDs, uncovering hitherto hidden properties of auditory cortical processing (21). Specifically, the MID analysis revealed a second STRF that influences the neuron's responsiveness, in conjunction with the first STRF.

Past research tried to find single stimulus-based parameters that remain constant across laminae (30) but had limited success and identified only a few parameters that changed little across cortical depth (7–11). By contrast, systematic laminar changes of receptive field parameters exist and are related to the coding of stimulus parameters, including spectral bandwidth, sound intensity, frequency sweeps, spectral and temporal modulations, and vocalizations (11, 31–34, 46). Despite some inconsistencies among studies (4), they confirm the observations from other modalities, that processing in layers is specific to their different tasks and their different projection targets. In addition, no consistent functional or task-specific interpretations or sequential/hierarchical schemes for intracolumnar processing have emerged from these studies (4).

Here, we found that the majority of receptive field parameters that capture general processing strategies, as opposed to specific processing content, changed with laminar position, and these changes correlated with the synaptic distance from granular layers. Seven of 11 parameters monotonically changed across the three levels of the canonical columnar circuit. Two main exceptions were response latency and firing rate. That latencies of infragranular neurons were shorter than those in supragranular layers is likely caused by additional direct thalamic inputs (32, 33, 35). The nonordinal changes in firing rate from granular to nongranular layers likely reflect laminar differences in the composition of cell types with different membrane and synaptic properties and in the differing nature of the input sources. Overall, however, laminar changes in how auditory information is processed support a sequential scheme in general agreement with the canonical columnar circuit. This congruence of functional and connectional aspects is remarkable, given that each layer receives numerous and diverse feed-forward and feedback inputs that impinge on the determination of the functional properties of auditory cortical neurons. Noncolumnar inputs appear to take a stronger role in shaping the content of the processing as opposed to the columnar circuit that dominates processing strategy. Thus, granular, supragranular, and infragranular layers may be thought of as separate nuclei, with significantly differing processing in each, although still maintaining interdependence (36).

How does the columnar processing in auditory cortex differ from other primary sensory cortices? Unlike visual cortex, distinct functional cell classes are not created. Instead, there is a gradient for processing complexity in AI; nonlinearity structure and STRF interactions change within the local circuit. This represents a significant difference from visual cortex, where spiking responses, but not subthreshold responses, can be nearly bimodally distributed into simple and complex cells (37, 38, 39). In AI, by contrast, a similar bimodality does not appear, indicating that modality analogies must be considered with caution. AI cells combine aspects of simple and complex cells, because they appear to contain STRFs with both an asymmetric (like simple cells) and a symmetric (like complex cells) nonlinearity. A direct analog of an envelope-phase invariant complex cell, which has no STA, has yet to be found in auditory cortex (21).

Our findings resemble recent receptive field modeling in primate primary visual cortex that revealed multiple STRFs for simple cells (40, 41). Additionally, in both the visual and auditory systems, the structure of the nonlinearities varies with depth. The first MID nonlinearity in AI is most asymmetric in granular layers whereas the structure of the 2D nonlinearity, characterizing joint STRF processing, becomes more inseparable and complex outside of granular layers.

The processing by auditory cortical STRFs evolves within the columnar circuit. Processing in all layers is more completely captured with a two-STRF characterization. In granular layers, the first STRF is more dominant and possesses a high degree of separability and feature selectivity. Its nonlinearity is highly asymmetric reflecting the high feature selectivity of the STRF (22). In supragranular layers, the MID1 contribution is reduced, MID2 strengthens, synergy increases, and the 2D nonlinearity is less separable. In the infragranular layers, this trend toward more cooperative processing and higher receptive field complexity is continued. Thus, the sequential information processing in AI is progressive and becomes more complex and synergistic, as the auditory information moves from thalamic input to cortical output layers.

The processing strategy in AI follows a continuum of emphasis, with one major mode representing the response of a neuron, another representing interactions between the STRFs that comprise the receptive field of a neuron, and a third relating the nature of the nonlinearities, reflecting neuronal stimulus preferences and intrinsic membrane properties. These three processing aspects of auditory information undergo modifications in the AI microcircuit. The laminar progression of stimulus processing complexity, achieved by an increasing influence of a second STRF, represents a departure from traditional models of auditory cortical stimulus feature extraction and representation. The interactions between the first and second STRFs are reminiscent of combination sensitivity prevalent in biosonar signal processing (42), because the joint processing of the two STRFs leads to greater responsiveness and is not predictable from the independent processing of the STRFs. However, a symmetric nonlinearity introduces a processing strategy beyond the combination of highly defined stimulus features and may provide a key step in our understanding of cortical transitions toward increasingly more complex, nonlinear, robust, categorical, and/or abstract processing principles.

Materials and Methods

Neural recordings were made in the right AI of adult, anesthetized female cats. Multichannel silicon recording arrays were used to record neural responses. Each array (kindly provided by the University of Michigan Center for Neural Communication, Ann Arbor) consisted of 16 linearly spaced recording contacts, with each contact separated by 0.15 mm. Arrays were positioned orthogonally to the cortical surface and then inserted (see SI Text and Fig. S1). Recordings were obtained by using a Neuralynx Cheetah A/D system, with sampling rates between 18 and 27 kHz, and a passband filter setting of 0.6–6 kHz. Single neurons were obtained by using a Bayesian spike-sorting procedure. Neuron locations were estimated from depth readings and latency profiles. Stimuli consisted of a 15- or 20-min dynamic moving ripple stimulus that had randomly varying temporal modulations from −40 to 40 Hz and randomly varying spectral modulations from 0 to 4 cycles per octave (17). All experimental details were as reported and were in strict accordance with the policies of the University of California, San Francisco Committee for Animal Research. The STA and the MIDs were calculated as reported (see SI Text). Briefly, to compute the STA and the MIDs, we separated the data into training (3/4 of the data) and test (1/4 of the data) subsets, which resulted in four different estimates for each type of STRF. Information values were calculated from the 1/4 of the data that was not used to calculate the STRFs. Information values were adjusted for sampling bias by extrapolating to infinite dataset size, where information values were plotted versus the inverse of the data fraction used to calculate them (80%, 85%, 90%, 92.5%, 95%, 97.5%, and 100%), and the ordinate intersection of the line to the values was taken as the estimated information value (43, 44). Neurons were assigned to layers according to cortical depth by using standard boundaries: supragranular, 0–0.6 mm; granular, 0.6–1.1 mm; and infragranular, 1.1–1.85 mm. To minimize depth-measure variance, when data were grouped into layers and analyzed for statistical significance, layers were defined as: supragranular, 0–0.6 mm; granular, 0.7–1.1 mm; and infragranular, 1.2–1.85 mm (5). Statistical tests were consistent whether the original or analysis layer definitions were used. We used Statview (SAS Institute) to apply factor analysis using the varimax technique (45). Only factors with corresponding eigenvalues more than one were considered to explain the variability in the dataset.