The local cell curvature guides pseudopodia towards chemoattractants

Abstract

Many eukaryotic cells use pseudopodia for movement towards chemoattractants. We developed a computer algorithm to identify pseudopodia, and analyzed how pseudopodia of Dictyostelium cells are guided toward cAMP. Surprisingly, the direction of a pseudopod is not actively oriented toward the gradient, but is always perpendicular to the local cell curvature. The gradient induces a bias in the position where the pseudopod emerges: pseudopodia more likely emerge at the side of the cell closer to the gradient where perpendicular pseudopodia are pointed automatically toward the chemoattractant. A mutant lacking the formin dDia2 is not spherical but has many invaginations. Although pseudopodia still emerge at the side closer to the gradient, the surface curvature is so irregular that many pseudopodia are not extended toward cAMP. The results imply that the direction of the pseudopod extension, and therefore also the direction of cell movement, is dominated by two aspects: the position at the cell surface where a pseudopod emerges, and the local curvature of the membrane at that position.

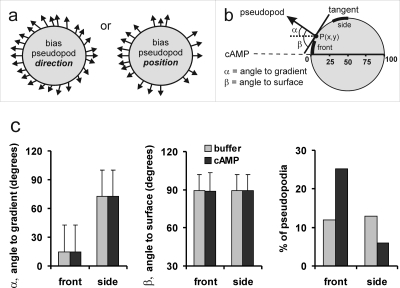
Chemotaxis is important for diverse functions such as finding nutrients, tracking bacterial infections, guiding axon growth, and organizing the embryo (Baggiolini, 1998; Campbell and Butcher, 2000; Crone and Lee, 2002; Van Haastert and Devreotes, 2004). It has been well established that cells can sense the direction of the gradient, and that they move by extending cytoplasmic protrusions, called pseudopodia (Mato et al., 1975; Zigmond, 1977). To understand how a cell converts this spatial information into directed pseudopod extension, we developed an algorithm that defines the cell contour and its protrusions [Bosgraaf and Van Haastert (submitted); Bosgraaf and Van Haastert, 2009]. Dictyostelium cells were exposed to a shallow cAMP gradient with a concentration difference of ∼1% across the cell (Veltman and Van Haastert, 2006). We analyzed ∼1600 pseudopod extensions before and after application of the cAMP gradient. The automatic pseudopod tracking algorithm describes the contour of a cell as a polygon of ∼150 nodes, and the pseudopod as a vector that connects the tip of the pseudopod at the start and end of its growth period, respectively [Bosgraaf and Van Haastert (submitted); Bosgraaf et al., 2009]. For each pseudopod we measured the angle α towards the gradient and the angle β towards the local surface contour of the cell [Fig. 1a]. In buffer, the direction of the pseudopod extension appears to be perpendicular to the curvature of the surface at the point where the pseudopod emerges [89.1±12.6 deg, mean and standard deviation (SD), n=750; Fig. 1b], as was shown before (Bosgraaf and Van Haastert, 2009). The cAMP gradient may induce bias in this direction such that the pseudopodia are bent toward the gradient. Alternatively, the cAMP gradient may induce a bias in the position where the pseudopod emerges, such that more pseudopodia start at the side of the cell closer to the gradient [Fig. 1a]. We compared pseudopod extensions in buffer and a cAMP gradient for two regions of the cell, at the front and at the side of the cell, respectively. The results of Fig. 1b reveal that pseudopodia emerging at the front of the cell are pointed toward the gradient, whereas pseudopodia that are formed at the side of the cell make a large angle to the gradient. These angles toward the gradient are not different for pseudopodia in buffer or a cAMP gradient, both with respect to the means and SD. Furthermore, in a cAMP gradient, the pseudopodia are still extended exactly perpendicular to the surface. We observed 89.0±13.2 deg for all 835 pseudopodia, which is statistically not significantly different from 90 deg; at this number of observations and variance, 88.0 deg would be significantly different from 90 at P<0.01, indicating that pseudopodia may bend toward the gradient by less than 2 deg. In contrast to the direction of the pseudopod extension, the gradient strongly increases the fraction of pseudopodia emerging at the front of the cell [Fig. 1b]. These experiments reveal that the direction of the pseudopod extension depends predominantly on the curvature of the cell surface at the point where a pseudopod emerges.

Figure 1. Pseudopodia are extended perpendicular to the cell surface.

Dictyostelium cells were exposed to a shallow cAMP gradient in a modified Zigmond chamber using 1 μM cAMP in Veltman and Van Haastert (2006). From 4 independent movies we analyzed 28 cells providing data on 750 pseudopodia before cAMP addition (buffer) and 835 pseudopodia in a stable cAMP gradient. (a) Schematic with pseudopodia emerging from a spherical cell. In buffer the pseudopodia are extended evenly around the cell, and emerge perpendicular to the cell surface. The cAMP gradient may induce a bias in the direction of the pseudopod extension, or a bias in the position where pseudopodia emerge. For each pseudopod we calculated the angle α towards the gradient and the angle β towards the surface tangent. (b) shows the results for two sections of the cell that each represent 1∕8th of the hemisphere, at the front and the side, respectively. Data are the means and SD.

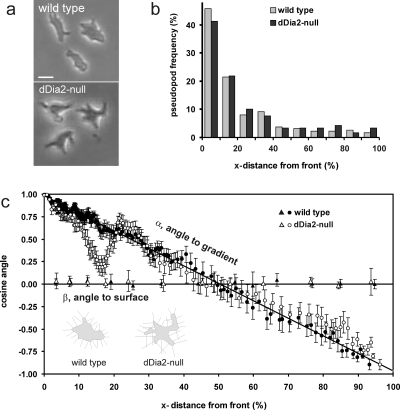
This model may be tested in a mutant that has normal gradient sensing but has a deformed cell surface (see Supplemental Information for calculations on of the effect of cell shape on the direction of pseudopod extension). Cells lacking the gene encoding the Dictyostelium homologue of formin, dDia2-null cells (Schirenbeck et al., 2005), have many invaginations of the cell surface [Fig. 2a]. In a cAMP gradient, pseudopodia are extended predominantly at the side of the cell closer to the gradient, as in wild type cells [Fig 2b]. We measured for 605 pseudopodia the angle α toward the gradient and the angle β toward the surface, and present the cosine of these angles as a function of the distance from the pseudopod start site to the front of the cell [Fig 2c]. The results demonstrate that pseudopodia of both wild type and mutant dDia2-null cells are extended perpendicular to the surface, irrespective where on the surface the pseudopodia emerge (cos β=∼0 deg; β=∼90 deg). The cosine of the angle α to the gradient is identical to the frequently used chemotaxis (CI) of each pseudopod. Geometry predicts that for straight pseudopodia extending perpendicular from a circle this plot will yield a straight line from cos α=1 for pseudopodia emerging at the front to cos α=−1 for pseudopodia emerging at the rear of the cell. The pseudopodia that are extended by wild type cells fully comply with the predictions for a smooth and regular spherical cell. In contrast, the deformed mutant dDia2-null cells are defective. Pseudopodia extended at the front 5% of dDia2-null cells are pointed perfectly toward the gradient (cos α∼1), but pseudopodia extended behind the front, especially between 10% and 25% of the cell length, are not pointing correctly toward the gradient. Since these “wrong” pseudopodia are still extended perpendicular to the surface, the results strongly suggest that the altered surface curvature of the dDia2-null cells guide the perpendicular pseudopodia not effectively toward the chemoattractant. The shape of the chemotaxis index curve showing a local minimum of the chemotaxis index for dDia2-null cells is surprising, but also predicted by model calculations (see Supplemental Information). In cells with a very irregular shape, the cell surface closest to the gradient is still perpendicular to the gradient and therefore the CI=∼1 for pseudopodia that appear at the front. However, shortly behind the front the cell surface may be curved in many different directions, by which at increasing distance from the front the CI declines much faster than in a cell with a regular shape. A local minimum of the chemotaxis index appears because the frontal pseudopod is directed well toward the gradient, as was observed experimentally [Fig. 1c], resulting in a spatial pattern of very irregular shapes just after the frontal pseudopod as indicated in the supplemental figures.

Figure 2. Reduced chemotaxis due to morphology changes in dDia2-null cells.

(a) shows the shape of representative spherical wild type cells and starlike dDia2-null cells; the cAMP source is at the left. (b) The number of pseudopodia that emerge at different distances from the front of the cell (x-distance, defined from front to rear of the cell). (c) The cosines of the angles α and β are presented as function of the x-distance from the front. For pseudopodia perpendicular to a circle, this will yield straight lines for α and β as drawn. To present the large dataset in an optimal way, the data were placed in an array with increasing values of x-distance. To calculate cos(α), gliding blocks of 15 adjacent data points were taken with increments of 5 data points (i.e. 1–15, 6–20, 11–25, etc.); the mean and SEM of these 15 data points are shown. The data for cos(β) are averaged for 5% or 10% intervals of the x-distance and presented as the mean and 3×SEM (the intervals are 5% for 0–30%, and 10% for 30–100%; 3×SEM to obtain error bars that are larger than the symbols). The total number of pseudopodia is 835 for wild type cells and 605 for dDia2-null cells (inset) (c) shows schematic drawings of two cells [redrawn from the cells at the right in (a)] with perpendicular lines to illustrate the effect of cell shape on the direction of pseudopod extension.

Statistics, especially the variance, may be used to explore a process, because the variance of the final response is composed of the variances of the underlying mechanisms. In our model the variance of the pseudopod angle toward the gradient $\left({\sigma }_g^2\right)$ depends on the variance of cell curvature $\left({\sigma }_c^2\right)$ and the variance of the pseudopod angle perpendicular to the surface $\left({\sigma }_p^2\right)$, which, for independent variables, is given by ${\sigma }_g^2={\sigma }_c^2+{\sigma }_p^2$. We observed that the variance of the angle toward the gradient (σ_g=27.8 deg) is much larger than the variance of the angle to the surface (σ_p=13.3 deg), predicting σ_c=24.4 deg. We measured the cell curvature as the angle of the tangent relative to the gradient at a specific point on the surface (25% from the front of 247 cells), and obtained a mean of 29.2, close to the predicted value of 30 deg for a circle; the observed variance is large (σ_c=24.9 deg), and close to the predicted value of 24.4 deg. Thus, although the average contour of ∼800 wild type cells may be close to a circle, the contour of individual cells deviates from a perfect circle.

The results strongly support a model for chemotaxis in which the direction of a pseudopod is strictly dependent on the local curvature of the cell, and is affected for less than 2 deg by the gradient of cAMP. Instead of changing the direction of the pseudopod extension, the gradient stimulates the cell to form pseudopodia at the side of the cell closer to the gradient. At that side of the cell, the curvature of the membrane is approximately at a right angle to the gradient, and thus a pseudopod that emerges perpendicular to this surface will automatically point toward the gradient. The current observations can be incorporated in many models on chemotaxis, including compass models (Bourne and Weiner, 2002), pseudopod splitting (Andrew and Insall, 2007), local extension (Arrieumerlou and Meyer, 2005), and directional bias (Van Haastert and Postma, 2007). The key of our observations is that the gradient somehow induces a bias in the position where a pseudopod emerges, most likely because at the side of the cell closest to the gradient more receptors are occupied with chemoattractant, resulting in the production of more pseudopod-inducing signaling molecules such as PIP3. For the current model, it is irrelevant whether this positioned pseudopod emerges as a consequence of splitting or local extension.

We have observed no statistically significant effects of the position where pseudopodia emerge on the properties of the pseudopod, such as size, frequency, and lifetime (data not shown). The relative uniformity of pseudopodia supports the notion that they are self-organizing structures (Bourne and Weiner, 2002; Bretschneider et al., 2004; Misteli, 2001; Nicolis and Prigogine, 1977; Postma et al., 2004; Varnum and Soll, 1984; Verkhovsky et al., 1999). The main advantage of a switchable self-organizing element in motility and chemotaxis is the ease by which it can be locally triggered, which thereby simplifies the problems of integrating cues from throughout the cell (Postma et al., 2004).

Dictyostelium and neutrophils can detect very shallow gradients of chemoattractant (Mato et al., 1975; Zigmond, 1977). The threshold steepness of the gradient that these cells can still detect depends on the background concentration, and will activate ∼10 receptors more at the half of the cell pointed toward the chemoattractant than at the other half of the cell (Endres and Wingreen, 2008; Rappel and Levine, 2008; Ueda and Shibata, 2007; Van Haastert, 1983; Van Haastert and Postma, 2007). Recent investigations are beginning to uncover the signaling pathways that can transduce such minute signals in a strong cellular response, which is the extension of a pseudopod in the direction of the gradient (Franca-Koh et al., 2007; Janetopoulos and Firtel, 2008;Kay et al., 2008). Multiple signaling pathways are involved with complex feed-back and feed-forward control loops, leading to amplification and symmetry breaking of pseudopod inducing activities (Kamimura et al., 2008; Veltman et al., 2008; Zhang et al., 2008). It is likely that computational models are required to fully understand these complex signaling networks (Arrieumerlou and Meyer, 2005; Iglesias and Devreotes, 2008; Satulovsky et al., 2008; Ueda and Shibata, 2007). The present observations imply that such models do not have to take into account any direct coupling between the gradient and the direction of pseudopod extension, but can be restricted to predictions on the position at the cell surface where pseudopodia emerge.

MATERIALS AND METHODS

The strains used are wild type AX3 and dDia2-null cells lacking the forH gene encoding the Dictyostelium homologue of formin (Schirenbeck et al., 2005). Cells were grown in HG5 medium (contains per liter: 14.3 g oxoid peptone, 7.15 g bacto yeast extract, 1.36 g Na₂HPO₄⋅12H₂O, 0.49 g KH₂PO₄, 10.0 g glucose), harvested in PB (10 mM KH2PO4∕Na2HPO4, pH 6.5), and allowed to develop in 1 ml PB for 5 h in a well of a 6-wells plate (Nunc). Starved cells were exposed to a shallow cAMP gradient in a modified Zigmond chamber using 1 μM cAMP in the source (Veltman and Van Haastert, 2006). Movies were recorded before and after application of the cAMP gradient with an inverted light microscope (Olympus Type CK40 with 20× objective) and images were captured at a rate of 1 frame∕s with a JVC charge-coupled device (CCD) camera.

Images were analyzed with the fully automatic pseudopod-tracking algorithm Quimp3, which is described in detail in Bosgraaf and Van Haastert (submitted). The phase contrast movie was converted to a black and white movie using the “phase contrast to BW” macro that is included in the Quimp3 package. Some manual adjustment was required to close a few gaps in the cell silhouette. The resulting file was used as input file for the Quimp3 analysis. In short, the program uses an active contour analysis to identify the outline of the cell as ∼150 nodes (Bosgraaf et al., 2009). With the convexity and area change in the nodes, extending pseudopodia were identified that fulfill the requirement of used-defined minimal number of adjacent convex nodes and minimal area change. The x,y and time coordinates of the central convex node of the convex area at the start and end of growth were recorded, which identifies the direction of the extending pseudopod. The tangent to the surface at the node where the pseudopod started was calculated using the position of the adjacent nodes. The pseudopodia were detected using the default parameters of the Quimp3 macro. The output files containing the x,y-coordinates of the start and end position of the pseudopod and the tangent of the surface were imported in Excel to calculate pseudopod size, interval, direction to gradient, direction to tangent, etc.

We analyzed 28 wild type cells from 4 independent movies providing data on 750 pseudopodia before cAMP addition (buffer) and 835 pseudopodia in a stable cAMP gradient; and 605 pseudopodia from 21 mutant dDia2-null cells in a cAMP gradient. The data are presented as the means and SD, or standard error of the means (SEM) where n represents the number of pseudopodia or number of cells analyzed, as indicated.