Real-Time Cardiac MRI using Prior Spatial-Spectral Information

Abstract

Cardiac MRI performed while the patient is breathing is typically achieved using non-real-time techniques such as ECG triggering with respiratory gating; however, modern dynamic imaging techniques are beginning to enable this type of imaging in real-time. One of these dynamic imaging techniques is based on forming a Partially Separable Function (PSF) model of the data, but the model fitting process is known to be sensitive even when truncated SVD regularization is used. As a result, physiologically meaningless artifacts can appear in the dynamic images when the total number of measurements is limited. To address this issue, the dynamic imaging problem is formulated as a generalized Tikhonov regularization problem with the PSF model as a component of the forward data model, and a penalty function is used to introduce spatial-spectral prior information. This new method both reduces data acquisition requirements and improves stability relative to the original PSF based method when applied to cardiac MRI.

Introduction

The vast majority of Cardiac Magnetic Resonance (CMR) is performed using non-real-time techniques based on either prospective or retrospective processing of physiological signals such as using the ECG to synchronize MRI data acquisition with the cardiac phases, but real-time CMR at high spatial resolution has long been a goal of the field. CMR has experienced significant progress over the past 10 years largely due to the introduction of parallel imaging, and its use is now commonplace in clinical CMR [1], [2], [3]. Parallel imaging not only speeds up non-real-time CMR but has made it possible to achieve real-time MRI with acceptable spatial resolution in many two dimensional CMR scenarios [1], [3].

Another contributor to real-time CMR research is known as dynamic imaging. Dynamic imaging in MRI is fundamentally concerned with reconstructing real-time movies of patients that are sampled insufficiently in the (k, t)-space [4]. UNFOLD and k-t SENSE are the most well known examples of the dozens of dynamic imaging algorithms that are well suited to CMR. These methods make use of redundancies in the data to improve the imaging speed of MRI [5], [6].

Unfortunately, all acceleration techniques for MRI can only be pushed so far until image artifacts destroy the reconstructions, and each method has its own unique limitations. For example in CMR, partial Fourier methods are prone to reduced spatial resolution and ringing artifacts; segmented acquisitions can result in temporal blurring; EPI suffers from spatial blurring; parallel imaging is limited by spatial aliasing and noise amplification; and dynamic imaging reconstructions are degraded by motion artifacts. The artifacts of dynamic imaging are the ones addressed in this paper.

An important feature of most motion artifacts in CMR is that they are relatively obvious when viewed by someone with a background in cardiac physiology. For instance, the boundary of the patient's body can often be determined despite image artifacts, so artifacts that extend outside the body can often be easily identified. Also, motion artifacts can appear in areas of low signal intensity such as the lungs or in static regions such as near the spine. Another example is when replicas of cardiac structures appear superimposed on other organs that are known to have much simpler spatiotemporal characteristics. Such an artifact may be obvious to a radiologist or physician even though its existence may render the images diagnostically useless.

Unfortunately, not all of the recently developed techniques for dynamic imaging provide a way to incorporate practical physiological information such as: 1) the heart is inside the body, 2) the heart is roughly within a certain spatial range, and 3) some tissues are more static than others. The main purpose of this paper is to enable this capability while taking advantage of a recently developed method based on the Partially Separable Function (PSF) model [7].

The potential of dynamic imaging using the PSF model has been demonstrated recently by developing a technique based on it to perform real-time CMR in breathing rats [8]. Not only are the spatio-temporal requirements very high for rat CMR, but the breathing motion introduces complexity into the spectral content of the raw data. The PSF method works in many cases, but sometimes it is very sensitive to the model fitting resulting in image artifacts. Reducing these artifacts would improve the practical usefulness of this method of CMR.

Also, there is a need to push to even higher spatial resolutions toward the goal of three dimensional, real-time CMR. The PSF model based method can already be used for 2D CMR with sparse sampling along the time dimension, but even less data are available for each k-space location in the three dimensional case (for a fixed MRI scan time). The authors propose a new method that addresses the stability of dynamic imaging using the PSF model as well as reduces its data acquisition requirements by reformulating the problem so that prior spatial-spectral information about the patient can be incorporated into the dynamic image reconstruction procedure.

This paper first introduces the theory of the new method along with its closed form solution. A simulation created to demonstrate the method is then described and followed by dynamic imaging reconstruction results. These results are discussed along with the usefulness of the proposed method, and the paper ends with the conclusion and references.

Theory

Recent work in the theory of Partially Separable Functions (PSF) has shown that it is possible to accelerate dynamic imaging to high levels of performance by allowing sparse temporal sampling [7]. In the PSF model based approach the (k, t)-space signal, s, is modeled as

$$s(\mathbf{\text{k}},t)=\sum _{\ell =1}^L{c}_{\ell }(\mathbf{\text{k}}){\phi }_{\ell }(t)$$ (1)

where {φ_ℓ(t)} are basis functions estimated from measured data, and {c_ℓ(k)} are the unknowns of the model. The dynamic images are found by fitting the model to the measured data by solving

$$\underset{{\{c_{\ell }(\mathbf{\text{k}})\}}_{\ell =1}^L}{\text{argmin}}\sum _{n=1}^N{\left|s(\mathbf{\text{k}},t_n)-\sum _{\ell =1}^L{c}_{\ell }(\mathbf{\text{k}}){\phi }_{\ell }(t_n)\right|}^2$$ (2)

at each point in the k-space using an energy constraint on {c_ℓ(k)} such as truncated SVD. Solving (2) will be referred to as applying the existing PSF based imaging method in the remainder of the paper.

It is unclear how to constrain the existing method to avoid physiologically incorrect reconstructions. To make this constraint possible, the dynamic imaging problem has been formulated as a generalized Tikhonov regularization problem [9], [10]

$$\underset{\mathbf{\text{a}}}{\text{argmin}}{\Vert \mathbf{\text{s}}-E\mathbf{\text{a}}\Vert }_2^2+{\lambda }^{\text{2}}{\Vert W(\mathbf{\text{a}}-{\mathbf{\text{a}}}_0)\Vert }_2^2$$ (3)

where s contains the measured (k, t)-space data for all coils (with a noise covariance Ψ), and E is the forward data model for the underlying unknowns describing the object, a. λ² is known as the regularization parameter. a₀ is an initial estimate of the unknowns, and W is a weighting matrix. The first term in the optimization problem encourages the solution to predict the measured data, while the second term penalizes undesirable solutions. In general, problems of this mathematical form have the solution

$$\mathbf{\text{a}}\ast ={\mathbf{\text{a}}}_0+{(E^H{\Psi }^{-1}E+{\lambda }^2{W}^{H}W)}^{-1}{E}^H{\Psi }^{-1}(\mathbf{\text{s}}-E{\mathbf{\text{a}}}_0).$$ (4)

The Partially Separable Function (PSF) model is incorporated by defining the general forward data model

$$E=\mathcal{U}{\stackrel{\sim }{\mathcal{F}}}_{\mathbf{\text{y}}}S\Phi$$ (5)

where Φ is a matrix of the PSF temporal basis functions whose product with a gives a vector containing the (y, t)-space reconstruction. S represents the time-varying coil sensitivities. 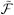_y transforms its input to the (k, t)-space with the options to window the discretized spatial domain data, represent the object using an arbitrary basis such as a pixel basis, account for magnetic field inhomogeneities, and allow for arbitrary k-space trajectories. 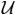is the sampling operator that retains only those data actually acquired in the (k, t)-space.

Prior spatial-spectral information is incorporated into the imaging method by defining the W operator as

$$W=P{\mathcal{F}}_t\Phi$$ (6)

where 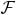_t is a Fourier transform over the time domain, and the entries of P define a spatial-spectral penalty to discourage energy from being assigned to certain (y, f)-space locations thereby reducing physiologically meaningless artifacts as well as the data acquisition requirements.

Methods

Experimental Conditions

All experimental data in this paper were collected using a Bruker (Billerica, MA) Avance DRX 4.7 T, 40 cm equipped with a 12 cm, 40 G/cm shielded gradient set. A 5.5 cm custom built surface coil was used for the collections. A FLASH pulse sequence was used to acquire an ECG triggered, respiratory gated set of cardiac images at 256 × 256 resolution over a 5 × 5 cm Field of View (FOV) with a 2 mm slice thickness.

The animals used in the study were the same type of Dark-Agouti and Brown Norway rats as in reference [11]. All animals received humane care in compliance with the Guide for the Care and Use of Laboratory Animals, published by the National Institutes of Health, and the animal protocol was approved by the Carnegie Mellon University Institutional Animal Care and Use Committee.

Simulation

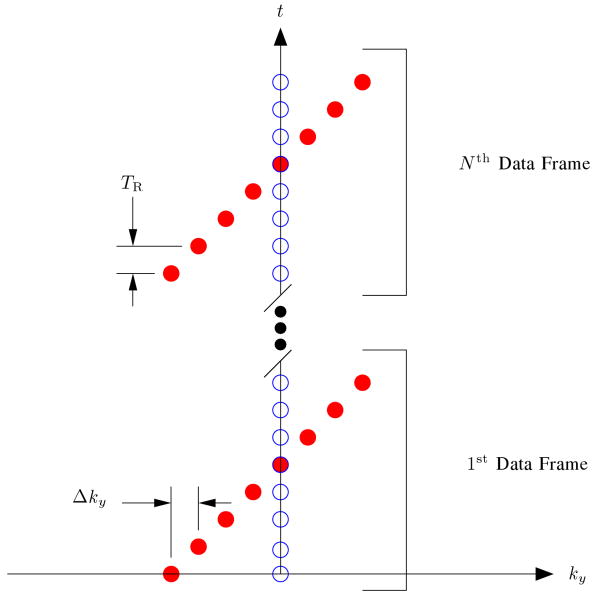
A single channel cardiac phantom was created using denoised images from the gated acquisition. The phantom was time sequentially sampled using phase encoding with the sampling pattern shown in Figure 1 over a time duration of 15 sec with a T_R of 3 msec.

Fig. 1.

The k-t sampling pattern used for phase encoding where the readout direction is into the page. The open circles represent the training data, and the filled circles represent the (k, t)-space sparse samples.

The data were then reconstructed using (2) as well as (3). The definition of P used in (4) was (I – Ω) where I is the identity matrix, and Ω is a diagonal matrix formed from an indicator function defining the Region of Support (ROS) in the (y, f)-space. Ω has a value of 1 when significant energy is present and 0 when it is not, so P penalizes only those (y, f)-space locations outside the ROS. Ω was chosen to be a coarse approximation to the true ROS that forms a cross shape over the heart [5]. Ω was given a value of 1 over a range of y locations containing the heart, while other spatial locations were assigned a value of 1 only near the DC frequency, and Ω was kept constant over all x locations. λ² = 10⁻⁷ was used, and a₀ was set equal to zero. Because phase encoding was used, the reconstruction problem was solved at each x location separately. This means that a contains the PSF model coefficients for all y locations at each particular x.

Results

The reconstruction in Figure 2 (a) shows a single image of the dynamic reconstruction using the existing PSF based method. The vertical streaking artifacts are in the phase encoding direction, and they corrupt the heart region significantly enough to render the image diagnostically useless. These artifacts are eliminated when the proposed method is applied to exactly the same acquired data as shown in Figure 2 (b).

Fig. 2.

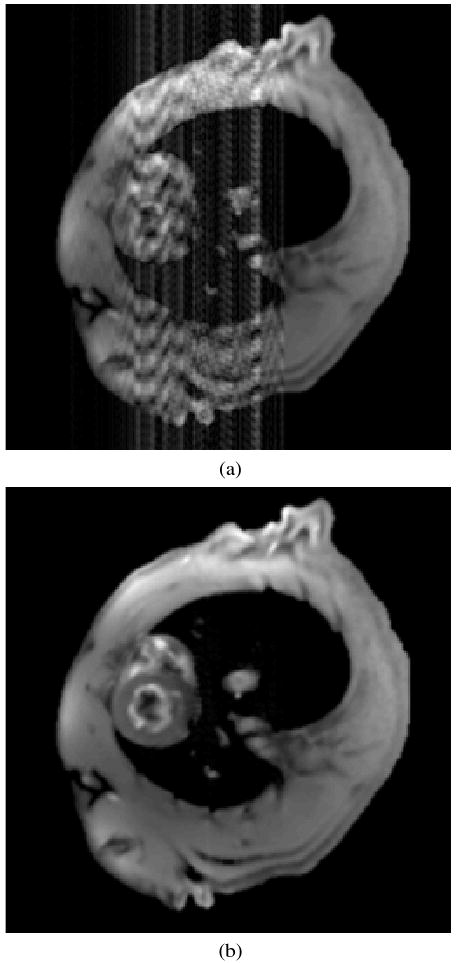
Comparison of simulated reconstruction (a) existing PSF method and (b) proposed method with spatial-spectral prior information.

Another view of the artifacts is shown in Figure 3 by plotting a column of pixels passing through the heart (vertical axis) as a function of time (horizontal axis). Figures 3 (a) and (b) show the reconstruction results of the existing PSF based method and the proposed method respectively. The proposed method's reconstruction has a peak error of 7% and is nearly indistinguishable from the gold standard.

Fig. 3.

Comparison of simulation results for the (y, t)-space of a column of pixels through the heart: (a) existing PSF based method, and (b) proposed method with prior spatial-spectral information.

Discussion

One interesting result in Figure 3 (b) is that these simulation results demonstrate typical artifacts of the existing PSF model fitting when it is pushed to its performance limits. The reconstruction artifacts take on a character that appears much like time-varying noise, and some image frames are close to the true image while others are unintelligible. The artifacts corrupt regions of the image with and without signal from the body; however, the spatial-spectral penalty in the proposed method can largely eliminate these artifacts.

Another key point is that the proposed method reduces the number of measurements needed to reconstruct images with an allowable amount of error when compared to the existing PSF based method. This reduction in the number of measurements is equivalent to a speed improvement, so in the proposed method, the data acquisition resources can then be allocated to either increase the spatial resolution or reduce the scan time as appropriate for the specific application.

The proposed method has significant differences with other popular methods for CMR. It makes a very different use of the (y, f)-space ROS concept when compared to UNFOLD, TSENSE, UNFOLD-SENSE, PARADIGM, and PARADISE [5], [12], [13], [14], [15], [16]. Those methods rely on specialized sampling patterns, , that manipulate the (y, f)-space aliasing to pack the ROS. In these methods the ROS is a well defined region that is explicitly extracted using a linear filter, but the proposed method imposes the ROS in a soft fashion making it robust to errors in the ROS estimate. Also, spatial-spectral overlap is allowed in these other methods only when parallel imaging is used. In contrast, the PSF model can be used to overcome significant spatial-spectral aliasing even without parallel imaging and is considerably less dependent upon the choice of an optimal sampling pattern.

The proposed method's use of prior information is conceptually similar to k-t SENSE [6]; however, the direct extension of that method to take advantage of the PSF model is to use a magnitude estimate of the PSF model coefficients to constrain the solution [17]. The spatial-spectral penalty used here has some practical advantages since it has a very biological interpretation and can therefore be used to constrain dynamic motion to be within the patient's body, cardiac motion to be localized to the heart region, eliminate energy from air cavities inside the body, and discourage dynamic content from appearing in static tissues. In contrast, the coefficient magnitudes rarely have a physiologically meaningful interpretation since the temporal basis functions from the PSF model are purely mathematical constructions, so the only practical refinement to further constrain the reconstructed images is to set coefficients for selected spatial locations to zero. An important final note in this comparison is that even though the prior information in this demonstration has been manually defined, it can also be automatically derived from training data.

The proposed method also differs from Compressed Sensing (CS) inspired methods for dynamic imaging such as k-t FOCUSS, k-t SPARSE, and others [18], [19], [20]. CS assumes that the sparse basis is independent of the patient, while the PSF model's basis is patient specific. The proposed method is similar to already knowing the locations of the non-zero temporal basis coefficients in CS, so some reduction in the number of measurements may be possible.

Conclusion

A new method of dynamic imaging has been proposed for use in real-time CMR. The formulation solves the problem using generalized Tikhonov regularization and jointly uses the PSF model, parallel imaging, and spatial-spectral prior information to both reduce data acquisition requirements and improve stability over existing PSF model based methods. The results in this paper have demonstrated the potential usefulness of prior spatial-spectral information combined with the PSF model, and this new approach to dynamic imaging may find applicability in real-time Cardiac MRI as well as other real-time imaging scenarios.