Flipping DNA to Generate and Regulate Microbial Consortia

Abstract

Communities of interdependent microbes, found in diverse natural contexts, have recently attracted the attention of bioengineers. Such consortia have potential applications in biosynthesis, with metabolic tasks distributed over several phenotypes, and in live-cell microbicide therapies where phenotypic diversity might aid in immune evasion. Here we investigate one route to generate synthetic microbial consortia and to regulate their phenotypic diversity, through programmed genetic interconversions. In our theoretical model, genotypes involve ordered combinations of DNA elements representing promoters, protein-coding genes, and transcription terminators; genotypic interconversions are driven by a recombinase enzyme that inverts DNA segments; and selectable phenotypes correspond to distinct patterns of gene expression. We analyze the microbial population as it evolves along a graph whose nodes are distinct genotypes and whose edges are interconversions. We show that the steady-state proportion of each genotype depends on its own growth advantage, as well as on its connectivity to other genotypes. Multiple phenotypes with identical or distinct growth rates can be indefinitely maintained in the population, while their proportion can be regulated by varying the rate of DNA flipping. Recombinase-based synthetic constructs have already been implemented; the graph-theoretic framework developed here will be useful in adapting them to generate microbial consortia.

MICROBES typically live in interdependent multiphenotype or multispecies communities (Wingreen and Levin 2006; Brown and Buckling 2008). Metabolic tasks are often distributed over distinct species, as has been observed in cases ranging from loose ecological groups in the open ocean and the soil (Boetius et al. 2000; Kent and Triplett 2002; Delong 2005) to tightly knight biofilm communities on animal body surfaces, mucosal membranes, and teeth (Kolenbrander et al. 2002; Vial and Déziel 2008). Phenotypic diversity might play a role in allowing pathogens to evade a host immune response (Thattai and van Oudenaarden 2004; van der Woude and Bäumler 2004): many infectious diseases are caused by polymicrobial populations (Brogden et al. 2005) or by heterogeneous but coordinated populations of a single pathogenic strain (Williams et al. 2000). These same features—metabolic distribution and immune evasion—underlie possible applications of engineered microbial consortia (Brenner et al. 2008; Hooshangi and Bentley 2008): fermentations can be more efficient when reactions are compartmentalized between distinct bacterial strains (Eiteman et al. 2008); research on bioremediation has drawn attention to microbial communities capable of complex pollutant degradation (Pelz et al. 1999); engineered commensual bacteria, the basis of live-cell microbicide therapies (Rao et al. 2005), might be better able to colonize body surfaces by mimicking the multiphenotype strategy of native microflora.

The mechanisms by which individual cells in a microbial consortium communicate with one another are currently being elucidated. Diffusible chemical messengers are involved in inter- and intraspecies communication—a process referred to as quorum sensing—in cases ranging from biofilm formation to virulence regulation (Williams et al. 2000; Bassler and Losick 2006). More recently, it has become clear that physical contact between cells on surfaces and in biofilms plays a key role in their coordination (Rickard et al. 2003; Bassler and Losick 2006). These regulatory mechanisms help coordinate the different components of a microbial consortium, preventing a single strain with a small fitness advantage from dominating the population. Implementing such coordination to suppress monoculture is a key challenge in generating engineered microbial consortia. Brenner et al. (2008) review two possible strategies to achieve this, involving either direct or indirect communication: first, mutual population regulation as implemented in an artificial microbial predator–prey system (Balagaddé et al. 2008); and second, metabolic cooperation where each strain depends on another for essential nutrients (Shou et al. 2007). Here we suggest a third strategy, borrowing from a natural microbial tactic known as phase variation: continual regeneration through interconversion between phenotypically distinct strains.

Phase variation—a stochastic, heritable but reversible switching of phenotype—was first described in the pathogen Salmonella typhimurium and has since been studied in a variety of bacterial species (van der Woude and Bäumler 2004). In Salmonella, as in a number of other cases, the phenotypic switch is driven by a DNA inversion recombination event (Silverman et al. 1979) in which the Hin DNA recombinase protein flips the region between two 26-bp palindromic hix sequences (Glasgow et al. 1989). The inversion process involves a looped intermediate known as an invertasome in which two hix sites are brought into alignment by the recombinase (Heichman and Johnson 1990), a process that is accelerated in the presence of an enhancer DNA sequence (Moskowitz et al. 1991). Hin–hix binding depends on Hin concentration, allowing the recombination rate to be regulated (Bruist and Simon 1984; Gates and Cox 1988; Glasgow et al. 1989). The Hin/hix system lends itself to the modular engineering approach advocated by the synthetic biology community (Andrianantoandro et al. 2006; Boyle and Silver 2009; Purnick and Weiss 2009). The Hin protein along with an artificial hixC site (Lim et al. 1992) was recently used in three synthetic genetic constructs: a multistate genetic memory device (Ham et al. 2008) and two systems designed to solve combinatorial mathematics problems (Haynes et al. 2008; Baumgardner et al. 2009). We propose that recombinase-based synthetic constructs such as these can be used to engineer regulated microbial consortia. We first describe how DNA flipping on an ordered set of genetic elements can be used to drive phenotypic interconversions. We then develop a general mathematical framework to understand the dynamics of an interconverting microbial population, which naturally leads us to consider the concept of neutral networks on a genotype graph. We argue that by exploiting the properties of neutral networks, it is possible in principle to engineer a regulated microbial consortium. Finally, we use specific designs to demonstrate that a population of phenotypically diverse bacteria can be maintained regardless of their respective growth rates, while the proportion of each phenotype can be regulated by varying the rate of interconversion through DNA flipping.

METHODS

Population dynamics and steady-state distributions:

Let G be the graph of genotypes, as defined in the main text, with its nodes indexed by i. The square connectivity matrix E stores the edges of G as follows:

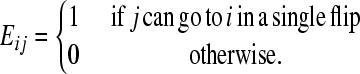(1)

Each flip is its own inverse so E is a symmetric matrix. Let x_i(t) be the number of cells with genotype i at time t. The population evolves as

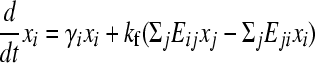(2)

(e.g., see Thattai and van Oudenaarden 2004), where the first term captures cell growth, the second one accounts for transitions into state i, and the third one accounts for transitions out of state i. Here, γ_i = γ_H for the high-fitness genotypes, γ_i = γ_L < γ_H for the low-fitness genotypes, and k_f is the rate of DNA flipping, which we assume is equal between any pair of connected nodes (Figure 2B). This equation can be rewritten as

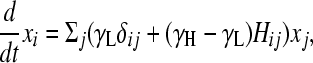where

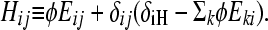(3)

Here, φ ≡ k_f/(γ_H − γ_L) is the normalized rate of flipping; δ_ij = 1 if and only if i = j; and δ_iH = 1 if and only if i is a high-fitness node. After sufficient time elapses, the population will evolve as

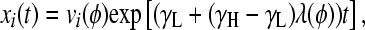(4)

where 0 < λ(φ) < 1 is the largest eigenvalue of H (giving the steady-state fraction of cells in high-fitness genotypes; Figure 4) and v(φ) is the corresponding eigenvector (giving the steady-state distribution of cells over all genotypes; Figure 3, D and H). Note that while the distribution v(φ) equilibrates, the total number of cells continues to increase exponentially, with growth rate γ_L + (γ_H − γ_L)λ(φ). Since H depends on a single adjustable parameter φ, its eigenvectors and eigenvalues are functions solely of φ.

Figure 2.—

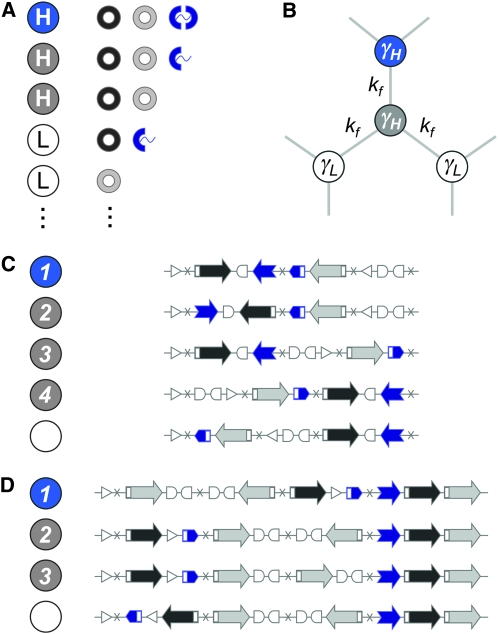
Genotype-to-phenotype maps. (A) Genotypes fall into two classes, as defined by their growth rate under selection: low fitness (L, white circles) and high fitness (H, colored circles). For a high-fitness phenotype, proteins Q and R must be expressed simultaneously; otherwise, a low-fitness phenotype results. Among the high-fitness states, we distinguish between those that express the full-length reporter protein S (blue circles) and those that do not (gray circles). Only two of the nine possible protein combinations that produce low-fitness states are shown. (B) Population dynamics: cells can transition reversibly between different genotypic states (circles) through DNA flips (light gray lines), which occur at rate k_f. Low-fitness states have growth rate γ_L, and high-fitness states have growth rate γ_H > γ_L. Steady-state distributions are governed by a single dimensionless parameter φ = k_f/(γ_H − γ_L). (C and D) Two specific designs. In both cases we have used three flippable DNA elements flanked by four hix sites. Here we show a few of the 48 possible genotypes (schematic DNA layouts) along with their phenotypes (colored and white circles). It is a useful exercise to work out exactly how to go from one genotype to another through flips and how different orders and orientations of the same three elements determine which proteins are expressed. Figure 3 shows that the high-fitness neutral network (HNN) breaks up into several equivalence classes; here we list one sample genotype from each class, labeled by integers. (C) Design 1: the robust core. Also see Figure 3, A–D. (D) Design 2: disjoint islands. Also see Figure 3, E–H.

Figure 4.—

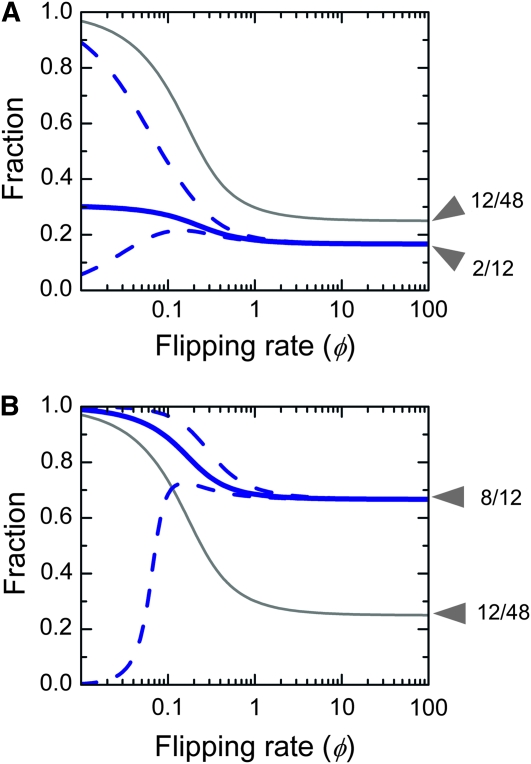
Phenotypic tuning. (A) Design 1: the robust core. (B) Design 2: disjoint islands. (A and B) The thin gray line shows the steady-state fraction λ(φ) of cells in the HNN compared to the total number of cells. The population as a whole increases exponentially with growth rate γ_L + (γ_H − γ_L)λ(φ) (Equation 4). For φ ≪ 1 almost all cells are in the HNN; for φ ≫ 1 the population spreads uniformly over the graph, so the chance of being in one of the 12 high-fitness states is simply 12/48. The thick blue line shows the steady-state fraction of S-expressing cells within the HNN, compared to all the cells within the HNN. For φ ≪ 1 cells preferentially populate S-expressing genotypes, but at φ ≫ 1 they spread uniformly over the HNN. The dashed blue lines indicate what happens when S expression influences fitness. The bottom line shows the result of a 10% growth rate decrease, and the top line shows the result of a 25% growth rate increase, relative to the (γ_H − γ_L) baseline. These changes have very little impact for large φ. As φ approaches zero, any growth rate increase or decrease, respectively, causes the S-expressing population to either dominate the population or completely vanish.

Figure 3.—

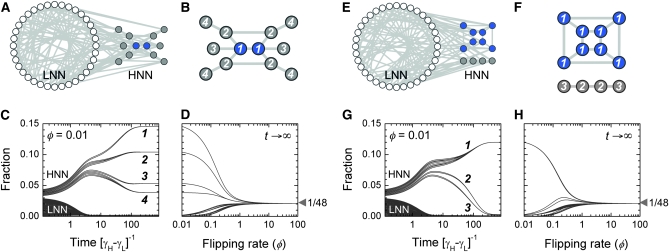
Neutral networks and equivalent genotypes. (A–D) Design 1: the robust core; see Figure 2C for the underlying DNA elements. (E–H) Design 2: disjoint islands; see Figure 2D for the underlying DNA elements. (A and E) The complete graph G for 48 genotypes, split into the 36-node low-fitness neutral network (LNN; white circles) and the 12-node high-fitness neutral network (HNN; colored circles). Two nodes are connected by an edge (light gray line) if it is possible to go from one to the other through a single DNA flip; each node is connected to exactly six edges. (B and F) The HNN subgraph. All nodes are high-fitness types, but some express S (blue circles) and others do not (gray circles). We only show edges that connect pairs of high-fitness genotypes. These nodes break up into different equivalence classes (indicated by integer labels) on the basis of the symmetries of the HNN subgraph. (B) In design 1, the HNN is a single connected network of 12 genotypes. There are two axes of symmetry, so these partition into four equivalence classes. Within the HNN, the 2 S-expressing genotypes have the fewest connections to external low-fitness genotypes: they form the robust class 1 core. These genotypes have two inward-facing promoters at their termini (Figure 2C), so only two of six possible flips can disrupt transcription. (F) In design 2, the HNN breaks up into two disjoint islands comprising 8 and 4 genotypes respectively, separated by a sea of low-fitness states. The 8-node set has a cubic topology with few external connections; these compose equivalence class 1. The 4-node set is arranged in a line with one axis of symmetry and so breaks into two further equivalence classes. The 8 genotypes of the S-expressing class 1 island all involve expression of flanking genes from an internal promoter (Figure 2D); as long as this element is correctly positioned, all 8 configurations of the other two pieces will have high fitness. (C and G) Time evolution of the bacterial population. The flipping rate is set at φ = 0.01, and all genotypes are mixed together at t = 0. The subsequent behavior of the population is given by Equation 2. We show the fraction of cells in each of i = 1, …, 48 genotypes. For clarity, the initial conditions are chosen so that trajectories do not cross; equivalent genotypes converge, while inequivalent genotypes diverge. The population eventually reaches a steady-state distribution v_i(φ) (Equation 4). All equivalent genotypes will be present at the same fraction in steady-state; we label equivalence classes in descending order of this fraction. Note that the most successful genotypes are those that are most connected to others within the HNN. (D and H) Genotypic tuning. We show how the steady-state distribution v_i(φ) changes as the flipping rate φ is varied. For φ ≪ 1, cells are overwhelmingly found in the HNN, where they preferentially populate nodes with the most internal connections. As φ is increased, differences between genotypes become less important. For φ ≫ 1, the population distributes uniformly over all 48 nodes. [Genotype graphs were generated in Cytoscape version 2.6.2 (Shannon et al. 2003)].

Automorphisms of the genotype graph:

Let G be the simple undirected graph comprising the set N of nodes representing genotypes and the set E of edges between nodes connected by single DNA flips. The nodes are partitioned into M_N classes labeled by their phenotypes; the edges are partitioned into M_E classes corresponding to distinct DNA flips. (Two flips are distinct if and only if they relate to a distinct indexed pair of hix sites.) Each node is by definition connected to precisely M_E distinct undirected edges. If the construct comprises n flippable DNA elements bracketed by (n + 1) successive hix sites, then the total number of nodes and edges is given by

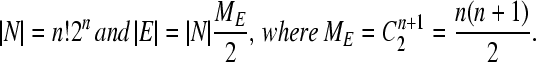(5)

Let F be the group generated by single flips, and consider a permutation α of the nodes of G that commutes with flips. That is, if n₁ and n₂ are nodes in N related by some flip f ∈ F, then their images under the permutation α are related by the same flip:

(6)

The set of all permutations α that satisfy this property forms a group Aut_E(G) of edge-preserving automorphisms of G (Cameron 2004). For any α ∈ Aut_E(G), once its action on any node in N is specified, then its action on every node in N is determined by repeated application of flips. It follows that Aut_E(G) is the same size as N. To help understand the nature of Aut_E(G), we now define another group Z of substitution rules that also act as special permutations on N, by swapping individual DNA elements and either preserving or reversing their orientation. Consider a construct assembled from three directed DNA elements 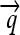, , 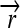and 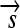whose order and orientation can be independently modified. Elements z ∈ Z are defined as in the following example:

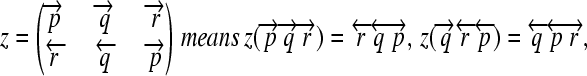(7)

and so on.

For any z ∈ Z, once its action on any node in N is specified by a substitution rule, then its action on every node in N is determined. It follows that Z is the same size as N and, therefore, as Aut_E(G). It is also straightforward to verify that all elements of Z commute with flips, so Z ⊂ Aut_E(G). Since these two sets are the same size, we must have Aut_E(G) = Z. Finally, the elements of Z or Aut_E(G) that, in addition, preserve node classes form the subgroup Aut_NE(G) ⊂ Aut_E(G) of node-class- and edge-class-preserving automorphisms of G. In the event that all flips are identical, so edges are not partitioned into classes, additional symmetries might emerge. Aut_NE(G) is therefore a subgroup of Aut_N(G), the group of all node-class-preserving automorphisms of G discussed in the main text. The nodes of G can be partitioned into Aut_N(G) orbits that are the nonoverlapping sets of equivalent genotypes.

RESULTS

The genotype graph and neutral networks:

We consider a population of bacteria whose genotypes are defined as an ordered and oriented combination of directed DNA elements (e.g., Figure 1A). Successive elements of such a construct are separated by hix sites so that, in the presence of the Hin recombinase, they can be shuffled into every possible combination through a series of flips (Figure 1B). For a given order and orientation, the resulting gene expression state defines the selectable phenotype; the same elements arranged differently might give rise to a different phenotype, while many distinct arrangements of the elements might give rise to the same phenotype (Figure 2). The total number of distinct genotypes is a rapidly increasing combinatorial function of the number of DNA elements involved: if the construct comprises n successive flippable elements, then permutations and reorientations can produce n! × 2ⁿ distinct states. DNA flips will drive repeated rearrangements in individual bacterial cells, allowing them to explore the space of possible genotypic states (Figure 2B). The population thus evolves along the genotype graph G, where each node represents a genotype, and there is an edge between nodes i and j if it is possible to convert from genotype i to genotype j in a single flip. The final population distribution can be obtained analytically and depends on details such as selective advantage, interconversion rates, and connectivity (see methods: Population dynamics and steady-state distributions).

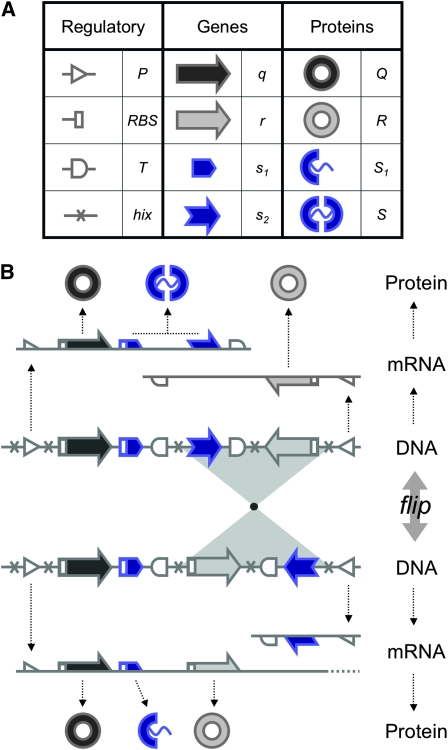
Figure 1.—

Engineering interconvertible genotypes using DNA recombination. (A) Basic DNA parts: regulatory elements include promoters (), ribosome binding sites (RBSs), transcription terminators (), and hix sites; proteins Q, R, and S are encoded by the genes 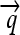, , 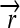and the “split gene”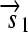 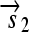. All basic parts are directed except for the palindromic hix site. (B) Example of interconversion through DNA flipping. We show a construct consisting of three flippable DNA elements, flanked by four hix sites. The Hin recombinase can flip the region between any pair of hix sites. Note that a flip reverses both the order and the orientation of each part on the flipped element. DNA parts on flanking regions are not subjected to flips. mRNA transcription is initiated in the appropriate direction at each promoter and is halted by the nearest correctly oriented terminator. For clarity, we have indicated only correctly (5′–3′) oriented coding sequences on the resulting polycistronic mRNA strands. Coding sequences that are prefixed by RBSs are translated into proteins. The gene fragment 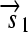is translated into the protein fragment S₁ but the gene fragment 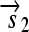that lacks an RBS is not translated (bottom). The complete gene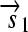 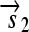is translated into the full-length reporter protein S (top). The flip thus changes the observable phenotype.

The nodes of the genotype graph can be partitioned into different classes on the basis of their fitness under selection. This allows us to identify neutral networks: sets of interconvertible genotypes of selectively identical phenotype (Figure 3, A and E). In the present context, these would be a set of distinct orderings of the basic DNA elements, all having the same selectable gene expression state and connected to one another by single DNA flips. Neutral networks were first studied in the context of the genotype-to-phenotype maps of protein and RNA secondary structure (Lau and Dill 1990; Schuster et al. 1994; Reidys et al. 1997), but their utility extends beyond the study of individual molecules (Wagner 2005). For example, the neutral-network structure of accessible mutations influences the nature of viral evolution (Burch and Chao 2000; Koelle et al. 2006; van Nimwegen 2006). Although the genotypes in a neutral network are by definition identical under selection, they can be distinguished on the basis of their connectivity to nonidentical genotypes: within a high-fitness neutral network, those nodes that are more connected to low-fitness neighbors outside it will become underrepresented. As a result, even selectively neutral genotypes will show diverging trajectories (Figure 3, C and G) and become nonuniformly represented in steady state (van Nimwegen et al. 1999).

Graph automorphisms and genotype inequivalence:

For two genotypes to follow identical trajectories they must be selectively neutral, but must also somehow occupy equivalent positions in the context of the entire genotype graph. More formally, they must be related by a graph automorphism (see methods: Automorphisms of the genotype graph). An automorphism of G is a special permutation of node identities that satisfies two properties (Cameron 2004): nodes of any given class are permuted only among themselves; and two nodes in the new permuted graph are connected by an edge if and only if they were connected by an edge in the original graph. A graph might have several distinct automorphisms, although the vast majority of permutations will not be automorphisms. The existence of a nontrivial automorphism tells us that the graph is symmetric in some way. Automorphisms are important because they allow us to connect the global properties of G—its topology and partitioning—to local properties of individual genotypes. Suppose there is an automorphism α of the graph that carries node i to node j. Then i and j must belong to the same class. In addition, for every point that node i connects to, node j connects to a corresponding point of the same class, and so on for higher-order connections as well. If we impose population dynamics rules on this graph, then since by definition nodes of the same class obey the same rules under selection, the population distribution over genotypes i and j must converge to identical trajectories (Figure 3, C and G): these two genotypes will be equivalent.

Let Aut_N (G) = {α₀, α₁, α₂, … , α_m} be the group of all node-class-preserving automorphisms of G, with α₀ representing the trivial identity permutation. If we start with some node i, then the set of nodes {i, α₁(i), α₂(i), … , α_m(i)} (not necessarily all distinct) is equivalent to i and to one another. By applying this procedure to each node in turn, we can break up the entire graph into nonoverlapping sets of equivalent genotypes (Figure 3, B and F). If the nodes of G are arbitrarily partitioned into a large number M_N of classes, then Aut_N(G) will almost always consist only of the identity permutation, reflecting a lack of symmetry. As the number of node classes is reduced, more automorphisms might emerge. For the trivial case M_N = 1 the graph is fully symmetric so all nodes become equivalent. However, as we show below using specific designs, biologically relevant graphs with as few as M_N = 2 node classes permit few automorphisms and have some irreducible asymmetry. Therefore, the set of nodes equivalent to any given node is small, and most pairs of nodes are inequivalent, even if they are of identical phenotype. An immediate corollary is that phenotypes with identical fitness also generically become inequivalent because they are encoded by inequivalent mixtures of genotypes. This implies that their proportion can, at least in principle, be regulated by varying parameters such as the flipping rate.

Specific implementations:

We now illustrate these general ideas in the context of two concrete examples. We consider interconvertible genotypes built from the same basic set of functional parts (Figure 1A): constitutive promoters (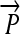); three distinct protein-coding genes prefixed by ribosome binding sites (RBSs) at their 5′ ends (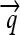, , 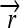and a “split gene” 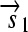and 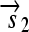), along with their corresponding protein products (Q, R, and S); and transcription terminators (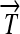). The precise placement of hix sites will determine the DNA flipping pattern. Note that hix sites are palindromic, while the remaining elements are directed (meaning that their orientation matters), as indicated by arrows. These basic parts obey the following rules (Figure 1B):

• R1. Transcription: RNA polymerase initiates mRNA transcription in the appropriate direction at any promoter 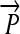, but is halted by the nearest correctly oriented terminator .

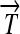• R2. Translation: All correctly oriented RBS-prefixed genes on mRNAs will be translated into proteins. The gene fragment 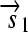is translated into a protein fragment S₁, while the complete gene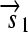 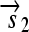is translated into the full-length protein S. The gene fragment 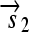cannot be translated since it lacks an RBS.

• R3. Fitness: The presence of Q and R simultaneously results in a high-fitness phenotype H (with growth rate γ_H); all other cases result in a low-fitness phenotype L (with growth rate γ_L < γ_H). The number of gene copies has no impact on fitness.

• R4. Reporter: The full-length protein S serves as a passive reporter. The protein fragment S₁ cannot be detected. By definition, the presence or the absence of either S or S₁ has no impact on fitness.

• R5. Flipping: The Hin recombinase can flip the region of DNA between any pair of hix sites. The presence of hix sites has no impact on transcription, translation, or fitness.

These rules are biologically reasonable. Synthetic systems have demonstrated the feasibility of flipping multiple overlapping regions flanked by a series of hix sites (Ham et al. 2008; Haynes et al. 2008; Baumgardner et al. 2009). The flipping reaction appears to operate efficiently over inter-hix distances ranging from 100 bases to 5 kb (Ham et al. 2008 and references therein), and the enhancer sequence can function several kilobases from these sites (Moskowitz et al. 1991). Introducing a distance dependence to the flipping rate (for example, an exponential suppression) does not qualitatively change the population dynamics (see supporting information, Figure S1), except that some previously equivalent genotypes might become inequivalent (see methods: Automorphisms of the genotype graph). Several examples exist of efficient and modular constitutive promoters and transcription terminators (Voigt 2006; Shetty et al. 2008; Boyle and Silver 2009). The proteins Q and R might be enzymes in a double auxotroph strain; alternatively, they might confer resistance when cells are grown in a medium containing two different antibiotics. Finally, it has been shown that a hixC site can be inserted in the coding region of the green fluorescent protein (GFP) gene, allowing it to be reversibly “split” by DNA inversion events (Baumgardner et al. 2009). The utility of this unusual property will become clear as our discussion proceeds.

As the bacterial population evolves, the genotypes of individual cells will change due to the stochastic occurrence of DNA flips; cells can transition reversibly between low- and high-fitness states, but the latter will dominate due to growth. The model (see methods: Population dynamics and steady-state distributions) admits a single dimensionless parameter φ: the rate of flipping (k_f) measured relative to the growth rate differences between the high- and low-fitness individuals (γ_H − γ_L). As this parameter is varied, we track the fraction of cells in low- and high-fitness states and their distribution over the low-fitness and high-fitness neutral networks (LNN and HNN) (Figure 3, A and E). For the special case of zero flipping rate (φ = 0) the genotypes of cells cannot change: only the high-fitness individuals will be present, but their distribution over the HNN will be precisely the same as the arbitrary initial condition. At any nonzero but finite flipping rate, there is a unique nonuniform equilibrium distribution that any population will tend to. Suppose the flipping rate is low (φ ≪ 1), and cells of all possible genotypes are mixed together at t = 0 (Figure 3, C and G). Very rapidly (t ∼ (γ_H − γ_L)⁻¹), differential growth will cause the high-fitness fraction to increase and the low-fitness fraction to plunge; as DNA flips begin to occur (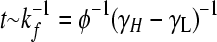), cells will redistribute themselves across the HNN, with equivalent genotypes converging, inequivalent phenotypes diverging, and genotypes strongly connected to other high-fitness states being overrepresented. In this limit, population dynamics essentially occur on the HNN alone, so symmetries of this subgraph will determine the sets of equivalent genotypes (Figure 3, B and F). At high flipping rates (φ ≫ 1) the growth rate differences between the HNN and the LNN become unimportant: as cells transition rapidly between genotypes, the population spreads uniformly over the entire graph, and the steady-state proportions of all genotypes converge to the same value (Figure 3, D and H).

Phenotypic tuning:

Consider now a situation in which two distinct phenotypes have identical growth rates. Their underlying genotypes will then be part of the same HNN, but will be partitioned into various inequivalent subsets. For the proportion of these two phenotypes to be independently tunable, it must happen that the genotypic mixtures corresponding to these two phenotypes respond quite differently to variations in φ. Such phenotypic tuning can indeed be achieved, through careful design of the underlying DNA elements. In our two specific designs (Figure 2, C and D) we combine the basic parts into three flippable DNA elements, resulting in a graph with 48 nodes, each connected to 6 others via flips. In both cases (Figure 3, A and E), G consists of precisely 12 high-fitness nodes (gray and blue circles) and 36 low-fitness nodes (white circles); the difference between them lies in how phenotypes are distributed over the graph, resulting in topologically distinct neutral networks. We focus on three distinguishable phenotypes (Figure 2A): low-fitness states, ignoring S expression (white circles), high-fitness states that do not express S (gray circles), and high-fitness states that do express S (blue circles). As we have seen, symmetries of the HNN cause it to break up into nonoverlapping equivalence classes. We can label each node by its equivalence class, for example, by listing them in order of steady-state fractions (so class 1 is the highest, class 2 is second, and so on; see Figure 3, B, C, F, and G). This breakup would remain the same no matter which subset of HNN nodes were to express S, since fitness is unaffected by S. However, when it comes to being able to independently tune the proportion of S-expressing to non-S-expressing cells, we would prefer the genotypic mixtures underlying these two phenotypes to be as different as possible. In our two designs the class 1 nodes are precisely those that express S (Figure 3, B and F). The key point is that we have designed them to express S because they are class 1, not the other way around; the fact that they express S has no influence on their equivalence class.

To understand the circumstances under which microbial subpopulations with distinct growth rates can be indefinitely maintained, we look at an aggregate fraction of cells in the HNN compared to the total number of cells (gray and blue circles vs. gray and blue circles plus white circles in Figure 3, A and E; thin gray lines in Figure 4, A and B). When φ ≪ 1, cells are overwhelmingly likely to be in high-fitness states; for φ ≫ 1 the population spreads uniformly over the graph. The fraction of high-fitness cells can thus be regulated over a 4-fold dynamic range. To understand how subpopulations with identical growth rates may be independently regulated we must consider just cells within the HNN, tracking the aggregate fraction of S-expressing cells compared to all high-fitness cells (blue circles vs. blue plus gray circles in Figure 3, B and F; thick blue lines in Figure 4, A and B). At low φ, cells will preferentially populate the S-expressing genotypes; for φ ≫ 1 cells spread uniformly over the whole HNN, so the fraction of S-expressing cells becomes identical to the fraction of S-expressing genotypes in the HNN. As φ is varied, the “robust core” design (Figure 3, A–D, and Figure 4A) achieves a 1.8-fold dynamic range of the S-expressing fraction, while the “disjoint islands” design (Figure 3, E–H, and Figure 4B) achieves a 1.5-fold dynamic range. Here, we have deliberately assumed that S expression has no influence on growth, to demonstrate that phenotypic tuning can arise just from topological properties of the genotype graph. In practice, different nodes of the HNN might have slightly different growth rates. Growth differences smaller than the flipping rate will only weakly influence the outcome; conversely, at the very lowest flipping rates even a small growth advantage can cause a subset of genotypes to take over the population (Figure 4, A and B, dashed blue lines).

The practical range over which φ can be modulated depends on the flipping rate as well as the growth rates of the various phenotypes. In Salmonella the flipping rate k_f is ∼10⁻³–10⁻² per cell generation (approximately, per hour) (Scott and Simon 1982) but this can be increased at least 30-fold in vivo, in proportion to Hin protein concentration (Bruist and Simon 1984). More direct in vitro measurements suggest that when Hin–DNA binding is in saturation (at a protein concentration in excess of 10 nm), k_f is on the order of 1 per hour (Lim et al. 1992). The growth rate of the high-fitness phenotypes (γ_H) will be on the order of 1–2 per hour, while that of the low-fitness phenotypes (γ_L) will be some fraction of this value. (We do not consider exponentially diminishing populations with negative growth rates here.) The term γ_H − γ_L will therefore be on the order of ≤1 per hour. Taken together, these estimates show that φ = k_f/(γ_H − γ_L) can be varied in the range 10⁻³–1, which brackets the useful range of control.

DISCUSSION

By using DNA flips to drive genotypic interconversions on neutral networks, we have shown it is possible to generate, maintain, and regulate a phenotypically diverse population of microbes. A key feature of our proposal is that phenotypic diversity can be regulated by varying the rate of DNA flipping. This is important because, in practice, we might not have much control over the growth rates of the constituent phenotypes. The mathematical basis of these results is extremely general: the more asymmetric the genotype graph, the easier it is to independently regulate different phenotypes. Nevertheless, there are several issues that limit their practical implementation. To maintain the microbes' genomic integrity, we imagine that our constructs will be plasmid borne. Plasmids will be present in multiple copies per cell, each possibly having a different genotypic arrangement (although at low flipping rates, genetic drift through random plasmid segregation will lead to a single arrangement becoming fixed between successive flipping events). We must also be wary of undesirable outcomes such as interplasmid recombination and deletion of inter-hix regions. A more challenging issue is control of cell growth. We have assumed that populations are exponentially growing, but this requires a chemostat or batch-culture setup; if stationary-phase effects are phenotype dependent, this will complicate the final outcome. We have assumed that the number of copies of crucial genes does not affect fitness, but it will in practice. We must ensure that the growth rate differences between high-fitness and low-fitness phenotypes are much greater than the variation within each group. Also, this growth advantage must be correctly matched to the range of achievable DNA flipping rates, requiring tight control over Hin recombinase expression. Even if we were able to overcome these various practical hurdles, the extent of our control over multiphenotype populations would be limited. In our proof-of-principle designs, the dynamic range over which phenotypic fractions can be regulated is moderate. This can be improved by using more DNA elements and more “context-dependent” parts like split genes, which can help generate observable phenotypic distinctions between genotypic equivalence classes. More fundamentally, the fact that we have a single control parameter—the flipping rate—constrains our ability to independently regulate the proportion of several different phenotypes. To achieve more intricate regulation of multiphenotype populations, we might consider using two or more independently tunable DNA inversion systems (e.g., Ham et al. 2008). This opens up a range of interesting possibilities that can be explored using the genotype graph framework presented here.

Far from being just another entry in the long list of gene-regulatory mechanisms, DNA inversions add a fundamentally new dimension to biological control. Genetically specified systems have two levels of structure: gene expression drives a cell's physical and chemical program, mapping genotype to phenotype; and DNA modifications alter that program, converting one genotype to another. By building DNA flips into a system's basic architecture we can specify structure at both levels: we can design individual genotypes, but also define how different genotypes connect to one another. A great variety of genotype graphs can be built using just a handful of genes, and the range of options combinatorially explodes as the number of DNA elements is increased. Features like interphenotype feedback loops, spatial variation, and differential control of flipping add a rich layer of dynamic phenomena onto this large canvas. Engineered microbial consortia, like their natural counterparts, can exploit these mechanisms to generate adaptive, nimble cell populations in which heterogeneity is a virtue, bringing efficiencies in metabolism and resilience against external shocks.