Abstract
Rates of brain atrophy derived from serial magnetic resonance (MR) studies may be used to assess therapies for Alzheimer's disease (AD). These measures may be confounded by changes in scanner voxel sizes. For this reason, the Alzheimer's Disease Neuroimaging Initiative (ADNI) included the imaging of a geometric phantom with every scan. This study compares voxel scaling correction using a phantom with correction using a 9 degrees of freedom (9DOF) registration algorithm. We took 129 pairs of baseline and 1-year repeat scans, and calculated the volume scaling correction, previously measured using the phantom. We used the registration algorithm to quantify any residual scaling errors, and found the algorithm to be unbiased, with no significant (p = 0.97) difference between control (n = 79) and AD subjects (n = 50), but with a mean (SD) absolute volume change of 0.20 (0.20) % due to linear scalings. 9DOF registration was shown to be comparable to geometric phantom correction in terms of the effect on atrophy measurement and unbiased with respect to disease status. These results suggest that the additional expense and logistic effort of scanning a phantom with every patient scan can be avoided by registration-based scaling correction. Furthermore, based upon the atrophy rates in the AD subjects in this study, sample size requirements would be approximately 10–12% lower with (either) correction for voxel scaling than if no correction was used.
Keywords: Scanner drift, Registration, Brain atrophy, Boundary shift integral, Alzheimer's disease
Introduction
Alzheimer's disease is associated with an insidious onset and relentless progression of cognitive decline. This cognitive deterioration reflects a loss of synaptic function and neuronal destruction secondary to the underlying pathological process which is characterised histologically by the deposition of amyloid plaques, neurofibrillary tangles and neuronal loss (Braak and Braak, 1995). The macroscopic concomitant of that neuronal loss is cerebral atrophy with brain weights at death being typically 10–20% lower than in age-matched healthy controls (Silbert et al., 2003). Serial magnetic resonance imaging (MRI) allows in vivo visualisation and quantification of progressive cerebral atrophy: each individual acts as their own control and change relative to baseline volume can be calculated (Fox et al., 1996; Jack et al., 1998). Registration of serial images and application of a direct method to quantify loss such as the Brain Boundary Shift Integral (BBSI) (Freeborough and Fox, 1997) allow a more precise measure of this volume change (Frost et al., 2004). Rates of cerebral atrophy in established AD are typically around 1.5–2.5% per annum (O'Brien et al., 2001; Wang et al., 2002; Fox and Schott, 2004; Archer et al., 2006) although this can depend on the rate of progression of AD, where faster progressors (Jack et al., 2004) and more severely cognitively impaired individuals have higher brain atrophy rates (Mungas et al., 2005). More specifically, as subjects progress from a pre-clinical state to amnestic mild cognitive impairment (MCI) (an isolated memory deficit) and then to AD there is an acceleration in rates of atrophy (Chan et al., 2003; Ridha et al., 2006; Carlson et al., 2008). There is great interest in using rates of atrophy to distinguish individuals who are likely to progress from MCI to AD from those who may remain cognitively stable or even improve (Jack et al., 2005; Carlson et al., 2008). In addition, the rates of brain atrophy are increasingly included as endpoints in clinical trials of potentially disease modifying therapies in AD (Fox et al., 2000, 2005; Wang et al., 2002; Jack et al., 2003).
In order to quantify precisely the rates of brain atrophy from serial MRI it is important that the MR acquisitions at baseline and a later time point are as similar as possible, in particular any changes in the voxel size (a scaling change) introduced by some scanner instability may either mimic or obscure true atrophy changes. For this reason ADNI included the imaging of a geometric phantom (test object) with every subject's scan to measure and correct for voxel size fluctuations (Gunter et al., 2006; Jack et al., 2008). While correction using phantoms can be extremely robust, practical considerations such as the possibility of damage to or leakage of phantoms and the expense and logistical effort of imaging a phantom with every scan in a multi-centre trial means that an alternative correction procedure would be highly desirable. One approach is to use image registration of each individual's scan to their baseline scan and incorporating scaling changes within the registration to correct for any potential scanner drift or change in voxel size.
Image registration is the process of aligning images so that corresponding features can be easily related (Hajnal et al., 2001). The alignment process can include 3 rotations and 3 translations, known as rigid-body or 6 degrees of freedom (6DOF), or can additionally include 3 scale parameters, known as 9 degrees of freedom (9DOF). There are many image registration algorithms, see Hill et al. (2001) for a review. In this study we chose to use the software package AIR (http://bishopw.loni.ucla.edu/AIR5/), as it has been well validated over a long period of time (Woods et al.,1993,1998), performs well compared with other algorithms (West et al.,1997), is readily available with 6DOF and 9DOF modes and is frequently used in serial MR registration (Fox and Freeborough, 1997; Fox et al., 2000; Gunter et al., 2003).
Strategies to correct for voxel scaling errors have included measuring total intra-cranial volume (TIV) on each scan and using the ratio to correct volume measurements (Jenkins et al., 2000), registering two scans of a phantom taken at different time points (Lemieux and Barker, 1998), registering a scan of a phantom and a computerised model of the phantom (Hill et al., 1998), extracting a known rigid structure such as the skull in the baseline and repeat image and registering the two structures (Freeborough et al., 1996) and by registering the repeat scan directly to the baseline scan (Whitwell et al., 2004) using a 9DOF registration algorithm (Woods et al., 1993). Whitwell et al. showed that a 9DOF registration algorithm can successfully correct for artificially added scaling errors in the range 1.5%–6.1% of volume, that the 9DOF registration algorithm did not affect the measurements of brain atrophy and that the scaling correction was less variable than using TIV. These methods may all be valid, but previous studies have not quantified the benefit of these approaches to scaling correction in large scale multi-site studies.
In this study we specifically compare 9DOF registration (Woods et al., 1993, 1998) with the geometric scaling phantom used in ADNI (Gunter et al., 2006). We used a subset of the ADNI dataset, which is the first large dataset to have a geometric scaling phantom scanned with every subject's MRI. Our aim was to assess the extent of within-scanner scaling geometric drift over time that is encountered in a large multi-site study (using serial phantom measurements on each scanner), and to examine whether or not a post-processing alternative based on image registration of the brain scans themselves is an equivalent scaling error correction and whether this is robust for AD patients with progressive atrophy. The atrophy measurement method used in this comparison is the Brain Boundary Shift Integral (BBSI) (Freeborough and Fox, 1997).
Materials and methods
Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (http://www.loni.ucla.edu/ADNI). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, M.D., VA Medical Center and University of California—San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55 to 90, to participate in the research—approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years, and 200 people with early AD to be followed for 2 years. For up-to-date information see http://www.adni-info.org.
Subjects and scan selection
A sample of 129 subjects were selected (79 control and 50 AD, see Table 1), where to the best of the knowledge of the core QC site (Mayo Clinic) there had not been any (1) phantom replacement at the scanner sites or problems such as leakage or dropping of the phantom, and (2) technical difficulties with the MRI protocol or scanner that could have adversely impacted scan geometry. These 129 subjects had been scanned at 34 different sites, on 1.5 Tesla, Siemens (n = 49) or General Electric (GE) Medical Systems (n = 80) MR clinical scanners. Each individual was scanned with different sequences but for this study we only used the T1-weighted volumetric scans. Representative imaging parameters were TR = 2400 ms, TI = 1000 ms, TE = 3.5 ms, flip angle = 8°, field of view = 240 × 240 mm and 160 sagittal 1.2 mm-thick-slices and a 192 × 192 matrix yielding a voxel resolution of 1.25 × 1.25 × 1.2 mm, or 180 sagittal 1.2 mm-thick-slices with a 256 × 256 matrix yielding a voxel resolution of 0.94 × 0.94 × 1.2 mm. The details of the ADNI MR imaging protocol are described in Jack et al. (2008), and listed on the ADNI website (http://www.loni.ucla.edu/ADNI/Research/Cores/).
Table 1.
Subject characteristics.
| Characteristic | Controls | AD |
|---|---|---|
| Number of subjects | 79 | 50 |
| Number of women (%) | 35 (44) | 27 (54) |
| Mean (SD) age at baseline (years) | 76.0 (4.9) | 75.1 (6.9) |
| Mean (SD) scan interval (days) | 389 (16) | 387 (13) |
The standard ADNI processing pipeline includes post-acquisition correction of gradient warping (Jovicich et al., 2006), B1 non-uniformity correction (Narayana et al., 1988) depending on the scanner and coil type, intensity non-uniformity correction (Sled et al., 1998) and phantom-based scaling correction (Gunter et al., 2006)—the geometric phantom scan having been acquired with each patient scan. 129 pairs (baseline and 1 year repeat) of images with all necessary corrections including the phantom-based scaling correction were downloaded from the ADNI website (http://www.loni.ucla.edu/ADNI), and in this study are called phantom corrected images. Mayo Clinic provided the phantom scale correction parameters for each image, and so a second dataset of 129 pairs of images was created by reversing-out the phantom scaling correction by changing the image header, and in this paper are called uncorrected images. So, in this paper, the two datasets are referred to as “uncorrected” and “phantom corrected”, and each dataset has 129 pairs of baseline and repeat scans, with the only difference between the two datasets being the phantom scaling correction.
Image registration
Images were registered using AIR 5.2.5, minimising the standard deviation of the ratio image (Woods et al.,1993) (http://bishopw.loni.ucla.edu/AIR5). For each baseline scan, whole brain regions were delineated using a semi-automated, iterative, 3D morphological technique, whereby the brain region is initially identified by manually selecting two intensity thresholds, the largest connected component is extracted, conditional dilations and erosions are applied and the resultant region is manually edited as necessary (Freeborough et al., 1997). Brain regions for the repeat scans were found using automated region propagation (Evans et al., 2008). The propagation is achieved by registering the baseline scan to the repeat scan using affine registration and then a non-linear technique based on B-Splines (Rueckert et al., 1999) and then using these two transformations to deform the baseline region into the co-ordinate space of the repeat scan. The registration experiments in this paper were performed over the brain volumes dilated 8 times with a 6-neighborhood structuring element. In the literature, methods that measure brain atrophy vary with regard to the registration step. Registration has been performed using the whole image, using just the brain region (Woods et al., 1998), using a dilated brain mask (Gunter et al., 2003), or using a skull extraction procedure to ensure registration does not affect atrophy measurement (Freeborough et al., 1996; Smith et al., 2002). Eight dilations were performed on each brain mask to include the edges of the skull and scalp in order to reduce the likelihood that the optimisation of the scale parameters would affect any measurement of atrophy, and to provide a comparable approach with other groups.
Measurement of atrophy
Registered images were corrected for differential intensity bias (Lewis and Fox, 2004) and then the Brain Boundary Shift Integral (BBSI) (Freeborough and Fox, 1997) was calculated as a measure of brain atrophy. The BBSI is calculated by integrating the intensity change between two thresholds in a region around all brain/non-brain boundaries.
Statistical analysis
Both the phantom and registration scaling correction procedures result in multiplicative scale factors for each of the X, Y and Z voxel dimensions. In this paper we define the volume scale factors as the product of the X, Y and Z scale factors. These may, for example, range from 0.97 to 1.03, and where we believe it adds clarity, we convert these to percentage values, e.g. 0.97 → − 3% and 1.03 → + 3%. Where we discuss the magnitude of these changes, we take the absolute percentage change as a measure of the amount of scale change, regardless of whether that change was an increase or decrease. Throughout this paper, we compare the differences of mean absolute percentage scale change, and differences of the mean, annualized, percentage BSI measures using two tailed t-tests. In the Experiments section, we compare the difference in variance of BBSI measures using Pitman's tests. In each significance test, the null hypothesis is that there is zero difference, and the significance level is set at p <0.05 unless otherwise stated. All tests were performed using Stata 10.0 (StataCorp, Texas, USA).
Experiments
Assessing the magnitude of phantom scaling corrections
This section addresses only phantom images. The scaling correction for each scan, derived from scanning the phantom (Gunter et al., 2006) provides scale factors in the X, Y and Z image directions. For each image, the volume scale factor was calculated as the product of the X, Y and Z phantom scale factors and converted to a percentage volume change. The distribution of volume scale factors at baseline and repeat was compared using an independent samples two tailed t-test.
Results
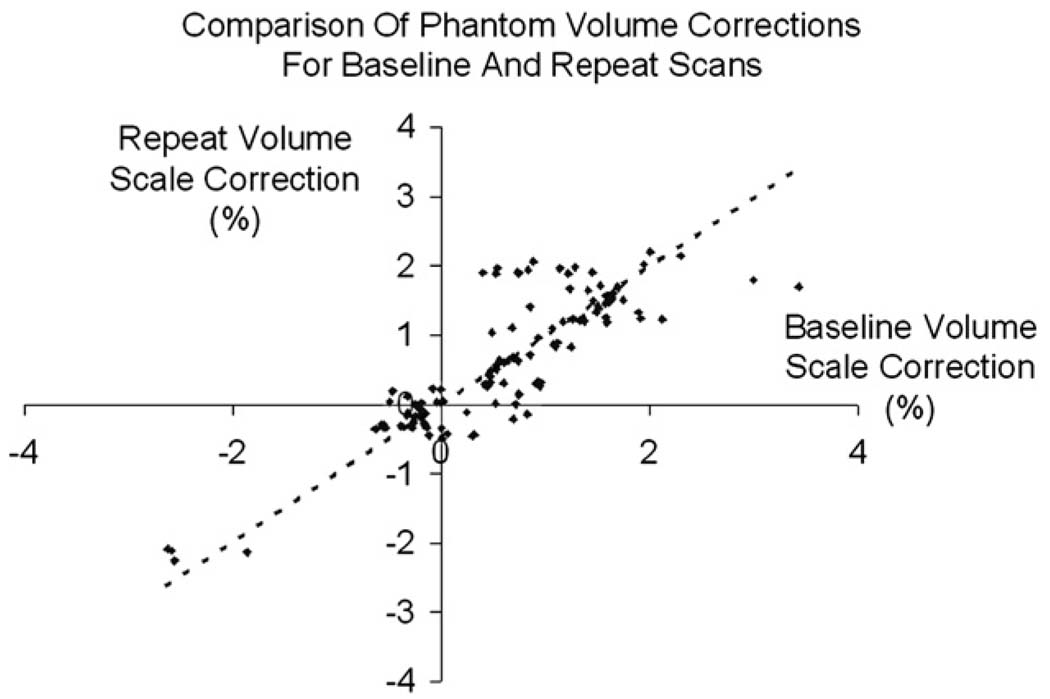
Table 2 shows the mean (SD) and range of absolute percentage scale corrections applied to baseline and repeat scans by the phantom correction procedure—voxel volumes in each scan being corrected to the absolute geometric standard of the phantom. The mean absolute volume change was 0.90% for baseline scans and 0.87% for the repeat scans. There was no significant difference between the distribution of volume scale factors found in the baseline images and repeat images (p = 0.97) indicating no systematic bias in the phantom scaling correction procedure over the time interval of 1 year. Fig. 1 shows the baseline percentage volume change against the repeat percentage volume change calculated using the phantom. Visually, there is some correlation between these values indicating that the scanners are relatively stable in terms of scaling.
Table 2.
Absolute percentage scale corrections calculated using the phantom for baseline scans and repeat scans.
| X-axis (%) | Y-axis (%) | Z-axis (%) | Volume (%) | ||
|---|---|---|---|---|---|
| Baseline | Mean (SD) | 0.41 (0.39) | 0.56 (0.26) | 0.40 (0.32) | 0.90 (0.69) |
| Baseline | Range | 0.03–2.18 | 0.05–1.65 | 0.01–1.54 | 0.00–3.42 |
| Repeat | Mean (SD) | 0.38 (0.36) | 0.53 (0.30) | 0.43 (0.36) | 0.87 (0.69) |
| Repeat | Range | 0.01–2.03 | 0.01–1.59 | 0.00–1.67 | 0.01–2.25 |
| Baseline/repeat | Mean (SD) | 0.20 (0.27) | 0.17 (0.20) | 0.14 (0.16) | 0.33 (0.36) |
| Baseline/repeat | Range | 0.00–1.39 | 0.00–1.21 | 0.00–0.71 | 0.00–1.66 |
For each image in our phantom corrected dataset, we have the scale factor calculated using the phantom for each axis. We calculate the volume change as X × Y × Z for each image and convert to an absolute percentage, and display the mean (SD) and range aggregated over the 129 baseline images (rows 1, 2) and the 129 repeat images (rows 3, 4). Furthermore, we take the baseline and repeat volume scale factors, and calculate the ratio of Baseline/Repeat, and display the mean (SD) and range in rows 5 and 6.
Fig. 1.
The baseline percentage volume correction (X-axis) against the corresponding repeat image percentage volume correction (Y-axis), calculated using the phantom correction procedure. Any points that lie off the y = x line represent where the phantom correction differed between baseline and follow-up—which should indicate the presence of a scaling change on the scanner between the two MRI exams.
Quantification of the residual scaling errors after phantom correction
The 129 pairs of phantom corrected baseline and repeat scans were registered using the 9DOF registration algorithm. The registration algorithm produces X, Y and Z scale factors, from which the volume scale factor was calculated as the product of the X, Y and Z registration scale factors, and then converted to a percentage volume change. If no scaling is needed the X, Y and Z scale parameters produced by the registration algorithm would each be 1.00 indicating 0% volume change. The registration volume scale change was compared to the expected volume scale change of 0%. The distribution of volume scale factors for control and AD groups was compared using an independent samples two tailed t-test.
Results
The mean (SD) percentage volume change was 0.04 (0.29) % for control and 0.04 (0.32) for the AD group. Re-running the experiment with the baseline and repeat scans reversed gave, as expected, a mean percentage change of −0.04% for both groups. The mean (SD) absolute percentage volume change was 0.20 (0.20) % for the control group and 0.19 (0.26) % for the AD group. There was no significant difference between the distribution of the volume scale factors calculated using 9DOF registration for the control and AD groups (p = 0.95).
Comparison of the 9DOF registration method and phantom correction method
When a repeat scan is registered using 9DOF to a baseline scan, the registration algorithm calculates X, Y and Z scale factors to scale the repeat scan directly to the baseline scan, from which the volume scale change is calculated (the scaling change over time). The volume scale factor obtained using registration should therefore match the ratio of the baseline and repeat volume scale factors calculated using the phantom. The 129 pairs of uncorrected baseline and repeat scans were registered using the 9DOF registration algorithm. As above, we took the registration result, and calculated the volume scale factor, and compared it to the ratio of the baseline and repeat volume scale factor calculated using the phantom. The distribution of volume scale corrections calculated using the phantom was compared to the distribution of volume scale corrections calculated from the registration using a paired samples two tailed t-test.
Results
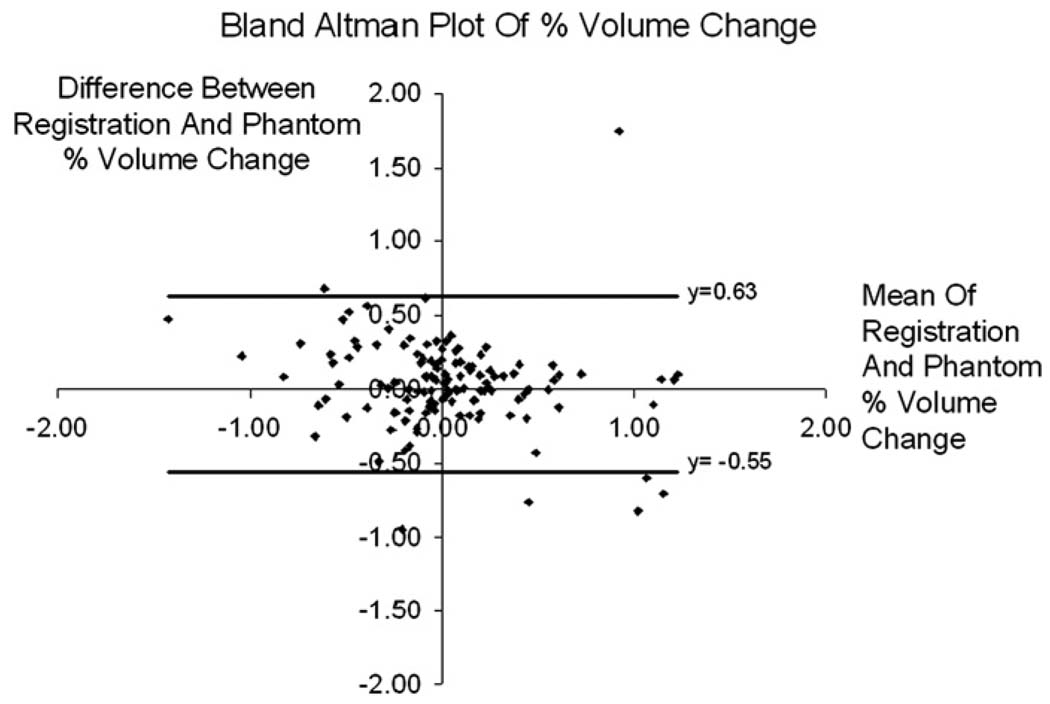
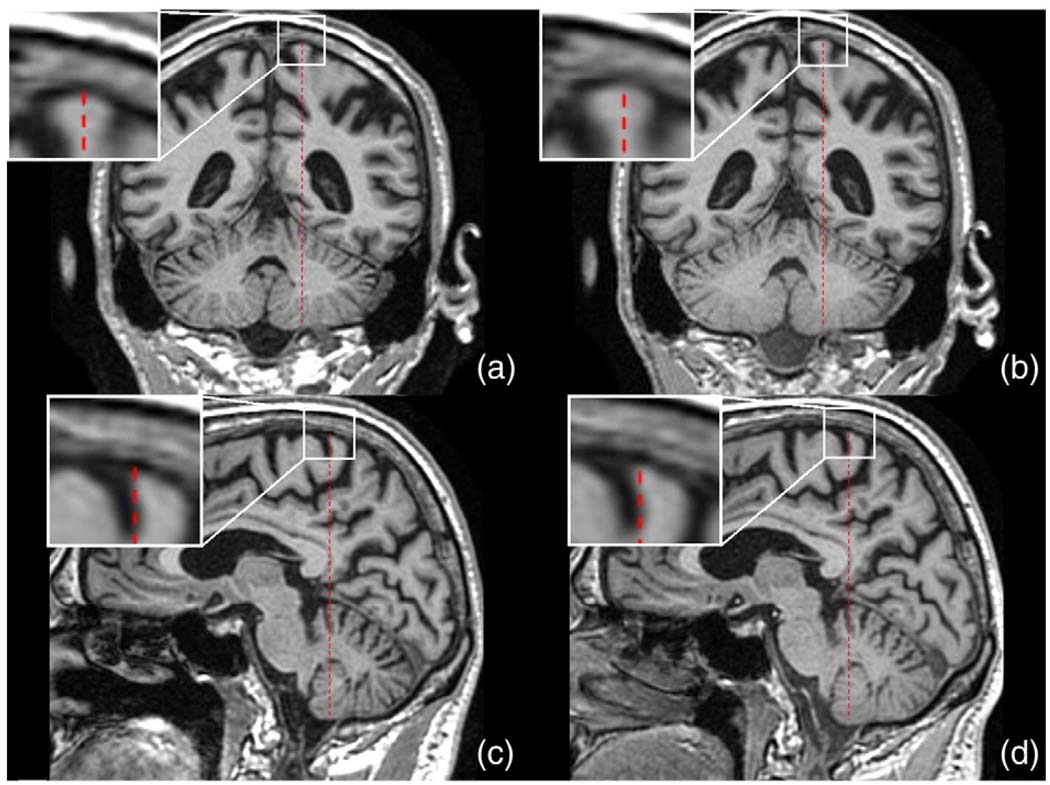
Table 2 rows 5 and 6, shows the mean (SD) and range of baseline to repeat volume scale change calculated from the phantom scaling procedure. While the baseline scans have a mean volume change of 0.90% and the repeat images have a mean volume change of 0.87% (see Table 2), the ratio of the two measurements is much smaller at 0.33%. Table 2 shows the range of the size of correction that the 9DOF registration was trying to correct for. The distribution of the phantom calculated repeat image to baseline image volume scale change is shown in Fig. 2. A two tailed paired t-test, comparing the phantom scaling percent volume change and the registration percent volume change gave p = 0.15. Fig. 3 shows a Bland–Altman plot of these results. In this plot, there are 7 registrations that lie outside the 95% confidence interval (mean ± 1.96 × SD). The 7 outliers consisted of 5 control and 2 AD subjects. A further 7 subjects (3 control and 4 AD) were randomly selected from our 129 subjects, and in a randomised test, blinded to scaling correction method, an expert reviewer was asked to visually inspect and rank corresponding pairs of images with 1) no correction, 2) phantom correction and 3) registration correction. For all 7 outliers, the 9DOF registration was the preferred scaling correction—in that there was no residual scaling artifact after the correction. In 5 out of 7 outliers, the phantom was deemed to have had a detrimental effect, i.e. worse than no scaling correction at all, and in the remaining two cases the phantom correction was better than no correction at all, but not better than the 9DOF registration. Fig. 4 shows an example of a large scaling error from the ADNI cohort, similar to those visually assessed.
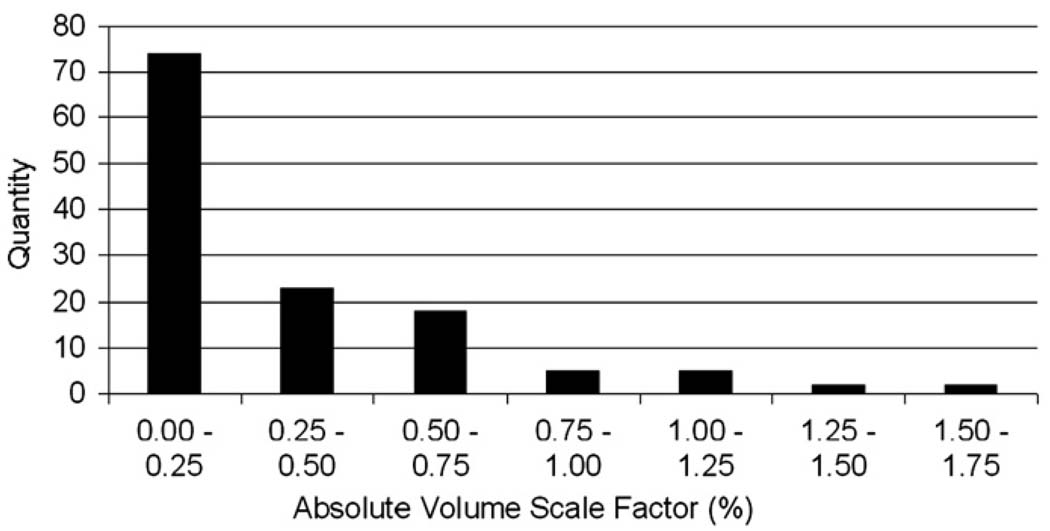
Fig. 2.
The distribution of the absolute repeat scan to baseline scan phantom corrected volume scale factors as a percentage. 97 of the 129 cases have a volume scale correction of <0.5%, and 115 examples have a volume scale correction of <0.75%.
Fig. 3.
A Bland–Altman plot showing the mean and difference between the percentage volume scale correction calculated using the phantom procedure, and the percentage volume scale correction calculated using the 9DOF registration on the uncorrected images.
Fig. 4.
Example images, to demonstrate the scaling errors visually inspected in the Experiments section. Image (a) is a baseline image, coronal view, and figure (b) is the 6DOF registered repeat image. The red bar is the same size in all images, and yet the enlarged section shows clear differences between (a) and (b), most visible at the end of the bar. The difference is a superior–inferior scaling issue. Images (c) and (d) show the same subject as (a) and (b) but in saggital view. Image (c) is the baseline, and (d) is the 6DOF registered repeat image.
Assessing the effect of 9DOF registration on the measurement of brain atrophy using the BBSI
The 129 uncorrected repeat scans were registered to the corresponding baseline scan using 6DOF, thereby having no scaling correction. In addition, the 129 phantom corrected repeat scans were registered using 6DOF to the corresponding baseline scan and finally the 129 uncorrected repeat scans were registered to the corresponding baseline scan using 9DOF. After differential bias correction we measured the BBSI for each pair. The annualized mean (SD) BBSI was calculated for control and AD groups, for each set of images.
Results
Table 3 shows the performance of the phantom scaling correction, and the registration algorithm in terms of the Brain Boundary Shift Integral (BBSI) measurement for control and AD subjects. The BBSI value gives a measure of overall brain atrophy. This is a volume change expressed as a percentage of baseline brain volume, per year. The first line, showing uncorrected images registered with 6DOF has no scaling correction at all. The second and third lines show the impact on mean (SD) BBSI values for phantom scaling correction, and 9DOF registration scaling correction respectively. We did not find a significant difference in the mean BBSI values for either scaling correction method, in either control or AD groups (all p > 0.3). Overall, the phantom correction procedure reduced the SD of BBSI by 7% for both control and AD groups, and the 9DOF registration reduced the SD of BBSI by 13% for control subjects and 9% for AD subjects. This corresponds to a reduction in variance of BBSI of around 20%. Table 4 shows the significance of these results in terms of the Pitman's tests.
Table 3.
The mean (SD) annualized Brain Boundary Shift Integral (BBSI) value for uncorrected and phantom corrected images, registered using 6 or 9DOF, and for control and AD subjects.
| Correction | Control (n = 79) | AD (n = 50) |
|---|---|---|
| None | 0.51 (0.93) | 1.38 (0.98) |
| Phantom corrected | 0.51 (0.86) | 1.37 (0.91) |
| 9DOF registration | 0.49 (0.81) | 1.34 (0.89) |
The BBSI value gives a measure of overall brain atrophy. This is a volume change expressed as a percentage of baseline brain volume, per year.
Table 4.
Comparing BBSI values from Table 3, showing Pitman's test (a comparison of variance) p-values.
| Comparison of scaling correction method | Control | AD |
|---|---|---|
| None versus phantom corrected | 0.091 | 0.095 |
| None versus 9DOF registration | <0.001 | 0.070 |
| Phantom corrected versus 9DOF registration | 0.026 | 0.642 |
Discussion
In this paper, we calculated the magnitude of phantom derived voxel scaling changes in structural MRI images collected in the ADNI trial. We assessed whether a scaling correction method based on a post-processing of the brain scans themselves using a widely available registration algorithm (Woods et al., 1993) can correct for scaling changes as effectively as a scaling phantom. In all cases, scan pairs were within-scanner.
The phantom scans gave a mean absolute percentage volume scale change of 0.90% for baseline scans and 0.87% for the repeat scans with no significant difference (p = 0.97) in the magnitude of the correction between baseline and repeat scans. The implication of this finding is, as would be expected, that on average there was neither a systematic scaling difference (bias) in the scanners over time, nor a systematic change in the phantom scaling correction. The phantom corrections at baseline and follow-up for individual subjects were correlated with a mean absolute % volume change between repeat and baseline scans of only 0.33%. This suggests that scanner-related change in voxel sizes resulted in artifactual errors in the measurement of brain volume change that were on average of a similar magnitude as those seen in normal ageing over 1 year, typically 0.3–0.5% for healthy individuals aged 50–75 years (Scahill et al., 2003). This is considerably less than the annual losses in MCI or AD (1–2% of baseline brain volume per year) (Fox and Schott, 2004). However, this finding must come with a number of caveats. First, because this study was designed to compare methods of correction for scaling change, the scanners chosen were not representative of scanners generally; they had to have been “qualified” to be included in ADNI; they were part of an ongoing QC programme and importantly scans from scanners with an obvious problem had been excluded by the central QC site (Mayo Clinic) that selected the scans for this comparison. For these reasons, the temporal stability of the scanners analyzed here is most likely better than what might be expected in a typical clinical trial. Thus these data likely underestimate the deleterious impact of scanner scaling instability in most clinical trials. Secondly, although some scanners showed no change at all in voxel sizes, there was quite a range (Table 2 and Fig. 1) in the individual scanner-related change with a number of scan pairs showing more than 1% volume change as measured by the phantom.
Nine degrees of freedom (9DOF) registration of the phantom corrected images was used to test if there is any residual scaling error after phantom correction. In an ideal world, if both methods of scaling correction were perfect, the phantom correction would correct the images perfectly, and having done so the registration algorithm would correctly recover scalings change of exactly 1.0 for all scan pairs and would give a mean volume change and mean absolute volume change of 0.0%. Any deviation from this could be caused by either the phantom correction algorithm, whereby data that we are assuming is phantom corrected is in fact not perfectly corrected, or the registration algorithm is inaccurate (e.g. adjusting for scaling unnecessarily), or both. The mean percentage volume change was only 0.04%, which is negligible in practical terms, and importantly, when we reversed the images and re-ran the experiment, the result was −0.04%. This indicates that the registration algorithm is performing symmetrically, and hence there is a small bias in the data. There was no significant difference (p = 0.97) between the control and AD groups indicating no disease-related bias: implying that progressive atrophy in the AD group did not influence the registration-based correction. The majority of scan pairs in our data (98 out of 129 pairs, 76%) had a phantom scaling correction of less than 0.5% (arbitrarily chosen). For small scale changes (e.g. <0.05%) the phantom and the registration-based scalings are not tightly correlated perhaps implying we are at the practical limits of correction with this method. Future work should seek ways of improving the precision of scaling correction. Importantly however, for large scale changes we found a small number of cases (7) where there was a marked and material difference between the phantom derived scalings and the registration derived scalings. Visual inspection (blind to method of correction) suggested that the 9DOF registration produced a more correct solution. We feel that this implies that in a small number of cases the phantom produced an incorrect scale change which could be corrected by the 9DOF registration. These results combined, suggest that the additional expense and logistic effort of scanning a phantom with every patient scan can be avoided by registration-based scaling correction.
In terms of the effect on the measurement of brain atrophy (Materials and methods), the mean BBSI values were similar whether measured from the uncorrected, phantom, or 9DOF registration corrected scans (Table 3). Although not significantly different it is worth noting that the BBSI values were on average about 3% lower with 9DOF correction. Importantly however, there was a trend towards a reduction in the variability (standard deviation) of the BBSI value scans when corrected for scaling errors with either method. The reduction in variability was greatest with 9DOF correction for the control group and was statistically significant. Both forms of correction reduced the SD of the mean atrophy rates: the 9DOF correction producing about 10% reduction in the SD for both control (13%) and AD (9%) groups—this is equivalent to approximately 20% reduction in variance which if there were no changes in mean rates of atrophy equate to approximately 20% reduction in sample sizes. Sample size estimates for disease modifying trials in AD are driven by the variance in the outcome measure and the expected difference in the mean rate of atrophy in the treated group versus the placebo group. The maximum effect one could reasonably expect for an atrophy slowing therapy would be to reduce the AD rate to the control rate, as such, sample sizes are proportional to (SD/(difference in means))2 (Fox et al., 2000)—sample size estimates based upon the atrophy rates in the AD subjects in this study would therefore be 10–12% lower with (either) correction for voxel scaling than if no correction was used. This could improve group separation of atrophy rates in AD and controls and make a material difference in therapeutic trials especially if less well controlled scanners are included.
An important aspect of the method is the pre-segmentation of the brain prior to the use of the registration step. The original Woods method (Woods et al., 1993) required a segmented image of the brain. Subsequent validation studies showed that this significantly improved the accuracy of the overall registration compared with unsegmented images (Freeborough et al., 1996; Woods et al., 1998). Gunter et al. (2003) later showed better group separation (AD and control groups) using a dilated brain mask. For this paper we used 8 dilations which include the skull/scalp boundary. In this paper we did not assess different registration algorithms for correction of voxel scaling changes in longitudinal MR studies. We focused on a single widely used algorithm. Future work could investigate different interpolation methods to smooth the cost function near the registration point, with the aim of improving the precision. Additionally, it would be useful to understand further which parts of the image are most important for this type of registration—a highly complex structure such as the brain provides good 6DOF registration, but the skull or scalp/skull high contrast boundary may be more important to constrain scaling, either as part of a 9DOF algorithm or a 3DOF algorithm (just scalings). Another alternative, is to use an intensity based method that is robust to large percentages of statistical outliers. Approaches like this have been proposed (Smith et al., 2002; Freeborough et al., 1996; Ourselin et al., 2000) and the ADNI dataset may be a way of assessing their performance at correcting for these scaling issues. Furthermore having run these experiments on a subset of 129 well controlled pairs of scans, it would be interesting to examine the whole ADNI dataset. This should have greater power to assess 9DOF registration correction of scaling errors and assess whether the trend towards a reduction in variance is significant with larger datasets.
The ADNI study went to great lengths to image a phantom with every subject scan, and has provided us with realistic, quantitative data such as might be obtained in future clinical trials. In this dataset, the mean correction to baseline and repeat scans was small, and the ratio of the measurements (i.e. change over time) was smaller. In addition the effects of phantom correction on the BBSI were not significant, and there was a correlation between the size and direction of the correction applied to baseline and repeat scans. This suggests that it is more important to ensure that a subject is scanned at the same centre and on the same quality controlled scanner than it is to scan the phantom with every subject. In this way, as long as the scanner was regularly and carefully serviced, the relative change would be small enough to not have a significant effect on measurements of atrophy, even if larger absolute scaling errors are present and unchanging over time. Phantoms will clearly play an important role in calibrating the scanner as part of routine maintenance due to the high level of accuracy and precision thus obtained, and the use of high quality phantoms to accredit imaging sites for clinical trial could have great value in ensuring that all sites in multi-site trials have similar stability to the carefully monitored sites used in the ADNI study. The results from the visual assessment also suggest alternative strategies. In general the 9DOF registration was the preferred solution where the scaling factors found by the phantom and the 9DOF registration method were most different. However, we can imagine cases where the 9DOF registration will fail. The 9DOF registration is most likely to be inaccurate when there is significant motion artifact, excessive amounts of atrophy or large intensity differences. If any of these factors are known to be likely, then a phantom scan may be prudent. For example phantom scaling correction may be preferable for patients that are more likely to move during the scan, for longer running trials, or if a known scanner upgrade is unavoidable. The results from the visual assessment also showed an example with a warping distortion presumably due to uncorrectable gradient non-linearity. This suggests that it is also important to place subjects consistently as close as possible to the iso-centre of the magnet and to position subjects in the same location for each visit. In addition, it may be the case that the organizers of a clinical trial should invest in a pre-qualifying phase, where an imaging centre uses a phantom to benchmark their quality control processes and prove to a hub site that they can routinely scan subjects to a known quality standard (Jack et al., 2003). These recommendations may provide an alternative, more cost effective method of control than a phantom scan with every subject. The comparison of the value of the two scaling change correction methods was done using a single structural MRI endpoint, namely the BBSI for quantification of global brain atrophy. For other endpoints, especially those involving local measurements of atrophy or of cortical thickness, the relative merits of the two approaches may possibly differ, however it is likely that scaling changes would affect any measure of volume change over time. Also, this paper has focused on longitudinal measurements of brain atrophy. For cross-sectional studies, although absolute voxel scaling errors (which the registration method does not correct) may have an impact, any effect will be small compared to inter-individual variation in brain volumes and morphology.
Conclusions
The ADNI study is the first publicly-available, large scale, multi-site study to routinely scan a geometric phantom with each subject. Consequently this paper is the first to study and quantify the benefit of the phantom in a multi-centre trial context, and to compare the phantom with an image processing based solution to correct for change in scaling values using a 9 degree of freedom registration algorithm. The 9DOF registration approach was found to produce essentially equivalent results to phantom scale correction when the images were used to quantify brain atrophy. We suggest that 9DOF registration is unbiased, can be automated as part of image processing pipelines, can be applied retrospectively, is less expensive than using a scaling phantom and avoids the risk of errors introduced by faulty phantoms. These conclusions have practical implications on the implementation of future clinical trials.
Acknowledgments
Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI; Principal Investigator: Michael Weiner; NIH grant U01 AG024904). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering (NIBIB), and through generous contributions from the following: Pfizer Inc., Wyeth Research, Bristol-Myers Squibb, Eli Lilly and Company, GlaxoSmithKline, Merck & Co. Inc., AstraZeneca AB, Novartis Pharmaceuticals Corporation, Alzheimer's Association, Eisai Global Clinical Development, Elan Corporation plc, Forest Laboratories, and the Institute for the Study of Aging, with participation from the U.S. Food and Drug Administration. Industry partnerships are coordinated through the Foundation for the National Institutes of Health. The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory of Neuro Imaging at the University of California, Los Angeles. This work was undertaken at UCL/UCLH which received a proportion of funding from the Department of Health's NIHR Biomedical Research Centres funding scheme. The Dementia Research Centre is an Alzheimer's Research Trust Co-ordinating centre. MC and KL were supported by TSB grant M1638A, JB is supported by an Alzheimer’s Research Trust (UK) Research Fellowship and NCF by the MRC (UK). The authors would like to thank Shona Clegg, Raivo Kittus and Lois Kim at the Dementia Research Centre for their invaluable help in assessing registration quality and statistical analysis, and also the ADNI study subjects and investigators for their participation.
Footnotes
Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (http://www.loni.ucla.edu/ADNI). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. ADNI investigators include (complete listing available at http://www.loni.ucla.edu/ADNI/Collaboration/ADNI_Citation.shtml).
References
- Archer HA, Edison P, Brooks DJ, Barnes J, Frost C, Yeatman T, Fox NC, Rossor MN. Amyloid load and cerebral atrophy in Alzheimer's disease: an 11C-PIB positron emission tomography study. Ann. Neurol. 2006 Jul;60(1):145–147. doi: 10.1002/ana.20889. [DOI] [PubMed] [Google Scholar]
- Braak H, Braak E. Staging of Alzheimer's disease-related neurofibrillary changes. Neurobiol. Aging. 1995;16(3):271–278. doi: 10.1016/0197-4580(95)00021-6. discussion 278–84. [DOI] [PubMed] [Google Scholar]
- MarCarlson NE, Moore MM, Dame A, Howieson D, Silbert LC, Quinn JF, Kaye JA. Trajectories of brain loss in aging and the development of cognitive impairment. Neurology. 2008;70(11):828–833. doi: 10.1212/01.wnl.0000280577.43413.d9. [DOI] [PubMed] [Google Scholar]
- Chan D, Janssen JC, Whitwell JL, Watt HC, Jenkins R, Frost C, Rossor MN, Fox NC. Change in rates of cerebral atrophy over time in early-onset Alzheimer's disease: longitudinal MRI study. Lancet. 2003 Oct;362(9390):1121–1122. doi: 10.1016/S0140-6736(03)14469-8. [DOI] [PubMed] [Google Scholar]
- Evans MC, Nielsen C, Douiri A, Barnes J, Clegg SL, Lehmann M, Mellow T, McNaught E, Ahsan L, Boyes R, Pepple T, Foster J, Rosser MN, Fox N. Automating the BSI brain atrophy rate calculation: comparison of using automated and semi-automated brain regions. Alzheimer's Dement. 2008 July;4(4) Supplement 1:T84–T85. [Google Scholar]
- Fox NC, Schott JM. Imaging cerebral atrophy: normal ageing to Alzheimer's disease. Lancet. 2004 Jan;363(9406):392–394. doi: 10.1016/S0140-6736(04)15441-X. [DOI] [PubMed] [Google Scholar]
- Fox NC, Freeborough PA. Brain atrophy progression measured from registered serial MRI: validation and application to Alzheimer's disease. J. Magn. Reson. Imaging. 1997;7(6):1069–1075. doi: 10.1002/jmri.1880070620. [DOI] [PubMed] [Google Scholar]
- Fox NC, Freeborough PA, Rossor MN. Visualisation and quantification of rates of atrophy in Alzheimer's disease. Lancet. 1996 Jul;348(9020):94–97. doi: 10.1016/s0140-6736(96)05228-2. [DOI] [PubMed] [Google Scholar]
- Fox NC, Cousens S, Scahill R, Harvey RJ, Rossor MN. Using serial registered brain magnetic resonance imaging to measure disease progression in Alzheimer disease: power calculations and estimates of sample size to detect treatment effects. Arch. Neurol. 2000 Mar;57(3):339–344. doi: 10.1001/archneur.57.3.339. [DOI] [PubMed] [Google Scholar]
- Fox NC, Black RS, Gilman S, Rossor MN, Griffith SG, Jenkins L, Koller M N1792 (Q. S-21)-201 Study, A. Effects of Abeta immunization (AN1792) on MRI measures of cerebral volume in Alzheimer disease. Neurology. 2005 May;64(9):1563–1572. doi: 10.1212/01.WNL.0000159743.08996.99. [DOI] [PubMed] [Google Scholar]
- Freeborough PA, Fox NC. The boundary shift integral: an accurate and robust measure of cerebral volume changes from registered repeat MRI. IEEE Trans. Med. Imag. 1997;16(5):623–629. doi: 10.1109/42.640753. [DOI] [PubMed] [Google Scholar]
- Freeborough PA, Woods RP, Fox NC. Accurate registration of serial 3D MR brain images and its application to visualizing change in neurodegenerative disorders. J. Comput. Assist. Tomogr. 1996;20(6):1012–1022. doi: 10.1097/00004728-199611000-00030. [DOI] [PubMed] [Google Scholar]
- Freeborough PA, Fox NC, Kitney RI. Interactive algorithms for the segmentation and quantitation off 3-D MRI brain scans. Comput. Methods Programs Biomed. 1997;53:15–25. doi: 10.1016/s0169-2607(97)01803-8. [DOI] [PubMed] [Google Scholar]
- Frost C, Kenward MG, Fox NC. The analysis of repeated ‘direct’ measures of change illustrated with an application in longitudinal imaging. Stat. Med. 2004;23:3275–3286. doi: 10.1002/sim.1909. [DOI] [PubMed] [Google Scholar]
- Gunter JL, Shiung MM, Manduca A, Jack CR. Methodological considerations for measuring rates of brain atrophy. J. Magn. Reson. Imaging. 2003 Jul;18(1):16–24. doi: 10.1002/jmri.10325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunter JL, Bernstein MA, Borowski BJ, Felmlee JP, Blezek DJ, Mallozzi RP, Levy JR, Schuff N, Jack CR. Validation testing of the MRI Calibration Phantom for the Alzheimer's Disease Neuroimaging Initiative Study. ISMRM 14th Scientific Meeting and Exhibition; Seattle, WA. 2006. 2006. [Google Scholar]
- Hajnal JV, Hill DLG, Hawkes DJ. Medical Image Registration. CRC Press; 2001. [Google Scholar]
- Hill DL, Maurer CR, Studholme C, Fitzpatrick JM, Hawkes DJ. Correcting scaling errors in tomographic images using a nine degree of freedom registration algorithm. J. Comput. Assist. Tomogr. 1998;22(2):317–323. doi: 10.1097/00004728-199803000-00031. [DOI] [PubMed] [Google Scholar]
- Hill DL, Batchelor PG, Holden M, Hawkes DJ. Medical image registration. Phys. Med. Biol. 2001 Mar;46(3):R1–R45. doi: 10.1088/0031-9155/46/3/201. [DOI] [PubMed] [Google Scholar]
- Jack CR, Petersen RC, Xu Y, O'Brien PC, Smith GE, Ivnik RJ, Tangalos EG, Kokmen E. Rate of medial temporal lobe atrophy in typical aging and Alzheimer's disease. Neurology. 1998 Oct;51(4):993–999. doi: 10.1212/wnl.51.4.993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Slomkowski M, Gracon S, Hoover TM, Felmlee JP, Stewart K, Xu Y, Shiung M, O'Brien PC, Cha R, Knopman D, Petersen RC. MRI as a biomarker of disease progression in a therapeutic trial of milameline for AD. Neurology. 2003 Jan;60(2):253–260. doi: 10.1212/01.wnl.0000042480.86872.03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Shiung MM, Gunter JL, O'Brien PC, Weigand SD, Knopman DS, Boeve BF, Ivnik RJ, Smith GE, Cha RH, Tangalos EG, Petersen RC. Comparison of different MRI brain atrophy rate measures with clinical disease progression in AD. Neurology. 2004 Feb;62(4):591–600. doi: 10.1212/01.wnl.0000110315.26026.ef. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Shiung MM, Weigand SD, O'Brien PC, Gunter JL, Boeve BF, Knopman DS, Smith GE, Ivnik RJ, Tangalos EG, Petersen RC. Brain atrophy rates predict subsequent clinical conversion in normal elderly and amnestic MCI. Neurology. 2005 Oct;65(8):1227–1231. doi: 10.1212/01.wnl.0000180958.22678.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Bernstein MA, Fox NC, Thompson P, Alexander G, Harvey D, Borowski B, Britson PJ, Whitwell JL, Ward C, Dale AM, Felmlee JP, Gunter JL, Hill DLG, Killiany R, Schuff N, Fox-Bosetti S, Lin C, Studholme C, DeCarli CS, Krueger G, Ward HA, Metzger GJ, Scott KT, Mallozzi R, Blezek D, Levy J, Debbins JP, Fleisher AS, Albert M, Green R, Bartzokis G, Glover G, Mugler J, Weiner MW. The Alzheimer's Disease Neuroimaging Initiative (ADNI): MRI methods. J. Magn. Reson. Imaging. 2008 Apr;27(4):685–691. doi: 10.1002/jmri.21049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins R, Fox NC, Rosser AM, Harvey RJ, Rosser MN. Intracranial volume and Alzheimer disease: evidence against the cerebral reserve hypothesis. Arch. Neurol. 2000;57:220–224. doi: 10.1001/archneur.57.2.220. [DOI] [PubMed] [Google Scholar]
- Jovicich J, Czanner S, Greve D, Haley E, van der Kouwe A, Gollub R, Kennedy D, Schmitt F, Brown G, Macfall J, Fischl B, Dale A. Reliability in multi-site structural MRI studies: effects of gradient non-linearity correction on phantom and human data. NeuroImage. 2006 Apr;30(2):436–443. doi: 10.1016/j.neuroimage.2005.09.046. [DOI] [PubMed] [Google Scholar]
- Lemieux L, Barker GJ. Measurement of small inter-scan fluctuations in voxel dimensions in magnetic resonance images using registration. Med. Phys. 1998;25(6):1049–1054. doi: 10.1118/1.598288. [DOI] [PubMed] [Google Scholar]
- Lewis EB, Fox NC. Correction of differential intensity inhomogeneity in longitudinal MR images. NeuroImage. 2004;23:75–83. doi: 10.1016/j.neuroimage.2004.04.030. [DOI] [PubMed] [Google Scholar]
- Mungas D, Harvey D, Reed BR, Jagust WJ, DeCarli C, Beckett L, Mack WJ, Kramer JH, Weiner MW, Schuff N, Chui HC. Longitudinal volumetric MRI change and rate of cognitive decline. Neurology. 2005 Aug;65(4):565–571. doi: 10.1212/01.wnl.0000172913.88973.0d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayana P, Brey WW, Kulkarni MV, Sievenpiper CL. Compensating for surface coil sensitivity variation in magnetic resonance imaging. Magn. Reson. Imaging. 1988;6:271–274. doi: 10.1016/0730-725x(88)90401-8. [DOI] [PubMed] [Google Scholar]
- O Brien JT, Paling S, Barber R, Williams ED, Ballard C, McKeith G, Gholkar A, Crum WR, Rossor MN, Fox NC. Progressive brain atrophy on serial MRI in dementia with Lewy bodies, AD, and vascular dementia. Neurology. 2001 May;56(10):1386–1388. doi: 10.1212/wnl.56.10.1386. [DOI] [PubMed] [Google Scholar]
- Ourselin S, Roche A, Prima S, Ayache N. Block matching: a general framework to improve robustness of rigid registration of medical images. Medical Image Computing and Computer Assisted Intervention. Lecture Notes in Computer Science. Heidelberg: InSpringer Berlin; 2000. [Google Scholar]
- Ridha BH, Barnes J, Bartlett JW, Godbolt A, Pepple T, Rossor MN, Fox NC. Tracking atrophy progression in familial Alzheimer's disease: a serial MRI study. Lancet Neurol. 2006 Oct;5(10):828–834. doi: 10.1016/S1474-4422(06)70550-6. [DOI] [PubMed] [Google Scholar]
- Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans. Med. Imag. 1999;18(8):712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- Scahill RI, Frost C, Jenkins R, Whitwell JL, Rossor MN, Fox NC. A longitudinal study of brain volume changes in normal aging using serial registered magnetic resonance imaging. Arch. Neurol. 2003 Jul;60(7):989–994. doi: 10.1001/archneur.60.7.989. [DOI] [PubMed] [Google Scholar]
- Silbert LC, Quinn JF, Moore MM, Corbridge E, Ball MJ, Murdoch G, Sexton G, Kaye JA. Changes in premorbid brain volume predict Alzheimer's disease pathology. Neurology. 2003 Aug;61(4):487–492. doi: 10.1212/01.wnl.0000079053.77227.14. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbox AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imag. 1998;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Smith SM, Zhang Y, Jenkinson M, Chen J, Matthews PM, Federico A, Stefano ND. Accurate, robust, and automated longitudinal and cross-sectional brain change analysis. NeuroImage. 2002 Sep;17(1):479–489. doi: 10.1006/nimg.2002.1040. [DOI] [PubMed] [Google Scholar]
- Wang D, Chalk JB, Rose SE, de Zubicaray G, Cowin G, Galloway GJ, Barnes D, Spooner D, Doddrell DM, Semple J. MR image-based measurement of rates of change in volumes of brain structures. Part II: application to a study of Alzheimer's disease and normal aging. Magn. Reson. Imaging. 2002 Jan;20(1):41–48. doi: 10.1016/s0730-725x(02)00472-1. [DOI] [PubMed] [Google Scholar]
- West J, Fitzpatrick JM, Wang MY, Dawant BM, Maurer CR, Kessler RM, Maciunas RJ, Barillot C, Lemoine D, Collignon A, Maes F, Suetens P, Vandermeulen D, van den Elsen PA, Napel S, Sumanaweera TS, Harkness B, Hemler PF, Hill DL, Hawkes DJ, Studholme C, Maintz JB, Viergever MA, Malandain G, Woods RP. Comparison and evaluation of retrospective intermodality brain image registration techniques. J. Comput. Assist. Tomogr. 1997;21(4):554–566. doi: 10.1097/00004728-199707000-00007. [DOI] [PubMed] [Google Scholar]
- Whitwell JL, Schott JM, Lewis EB, MacManus DG, Fox NC. Using nine degrees-of-freedom registration to correct for changes in voxel size in serial MRI studies. Magn. Reson. Imaging. 2004 Sep;22(7):993–999. doi: 10.1016/j.mri.2004.01.057. [DOI] [PubMed] [Google Scholar]
- Woods RP, Mazziotta JC, Cherry SR. MRI-PET registration with automated algorithm. J. Comput. Assist. Tomogr. 1993;17(4):536–546. doi: 10.1097/00004728-199307000-00004. [DOI] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, Holmes CJ, Cherry SR, Mazziotta JC. Automated image registration: I. General methods and intrasubject, intramodality validation. J. Comput. Assist. Tomogr. 1998;22(1):139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]