Barrier Compression and Its Contribution to Both Classical and Quantum Mechanical Aspects of Enzyme Catalysis

Abstract

It is generally accepted that enzymes catalyze reactions by lowering the apparent activation energy by transition state stabilization or through destabilization of ground states. A more controversial proposal is that enzymes can also accelerate reactions through barrier compression—an idea that has emerged from studies of H-tunneling reactions in enzyme systems. The effects of barrier compression on classical (over-the-barrier) reactions, and the partitioning between tunneling and classical reaction paths, have largely been ignored. We performed theoretical and computational studies on the effects of barrier compression on the shape of potential energy surfaces/reaction barriers for model (malonaldehyde and methane/methyl radical anion) and enzymatic (aromatic amine dehydrogenase) proton transfer systems. In all cases, we find that barrier compression is associated with an approximately linear decrease in the activation energy. For partially nonadiabatic proton transfers, we show that barrier compression enhances, to similar extents, the rate of classical and proton tunneling reactions. Our analysis suggests that barrier compression—through fast promoting vibrations, or other means—could be a general mechanism for enhancing the rate of not only tunneling, but also classical, proton transfers in enzyme catalysis.

Introduction

Enzymes are efficient and often unrivalled catalysts, yet uncertainty remains as to the precise origins of their catalytic power (1,2). Transition state theory (TST) (3) remains the dominant paradigm, but for reactions involving H (H⁺, H^•, or H⁻) transfer—comprising probably at least half of all enzymatic reactions—quantum mechanical tunneling of the transferring particle (H) must also be considered (4–10). H-transfer reactions are probed experimentally using isotope effects and, about 10 years ago, measurements of the temperature dependence of some enzymatic reactions began to uncover kinetic isotope effects (KIEs) with unusually strong temperature dependencies (11–14). The origin of such temperature dependencies is still hotly debated (see, e.g., (15–19)), but one popular explanation is that promoting vibrations—fast (subpicosecond) thermally activated vibrations of the enzyme-substrate binary complex—transiently compress (i.e., reduce the width of) the reaction barrier and consequently enhance the rate of the tunneling reaction (18–24). Saen-Oon et al. have also recently suggested that such vibrations may also enhance nontunneling reactions (25). Although it is possible to use computational studies to visualize putative promoting vibrations using spectral density analysis of molecular dynamics (MD) simulations (19,26,27), direct experimental observation of such vibrations remains elusive. Indeed, it has been argued that such vibrations might not be catalytically useful as, if they compress the reaction barrier, they will reduce the amount of H-tunneling that occurs (15,28). Contrary to this, we have recently presented experimental evidence that hydrostatic pressure causes both barrier compression (29), and significant enhancements to both the rate and KIE (30) of an enzymatic hydride transfer reaction that occurs predominantly by tunneling (31).

The rate of a tunneling reaction is sensitive to the overall shape of the reaction barrier (32–34) and, to the best of our knowledge, there has been no systematic computational study of the effect of barrier compression on the shape of enzymatic reaction barriers. Further, in many enzymes, the H-transfer step will occur by a mixture of classical (over-the-barrier) transfer and tunneling. In this case, the role of barrier shape is also important as the classical reaction will be influenced largely by the height of the barrier—which is also likely to be affected by barrier compression (35). In this study, we provide a systematic investigation of the role of both barrier height and barrier width on the kinetics of proton transfer. We focus initially on two model (partially nonadiabatic) proton transfer reactions, and then extend this study to look at the individual contributions of barrier height and width by using analytical barriers. Finally we apply the same methods to a well-characterized enzymatic proton tunneling reaction—that of aromatic amine dehydrogenase (AADH) (7,14,19,35–39). This work provides a general framework for understanding the effects of barrier shape (particularly barrier height and width) on the rates, KIEs, and tunneling contributions of H transfers in small molecule and enzymatic systems.

Methods and Theory

Model systems

The two (symmetrical) model systems used—linear proton transfer from CH₄ to CH₃⁻ (denoted CH₄/CH₃⁻) and internal proton transfer within malonaldehyde (MA)—are shown in Fig. 1. To ensure that our results can be applied to biological systems, we also compare the model systems to the proton transfer step during the reductive half-reaction of AADH with tryptamine (14,19,35,38,39) (Fig. 1 C) and to reactions modeled using analytical barriers (Fig. S1 in Supporting Material).

Figure 1.

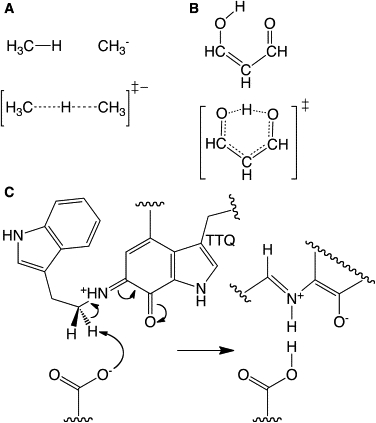
Reactant (top) and transition (bottom) states of the two model systems used in this study. (A) CH₄/CH₃⁻ and (B) malonaldehyde. Proposed reaction scheme for the proton tunneling step during the reductive half-reaction of AADH with tryptamine is also shown (C).

Theory

To model partially nonadiabatic proton transfer reactions, it is necessary to consider transfer that occurs both classically (over-the-barrier) and quantum mechanically (tunneling through the barrier) from any point along the reaction coordinate. The rate of the classical unimolecular reaction, k_TST, can be determined using TST,

$$k_{\text{TST}}\left(T\right)=\kappa \prime \left(k_{\mathrm{B}}T/h\right)\left(Q^{‡}\left(T\right)/Q_{\mathrm{r}}\left(T\right)\right)\exp \left(-{\varepsilon }_0/k_{\mathrm{B}}T\right),$$ (1)

where Q^‡(T) and Q_r(T) are the partition functions of the transition and reactant states, κ′ is the (nontunneling) transmission coefficient (set to unity in this study for simplicity), and ɛ₀ is the difference in barrier potential from reactant to transition states (TSs) including zero point energy (ZPE) contributions. Consequently, conventional TST (compare to canonical or variational TST (34)) requires little knowledge of the barrier shape beyond the barrier height. Calculation of the partition functions is nontrivial, as these require knowledge of all the vibrations in the system. However, for a preorganized enzyme active site, there is expected to be little activation entropy and Q^‡(T) ≈ Q_r(T) (see (40) and references therein). We will set the ratio of partition factors to unity in this study—equivalent to assuming that ɛ₀ ≈ ΔG^‡. To account for vibrational ZPE lost in the TS, ɛ₀ can be estimated crudely using an harmonic approximation,

$${\varepsilon }_0=V_0-\frac{1}{2}\hslash {\omega }_{\text{i}},$$ (2)

where ω_i is the (angular) D–H stretching frequency lost in the TS (41). Consequently, the protium barrier is lower than the deuterium barrier by ∼4.8 and 5.5 kJ mol⁻¹ for the CH₄/CH₃⁻ and MA reactions, respectively. Equation 2 assumes that no other frequencies change along the reaction coordinate and ignores the ZPE of the TS—two properties of the reaction that must be determined using frequency calculations. The consequences of these simplifications are that Eq. 2 will tend to underestimate ɛ₀ (and thus lead to an overestimation of the rate constants) and, because the values of ω_i have been fixed (they decrease at small barrier widths; see Fig. S2) the classical KIE ($k_{\text{TST}}^{\text{H}}/k_{\text{TST}}^{\text{D}}$) will not vary with changes to the barrier shape (also discussed in (28)). The free energy, ΔG^‡, for the various CH₄/CH₃⁻ and MA reactions was also determined from frequency calculations for both H and D transfer (see below and Fig. S2, Fig. S3, and Fig. S4). Rate constants and KIEs calculated (see below) from ɛ₀ and ΔG^‡ are compared later in Fig. 3 and Fig. S6. As there is typically <10-fold difference in the results, and the trends are identical, we feel that use of Eq. 2 provides an acceptable approximation when frequency calculations are not practical—such as with the analytical and AADH calculations (see below).

Figure 3.

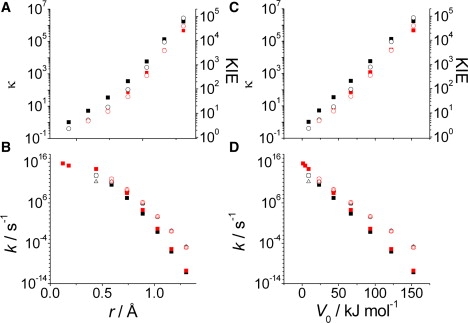
Effect of the barrier width r (A and B) and V₀ (C and D) on proton transfer within malonaldehyde. κ (for H; solid squares) and the KIE (open circles) are shown in panels A and C and k_TST (solid squares), k_tun (open triangles), and k_obs (open circles) shown in panels B and D. Note that the k_tun and k_obs values are essentially superimposed. Black data were calculated for free energy barriers and the red data for barriers were calculated using Eq. 2.

The probability, P_tun, of tunneling through a one-dimensional barrier can be calculated using the Wentzel-Kramers-Brillouin (WKB) action (32) with parabolic uniformization (42):

$$P_{\text{tun}}\left(q,i\right)={\left(1+\exp \left[\left(2/\hslash \right){\int }_{{\text{x}}_1}^{{\text{x}}_2}{\left[2{\mu }_i\left(V\left(x\right)-V\left(q\right)\right)\right]}^{1/2}dx\right]\right)}^{-1}\text{.}$$ (3)

The rate of tunneling can then be determined by integrating with respect to barrier energy,

$$k_{\text{tun}}^{\text{i}}\left(T\right)={\left(2\pi \hslash \right)}^{-1}{\int }_0^{V_{\text{max}}^{\text{i}}}Q\left(V,T\right)P_{\text{tun}}\left(V,i\right)dV,$$ (4)

where Q(V,T) is the Boltzmann probability of achieving an energy, V, relative to the reactant state. We will take V_max (which is isotope-dependent) to be either ΔG^‡ (when known) or ɛ₀ (Eq. 2). Note that the rate (but not the probability) of tunneling here is temperature-dependent, becoming temperature-independent at cryogenic temperatures. The overall rate of reaction is simply the sum of k_TST and k_tun. Equations 3 and 4 can be readily solved (approximately) by numerical integration. The apparent correction factor κ—the rate enhancement due to tunneling—can be calculated:

$$\kappa \left(T\right)=1+k_{\text{tun}}\left(T\right)/k_{\text{TST}}\left(T\right)\text{.}$$ (5)

Alternatively, κ can be directly calculated by multiplying Eq. 3 by a factor of (h/k_BT) when Q(V,T) is normalized to the transition (as opposed to the reactant) state. This approach generally gives equivalent results to Eqs. 3–5 but suffers due to machine precision when κ approaches unity.

Analytical barriers

To analyze the effect of barrier shape on proton transfer reactions, it is also useful to describe the reaction barrier using a simple model potential energy function such as the symmetrical quartic double-well potential (17). We have modified this function such that the barrier height, V₀, and width, r (the well-to-well separation), are adjustable independently:

$$V\left(q\right)=\left(V_0/\frac{1}{8}{r}^4\right){\left({\left(q-q_{\text{TS}}\right)}^2-\frac{1}{4}{r}^2\right)}^2\text{.}$$ (6)

Over the range of values used in this study for V₀ and r (50–200 kJ mol⁻¹ and 0.4–1.5 Å, respectively), barrier frequencies of ∼500–∼5000 cm⁻¹ were obtained from the curvature of V(q) at the TS (Fig. S1).

Computational methods

Numerical calculations (Eqs. 1–6) were performed using Mathematica version 6.5 or 7.0 (Wolfram Research, Champaign, IL). All computational chemistry was performed in vacuo using Gaussian 03 (43). Potential energy surfaces (PESs) along the proton-transfer coordinate were calculated at the MP2/6-31+G(d,p) level of theory for the two model systems, CH₄/CH₃⁻ and MA. Proton transfer from CH₄ to CH₃⁻ was calculated with the C–H–C angle restrained to 180.01° (to overcome Gaussian 03 (43) crashing with a restraint of 180.00°) and d(C–C) both unrestrained and fixed to values ranging from 2.7 to 4.2 Å (Fig. S3). Proton transfer within MA was calculated with d(O–O) both unrestrained and fixed to values ranging from 2.3 to 3.0 Å (Fig. 2 A and Fig. S4). Each transition state was verified using vibrational analysis and a single imaginary frequency was found in every case. As we wish to consider proton tunneling, the reaction coordinate was defined as

$$q=\frac{1}{2}\left(d\left(A-\text{H}\right)-d\left(D-\text{H}\right)\right),$$ (7)

where A and D are the donor and acceptor heavy atoms. To directly assess barrier-width in this study, we will use a reaction coordinate with units of Å in place of the more usual mass-weighted coordinate (with units of Bohr). The factor of one-half allows q to reflect the actual H-tunneling distance at a given energy along the PES for proton transfer. The well-to-well separation (Fig. S1) is equal to the distance between the transferred H in the superimposed reactant and product states. However, this is only the case if the D–H–A angle is linear and the system is symmetrical, which is the case for the CH₄/CH₃⁻ reactions here. If H-transfer is not linear then Eq. 7 becomes approximate and, in the case of MA, we corrected for this by using d(A–H) and d(D–H) values projected along the D–A vector.

Figure 2.

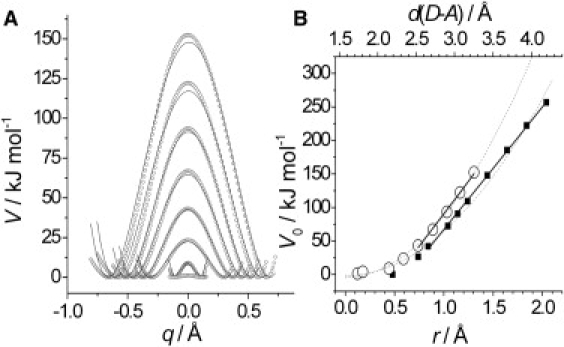
(A) Malonaldehyde potential energy surfaces for proton transfer calculated with fixed O-O separations. Equivalent data for the C₄H/CH₃⁻ reaction are shown in Fig. S3, as are free energies and barrier widths (Table S1 and Table S2). (B) Effect of fixed barrier width, r, on the height (potential energy) of the malonaldehyde (open circles) and C₄H/CH₃⁻ (solid squares) barriers. Acceptor-H distance is also shown. Data are fit to both linear (solid) and quadratic (V₀ ∝ r²; dotted) functions. Slope from the linear fit (for r > 0.7 Å) is 194 ± 7 and 186 ± 2 kJ mol⁻¹ Å⁻¹ for malonaldehyde and C₄H/CH₃⁻, respectively.

Approximately 200 one-dimensional PESs along the proton-transfer coordinate in AADH have previously been calculated at the AM1/CHARMM22 level on structures sampled during QM/MM MD simulations, with a harmonic constraint applied to the MM region (35). We chose a representative sample (with the same average barrier height as the total sample) of 35 of these PESs for this study, and we modified these data by redefining the approximate reaction coordinate as $q=\frac{1}{2}\left(d\left({\text{O}}_2-{\text{H}}_{\text{1}}\right)-d\left({\text{C}}_1-{\text{H}}_{\text{1}}\right)\right)$. Note that proton transfer was calculated to the aspartate O₂ as we have previously established that this is the more likely acceptor (38).

Results and Discussion

Barrier shape

First, PESs along the proton transfer coordinate (barriers) were calculated for two small and well-characterized model systems: proton transfer from CH₄ to CH₃⁻ with the D–H–A angle linearly restrained (44), and internal proton transfer within malonaldehyde (45,46) (Fig. 1). The potential barrier heights, V₀, are 57.6 kJ mol⁻¹ for CH₄/CH₃⁻ and 14.4 kJ mol⁻¹ for MA. As expected, the donor/acceptor heavy atom separation varied along the reaction coordinate for both reactions (Fig. S3 and Fig. S4). Compression of the donor/acceptor heavy atoms from the reactant to TS separation requires 10–15 kJ mol⁻¹ for both systems (Fig. S7). To investigate the effect of barrier compression on these reactions, we then calculated multiple PESs for both reactions with various fixed heavy atom separations. Note that, as we are interested in the relative change in barrier height with width, the absolute height of the barriers is not of central importance. The MA data are shown in Fig. 2 A (and both sets of PESs in Fig. S3 and Fig. S4). When the heavy atom separation is sufficiently large (∼2.5 Å), there is an approximately linear increase in barrier height with increasing width (H-transfer distance) (Fig. 2 B). The calculated barrier free energies also show the same trend (Fig. S2, Table S1, and Table S2). We would like to stress that a decrease in barrier height with decreasing width is not unexpected (see, e.g., (47)). Parabolic model barriers predict that V₀ ∝ r² (41) (also shown in Fig. 2 B) and, among others, Aqvist and Warshel's empirical valence bond method makes a qualitatively similar prediction (48). Somewhat unexpectedly, however, the magnitude of dV₀/dr is similar for both the CH₄/CH₃⁻ and MA reactions, suggesting that this relationship may be generalized to other proton transfer reactions.

KIEs

To convert the PESs to their corresponding free energy surfaces, the CH₄/CH₃⁻ and MA reactions were linearly scaled to ΔG^‡—the difference in free energy of the TS and reactant states. Although this scaling is obviously an approximation, it seems to work quite well as the free energy barriers map onto those calculated using vibrational analysis of points along the PES (Fig. S5). The rate constant and primary H/D KIE for proton transfer were then calculated using Eqs. 3 and 4. The calculated KIEs for proton transfer in the unrestrained MA and CH₄/CH₃⁻ reactions are 4.1 and 5.1, respectively. The KIE for MA is in good agreement with previous values calculated using molecular orbital methods (45), although it is in poor agreement with the experimentally determined KIE of ∼17 (extrapolated to 298 K) (46), which has proven difficult to accurately calculate (45). More importantly, there are clear trends among the barrier width for both restrained reactions and 1), the rate, 2), κ, and 3), the KIE. As the barrier becomes narrower (and lower), the rate increases roughly exponentially, whereas both κ and the KIE decrease approximately exponentially (Fig. 3 and Fig. S6; note log₁₀ scale). Interestingly, deconvolution of the calculated rate constants into classical and tunneling contributions show that both k_TST and k_tun show similar trends (Fig. 3 and Fig. S6). This is discussed further below.

We next calculated the rate of H and D transfer across a series of analytical barriers of differing height and width (Fig. 4). The barriers were calculated using Eq. 6 and scaled using Eq. 2 to account for the different ZPE contributions of H and D to the barrier height. Although this approach will underestimate the barrier height (ɛ₀, see above), it allows the practical deconvolution of the individual contributions of barrier height and width to the rate of H-transfer. The analytical barrier data in Fig. 4 are overlayed with the MA free energy data from Fig. 3. In general, barrier compression would be expected to roughly follow the path of the MA data. Clearly, almost any reduction in the barrier height and/or width will lead to a decrease in the KIE and increase in k_obs. The dependence of κ and the percentage of tunneling is more complicated as the MA data set almost follows the contours in Fig. 3, A and C. If barrier compression were to lead to a more reduced slope (dV₀/dr) than is seen in the linear portion of Fig. 2 B, then κ could become invariant with barrier compression. Otherwise, κ will decrease as the barrier is compressed. When κ decreases, the relative amount of H-transfer that occurs by tunneling also decreases (see below).

Figure 4.

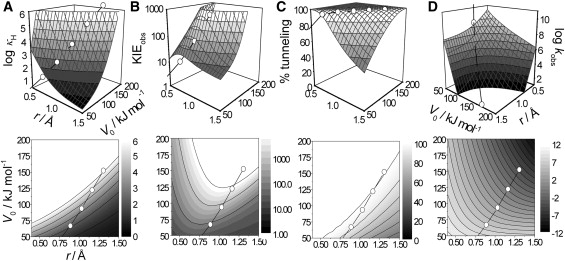
Three-dimensional and contour plots of the WKB calculations as a function of barrier height and width showing κ^H (A); KIE_obs (B); percentage of H (as opposed to D) tunneling (C); and k_obs (D). Values calculated from the malonaldehyde free energy barriers are overlayed as open circles. Note that for clarity, the x and y axes are the same in panels A–C. See text for more details.

Enzymatic proton transfer: AADH

To extend this study to enzyme-catalyzed reactions, we then investigated the rate-limiting proton transfer step during the reductive half-reaction of the tryptophan-tryptophylquinone-dependent quinoprotein AADH with tryptamine. The reaction scheme for this reaction is shown in Fig. 1 C and involves the transfer of a proton from the β-carbon of the tryptophan-tryptophylquinone iminoquinone intermediate to an aspartate oxygen (38). The reductive half-reaction of AADH with tryptamine is well characterized (7,36,37), and the proton transfer step has previously been shown to occur predominantly by tunneling (14,38,39). The experimentally observed rate of proton transfer is ∼3500 s⁻¹ at room temperature and the KIE is 55 ± 6 (38). Further, using spectral density analysis (26), we have previously identified a putative subpicosecond-promoting vibration inherent to the iminoquionone intermediate (19). This vibration corresponds to a rotation of the donor C1/H1 methylene group that reduces the heavy atom separation (and concomitantly causes barrier compression while lowering the activation energy (35)).

In a previous study, we calculated PESs for proton transfer in AADH sampled from multiple snapshots during an MD simulation (35). In this study, we analyzed 35 of these PESs using Eqs. 1–5. Accurate calculation of this number of enzymatic free energy barriers (using frequency calculations) would be very time-consuming, so again these were estimated using Eq. 2 (Fig. 5). The distribution of AADH barrier heights is roughly Gaussian so we calculated the apparent (i.e., observed) rate and KIE by taking the probability-weighted sum over all calculated rate constants (Fig. S8). We calculated (at 298 K) the KIE = 49, $k_{\text{obs}}^{\text{H}}$ = 8.1 × 10⁶ s⁻¹, κ^H = 1735, and κ^D = 71. Although, compared to experiment, the rate constants are too fast by ∼10³ (probably because Eq. 2 leads to an underestimation of the barrier height), κ is similar to the values previously determined using variational TST with multidimensional tunneling corrections (38, 39) and the KIE is in perfect agreement with the experimentally determined value (38). By comparing the MA and CH₄/CH₃⁻ free energy and ɛ₀ data (Fig. S2), we can estimate that Eq. 2 probably underestimates ɛ₀ by ≤10 kJ mol⁻¹. If we add an additional 10 kJ mol⁻¹ to each value of V₀, the KIE in AADH will increase from 49 to ∼86 (a similar magnitude to the KIE of 93 calculated previously using multidimensional tunneling calculations (38)), whereas the rate will decrease by ∼2 orders of magnitude (see Fig. 7 below). We are not advocating that this correction be made, but note that more realistic rate constants are expected if more-accurate ZPE corrections can be made. It is not obvious why our method reproduces the experimental KIE more accurately, but this may be due to the fortuitous cancellation of errors. We should also point out that although this method uses a one-dimensional tunneling model, by analyzing many barriers over time, we are effectively performing a multidimensional calculation.

Figure 5.

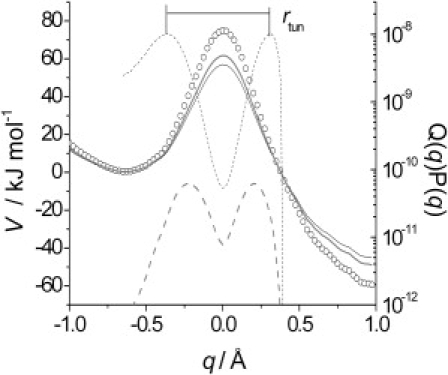
Representative barrier for proton transfer in AADH. The barrier (open circles) was approximately corrected for ZPE contributions (Eq. 2) and the corrected barriers for H and D transfer are shown (solid black and shaded lines, respectively). Overlayed is the transfer probability P(q)Q(q) for H and D (dashed solid and shaded lines, respectively). Representative tunneling distance, r_tun, is labeled for H-transfer.

Figure 7.

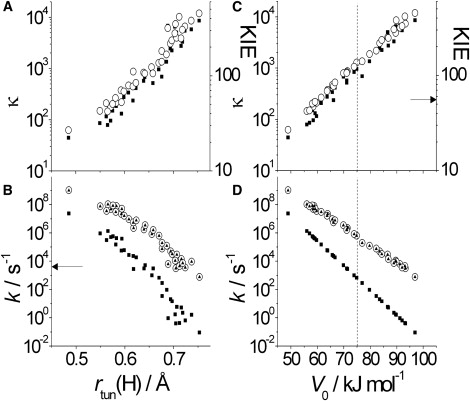
Dependence on r_tun (for H-transfer) (A and B) and V₀ (C and D) of proton transfer in AADH. κ (for H; solid squares) and the KIE (open circles) are shown in panels A and C; and k_TST (solid squares), k_tun (open circles), and k_obs (solid triangles) are shown in panels B and D. Note that the k_tun and k_obs values are essentially superimposed and the dotted horizontal lines in panels C and D mark the average barrier potential (see Fig. S8). Arrows mark the experimentally observed k_obs and KIE values (38). See text for more details.

The AADH potential energy barrier heights were found to vary from 49 to 97 kJ mol⁻¹ across the snapshots from the MD simulation. In addition, the heavy atom separation was not restrained during the calculation of the AADH PESs (compare to the CH₄/CH₃⁻ and MA calculations) and varied considerably along the reaction coordinate (35). It was difficult to determine barrier width, r, as the product states did not generally show a clear energy minimum. As an alternative, we can compare the proton tunneling distance—r_tun (shown in Fig. 5), which is isotope-dependent (r^H_tun > r^D_tun) and scales linearly with r (Fig. 6 A). There is a good correlation between V₀ and r_tun and, surprisingly, these data (V₀ vs. r_tun) overlay the MA and CH₄/CH₃⁻ data sets (Fig. 6 B). Although these combined data are best described by the quadratic relationship V₀ ∝ r²_tun (the prediction made for tunneling through a model parabolic barrier (41)), for a physically realistic spread of r or r_tun values—such as in the AADH data (Fig. 6 B)—the dependence of V₀ and r can be described by a linear relationship (as we have done in Fig. 2 B). Fig. 7 shows the dependence of κ, the KIE and the deconvoluted rate constants on both the barrier height and r_tun. The trends match those seen for the restrained MA and CH₄/CH₃⁻ calculations (Fig. 3 and Fig. S6), i.e., roughly exponential decreases in κ and KIE and exponential increases in both k_TST and k_tun with decreasing barrier width or height. Clearly, barrier compression will lead to an increase in observed rate, and a decrease in KIE and κ. A reduction in κ corresponds to a decrease in the fraction of proton transfers that occur by tunneling rather than over the barrier, i.e., the percentage of tunneling. This trend is also seen in Fig. 4. Liu and Warshel made a similar observation for dihydrofolate reductase (15), and this is probably a general consequence of barrier compression (47). It has previously been suggested that the decrease in κ (and thus the relative amount of tunneling) caused by barrier compression means that the increase in rate is primarily due to an increase in k_TST (17,28). We emphasize that in AADH, the absolute magnitude of k_tun increases significantly more than that of k_TST for a given barrier compression (decrease in r_tun; Fig. 7 C, note the log₁₀ scale). Consequently, the rate increase is due, mostly, to the tunneling contribution. This will be the case generally whenever κ ≫ 2.

Figure 6.

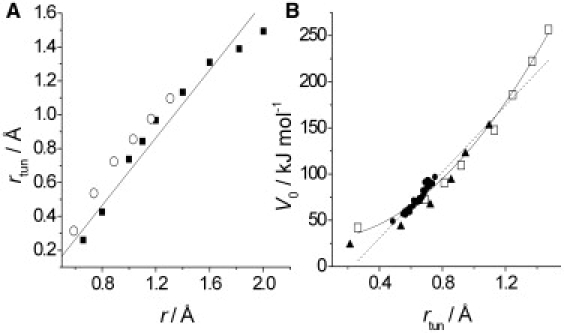
Correlation between r_tun and r for H (as opposed to D) transfer in CH₄/CH₃⁻ (solid squares) and malonaldehyde (open circles) (A); solid line shows a slope of 1:1. (B) Relationship among V₀ and r_tun (for H transfer) in CH₄/CH₃⁻ (open squares), malonaldehyde (solid triangles), and AADH (solid circles). Combined data are fit to linear (dotted line) and quadratic (V₀ ∝ r²_tun; solid line) functions.

Nonadiabatic models

The decrease in KIE and increase in k_tun with barrier compression seen in Figs. 3 and 7 is also the prediction made by nonadiabatic, vibronic (Marcus-like full-tunneling) models of H-transfer (18–23,30,49–51). In these models, over-the-barrier proton transfer is ignored (i.e., k_obs = k_tun) and proton tunneling is modeled in a similar manner to electron transfer, but with extra terms to account for the H-wavefunction overlap and, in some cases, for barrier-compression (donor-acceptor fluctuations). Whereas it is generally agreed that this approach is not strictly valid for most H-transfers, it has become adopted by members of the experimental community (18,50,51)—including ourselves (14,19,20,30)—as it appears to be qualitatively useful, and is currently the only method that can routinely account for strongly temperature-dependent KIEs. In the context of this study, it should be possible to model the temperature-dependence of the KIE by calculating k_TST and k_tun at various temperatures. It is also necessary to account for the effect of temperature on the distribution of V₀ and/or r (e.g., by running the initial MD simulations at different temperatures). We will pursue this in future work.

We compared the dependence of the AADH KIE on r^H_tun (from Fig. 7) to the Kuznetsov and Ulstrup (K-U) (23) nonadiabatic model we have used previously to model the AADH reaction (19). There is a very good agreement, especially if the H wavefunction is modeled more accurately using a quantum Morse oscillator rather than a harmonic oscillator (51) (Fig. 8). There is also good agreement for MA (Fig. S10). It is interesting to note that the K-U model agrees well with the WKB model (Eqs. 1–5) even at fairly low κ-values, where proton transfer is largely adiabatic (i.e., occurs with significant over-the-barrier H-transfer). The agreement between these two approaches suggests that despite the oversimplified nature of the K-U model (and presumably other similar models), this type of model can provide a useful tool for fitting experimental data and extracting tunneling distances.

Figure 8.

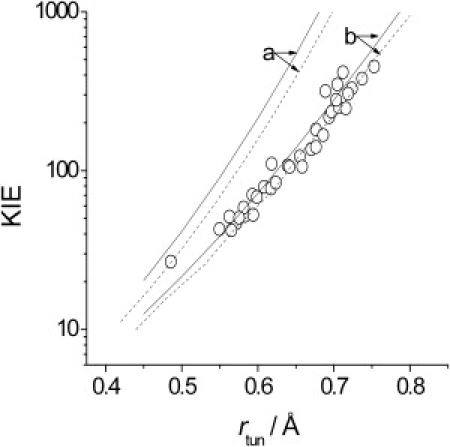
KIE versus r_tun for the Kuznetsov and Ulstrup vibronic model (19,23) compared to the AADH KIE calculated using Eqs. 1–5 and plotted versus r_tun for H (as opposed to D) transfer. The X-H bond in the vibronic model is described using both a quantum harmonic oscillator (a) and a quantum Morse oscillator (b) as described by Meyer and Klinman (51). Vibronic model was calculated both without a promoting vibration (solid lines) and with a fairly stiff promoting vibration (dashed lines), with the same force constant used in our previous study (160 J m⁻² (19)). Parameters for describing the proton wavefunction are given in Fig. S9.

Conclusions

The role of promoting vibrations and barrier compression are usually discussed in the context of H-tunneling reactions. However, as there is 1), a roughly exponential dependence of the rate of a tunneling reaction on barrier width; 2), an exponential dependence of the rate of a classical reaction on barrier free energy; and 3), what appears to be a roughly linear dependence between barrier height and width (Fig. 2 and Fig. S2), then the rate enhancement caused by any barrier compression—whether it be by promoting vibration or other mechanism—should be of a similar magnitude for both classical (over-the-barrier) and quantum reactions. As the enzyme only feels evolutionary pressure on the rate of the reaction and not the mechanism (i.e., on tunneling versus over-the-barrier), then it would appear that promoting vibrations, if present, and any other mechanism for barrier compressions, may be more important than is (as of this writing) generally acknowledged.

Supporting Material

Ten figures and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01557-4.