Denoising Single-Molecule FRET Trajectories with Wavelets and Bayesian Inference

Abstract

A method to denoise single-molecule fluorescence resonance energy (smFRET) trajectories using wavelet detail thresholding and Bayesian inference is presented. Bayesian methods are developed to identify fluorophore photoblinks in the time trajectories. Simulated data are used to quantify the improvement in static and dynamic data analysis. Application of the method to experimental smFRET data shows that it distinguishes photoblinks from large shifts in smFRET efficiency while maintaining the important advantage of an unbiased approach. Known sources of experimental noise are examined and quantified as a means to remove their contributions via soft thresholding of wavelet coefficients. A wavelet decomposition algorithm is described, and thresholds are produced through the knowledge of noise parameters in the discrete-time photon signals. Reconstruction of the signals from thresholded coefficients produces signals that contain noise arising only from unquantifiable parameters. The method is applied to simulated and observed smFRET data, and it is found that the denoised data retain their underlying dynamic properties, but with increased resolution.

Introduction

In the past decade several single-molecule techniques have moved to the forefront of spectroscopic research, and their application spans a broad scope from spectroelectrochemistry (1) to smFRET (2), which is particularly applicable to biological systems (3–5). Many single-molecule studies have exposed mechanistic and conformational heterogeneities in these biological systems (6–14). Although the realization of heterogeneities provides the opportunity to expand our understanding of biological systems, their detection and characterization provides many experimental challenges.

The effects of experimental noise in single-molecule studies often limit their scope. Low signal/noise ratios are inherent to these experiments (15), and various statistical implementations have been applied in attempt to reduce the effects of experimental noise (16–26). These implementations include the use of Fisher information matrices to achieve optimal time resolution (27) and positional accuracy (28), statistical correlation functions to show single-molecule kinetic heterogeneities (29), and hidden-Markov models to extract the most likely sequence of events from smFRET time trajectories (30). Most recently, statistical correlation is combined with wavelet decomposition in attempt to describe kinetic heterogeneities in single-molecule systems (31). Despite the relative success of these implementations, much remains left to be desired from the resolution of single-molecule experiments. Physical events in these experiments still remain hidden under guesses, optimization parameters, and the artifacts of experimental noise.

Reversible photoblinks that result in the fluorophore's occupation of a nonabsorbing and nonemitting, or dark, electronic state (32–34) are a problematic source of noise in single-molecule experiments. Many of the aforementioned implementations require preprocessed data that is free of photoblinks, but their identification becomes an issue when considering that smFRET experiments are most often designed so that conformational shifts lead to changes in smFRET efficiency (3–5). Furthermore, these events are most often removed manually, leading to bias in the smFRET time trajectories. Therefore, an unbiased method of photoblink identification that recognizes photoblinks on all timescales is desirable.

Many analyses also rely on the assumption that the system's states are well-defined, and that transitions among these states are purely Markovian in nature (30,35). However, the observation of memory effects in single-molecule enzymatic turnover (36), large variations in the folding kinetics of a ribozyme (37), and the occurrence of overlapping efficiency states in single DNA aptamer molecules (12) all offer recent experimental results that violate these assumptions. As such, a means of processing single-molecule data that provides a more accurate representation of a physical setting remains a pressing need.

A dual-component interpretation of noise in smFRET photon distributions results in a quantifiable component arising from known sources such as shot-noise and photoblinks, and an unquantifiable component arising from molecular phenomena like conformational fluctuations. Methods that discriminate the former component from the latter are known in signal processing, and wavelet-based approaches are directly applicable to time-series data (38–41). Similar to Fourier transforms, wavelet transforms are mathematic constructs that convert a time-series signal into a representation in another domain. Wavelet transforms, however, offer the advantage of localization in both time and frequency (42).

The first and simplest of all wavelets was presented by Haar (43). Since its invention a century ago, this wavelet and more sophisticated varieties have evolved into important tools in the fields of data compression and signal processing. Contributions by Mallat (44), Daubechies (45), and others (46–48) have extended the impact of such analyses to nearly all subdivisions of these fields. Wavelet-based analyses now enjoy a broad range of applicability, and have supplanted the use of the traditional Fourier transform in many areas (42,49).

A framework that paved the way for the use of wavelets in signal processing was introduced as multiresolution analysis in the late 1980s (44,45). The basic scheme decomposes the signal into two components: an approximation component containing coefficients that multiply a scaling function, and a detail component containing coefficients that multiply the wavelet function. Thresholding the detail components of a signal's wavelet decomposition that are smaller than a certain value, a threshold, effectively removes noise components from a noisy signal (50). There are many eloquent thresholding methods (42,46,47,49,51), but our aim in thresholding smFRET detail components is simple: we wish to discard the noise components we can quantify while keeping those we cannot.

We present an algorithm for quantifiable noise suppression in smFRET time trajectories. Bayesian methods make use of observations in such a way as to provide insight into unknown events based on known properties of a system (52). Such methods are often used in model (53) and hypothesis testing, and in the case of photoblinking events in smFRET time trajectories, we use the power of Bayesian inference to identify these events. We then use the Haar wavelet to decompose each of the two photon signals acquired in dual-channel smFRET experiments. Noise parameters in each signal are quantified as a means of generating a universal threshold, and quantifiable noise is removed from each photon signal via soft thresholding of the detail components. Signals are then reconstructed from the highest level approximations and thresholded details, producing denoised signals that contain noise artifacts arising only from unquantifiable sources.

Algorithms

Parameters in smFRET trajectories

The acquisition of a two-channel smFRET time trajectory results in two data vectors that contain acceptor and donor photon counts in discrete time steps. The standard collection window contains both acceptor and donor fluorophore photobleaching events, and results in three distinct regions within each of these vectors: background, crosstalk, and FRET regions. Fig. S1 in the Supporting Material illustrates these regions in detail, and Part S1 describes the calculation of the mean background intensities, the crosstalk parameter, the calculation of the numbers of crosstalk photons, correction of the detected numbers of photons to obtain fluorophore-emitted photon intensities, and the calculation of smFRET efficiency in detail.

Bayesian inference to detect photoblinks

Photoblinks involving either fluorophore are characterized by observation of a sharp drop in the detected number of acceptor photons. In the instance of a donor photoblink, photon counts on both channels fall to background levels due to the donor's occupation of a dark electronic state, thereby rendering it unable to transfer energy to the acceptor fluorophore. Similarly, during an acceptor photoblink, donor emission is observed in the absence of energy transfer, and the numbers of detected acceptor photons during fall to levels similar to those observed in the crosstalk region.

A caveat arises in the preceding logic in that, if one is searching for smFRET efficiencies approaching zero, then one cannot distinguish low efficiencies from acceptor photoblinks. However, if experiments are designed such that low efficiencies cannot be “real” observations, as will be addressed in more detail below, or if photoblinks are typically on a much faster timescale than experimental observations, this caveat can be avoided entirely.

As a means to detect photoblinks, Bayes' Law (52) is used to estimate the probability that the detected number of acceptor photons N_A arises due to a photoblink. To accomplish this, we need the conditional probability distributions of N_A given two alternatives, the “no blink” hypothesis (NB) and the “blink” hypothesis (B). After we obtain these distributions, we use Bayes' Law to reverse this logic and calculate the probabilities of each hypothesis given the observation of acceptor intensity N_A. This allows us to select those time steps that arise due to a photoblink, and remove them from the time trajectory in an unbiased manner. Details of the algorithm's implementation are described completely in Part S2 in the Supporting Material.

Application of the Haar wavelet to denoise smFRET trajectories

Denoising methods are generally designed to separate the essential component of the signal from the random noise generated by experimental error. The simplest example of denoising is the removal of high frequency noise via the application of a low pass filter to the original signal. Mathematically, this is accomplished by suppressing the high frequency Fourier components of the signal, which is comprised of 1), applying the Fourier transform to the signal; 2), modifying the high frequency components according to a certain rule; and 3), applying the inverse Fourier transform to obtain the denoised signal.

From this example it is clear that there are two ingredients in a denoising method: 1), the choice of the basis set used to represent the signal (e.g., the sine and cosine functions are chosen as the basis for the Fourier transform); and 2), the rule according to which certain components of the signal—that are presumably associated with noise—are suppressed. For example, the above smoothing method assumes implicitly that the signal is contained in the low frequency part of the Fourier spectrum whereas the noise is associated with high frequency components of the signal. A successful method takes advantage of existing knowledge about the noise. Furthermore, if the basis functions that are chosen to represent the signal do so poorly (under the inevitable constraint of using a finite basis set), the method will not be successful. The keys then, to a successful denoising method, lie in making the proper choices regarding basis sets and noise suppression rules.

The orthonormal basis set used in the denoising method presented here is comprised of the Haar (43) wavelet and scaling functions. In general, wavelets offer the advantage over more conventional basis sets that they are localized in both the frequency and time domains. In contrast, the sines and cosines of Fourier transforms are localized only in the frequency domain. This time locality is particularly suitable for nonstationary time series, as in the famous example of the wavelet-denoised recording of Brahms at the piano (54).

Returning to the context of smFRET time trajectories, we recall that the trajectory consists of two data vectors containing detected numbers of photons in discrete time steps. In this discussion we consider only the acceptor photon trajectory N_A (= N_A(0), N_A(Δt),...), in discrete time steps Δt, which is written in the form

$$N_{\mathrm{A}}=S_{\mathrm{A}}+\sigma Z\text{.}$$ (1)

Here, at each time step Δt, Z is a Gaussian white noise component, and each element of Z is independently and identically distributed on a normal distribution with mean 0 and variance 1, σ is a known noise level, and S_A is the “true” signal that we wish to recover. Similarly to the smoothing method described above, we accomplish the recovery of the true signal S_A in three steps: 1), transform the observed data N_A into the wavelet domain; 2), suppress the presumed noise component of the signal; and 3), invert the wavelet transform to obtain the denoised signal. Part S3 in the Supporting Material provides details regarding the specifics of wavelet transformation of our smFRET data, and the rules applied for noise suppression.

Application to Simulated smFRET Data

Photoblink detection in simulated data

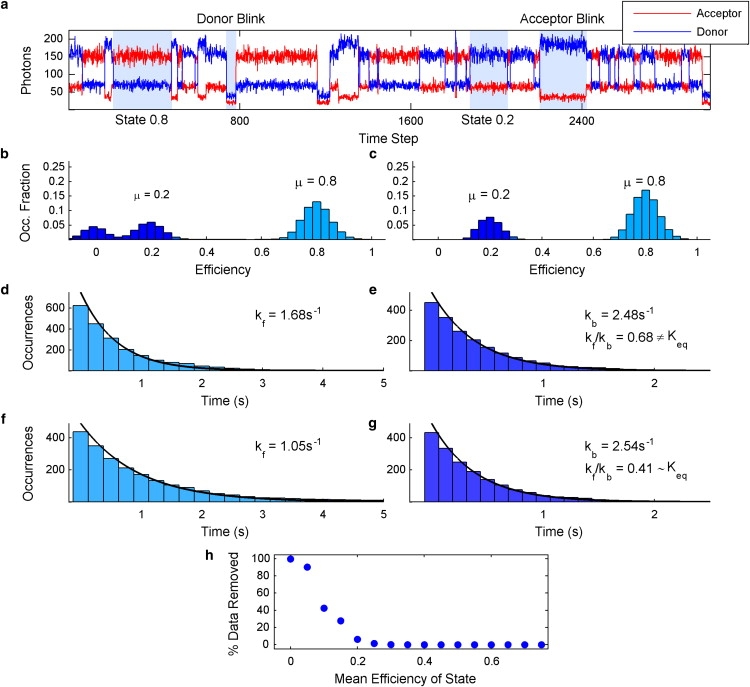
To assess the strengths and weaknesses of the photoblink detection method, we generate simulated smFRET trajectories using the kinetic Monte Carlo method (55–58), and apply the photoblink detection algorithm to the simulated data. We simulate a three-state system that represents the equilibrium of two efficiency states having central efficiencies of 0.8 and 0.2, respectively, as well as a photoblink state that represents both acceptor and donor photoblinks. An equilibrium constant, K_eq, of 0.4 is chosen for the 0.8 ↔ 0.2 equilibrium. The average photoblink lifetime is described by exponential kinetics, and is chosen such that realistic photoblinking statistics are obtained (59). The lifetimes of states 0.2 and 0.8 are also described by exponential kinetics, and are chosen to mimic realistic physical conditions (60). After the simulation generates the states that are present at each time step, shot-noise laden acceptor and donor photon trajectories are constructed from the simulated state trajectories. The photoblink detection algorithm is applied to the constructed photon trajectories, and time steps identified as photoblinks by the algorithm are removed. State lifetimes are extracted from the simulated data both before and after photoblink detection as a means to obtain the forward and backward rate constants for transition between the two real states. The equilibrium constant is estimated from the ratio of these rate constants as well as the ratio of the occurrences of each state in the efficiency distribution.

As shown in Table 1, the photoblink detection algorithm removes 99.8% of the total number of generated photoblinks. Additionally, the algorithm's selectivity is shown by the removal of only 1.8% of the actual data points. Even in the presence of shot-noise, state 0.2 is only marginally affected by the removal of photoblinks, as a meager 5.8% of the data points originally assigned to this state are removed during photoblink detection.

Table 1.

Statistics of simulated data before and after photoblink detection

	Before blink filter	After blink filter
Total data points	100,078	74,594
State 0.8 (N)	52,665	52,651
State 0.2 (N)	23,218	21,882
Blinks (N)	24,195	52
Blinks removed (%)	—	99.8
Identified as blinks (N)	—	25,484
State 0.8 removed (%)	—	<0.1
State 0.2 removed (%)	—	5.8

Fig. 1 illustrates the data simulation and the application of the photoblink detection algorithm in more detail. A sample acceptor and donor photon trajectory is shown in Fig. 1 a, demonstrating the following chemical and photophysical transitions: transitions between the two designated FRET states, donor photoblinks, and acceptor photoblinks. Fig. 1 b contains the efficiency distribution of the simulated data before photoblink detection, and Fig. 1 c shows the efficiency distribution of the simulated data after photoblink detection. This comparison shows that the denoising algorithm effectively removes photoblinks, resulting in an efficiency distribution that accurately reflects the two states of the system, even though the shot-noise broadened signal from state 0.2 overlaps with blink values.

Figure 1.

Applying photoblink detection to simulated smFRET trajectories. (a) Sample acceptor (red) and donor (blue) photon trajectories. The mean of the sum of acceptor and donor photon counts at each time step was held constant at 220. (b) Efficiency distribution of the model system before photoblink removal. (c) Efficiency distribution of the model system after photoblink removal showing K_eq to be 0.4. (d) The lifetime distribution of state 0.8 before photoblink detection overlaid by a fit to a single exponential decay. (e) The lifetime distribution of state 0.2 before photoblink detection overlaid with its fit to an exponential decay. (f) The lifetime distribution of state 0.8 after photoblink detection overlaid with a fit to an exponential decay. (g) The lifetime distribution of state 0.2 after photoblink detection overlaid with its fit to an exponential decay. (h) The fraction of total data points removed from a state's efficiency distribution versus the mean efficiency of the state.

Effective blink removal also improves dynamic analyses. Fig. 1, d and e, show the lifetime distributions before photoblink detection for state 0.8 and state 0.2, respectively, overlaid with their respective fits to single exponential decays. Fig. 1, f and g, show the same data, after photoblink detection and removal. The simulated data shown in Fig. 1 show that the removal of photoblinks from the simulated data results in more accuracy in the extracted kinetic rates. The ratio of forward to backward rate constants before photoblink detection and removal extracted from Fig. 1, d and e, is 0.68, showing poor agreement with the equilibrium constant of 0.4. However, the corresponding ratio obtained after the removal of photoblinks extracted from Fig. 1, f and e, is 0.41, thus showing excellent agreement with the equilibrium constant of 0.4. It is therefore shown that carrying out Bayesian photoblink removal on the simulated data results in a fitted equilibrium constant that differs by only 2.5% from the actual value. In comparison, the error before photoblink removal is 70%. These results confirm that more accurate dynamic information can be extracted from smFRET trajectories after the removal of photoblinks.

To address the resolution of photoblinks from states having low central efficiencies, we carried out a series of simulations as a function of mean state efficiency as a means to determine a lower limit for this method. The results of these simulations are shown in Fig. 1 h. We find that, to distinguish photoblinks from actual data, a state's mean efficiency needs to be higher than a lower bound of ∼0.2. It is of note that this lower bound is a function of total acquired photons per time step, and will move toward zero as the total number of acquired photons increases. In the context of the current discussion, the mean number of total photons per time step is 220, and at this value the simulations confirm that the algorithm, although removing all but a negligible amount of photoblinks, leaves occurrences of states with mean efficiencies higher than ∼0.2 essentially unaltered.

It is also important to note that the effects of intermediate timescale photoblinks that are less than one time step in duration. These photoblinks limit the Bayesian method presented here in that, relative to the length of the event, intensity falls, but does not fall low enough to be designated a photoblink. As such, the time step remains. Such events fall into the unquantifiable noise contribution discussed above.

Fig. S4 compares the performance of this method to a more traditional method involving a simple thresholding technique, and Fig. S5 analyzes the performance of the Bayesian photoblink filter over a range of K_eq.

Denoising an oscillatory system

As a means to quantify the effects of the wavelet denoising algorithm to smFRET trajectories, simulated trajectories were generated for two types of systems. The first, a two-state equilibrium, was simulated using kinetic Monte Carlo methods. Each of the simulated trajectories was denoised by the wavelet denoising algorithm as well as the hidden-Markov model (HaMMy) described by McKinney et al. (30). Both methods are effective at denoising trajectories comprised of well-defined FRET states. A figure showing this comparison of the two methods is included as Fig. S6. Additional details about the simulation are also included in the Supporting Material.

The next simulation was carried out for a system without defined FRET states. The wavelet denoising algorithm does not make use of Markovian and/or distinct-state assumptions. Given that these assumptions are not valid in all cases, wavelet denoising offers a significant advantage. Examples include the wormlike multi-dT chains discussed by Murphy et al. (61), the aV aptamer (12), or any system that undergoes breathing dynamics with a continuously changing conformation. An example of such behavior is shown by green fluorescent protein, which has been observed recently to exhibit periodic oscillation between two conformational extremes during the unfolding process (62).

As an extreme example of a system without well-defined states, we simulate a system showing conformational oscillation. Assuming the efficiency E of such a system oscillates around a central value E_c with amplitude E₀ according to the equation E(t) = E₀cos(ωt) + E_c, the probability distribution p(E) of the efficiency is given by:

$$p\left(E\right)=\frac{1}{\pi {\left[E_0^2-{\left(E-E_{\mathrm{c}}\right)}^2\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\text{.}$$ (2)

Although p(E) is weakly singular at E = E_c ± E₀, the singularities are readily removed when a discrete probability distribution is used. The constructed trajectories are analyzed by the wavelet-denoising algorithm, and again compared with analyses produced by HaMMy.

Fig. 2 a shows a typical trajectory generated for these analyses. The original, noisy efficiency trajectory (cyan) is overlaid with the results produced by the wavelet denoising algorithm (red) and HaMMy (black). Fig. 2 b depicts the efficiency distribution of the noisy trajectory, and Fig. 2 c shows that of the wavelet-denoised trajectory. Lastly, Fig. 2 d shows the efficiency distribution as predicted by HaMMy. Each of the efficiency distributions in Fig. 2, b–d, are overlaid with the probability distribution p(E) in blue, depicted in discrete steps.

Figure 2.

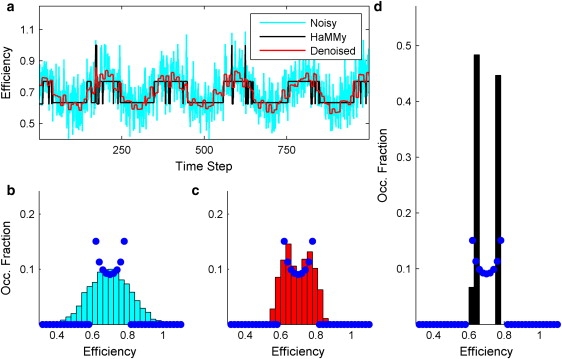
Denoising an oscillatory system. (a) The original, shot-noise laden efficiency trajectory (cyan) is overlaid with the denoised efficiency trajectory (red) and the efficiency trajectory generated by HaMMy (black). (b) The efficiency distribution of the original data. (c) The efficiency distribution of the denoised data. (d) The distribution of efficiencies generated by HaMMy. The efficiency probability distribution p(E) is overlaid in blue on each efficiency distribution.

Although the period of oscillation is identified nicely by HaMMy, it is obvious in Fig. 2 a that the assumption of distinct states in the trajectory poses a major hindrance to the hidden-Markov analysis. In fact, this is a system that does not possess “states” and lifetimes, but a system that merely oscillates between two efficiency extremes. This is illustrated in the efficiency distributions shown in Fig. 2, b and d, as well. Whereas the efficiency distribution in Fig. 2 b shows the occupation of a broad range of efficiencies, that which is produced by HaMMy in Fig. 2 d shows the molecule to occupy two major conformations.

In contrast, both the denoised trajectory and the denoised efficiency distribution show improved agreement with the noisy data. It is seen in the trajectories shown in Fig. 2 a that the denoised data constitutes a better representation of this system's dynamics than does that produced by the hidden-Markov analysis. In comparing the efficiency distributions, one can also see that, although there is a slight discrepancy that arises at the efficiency extremes of E_c ± E₀ due to a small amount of remaining noise in the trajectories, there is good agreement between the efficiency probability distribution p(E) and the denoised distribution. The distribution produced by the wavelet denoising algorithm in Fig. 2 c is, therefore, a more accurate representation of the system's actual properties. Thus, the comparison shown in Fig. 2 shows the value of the wavelet denoising algorithm when applied to data derived from systems that exhibit nonMarkovian kinetics, and/or do not possess distinct conformational states.

Denoising a system with indistinguishable states

Fig. 3 a depicts the efficiency distribution of a two-state equilibrium that was simulated using kinetic Monte Carlo methods. As shown by this efficiency distribution, the two states, having mean efficiencies of 0.89 and 0.81, are indistinguishable in the presence of shot-noise. However, it is clearly shown by Fig. 3 b that the states in the underlying equilibrium are distinguishable after the trajectories are denoised by the wavelet denoising algorithm.

Figure 3.

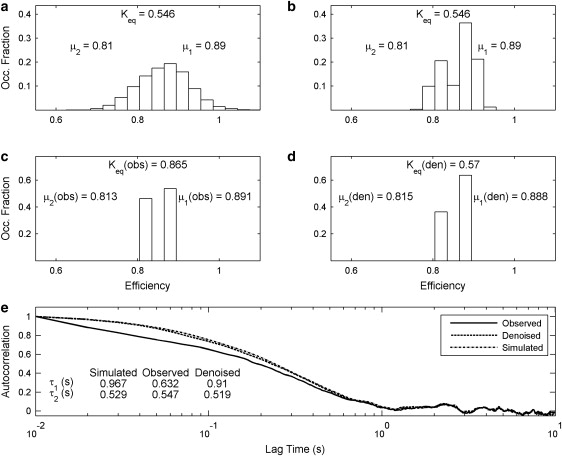
Denoising a system with indistinguishable states. (a) The efficiency distribution of the simulated equilibrium showing the central efficiency of each state, μ₁ and μ₂, as well as the simulated equilibrium constant, K_eq. (b) The efficiency distribution produced after denoising the trajectories with the wavelet denoising algorithm. (c) The distribution of efficiencies produced by acting on the noisy trajectories with HaMMy, showing the central efficiencies of each state, μ₁(obs) and μ₂(obs), as well as the equilibrium constant, K_eq(obs), produced by this operation. (d) The distribution of efficiencies produced by acting on the denoised data with HaMMy, showing central efficiencies of each state, μ₁(den) and μ₂(den), as well as the equilibrium constant, K_eq(den), produced by this operation. (e) Autocorrelation curves produced from the trajectories generated by HaMMy acting on the noisy data (solid), the denoised data (dotted), and the simulated state trajectories (dot-dash). The average lifetimes of each state, as extracted from the autocorrelation curves, are shown in the inset table for each of the simulated, observed, and denoised data.

To show the wavelet denoising algorithm's value as a companion to other methods, the hidden-Markov model of HaMMy (30) was used to further identify the central efficiency the states as well their relative populations, and the statistical correlation method described by Schenter et al. (29) was used to extract the kinetics that underlie the equilibrium. This method requires that a state be assigned to each time step in the trajectories, and HaMMy was also used to accomplish this task.

Acting on the shot-noise laden trajectories of the distribution shown in Fig. 3 a produces the idealized efficiency distribution in Fig. 3 c. Carrying out the same operation on the denoised trajectories produces the distribution shown in Fig. 3 d. It is seen that, whereas HaMMy ably identifies the central efficiency of each state, the equilibrium constant, K_eq(obs), that is produced by this operation differs from the actual equilibrium constant, K_eq, by 58%. In contrast, the equilibrium constant produced by acting on the denoised trajectories with the hidden-Markov model, K_eq(den), differs from the actual value of K_eq by only 4.4%. In addition, the central efficiencies that are produced by acting on the denoised trajectories with the hidden-Markov model differ only trivially from the actual efficiencies. It is quite obvious from this comparison that the denoised data produces an accurate representation of the thermodynamics that underlie the states this equilibrium.

The autocorrelation curves shown in Fig. 3 e were produced from idealized trajectories produced by HaMMy. Fitting these curves to exponential decays allows for the extraction of rate constants, and thus for the extraction of mean lifetimes of each state in the equilibrium. These lifetimes are also reported in Fig. 3 e. Inspection of each of the autocorrelation curves in Fig. 4 e reveals good agreement between the denoised and simulated curves, but poor agreement between the observed and simulated curves. Also, as seen in Fig. 3 e, the lifetimes of each state, as calculated from the autocorrelation of the noisy trajectories, are 0.632 s and 0.547 s. These values differ from the simulated lifetimes by 34.6% and 3.4%, respectively. The lifetimes produced by the autocorrelation of the denoised data are 0.91 s and 0.519 s, respectively, and these values differ from the simulated lifetimes by 5.9% and 1.9%, respectively.

Figure 4.

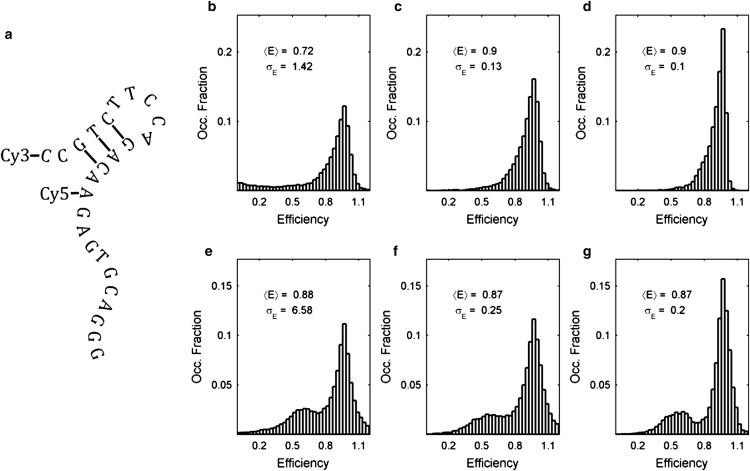
aV aptamer as a multiple state system. (a) The 2° of the aV aptamer. (b) The observed efficiency distribution of the aV aptamer at Mg²⁺ concentration of 2 mM, before blink-filtering. (c) The blink-filtered efficiency distribution of the aV aptamer. (d) The denoised distribution corresponding to b. (e) The observed efficiency distribution, before blink-filtering, resulting from the addition of 2 μM VEGF. (f) The blink-filtered efficiency distribution corresponding to e. (g) The denoised distribution corresponding to d.

Given the accuracy of each state's central efficiency and of the extracted equilibrium constant, we conclude that denoising the trajectories of this simulated system with the wavelet denoising algorithm successfully removes noise while retaining the actual data. Furthermore, acting on the denoised trajectories with the hidden-Markov model allows for the extraction accurate kinetic data, thereby completely characterizing two states in an equilibrium that were, before denoising, indistinguishable.

Application to Experimental smFRET Data

Application of the wavelet denoising algorithm and the Bayesian photoblink filter to a single, experimental smFRET trajectory is illustrated by Fig. S7. Extension of this application to a collection of experimental trajectories representing a single-state system is shown in Fig. S8, and Fig. S9 describes the application to a two-state experimental system.

The aV aptamer: a multistate experimental system

Trajectories acquired from studies reported previously (12) on the aV aptamer and its interaction with its binding target, vascular endothelial growth factor (VEGF), are chosen to represent a multiple state system. These experimental studies showed a highly dynamic secondary structure that ranged from the closed hairpin, illustrated in Fig. 4 a, to an irresolvable continuum of open states with lower smFRET efficiencies. To complicate matters, the aptamer interaction with VEGF was found to be similarly dynamic. Although the smFRET studies suggested that the VEGF-bound aptamer structure was the open state, quantitative analysis was hampered by contributions of both shot-noise and structural fluctuations to the measured smFRET distributions.

The global efficiency histogram containing ∼15,000 data points of the aV aptamer in 2 mM Mg²⁺ buffer solution is shown in Fig. 4 b. The distribution shows a skewed mean with an anomalously large standard deviation (SD) that is a result of the trajectories containing photoblinks. Application of the Bayesian photoblink filter to the trajectories results in the distribution shown in Fig. 4 c. This efficiency distribution has a mean efficiency of 0.9 with SD of 0.13. Application of the wavelet-denoising algorithm to this collection of trajectories results in the efficiency distribution shown in Fig. 4d. We observe that the mean efficiency is unaffected, and that the SD has been reduced by 25%. As such, we conclude that the algorithm has the capability to simultaneously refine the distributions of multiple, efficiency states, even if the efficiency state distributions have significant overlap.

Fig. 4 d shows a global efficiency histogram of the aV aptamer while in the presence of VEGF that contains ∼26,000 data points. Again, due to the presence of photoblinks in the trajectories, the distribution shows an anomalously large SD. Despite photoblinks, the VEGF-induced shift in the aptamer conformational equilibrium shown previously (12) is seen quite clearly in Fig. 4 e. It is not, however, clear that this shift arises due to a shift in the conformational equilibrium until the application of the Bayesian photoblink filter, which results in the distribution shown in Fig. 4 f. This collection of trajectories shows an overall mean efficiency of 0.87 with a large SD of 0.25 efficiency units, and shows that a shift in the aptamer equilibrium is indeed observed in the presence of VEGF.

The wavelet-denoised complement to this collection is shown in Fig. 4 g. Again, the effects of the denoising algorithm are quite clear. Whereas the mean efficiency once again remains constant, the SD is decreased by 20%. More importantly, the shape of the distribution is visibly refined. Although the distribution is broadened, presumably by effects of the fluorophores' respective orientations (63–65), efficiencies representative of a conformation yielding lower efficiencies are noticeably increased, in good agreement with the presumed interaction with VEGF (12). As a result of Fig. 4, d and g. we conclude that, although improving the finer aspects of the analysis, the application of the wavelet-denoising algorithm does not affect the overall outcome of the analysis of a system containing a complex combination of multiple and overlapping efficiency states. Furthermore, we conclude that the wavelet denoising algorithm enhances the analysis of this system by confirming the presence of a continuum of irresolvable conformations in the aptamer conformational equilibrium, as in Fig. 4 c, as well as improving the visibility of the presumed aV-VEGF interaction as in Fig. 4 g.

Conclusions

In conclusion, we have developed methods to identify, quantify, and remove two considerable sources of uncertainty in smFRET time trajectories—photoblinks and shot-noise. Using a two-component interpretation of noise observed in such signals allows us to remove the component we can quantify, thereby enhancing the accuracy of these measurements. In addition, the development of an unbiased method of photoblink detection eliminates the need to manually preprocess the trajectories, and perhaps more importantly, removes bias introduced into the measurement by manual selection of photoblink regions.

The algorithms' efficacy has been tested using simulated data. Acceptor and donor photon trajectories containing photoblinks were generated, and photoblink detection in these trajectories resulted in nearly complete elimination of photoblinks with little effect on the actual data. Similarly, wavelet denoising was applied to simulated acceptor and donor trajectories, and significantly decreased the width of a state's efficiency distribution. Additionally, trajectories representing a system showing oscillatory behavior were simulated as a means to show the efficacy of denoising in complex systems. These simulations showed that the denoised data formed a most accurate representation of the system at hand.

We have also shown that application of the Bayesian photoblink detection method in combination with the application of the wavelet denoising algorithm significantly improves the quality of experimental smFRET data. This improvement is observed both in the ensemble analysis of structural distributions, and in kinetic analysis of dwell times. Although there are caveats involved with the method of photoblink detection, we have also shown that the caveats can be avoided through establishment of a lower efficiency bound.

We expect that the methods presented here will have immediate impact on the smFRET community. We also expect the method to have a broad scope of applicability because the wavelet denoising algorithm is not strictly limited to smFRET measurements. Many wavelet-based applications have already been realized, and this particular method requires only slight adjustment for application to other types of time-series photon measurements, single-molecule or otherwise.

Supporting Material

Parts S1–S9, nine figures, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01559-8.