Abstract
We present a quantification method for affinity-based DNA microarrays which is based on the real-time measurements of hybridization kinetics. This method, i.e. real-time DNA microarrays, enhances the detection dynamic range of conventional systems by being impervious to probe saturation in the capturing spots, washing artifacts, microarray spot-to-spot variations, and other signal amplitude-affecting non-idealities. We demonstrate in both theory and practice that the time-constant of target capturing in microarrays, similar to all affinity-based biosensors, is inversely proportional to the concentration of the target analyte, which we subsequently use as the fundamental parameter to estimate the concentration of the analytes. Furthermore, to empirically validate the capabilities of this method in practical applications, we present a FRET-based assay which enables the real-time detection in gene expression DNA microarrays.
INTRODUCTION
Affinity-based detection is a fundamental method to identify and measure the abundance of biological and biochemical analytes. Affinity-based detectors (or so-called biosensors in case of detecting biological analytes) take advantage of the selective interaction and binding (affinity) of the target analyte with the immobilized capturing probes to specifically capture the target analyte onto a solid surface (1). One of the fundamental advantages of affinity-based biosensors is their inherent capability to be used in parallel to simultaneously detect a large number of different analytes in a single sample. The foremost example of massively parallel affinity-based biosensors is the microarray technology, which is widely adopted in Genomics and Proteomics (2). In particular DNA microarrays, devised for the analysis of complex nucleic acid samples, use the base pairing of nucleic acid molecules (3) as both the targets and the capturing probes to obtain thousands of concurrent measurements (4–8). Although relatively new, DNA microarrays have enabled a variety of important high-throughput applications, for example, genome-wide quantitative analysis of gene expression and large-scale single nucleotide polymorphism (SNP) discovery and genotyping (6–11).
To create target-specific signals in DNA microarrays the target analytes in the sample volume first need to collide with the capturing layer, interact and bind (hybridize) to the probes, and ultimately take part in some sort of transduction process to generate a signal. The analyte motion in typical microarray settings (e.g. aqueous biological mediums) is dominated by diffusion spreading, which from a microscopic point of view is a probabilistic mass-transfer process [i.e. random walk events for a single analyte molecule (12)]. Accordingly, the analyte collisions with the probes are probabilistic processes. In addition, because of the quantum-mechanical nature of chemical bond forming (13–16), interactions between the probes and the analyte molecules, are also probabilistic, adding more ‘uncertainty’ to the capturing events. Moreover, we also have the detector and the readout circuitry (e.g. fluorescent imaging systems), which likely add additional uncertainty to this already ‘noisy’ signal.
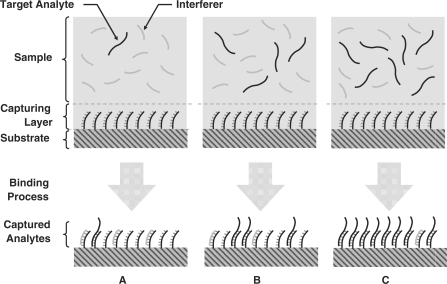
Besides the inevitable uncertainty associated with target analyte capturing and detection, in all practical biosensors, binding of other species to the probes (non-specific binding) is also possible. Non-specific binding [e.g. cross-hybridization in DNA microarrays (2)] is generally less probable and has a dissimilar binding kinetics compared to specific binding when the target analyte and the interfering species have the same abundance (3,17–18). Nonetheless, if the concentration of the non-specific species becomes much higher than that of the target analyte (e.g. in the case of genes expressed at low levels in DNA microarray experiments with complex biological background), non-specific bindings dominate the measured signal and hence limit the minimum detectable level (MDL) (19–23). Although the MDL is fundamentally noise- and interference-limited in microarrays, the highest detection level (HDL), is only a function of the capturing probe density and its associated saturation level (see Figure 1). It is imperative to realize that in order to reach this fundamental MDL and HDL, special care is necessary to minimize systematic errors such as probe density variations and washing artifacts. Such systematic errors, if present, can further degrade the quality of the acquired data and increase MDL while decreasing HDL.
Figure 1.
Capturing of analytes by the probes in affinity-based biosensors can be in the (A) interference-limited, (B) target analyte-limited and (C) saturation region.
Due to the aforementioned impediments, as of today, the accuracy and dynamic range of microarray systems do not satisfy the stringent requirements of many biotechnology applications, such as molecular diagnostics and forensics. Microarrays are considered semi-quantitative platforms and are best suited for applications such as whole genome gene expression profiling, where parallelism is the most imperative criteria. Enhancing the detection dynamic range of microarrays can not only improve the performance of the existing high-throughput systems, but also facilitate the adoption of microarrays in emerging high-performance applications.
In this work, we address some of the fundamental performance limitations of the conventional detection procedure in microarrays [i.e. incubation, washing, and scanning (2,5,24)] by proposing a kinetic assay for DNA microarray analysis, and demonstrate empirically its higher detection dynamic range. This method is based on real-time measuring of the total number of captured analytes during hybridization and, by calculating the kinetics of hybridization (as opposed to the total amount of captured analytes), estimating the target analyte concentrations. The presented practical implementation of this method for a set of analytes, i.e. real-time microarrays, makes use of fluorescent resonance energy transfer (FRET) donor and acceptor moieties (25–30) to enable real-time and non-invasive measurements during the hybridization. Moreover, we show, using both theory and experimental results, that this method is impervious to capturing probe saturation, washing artifacts, probe spotting or synthesis variations, and other signal amplitude-affecting non-idealities. This method introduces a paradigm shift in terms of how microarray experiments can be done, and because of its significant performance advantages over conventional methods, may become a preferred method of choice in future high-performance microarray-based applications.
MATERIALS AND METHODS
Target labeling
Real-time microarray experiments were performed using either target DNA oligonucleotides or target in vitro transcribed RNAs that were labeled with quencher residues. Target oligonucleotides were 3′-modified during synthesis with QSY9 (oligonucleotides were manufactured by TriLink BioTechnologies, USA). To prepare in vitro transcribed, QSY9-labeled target RNA, the Amino Allyl MessageAmpII aRNA Kit (Ambion) and QSY9 carboxylic acid, succinimidyl ester (Molecular Probes, USA) were used. Manufacturers’ protocols were used, with the following modifications: 50 ng of each spike RNA was used per cDNA synthesis reaction; the amount of amino allyl UTP used per in vitro transcription reaction was doubled; 5 mg of QSY9 were dissolved in 220 µl of DMSO, and 11 µl of the dissolved succinimidyl ester were used per labeling reaction. In vitro transcribed RNA was cleaved using Ambion's Fragmentation Reagent (following manufacturer's instructions) and purified using Sephadex Spin-50 Mini Columns (USA Scientific, USA). Approximately, one QSY9 residue was incorporated for every 20 nucleotides of the target IVT RNA.
Microarray setup
Probes for the real-time microarrays were designed against the ArrayControl RNA Spikes (Ambion Inc., USA). These RNA Spikes are a collection of eight individual RNA transcripts (Spikes 1 through 8) that range in size from 750 to 2000 bases, and each transcript has a 30-base 3′ poly(A) tail. Probes were custom synthetic DNA oligonucleotides modified during synthesis with a Cy3 fluorophore at the 5′ end and an amine residue at the 3′ end (oligonucleotides were manufactured by IDT). Control probes were designed such that they would not specifically hybridize to any of the targets (RNA Spikes) used. Probe sequences and the targets to which each one of them hybridizes are provided in Table 1.
Table 1.
Oligonucleotide sequences
| Oligonucleotide name | Sequence (5′–3′) |
|---|---|
| Probe A | [Cy3]-TACTTTCTCAGTACCATTAGGGCAA-[Amin] |
| Probe B | [Cy3]-CCCGGTTTCCCGGGTAAACACCACC-[Amin] |
| Control probe | [Cy3]-GTTGCCAAGTGCAGCAGGCGAAAGT-[Amin] |
| Target A | ACTTTCGCCTGCTGCACTTGGCAAC-[BHQ2] |
For microarray manufacture, dilutions of the Cy3-labeled DNA oligonucleotides were prepared in printing buffer (100 mM Na-phosphate pH 8.5; 0.005% w/v SDS) at the appropriate concentration (usually, 0.8, 4 and 20 μM DNA). Dilutions were dispensed in 384-well plates (15 μl of dilution per well), and DNA was spotted onto CodeLink activated slides (GE Healthcare) with a MicroGrid II microarrayer (Biorobotics/Genomics Solutions, USA). After printing, the slides were processed (DNA coupling and slide blocking) following manufacturer's protocols with minor modifications: DTT was added to the wash buffer (1 mM DTT, final concentration), and slide exposure to light was minimized. The printed microarrays were packed individually under vacuum with a flush of nitrogen gas, and stored at room temperature until use.
Microarray hybridization and data acquisition
For real-time microarray hybridizations, labeled target oligonucleotides or IVT RNAs were diluted at the indicated concentration in 50 μl of hybridization buffer (SlideHyb Glass Array Hybridization Buffer #1, Ambion). To initiate the hybridization, the microarray was first put in contact with 50 μl of hybridization buffer (without labeled target), and then (t = 0) the labeled target(s) were added in a volume of 50 μl of hybridization buffer (i.e. hybridization volume was 100 μl).
The hybridization was carried out within an individual well of a 24-well hybridization cassette (TeleChem International, Inc., USA). Hybridization temperature was controlled (with an accuracy of 1°C) using Peltier thermoelectric heating and cooling modules and a 5C7-195 benchtop temperature controller (McShane Inc., USA).
The imaging was done using a Zeiss LSM Pascal Inverted Laser Scanning Microscope, Zeiss, Germany) from below the microarray slide which was mounted in the hybridization cassette. The images were analyzed using our own software developed in Matlab (Mathworks, USA).
RESULTS AND DISCUSSIONS
Theoretical formulations
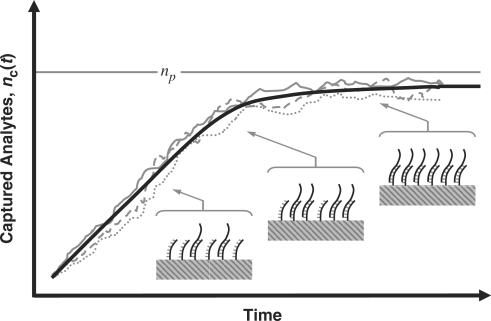
The binding process (for both specific and non-specific analytes) is a dynamic process that occurs over time and is a function of the analyte diffusion coefficient and concentration, the temperature, solution ionic strength, the density of the capturing probes, and the reaction surface-to-volume ratio. In Figure 2, we have illustrated a typical dynamical process for an individual capturing process where the total number of captured analytes is denoted by nc(t). It essentially starts with nc(0) = 0, and monotonically increases until it reaches the biochemical steady state, i.e. where the capturing and release processes have equal rate, thus making 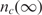 constant.
constant.
Figure 2.
Typical binding kinetics in DNA-based biosensors where the total amount of captured analytes increases until there is no free DNA capturing probes, i.e. saturation region. Expected behavior (thick solid line); Experiment (1, thin solid line); Experiment (2, dashed line); Experiment (3, dotted line).
Molecular binding, like any other biochemical process, is a random process, making nc(t) a random variable (13,16). Nevertheless, 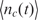 , the expected value (ensemble average) of nc(t), can be still approximated by the rate equation such that
, the expected value (ensemble average) of nc(t), can be still approximated by the rate equation such that
| 1 |
where k1 and k−1 are the association and dissociation rates of the binding (hybridization for DNA molecules), respectively, 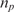 is the total number of DNA capturing probe molecules immobilized on the surface, and nt is the number of existing analyte molecules in the sample.
is the total number of DNA capturing probe molecules immobilized on the surface, and nt is the number of existing analyte molecules in the sample.
The binding process in affinity-based microarrays is slightly different from reactions in homogeneous solutions where both species are subject to diffusive spreading. In solid-phase reactions (e.g. hybridization in DNA microarrays), only the analyte (target nucleic acid strand) can freely move, and therefore binding can only occur at the intimate proximity (i.e. reaction distance) of the immobilized probes. To take this constraint into account, we need to modify Equation (1) to
| 2 |
In Equation (2), k1* is the association rate when there is unlimited abundance of capturing probes and the term 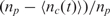 represents the availability of the probes, i.e. the probability of finding an unoccupied probe. It is important to recognize that in Equation (2), k1* is a function of the reaction chamber dimensions and the surface-to-volume ratio, but k−1 is not. However, both k1* and k−1 are also a strong function of temperature and ionic strength of the solution (3,31,32). Now, we can also further simplify Equation (2) for typical DNA microarray applications where the surface-to-volume ratio is relatively small. In these cases, we can assume that there is negligible analyte depletion in the system due to hybridization (nt remains relatively constant during the experiment); thus Equation (2) becomes
represents the availability of the probes, i.e. the probability of finding an unoccupied probe. It is important to recognize that in Equation (2), k1* is a function of the reaction chamber dimensions and the surface-to-volume ratio, but k−1 is not. However, both k1* and k−1 are also a strong function of temperature and ionic strength of the solution (3,31,32). Now, we can also further simplify Equation (2) for typical DNA microarray applications where the surface-to-volume ratio is relatively small. In these cases, we can assume that there is negligible analyte depletion in the system due to hybridization (nt remains relatively constant during the experiment); thus Equation (2) becomes
| 3 |
and accordingly the solution for Equation (3) with the assumption of, 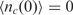 , is
, is
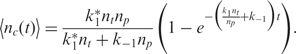 |
4 |
Now, we can define the random variable nc(t) which is the number of captured target analytes in a specific spot as
| 5 |
where 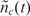 is the zero-mean random deviation from the expected behavior. Previously, it has been shown that
is the zero-mean random deviation from the expected behavior. Previously, it has been shown that 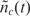 is essentially the biochemical ‘noise’ of the process, and that it has characteristics similar to shot-noise (Poisson noise) which can be formulated using stochastic differential equations methods (19–22). The challenge in all affinity-based sensors and DNA microarray systems is to estimate nt by measuring the noisy nc(t) in the presence of biological interference and transduction noise.
is essentially the biochemical ‘noise’ of the process, and that it has characteristics similar to shot-noise (Poisson noise) which can be formulated using stochastic differential equations methods (19–22). The challenge in all affinity-based sensors and DNA microarray systems is to estimate nt by measuring the noisy nc(t) in the presence of biological interference and transduction noise.
Microarray protocols generally allocate a fixed (and consistent) amount of time for the incubation step (e.g. 5–24 h for the hybridization step for gene expression DNA microarrays). At the end of this step with duration of t0, the solution containing the sample is carefully removed (washing step), and the intensity of the fluorescent signal is measured in each capturing spot, which is an indication of the amount of captured analytes at different capturing regions (2). Based on Equation (4), this procedure creates a non-linear relationship between nt and 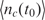 which is a strong function of t0. Moreover, the rate of binding depends not only on nt, but also on
which is a strong function of t0. Moreover, the rate of binding depends not only on nt, but also on 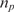 , as well as temperature-, ionic strength- and reaction-dependent parameters k1* and k−1. This clearly makes the quantitative estimation very complicated (33,34).
, as well as temperature-, ionic strength- and reaction-dependent parameters k1* and k−1. This clearly makes the quantitative estimation very complicated (33,34).
One can argue that the time-dependency of hybridization is not a major predicament in applications where comparative detection techniques are used, such as in two-color assaying methods in gene expression DNA microarrays (24). However, this statement is not generally valid since comparative assaying (ratio analysis) techniques can only be accurate when the reaction kinetics for the anlaytes are identical. Applying such techniques to estimate multi-analyte (multiplexed) systems with dissimilar values of k1* and k−1 is not optimal. This is even without considering the signal-corrupting effects of unspecific binding and biochemical noise.
One option to simplify the estimation of nt is to carry out the measurements early on, i.e. in the initial stages of hybridization (linear region), where we have
| 6 |
Although Equation (6) shows that we have a linear relationship between nt and nc(t), since t ≪ 1, the signal-to-noise ratio (SNR) is very small (19,21). Thus, proper estimation of 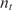 from such an early measurement may not be feasible in presence of imaging system noise. This gets particularly challenging if we take into consideration cross-hybridization, the signal-corrupting washing artifacts, and other systematic errors associated with conventional microarray procedures.
from such an early measurement may not be feasible in presence of imaging system noise. This gets particularly challenging if we take into consideration cross-hybridization, the signal-corrupting washing artifacts, and other systematic errors associated with conventional microarray procedures.
The other option is to carry out the measurement in the other extreme and wait long enough for the reaction to reach its steady state as value as  . In this case we can have enough signal and therefore a high output SNR (e.g. bright spots in fluorescent-based microarrays). If we assume that the measurement time much larger than the time constant of the reaction, then we may write the following using Equation (4)
. In this case we can have enough signal and therefore a high output SNR (e.g. bright spots in fluorescent-based microarrays). If we assume that the measurement time much larger than the time constant of the reaction, then we may write the following using Equation (4)
| 7 |
Although this is the approach typically used in many systems, there are two fundamental challenges associated with it. The first is that the relationship between the measured nc (t) and the desired nt is nonlinear (35). Probes are conventionally designed such that their affinity for their corresponding analytes is high. This implies that k1* ≫ k - 1, and consequently, if nt and 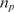 are comparable, then k1*
nt ≫ k - 1
np. Therefore nc(t), which in turn implies that
are comparable, then k1*
nt ≫ k - 1
np. Therefore nc(t), which in turn implies that 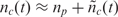 , which means that all probes will be effectively occupied [saturated (36)] at the biochemical steady state (Figure 2). Hence, the measurement bears little information regarding the concentration of nt. The only regime where the measured signal is proportional to nt is when the target concentration is very low so that nc (t) ≈ k1*
nt / k - 1 + ñc (t). For concentration levels of nt between these two extremes, the relationship between the measured nc(t) and the desired nt is nonlinear, as given by Equation (7). The second problem is that the time for the binding reaction to reach equilibrium can be very long, especially for low concentration analytes. Accordingly, it again may not be impractical to estimate nt from
, which means that all probes will be effectively occupied [saturated (36)] at the biochemical steady state (Figure 2). Hence, the measurement bears little information regarding the concentration of nt. The only regime where the measured signal is proportional to nt is when the target concentration is very low so that nc (t) ≈ k1*
nt / k - 1 + ñc (t). For concentration levels of nt between these two extremes, the relationship between the measured nc(t) and the desired nt is nonlinear, as given by Equation (7). The second problem is that the time for the binding reaction to reach equilibrium can be very long, especially for low concentration analytes. Accordingly, it again may not be impractical to estimate nt from 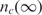 , in the presence of
, in the presence of 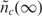 and other typical measurement non-idealities.
and other typical measurement non-idealities.
The alternative approach that we propose here is to estimate nt, not based on a single measurement of Equations (4) and (5) but, by looking at the full trajectory of nc (t). Using this full trajectory, one may estimate the time constant (or, its inverse, the rate) of the hybridization for a certain analyte in a capturing spot, τc. Using Equation (4), it is easy to see that
| 8 |
and for high-affinity probe-analyte moieties, we have
| 9 |
which shows that the time constant of binding can become proportional to the number of probe molecules and inversely proportional to the analyte concentration. Alternatively, the reaction rate 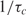 is proportional to the analyte concentration. Thus, we can in theory compute analyte concentration by determining the time-constant of hybridization in individual spots of a microarray. Again, it is imperative to realize that k1* for a certain reaction depends on the molecular structure of probe and the anlayte, temperature and ionic strength of the solution (3,31–34).
is proportional to the analyte concentration. Thus, we can in theory compute analyte concentration by determining the time-constant of hybridization in individual spots of a microarray. Again, it is imperative to realize that k1* for a certain reaction depends on the molecular structure of probe and the anlayte, temperature and ionic strength of the solution (3,31–34).
Now if we want to quantify the concentrations of the analytes, we should non-invasively measure the capturing kinetics and evaluate Equation (4) from the change in the signal, rather than stop the reaction to measure the signal from the captured analytes, as done in conventional DNA microarray platforms; in other words, a paradigm shift in terms of detection in microarrays. To be more specific, we should make a sequence of N measurements at times 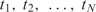 , i.e.
, i.e.
| 10 |
where A = k1*
nt
np /(k1*
nt + k - 1
np) and the time instants 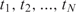 are typically equi-spaced, though they need not be so. The Equation (10) which is used for estimation has basically two unknowns, A and
are typically equi-spaced, though they need not be so. The Equation (10) which is used for estimation has basically two unknowns, A and 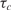 which include information regarding the analyte concentration. We have been shown that these two parameters and subsequently the analyte concentration can be estimated from the N measurements using a variety of methods, such as nonlinear least-squares (37).
which include information regarding the analyte concentration. We have been shown that these two parameters and subsequently the analyte concentration can be estimated from the N measurements using a variety of methods, such as nonlinear least-squares (37).
It is imperative to note that 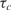 is estimated using the transient phase of the binding process and it has little bearing on the steady state value. Although it is true that early in the reaction the signal component of nc (t) is rather weak (i.e. low SNR), this can be compensated by increasing N and by taking measurements more frequently. In this manner, we can effectively ‘average out’ the noise and
is estimated using the transient phase of the binding process and it has little bearing on the steady state value. Although it is true that early in the reaction the signal component of nc (t) is rather weak (i.e. low SNR), this can be compensated by increasing N and by taking measurements more frequently. In this manner, we can effectively ‘average out’ the noise and  , which results in a significant improvement in the minimum detection level (MDL). On the other hand, since estimation is done in the transient phase and based on how fast the signal increases toward saturation, the saturation itself becomes not a predicament. This clearly increases the HDL. Therefore, compared to conventional microarrays, the accuracy of the estimate of the analyte concentration and the detection dynamic range, defined as the ratio of the analyte HDL to MDL, can be significantly improved. This is the fundamental advantage of the real-time analysis method independent of what transduction mechanism we use compared to conventional methods. We will demonstrate this empirically in the following section.
, which results in a significant improvement in the minimum detection level (MDL). On the other hand, since estimation is done in the transient phase and based on how fast the signal increases toward saturation, the saturation itself becomes not a predicament. This clearly increases the HDL. Therefore, compared to conventional microarrays, the accuracy of the estimate of the analyte concentration and the detection dynamic range, defined as the ratio of the analyte HDL to MDL, can be significantly improved. This is the fundamental advantage of the real-time analysis method independent of what transduction mechanism we use compared to conventional methods. We will demonstrate this empirically in the following section.
Real-time DNA microarray assay
Real-time measurement of the binding events poses challenging requirements for the detection system and the assay. The foremost challenge for real-time detection is that the aqueous solution where the analytes reside should be present during detection. This is in contrast with conventional procedure where the detection is carried out after the aqueous solution (hybridization buffer for DNA microarrays) is removed. From a detection point of view, the presence of the aqueous solution usually results in a significant amount of background signal which needs to be distinguished and extracted from the analyte-specific signal. In the systems where extrinsic reporters or labels are used such as fluorescence-based DNA microarrays, the solution background generally comes from the unbound and labeled analytes in the hybridization buffer which makes the real-time detection of captured analytes almost impossible. In the systems where the intrinsic characteristics of the analytes (e.g. charge or optical absorption) are used, the background originates from the neighboring molecules that have similar physiochemical characteristics to the captured analytes. Regardless of their origin, high level of background signals (or interferences) reduces the MDL, and becomes particularly problematic when the aqueous sample contains multiple analytes.
Although real-time detection in microarrays have not been demonstrated so far, real-time detection of binding kinetics in affinity-based biosensors have been previously demonstrated using a variety of modality and innovative instrumentations. To name a few, we can mention surface plasmon resonance (SPR) (18,33,34,38–41), intrinsic charge (42–44), molecular mass and surface acoustic wave (45–48), UV absorption-based (3,48), and optical waveguide-coupled (31,49,50) detection assays. While most of these techniques and methods can generate the data for Equation (10) for a number of analytes, they are not scalable in terms of number of capturing spots (except charge-based methods) and therefore not compatible for large biosensor arrays and microarrays.
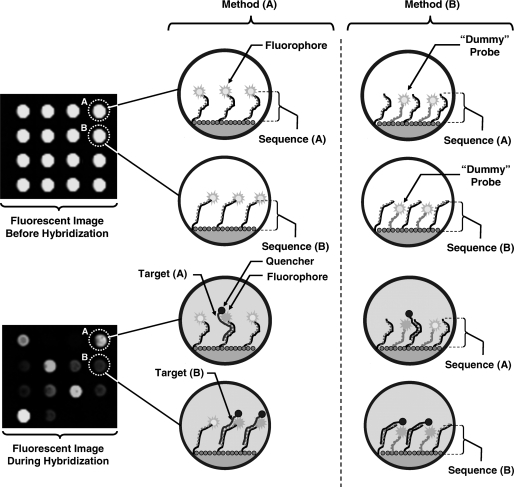
To enable real-time detection in microarrays with little background interference, we need to ensure that only the captured analytes in intimate proximity of the capturing probes contribute to the measured signal. Since intimate proximity in molecular scale in individual spots is critical, here we propose to use fluoresce resonance energy transfer (FRET) moieties to create binding-specific signals (25–30). In this technique, we attach radiating donor molecules (e.g. fluorescent molecules) to the capturing probes (method A in Figure 3) or to a ‘dummy’ probe near the capturing probes (method B in Figure 3) in each spot. This can be done prior to array spotting and during the synthesis of the capturing probes. For instance, in the case of DNA microarrays, as shown in Figure 3, the DNA oligonucleotides that act as the capturing probes are end-labeled with Cyanine (Cy) fluorophores. Subsequently, in the sample preparation process, we attach the acceptor molecules of the FRET system to the analytes. If the sample containing the analytes is applied to the array, which consists of capturing spots with donors, hybridization events bring the donor and acceptor into intimate proximity resulting in a molecular FRET system. To create a binding-specific signal, we use non-radiating acceptors (i.e. quenchers), such that hybridization ‘turns off’ the fluorophore of the capturing probe or the ‘dummy’ probe, and hence reduces the overall emitted fluorescent signal of the spot as shown in Figure 3. From a imaging point of view, this method requires identical instrumentation compared to other fluorescence-based assays, while the solution containing the sample introduces little fluorescence background. In addition, parallel measurements can be carried and the method is scalable to large size arrays. It is also important to recognize that the low background signal in this method enables the effective detection of the capturing events with high SNR during the DNA hybridization.
Figure 3.
Two FRET-based real-time DNA microarray assaying alternative methods. In method (A) the donor fluorophore is attached to the capturing probe, while in method (B) it is placed near the capturing probe by attaching it to a ‘dummy’ probe. In both methods, successful hybridization of the analyte which contains the quencher results in the quenching of the nearby donor fluorophore.
The emitted fluorescent signal for the spots during binding is proportional to the number of probes which have active fluorophores, assuming that there is negligible self-quenching among the donor fluorophores. The number of free capturing probes is 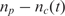 . Based on Equation (4), we can calculate its expected number of free fluorophores during hybridization by
. Based on Equation (4), we can calculate its expected number of free fluorophores during hybridization by
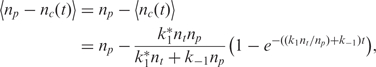 |
11 |
which illustrates that the rate of quenching due to capturing is identical to the rate of capturing and hence it is possible to implement the rate-based analyte quantification method described earlier.
In Figure 4, we illustrate the experimental results of our real-time method for a typical DNA microarray system. The donor and acceptor are Cy3 and BHQ2, respectively, with Förster distance of ∼6 nm. The sequences of the three different sequences of printed oligonucleotides are listed in Table 1 and they all are printed in four replicates from a solution at 10 and 20 µM concentration. At 100% coupling efficiency such concentrations will create probe surface densities of 1 × 1011 to 2 × 1011 oligonucleotides per mm2 (33,51). For example, a 50 µm diameter microarray spot contains approximately 0.2 × 109 to 0.4 × 109 oligonucleotide molecules for printing concentrations of 10–20 µM.
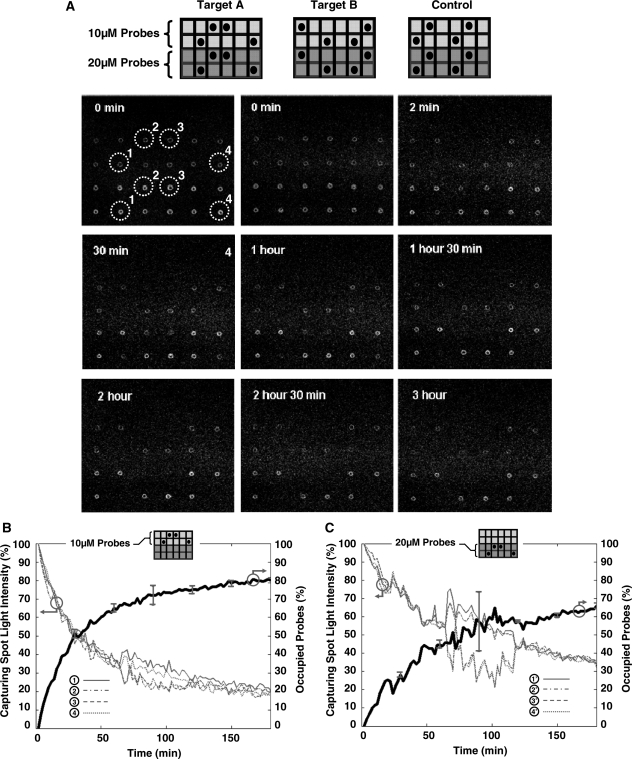
Figure 4.
Experimental results of a real-time DNA microarray system using Cy3 and BHQ2 as the donor and acceptor moieties according to method A of Figure 3. In (A), selected fluorescent images (every 30min) are shown during the first 3 h of the hybridization step when 20 ng/100 µl of Target A is introduced to the array. In (B), we show the time series acquired fluorescent light intensity and the calculated average percentage of the occupied probes for four identical capturing spots within this array which have Probe A printing concentration of 10 µM. In (C), we show similar data as of (B), but for capturing spots which have Probe A printing concentration of 2 µM.
In Figure 4A, the layout of the array and the real-time fluorescent image of the array acquired by an inverted fluorescent laser-scanning microscope is shown, when 20 ng/100 µl of Target A is applied to the array at 44°C. Individual images were taken every 2 min and representative images are shown in Figure 4A. At the beginning, when the solution is not present, the fluorescent density in the image shows the printed probes and the potential printing artifact and non-idealities. When the solution with DNA target is added, the fluorescent intensity in spots 1–4 associated with Probe A where capturing is occurring, gradually goes down. As evident, there is little background fluorescence from the solution and light intensity of the other spots remains relatively unchanged.
In Figure 4B and C, we show the real-time measured fluorescent intensity of Probe A spots with oligonucleotide printing concentration of 10 and 2 µM, respectively. The light intensities of individual spots illustrate an exponential decay as predicted by Equation (10). By using the light intensity quenching data, we were able to compute not only the kinetics of hybridization (time-constant of the reaction), but also the saturation levels of each spot. It is also worth mentioning that even with spot-to-spot size and area variations in the printed arrays, we were able to estimate the spot boundaries and compensate for the printing artifacts. This correction procedure was done using the t = 0 image to delineate the outline of each spot and choosing the ‘acceptable’ capturing region by differentiating it from the surrounding background. Selecting this region was simply carried out by finding the coordinates (pixels) within each spot of t = 0 image where fluorescent intensities were close to its spot median intensity. The justification for this particular method is based on the fact that hybridization kinetics is a function of capturing probe density. Therefore, if we create non-uniform probe densities during array printing, we expect a mixture of time-constants in each capturing spot which in turn undermines the applicability of Equation (10) for the generated real-time signal. The typical ‘coffee stain’ artifacts created by printing pins during printing (see Figure 4) are examples of such a phenomenon which need to avoided or considered during measurements. This compensation approach is not feasible in conventional DNA microarrays since the printed probes in their case do not generate signal. In addition, we used the light intensity of the spots which do not capture any targets (i.e. control oligonucleotide in Table 1) in our experiments as the control signal to compensate for the instrument gain drifts and possible fluorophore bleaching. In this 3-h experiment, we did not observe more than 3–5% light variation in the control spots using this setup.
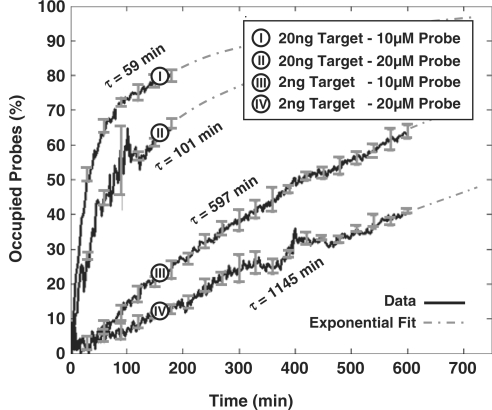
In Figure 5, we show the real-time results of four microarray experiments, with the same target and probe sequence (i.e. Probe A and Target A), but different concentrations. Each curve is generated using the results of eight independent spots on the array. Based on Equation (9), τ should be proportional to 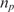 and inversely proportional to nt. As evident, this indeed the case, i.e. doubling the probe density doubles the time-constant and reducing the target concentration by one order of magnitude decreases the time-constant by one order of magnitude. We should note that the estimation of τ is robust with respect to the probe printing variations and artifacts. Namely, the coefficients of variation of the initial probe light intensity in probe spots with printing concentrations of 10 and 20 µM were 22 and 15%, respectively. Nevertheless, coefficients of variation of the corresponding estimates of τ were 6 and 4.4% in the experiment with 20 ng/100 µl of the target, and 4.8 and 2.1% in the experiment with 2 ng/100 µl of the target, respectively.
and inversely proportional to nt. As evident, this indeed the case, i.e. doubling the probe density doubles the time-constant and reducing the target concentration by one order of magnitude decreases the time-constant by one order of magnitude. We should note that the estimation of τ is robust with respect to the probe printing variations and artifacts. Namely, the coefficients of variation of the initial probe light intensity in probe spots with printing concentrations of 10 and 20 µM were 22 and 15%, respectively. Nevertheless, coefficients of variation of the corresponding estimates of τ were 6 and 4.4% in the experiment with 20 ng/100 µl of the target, and 4.8 and 2.1% in the experiment with 2 ng/100 µl of the target, respectively.
Figure 5.
Capturing curves and the computed time-constants from a real-time DNA microarray system for 2 ng/100 μl and 20 ng/100 μl analyte concentrations.
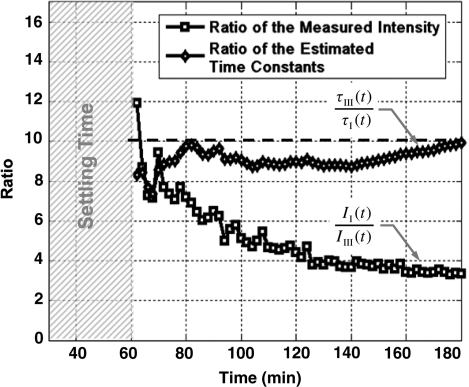
In Figure 6, we show the results of a comparison between the conventional ratio-based method of quantification in microarrays (24,52,53) with the real-time method for using the results of experiments (I) and (III) of Figure 5. In this particular experiment, the ratio of the computed τ in real-time analysis is compared to the ratio of the fluorescent intensity of the spots every 2 min after the first hour of the hybridization until the end of the third hour. As evident, the real-time technique does a much better quantitative job in estimating the concentrations compared to the conventional technique. We believe that the error of the conventional methods can be explained using Equation (4).
Figure 6.
Ratio of hybridized analytes versus ratio of computed time-constants for experiments (I) and (III) of Figure 5 as a function time.
The result of these sets of experiments, which emulates DNA microarray assays, not only demonstrates the feasibility of our proposed FRET-based real-time microarray assay, but also offers key insights into the characteristics of DNA microarray signals. One important result demonstrated by these experiments is that the DNA microarray assays reach equilibrium at a very different rate depending on the concentration of the analytes. This observation which was previously reported in different platforms (38–41,49,50) confirms our initial assertion regarding the kinetic nature of DNA microarray signals and supports the necessity of real-time measurements to quantify a wide range of concentrations. Another observation is the exponential relationship between the time-to-saturation and the analyte concentration level. Such a relationship points out that when target analytes have large concentration differences (e.g. two to three orders of magnitude) it is challenging to do an accurate quantification using a single measurement in time, as it is currently practiced. The reason is that at the time when high concentration analytes show sufficient SNR, low concentration analytes are well below the noise level. On the other hand, when low concentration analytes have sufficient SNR, the signals from high concentration analytes are well within the saturation region. Noticeably, real-time analysis and quantification based on the hybridization time-constants addresses this problem since the information is extracted in the linear, non-linear, and saturation regions of the capturing curve.
It is important to realize that the detection dynamic range and the necessary time for real-time analysis are both a function of how accurate we can measure τ for different analyte concentrations. For HDL, we are limited by the image acquisition speed since the hybridization kinetics can be very fast for high concentration analytes. On the other hand for MDL, we are limited by the maximum allowable hybridization time since the hybridization kinetics can be very slow for low concentration analytes. In both cases based on Equation (11), we require sufficient time (e.g. multiples of τ) for the analyte signal to come out of background signal and for us to properly estimate τ.
Although end-labeling of nucleic acid strands (targets) can be adopted in all forms of DNA microarrays, it is more efficient to use multiple labels per individual target DNA or RNA target molecule, as current standard microarrays normally do, using a variety of methods. One widely adopted method to label at multiple sites each target molecule is to incorporate amino allyl nucleotides during the cDNA synthesis or in vitro transcription (if such amplification step is used) reactions, followed by a secondary label coupling reaction (2). The coupling reaction includes bonding of the reactive amino group to a NHS ester modified label (e.g. biotin or Cy dye). For the real-time assay, we implemented this approach but used the QSY9 quencher (NHS ester modified) instead of conventional fluorescent labels (see Supplementary Figure 1). QSY9 was incorporated efficiently in the target molecules, and we determined an average distance of 20 nucleotides between incorporated quencher molecules. Using this labeling method, we conducted experiments wherein the real-time microarray platform was used to detect and quantify mRNA targets to emulate gene expression microarray assays. As targets, we used a commercially available set of 8 purified Escherichia coli RNA transcripts (ArrayControl RNA spikes, Ambion Inc., USA). We designed 8 complementary probes (25-mer oligonucleotides, one per target). Microarrays were manufactured by printing each probe at three different concentrations, and with 6 replicate spots each.
Table 2 shows, 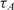 , the measured, time-constant of the hybridization process for different concentrations of Spike 2 752 bp mRNA using method A. We performed the real-time microarray experiments in which the concentration of the Spike 2 was diluted by a factor of 5 starting from 400 ng/100μl. The hybridization duration was 5 h, and the fluorescent images were collected 1 min apart. To estimate the sequence-dependant k1* and to create a reference spot, we chose the data of the experiment where the probe and target concentrations are both in the mid range (i.e. 16 ng/100 μl target and 10 μM probe printing concentration). Subsequently, we normalized the other time constants using this reference time-constant. We also applied log2 function on the normalized data to form a figure-of-merit for the quality of the data, similar to conventional microarray experiments (52,53).
, the measured, time-constant of the hybridization process for different concentrations of Spike 2 752 bp mRNA using method A. We performed the real-time microarray experiments in which the concentration of the Spike 2 was diluted by a factor of 5 starting from 400 ng/100μl. The hybridization duration was 5 h, and the fluorescent images were collected 1 min apart. To estimate the sequence-dependant k1* and to create a reference spot, we chose the data of the experiment where the probe and target concentrations are both in the mid range (i.e. 16 ng/100 μl target and 10 μM probe printing concentration). Subsequently, we normalized the other time constants using this reference time-constant. We also applied log2 function on the normalized data to form a figure-of-merit for the quality of the data, similar to conventional microarray experiments (52,53).
Table 2.
Real-time microarray experiment results for different concentrations of 720 bp mRNA target and oligonucleotide probes without any biological background
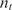 (ng/100μl) (ng/100μl) |
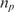 (μM) (μM) |
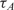 (min) (min) |
 (min) (min) |
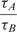 |
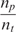 |
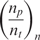 |
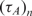 |
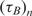 |
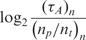 |
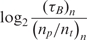 |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 20 | 120 | 188.6 | 0.636 | 0.05 | 0.08 | 0.097 | 0.082 | 0.285 | 0.033 |
| 80 | 20 | 442.5 | 979.4 | 0.451 | 0.25 | 0.4 | 0.354 | 0.425 | −0.154 | 0.088 |
| 16 | 20 | 2058.8 | 4040.9 | 0.509 | 1.25 | 2 | 1.672 | 1.754 | −0.258 | −0.190 |
| 400 | 10 | 68.8 | 161.9 | 0.425 | 0.025 | 0.04 | 0.056 | 0.070 | 0.482 | 0.8130 |
| 80 | 10 | 214.7 | 472.4 | 0.454 | 0.125 | 0.2 | 0.174 | 0.205 | −0.197 | 0.036 |
| 16a | 10 | 1230.8 | 2303.8 | 0.534 | 0.625 | 1 | 1 | 1 | 0 | 0 |
| 3.2 | 10 | 7073.5 | 11149.9 | 0.634 | 3.125 | 5 | 5.747 | 4.840 | 0.201 | −0.047 |
| 0.64 | 10 | 15 940.5 | 29 373.4 | 0.543 | 15.625 | 25 | 12.951 | 12.750 | −0.949 | −0.971 |
| 400 | 2 | 51.5 | 158.3 | 0.325 | 0.005 | 0.008 | 0.0418 | 0.0687 | 2.387 | 3.102 |
| 80 | 2 | 272.3 | 631.1 | 0.431 | 0.025 | 0.04 | 0.221 | 0.274 | 2.468 | 2.776 |
| 16 | 2 | 1603.7 | 3815.1 | 0.420 | 0.125 | 0.2 | 1.303 | 1.656 | 2.704 | 3.050 |
| 3.2b | 2 | 13 686 | 71 913.9 | 0.190 | 0.625 | 1 | 11.120 | 31.215 | 3.475 | 4.964 |
| 0.64b | 2 | 15 790.2 | 76 395.2 | 0.207 | 3.125 | 5 | 12.829 | 33.16 | 1.360 | 2.729 |
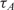 and
and 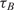 are the measured hybridization time-constants for Methods (A) and (B) of the FRET-based assay, respectively, according to Figure 3.
are the measured hybridization time-constants for Methods (A) and (B) of the FRET-based assay, respectively, according to Figure 3.
aThe reference experiment and the index (n) shows the normalized data using the results of the reference.
bThe experiments where the light intensity SNR was unacceptable (i.e. background variation was higher than the signal value).
One barrier for the adoption of method A in DNA microarray technology is the cost and the synthesis complexities of dual-labeled capturing oligonucleotides which in our case include Cy3 fluorophore at the 5′ end and an amine residue at the 3′ end. Although in small scale arrays, the synthesis and spotting of such probes are sensible, in large scale arrays, with 103 and above number of spots, it is not desirable. Also, for many applications libraries of capturing probes (without donor modification) have already been synthesized and the users might not be able to re-synthesize the whole library again. In order to address this drawback and make the real-time DNA microarray method compatible with the already capturing probe libraries, we repeated the previously described mRNA experiments with a different set of arrays using method B of Figure 3, where the contents of probe spots were modified. In this experiment, we used the same capturing probe as before, but did not modify them with the donor, i.e. Cy3 florophore, and only the amine residue modification was incorporated. These unlabeled probes were mixed with ‘dummy’ probes which had both modifications, but with a designed sequence with a very low alignment score with the mRNA targets. Our goal in these experiments was to demonstrate that quenching is feasible even if the fluorescent donor modifications are not attached to the capturing probe to which targets bind, but simply need to be in their intimate proximity. The ratio of the unlabeled specific probes and labeled ‘dummy’ probes was 50:50. The time-constants of experiments using method B are denoted by 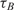 in Table 2.
in Table 2.
The first observation regarding the results in Table 2 is that, 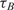 , the time-constant of experiments using method B is generally twice the value of
, the time-constant of experiments using method B is generally twice the value of 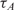 , expect in the experiment where the images SNR is low. This is consistent with the fact that the ratio of the unlabeled capturing probes and labeled ‘dummy’ probes was 50:50 in method B, making its probe density half of method A. In addition when we examine the normalized data of Table 3, we see that when the SNR is acceptable, the log2 function reveal strong correlation between the value of
, expect in the experiment where the images SNR is low. This is consistent with the fact that the ratio of the unlabeled capturing probes and labeled ‘dummy’ probes was 50:50 in method B, making its probe density half of method A. In addition when we examine the normalized data of Table 3, we see that when the SNR is acceptable, the log2 function reveal strong correlation between the value of 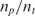 and
and 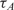 and
and 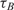 within 2 and 1 orders of magnitude dynamic range for mRNA target and probe concentrations, respectively.
within 2 and 1 orders of magnitude dynamic range for mRNA target and probe concentrations, respectively.
Table 3.
Real-time microarray experiment results for different concentrations for 720 bp mRNA target and oligonucleotide probes with 7.5 μg/50 μl aRNA prepared from total mouse RNA as the complex biological background
| nt (ng/100μl) | np (μM) |
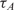 (min) (min) |
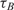 (min) (min) |
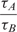 |
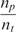 |
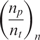 |
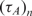 |
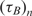 |
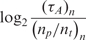 |
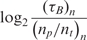 |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 20 | 251 | 562.3 | 0.446 | 0.05 | 0.08 | 0.159 | 0.225 | 0.987 | 1.4935 |
| 80 | 20 | 703.4 | 1420.1 | 0.495 | 0.25 | 0.4 | 0.444 | 0.569 | 0.152 | 0.508 |
| 16 | 20 | 2726.3 | 4519.4 | 0.603 | 1.25 | 2 | 1.722 | 1.810 | −0.215 | −0.143 |
| 3.2 | 20 | 9253.3 | 37 270.7 | 0.248 | 6.25 | 10 | 5.847 | 14.931 | −0.774 | 0.578 |
| 400 | 10 | 119.9 | 228.1 | 0.526 | 0.025 | 0.04 | 0.076 | 0.0913 | 0.921 | 1.192 |
| 80 | 10 | 394.1 | 944 | 0.417 | 0.125 | 0.2 | 0.249 | 0.378 | 0.316 | 0.919 |
| 16a | 10 | 1582.5 | 2496.1 | 0.633 | 0.625 | 1 | 1 | 1 | 0 | 0 |
| 3.2 | 10 | 5359.8 | 11 052.4 | 0.485 | 3.125 | 5 | 3.387 | 4.427 | −0.561 | −0.17 |
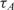 and
and 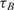 are the measured hybridization time-constants for Methods (A) and (B) of the FRET-based assay, respectively, according to Figure 3.
are the measured hybridization time-constants for Methods (A) and (B) of the FRET-based assay, respectively, according to Figure 3.
aThe reference experiment and the index (n) shows the normalized data using the results of the reference. The low SNR measurements are not reported in this table in contrast to Table 2.
In a second set of experiments, 7.5 µg/50 µl of aRNA prepared from total mouse RNA was added to the Spike 2 target to provide a complex biological background, in order to simulate a standard gene expression microarray experiment. Table 3 shows measured time-constants of the hybridization processes, using both methods A and B. As expected, the interference of the background degraded the quality of the data, but the quantification was still acceptable, even within two orders of magnitude difference in the target concentration.
CONCLUSION
To address the fundamental detection challenges of DNA microarrays, we need to better understand the relationship between the target analytes in the sample and the number of captured analytes in the capturing spots. In this article, we establish the fact that the hybridization process in microarrays, similar to any other affinity-based biosensor, is a kinetic stochastic process and a non-linear function of time, analyte concentration, and reaction kinetics. We also articulate that the limits of detection, i.e. MDL and HDL, in microarrays are a direct consequence of the kinetic nature of the system as well as of the inherent uncertainty of the binding events. Furthermore, we argue that the current method of analysis in microarrays, i.e. analyte quantification based on a single data point from the hybridization (binding) process, is not only susceptible to noise and systematic errors, but also incapable of providing sufficient information for systems which comprise of analytes with a very large concentration differences. Accordingly, real-time measurement of hybridization events and analyte quantification based on the rate of the hybridizations can be an alternative and preferred solution since it is impervious to many of the impediments. The enhanced performance of real-time microarrays compared to conventional analysis methods, which we show using both theory and empirical results, is very promising. We believe the real-time microarray technique to be a paradigm shift in terms of detection in microarrays, very general, and also applicable to a variety of analytes and not limited to nucleic acids.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Grubstake grant from Caltech; Millard and Muriel Jacobs Genetics Laboratory at the California Institute of Technology; David and Lucille Packard Foundation. Funding for open access charge: University of Texas at Austin New Faculty Startup Fund.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
The authors are grateful to Vijaya Kumar for experimental assistance with microarray manufacture and target labeling. They also want to thank Dr Scott Fraser for technical feedback in the imaging aspects of this project.
Footnotes
Present address: José Luis Riechmann, ICREA and Center for Research in Agricultural Genomics (CRAG)-CSIC-IRTA-UAB, Barcelona 08034, Spain.
REFERENCES
- 1.Hall EAH. Biosensors. Englewood Cliffs, NJ: Prentice-Hall; 1991. [Google Scholar]
- 2.Schena M. Microarray Analysis. New York, NY: Wiley; 2003. [Google Scholar]
- 3.SantaLucia J, Jr, Allawi HT, Seneviratne PA. Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry. 1996;35:3555–3562. doi: 10.1021/bi951907q. [DOI] [PubMed] [Google Scholar]
- 4.Pease AC, Solas D, Sullivan EJ, Cronin MT, Holmes CP, Fodor SP. Light-generated oligonucleotide arrays for rapid DNA sequence analysis. Proc. Natl Acad. Sci. USA. 1995;91:5022–5026. doi: 10.1073/pnas.91.11.5022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schena M, Shalon D, Davis RW, Brown PO. Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science. 1995;270:467–470. doi: 10.1126/science.270.5235.467. [DOI] [PubMed] [Google Scholar]
- 6.Chee M, Yang R, Hubbell E, Berno A, Huang XC, Stern D, Winkler J, Lockhart DJ, Morris MS, Fodor SP. Accessing genetic information with high-density DNA arrays. Science. 1996;274:610–614. doi: 10.1126/science.274.5287.610. [DOI] [PubMed] [Google Scholar]
- 7.Lockhart DJ, Dong H, Byrne MC, Follettie MT, Gallo MV, Chee MS, Mittmann M, Wang C, Kobayashi M, Horton H, et al. Expression monitoring by hybridization to high-density oligonucleotide arrays. Nat. Biotechnol. 1996;14:1675–1680. doi: 10.1038/nbt1296-1675. [DOI] [PubMed] [Google Scholar]
- 8.Lockhart DJ, Winzeler EA. Genomics, gene expression and DNA arrays. Nature. 2000;405:827–836. doi: 10.1038/35015701. [DOI] [PubMed] [Google Scholar]
- 9.Wang DG, Fan J-B, Siao C-J, Berno A, Young P, Sapolsky R, Ghandour G, Perkins N, Winchester E, Spencer J, et al. Large-scale identification, mapping, and genotyping of single-nucleotide polymorphisms in the human genome. Science. 1998;280:1077–1082. doi: 10.1126/science.280.5366.1077. [DOI] [PubMed] [Google Scholar]
- 10.Hardenbol P, Baner J, Jain M, Nilsson M, Namsaraev EA, Karlin-Neumann GA, Fakhrai-Rad H, Ronaghi M, Willis TD, Landegren U, et al. Multiplexed genotyping with sequence-tagged molecular inversion probes. Nat. Biotechnol. 2003;21:673–678. doi: 10.1038/nbt821. [DOI] [PubMed] [Google Scholar]
- 11.Kennedy GC, Matsuzaki H, Dong S, Liu WM, Huang J, Liu G, Su X, Cao M, Chen W, Zhang J, et al. Large-scale genotyping of complex DNA. Nat. Biotechnol. 2003;21:1233–1237. doi: 10.1038/nbt869. [DOI] [PubMed] [Google Scholar]
- 12.Berg HC. Random Walks in Biology. New Jersey, NJ: Princeton University Press; 1993. [Google Scholar]
- 13.Levine N. Quantum Chemistry. New York, NY: Prentice-Hall; 1999. [Google Scholar]
- 14.Van Kampen NG. Stochastic Processes in Physics and Chemistry. Amsterdam: North-Holland; 1981. [Google Scholar]
- 15.Steinfield JI, Fransisco JS, Hase WL. Chemical Kinetics and Dynamics. 2nd. New York, NY: Prentice-Hall; 1998. [Google Scholar]
- 16.Hubble J. Monte-Carlo simulation of biospecific interactions. Biotechnol. Lett. 2000;22:1483–1486. [Google Scholar]
- 17.Dai H, Meyer M, Stepaniants S, Ziman M, Stoughton R. Use of hybridization kinetics for differentiating specific from non-specific binding to oligonucleotide microarrays. Nucleic Acids Res. 2002;30:e86. doi: 10.1093/nar/gnf085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Heaton RJ, Peterson AW, Georgiadis RM. Electrostatic surface plasmon resonance: direct electric field-induced hybridization and denaturation in monolayer nucleic acid films and label-free discrimination of base mismatches. Proc. Natl Acad. Sci. USA. 2001;98:3701–3704. doi: 10.1073/pnas.071623998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hassibi A, Vikalo H, Hajimiri A. On noise processes and limits of performance in biosensors. J. Appl. Phys. 2007;102:0149091–01490912. [Google Scholar]
- 20.Das S, Vikalo H, Hassibi A. On scaling laws of biosensors: a stochastic approach. J. Appl. Phys. 2009;105:102021–102027. [Google Scholar]
- 21.Tu Y, Stolovitzky G, Klein U. Quantitative noise analysis for gene expression microarray experiments. Proc. Natl Acad. Sci. USA. 2002;99:14031–14036. doi: 10.1073/pnas.222164199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hassibi A, Zahedi S, Navid R, Dutton RW, Lee TH. Biological shot-noise and quantum-limited signal-to-noise ratio in affinity-based biosensors. J. Appl. Phys. 2005;97:1–10. [Google Scholar]
- 23.Linneti K, Kondratovich M. Partly nonparametric approach for determining the limit of detection. Clin. Chem. 2004;50:732–740. doi: 10.1373/clinchem.2003.029983. [DOI] [PubMed] [Google Scholar]
- 24.Shalon D, Smith SJ, Brown PO. A DNA microarray system for analyzing complex DNA samples using two-color fluorescent probe hybridization. Genome Res. 1996;6:639–645. doi: 10.1101/gr.6.7.639. [DOI] [PubMed] [Google Scholar]
- 25.Lacowicz R. Principles of Fluorescence Spectroscopy. 2nd. New York, NY: Plenum; 1999. [Google Scholar]
- 26.Ota N, Hirano K, Warashina M, Andrus A, Mullah B, Hatanaka K, Taira K. Determination of interactions between structured nucleic acids by fluorescence resonance energy transfer (FRET): selection of target sites for functional nucleic acids. Nucleic Acids Res. 1998;26:735–743. doi: 10.1093/nar/26.3.735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Okamura Y, Kondo S, Sase I, Suga T, Mise K, Furusawa I, Kawakami S, Watanabe Y. Double-labeled donor probe can enhance the signal of fluorescence resonance energy transfer (FRET) in detection of nucleic acid hybridization. Nucleic Acids Res. 2000;28:e107. doi: 10.1093/nar/28.24.e107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ghosh SS, Eis PS, Blumeyer K, Fearon K, Millar DP. Real time kinetics of restriction endonuclease cleavage monitored by fluorescence resonance energy transfer. Nucleic Acids Res. 1994;22:3155–3159. doi: 10.1093/nar/22.15.3155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rajendran M, Ellington AD. In vitro selection of molecular beacons. Nucleic Acids Res. 2003;31:5700–5713. doi: 10.1093/nar/gkg764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Marras SAE, Tyagi S, Kramer FR. Real-time assays with molecular beacons and other fluorescent nucleic acid hybridization probes. Clin. Chim. Acta. 2006;363:48–60. doi: 10.1016/j.cccn.2005.04.037. [DOI] [PubMed] [Google Scholar]
- 31.Watterson JH, Raha S, Kotoris CC, Wust CC, Gharabaghi F, Jantzi SC, Haynes NK, Gendron NH, Krull UJ, Mackenzie AE, Piunno PAE. Rapid detection of single nucleotide polymorphisms associated with spinal muscular atrophy by use of a reusable fibre-optic biosensor. Nucleic Acids Res. 2004;32:e18. doi: 10.1093/nar/gnh013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zeng J, Almadidy A, Watterson J, Krull UJ. Interfacial hybridization kinetics of oligonucleotides immobilized onto fused silica surfaces. Sensors Actuat. B. 2003;90:68–75. [Google Scholar]
- 33.Peterson AW, Heaton RJ, Georgiadis RM. The effect of surface probe density on DNA hybridization. Nucleic Acid Res. 2001;29:5163–5168. doi: 10.1093/nar/29.24.5163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Georgiadis R, Peterlinz KP, Peterson AW. Quantitative measurements and modeling of kinetics in nucleic acid monolayer films using SPR spectroscopy. J. Am. Chem. Soc. 2000;122:3166–3173. [Google Scholar]
- 35.Abdueva D, Skvortsov D, Tavare S. Non-linear analysis of GeneChip arrays. Nucleic Acids Res. 2006;34:e105. doi: 10.1093/nar/gkl435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Skvortsov D, Abdueva D, Curtis C, Schaub B, Tavare S. Explaining differences in saturation levels for Affymetrix GeneChip® arrays. Nucleic Acids Res. 2007;35:4154–4163. doi: 10.1093/nar/gkm348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vikalo H, Hassibi B, Hassibi A. Modeling and estimation for real-time microarrays. IEEE J. Select. Topics Signal Process. Special Issue Genomic Proteomic Signal Process. 2008;2:286–296. [Google Scholar]
- 38.Homola J, Yee SS, Gauglitz G. Surface plasmon resonance sensors: review. Sensors Actuat. B: Chem. 1999;54:3–15. [Google Scholar]
- 39.Smith EA, Corn RM. Surface plasmon resonance imaging as a tool to monitor biomolecular interactions in an array based format. Appl. Spectrosc. 2003;57:320A–332A. doi: 10.1366/000370203322554446. [DOI] [PubMed] [Google Scholar]
- 40.Chen SJ, Su YD, Hsiu FM, Tsou CY, Chen YK. Surface plasmon resonance phase-shift interferometry: real-time DNA microarray hybridization analysis. J. Biomed. Optics. 2005;10:034005-1–034005-6. doi: 10.1117/1.1924713. [DOI] [PubMed] [Google Scholar]
- 41.Bassil N, Maillart E, Canva M, Lévy Y, Millot M-C, Pissard S, Narwa R, Goossens M. One hundred spots parallel monitoring of DNA interactions by SPR imaging of polymer-functionalized surfaces applied to the detection of cystic fibrosis mutations. Sensors Actuat. B: Chem. 2003;94:313–323. [Google Scholar]
- 42.Fritz J, Cooper E, Gaudet S, Sorger PK, Manalis SR. Electronic detection of DNA by its intrinsic molecular charge. Proc. Natl Acad. Sci. USA. 2002;99:14142–14146. doi: 10.1073/pnas.232276699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schienle M, et al. A fully electronic DNA sensor with 128 positions and in-pixel A/D conversion. J. Solid-State Circuits. 2004;39:2438–2445. [Google Scholar]
- 44.Hassibi A, Lee TH. A programmable 0.18-µm CMOS electrochemical sensor microarray for biomedical detection. IEEE Sensors J. 2006;60:1380–1388. [Google Scholar]
- 45.Yamaguchi S, Shimomura T, Tatsuma T, Oyama N. Adsorption, immobilization, and hybridization of DNA studied by the use of quartz crystal oscillators. Anal. Chem. 1993;65:1925–1927. [Google Scholar]
- 46.Su H, Chong S, Thompson M. Kinetics of hybridization of interfacial RNA homopolymer studied by thickness-shear mode acoustic wave sensor. Biosens. Bioelectron. 1997;12:161–167. [Google Scholar]
- 47.Savran CA, Knudson SM, Ellington AD, Manalis SR. Micromechanical detection of proteins using aptamer-based receptor molecules. Anal. Chem. 2004;76:3194–3198. doi: 10.1021/ac049859f. [DOI] [PubMed] [Google Scholar]
- 48.Towery RB, Fawcett NC, Zhang P, Evans JA. Genomic DNA hybridizes with the same rate constant on the QCM biosensor as in homogeneous solution. Biosens. Bioelectron. 2001;16:1–8. doi: 10.1016/s0956-5663(00)00126-3. [DOI] [PubMed] [Google Scholar]
- 49.Stimpson DI, Hoijer JV, Hsieh WT, Jou C, Gordon J, Theriault T, Gamble R, Baldeschwieler JD. Real-time detection of DNA hybridization and melting on oligonucleotide arrays by using optical waveguides. Proc. Natl Acad. Sci. USA. 1995;92:6379–6383. doi: 10.1073/pnas.92.14.6379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bishop J, Chagovetz A, Blair S. Competitive displacement of DNA during surface hybridization. Biophys. J. 2007;92:L10–L12. doi: 10.1529/biophysj.106.097121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Belosludtsev Y, Iverson B, Lemeshko S, Eggers R, Wiese R, Lee S, Powdrill T, Hogan M. DNA microarrays based on noncovalent oligonucleotide attachment and hybridization in two dimensions. Anal. Biochem. 2001;292:250–256. doi: 10.1006/abio.2001.5088. [DOI] [PubMed] [Google Scholar]
- 52.Beissbarth T, Fellenberg K, Brors B, Arribas-Prat R, Boer JM, Hauser NC, Scheideler M, Hoheisel JD, Schuetz G, Poustka A, et al. Processing and quality control of DNA array hybridization data. Bioinformatics. 2000;16:1014–1022. doi: 10.1093/bioinformatics/16.11.1014. [DOI] [PubMed] [Google Scholar]
- 53.Huber W, von Heydebreck A, Sültmann H, Poustka A, Vingron M. Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics. 2002;18:96–104. doi: 10.1093/bioinformatics/18.suppl_1.s96. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.