Predicting response to short-acting bronchodilator medication using Bayesian networks

Abstract

Aims

Bronchodilator response tests measure the effect of β₂-agonists, the most commonly used short-acting reliever drugs for asthma. We sought to relate candidate gene SNP data with bronchodilator response and measure the predictive accuracy of a model constructed with genetic variants.

Materials & methods

Bayesian networks, multivariate models that are able to account for simultaneous associations and interactions among variables, were used to create a predictive model of bronchodilator response using candidate gene SNP data from 308 Childhood Asthma Management Program Caucasian subjects.

Results

The model found that 15 SNPs in 15 genes predict bronchodilator response with fair accuracy, as established by a fivefold cross-validation area under the receiver-operating characteristic curve of 0.75 (standard error: 0.03).

Conclusion

Bayesian networks are an attractive approach to analyze large-scale pharmacogenetic SNP data because of their ability to automatically learn complex models that can be used for the prediction and discovery of novel biological hypotheses.

Asthma is a chronic respiratory disease that affects over 20 million Americans and 300 million people worldwide [1,2]. There are two main types of asthma therapies that differ in their onset time: reliever drugs, which are fast-acting and traditionally target acute bronchoconstriction, and controller drugs, which act long-term to reduce the severity of airway inflammation and obstruction [3]. The most common short-acting reliever drugs are inhaled β₂-agonists (e.g., albuterol) that stimulate β₂-adrenergic receptors (β₂-AR) on airway smooth muscle cells to reduce bronchoconstriction [4]. Despite their routine clinical use, β₂-agonist drugs have variable efficacy among patients [5]. The effect of β₂-agonists is commonly measured by the acute bronchodilator response (BDR) test, which is a lung function test used to evaluate reversible airway obstruction and aid in the diagnosis of asthma. The physiological response to a bronchodilator is a complex trait that is heritable and partly under genetic control [6], involving intricate interactions among airway epithelial and smooth muscle cells as well as sympathetic nerves. Although a comprehensive pathophysiologic understanding of BDR has not been realized, some evidence for the genetic basis of variable BDR has been established by genetic association studies [7–15].

The most studied gene related to BDR is that encoding the β₂-AR (ADRB2). This transmembrane G protein-coupled receptor mediates airway smooth muscle relaxation when β₂-agonist drugs bind to it. Several studies have looked at SNPs and haplotypes in this gene and related them to decreased pulmonary function [7], response to β₂-agonist treatment [8], an increased frequency of asthma exacerbations [9] and BDR [10,11]. A meta-analysis of 21 studies of ADRB2 polymorphisms found that most of the positive associations identified in individual studies cannot be compared with findings in other studies due to different study designs, different phenotypes considered and potentially, selective reporting, making the number of variants with true replications very small [12]. Other candidate genes have been reported to be associated with BDR, including adenylyl cyclase type 9 (AC9) [13], corticotrophin-releasing hormone receptor 2 (CRHR2) [14] and arginase 1 (ARG1) [15]. Overall, these candidate gene studies suggest that genetic polymorphisms play a role in the success of β₂-agonist therapy and that a set of variants that accurately predicts successful treatment may be identified. Unraveling the genetic basis of BDR would be helpful to identify which patients are responsive to β₂-agonists and which biological mechanisms are responsible for variability in patient response to such drugs.

In this study, a genetic predictive model of BDR was created with Bayesian networks, multivariate models that are able to account for simultaneous associations and interactions among variables to make predictions of BDR [16–18]. In addition to Bayesian networks, other machine learning techniques have been successfully developed to create multivariate predictive models, including artificial neural networks [19], support vector machines [20] and random forests [21]. Among these techniques, Bayesian networks have the advantage of representing relationships among variables in intuitive graphical models and of calculating probabilities for individual outcomes that help to determine the reliability of predictions. Bayesian networks have been used to study a wide variety of clinical phenotypes, including the prediction of risk of death among cardiac surgery [22] and sickle cell anemia [23] patients, the diagnosis of acute appendicitis [24], the assessment of ballistic penetrating trauma [25] and the identification of asthma patients at risk for chronic obstructive pulmonary disease [26]. In addition, genetic data has been used to create Bayesian networks for the assessment of stroke risk in sickle cell anemia patients [27], and the probability of cardioembolic stroke [28]. Here, Bayesian networks are being applied to pharmacogenetics to try to identify a set of genetic variants that may be used to predict drug response.

Methods

Subject population

The Childhood Asthma Management Program (CAMP) is a clinical trial that followed 1041 asthmatic children for 4 years and nearly 80% of the original participants for an additional 12 years [29]. Stringent inclusion criteria ensured that participants had mild-to-moderate asthma, which was assessed as having asthma symptoms at least twice per week, using asthma medication daily, or using an inhaled bronchodilator twice per week for 6 or more months of the year prior to recruitment. CAMP subjects had increased airway responsiveness, as established by a 20% or greater decrease in forced expiratory volume in 1 second (FEV₁) after administration of up to 12.5 mg/dl of methacholine. At thrice yearly follow-up visits, spirometry was performed according to American Thoracic Society recommendations with a volume-displacement spirometer [29]. Spirometry testing was performed by pulmonary function technicians trained and certified specifically for the CAMP protocol and procedures, and took place at least 4 h after the use of a short-acting bronchodilator and 24 h after the use of a long-acting bronchodilator. Post-bronchodilator (two puffs albuterol by metered-dose inhaler) measurements were taken at each spirometry session. After administration of the bronchodilator, the minimal elapsed time before the post-bronchodilator test was 15 min. BDR was defined as the percentage change in FEV₁ after bronchodilator administration. Additional data collected for CAMP subjects has been described previously [29]. CAMP participants and their parents provided DNA for genetic studies. Informed consent was obtained from all CAMP participants and their parents. The studies were approved by the Institutional Review Board of Partners’ Healthcare and by all eight CAMP clinical centers and the CAMP Data Coordinating Center.

A cohort of 308 Caucasian CAMP probands who had data on multiple genetic polymorphisms gathered for various candidate genes were selected to create a predictive model of BDR. These subjects were not part of the inhaled corticosteroid treatment group of CAMP, as inhaled corticosteroid treatment can influence BDR [30], and had at least nine out of 11 BDR measures available from follow-up visits. Subjects were classified as cases (n = 113) if they had a mean BDR across all visits of 12% or greater, and controls (n = 195) if they had a mean BDR across all visits of less than 8%. These thresholds of BDR are established clinical thresholds for classifying patients as ‘responders’ (12% or greater BDR) and being within natural measurement variability (8% or smaller BDR) [31,32]. Because it is less clear how to classify subjects with BDR between 8 and 12%, we focused on subjects with extreme values to maximize any potential underlying genetic difference.

Genetic data

Candidate gene & variant selection

Candidate genes were selected for genotyping based on previously published associations with asthma or related phenotypes, including involvement in innate immunity and steroid and β-agonist pharmacogenetic pathways. SNP selection was performed such that a small set of SNPs distinguished the common haplotypes of the genes of interest [33]. Haplotypes were inferred using Bayesian methods as implemented in PHASE [34]. SNPs that distinguished the most common haplotypes were identified using the best enumeration of SNP tags (BEST) algorithm [35]. Only haplotypes that were found in the Caucasian population at a frequency of 5% or greater were considered. Rare SNPs (minor allele frequency <5%) were considered for genotyping only if the SNP led to a nonconservative amino acid change, implying greater potential for functional significance.

Genotyping

As described previously, SNPs were genotyped either with an Illumina BeadStation 500G (Illumima Inc., CA, USA) using the GoldenGate assay [15] or a Sequenom MassARRAY^® matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) mass spectrometer (Sequenom, CA, USA) [36].

Data quality control & preprocessing

Prior to quality control filters, there were 329 subjects and 3305 SNPs. Subjects missing more than 5% of SNP data (n = 19), and SNPs missing in more than 5% of subjects (n = 590) were dropped from further analysis. Hardy–Weinberg equilibrium was checked in all SNPs among control subjects using the exact procedure used by Wigginton et al. [37], with a p = 0.01 significance threshold, and those that were not in equilibrium (n = 27) were dropped from further analysis. SNPs with minor allele frequency less than 5% (n = 244) and intergenic SNPs (n = 402) were dropped from further analysis. PLINK was used to obtain a subset of the 2042 SNPs that were independent, as established by an r² threshold of 0.10 [38]. Missing alleles were imputed by randomly selecting a genotype based on the observed genotype frequency distribution among controls. The resulting data corresponded to 426 SNPs from 254 candidate genes. The number of SNPs in each of these genes, assigned according to the September 2006 NCBI data (Build 36.2), are given in Supplementary Table 1.

Statistical analysis

Clinical variable differences among cases and controls were measured in R [39], with Fisher’s Exact test for categorical variables and with Welch Two Sample t-tests for continuous variables. Logistic regression and forward stepwise logistic regression procedures in R were used to create SNP multivariate models of BDR [39]. Genetic case–control analyses measuring the association of individual SNPs to BDR were performed in PLINK using genotypic tests [38]. Power calculations were performed using the Genetic Power Calculator by Purcell et al. with high risk allele frequency of 0.17, prevalence of 0.30, D′ of 1, marker allele frequency of 0.30 and with default error rates (α= 0.05, power = 0.80) [40].

Bayesian network creation

A Bayesian network is a directed acyclic graph where nodes represent variables and edges between nodes represent probabilistic relationships between variables (i.e., a node that has an incoming arrow is dependent on the node from which the arrow originates). The topology of a Bayesian network and the associated probabilistic relationships among variables can be learned directly from data, making Bayesian networks suitable for extracting complex and unbiased relationships among variables. In this work, a Bayesian network was constructed using a ‘phenocentric’ search algorithm developed by some of the authors (Blanca E Himes, Marco F Ramoni) in which SNPs that directly modulate BDR were found [17]. This set consisted of nodes with edges originating from BDR (i.e., children of BDR) and those with edges directed to children of BDR (i.e., parents of children of BDR). The search algorithm proceeded by greedily selecting SNPs to become children of BDR based on Bayes factors comparing the likelihood that BDR was dependent versus independent on each SNP, and, for each BDR child, greedily selected its parental SNPs based on Bayes factors comparing the likelihood that the new SNP should be connected versus not connected to the BDR child. The final network returned is that with the highest likelihood of predicting BDR, given a set of SNPs, among the networks explored. More details regarding Bayesian networks can be found in [16–18].

Predictive validation

The network’s goodness of fit to the data used in its creation was assessed using fitted values corresponding to BDR prediction for each subject used in the Bayesian network construction. The predictive accuracy of the network was determined via a fivefold cross-validation in which each of five non-overlapping data subsets, obtained by randomly splitting the original dataset, is used as an independent dataset while the remaining four are used to learn the network dependencies. The probability of BDR given the genotype of an individual subject was calculated using the Clique algorithm implemented in Bayesware Discoverer [27]. The predictive performance of the network was evaluated with receiver operating characteristic (ROC) curves calculated with both fitted values and cross-validation results. Predictive accuracy was measured as the area under the ROC curve (AUROC), and significance for this accuracy was obtained by comparing the classification ability of models obtained to random classification. The standard error (SE) for AUROCs and for the difference between AUROCs of two curves were estimated using the nonparametric asymptotic method proposed by DeLong et al. [41] and described in Lasko et al. [42]. For ROC plots, convex hulls were estimated. All ROC analyses were performed in R [39]. To compare the performance of the Bayesian Network to a single-SNP approach, the predictive performance of single SNPs was compared with the performance of all SNPs in the network using corresponding fitted value and fivefold cross-validation procedures.

Results

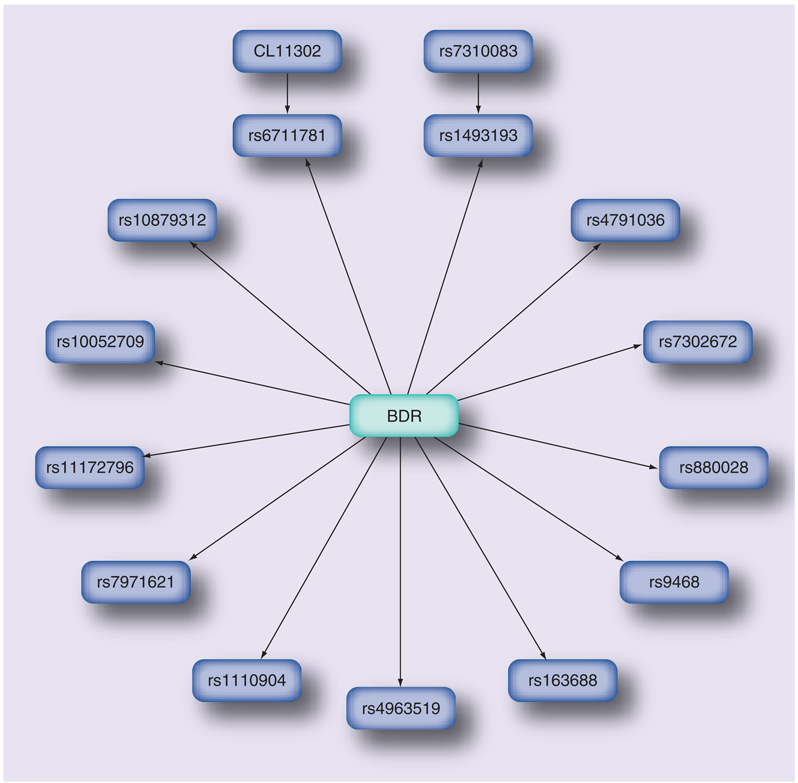
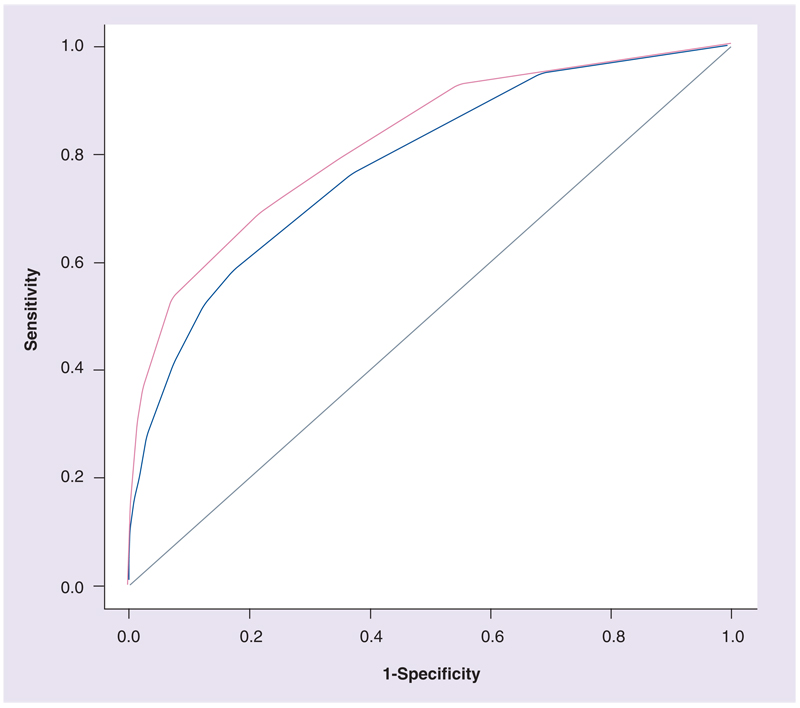
Clinical characteristics of the subjects are provided in Table 1. In a Bayesian network that was learned directly from the genetic data, it was found that 15 of 426 (3.5%) SNPs from 15 of 254 (5.9%) genes were predictive of BDR (Figure 1). The model’s goodness of fit, assessed using fitted values, had an AUROC of 0.81 (SE: 0.03) and was significantly better than a random classifier (p < 10⁻¹⁶). Fivefold cross-validation was performed to test model robustness, and the corresponding AUROC of 0.75 (SE: 0.03), which was also significantly better than a random classifier (p = 2 × 10⁻¹³), demonstrated that the network had fair predictive accuracy (Figure 2). The genotypic p-values measuring the association of individual SNPs with BDR are consistent with Bayes factors measuring the likelihood that each SNP in the network is related directly to BDR (Table 2). Corresponding allelic odds ratios demonstrate that some of the SNPs increase the risk of having higher BDR, while others confer a protective effect.

Table 1.

Baseline clinical characteristics of cases and controls.

Variable	Cases	Controls	p-value
Sex			0.63
– Female	66 (58.4)	120 (61.5)
– Male	47 (41.6)	75 (38.5)
Age (years)	9.0 (2.3)	8.8 (2.1)	0.37
Age at asthma onset (years)	3.0 (2.4)	3.2 (2.5)	0.53
Prebronchodilator FEV1 (L)	1.5 (0.5)	1.7 (0.5)	0.0003
Bronchodilator response	0.18 (0.12)	0.05 (0.05)	<10−15
Log-transformed PC20 (log mg/ml)	−0.6 (0.9)	0.7 (1.1)	<10−15
Log-transformed IgE level (log IU/l)	2.9 (0.6)	2.4 (0.7)	1.30 × 10−8
Eosinophil level	2.7 (0.5)	2.4 (0.6)	2.20 × 10−6
BMI (kg/m2)	17.2 (2.8)	18.3 (3.3)	0.002

Cases are subjects with mean BDR across CAMP trial follow-up visits greater than 12%. Controls are those with mean BDR less than 8%. For ‘sex’, number (%) are reported and p-value was computed using Fisher’s Exact test. For all other variables, Mean (standard deviation) are reported and p-values were computed using Welch Two Sample t-tests.

CAMP: Childhood Asthma Management Program; FEV₁: forced expiratory volume in 1 second; PC₂₀ Provocative concentration of methacholine causing a 20% drop in FEV1.

Figure 1. BDR Bayesian network.

BDR is predicted by 15 SNPs from 15 genes. BDR: Bronchodilator response

Figure 2. Predictive accuracy of bronchodilator response Bayesian network.

Shown are the receiver operating curves corresponding to fitted values (pink) and to fivefold cross-validation (blue). Corresponding area under the receiver operating curves are 0.81 (standard error: 0.03) and 0.75 (standard error: 0.03), respectively, demonstrating that the network has fair predictive accuracy.

Table 2.

Genetic association results for SNPs in the bronchodilator response Bayesian network.

SNP	CHR	BP	Gene	Minor allele	Observed genotypes		Allelic OR	Allelic p-value	Genotypic p-value	Bayes Factor
					Cases*	Controls*
rs880028	7	50537630	DDC	3	11/36/66	2/74/119	1.38	0.10	0.0011	18.95
rs163688	12	61378399	PPM1H	4	13/39/61	7/50/138	2.06	0.00028	0.0025	8.56
rs6711781	2	218727362	IL8RA	3	5/17/91	0/42/153	1.12	0.66	0.0060	5.90
rs7971621	12	62546881	SRGAP1	3	0/18/95	1/12/182	2.32	0.018	0.016	4.45
rs10052709	5	158693055	IL12B	3	4/16/93	1/50/144	0.77	0.32	0.011	3.94
rs4791036	17	62227597	PRKCA	2	1/32/80	0/32/163	1.98	0.0082	0.017	3.21
rs1110904	12	123549569	NCOR2	4	7/29/77	5/81/109	0.77	0.21	0.010	3.09
rs11172796	12	57565927	LRIG3	4	0/27/86	1/24/170	1.90	0.024	0.024	2.50
rs10879312	12	70361002	TMEM19	4	1/29/83	0/29/166	1.98	0.011	0.025	2.32
rs9468	17	41457408	MAPT	2	6/54/53	13/60/122	1.46	0.047	0.012	1.93
rs7302672	12	62512629	LOC341315	3	7/25/81	5/70/120	0.81	0.32	0.019	1.65
rs4963519	12	6801913	GPR162	4	4/29/80	0/45/150	1.50	0.089	0.024	1.46
rs1493193	12	50192616	LOC283400	2	0/16/97	0/15/180	1.91	0.077	NA	1.07
rs7310083	12	68347053	VMD2L3	4	1/12/100	0/27/168	0.89	0.73	0.31	0.23
CL11302‡	17	43186946	TBX21	4	3/16/94	1/27/167	1.34	0.32	0.27	0.20

The Bayes Factor column contains Bayes factors that indicate how many times more likely it is that bronchodilator response is dependent on, rather than independent of, a SNP. It is the most consistent with the genotypic model p-values because it is also based on the genotype distribution of each SNP.

^*Shows homozygous minor/heterozygous/homozygous major allele genotype counts.

^‡No NCBI ID available for this marker.

BP: Base pair; CHR: Chromosome; OR: Odds ratio.

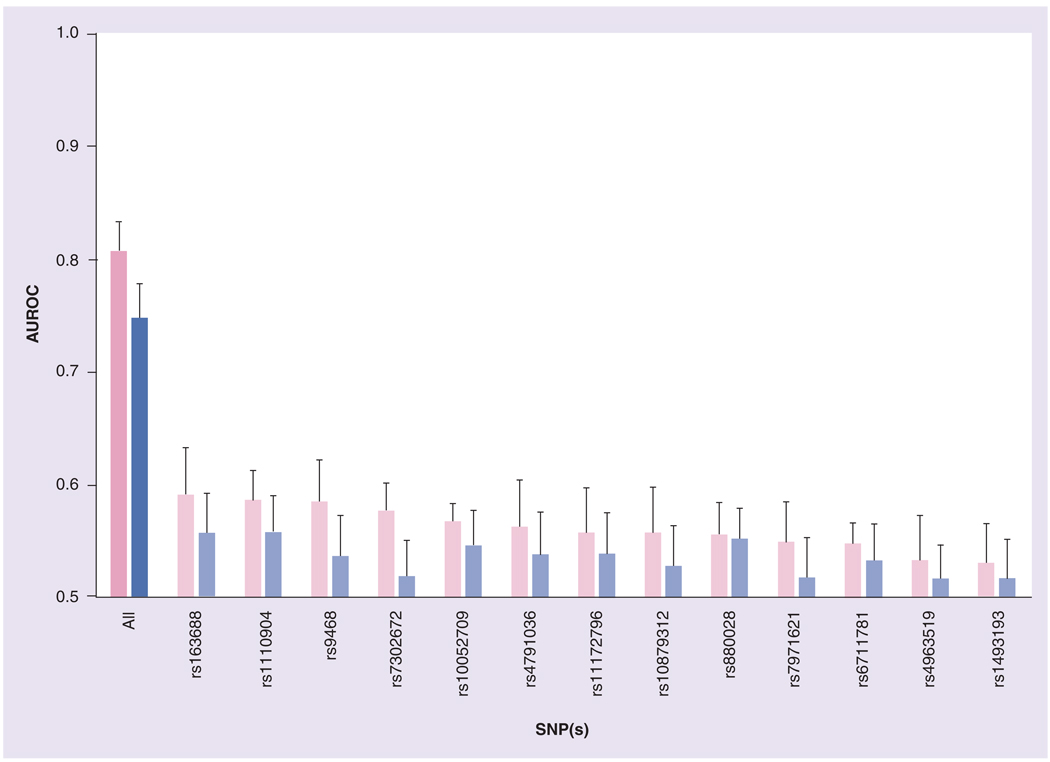
Comparison of the performance of single SNPs to all SNPs in the Bayesian network found that the predictive accuracy, according to fitted value AUROCs having an area significantly greater than 0.5 (p < 0.05), of 13 SNPs individually is slightly better than a random classifier (Table 3 & Figure 3). However, according to fivefold cross-validation AUROCs, only three SNPs (rs880028, rs1110904 and rs163688) performed better than a random classifier. By either fitted value or cross-validation results comparison, the model performed considerably worse individually at predicting BDR than did using all SNP information (p < 10⁻¹⁴).

Table 3.

Individual predictive ability of SNPs in the bronchodilator response Bayesian network.

SNP(s)	Fitted values		Fivefold cross validation
	AUROC (standard error)	p-value	AUROC (standard error)	p-value
All	0.81 (0.03)	<10−16	0.75 (0.03)	2 × 10−13
rs163688	0.59 (0.04)	0.0006	0.56 (0.04)	0.05
rs9468	0.59 (0.04)	0.002	0.54 (0.04)	0.13
rs1110904	0.59 (0.03)	0.001	0.56 (0.03)	0.04
rs7302672	0.58 (0.02)	0.003	0.52 (0.03)	0.28
rs10052709	0.57 (0.02)	0.003	0.55 (0.03)	0.08
rs11172796	0.56 (0.04)	0.003	0.54 (0.04)	0.12
rs4791036	0.56 (0.04)	0.004	0.54 (0.04)	0.12
rs10879312	0.56 (0.04)	0.006	0.53 (0.04)	0.20
rs880028	0.56 (0.03)	0.03	0.55 (0.03)	0.02
rs7971621	0.55 (0.04)	0.002	0.52 (0.04)	0.29
rs6711781	0.55 (0.02)	0.02	0.53 (0.03)	0.16
rs4963519	0.53 (0.04)	0.09	0.52 (0.03)	0.26
rs1493193	0.53 (0.03)	0.03	0.52 (0.04)	0.30

p-values indicate whether AUROC are significantly higher than 0.05, the AUROC of a random predictor.

AUROC: Area under the receiving operating characteristic curve.

Figure 3. Predictive accuracy of single SNPs in the bronchodilator response Bayesian network.

The fitted value and fivefold cross-validation AUROCs corresponding to single SNPs show that the full bronchodilator response Bayesian network (fitted values: dark pink; fivefold cross-validation: dark blue) has far better predictive performance than single SNPs (fitted values: light pink; fivefold cross-validation: light blue), as indicated by p-values less than 10⁻¹⁴ comparing any of the single-SNP AUROCs to those using all SNPs. AUROC: Area under the receiver operating characteristic curve.

A forward stepwise logistic regression performed with the same SNPs that were used to learn the Bayesian network found that 47 SNPs were predictive of BDR, though none had a significant p-value for its individual effect in the model (Supplementary Table 2). The logistic regression model had a fitted value AUROC of 1.0 (SE: 0.0; p < 1 × 10⁻¹⁶) and a fivefold cross-validation AUROC of 0.55 (SE: 0.04; p = 0.04). A logistic regression model created using the SNPs that were in the BDR Bayesian network had an AUROC of 0.73 (SE: 0.03; p = 3 × 10⁻¹²) for fitted values and 0.66 (SE: 0.03; p = 1 × 10⁻⁶) for fivefold cross-validation. Six of the 15 SNPs in this smaller regression model had significant individual effects (Table 4).

Table 4.

Bronchodilator response logistic regression model using SNPs in the bronchodilator response Bayesian network.

Variable	p-value
(Intercept)	0.41
rs6711781	0.36
rs10052709	0.28
rs880028	0.51
rs4963519	0.18
rs1493193	0.12
rs11172796	0.030
rs163688	0.0031
rs7302672	0.57
rs7971621	0.019
rs7310083	0.42
rs10879312	0.024
rs1110904	0.071
rs9468	0.014
CL11302	0.94
rs4791036	0.022

Discussion

An important aspect of the growth of pharmacogenetics over the past 15 years has been the collection of candidate gene data from participants of drug trials to find genetic variants correlated with drug response [43]. Consistent with the approach taken in most genetic studies, the analyses in pharmacogenetics have been mostly limited to consideration of individual gene variants in single genes. When the effect of multiple genes and variants is taken into account, it is usually done so using traditional additive models (e.g., logistic regression). The consensus reached from these small-scale genetic association studies, and even from more recent genome-wide studies, is that SNPs individually contribute very modestly towards phenotypic differences and a very large number of variants are required to explain the genetic underpinnings of each complex trait [44,45]. Traditional approaches that analyze individual variants one at a time do not address the complex interactions that are known to underlie complex traits. If such interactions were taken into account by attempting to directly model epistasis, it is likely that a larger portion of phenotypic variance could be explained with fewer SNPs than the number estimated using additive models [46,47]. Therefore, pharmacogenetic studies will benefit from analytical methods that consider complex genetic interactions because such approaches may more accurately predict drug responses and characterize their complex biological underpinnings.

Bayesian networks are a promising approach for the analysis of complex traits because of their ability to model complex multivariate dependencies and make predictions [16–18]. Unlike traditional regression models, they are not limited to representing the dependencies of a single outcome variable on predictor variables. Instead, Bayesian networks go beyond single or pairwise gene interactions with a phenotype to account for complex multivariate interactions. In addition, they can be used to make predictions of a phenotype of interest for individual subjects that allow for ascertainment of model validity. Relationships found in a Bayesian network suggest true relationships among variables and may even reflect causal relationships. However, proof of any causal relationship among variables requires experimental verification. In this work, we have demonstrated that Bayesian networks can automatically integrate candidate gene data to make predictions of BDR, a pharmacogenetic phenotype. The resulting network provides a model that can also be used for both clinical prediction and to investigate potential biological relationships among the genes that compose it.

An important test of model goodness is its ability to make accurate predictions. Initially, a model is tested by using fitted values to ensure that it is adequate for the data used to construct it. The BDR Bayesian network had an AUROC of 0.81 (SE: 0.03) on the fitted values, demonstrating that it is good at predicting BDR in the subjects who were used to learn the model. Ideally, the next step in testing the generalizability of the model is to use it for prediction in an independent population to ensure that the predictive accuracy in fitted values is generalizable. Because we did not have access to an independent population with similar clinical characteristics as our training population, we used cross-validation, a standard procedure used to estimate the predictive accuracy of a model in the absence of an independent population. The fivefold cross-validation AUROC, 0.75 (SE: 0.03), demonstrated that some overfitting was present in the fitted values because the AUROC dropped significantly by 0.05 (p < 10⁻¹⁶). However, as shown in Table 3 & Figure 3, when the information of multiple SNPs is used to predict BDR, the accuracy of prediction is significantly higher than when using the information of single SNPs. The fairly good predictive accuracy of the network and the better predictive performance when using all, rather than single, SNP information, suggest that some of the relationships among SNPs and BDR are not due to overfitting and potentially, reflect true biological relationships.

Some of the genes corresponding to SNPs in the BDR Bayesian network belong to biological pathways expected to be involved in BDR: DDC and PRKCA are part of the β-agonist pathway, and IL12B and IL8RA are involved in immune responses. Some genes that are intuitively expected to be in the network are absent. Most notably, polymorphisms of ADRB2, the most studied gene related to BDR, are not part of the network despite this gene having three SNPs in our candidate gene set. Because ADRB2 variants have been associated with BDR [10] and related phenotypes (decreased pulmonary function, response to β₂-agonist treatment [7,8], increased frequency of asthma exacerbations [9]), it might be expected that ADRB2 SNPs would be part of the network. Even in CAMP families, some ADRB2 SNPs were previously found to be associated with spirometric measures of lung function [11]. In the current study, traditional genetic association results for the three ADRB2 SNPs that were part of the set of SNPs used to learn the BDR Bayesian network failed to show any association to BDR (Supplementary Table 3). These results are in agreement with some of the inconsistent ADRB2 association results observed when considering different phenotypes and populations as mentioned in the Introduction.

Traditional association statistics of the SNPs in the BDR Bayesian network reveals that the SNPs that are children of BDR have significant genotypic p-values, ranging from 0.0011 to 0.025 (Table 2). By contrast, some of the SNPs have significant allelic p-values, while others do not. The Bayes Factor column in this table contains the Bayes factors that tested whether each SNP should be a child of BDR. Those SNPs for which the Bayes factor was greater than 1 were selected as children of BDR. A significant p-value is, therefore, analogous to a Bayes factor greater than 1. The genotypic model p-value results are more consistent with those of the Bayes factors than those of the allelic p-values because both genotypic p-values and the Bayes factors are based on a SNPs genotype distributions. The two SNPs (rs7310083 and CL11302) from parents of BDR children were selected to be part of the Bayesian network based on Bayes factors indicating that it was more likely that both they and BDR should be parents of SNPs rs6711781 and rs1493193, rather than not. This type of relationship cannot be captured using individual allelic or genotypic p-values, but is readily found by the Bayesian network search algorithm.

The results from a stepwise logistic regression procedure performed on the 426 SNPs that were available to create the Bayesian network demonstrate that the Bayesian network learning algorithm was much better at selecting predictors of BDR and not as prone to overfitting. Although the fitted value AUROC of the stepwise logistic regression, 1.0 (SE: 0), suggested that the logistic regression model was perfect at predicting BDR, a fivefold cross-validation procedure had an AUROC of 0.55 (SE: 0.04), showing that the regression procedure was very poor at creating a generalizable model of BDR. If instead of using a stepwise procedure to select the predictors from the list of all SNPs, a logistic regression model is built with the same SNPs that were in the BDR Bayesian network, the results improve. The fitted values AUROC drops to 0.73 (SE: 0.03), but there is less overfitting as indicated by a cross-validation AUROC of 0.66 (SE: 0.03). However, the BDR Bayesian network, which had cross-validation AUROC of 0.75 (SE: 0.03), is much better at predicting BDR than the logistic regression model. Therefore, the logistic regression model is adequate to predict BDR when the appropriate SNPs are used in the model, but it is not an appropriate procedure to determine the best predictive SNPs from a long list of candidates.

As the cross-validation AUROC (0.75, SE: 0.03) of our model demonstrates, there is room for improvement in predictive accuracy. Some notable limitations of this work that may have reduced the predictive accuracy are: BDR phenotype definition, selection of candidate genes, and low power to detect genetic effects. The definition we chose for BDR was percentage change in FEV₁ after bronchodilator administration, which is the phenotype most commonly used in a clinical setting. Because BDR is a continuous trait, with no clear boundary separating responders from nonresponders, arbitrary thresholds must be chosen to distinguish these groups. We used the average of multiple measures of BDR and selected subjects with values at two extremes, according to clinical standards, to define cases and controls. In so doing, we hoped to maximize any genetic difference between the two phenotype groups with a stable BDR. In addition to BDR being a continuous trait that is influenced by many environmental factors, it is a trait that is difficult to isolate from other factors that indicate poor lung function, such as baseline FEV₁. As shown in Table 1, baseline measures of prebronchodilator FEV₁, log-transformed provocative concentration of methacholine causing a 20% drop in FEV₁ (PC₂₀), log-transformed IgE level, eosinophil level and BMI are different in cases and controls. Most of these factors have trends that reflect more severe disease in cases, and therefore, it is likely that the BDR phenotype that we defined does not exclusively reflect bronchodilator response. These trends are also consistent with previous work in CAMP subjects that has demonstrated that bronchodilator response, bronchoconstriction, and baseline lung function effects are difficult to isolate [30,48]. Attempts to adjust for these known confounders of BDR may diminish the phenotype’s magnitude erroneously because all may be partly due to some overlapping genetic risk factors. Therefore, we chose to use BDR measures only to define our BDR phenotype. In future studies, it may be informative to look at genetic models that predict other lung function phenotypes to measure the extent to which the SNPs and genes composing them overlap.

The second limitation influencing the model’s predictive accuracy is that the genetic data used to learn the Bayesian network was a set of SNPs gathered from candidate gene studies. The selection of such SNPs is limited in number and biased as it was based on previous literature and not on the whole genome. It is therefore highly likely that important genes contributing to BDR were not included in the search. Inclusion of such genes may have resulted in higher predictive accuracy and lead to the discovery of more novel biological pathways. In future studies, it will be interesting to find out whether an unbiased genome-wide search leads to finding the same SNPs in the BDR Bayesian network presented here. Lastly, the number of subjects used to create the network (113 cases, 195 controls) is not of adequate size to measure small genetic effects, as exemplified by power calculations using the mean allelic frequencies and effect sizes observed for the children SNPs in the BDR Bayesian network yielding estimates of 0.32 for a genotypic model and 0.40 for an allelic model. Although these power estimates do not directly apply to the Bayesian network, having adequate sample sizes and large genetic effects increases the ability of any search algorithm to find true relationships. Low power to detect genetic effects is a limitation of many previous pharmacogenetics studies because the number of subjects in clinical trials is smaller than necessary for highly powered association studies. This limitation may be reduced with newly available subject populations that are being recruited through electronic medical records [26]. Due to the limitations of our study, we would not recommend that the current BDR Bayesian network be used clinically at this time. Eventually, if a successful predictive model of BDR is found, it could be used clinically as a genetic test to help determine which patients will have a poor response to bronchodilator medications. In addition, a successful predictive model of BDR would likely contain polymorphisms that suggest novel hypotheses regarding biological variants involved in asthma pathophysiology.

Conclusion

A genetic predictive model of BDR was made using Bayesian networks. This model found that 15 of 426 (3.5%) SNPs from 15 of 254 (5.9%) genes were predictive of BDR. The predictive accuracy of the model is fair, as established with a fivefold cross-validation having an AUROC of 0.75 (SE: 0.03). The multivariate model was compared with a single-gene approach, and the superior predictive accuracy of the multivariate approach was demonstrated. Bayesian networks are an attractive approach to analyze pharmacogenetic data because of their ability to automatically learn complex models that can be used for prediction and the exploration of biological hypotheses.

Executive summary

• Bronchodilator response (BDR) tests measure the effect of β₂-agonists, the most common reliever drugs used in asthma therapy.

• Few attempts have been made to integrate genetic data in the analysis of complex traits, despite the knowledge that these traits are due to the complex interplay of many variables.

Materials & methods

• Bayesian networks are multivariate models that are able to account for simultaneous associations and interactions among variables. They can be created automatically from data and can be used for prediction.

• Using candidate gene study data from the Childhood Asthma Management Program (CAMP), a Bayesian network was created.

Results

• A BDR network in which 15 SNPs in 15 genes predict BDR was created. It had fair predictive accuracy, as established by a fivefold cross-validation area under the receiver operating characteristic curve of 0.75 (standard error: 0.03).

• Individual SNPs had prediction area under the receiver operating characteristic curves less than 0.60.

• A logistic regression model of the 15 SNPs in the BDR had a fivefold cross-validation area under the receiver operating characteristic curve of 0.66 (standard error: 0.03).

Discussion

• The BDR Bayesian network was better at predicting BDR than single SNPs or logistic regression models.

• Limitations of this work include those related to BDR phenotype definition, selection of candidate genes and low power to detect genetic effects.

Conclusion

• Bayesian networks are an attractive approach to analyze pharmacogenetic data because of their ability to automatically learn complex models that can be used for prediction and the discovery of biological hypotheses.