Abstract
Conformational changes of filamin A under stress have been postulated to play crucial roles in signaling pathways of cell responses. Direct observation of conformational changes under stress is beyond the resolution of current experimental techniques. On the other hand, computational studies are mainly limited to either traditional molecular dynamics simulations of short durations and high forces or simulations of simplified models. Here we perform all-atom discrete molecular dynamics (DMD) simulations to study thermally and force-induced unfolding of filamin A. The high conformational sampling efficiency of DMD allows us to observe force-induced unfolding of filamin A Ig domains under physiological forces. The computationally identified critical unfolding forces agree well with experimental measurements. Despite a large heterogeneity in the population of force-induced intermediate states, we find a common initial unfolding intermediate in all the Ig domains of filamin, where the N-terminal strand unfolds. We also study the thermal unfolding of several filamin Ig-like domains. We find that thermally induced unfolding features an early-stage intermediate state similar to the one observed in force-induced unfolding and characterized by N-terminal strand being unfurled. We propose that the N-terminal strand may act as a conformational switch that unfolds under physiological forces leading to exposure of cryptic binding sites, removal of native binding sites, and modulating the quaternary structure of domains.
Introduction
Filamin family members (A, B, and C) are composed of an actin-binding domain and subsequent 24 immunoglobulin(Ig)-like domains. Filamins have been shown to play an important role in maintaining the rheological properties of the actin cytoskeleton.1 Filamin molecules can cross-link actin fibrils into actin-networks. As mechanical proteins, filamins localize to the cortex, stress fibers, and muscle Z-line. Besides their critical roles as mechanical proteins, filamins are also involved in cellular response to stress. Filamin A has been postulated to respond to cues from the stress environment of cells, as reported from its involvement in cell-fate determination,2 activation of platelets,3-5 and mechanoprotection.6,7 How could filamin A transduce the stress state of cells? Some studies report that filamin A turnover and ability to bind actin can be regulated through its interactions with calmodulin and calpain, proteins that are activated by changes in cellular calcium level.2,8,9 Calcium levels in turn fluctuate with cellular stress levels.10 Other studies suggest that filamin A’s role as a scaffold protein, binding over 70 proteins,11 is modulated by its quaternary structure, which in turn could be regulated by either physical or thermal stress.12,13 Based on these studies, we hypothesize that stress-induced conformational changes of filamin A play a direct role in signaling either by disrupting existing interactions or by introducing new interactions. Therefore, it is important to investigate possible stress-induced conformational changes that could play a functional role.
Atomic force microscope (AFM) has been commonly used to study a protein’s response to mechanical stress at the single molecule level. Several AFM studies on other proteins with Ig-like fold indicate that Ig domains can have force-induced metastable conformations. D. discoideum filamin (ddFLN), a six Ig-like domain homolog of mammalian filamin, has been reported to have a metastable conformation in domain 4 (ddFLN4), which lacks β strands A and/or B.14-16 The 27th Ig-like domain of titin (TNI27) has been reported to have a force-induced17-19 stable intermediate that lacks β strand A.20 Fibronectin has been reported to have a forced-induced21 conformation in its fribronectin III domain 10 (FN-III10) that lacks β strand A and B.22 Although AFM by itself has been used to detect the presence of intermediate state in these domains, complementary studies have been used to determine the atomistic conformation of the intermediate states. Mutational studies, such as amino acid inserts and φ-value analysis, have been used to obtain structural insights into conformational changes in proteins under stress. These studies have been successful at proposing hypotheses about the conformation of intermediates of ddFLN414 as well as identifying critical residues for the mechanical stability of N-terminal β strands of TNI27.23 However, a limitation of these studies is that mutations can alter the conformational changes under stress. Thus, while existing biochemical and biophysical techniques are effective at generating hypotheses about stress-induced metastable states, they are lack detailed direct structural information about these conformations.
Being able to provide a direct atomistic picture of conformational changes under forces, computational modeling has been used in the study protein conformational changes under mechanical stress. However, the time-scales accessible by traditional molecular dynamic simulations are severely limited (∼10-100 nanoseconds) and are not sufficient to study large-scale conformational dynamics of proteins (sub-microsecond to millisecond time-scales). Two major strategies have been employed to overcome this limitation. The first approach is to use simplified proteins models, in which residues are represented as one or several pseudo-atoms having empirical structural-based interactions.24,25 For example, West et al. used a simplified model to study the thermal and forced unfolding of TNI27, and found distinct unfolding pathways.26 The second approach often relies on simulating the system under extreme conditions, such as high temperatures or high forces, to promote rapid protein unfolding events.27 For example, Fowler et al., used traditional MD and a pulling protocol similar to AFM with pulling forces approximately two times the experimentally observed critical unfolding force (>=300 pN) for TNI27.19 Steered molecular dynamics was used by Lu et al. to understand the unfolding pathways of TNI27 with very high forces (∼1,000 pN).28 Many other studies have been recently reviewed by Sotomayor et al.29. One major limitation of these approaches is that unfolding pathways could be altered under extreme conditions.
To avoid the artifacts arising out of using unphysical simulation parameters and coarse-grained models in the study of force-induced filamin A conformational changes, we employ all-atom discrete molecular dynamics (DMD) simulations.30-35 DMD is similar to traditional MD in that it calculates the evolution of the coordinates of the system under study as a function of time and follows the same laws of conservation of energy and momentum as MD, but it affords much more rapid and diverse sampling. DMD solves the ballistic equations of motion rather than Newtonian ones, which reduces the simulation algorithm to an iterative search of the immediate collision events in the system, making it several orders of magnitude faster compared to MD. The reduction in simulation time achieved by DMD gives us the ability to study conformational dynamics over physiologically relevant time-scales. DMD has been shown to have a higher sampling efficiency than traditional molecular dynamics and has been used to study protein folding thermodynamics and protein aggregation.36 All-atom DMD features a transferable force field and has been successfully used to fold several small proteins ab initio (<60 amino acids)35 and to investigate the conformational dynamics of superoxide dismutase.37
To study force-induced unfolding of filamin A using DMD we need an atomistic structure of filamin A. However, structures of only five of the 24 Ig-like domains of filamin A have been experimentally determined.12,38-40 Hence, in this study we use the all-atom structure of filamin A derived from comparative modeling in an earlier study (Kesner, et al. submitted). The average sequence similarity of all the Ig-like domains is > 40%. Therefore, we expect the homology-derived structures to be close to their native structures.41 In that study we observed that there are two classes of Ig-like domains in filamin: six-stranded (lacking the N-terminal strand) and canonical seven-stranded. Domains 16, 18, and 20 are six stranded. In a recent crystal structure of domains 19-21 it was observed that the putative first strand of domain 20 interacts with domain 21 instead of forming a β sheet with the second strand. This interaction has been proposed to inhibit domain 21’s interaction with other binding partners.12 Based on this quaternary structure it is possible that β strand A of an Ig-like domain could form complementary strands with adjacent Ig-like domains. Hence, we hypothesize that unraveling of the N-terminal strand of Ig-like domains could initiate inter-domain interactions through that strand. We study the six-stranded Ig-like domains from two perspectives. First, we compare domains 16 and 18 to that of domain 20 (whose structure has been determined)12 to study if the six-stranded domains have similar physical characteristics. Second, we compare these domains to the seven-stranded domains to understand the role of the missing strand.
For each of the 24 Ig-like domains that make up filamin, we perform constant-force simulations by applying a set of physiologically relevant ranges of forces (0-315 pN).42 Based on these systematic DMD simulations, we estimate the critical force of unfolding of each individual domain and characterize the conformational changes under mechanical stress. We find that the critical forces are heterogeneous among the 24 domains due to the sequence differences. We also find that there is no significant difference between the critical unfolding forces of domains with and without N-terminal strands. We find that under small forces up to ∼35 pN, which correspond to the physiological forces43, most Ig-like domains remain in the native states. As the force increases up to the intermediate force levels of ∼70 pN, large conformational changes takes place. Interestingly, Ig-like domains feature a common initial conformational change, where the first β strand unfurls. Domains that lack their N-terminal β strands appear similar to one another, maintaining their native-like conformation under low forces. At intermediate forces, they unfold to a heterogeneous population of intermediate states similar to seven-stranded domains.
Additionally, the effect of temperature versus mechanical stress on unfolding pathways has been the subject of much debate.44 The general hypothesis is that thermally induced and force-induced unfolding pathways are independent from one another since the thermal fluctuations are exerted on the protein globally, while the effect of mechanical forces is localized and non-homogeneous. To examine whether the thermally and force-induced unfolding of filamin Ig-like domains are different from each other, we also perform thermal unfolding of three Ig-like domains, 14, 21, and 24. Interestingly, we find that thermally induced unfolding shares the same initial unfolding intermediate state as forced unfolding, where the first strand unfolds. This observation suggests that filamin evolved to feature the intermediate state of unfolded N-terminal strand(s). Given the observation that the putative first strand of domain 20 interacts with domain 21 instead of forming a β sheet with the second strand, we propose that N-terminal strand may act as a conformational switch that unfolds under stressed physiological conditions leading to exposure of cryptic binding sites, removing of native binding sites, and modulating the quaternary structure of domains.
Materials and Methods
All-atom DMD
A detailed description of the DMD algorithm can be found elsewhere.35,45 Briefly, interatomic interactions in DMD are governed by square-well potential functions. Neighboring interactions along the sequence (such as bonds, bond angles, and dihedrals) are modeled by infinitely deep square-well potentials to model the geometry of residues and peptide bonds. During a simulation, an atom’s velocity remains constant until a potential step is encountered, during which it changes instantaneously according to the laws of conservation of energy, momentum and angular momentum. Simulations proceed as a series of such collisions, with a rapid sorting algorithm employed at each step to determine the next collision.
The all-atom DMD method employs a united atom protein model, where heavy atoms and polar hydrogen atoms are explicitly modeled.35 We include van der Waals, solvation, and environment-dependent hydrogen bond interactions. For solvation, we adopt the Lazaridis-Karplus solvation model46,47 and use the fully-solvated conformation as the reference state. Due to the strong screening effect of solvent, distant charges have weak polar interactions. For salt-bridges, we expect the hydrogen bonds to partially account for their polar interactions.
Protein Models
As described in the introduction filamin A is composed of an ABD followed by 24 Ig-like domains. Ig-like domains are seven-stranded β sandwich folds (Fig. 1A). Loops with conserved residues GPG and SPF bisect the first and last strands. We refer the resulting subdomains as A, A’, G’, G. Subdomain A forms a β sheet with B (A-B region) and in some domains A’ and G (A-G’ region) form a β sheet. We use the homology models of human filamin A Ig-like domains (Fig. 1A) that were derived from an earlier work (Kesner et al., submitted). Briefly, closest matching homology templates were derived from a structural alignment of homologous filamin domains in the protein data bank (PDB).48 Insight II (Accelrys, CA) was then used to perform homology modeling of each filamin A Ig-like domain. Domain 16, 18 and 20 have only six complete strands since the best-match template lacks all (16), or substrand A (18, 20), of β strand A.
Figure 1. Critical unfolding parameters of filamin Ig-like domains.
(A) Seven-stranded Ig-like domain with subdomain termini and β strands A-G labeled. (B) Graph depicting the free energy landscape along the extension length as the reaction coordinate at different levels of constant-force pulling. Fc is the critical unfolding force and xu is the distance to the center of the unfolding energy barrier. (C) Unfolding behavior of a domain pulled apart with a constant force (122.5 pN) is described by plotting the extension length as a function of time. Replicates with differing initial velocities vary in their unfolding behavior. (D) A linear natural log plot of the pulling force versus mean first passage time. Fc is the critical unfolding force. A linear fit of forces is shown for the barrier (left of Fc) and barrierless (right of Fc) regimes. (E) Critical unfolding forces observed for each domain. The error bars are determined as described in Methods. (F) Histogram of mean Fc.
Each model is validated using the sequence-structure compatibility score from the Verify-3d module of InsightII (Accelrys Inc.). This analysis measures the compatibility of modeled residues with their strucutral environment.49 Quality scores of greater than 0.1 indicates valid strucutral models49 and typical biochemical structures have a score of 1. The mean Verify-3d score obtained for Ig-like domain models was 0.89 with standard deviation 0.30. IgFLNa18 is the only model to produce a low score (0.11). However, IgFLNa18’s homology model has high sequence identity (64% id), and a low RMSD (0.23 Å) when compared to its IgFLNb18 (PDB ID 2dmc) template, suggesting that the IgFLNa18 model was correctly built based on the experimental template. Furthermore, the experimental structure of the template itself has a low quality score of 0.56. Overall, Ig-like domains have high quality scores indicative of their high accuracy.
Following homology modeling, each structure is relaxed using 1000 steps of steepest descent energy minimization as in the AMBER50 9.0. In addition, each model is minimized using the Medusa modeling suite.51-53
Constant-force Unfolding
For each domain, we start the constant-force simulations from the homology-derived native state. The dimension of a cubic simulation box is 500 Å and the periodic boundary condition is used. We use an Anderson thermostat54 to maintain constant temperature at the room temperature (300 Kelvin). Constant-force pulling is achieved by applying a discretized step-function with a constant energy jump, dE, at the distance step of dR (1 Å) between the N- and C-termini. The pulling force equals to dE/dR. For example, dE of 0.5 kcal/mol is equivalent to approximately 35 pN. The applied forces range from zero to 315 pN. From zero to 210 pN, we sample the force values with an interval of 17.5 pN. From 245 to 315 pN, the interval is 35 pN. For each force, we perform 10-20 realizations of pulling simulations, each of which start with randomized velocities. We perform 10 simulations for pulling simulations at low forces (70 pN or less), since there is a low probability of unfolding during the simulation time. For higher forces, we perform 20 realizations.
Derivation of Critical Unfolding Forces
Under external force F, the unfolding time under pulling forces can be approximated as T = Ae(δG‡-Fxu)*β. Here, A is the Arrhenius prefactor, ΔG‡ is the zero force activation energy barrier, xu is the distance to the center of the activation energy barrier, and β is the inverse of kbT, where kb is the Boltzmann constant and T is the temperature. We use the mean first passage time (MFPT) of unfolding as the approximation of the unfolding time. We use 200 Å as the cutoff distance to assess whether a protein is unfolded. This cutoff was determined base upon observations that after an extension of 200 Å most domains lack metastable states, although the minimum full extent for an unfolded domain is 240 Å (Supplementary Fig. 1). If the protein has not unfolded within the maximum simulation time (one million time units), we use this time as the first passage time.
We plot the ln(MFPT) versus force and obtain linear fits in the barrier and barrierless unfolding regions. The intersection of the two linear fits determines the critical force of unfolding (Fc). We use the error bar of the linear regression to estimate the error bar of the estimated critical forces with a simple Monte Carlo method. In each Monte Carlo step, linear lines constructed based on the Gaussian distribution of error bars (derived form the linear regression) is used to determine a new intersection. The mean and standard deviation of the critical unfolding force is derived from the set of intersections.
Forced Unfolding Pathways Analysis
For each domain and each force, we combine trajectories of all realizations and compute the histogram of extension lengths. Gaussian curve fitting of the histogram is used to identify metastable states. Only the states that are present for more than 1% of the total simulation time are considered stable. To determine the representative structure of each metastable state, we first extract all conformations having extension length within the mean ± 2 SD of the corresponding Gaussian fit. Then, we compute a contact frequency map for each extracted ensemble. Finally, we select the representative structure as the one that has the least contact distance from the average contact frequency of the ensemble.
We characterize the unfolding pathway using a directed graph. The nodes of the graph are formed by the states identified from the extension length histogram and the edges are the transitions between the different states. Occupancy of each node corresponds to the number of conformations associated with that state normalized by the total number of conformations. Edges have an associated transition probability determined by counting the number of transitions between a node and its neighbor and then dividing by total number of transitions to all its neighbors in the same direction. The graph representation of the unfolding pathway is visualized using Cytoscape.55
Thermal Unfolding
Equilibrium simulations are performed at a wide range of temperatures: 300, 330, 360, 390, and 420 Kelvin. We use the percentage of native contacts, Q, to approximate the reaction coordinate. We define a contact when the distance between two Cβ atoms (Cα for Glycine) is less than 8.5 Å. We use a similar approach to identify the representative structure of each state, where the Q-value rather than the extension distance is used as the approximation of the reaction coordinate. To determine the localization of loss of contacts during thermal unfolding simulations we calculate a subdomain average Q-value. Subdomains are delineated based upon a strand-by-strand analysis of each Ig-like domain homology model. Average Q-values for an ensemble are obtained by dividing the marginal sum of native contacts from the residue-by-residue contact frequency map by the marginal native contacts from the reference structure contact map.
Results
We model constant-force unfolding by applying a pulling force between the Cα atoms of the N- and C-terminal residues (Materials and Methods). The force is modeled by assigning a corresponding potential between the corresponding atom pair. For each force value, we perform 10-20 independent simulations with randomized initial velocities. Each simulation lasts a million DMD time units.
Computationally identified critical unfolding forces of filamin Ig-like domains agree with AFM experiments
Most single domain proteins, such as the Ig-like domains in filamin, feature a two-state folding/unfolding dynamics without external forces. At room temperatures, a protein stays folded and its native state corresponds to the lowest energy state in the free energy landscape (Fig. 1B). Unfolding requires overcoming a free energy barrier (the folding/unfolding transition state) separating the folded and unfolded states, ΔG‡. The unfolding time is proportional to the exponential of ΔG‡/kBT. As the force (F) applied to the N- and C-termini of a protein increases, the unfolded states with large end-to-end extensions are favored (Fig. 1C), and the corresponding free energy barrier decreases (ΔG‡-Fxu (Fig. 1B)). Here, xu denotes the difference of end-to-end distances between the transition and native states. Assuming that xu does not change for different external forces, the natural logarithm of the unfolding time is linearly dependent on the external force. As the force reaches the critical value (Fc), the barrier will disappear and activation driven unfolding dynamics is reduced to barrierless unfolding. As a result, the dependence of the unfolding time with respect to the external force changes near the Fc (Fig. 1D). We estimate the critical unfolding forces based on the change of the scaling of the unfolding time with respect to external forces (see Methods). For each applied force, we compute the mean first passage time (MFPT) over 20 trajectories to estimate the unfolding time. We use a cutoff distance of 200 Å to assess whether a protein is unfolded. We estimate the critical force as the crossover point in the plot of ln(MFPT) as a function of external forces (Fig. 1D). We compute the critical unfolding forces for each domain (Fig. 1E). The mean critical unfolding force over all domains is 179□19 pN. We find that the distribution of Fc values features a peak around 155-180 pN with a long tail from 185-205 pN (Fig. 1F). Therefore, most of the Ig-like domains of filamin A can withstand the stretching forces up to 150 pN with a few domains being able to resist higher forces. For example, domains 6 (217□68 pN) and 14 (238□36 pN) have Fc values greater than 205 pN. Our calculated critical forces are consistent with the experimental measurements (50-220 pN as identified by AFM pulling study of Filamin A).42
Sequence alignment during the homology modeling of domains 16, 18, and 20 suggested that these domains lack the N-terminal β strand of the canonical Ig fold. Such a deviation from the canonical Ig-like domain suggests a unique biological function for these domains. Interestingly, the absence of these structural features did not significantly change the mechanical stability of these domains with respect to other domains. The two domains, 18 and 20, have Fc of 170±18 pN, and domain 16, has an Fc of 188±68 pN. These data suggest that the mechanical stability of Ig domains is independent of the N-terminal β strand and likely to be caused by sequence difference in the core of the protein.
Recent in vitro pulling experiments on filamin-actin networks suggest that filamin A Ig-like domains are subjected to equilibrium forces up to 80 pN.43 Hence, we analyze the conformational changes of each of the 24 Ig-like domains under 35 and 70 pN of constant pulling force next (see Forced Unfolding Pathways Analysis in Materials and Methods).
Under the 35 pN pulling force, most filamin Ig-like domains remain in a native-like state with a few domains featuring intermediate conformations that could potentially play a role in stress signaling
We analyze the population of conformations of each Ig-like domain under the 35 pN pulling force, which we expect to be physiologically relevant. We find that most of the domains stay in their near-native conformations as shown for domain 21 (Fig. 2B). The average end-to-end extension of these conformations is increased by ∼10 Å, compared to the extension length seen in zero force extension (Supplementary Fig. 2 A and B). This is the result of pulling out leading N-terminal residues (Supplementary Fig. 3 A and B), which make little contacts in the native state. The rest of the structure remains intact (Supplementary Fig. 3A).
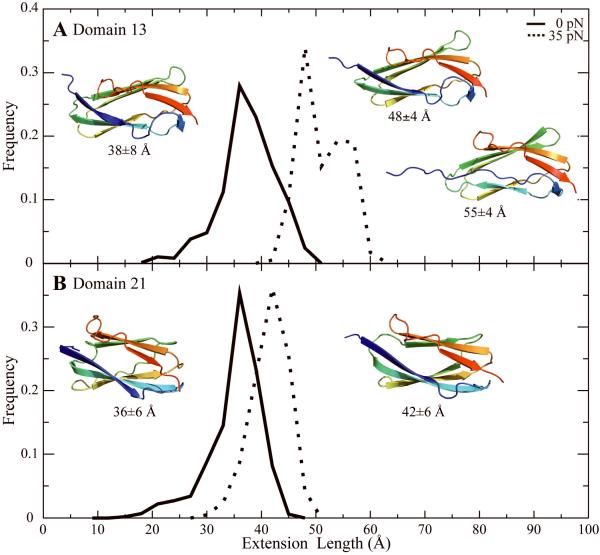
Figure 2. Equilibrium stable intermediate states of domains at 35 pN of constant-force pulling.
Histogram of extension lengths for domains 13 (A) and 21 (B). A representative conformation for each state is shown. The solid line represents the distribution from simulations at 0 pN pulling and the dotted line represents the distribution from simulations at 35 pN pulling.
Interestingly, we find that at the 35 pN pulling force a few domains feature a partially unfolded intermediate state in addition to a near-native conformation. This is exemplified by partially unfolded state of domain 13 (Fig. 2A), which has the interaction between strands A and B lost while maintaining A’-G region contacts (Fig. 2A; the 55 Å conformation). This conformation is analogous to changes hypothesized for TNI27 when it was pulled at much higher forces.19,20 The loss of β-strand A contacts while other β strands are left intact is common to most of the intermediate states of these domains, although domain 3 is unique in having a large loss of contacts in the G’ region (Supplementary Fig. 3B). We do observe one exception: domain 15 loses its entire β strand A (Supplementary Fig. 4). This major conformational shift occurs in a small number of ensembles and produces an extension length of ∼86 Å (Supplementary Fig. 2B). Thus, while several domains have a modest conformational shift pulled at the 35 pN force, at least one domain has a major conformational shift that could serve as a potential signal of relatively low level of cellular stress.
At 70 pN, filamin domains have a diverse set of metastable states. The unfolding pathway of all domains is initiated by the loss of contacts in the N-terminal β strands
Under 70 pN pulling force, all Ig-like domains undergo large conformational changes (Fig. 3 and Supplementary Fig. 2C). The most populated states are those with end-to-end extension within 20 Å of native state, where β strands A and/or G has been pulled out slightly leaving the remaining structure native-like (Fig. 3). The stretched conformations with longer extensions (>20 Å) have one β strand sliding past another (Fig. 3A) and/or lose contacts between strand A’ and G (63 Å extension in Fig. 3B; and 72 Å extension in Fig. 3C). Interestingly, TNI27 is reported to have similar initial unfolding pathways which features loss A-B contacts, loss of contacts in the A’-G region, and then quickly unfolding.19,20 However, at 70 pN stretching force filamin Ig-like domains do not traverse directly to the unfolded state, instead they get trapped in several metastable states (Supplementary Fig. 2C). These states include domains in which strand A (130 Å extension in Fig. 3B) or strands A and B has been unfolded (150 Å extension in Fig. 3A, and 149 Å extension in 3B) from the rest of the domain resulting in conformations such as a single β sheet (150 Å in Fig. 3A) or a β sandwich (149 Å in Fig. 3B). These conformations are analogous to those observed in the metastable intermediate of ddFLN4 when unfolded using forces in the order of 60 pN.14,15 Also, FN-III10 has been observed to lose N-terminal β strands when forced to unfold using ∼100 pN.21,22 Domain 21 has a proclivity to also lose β strand G entirely (Fig. 3B 149Å), which could potentially be related to its role in the previously mentioned interdomain conformation involving domain 20. Most other domains only lose β-strands at the N-terminus.
Figure 3. Equilibrium stable intermediate states of domains at 70 pN of constant-force pulling.
Histogram of extension lengths for domains 13 (A), 21 (B) and 23 (C). A representative conformation for each state is shown. The solid line represents the distribution from simulations at 0 pN pulling and the dotted line represents the distribution from simulations at 70 pN pulling.
The most stable domains at 70 pN unfolding force are 3, 9, and 22, which have metastable states close to that of their native state (extension length < 86Å) (Supplementary Fig. 3C). The frequent interconversion between intermediate states of these domains suggests a low energy barrier between successive extension length states (e.g. Fig. 3C domain 3). Domains 1, 6, 12, 13, and 14 also feature the near-native state being highly populated. However, these domains also feature an intermediate state missing the N-terminal β strands. Interestingly, we found other domains (e.g. 21) (Supplementary Fig. 3C) are fully unfolded using a force ∼70 pN, suggesting a lesser stability of these domains. Domains in the range 9 to 15 are considered secondary sites for binding actin, and having unusually stable domains in this range could be critical to the structural role of filamin in cells.56 We hypothesize that domains near the actin-binding boundary could have added stresses in the cell since they could act as the actin-binding fulcrum. It is also conceivable that domains near the end of the actin-binding range could require additional flexibility. Thus domains 13 and 14 having stable intermediates lacking β strands could meet this potential requirement.
We also find that the mechanical stability of some Ig-like domains does not depend entirely on N-terminal β strands. We modeled domains 16 (N-terminal residues up to and including β strand A’), 18 and 20 (N-terminal residues up to and including β A) lacking N-terminal β strands (Kesner, et al., submitted) as their templates lacked β strand integrity in this region. We find that at both 35 and 70 pN, these domains have similar unfolding pathways and metastable conformations as seven-stranded domains. Domain 20 maintains a highly populated native-like conformation featuring an A’-G region β sheet at 35 pN (Supplementary Figs. 3A, 4B) and an unfolding pathway where the most populated state is native-like at 70 pN similar to seven-stranded domains. Domain 18 at 35 pN features two metastable states and does not unfold entirely. The most populated state is native-like with few of the native contacts lost (Supplementary Fig. 3A). However, domain 18 also features a lowly populated state with a conformation that has an unfurled N-terminal β strand B at 35 pN (Supplementary Fig. 4B), thus making it somewhat distinct from seven-stranded domains in which we observe the unfolding of β strand B only at 70 pN. At 70 pN domain 18 has a similar unfolding pathway as that of domain 24, featuring highly populated intermediate states that have extension lengths much greater than that of their native states (Supplementary Fig. 2C). Domain 16 features the greatest differences in the unfolding pathway compared to seven-stranded domains: it has an unfolding pathway that is distinct from that of domains 18 and 20 and most seven-stranded Ig-like domains unfolding from the C-terminus at 35 pN (Supplementary Fig. 4 B). However, domain 16 is very stable because at 70 pN, its most populated state is a metastable and not the fully unfolded state. Thus, all three domains lacking N-terminal β strands are highly stable at 35 and 70 pN of force, although domain 18 and 20 are more similar to each other than to domain 16, which unfolds from the C-terminus.
This systematic analysis of our in silico pulling studies of filamin Ig-like domains reveals metastable intermediate states as observed in AFM experiments. Our simulations are able to reproduce experimentally derived critical unfolding forces. The conformational changes of all the Ig-like domains feature a common intermediate state where the N-terminal strand is unfolded, which could play a role in the signaling pathway of cell responses to mechanical stress. Next, we study the thermally induced unfolding of the filamin domains to test whether the intermediate states observed in forced pulling are also observed in thermally induced unfolding pathways. We restrict our study to three Ig-like domains, 14, 21 and 24. These domains are selected due to distinct kinetic properties and biological significance: domain 14 has the highest critical force, domain 21 has well-characterized thermodynamics13, and domain 24 is involved in dimerization.38
Thermal unfolding of filamin Ig-like domains features a common initial unfolding of the N-terminal β strand
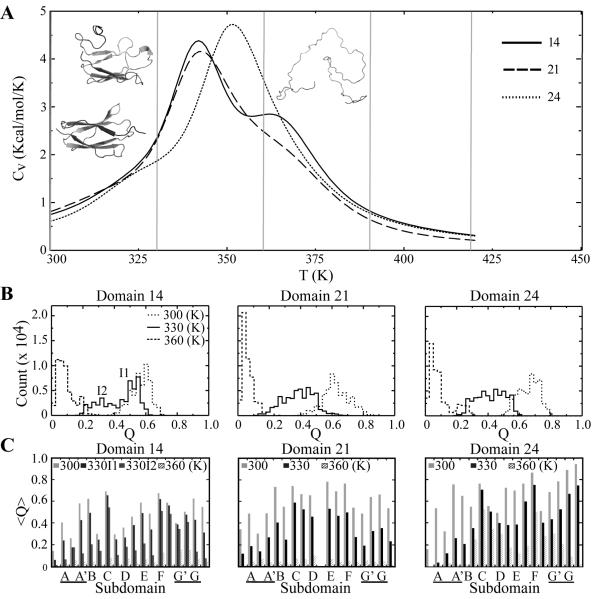
We perform equilibrium DMD simulations of Ig-like domains 14, 21 and 24 over a wide range of temperatures (300-420 K). We use the weighted histogram analysis method (WHAM)35 to compute the specific heat (Fig. 4A). The highest peak in the specific heat corresponds to the unfolding transition. The shoulders in the specific heat plot suggest the existence of an intermediate state. Our results indicate that domain 14 and 21 have similar unfolding temperature of ∼340 K. Domain 24 is the most stable of these domains with unfolding transition temperature ∼10 degrees higher than either 14 or 21 (Fig. 4A). The increased stability of domain 24 is possibly the result of its well-characterized role in dimerization of filamin monomers.38 Domain 14 has a prominent shoulder at temperature ∼370 K that is absent in domain 21, suggesting the existence of a thermally stable intermediate state.
Figure 4. Thermal unfolding of filamin domains.
(A) Plot of the specific heat as a function of temperature for domains 14, 21, and 24 calculated using the WHAM. Representative conformations of the metastable states of domain 21 at temperatures 300, 330 and 360 are also shown. (B) Histogram of Q-values for compiled replicated trajectories at each temperature (300, 330, 360 K) for domains 14, 21 and 24. Metastable states of domain 21 at 330 K are labled I1 and I2. (C) Average Q-value for metastable state for each subdomain (Fig. 1A) at each temperature (300, 330, 360 K).
To further investigate the conformational states of these domains, we use the fraction of native contacts (Q) as the approximation of the reaction coordination to analyze the conformational state at different temperatures (Fig. 4B). We also compute the Q-value of each of segments in the native state (Fig. 1A, 4C). At the low temperature of 300 K, all domains have near-native conformation with high Q-values (Fig. 4B). As the temperature increases to 330 K, we find domain 14 features two states, I1 and I2, while domains 21 and 24 have only one. We examine the Q-values of each secondary structure segment at 330 K (Fig. 4C). For domain 14 both states I1 and I2 have large losses in A-B region contacts, I2 however has more contacts lost in A’, B and G than does I2. Furthermore, the conformation in I1 is a closed β sandwich whereas the conformation of I2 is an open β sandwich (Supplementary Fig. 5A). Thus it is likely that A’-G region contacts are involved in maintaining the closed conformation of I1. Domain 21 has lost significant amount of native contacts in both the N- and C- terminal β strands. Domain 24 loses contacts of mainly in β strand A. The existence of two states of domain 14 is consistent with the shoulder in the specific heat. At high temperature of 360 K, the most populated state of each domain is the unfolded conformation. Consistent with the high thermal stability, the β strands CDFG of domain 24 still retain partial native interaction at 360 K (Fig. 4C).
Jiang et al., using an NMR based approach determined the unfolding temperature of domain 21 to be 319 K. They also reported that different filamin Ig-like domains have different thermal stabilities. Domain 19 and 17 are fully folded at 333 K while domain 21 is unfolded.13 They have also reported a partially unfolded fraction of domain 21 under mild conditions (298 K). It is possible that the differences between domains observed were the result of β strand A’s displacement that we observed in domain 21 in our simulations at 330 K (Supplementary Fig. 5 B) since the residue they used as a folding marker is adjacent to β strand A. Our results are quite distinct from those of other reported simulations of thermal unfolding of Ig-like domains. For example, Paci et al., simulated the unfolding of TNI27 at 450 K and found unfolding pathways in which the last strands to unfold were the terminal β strands.57 Given the high temperatures used, it is possible that these observations were the result of nonequilibrium simulations.
Discussion
Mounting experimental evidence suggests that filamin A molecules act not only as structural and mechanical proteins that cross-links actin fibrils, but also as scaffold proteins that play a critical role in cellular response to external mechanical stress.2-7 We hypothesize that conformational changes of filamin A due to mechanical stress are important for signaling, where stress-induced conformational changes can either disrupt existing interactions or introduce new interactions. We systematically studied the conformational dynamics of forced unfolding of filamin Ig-like domains using DMD. We developed a novel technique to derive the critical unfolding force from constant-force trajectories that is based upon finding the intersection between two unfolding regimes with respect to pulling forces. As a validation of our methodology, our computationally estimated forced unfolding dynamics of filamin A Ig-like domains agree with AFM experiments. For example, our simulation suggests the average critical unfolding force is 150-240 pN, which is consistent with the experimental measurements of 50-220 pN. Our analysis of the force-induced unfolding trajectories suggests the existence of multiple intermediate states corresponding to partially unfolded β sandwich of Ig-like domains. Additionally, an intermediate state observed in the simulations common to most filamin A Ig-like domains is characterized by the unfolding of the first N-terminal β strand. This intermediate state is consistent with the intermediate state observed in the force-induced unfolding of D. discoideum filamin domain 4, 27 Ig-like domain of titin, and fibronectin type three domain 10.14,16-22 Thus, our stretching simulations using all-atom DMD is able to recapitulate the conformational dynamics of Ig-like domains under force.
Our simulation results suggest that at low force (35 pN) most of the Ig-like domains remain in the native state with only a few domains featuring a weak population of a partially unfolded N-terminal strand. As the force increases (up to ∼70 pN, which is close to the maximal forces observed in vivo),58 we observe an increased population of intermediate states. Most of the domains still remain in their native or near-native conformations since these forces are still below the Fc. We find a large heterogeneity in both the population of the force-induced intermediate states and the transitions between them. However, we do find a common initial unfolding intermediate common to all Ig-like domains, where the N-terminal strand unfolds, similar to those observed in AFM experiments on TNI27.18,20
Studies with TNI27 have suggested that contacts within A’-G region are important for maintaining the stability of its metastable state.23 We observe a similar phenomenon in domain 20’s metastable states. However, the stability of other six-stranded domains appears to be independent of this region. Domain 18 loses A’-G region contacts during unfolding, and yet does not completely unfold. Also, domain 16 which lacks subdomain A’, has a similar critical unfolding force as other domains. These three domains might not be representative of all domains since in their native-like state they are stable absent N-terminal β strands. On the other hand both thermally and forced unfolding pathways of most seven-stranded Ig-like domains feature metastable states that lack any A’ contacts. Thus, it is likely the A’-G region plays a minor role in filamin Ig-like domain stability.
Our results from thermal unfolding of Ig-like domains suggest that there is no correlation between thermal and mechanical stability. For example, domain 14, which has the highest critical unfolding force, is thermally less stable than domain 24. However, there does appear to be a correlation between thermal unfolding and force-induced unfolding pathways. In the case of both low force unfolding and low temperature thermal unfolding, unfolding is mostly initiated with the loss of contacts in N-terminal β strands. In the few cases where we observe initiation of forced unfolding at both the N- and C- terminus (domain 21) we also observe loss of contacts at both termini due to thermal denaturation. Thus, as evidenced by both thermal and force-induced unfolding pathways, Ig domains of filamin have a similar initial unfolding intermediate state. This similarity may be the result of evolutionary optimization of filamin due to its role as a structural and scaffold protein.
Filamins interact with a wide range of cell signaling proteins, and the conformational changes upon stress can either disrupt or promote these interactions. Additionally, the exposure of partially unfolded strands can promote modifications such as phosphorylation, which in turn can activate downstream signaling pathways. Therefore, we postulate that intermediates with their N-terminal strands unfolded could be involved in the cellular response to external mechanical stress. Further experimental studies are required to verify this hypothesis.
Conclusion
Stress levels in cells can be very large, especially in the cortex where the amount of stress depends on its compliance to the surrounding surface. 59 In this study, we find that under forces between 150-240 pN filamin domains readily unfold. However, under lower forces, domains unfold in stages producing a heterogeneous population of metastable states lacking N-terminal β strands. Our simulations of thermal unfolding reveal similar metastable states. Furthermore, we observe that the domains that were modeled lacking all or part of the N-terminal β strand (16, 18 and 20) have similar forced unfolding characteristics as canonical Ig-like domains. Thus, it appears that the stability of Ig-like domains is independent of N-terminal β strands. Domain 20 has been shown to have an N-terminal β strand playing an inhibitory role for protein-protein interactions involving filamin A.12 Since domain 18 has a similar forced unfolding pathway as domain 20, it is possible that domain 18’s β strand A has a similar biological function. Moreover, it is possible that unraveling of N-terminal β strands as observed during forced unfolding leads to interdomain interactions that could produce the inhibitory behavior that Lad et al.12 observed. Other possible ramifications to having exposed β strands include exposure of cryptic binding sites or post translational modification sites; higher degree of connectivity between filamin monomers as more β strand edges are exposed; a higher turnover rate as more residues are exposed to potential cleavage; forming of new actin structures (cross-links vs. bundles); attraction of heat shock proteins to refold domains as stress increases; allowing Ig-like domains to more quickly refold back to their native fold when stresses and then relaxed; or allowing multiple domains to fold properly60. For example, proteomic screens revealed two phospho-serines (S1081 and S1084)61,62 in the loop between β strands A and B of domain 9 of filamin A. Thus, we postulate that the stress-induced unfurling of the N-terminal β strands of filamin domains could play an important cellular role as a conformational switch.
Supplementary Material
Acknowledgements
We thank the discussion and critical reading of the manuscript by Srinivas Ramachandran, Pradeep Kota, and Adrian Serohijos. We also thank Shuangye Yin for assistance in statistical analysis. This work is supported in part by the National Institutes of Health grant R01GM080742.
References
- 1.Gardel ML, Nakamura F, Hartwig JH, Crocker JC, Stossel TP, Weitz DA. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(6):1762–1767. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mammoto A, Huang S, Ingber DE. Filamin links cell shape and cytoskeletal structure to Rho regulation by controlling accumulation of p190RhoGAP in lipid rafts. Journal of cell science. 2007;120(Pt 3):456–467. doi: 10.1242/jcs.03353. [DOI] [PubMed] [Google Scholar]
- 3.Andrews RK, Fox JE. Interaction of purified actin-binding protein with the platelet membrane glycoprotein Ib-IX complex. The Journal of biological chemistry. 1991;266(11):7144–7147. [PubMed] [Google Scholar]
- 4.Christodoulides N, Feng S, Resendiz JC, Berndt MC, Kroll MH. Glycoprotein Ib/IX/V binding to the membrane skeleton maintains shear-induced platelet aggregation. Thrombosis research. 2001;102(2):133–142. doi: 10.1016/s0049-3848(01)00243-2. [DOI] [PubMed] [Google Scholar]
- 5.Feng S, Resendiz JC, Lu X, Kroll MH. Filamin A binding to the cytoplasmic tail of glycoprotein Ibalpha regulates von Willebrand factor-induced platelet activation. Blood. 2003;102(6):2122–2129. doi: 10.1182/blood-2002-12-3805. [DOI] [PubMed] [Google Scholar]
- 6.Glogauer M, Arora P, Chou D, Janmey PA, Downey GP, McCulloch CA. The role of actin-binding protein 280 in integrin-dependent mechanoprotection. The Journal of biological chemistry. 1998;273(3):1689–1698. doi: 10.1074/jbc.273.3.1689. [DOI] [PubMed] [Google Scholar]
- 7.Shifrin Y, Arora PD, Ohta Y, Calderwood DA, McCulloch CA. The role of FilGAP-filamin A interactions in mechanoprotection. Mol Biol Cell. 2009;20(5):1269–1279. doi: 10.1091/mbc.E08-08-0872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nakamura F, Hartwig JH, Stossel TP, Szymanski PT. Ca2+ and calmodulin regulate the binding of filamin A to actin filaments. The Journal of biological chemistry. 2005;280(37):32426–32433. doi: 10.1074/jbc.M502203200. [DOI] [PubMed] [Google Scholar]
- 9.O’Connell MP, Fiori JL, Baugher KM, Indig FE, French AD, Camilli TC, Frank BP, Earley R, Hoek KS, Hasskamp JH, Elias EG, Taub DD, Bernier M, Weeraratna AT. Wnt5A Activates the Calpain-Mediated Cleavage of Filamin A. The Journal of investigative dermatology. 2009 doi: 10.1038/jid.2008.433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Holtzclaw JD, Brown RC, O’Neil RG. Shear stress-sensitive TRP channels modulate calcium influx in activated T cells. FASEB. 21:945.942. [Google Scholar]
- 11.Zhou X, Boren J, Akyurek LM. Filamins in cardiovascular development. Trends in cardiovascular medicine. 2007;17(7):222–229. doi: 10.1016/j.tcm.2007.08.001. [DOI] [PubMed] [Google Scholar]
- 12.Lad Y, Kiema T, Jiang P, Pentikainen OT, Coles CH, Campbell ID, Calderwood DA, Ylanne J. Structure of three tandem filamin domains reveals auto-inhibition of ligand binding. Embo J. 2007 doi: 10.1038/sj.emboj.7601827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jiang P, Campbell ID. Integrin binding immunoglobulin type filamin domains have variable stability. Biochemistry. 2008;47(42):11055–11061. doi: 10.1021/bi8011466. [DOI] [PubMed] [Google Scholar]
- 14.Schwaiger I, Kardinal A, Schleicher M, Noegel AA, Rief M. A mechanical unfolding intermediate in an actin-crosslinking protein. Nature structural & molecular biology. 2004;11(1):81–85. doi: 10.1038/nsmb705. [DOI] [PubMed] [Google Scholar]
- 15.Schwaiger I, Schleicher M, Noegel AA, Rief M. The folding pathway of a fast-folding immunoglobulin domain revealed by single-molecule mechanical experiments. EMBO reports. 2005;6(1):46–51. doi: 10.1038/sj.embor.7400317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yew ZT, Krivov S, Paci E. Free-energy landscapes of proteins in the presence and absence of force. J Phys Chem B. 2008;112(51):16902–16907. doi: 10.1021/jp807316e. [DOI] [PubMed] [Google Scholar]
- 17.Rief M, Gautel M, Oesterhelt F, Fernandez JM, Gaub HE. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science (New York, NY. 1997;276(5315):1109–1112. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- 18.Marszalek PE, Lu H, Li H, Carrion-Vazquez M, Oberhauser AF, Schulten K, Fernandez JM. Mechanical unfolding intermediates in titin modules. Nature. 1999;402(6757):100–103. doi: 10.1038/47083. [DOI] [PubMed] [Google Scholar]
- 19.Fowler SB, Best RB, Toca Herrera JL, Rutherford TJ, Steward A, Paci E, Karplus M, Clarke J. Mechanical unfolding of a titin Ig domain: structure of unfolding intermediate revealed by combining AFM, molecular dynamics simulations, NMR and protein engineering. Journal of molecular biology. 2002;322(4):841–849. doi: 10.1016/s0022-2836(02)00805-7. [DOI] [PubMed] [Google Scholar]
- 20.Lu H, Krammer A, Isralewitz B, Vogel V, Schulten K. Computer modeling of force-induced titin domain unfolding. Advances in experimental medicine and biology. 2000;481:143–160. doi: 10.1007/978-1-4615-4267-4_9. discussion 161-142. [DOI] [PubMed] [Google Scholar]
- 21.Li L, Huang HH, Badilla CL, Fernandez JM. Mechanical unfolding intermediates observed by single-molecule force spectroscopy in a fibronectin type III module. Journal of molecular biology. 2005;345(4):817–826. doi: 10.1016/j.jmb.2004.11.021. [DOI] [PubMed] [Google Scholar]
- 22.Gao M, Craig D, Vogel V, Schulten K. Identifying unfolding intermediates of FN-III(10) by steered molecular dynamics. Journal of molecular biology. 2002;323(5):939–950. doi: 10.1016/s0022-2836(02)01001-x. [DOI] [PubMed] [Google Scholar]
- 23.Fowler SB, Clarke J. Mapping the folding pathway of an immunoglobulin domain: structural detail from Phi value analysis and movement of the transition state. Structure. 2001;9(5):355–366. doi: 10.1016/s0969-2126(01)00596-2. [DOI] [PubMed] [Google Scholar]
- 24.Go N. Theoretical studies of protein folding. Annual review of biophysics and bioengineering. 1983;12:183–210. doi: 10.1146/annurev.bb.12.060183.001151. [DOI] [PubMed] [Google Scholar]
- 25.Klimov DK, Thirumalai D. Native topology determines force-induced unfolding pathways in globular proteins. Proceedings of the National Academy of Sciences of the United States of America. 2000;97(13):7254–7259. doi: 10.1073/pnas.97.13.7254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.West DK, Olmsted PD, Paci E. Mechanical unfolding revisited through a simple but realistic model. The Journal of chemical physics. 2006;124(15):154909. doi: 10.1063/1.2185100. [DOI] [PubMed] [Google Scholar]
- 27.Paci E, Karplus M. Forced unfolding of fibronectin type 3 modules: an analysis by biased molecular dynamics simulations. Journal of molecular biology. 1999;288(3):441–459. doi: 10.1006/jmbi.1999.2670. [DOI] [PubMed] [Google Scholar]
- 28.Lu H, Schulten K. The key event in force-induced unfolding of Titin’s immunoglobulin domains. Biophysical journal. 2000;79(1):51–65. doi: 10.1016/S0006-3495(00)76273-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sotomayor M, Schulten K. Single-molecule experiments in vitro and in silico. Science (New York, NY. 2007;316(5828):1144–1148. doi: 10.1126/science.1137591. [DOI] [PubMed] [Google Scholar]
- 30.Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Discrete molecular dynamics studies of the folding of a protein-like model. Folding & design. 1998;3(6):577–587. doi: 10.1016/S1359-0278(98)00072-8. [DOI] [PubMed] [Google Scholar]
- 31.Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Identifying the protein folding nucleus using molecular dynamics. Journal of molecular biology. 2000;296:1183–1188. doi: 10.1006/jmbi.1999.3534. [DOI] [PubMed] [Google Scholar]
- 32.Ding F, Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Direct molecular dynamics observation of protein folding transition state ensemble. Biophysical journal. 2002;83:3525–3532. doi: 10.1016/S0006-3495(02)75352-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dokholyan NV, Li L, Ding F, Shakhnovich EI. Topological determinants of protein folding. Proceedings of the National Academy of Sciences USA. 2002;99:8637–8641. doi: 10.1073/pnas.122076099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ding F, Dokholyan NV. Simple but predictive protein models. Trends in biotechnology. 2005;23(9):450–455. doi: 10.1016/j.tibtech.2005.07.001. [DOI] [PubMed] [Google Scholar]
- 35.Ding F, Tsao D, Nie H, Dokholyan NV. Ab initio folding of proteins with all-atom discrete molecular dynamics. Structure. 2008;16(7):1010–1018. doi: 10.1016/j.str.2008.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dokholyan NV. Studies of folding and misfolding using simplified models. Current opinion in structural biology. 2006;16(1):79–85. doi: 10.1016/j.sbi.2006.01.001. [DOI] [PubMed] [Google Scholar]
- 37.Wilcox KC, Zhou L, Jordon J, Huang Y, Yu Y, Redler RL, Chen X, Caplow M, Dokholyan NV. Modifications of superoxide dismutase (SOD1) in human erythrocytes: a possible role in amyotrophic lateral sclerosis (ALS) The Journal of biological chemistry. 2009 doi: 10.1074/jbc.M809687200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pudas R, Kiema TR, Butler PJ, Stewart M, Ylanne J. Structural basis for vertebrate filamin dimerization. Structure. 2005;13(1):111–119. doi: 10.1016/j.str.2004.10.014. [DOI] [PubMed] [Google Scholar]
- 39.Nakamura F, Pudas R, Heikkinen O, Permi P, Kilpelainen I, Munday AD, Hartwig JH, Stossel TP, Ylanne J. The structure of the GPIb-filamin A complex. Blood. 2006;107(5):1925–1932. doi: 10.1182/blood-2005-10-3964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kiema T, Lad Y, Jiang P, Oxley CL, Baldassarre M, Wegener KL, Campbell ID, Ylanne J, Calderwood DA. The molecular basis of filamin binding to integrins and competition with talin. Molecular cell. 2006;21(3):337–347. doi: 10.1016/j.molcel.2006.01.011. [DOI] [PubMed] [Google Scholar]
- 41.Baker D, Sali A. Protein structure prediction and structural genomics. Science (New York, NY. 2001;294(5540):93–96. doi: 10.1126/science.1065659. [DOI] [PubMed] [Google Scholar]
- 42.Furuike S, Ito T, Yamazaki M. Mechanical unfolding of single filamin A (ABP-280) molecules detected by atomic force microscopy. FEBS letters. 2001;498(1):72–75. doi: 10.1016/s0014-5793(01)02497-8. [DOI] [PubMed] [Google Scholar]
- 43.Ferrer JM, Lee H, Chen J, Pelz B, Nakamura F, Kamm RD, Lang MJ. Measuring molecular rupture forces between single actin filaments and actin-binding proteins. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(27):9221–9226. doi: 10.1073/pnas.0706124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Evans E, Ritchie K. Dynamic strength of molecular adhesion bonds. Biophysical journal. 1997;72(4):1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhou Y, Karplus M. Folding thermodynamics of a model three-helix-bundle protein. Proceedings of the National Academy of Sciences of the United States of America. 1997;94(26):14429–14432. doi: 10.1073/pnas.94.26.14429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lazaridis T, Karplus M. Discrimination of the native from misfolded protein models with an energy function including implicit solvation. Journal of molecular biology. 1999;288(3):477–487. doi: 10.1006/jmbi.1999.2685. [DOI] [PubMed] [Google Scholar]
- 47.Lazaridis T, Karplus M. Effective energy function for proteins in solution. Proteins. 1999;35(2):133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 48.Helen M, Berman, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov lN, Bourne PE. The Protein Data Bank. Nucleic acids research. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Luthy R, Bowie JU, Eisenberg D. Assessment of protein models with three-dimensional profiles. Nature. 1992;356(6364):83–85. doi: 10.1038/356083a0. [DOI] [PubMed] [Google Scholar]
- 50.Case DA, Darden TA, Cheatham TE, Wang J, Duke RE, Luo R, Crowley M, Walker RC, Zhang W, Merz KM, Wang B, Hayik S, Roitberg A, Seabra G, Kolossváry I, Wong KF, Paesani F, Vanicek J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Mathews DH, Seetin MG, Sagui C, Babin V, Kollman PA. AMBER 10. University of California; San Francisco: 2008. III CLS. [Google Scholar]
- 51.Yin S, Ding F, Dokholyan NV. Modeling backbone flexibility improves protein stability estimation. Structure. 2007;15(12):1567–1576. doi: 10.1016/j.str.2007.09.024. [DOI] [PubMed] [Google Scholar]
- 52.Yin S, Ding F, Dokholyan NV. Eris: an automated estimator of protein stability. Nature methods. 2007;4(6):466–467. doi: 10.1038/nmeth0607-466. [DOI] [PubMed] [Google Scholar]
- 53.Ding F, Dokholyan NV. Emergence of protein fold families through rational design. PLoS computational biology. 2006;2(7):e85. doi: 10.1371/journal.pcbi.0020085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Andersen HC. Molecular dynamics at constant pressure and/or temperature. The Journal of chemical physics. 1980;72(4):2384–2393. [Google Scholar]
- 55.Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, Amin N, Schwikowski B, Ideker T. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13(11):2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nakamura F, Osborn TM, Hartemink CA, Hartwig JH, Stossel TP. Structural basis of filamin A functions. The Journal of cell biology. 2007;179(5):1011–1025. doi: 10.1083/jcb.200707073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Paci E, Karplus M. Unfolding proteins by external forces and temperature: the importance of topology and energetics. Proceedings of the National Academy of Sciences of the United States of America. 2000;97(12):6521–6526. doi: 10.1073/pnas.100124597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bendix PM, Koenderink GH, Cuvelier D, Dogic Z, Koeleman BN, Brieher WM, Field CM, Mahadevan L, Weitz DA. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophysical journal. 2008;94(8):3126–3136. doi: 10.1529/biophysj.107.117960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kumar S, Weaver VM. Mechanics, malignancy, and metastasis: The force journey of a tumor cell. Cancer Metastasis Rev. 2009 doi: 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Raman EP, Barsegov V, Klimov DK. Folding of tandem-linked domains. Proteins. 2007;67(4):795–810. doi: 10.1002/prot.21339. [DOI] [PubMed] [Google Scholar]
- 61.Daub H, Olsen JV, Bairlein M, Gnad F, Oppermann FS, Korner R, Greff Z, Keri G, Stemmann O, Mann M. Kinase-selective enrichment enables quantitative phosphoproteomics of the kinome across the cell cycle. Molecular cell. 2008;31(3):438–448. doi: 10.1016/j.molcel.2008.07.007. [DOI] [PubMed] [Google Scholar]
- 62.Dephoure N, Zhou C, Villen J, Beausoleil SA, Bakalarski CE, Elledge SJ, Gygi SP. A quantitative atlas of mitotic phosphorylation. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(31):10762–10767. doi: 10.1073/pnas.0805139105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.