TMAO influence on the backbone of proteins: an oligoglycine model

Abstract

The study of organic osmolytes has been pivotal in demonstrating the role of solvent effects on the protein backbone in the folding process. Whereas a thermodynamic description of the interactions between the protein backbone and osmolyte has been well defined, the structural analysis of the effect of osmolyte on the protein backbone has been incomplete. Therefore, we have carried out simulations of a peptide backbone model, glycine₁₅ in protecting osmolyte TMAO solution in order to determine the effect of the solution structure on the conformation of the peptide backbone. We demonstrate that the models chosen show that the ensemble of backbone structures shifts towards a more collapsed state in TMAO solution as compared to pure water solution. The collapse is consistent with preferential exclusion of the osmolyte caused by unfavorable interactions between osmolyte and peptide backbone. The exclusion is due to strong triplet correlations of osmolyte, water, and peptide backbone. This provides a clear mechanism demonstrating that even a modest concentration of TMAO forces the protein backbone to adopt a more collapsed structure in the absence of sidechain effects.

Introduction

Important clues regarding the transition of a protein from its denatured to native state have been revealed by considering the effect the solvent has on the stability of the entire manifold of states of the protein. The information gained by the study of a specific class of biological cosolvents, the organic osmolytes, has created the basis for a mechanism of protein folding that emphasizes the importance of the peptide backbone, as opposed to the sidechains, in the process ¹. Osmolytes are small cosolvents distinguished by their endogenous usage in maintaining cellular volume in response to osmotic stress; however, they can have profound effects on protein stability ². Osmolytes can be delineated into two groups based upon their effect on protein stability: protecting osmolytes are known to bias the structure towards the folded state, whereas the nonprotecting osmolyte urea biases the folding transition towards the unfolded state.

Experimental evidence has inferred that protecting osmolytes are selectively excluded from the local domain surrounding the protein, whereas the concentration of denaturing osmolyte is enhanced in the local region ³. Classical studies of sidechain model compounds in solution were interpreted as indicating the dominant role of sidechain solvation free energy changes in protein folding ^4,5. More recent experimental thermodynamics indicated that osmolytes predominately exert their effect on the denatured state of the peptide backbone, with the side-chains hardly modulating the overall effect ^6–8. Thus, a mechanism for osmolyte-conferred stability has been posited whereby protecting osmolytes are preferentially excluded from the peptide backbone due to less favorable interactions between the osmolyte and backbone ⁹. Some computational ¹⁰ and experimental studies ¹¹ of proteins in solution have been shown to be consistent with this. However, a necessary link between the thermodynamic description of just the peptide backbone and osmolyte with the preferential exclusion data has yet to be shown computationally or experimentally; namely, the preferential exclusion of protecting osmolyte from a robust peptide backbone in a model system.

Of the protecting osmolytes, trimethylamine N-oxide (TMAO) is among the most potent¹². Its propensity to strongly bolster a protein’s stability has allowed TMAO to be selectively adapted to counteract severe denaturing stress in a variety of organisms. For instance, elasmobranches, which include sharks, skates and rays, are known to accumulate TMAO in order to counteract urea denaturation at urea to TMAO molar concentration ratios ranging from 3:2 to 2:1 ². TMAO also may be used to counteract the deleterious effects of the high hydrostatic pressure environment of deep-sea organisms ¹³. Additionally, mammals possess glycerophorylcholine (GPC), an osmolyte with an analogous function to TMAO but a different chemical structure, for use within the kidneys’ urea-rich environment ². As much has been learned about protein stability via the study of the strongly denaturing osmolyte urea, TMAO has similarly proven to be an increasingly valuable tool for the understanding of protein stability. The protein folding ability of TMAO has also been utilized to study the mechanisms associated with protein misfolding diseases, such as Alzheimer’s ^14–16 and prion diseases ^17–19, as well as neuroblastoma ²⁰ and glaucoma ²¹. The usage of chemical chaperones to correct for misfolding diseases is emerging as a potential therapeutic ²². TMAO itself may prove to have promising treatment applications ²¹. However, no clear mechanism for the conjectured osmolyte activity with the backbone has been devised. Recent work has argued that the presence of osmolyte alters protein stability indirectly by affecting the water structure^23–25, whereas a case has been made that it is the direct interaction, or lack of, between the osmolyte and backbone that causes the osmolyte effect ^26–28.

Considering the transfer free energy decompositions, ^8,12,29,30 the importance of protein backbone solvation to the understanding of the protein folding equilibrium process has become apparent ¹. Several backbone model systems have been suggested, including oligoalanine and oligoglycine. However, due to solubility and detection issues ³¹, there is yet little structural experimental characterization of long peptide backbones in osmolyte solution. There is also a lack of simulation studies that fully investigate the molecular mechanism of TMAO-conferred protein stability as it relates to the peptide backbone. Initial simulation studies of TMAO and protein functional groups have demonstrated a modest enhancement of water structure near TMAO, as indicated by increased angular orientation of waters as well as an increase in bulk water-water hydrogen bonding ²⁵. However, recently differing views on the analysis of the simulation data have been suggested ^26,28. Simulations of proteins in TMAO solutions have demonstrated TMAO rescue of prion protein misfolding ³², and counteraction of urea induced denaturation ³³, but did not reveal the effective interactions between osmolyte and peptide backbone. Previous simulations have also focused on the affect TMAO has on hydrophobic interactions between solutes ^26,34, yet provided differing results on the ability of TMAO to disrupt hydrophobic interactions, perhaps due to theory and model inconsistencies ³⁴.

Here, we are interested in a molecular-level interpretation of the structural ensembles of a peptide backbone in osmolyte solution and in characterizing the correlations between osmolyte and the peptide backbone itself. Utilizing molecular dynamics, we have simulated the “sidechainless” peptide backbone model, oligoglycine, in two different solvent systems, pure water and TMAO solution, thus allowing us to attribute any structural changes in the peptide oligomer to the osmolyte TMAO. Previous simulations of a glycine₁₅ peptide backbone model in water and urea demonstrated that urea created a better solution environment for the backbone model, as the peptide adopted significantly more swollen states as compared to the model in pure water ³⁵. By analyzing our simulations to capture structural properties of the peptide and distribution of the surrounding solution, we show how TMAO forces the peptide backbone to collapse in a manner consistent with preferential exclusion of osmolyte.

Methods

In previous experimental thermodynamic analyses short glycine oligomers were chosen to model the peptide backbone ^6,29. Here, we chose a peptide length of fifteen glycines to create a model of a sidechainless protein polymer. The system was built initially in an extended form ³⁶, and subsequently energy minimized using the steepest descent method. Coordinates for the TMAO molecules were built using InsightII from Accelrys Inc., and subjected to energy minimization using the steepest descent method.

The all-atom CHARMM-27parameter set ³⁶ was used for the peptide backbone model with TIP3P water ⁴⁰, whereas the force field parameters for the TMAO molecules were obtained from Kast et al. ³⁷. A microcanonical ensemble (NVE) was used with a velocity Verlet-algorithm to integrate the equations of motions with a 2 fs time step, while saving coordinates/velocities every 25 steps. An Ewald summation, implemented with a linked-cell algorithm ³⁸, with a real space cutoff of 1.9 nm was used to calculate long-range electrostatic interactions. To constrain the bonds we used RATTLE ³⁹.

Two simulations were created, which differed in their solvent composition: pure water and TMAO and water (for brevity referred to simply as the TMAO solution). To create the initial conditions for the peptide in pure water simulation, the peptide was solvated using 11440 TIP3P water molecules ⁴⁰, in a cubic box 7.00 nm on a side. The initial placement of proximal water molecules was chosen so that no water molecule oxygen was within 0.25 nm from a heavy atom of the peptide. To create the TMAO solution 650 TMAO molecules were placed in a uniform lattice outside of the box with water and peptide. The solution was allowed to spontaneously mix while shrinking the box to a target volume as done in other recent work ⁴¹. The final TMAO solution simulation box is thus larger than the pure water because of the increase in volume caused by the addition of the TMAO molecules to the water system. The resulting final concentration of the TMAO simulation was 2.6 M in a 7.43 nm³ simulation box. The solvent of each system was equilibrated by running each simulation for 1.8 ns while reassigning the velocities at a target temperature of 300K in the NVE ensemble. Following this, each system was simulated, without velocity modifications, for 1.5 ns, thus completing our equilibration phase. We allowed both simulations to run for 20 ns (post-equilibration). The results are based upon the subsequent data.

The radius of gyration was calculated to characterize some structural properties of the peptide backbone model. The radius of gyration represents the deviation of the atoms in a molecule from its center of mass, thus describing the extent of collapse or extension of the backbone:

$$R_g=\sqrt{{\displaystyle \sum _{i=1}^N\frac{m_i{(r_i-r)}^2}{m}}}$$

where m is the total mass of the protein, m_i and r_i are the mass and position of the ith atom (respectively) and r is the center of mass for the protein. A low radius of gyration value corresponds to a compact state, whereas a high radius of gyration is indicative of a broader distribution of the atoms of the protein from the center of mass.

Hierarchical agglomerative clustering was used to classify the dominant structure cluster sets in each solution ⁴². Clustering was accomplished by grouping the two closest structures based upon root mean square deviation (RMSD). The process was continued for several iterations until the smallest difference between the groups was greater than a threshold value of 5.5 Å. The same threshold value was used for each data set.

The nature of solvent composition surrounding the peptide backbone was described by calculating the preferential interaction parameter Γ_os,bb. This parameter provides a relationship between the distribution of cosolvent around a solute species at a particular distance to that of the bulk solution. A negative preferential interaction parameter indicates a deficit of osmolyte molecules in the local region of the peptide backbone as compared to the bulk region (random). The preferential interaction parameter between osmolyte and peptide backbone is defined as ⁴³:

$${\mathrm{\Gamma }}_{\mathit{\text{os,bb}}}=\langle n_{\mathit{\text{osmolyte}}}^{\mathit{\text{local}}}-n_{\mathit{\text{water}}}^{\mathit{\text{local}}}\left(\frac{n_{\mathit{\text{osmolyte}}}^{\mathit{\text{bulk}}}-n_{\mathit{\text{osmolyte}}}^{\mathit{\text{local}}}}{n_{\mathit{\text{water}}}^{\mathit{\text{bulk}}}-n_{\mathit{\text{water}}}^{\mathit{\text{local}}}}\right)\rangle .$$

Results

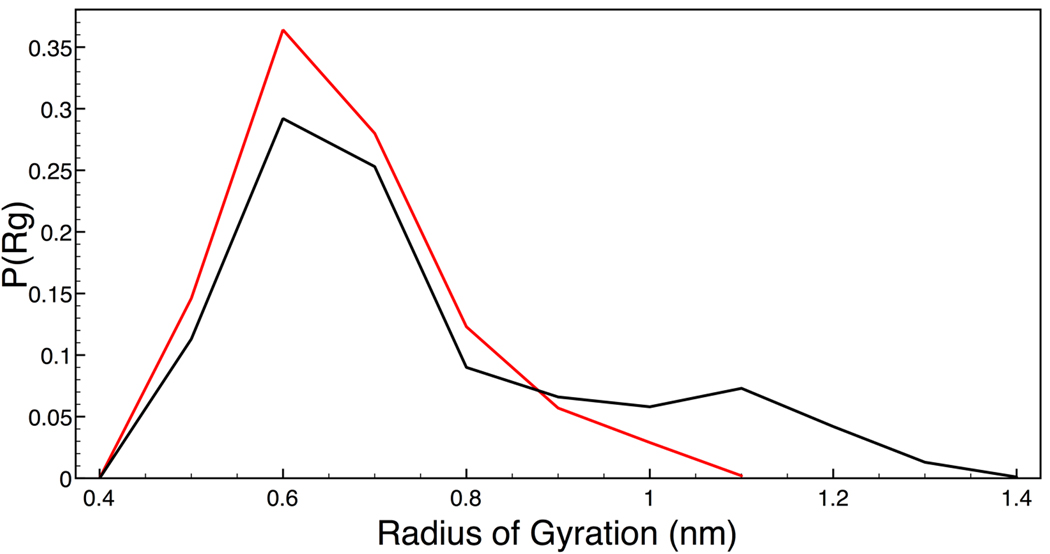
The oligoglycine peptide was quite flexible and did not sustain substantial alpha or beta structures for any meaningful period of time. The radius of gyration of the backbone in each solution was calculated over the entire trajectory for each simulation and Figure 1 shows the breadth of the probability distributions. It is clear that the presence of TMAO causes a significant shift in the distribution of structures sampled by the backbone degrees of freedom. Specifically, the ensemble of possible conformations of the backbone in TMAO solution is shifted towards a smaller radius of gyration as compared to a simple aqueous environment. The peptide backbone in water solution is able to sample structures of larger radius of gyration (greater than 1.08 nm) that are essentially unavailable to the peptide backbone in TMAO solution. As a value of lower radius of gyration corresponds to a more collapsed structure, it is evident that our model of TMAO solution causes the shift in the ensemble of conformations of the backbone model to a more collapsed and compact state. This is in contrast to the effect of the denaturing osmolyte urea has on a similar peptide backbone model, as the osmolyte causes the backbone model to adopt structures of larger radius of gyration as compared to that in pure water ³⁵.

Figure 1.

Radius of gyration probability profile. Black is for the peptide backbone in water solution and red is for the peptide backbone in TMAO solution.

To complement the general description of the shape of the backbone obtained from the computed radius of gyration profile, we have calculated distances between pairs of Cα atoms along the peptide backbone. The result provides a more detailed description of the curvature and local orientation of the peptide backbone structures in each solution. The probability distribution of the distances between select Cα atom pairs, Figure 2a, is shown in Figure 2b–e. For the majority of the pair distance profiles, there is a pronounced increase in the distribution of close Cα pair distances for the peptide backbone in TMAO solution, as compared to in pure water. The profile for the distances between the two end Cα atoms for the peptide backbone in pure water shows significant sampling of very close distances (less than 0.5 nm). A corresponding peak in TMAO solution is present although not as pronounced; however, there is a clear overall increase in the percentage of close distances between 0.8 – 2 nm for the peptide backbone in TMAO solution even for this end-to-end measure.

Figure 2.

Distance between Cα pairs (a) Numbering of Cα atoms. (b–e) Probability profile for distance between Cα pairs. Black is the peptide backbone in pure water solution and red is for the peptide backbone in TMAO solution. (b) Cα1–Cα15 (c) Cα2–Cα14 (d) Cα3–Cα13 (e) Cα4–Cα11

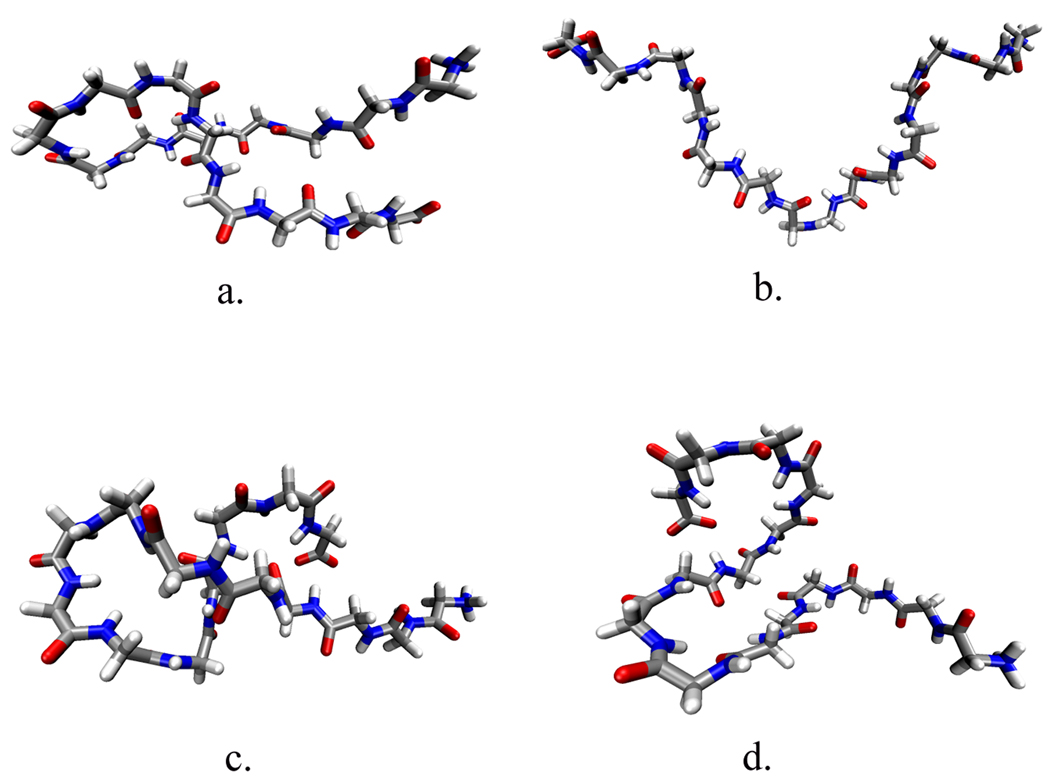
We further characterized the difference in conformation caused by the addition of TMAO by clustering similar structures independently in each simulation as outlined in the Methods section. The results from our structural clustering analysis are presented in Table 1. We analyzed the structures independently using the same threshold value, which yields a different number of clusters for each solution. The peptide backbone conformations in TMAO yield six clusters, whereas in pure water the peptide backbone shows nine. This is consistent with the radius of gyration profile seen in Figure 1 where we see that the backbone model in pure water samples more extended states than the backbone model in TMAO. Each cluster in Table 1 is listed by the RMSD between the average structure of the cluster and that of a perfectly elongated peptide. It is clear that the peptide backbone in TMAO solution samples more conformations that deviate significantly from a linear shape (higher RMSD) than that of the backbone in pure water. Figure 3 demonstrates this pictorially by showing representative structures from the two highest populated clusters for the two solutions. Comparing these two clusters between the two solutions shows that though the largest percentage cluster in each solution appear similar in conformation (Figure 3a,c), the second largest cluster display significant differences (Figure 3b,d). In pure water this cluster is more extended than the structure in TMAO solution.

Table 1.

Clustering analysis of the peptide backbone structures in (a) water solution and (b) TMAO solution. Clusters are listed in decreasing RMSD (in nm) of the average structure for that cluster from a perfectly linear peptide backbone. The RMSD values listed are for reference and are different from the RMSD calculations used to create the clusters, thus explaining similar RMSD values for different clusters. Clusters were made by taking structures every 5ps of the entire 20 ns trajectory, resulting in 4000 conformations.

a.		b.
RMSD	Probability	RMSD	Probability
1.3	32%	1.2	40%
1.3	13%	1.1	20%
1.2	7%	1.0	12%
1.1	7%	1.0	14%
1.1	4%	0.6	4%
1.0	9%	0.4	10%
0.9	2%
0.8	20%
0.7	5%

Figure 3.

Representative structures from the two highest populated clusters from Table 1. (a) most populated cluster in water solution (b) second most populated cluster in water solution (c) most populated cluster in TMAO solution (d) second most populated cluster in TMAO solution

The preferential interaction parameter, as outlined in the Methods section, was used to characterize the distribution of TMAO surrounding the peptide backbone. Figure 4 shows the preferential interaction parameter at increasing cutoff distances. The entire curve for the parameter is negative, which indicates a decrease in the number of osmolyte molecules within the local region as compared to the bulk region. This is to be expected for extremely close distances, where the excluded volume effect dominates, but the preferential interaction parameter between the peptide backbone and TMAO is negative even out to 1.2 nm; a distance encompassing several solvation layers. Therefore, in accord with the established experimental interpretation and recent predictions based upon Kirkwood-Buff theory ⁴⁴, TMAO is preferentially excluded from the peptide backbone model used here.

Figure 4.

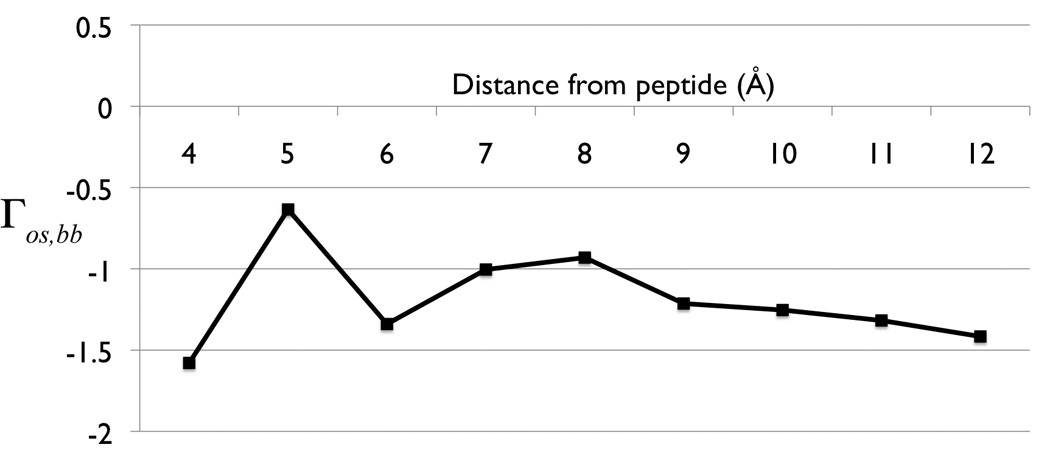
Preferential interaction parameter, Γ_{os, bb} as a function of cutoff distance between local and bulk domains.

We analyzed the solvent composition in radial shells from the peptide backbone by calculating the average number of TMAO and water molecules in the radial shells. This allows for a picture of the changes in the solvent environment and the distance at which the solution approaches bulk properties. In Table 2 these results are tabulated, in addition to the fraction of water to TMAO molecules. Within the first solvation shell of the backbone model there is a significant increase in the proportion of water to TMAO molecules as compared to the successive hydration layers (a ratio of about 1.5 times greater). At about 1.2 nm the solution environment becomes better mixed and gradually approaches the ideal ratio of water to TMAO molecules. Thus, the preferential exclusion of TMAO from the local domain of the peptide backbone creates an increased water hydration layer of the backbone model.

Table 2.

Solvent distribution in radial shells from the peptide backbone. Ideal water:TMAO ratio 17.6:1. Water oxygen is within 4.0Å from the nearest peptide backbone heavy atom, TMAO nitrogen is within 4.0Å from the nearest solute atom. Error estimate of the data was obtained by dividing the simulation trajectory into four equal batches and computing the averages and standard deviations (shown in parenthesis).

Distance from peptide backbone	Avg # of water	Avg # of TMAO	Water:TMAO
<4Å	92.5 (4.4)	3.7 (0.3)	25:1
4–8Å	245.3 (12.3)	14.6 (0.9)	16.8:1
8–12Å	426.9 (17.6)	23.8 (1.5)	17.9:1

The first hydration layer of the peptide backbone was further analyzed by determining the number, and duration, of direct contact or collision events. These results are presented in Table 3. As a result of the more collapsed backbone structure in TMAO solution, there is a reduction in the number of average water contact events with the backbone model as compared to in pure water solution. Interestingly, the residence time of backbone-water contact events in TMAO solution (14.5 ps) is longer than that in pure water solution (8.4 ps). The preferential exclusion manifests as an intertwining of correlations that results in a change in the protein state, even for a sidechainless peptide. There is a change in the first hydration shell, an increase in that first shell waters' residence time and a modification of the backbone structure. This is an expression of the effect of the triplet correlation between osmolyte, water and peptide backbone.

Table 3.

Solvent contact collision events with the peptide backbone model. Contact occurs when any solute atom is within 3.0 Å of any solvent atom. Residence time indicates the duration of the contact event.

Solution	TMAO Events	TMAO Residence Time (ps)	Water Events	Water Residence Time (ps)
TMAO	6.4 (0.6)	28.5 (3.4)	66.6 (14.5)	14.5 (1.)
Water	-	-	77.2 (3.8)	8.4 (0.5)

Hydrogen bonds are a traditional means to quantify aqueous solution structure although different definitions can produce a corresponding spread in interpretations. To determine the effect of TMAO on the water hydrogen bond network (water structure), the average number of hydrogen bonds per water molecule was calculated using a more and a less strict hydrogen bond criteria tabulated in Table 4. Using either criterion, there is no statistically significant difference in the number of hydrogen bonds per water molecule, regardless of distance from the backbone. This is in contrast to previous studies that have shown an increase in hydrogen bonds per water molecule upon the addition of TMAO to pure water ²⁵. The values using the second geometric criterion for hydrogen bonds (2.5 hydrogen bonds per water molecule) correspond very well with some previous simulations studies which showed an average of 2.4 hydrogen bonds per water molecule at a similar mole fraction of TMAO ⁴⁵.

Table 4.

Average number of hydrogen bonds. Values were calculated according to two different geometric criteria. (a) Criterion 1: distance between donor and acceptor within 3Å and the angle spanned by the donor-hydrogen-acceptor less than 60° (a value of 180° corresponds to fully planar). (b) Criterion 2: distance between donor and acceptor is within 3.5Å and the donor-hydrogen-acceptor angle is less than 30°⁴⁵.

Simulation	Distance from Backbone	Average hydrogen bonds per Water Molecule	Average water-water hydrogen bonds per Water Molecule	Average water- TMAO hydrogen bonds per TMAO	Average number of peptide-water hydrogen bonds
Water Solution	<4Å	2.7	2.4	-	40.1
	4 – 8Å	2.7	2.7	-	-
	8 – 12Å	2.7	2.7	-	-
TMAO Solution	<4Å	2.7	2.3	1.7	36.7
	4 – 8Å	2.7	2.6	2.0	-
	8 – 12Å	2.7	2.6	2.0	-
a.

Simulation	Distance from Backbone	Average hydrogen bonds per Water Molecule	Average water-water hydrogen bonds per Water Molecule	Average water- TMAO hydrogen bonds per TMAO	Average number of peptide-water hydrogen bonds
Water Solution	<4Å	2.5	2.2	-	29.0
	4 – 8Å	2.5	2.5	-	-
	8 – 12Å	2.5	2.5	-	-
TMAO Solution	<4Å	2.5	2.1	1.8	27.3
	4 – 8Å	2.5	2.4	2.1	-
	8 – 12Å	2.5	2.4	2.1	-
b.

Peptide-water and intrapeptide hydrogen bonds are also shown in Table 4. Peptide-TMAO hydrogen bonds were neglected, as these values were small (less than a half a hydrogen bond per structure) due to the preferential exclusion of TMAO. For both hydrogen bond criteria there is a decrease in the number of peptide-water hydrogen bonds in TMAO solution, as compared to the pure water simulations. This is marked by a slight increase in intrapeptide hydrogen bonds in TMAO solution. The average number of intrapeptide hydrogen bonds is small (as are the differences between the backbone model in TMAO and water) due to the large number of conformations with zero intrapeptide hydrogen bonds in both solutions, thereby heavily influencing the magnitude of the averages. However, the trend towards some increase in intrapeptide hydrogen bonds based upon our criteria is expected, as a collapse in the peptide backbone promotes an increase in such intrapeptide correlations as well as a decrease in peptide-water interactions.

Discussion

Transfer of free energy values have been used to provide testable hypotheses into the mechanism of the observed thermodynamics of protein folding ¹. However, the lack of structural characterization of the effect of osmolyte on the peptide backbone, in the absence of sidechains, has prevented describing a clear mechanism emphasizing the importance of the peptide backbone in the folding process versus the traditional view dominated by sidechains. Our study addressed this issue by simulating a “sidechainless protein” in the presence of osmolyte to model structural insight into the effect of the osmolyte TMAO on the peptide backbone.

Oligoglycine is a unique backbone model in that it has no sidechain sterics and lacks a stable folded structure. Inherent to this choice of system, there is neither a definitive native nor unfolded state. Thus, the system chosen has no intrinsic propensity to form traditional backbone structures. In order to characterize the nature of conformations sampled by the backbone model, we utilized several analysis methods to probe a variety of structural properties. Use of the radius of gyration, as in Figure 1, demonstrated the differences between the overall state of compaction or extension the peptide backbone adopts in both simulations. The change of the ensemble of backbone structures towards a region of lower radius of gyration indicates that the addition of TMAO caused the collapse of a peptide backbone without the influence of sidechains. Similar analysis of the distances between Cα pairs demonstrates that in TMAO solution the peptide backbone Cα pair distances are closer than in pure water, also indicating collapse of the peptide backbone.

By using complementary methods of structural analysis we characterized the conformations that the backbone samples in both solutions and subsequently have somewhat arbitrarily defined a criterion for the collapsed state of the peptide. This was accomplished by selecting a radius gyration of 0.8 nm as our cutoff value for defining a collapsed and extended conformation, and grouping similar collapsed and extended structures from the cluster analysis. The degree by which the addition of TMAO causes a change in the distribution of the radius of gyration was thus made quantitative: in TMAO solution 81% of the structures are in the collapsed state, whereas only 67% of the peptide backbone structures are collapsed in pure water. Similarly, grouping the structures that are in collapsed and extended conformations in our cluster analysis shows that 86% of the cluster structures at this TMAO concentration can be defined as collapsed whereas in pure water only 73% of the cluster structures are collapsed. Previous simulations found water to be a more poor solvent for a peptide backbone model in which 83% of the conformations in pure water were collapsed, based upon a 0.7nm radius of gyration cutoff ³⁵. This difference could perhaps be attributed to model differences, as the parameters used by the previous authors are different from those used in this study.

This provides a clear demonstration that TMAO does indeed force the protein backbone to fold upon itself into a more collapsed state in the absence of sidechains. Our computations are in accord with the previous experimentally shown contraction of a larger, truly disordered protein by TMAO ³¹ and by a decrease of the radius of gyration of a prion protein in simulations with TMAO present ³². However, in this study we demonstrated that TMAO could induce contraction of the peptide backbone itself, in the absence of sidechains.

The biasing of the peptide backbone towards a more compact state upon the addition of TMAO could be initially seen to be reconciled by crowding-induced stability as has been shown in the reduction of the radius gyration of proteins in recent simulations ^46–48. However, there are a few notable differences between those studies and the ones carried out here, suggesting that the collapse of the peptide backbone caused by TMAO is not easily described as a similar crowding effect. First, the crowding simulation studies utilized very large crowding agents, essentially the size of the folded state of the protein of interest or greater^46,48. The choice in size of the crowding agents was intentional in order to recreate the effect of globular macromolecules ⁴⁸, whereas the TMAO and water models used here are significantly smaller than our solute of interest. Also, were TMAO-induced collapse of the protein backbone to be like a macromolecular crowding effect, we would expect a similar subtle change in the radius of gyration profile as seen previously using large crowders ⁴⁷. However, the significant increase in small radius of gyration structures and a complete lack of population of large radius of gyration structures of the peptide backbone in TMAO solution suggests that the collapse of the peptide backbone is not consistent with a decrease in the radius of gyration caused by simple crowding. The distinct changes in the hydration properties caused by TMAO also indicate that the effect seen here is unlikely to have been caused purely by the addition of an inert molecular crowder.

Calculation of the preferential interaction parameter of TMAO and the peptide backbone demonstrated that this model of TMAO is preferentially excluded from the local region surrounding the peptide backbone. The preferential exclusion seen here corresponds with the recent predictions of a deficit of protecting osmolyte in 1M TMAO solution around a peptide backbone unit utilizing Kirkwood-Buff theory and experimental thermodynamic measurements ⁴⁴. Additionally, this preferential exclusion caused an increase in the first hydration layer of the peptide backbone evident by an increase in the ratio of water to TMAO molecules as well as an increase in the residence time of water contacts with the backbone and is in contrast to the direct interaction of urea with a similar peptide backbone model ³⁵. Therefore, even though TMAO is excluded from the local domain of the protein, the osmolyte still possesses the ability to alter the hydration of the peptide backbone, and suggests that the triplet correlation between osmolyte, peptide backbone, and water must be explicitly considered. While triplet correlations are notoriously difficult to manage computationally, this correlation can be seen pictorially in a representative snapshot from our aqueous TMAO simulations in Figure 5. In this snapshot we have included the first two solvation shells of the peptide, colored to emphasize particular features. We see quite clearly the exclusion of TMAO within the first hydration layer of the peptide. TMAO was found to make only very rare direct contacts with the peptide. As we progress outwards, the number of TMAO molecules increases and we can see the strong hydration layer of TMAO ^{23,45,49–51} influencing the hydration layer of the peptide backbone. The TMAO molecules essentially bring water to the peptide via the strong correlation of water with TMAO. The subsequent layer of water between TMAO and the peptide is no longer unaffected first solvation shell peptide waters or simply TMAO solvation shell waters but waters that now occupy a unique shared position between both the peptide and the TMAO. The waters are thus non-optimally structured for the peptide and prove to be a poorer solvent causing compaction. This triplet correlation drives the peptide to a preferred lower radius of gyration structure.

Figure 5.

Representative snapshot from the aqueous TMAO simulation demonstrating solvation of TMAO, water and peptide backbone. Peptide backbone in center with first hydration shell (within 4.0Å from the peptide surface) waters (black) and TMAO (yellow). Orange TMAO molecules that are excluded from the first hydration shell of the peptide, yet still influence the hydration shell of the peptide. Purple waters represent second hydration waters of the peptide (8Å from the peptide).

It has been proposed that the mechanism for osmolyte-induced stability is predicated based upon the potential number of interaction sites of the osmolyte with the peptide backbone ⁹. Based on a simple statistical mechanics model, it was suggested that protecting osmolytes, such as TMAO, are excluded from the domain because there is a lack of favorable (complementary charged sites) interactions. Conversely, the nonprotecting osmolyte accumulates near the backbone because of the higher probability of favorable interactions with the backbone, as compared to water ⁹. However, hydrogen bonding of TMAO as an acceptor is favorable although donating is clearly not. So it is true that there may be fewer complementary interactions for TMAO than urea, for example. However, this description does not make clear the role of water as a marginal backbone solvent. Thus, excluding TMAO from the peptide is not enough or there would be little difference between pure water and TMAO solution. The vicinal water must become a poorer backbone solvent in the presence of TMAO.

By connecting the thermodynamic definition of the preferential binding coefficient with the deficit (or excess) number of osmolytes surrounding a protein it becomes apparent how preferential exclusion and hydration affect protein stability. The exclusion of osmolyte from the protein domain increases the chemical potential of the protein by having the osmolyte-shared water be not as orientationally available for optimal interactions with the protein, shifting the equilibrium to the compact state of the protein. For osmolytes that are found in excess around the protein surface a more direct interaction model is reasonable ^52,53. The demonstration that the sidechains are not necessary for the compaction from preferential exclusion of the protecting osmolyte TMAO allows for the connection between the classic preferential exclusion model ^3,53,54 with the thermodynamic transfer free energies demonstrating the importance of the peptide backbone in the folding process. Our data suggests that the unfavorable interactions with the peptide backbone are caused by the preferential layering of TMAO and its hydration water around the peptide backbone thus accounting for the experimentally seen increase in transfer free energy for the backbone component.

The role that the structure of the water network has in osmolyte-induced conformational stability has been a point of some contention. Therefore, we analyzed the hydrogen bond network of the water structure using two hydrogen bond criteria for thoroughness. There was no evidence for a reduction (or increase) in the water hydrogen bond network caused by the addition of the osmolyte TMAO. Previous simulations using the same parameters for TMAO as used in this study ^26,28 as well as a modified TMAO model ⁴⁹, also did not see an increase in the strength or number of water hydrogen bonds as seen previously using older parameters for TMAO ²⁵. The prime difference found was a decrease in the number peptide-water hydrogen bonds in TMAO, as seen in Table 4, and is consistent with the water in the proximal layer being a somewhat less good solvent for the peptide.

Conclusions

The usage of osmolyte transfer of free energy values has allowed for the development of the backbone-based protein folding model which, like Pauling’s original work ⁵⁵, deemphasizes the role of sidechains structure in the thermodynamic process of protein folding. The demonstration of additivity of transfer of free energy values for backbone plus sidechain model compounds has validated the polyglycine peptide as a viable model for the protein backbone ²⁹. However, structural insight into the effect of osmolyte on this backbone model has been lacking. Using model simulations of an oligoglycine we have provided structural arguments regarding the interactions and correlations between the osmolyte TMAO, water and the protein backbone. The benefit of this analysis is that we were able to avoid previous experimental hurdles associated with solubility of the compound series and provide an atomistic-level view of the osmolyte-water-protein backbone interactions in a sidechain free system. We remark that this study would have been difficult experimentally due to solubility issues with G₁₅.

Through various structural analyses we have shown that TMAO causes collapse of the most fundamental unit of proteins, the protein backbone, in the absence of sidechains. The calculation of the preferential interaction parameter between osmolyte and peptide backbone has shown preferential exclusion of the TMAO from the local region surrounding the protein backbone due to a lack of release of waters from TMAO. As a result of this preferential exclusion there exists a first hydration layer surrounding the peptide backbone, caused by the proximity of the hydrated TMAO, which is less favorable thermodynamically for the extended forms of the peptide than pure water. Our analysis of both the backbone conformations and solution properties gives a molecular justification for the classical view of the osmophobic effect in the collapse of the peptide backbone.