Modeling the resonant release of synaptic transmitter by hair cells as an example of biological oscillators with cooperative steps

Abstract

The initial synapses of the auditory system, which connect hair cells to afferent nerve fibers, display two unusual features. First, synaptic transmission occurs in a multiquantal fashion: the contents of multiple synaptic vesicles are discharged simultaneously. Second, synaptic transmission may be tuned to specific frequencies of stimulation. We developed a minimal theoretical model to explore the possibility that hair-cell synapses achieve both multiquantal release and frequency selectivity through a cooperative mechanism for the exocytotic release of neurotransmitter. We first characterized vesicle release as a four-step cycle at each release site, then generalized the result to an arbitrary number of steps. The cyclic process itself induces some degree of resonance, and may display a stable, underdamped fixed point of the release dynamics associated with a pair of complex eigenvalues. Cooperativity greatly enhances the frequency selectivity by moving the eigenvalues toward the imaginary axis; spontaneously oscillatory release can arise beyond a Hopf bifurcation. These phenomena occur both in the macroscopic limit, when the number of release sites involved is very large, and in the more realistic stochastic regime, when only a limited number of release sites participate at each synapse. It is thus possible to connect multiquantal release with frequency selectivity through the mechanism of cooperativity.

The principal means of intercellular signaling in the nervous system is chemical neurotransmission, in which an electrically excited presynaptic cell releases transmitter from an intracellular storage site. Upon binding to postsynaptic receptors, the transmitter molecules produce a postsynaptic current that can be recorded with a microelectrode. Observations made in the presence of a reduced extracellular concentration of Ca²⁺, the ion whose entry into a presynaptic terminal initiates exocytosis, established that transmitter release is quantal in nature. Several lines of experimentation further demonstrated that transmitter accumulates in membrane-bounded synaptic vesicles and that each stochastic fusion of a vesicle with the surface membrane yields a quantal postsynaptic event. Exocytosis occurs at a presynaptic active zone that comprises an array of release sites surrounded by hundreds of synaptic vesicles.

Synaptic transmission faces serious challenges in the auditory system, which has evolved to process high-frequency stimuli with great temporal precision. Our ability to localize a sound source by detecting the interval between the arrival times of the signal at the two ears, for example, requires a neural precision of less than 20 μs (1). In a second example, the firing of neurons in some animals displays significant phase-locking to stimuli at frequencies approaching 10 kHz (2). The first synaptic relay of the auditory pathway connects a hair cell, the sensory receptor of the ear, to an afferent nerve fiber of the eighth cranial nerve. As if to underscore the magnitude of the challenge facing this contact, it displays a morphological specialization characteristic of several sensory systems: the ribbon synapse, without which precise transmission is impaired (3). Although the role of the synaptic ribbon remains obscure, it is plausible that the organelle contributes to the unusual properties of neurotransmission by hair cells.

Two important qualitative features of synaptic transmission by hair cells have yet to be explained. First, the neurotransmitter content of multiple vesicles can be released synchronously, yielding large, multiquantal postsynaptic responses (4–6). Although this behavior might originate from prefusion of several vesicles, it could alternatively stem from the tight coordination of vesicle release at the synaptic ribbon. Second, in keeping with the auditory system’s strategies for frequency tuning of its constituent hair cells and neurons, vesicle release appears to be frequency-tuned as well: When a hair-cell is stimulated by sinusoidal oscillation of its membrane potential, the rate of vesicle fusion as a function of stimulus frequency displays a peak (7). To explore a possible basis of multiquantal release and frequency selectivity at synapses, we developed a minimal model of cooperative vesicle release.

Description of the Model.

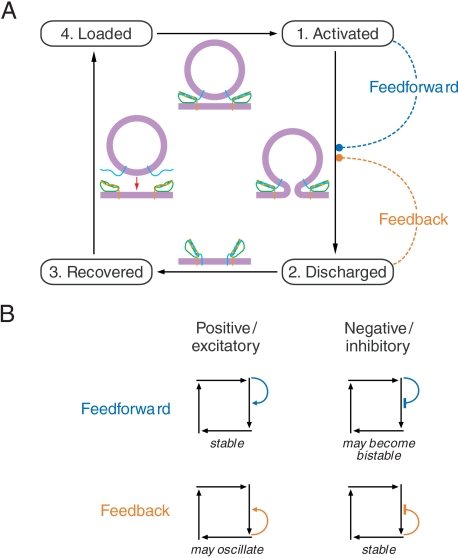
Vesicle release is a cyclical stochastic process. Because a presynaptic terminal contains myriad vesicles but only a limited number of release sites, our modeling centered not on the life cycle of a vesicle, but rather on that of a release site (8, 9). For a biologically plausible model, each site must cycle through a minimum of four distinct states (Fig. 1). First, the site is activated by Ca²⁺, which binds to a protein such as synaptotagmin or otoferlin to initiate exocytosis. Next, after the vesicle’s membrane has fused with the surface membrane and transmitter has been released by diffusion, the discharged site retains the complex of SNARE proteins that mediate exocytosis. In the third state, the recovered site is prepared by a series of biochemical reactions to accept the next vesicle. Finally, the site is loaded with a new vesicle and primed for exocytosis. Because there are likely to be additional configurations, we defined the state space of the system at a given time by the possibility that any of R release sites occupies any of N states.

Fig. 1.

The Markov ring model expressed as a four-state diagram. A. Each release site undergoes a cycle of irreversible, monomolecular steps: Activated, the site initiates the fusion of a vesicle to release its contents; discharged, the site completes the exocytotic process; recovered, the site prepares to accept the next vesicle; and loaded, the site docks and primes a new vesicle for release. The central cartoons depict a release site and an associated vesicle during the transitions between successive states. Cooperative effects in the fusion process can take two forms: Feedforward in which the population of activated sites influences the rate coefficient for the transition from activated state 1 to discharged state 2, and feedback in which this transition is modulated instead by the population of discharged sites. B. Positive cooperativity means that a transition’s rate coefficient is augmented by an increase in the relevant population, whereas negative cooperativity implies a decrease in the rate coefficient. Flow through the cycle is stabilized by either positive feedforward, in which a larger number of activated sites increases the fusion rate coefficient, or negative feedback, in which a greater number of discharged sites decreases the rate coefficient. Negative feedforward, in which a large number of activated sites decreases the rate coefficient for fusion, exhibits an instability at high cooperativity in which the flow becomes bistable. A large population of activated sites remains large by allowing only a few vesicles to fuse; a small population stays small by permitting more fusions. The case examined in this paper involves positive feedback. For a sufficient amount of cooperative interaction this model becomes oscillatory, and in the vicinity of the oscillatory transition, a Hopf bifurcation, the model displays resonance and frequency selectivity.

We examined the system at two levels of detail. The more detailed representation involves a master equation that treats the sites as identical and represents a Markov process (10) defined by the probability of a population of n_i sites residing in state i at a given time. We used this approach to conduct stochastic simulations that are described in the second half of this paper. To begin, we considered a more schematic approach that tracks the deterministic evolution of the macroscopic ensemble average of the number of sites in a given state. We defined the dynamical variable

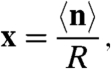[1]

in which the components of the vector n are the populations n_i and therefore a proportion x_i of sites are in state i∈{1…N}. The dynamics of the system is governed by differential equations of the form

[2]

with N transition-rate coefficients k_i,i+1. Arranged in a chain, the states interact only with neighbors and only through irreversible reaction steps; allowing the index to wrap around, k_N,N+1 ≡ k_N,1, closes the chain into a ring (Fig. 1A). There is a straightforward correspondence between these rate equations that govern x and the master equation for n (Supplementary Information). The loss of detail associated with the simpler form is offset by the tractability of the resulting model: The presence of frequency selectivity can be rigorously proven in the deterministic framework and exhibited as a numerical result by stochastic simulation.

The Markov ring model incorporates three different dynamical processes. First, there is a background rate of transitions from each state to the next. This step manifests itself as the linear component of the dynamics of x. Second, we introduce an autocatalytic transition between the states labeled activated and discharged, designated without loss of generality as states 1 and 2, such that the rate of the transition depends on the occupancy of those two states. This term captures the cooperativity between release sites and provides a nonlinear contribution to the dynamics that affects only the two states in question. Finally, we include as the input to our system a periodic parametric forcing of the rate of transition to the activated state. The rate equation for x can then be rewritten compactly as

[3]

in which the separate contributions of the linear, nonlinear, and parametrically forced components of the dynamics are evident. The function g captures the nonlinearity, ε is its strength, F is the amplitude of forcing at frequency ω, and the matrices A, B, and C are constant. The rate coefficients of Eq. 2 are connected to the variables of Eq. 3 through k_ij ≡ A_ij + εg(x₁,x₂)B_ij + F sin(ωt)C_ij. A consequence of Eq. 2 is that, by construction, the total number of release sites is a conserved quantity of the dynamics, such that 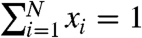and the matrices satisfy u^TA = u^TB = u^TC = 0, with u an array of ones.

We set the rate coefficients between states 2,...,N as identical and normalized to unity, which is equivalent to rescaling time. The remaining transition, that between states 1 and 2, represents the cooperative vesicle-fusion step for which the rate coefficient k₁₂ is

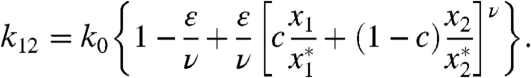[4]

Here ν is a Hill coefficient and c determines the relative contributions of feedforward (c = 1) and feedback (c = 0). The vector x^∗ is the unique steady state of the linear Markov ring that arises when the strength of the nonlinearity ε and forcing F are set to zero; k₀ is the rate coefficient of the fusion step in that linear case. Because negative cooperativity in this model cannot lead to increased frequency selectivity, we explored only positively cooperative interactions wherein k₁₂ is a monotonically increasing function of x₁ and x₂. The advantage of writing the nonlinearity in the form of Eq. 4 is that the steady state of the linear problem, x^∗, remains a known fixed point of the nonlinear system, facilitating the analysis of its stability.

Response in the Absence of Cooperativity.

Given this simple Markov ring model, we examined the influence of the parameters on the system’s ability to resonate. Consider the time dependence of the Markov ring in the linear case,

[5]

determined by the sparse N-by-N transition-rate matrix A. For N = 4,

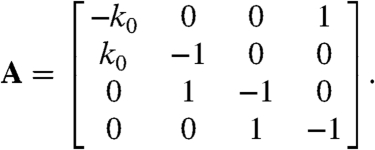[6]

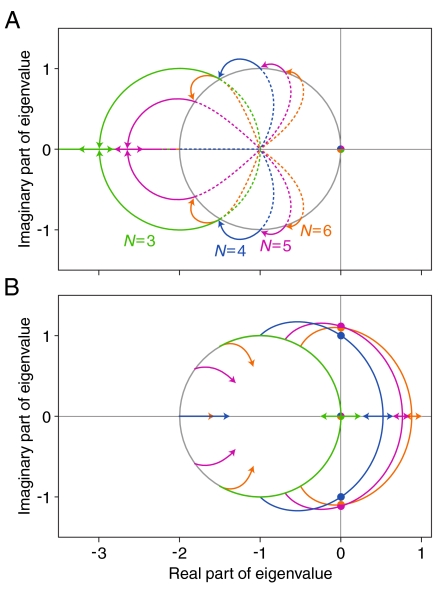
The response characteristics of the system are defined by the N eigenvalues λ_n of A. The solution to Eq. 5 is x = e^Atx₀ for some initial distribution x₀ (10), so the eigenvalues λ_n represent the complex frequencies at which the system’s eigenmodes oscillate or decay. The quality factor, defined in terms of the eigenvalues as Q_n = |ℑmλ_n/ℜeλ_n|, describes the system’s sharpness of tuning and its degree of resonance. When k₀ = 1, the complete symmetry of the system implies that the steady state is 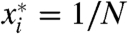. In this instance, the eigenvalues of A, which are specified by the equation (1 + λ)^N = 1, are equally spaced in the complex plane along a circle of unit radius about the point (-1,0) (Fig. 2A). The eigenvalues closest to the imaginary axis determine the maximal quality factor Q_max.

Fig. 2.

Properties of the linear Markov ring for models of four different sizes. A. The arrows show the motion of the system’s eigenvalues as the rate coefficient k₀ varies. Increasing (solid lines) or decreasing (dotted lines) k₀ from a value of one always reduces the quality factor and eventually moves the eigenvalues away from the imaginary axis. In the limit k₀ → ∞, an N-state system becomes a system with one less state, represented here by the joining of the end of each solid arrow to the origin of an adjacent arrow of a different color. The limit k₀ → 0 moves the eigenvalues onto the point (-1,0). B. Stability analysis shows the effect on the fixed point x^* of increasing feedback while k₀ = 1 remains constant. Increasing cooperative interactions by raising ε in Eqs. 3 and 4 boosts the quality factor, eventually pushing a conjugate pair of eigenvalues across the imaginary axis at a Hopf bifurcation (filled circles). The constant eigenvalue at the origin corresponds to the conservation of the number of release sites.

For a general k₀, the eigenvalues of A are solutions to (k₀ + λ)(1 + λ)^N-1 = k₀. To understand qualitatively how the eigenvalues are displaced from the unit circle as k₀ varies, consider two limits (Fig. 2A). As the rate coefficient k₀ becomes very large, states 1 and 2 are effectively unified, so the system tends to a new system with N - 1 states and k₀ = 1. In the opposite limit, as k₀ approaches zero, the ring of states is broken and we are left with a linear chain. Owing to this change in the topology of the graph, there can be no oscillatory behavior and the imaginary parts of all the eigenvalues must collapse onto the real axis.

The quality factor reaches a maximum of Q_max = tan{[(N - 2)/2N]π} at k₀ = 1 and approaches zero in the limits k₀ → 0 and k₀ → ∞. Although we have demonstrated the maximum in the quality factor by a perturbation of a single element of the cyclic chain, the maximum is global (Supplementary Information).

The Effect of Cooperativity.

We next examined a minimal model in which the Markov ring is locally enhanced by cooperativity that takes the form of a feedback or feedforward step (Fig. 1). Although negative feedforward can lead to bistability, we are concerned here with oscillatory instabilities, which can occur in this model only through positive feedback. When nonlinearity in the form of Eq. 4 is introduced, multiple attractors may arise. Fixed points occur as those solutions to a νth-order polynomial equation, for which the x_i are nonnegative and sum to one. Because it is the only fixed point to exist for all parameter values, we termed x^∗ the central fixed point. Although we were aware of attractor sets other than x^∗ and could not rule out their significance, during our numerical simulations we encountered none that significantly influenced the behavior of the system in the parameter range of interest.

In order to explore the behavior of the fixed point x^∗ as we varied the parameters, we constructed the linearized stability matrix. When the strength of cooperativity ε increases from zero, the matrix B and function g begin to play a role. For N = 4,

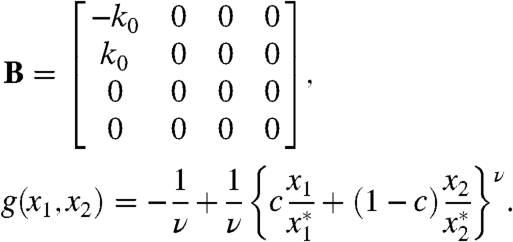[7]

Consider a small perturbation around the central fixed point, x = x^∗ + Δx. The character of the response to the perturbation is determined by the eigenvalues of the stability matrix in an analogous way to the role the eigenvalues of A play in Eq. 5. The stability matrix or Jacobian, which is

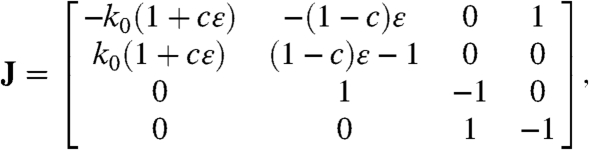[8]

includes a supradiagonal entry J₁₂ that depends purely on the nonlinear coupling term (Supplementary Information). Moreover, J₁₂ depends exclusively on the coupling to x₂; during positive feedforward, for which c = 1 and coupling occurs through x₁ alone, this off-diagonal component vanishes. The structure of the matrix J during feedforward accordingly does not differ from that of the linear, noncooperative Markov ring studied in the previous section, and feedforward cannot enhance the quality factor beyond that achieved in the noncooperative case.

We next concentrated on the positive-feedback mechanism by setting c = 0. We examined the (k₀,ε) plane to study the character of the fixed point x^∗. As cooperativity grows owing to an increase in ε from zero, the eigenvalues of J approach the imaginary axis, thereby enhancing resonance. In conspicuous contradistinction to the noncooperative case, the trajectories of the eigenvalues as a function of increasing ε demonstrate large increases in the quality factor (Fig. 2B). If ε continues to increase, the system eventually undergoes a supercritical Hopf bifurcation as a complex-conjugate pair of eigenvalues crosses the imaginary axis. Immediately before the bifurcation, the system offers the benefits of proximity to a critical point (11–13); at the bifurcation, the quality factor diverges. Beyond the bifurcation, the fixed point becomes unstable and the system produces limit-cycle oscillations. In those situations in which a purely real eigenvalue crosses the imaginary axis, a pitchfork bifurcation occurs in the absence of oscillations.

Phase Diagram of Bifurcations.

To chart the qualitative behavior of the Markov ring, we determined the locations of the bifurcations in (k₀,ε) space. The eigenvalues of the central fixed point of an N-state model are determined by the roots of an Nth-order polynomial in λ:

[9]

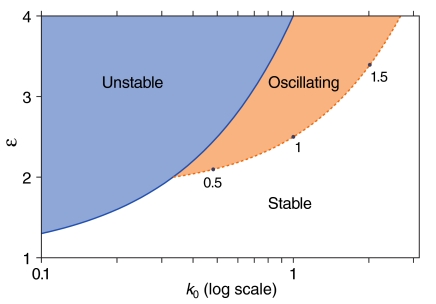
In general, different eigenvalues cross the imaginary axis for distinct sets of parameter values. We are interested in the first such crossing, when all but one of the eigenvalues are stable. One of the roots is always λ = 0 owing to the conservation of the number of release sites. To determine the remaining N - 1 roots, we divided the left hand side of Eq. 9 by λ. We sought additional λ = 0 roots and thus found that pitchfork bifurcations occur when the parameters satisfy ε_PB = 1 + (N - 1)k₀ (Fig. 3). The Hopf bifurcations, which reflect solutions for which λ is purely imaginary, occur for N = 4 along the line

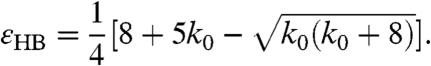[10]

Fig. 3.

Stability diagram of the central fixed point in a four-state system. The oscillating region of the diagram corresponds to at least one eigenvalue with a positive real part and a nonzero imaginary part. In the unstable region, at least one of the eigenvalues is positive and real, with zero imaginary part. The boundary separating the stable and oscillating regions represents a line of Hopf bifurcations; the normalized frequencies of the oscillations born there are indicated at three locations. Selecting a specific point along the line of Hopf bifurcations near which to operate tunes the resonance of the system to a specific frequency. A triple point occurs at (k₀ = 1/3, ε = 2).

Synchronous Release and Frequency Selectivity.

Upon introducing cooperativity in the fusion step, we expected to see highly correlated and hence synchronous release. We wished to study this phenomenon, along with the anticipated frequency selectivity of the Markov ring’s response, both in the macroscopic limit and in the presence of intrinsic noise owing to the finite number of release sites. In order to measure the system’s input-output relation, we first specified two details: how an external input couples to the system, and how the frequency selectivity of the output is quantified. We applied a small, periodic, parametric forcing at frequency ω and amplitude F. We depicted the formation of the activated state as linearly dependent on the periodic force, which in terms of vesicle release corresponds to a varying cytoplasmic Ca²⁺ concentration. The matrix C in Eq. 3 therefore assumes the form

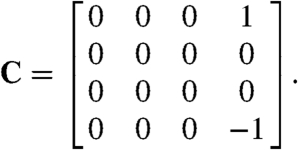[11]

The output consists of vesicle-fusion events, which are transitions between states 1 and 2 of the Markov ring, that occur at times t_j. With respect to the phase of the input, ωt, the relative phases of the fusion events are θ_j = ωt_j (modulo 2π). We computed the steady-state probability distribution P(θ) of event phases in the macroscopic limit by numerically solving differential Eq. 3 and noting that the time-dependent fusion rate is given by x₁(t)k₁₂(t). For the stochastic regime in which a finite number R of release sites participate, we developed a time-dependent Gillespie simulation (14) that allowed us to sample the distribution P(θ) (Supplementary Information). Output that is uncorrelated to the input leads to a uniform P(θ). When the output is phase-locked to the input, P(θ) exhibits a highly peaked distribution. The extent of phase-locking can be characterized by the vector strength or synchronization index,

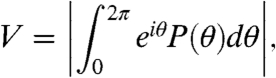[12]

which has the property of being equal to zero for phase-uncorrelated output events and equal to one only when the events always occur at exactly the same phase of the periodic input.

The degree to which events occur in bursts, in a synchronized manner analogous to multivesicular release, can be assessed from the distribution of interevent intervals. The probability that an event j + 1 occurs with a time delay τ after an event j can be written compactly as P₍₁₎(τ). In general, we may consider the delay between events separated by m - 1 other events, with distribution P_(m)(τ). For a Poisson process, the waiting-time distribution, P₍₁₎(τ), is an exponential, and the delays between larger separations are determined through the process’s Markov property: 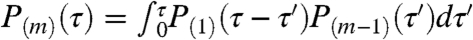. Coordinated release becomes apparent in deviations from these distributions.

Results from Simulations.

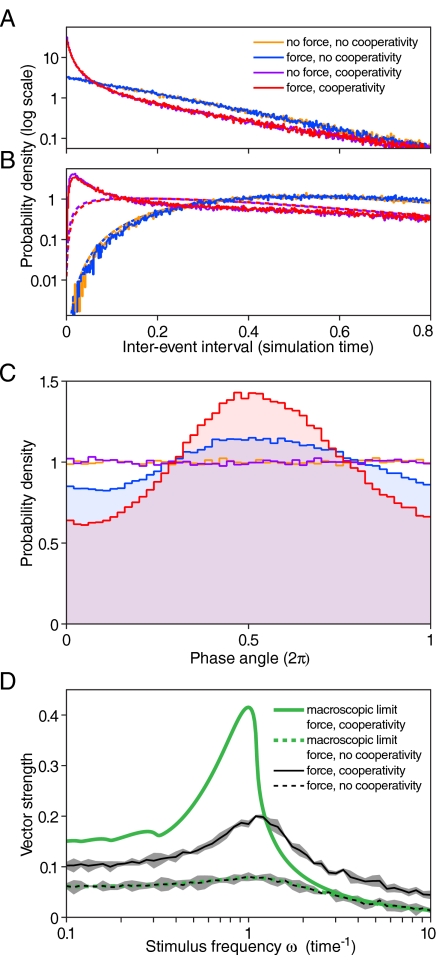
In the absence of cooperativity, release is essentially a Poisson process. By contrast, cooperativity greatly enhances the nearly synchronous release of multiple vesicles (Fig. 4A). By using the freedom to rescale time, we can choose the model system’s intrinsic frequency. For a synapse with R = 20 release sites and an intrinsic frequency of 100 Hz, as an example, the probability of releasing four or more vesicles during a 50 μs period increases by a factor of 400 in the presence of cooperativity. As observed experimentally, multiquantal release occurs in the absence of stimulation (F = 0) and independently of whether the stimulation is periodic or otherwise (4).

Fig. 4.

The effects of cooperativity on release statistics. A. The probability of release of two vesicles in quick succession is illustrated by plotting P₍₁₎(τ), which is elevated from its basal state (Blue, Orange: ε = 0) by the addition of cooperativity (Red, Purple: ε = 1.7). The effect is independent of external periodic forcing of amplitude F, demonstrated by the fact that the purple and orange lines (F = 0.5) are identical to their blue and red counterparts (F = 0). In the noncooperative case, P₍₁₎(τ) follows the exponential distribution expected of a Poisson process, as seen by the straight line on this log-linear plot. Stochastic simulation was performed with ω = 1.1, R = 20, k₀ = 0.55, and ν = 5, placing the cooperative system in the stable region near a Hopf bifurcation. B. The probability of release of four vesicles in quick succession, illustrated by P₍₃₎(τ), shows even greater elevation owing to cooperativity. The dashed lines show P₍₃₎(τ) based on P₍₁₎(τ) if the release process were Markovian. The noncooperative case satisfies the Markov condition, whereas the cooperative case does not. (C) Phase synchronization in the presence of a periodic stimulus is enhanced by cooperativity. The effect of forcing (Red, Blue) visible in C but not in A and B stems from a separation of timescales: the waiting time between events is dominated by delays smaller than 0.1, much less than the period 2π of the forcing. The deviations of the red and blue distributions from the uniform distributions shown in purple and orange, which constitute evidence of phase synchrony, are quantified by the vector strength defined by Eq. 12. The sharper the peak, the greater the vector strength D. The frequency dependence of synchronization is summarized by the vector strength calculated from a series of simulations, such as that in C, in which the stimulus frequency ω was varied for a constant force F = 0.5. The response in the presence of cooperativity is shown in solid black, surrounded by 95% confidence intervals in gray. Traces of subharmonic resonances of the macroscopic limit are visible in the solid green line at frequencies of 0.3 and less. The noncooperative case is portrayed with dashed lines. As indicated by the overlapping of the dashed black and dashed green lines, the macroscopic limit and finite-size simulations agree in the linear noncooperative case. The presence of intrinsic fluctuations limits the maximal synchrony achievable in the cooperative case.

On the timescale set by the mean interevent interval, which is much smaller than the period of stimulation, external forcing has no effect on cooperative or noncooperative release. Stimulation plays a role only on the timescale set by the period ω^-1 of forcing. Even on this much longer timescale, however, cooperative interaction has an effect. The presence of an external force dictates a certain degree of phase synchrony from any system. Cooperativity raises the phase synchrony of the response (Fig. 4B) and does so in a frequency-selective manner (Fig. 4C), even when the system is overwhelmed by intrinsic noise owing to a small number of release sites.

The maximal increase in the vector strength as a function of cooperativity depends on the magnitude of intrinsic fluctuations. Finite-size effects, which blur the macroscopic dynamics and dull the precision of phase-locking, have two sources. Both the number of steps N in the cycle and the number R of release sites affect the maximal vector strength and the sharpness of frequency dependence. This effect is apparent as a decrease in vector strength owing to finite values of R (Fig. 4C).

Discussion

Inspired by the vesicle-release machinery of auditory synapses, we explored a minimal model of a biological oscillator involving a locally enhanced Markov ring with one nonlinear, cooperative step. By introducing a cooperative step in the form of positive feedback, we were able to explain and connect two previously unrelated observations: multiquantal release, which we associate with temporal synchronization of transitions through the cooperative step; and the frequency selectivity of synchronized release in response to external forcing.

There are numerous models of biological oscillators, many of them based on genetic networks (15, 16). Some involve a time delay and negative feedback (17, 18), whereas others employ a repressive cycle, or rock-paper-scissors mechanism (19). The oscillating quantity is typically the rate of production of a target protein, which in our model is analogous to the rate of fusion events. Further similarities break down, however, because the site-based model that we present here fixes the total number of release sites, whereas the equivalent conservation law usually does not apply in genetic or biochemical networks. The constraint on state space imposed by a fixed population of release sites modifies the dynamics subtly but importantly. For instance, the common negative-feedback mechanism—which resembles negative feedforward in the current formulation—no longer elicits oscillation. It is also worth bearing in mind that the role of oscillation in the Markov ring considered here is not to establish an autonomous rhythm but instead to constitute a resonant filter in a sensory system.

The form taken by the coupling of external stimulation to the Markov ring is highly model-dependent. In the macroscopic limit and for a variety of coupling schemes, the system driven by a periodic stimulus develops chaotic behavior. Parametric forcing of the system can drive it into an unstable region—a likely outcome inasmuch as the system is intentionally poised near an instability—and engender chaos. Of many possibilities, we chose a simple forcing that captures the essentials of Ca²⁺ coupling at the synapse and avoids chaos. In any case, noise shifts the critical behavior (20), making it necessary to study the system in the stochastic, finite-size case.

What consequences might our model have for understanding the auditory synapse? Cooperative effects have previously been invoked to explain the dynamics and statistics of synaptic release in other systems. For example, negative cooperativity has been suggested to render release in hippocampal synapses more reliable by decreasing the standard deviation of the number of vesicles released by an action potential (21). The positive cooperativity examined here readily explains the multiquantal release characteristic of hair cells (4–6). More specifically, the large excitatory postsynaptic currents observed electrophysiologically could result from the essentially synchronous fusion of two to perhaps ten synaptic vesicles at adjacent release sites (Fig. 4). Positive cooperativity might arise because the fusion of a first vesicle releases some cytoplasmic factor that triggers the exocytosis of one or more nearby vesicles. Alternatively, as the membrane of a vesicle fuses with the presynaptic membrane, the flow of vesicle proteins or lipids into the presynaptic membrane—or perhaps a consequent change in the tension or fluidity of that membrane—might foster the fusion of additional vesicles. The cyclic nature of vesicle processing at release sites additionally lends itself to frequency tuning, an effect greatly enhanced by cooperativity. The observed sensitivity of the rate of exocytosis to the frequency of stimulation (7) would be expected of a cooperative release system operating near a Hopf bifurcation that would confer frequency selectivity (Fig. 3). The performance of the system depends straightforwardly on a few parameters, offering points for modulation by efferent control. This model establishes the foundation for future experimental exploration of frequency dependence at the synapse. For a more precise quantitative description of synaptic function, the model could be embellished with additional features such as reversible or deterministic transitions and a two-dimensional geometric arrangement of release sites. The statistics of multiquantal events and synaptic dynamics, including frequency selectivity, could then be fit to the model.

Along with the influence and stability of all the fixed points, the properties of the macroscopic limit might also be investigated in the continuum limit of large N. It is interesting from the mathematical point of view that this continuum limit corresponds to a modified version of the inviscid Burgers’ equation (22); viscosity would arise if reversible components were added to the system. Whether this limit might shed light on the analysis of synaptic dynamics remains a matter for future investigation. The possible existence of traveling shock waves around the ring and its eventual connection with the frequency selectivity of the dynamics also deserves consideration.