General principles of attraction and competitive attraction as revealed by large-cage studies of moths responding to sex pheromone

Abstract

Knowledge of how insects are actually affected by sex pheromones deployed throughout a crop so as to disrupt mating has lacked a mechanistic framework sufficient for guiding optimization of this environmentally friendly pest-control tactic. Major hypotheses are competitive attraction, desensitization, and camouflage. Working with codling moths, Cydia pomonella, in field cages millions of times larger than laboratory test tubes and at substrate concentrations trillions of times less than those typical for enzymes, we nevertheless demonstrate that mating disruption sufficiently parallels enzyme (ligand) –substrate interactions so as to justify adoption of conceptual and analytical tools of biochemical kinetics. By doing so, we prove that commercial dispensers of codling moth pheromone first competitively attract and then deactivate males probably for the remainder of a night. No evidence was found for camouflage. We generated and now validate simple algebraic equations for attraction and competitive attraction that will guide optimization and broaden implementation of behavioral manipulations of pests. This analysis system also offers a unique approach to quantifying animal foraging behaviors and could find applications across the natural and social sciences.

Mating disruption of insects is the agricultural practice of dispensing synthetic sex attractant into a crop so as to suppress pest reproduction by interfering with mate finding (1). The Environmental Protection Agency expects this environmentally friendly pest management tactic to effectively supplement the “softer” insecticides as well as to fill critical control gaps left as “harder” insecticides face withdrawal from the marketplace due to tightening governmental regulations (2–4), e.g., azinphos methyl (Guthion) in apple production. There are now more than 100 EPA registrations of insect pheromones for use as pest control agents in agriculture and forestry. Mating disruption for all pests encompasses ≈700,000 ha (5), 160,000 of which target codling moth, Cydia pomonella, the proverbial worm in the apple.

Despite 40 years of research and the emergence of a vigorous and expanding worldwide pheromone industry (5, 6), knowledge of how sex pheromones actually interact with target insects as individuals and groups under disruption has lacked a mechanistic framework sufficient for judging whether current practices for implementing mating disruption have been optimized. Here, we introduce and experimentally validate both attraction and competitive-attraction equations as well as a unique analysis system. Their utility in understanding and manipulating animal behaviors might parallel those of the Michaelis-Menten equation and classical enzyme kinetics in biochemistry.

Derivation of Equations.

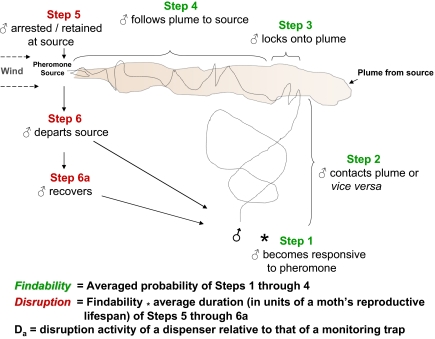
Wind traversing a pheromone point source sweeps out an odor plume whose active space and interactions with male moths are schematically represented in Fig. 1. Cumulative catch (C) of male moths (♂) in a trap (T) (Fig. S1 presents pictures of apparatus) baited with a pheromone lure is the culmination of Steps 1–5. The reasoning in Fig. 1 and SI Text 1A led to trapping Eq. 1 applying to the situation where: mobile males are randomly distributed in a bounded arena sized so that interactions with T are probable; T does not compete with other attractant sources; findability of T = probability of successful completion of Steps 1–4 of Fig. 1; efficiency of T = proportion of visiting males ensnared; retention time of T = proportion of a moth’s lifespan spent trapped; and the subscript den = density, meaning items per cage:

When retention of a moth is permanent (1.0) as is true for an effective trap, this parameter becomes silent. It is sometimes ignored below for traps. Then, rearrangement of Eq. 1 so as to isolate ♂_den yields Eq. 2:

Under competitive attraction operating in a crop treated with multiple point dispensers of synthetic pheromone, the frequency with which male insects find calling females or monitoring traps (surrogates for calling females) is reduced because males are diverted from orienting to females or traps due to preoccupation with more numerous nearby dispensers that first attract responders and then arrest and possibly deactivate them (9).* Analysis of 30 years of dosage–response profiles for moth mating disruption (10) documented that competitive attraction was involved in 11 of 13 available cases. Noncompetitive disruption includes: camouflage (masking) of traps and females by pheromone dispensers and desensitization of responder sensory systems without first requiring attraction (9).

Fig. 1.

Schematic representation of a pheromone plume, along with the designations for progressive steps leading a codling moth male to its source. *, starting point. Our treatment of attraction and disruption kinetics was inspired by conceptual parallels with enzyme kinetics (7) and ligand–receptor competition kinetics (8). The equivalents of: enzyme, male moth; substrate, female moth; enzyme-substrate complex, copulating pair; product, mated female; competitive inhibitor, dispensers; affinity, female and dispenser activity. Capacity for measuring rates of reactions was limited in this organismal system. By conducting experiments for one full reproductive lifespan of a male (4 d under these given conditions), durations of male–attractant complexes, normalized to one reproductive lifespan, could be derived from transformed graphical plots of catch in monitoring traps vs. density of pheromone dispensers.

Extension of Knipling’s (11) rudimentary competitive-attraction equations so as to account for findability of a trap [now referred to as T findability] and efficiency of a trap [T efficiency] less than 1.0 and variable retention of males at point-source dispensers of pheromone (D) led to (derivation explained in SI Text 1B):

Where ♀den = 0, Eq. 3 simplifies to:

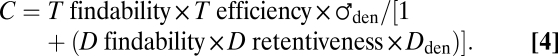Predictions of Eq. 4 as visualized by graphs rendered in Microsoft Excel when findability of D equals that for T are as follows: (i) untransformed plots of C vs. D_den descend concavely with rising D_den and always approach zero asymptotically (9, 10); and (ii) plots of C vs. D_den × C [Miller-de Lame plot (9, 10)] yield a straight line whose negative slope / (trap findability × efficiency) = D_a (a measure of dispenser disruption relative to that of a monitoring trap) and x-intercept = ♂_den / D_a. When D_a = 1.0, the x-intercept directly reveals functional ♂_den.

Results

Validation of Trapping Equation.

The predictions of Eq. 1 were tested by using lab-reared male codling moths in controlled, manipulative experiments unusual for insects under containment because of large spatial scale [each of 20 1,260 m³ cages (see Fig. S1) covered 12 apple trees] and unique for insect pheromone studies because moth density was known. Indeed, the straight line prescribed by Eq. 1 for a plot of C vs. ♂_den was realized (Fig. 2A) when various densities of codling moth males were released into cages having one central monitoring trap (Expt. 1). Averaged over time, male codling moth recaptures were consistent across cages and male densities. Trap findability × efficiency can be calculated as C / ♂_den (slope of Fig. 2A); it was a consistent 0.5 for this late-season test. Laboratory wind-tunnel tests conducted under the methods of ref. 12 revealed that 0.72 ± 0.04 (n = 35) of the males released in batches of 10 into the plumes of our trapping system became ensnared per visit, and that each visit can be comprised of up to four approaches to the trap. If trapping efficiency in Expt. 1 were 0.7, trap findability could have been 0.7, as 0.7 × 0.7 ≈ 0.5. This value suggests that the probabilities for each of the four successive steps of Fig. 1 required for source finding could have been as high as 0.91, as 0.91 raised to the power of 4 ≈ 0.7. Applying Eq. 2 to Expt. 1 yields ♂_den = 2C, showing how simply moth capture can be interpreted when the assumptions for Eqs. 1 and 2 are met.

Fig. 2.

Male codling moth catch per monitoring trap per cage as influenced by density of males released into large field-cages devoid of females (A); male capture as influenced by density of uniformly distributed monitoring traps in large field-cages devoid of females (B). Connecting lines were hand-drawn for (B).

Validation of Competitive-Attraction Equation.

The predictions of Eq. 3 were tested (Expt. 2) by deploying one central trap per cage in competition with varying densities of uniformly distributed pheromone dispensers. To set findability of dispensers (D) equal to that for traps (T), these dispensers were pheromone-baited trap bodies identical to the monitoring trap. Dispensers were of two types: either with or without a sticky liner—hereafter referred to as “sticky” and “nonsticky” dispensers. This design permitted quantification of catch suppression in monitoring traps when male moths were free to orient to nonsticky dispensers repeatedly vs. when males became permanently ensnared by sticky dispensers. With attractiveness of D set equal to T, findability would also be equal when all treatments were tested across the same nights on equivalent males. Because sticky dispensers were, in fact, traps, this experiment also quantified C as a function of the density of competing traps.

Over a male codling moth’s 4-day sexual lifespan as realized under these given conditions, a single trap/cage caught nearly as well as did many traps/cage (Fig. 2B). Trap findability and cumulative trapping efficiency were already approaching 1.0 and rose little as T_den increased from 1 to 18 traps per cage. One hundred three males were released per cage. However, maximum summed catch per one vs. many traps per cage reached a plateau at 65 and 75 males, respectively (Fig. 2B). In our laboratory, wind tunnel studies using the methods of ref. 12, 20 ± 0.02% of lab-reared codling moth males did not find an optimal pheromone lure upon their first exposure to the plume. These two lines of evidence suggest that ≈20% of the males released into the cages either died before capture or were incapable of responding strongly enough to pheromone to result in capture. The responsiveness-corrected (functional) ♂_den for Expt. 2 was therefore calculated at ≈82.

Trap findability × efficiency for Fig. 2B is calculated by dividing catch in the nondisrupted control cage by responsiveness-corrected ♂_den = 65 / 82 = 0.79. As cumulative trap findability approached 1.0, cumulative trapping efficiency approached 0.8. Likewise, dispenser findability must have also approached 1.0, because the same lure and trap body were used in the monitoring trap and both types of dispenser. That outcome left dispenser retentiveness as the only cause of differences in disruptive efficacy of sticky vs. nonsticky dispensers (see Eq. 4).

True to Prediction 1 of Eq. 4, the untransformed disruptive profile for the sticky dispensers was smoothly concave (Fig. 3A). It fit better to a profile for Eq. 4 having trap and dispenser findability set at a responsiveness-corrected 0.79 (65/82) rather than the uncorrected 0.63 (65/103). The disruptive profile for the nonsticky dispensers was considerably less concave than that for sticky dispensers (Fig. 3A). Males free to depart from dispensers could reorient repeatedly to the same or other dispensers; however, each selection of an attractive plume after departing from a dispenser raised the probability that a male would find the monitoring trap.

Fig. 3.

Untransformed (A) and Miller-de Lame plots (resembles but is not identical with Eadie-Hofstee plot of enzyme kinetics) (B) of the disruption profiles for sticky and nonsticky dispensers disrupting codling moth male captures per monitoring trap. Connecting lines were hand-drawn for (A). Data for nonsticky dispensers were generated from a single centrally placed monitoring trap; those for sticky dispensers are the average of the multiple sticky dispensers per cage. The pattern for the single centrally placed monitoring trap was nearly identical to the average capture for multiple sticky dispensers, but the error bars were larger.

True to Prediction 2 of Eq. 4, the Miller-de Lame plots for sticky and nonsticky dispensers fit straight lines (Fig. 3B) whose slopes divided by catch in the nondisrupted control reveal D_a values of 1.01 ± 0.08 vs. 0.08 ± 0.10, respectively (difference significant at P = 0.04 by paired t test). The D_a for the sticky dispensers was statistically indistinguishable from 1.0 (P = 0.97 by χ² test). A D_a of 1.0 for the sticky dispenser indicates that its ability to disrupt males from finding a monitoring trap was identical to that of an actual monitoring trap. This outcome is a reassuring tautology, because a sticky dispenser was a monitoring trap. The x-intercept for sticky dispensers as calculated from the individual Miller-de Lame slopes of the three replicate tests was 84 ± 6.8, placing functional male density very near the responsiveness-corrected 82 arrived at above. Upon confirmation of the theoretically predicted outcomes for the sticky dispensers, we confidently conclude that the nonsticky dispenser of Expt. 2 was only 0.08 ± 0.10 = 1/13th as disruptive as a monitoring trap would have been in its place.

When ♀_den = 0 and T_den = 1, both D_a and disruption time can be calculated from a single catch datum under disruption by competitive attraction along with its corresponding negative control (needed to measure trap findability × efficiency) as explained by Eqs. 5 and 6 of SI Text 1C. Disruption time for sticky vs. nonsticky dispensers was 1.01 ± 0.08 vs. 0.08 ± 0.10, respectively, of a male’s total sexual lifetime (estimated at 4 d × 2.5 h/d² = 600 min)^† = 606 vs. 48 min, respectively. As required by theory, disruption time equaled D_a in this special case where findability of D and T were equal. The number of complexes the average male moth formed with nonsticky dispensers over its lifetime can then be obtained as duration of reproductive lifespan / disruption time per visit, in this case: ≈600 min / 48 min per disruption event = 12.5, or 3 per d. But, the number of ♂–D complexes per male sexual lifetime is more directly given by 1/D_a when findability of D = T.

Inhibition of Male Capture in a Monitoring Trap due to Free-Flying Virgin Females.

As explained in SI Text 1D, this effect was measured at 0.04 in Expt. 3, whereas female retention of males was measured at 0.08. Thus, each female disrupted catch in a monitoring trap at a level similar to an Expt. 2 nonsticky dispenser (D_a = 0.08). Credibility of this finding that a female retained a male for 0.08 of a reproductive lifetime (48 min) is boosted by the knowledge that copulations by codling moths in the laboratory last from 40 to 60 min (13).

Determining the Mode-of-Action and Relative Efficacy of a Commercial Disruptive Product.

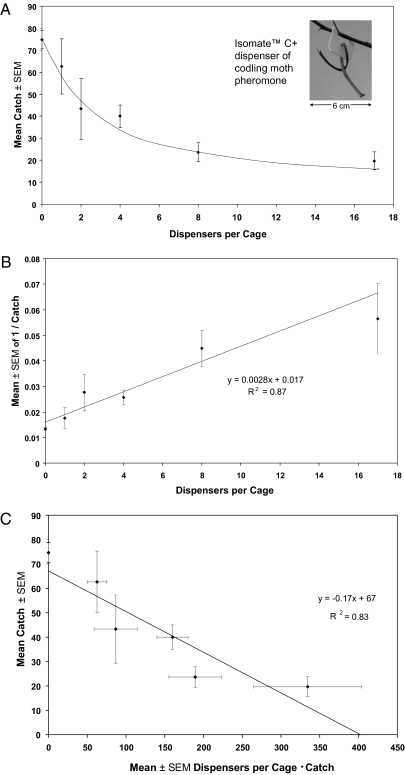
The calibrations of Expt. 2 were instrumental as we determined the mode-of-action and quantified D_a and disruption time for the Isomate tube dispenser (Expt. 4) manufactured by Shin-Etsu Chemical and marketed in the United States by Pacific Biocontrol. It and various mimics dominate the insect pheromone market currently. Its release rate of pheromone (≈5 μg/h) far exceeds that of the 0.1 mg lures (≈0.06 μg/h) used in our traps and as Expt. 2 dispensers. ♂_den for Expt. 4 was 118 per cage; trap findability × efficiency corrected for ≈20% nonresponders was 77 males caught in the negative control cages / 94 functional males = 0.82.

Dosage–response profiles for Isomate dispensers (Fig. 4) fit competitive rather than noncompetitive disruption (9, 10), i.e.: smoothly concave for untransformed data; linear with positive slope on Miller-Gut plot; and linear with negative slope on Miller-de Lame plot. Thus, the initial response of C. pomonella males to Isomate dispensers at the densities tested here was attraction, as also supported by direct behavioral observations of other tortricid moths (14) and pink bollworm (15). Had communication been disrupted noncompetitively by camouflage (masking) of traps or females, or desensitization not requiring attraction, Fig. 4 A–C would have been initially linear, upwardly concave, and parabolic, respectively (9, 10). Refutation of noncompetitive disruption suggests that the concentration of pheromone male moths experienced meters away from a dispenser is insufficient to achieve the disrupted physiological state and therefore unlikely to prohibit recovery of departed males that received a high exposure upon a close visit to a commercial dispenser.

Fig. 4.

Untransformed (A), Miller-Gut (resembles but is not identical with the Lineweaver-Burk plot of enzyme kinetics) (B), and Miller-de Lame (C) plots of the disruption profiles for Isomate dispensers of codling moth pheromone.

Retentiveness for the Isomate dispenser (calculated by using Eq. 6 of SI Text 1C) and D_a (derived from graphical data as per Expt. 2) fell between 0.2 and 0.25, substantially higher than the 0.08 for nonsticky dispensers of Expt. 2. The x-intercept of Fig. 4C reflected 400 total ♂–D complexes, whereas responsiveness-corrected ♂_den was 94 (ratio = 4.3 visits / 4 d). We conclude that each responsive male formed one complex with an Isomate dispenser per night, after which it was incapacitated but recovered before the next diel activity period. The dispenser specific activity [D_sa = D_a / μg of pheromone released by a dispenser per h (10)] of Isomate C+ dispensers (0.04) was far inferior to that for the nonsticky (1.3) or sticky (16.7) dispensers of Expt. 2.

Discussion

Congruence of the Expt. 1 and 2 data with the full suites of exacting predictions is proof that codling moth behavioral responses to point sources of its sex pheromone fit the trapping (Eq. 1) and competitive-attraction (Eq. 4) equations. Apparently, our large-cage system permitted all of the stochastic elements imbedded in these equations to be reliably expressed. The striking parallels between graphical plots of cage data and plots of enzyme (ligand) –substrate kinetic data (7, 8) reveal mechanistic convergence between these organismal and molecular phenomena. When time-averaged, both systems behave stochastically in accord with standard rules of probability as applied to substrates in a common pool and competing with differing affinities and binding longevities for a diffusible ligand. But the potency of sex pheromone communication permits these organismal reactions to run effectively at substrate concentrations trillions of times less than those typical for biochemical reactions. However, these molecular and behavioral phenomena demonstrate related kinetics, albeit in opposite zones with respect to overall speed.

Confirmation of these equations in other insect and animal systems is needed along with assessments of whether and how results obtained in large cages might differ from those obtained for uncontained systems. We postulate that the main effect of the cages was to forbid moth emigration or immigration so as to create an experimental context very similar to one where emigration would have been balanced by immigration. If widely substantiated, this explicit conceptual and analysis system could serve as the foundation for enhanced interpretation of catches in traps as well as for optimizing mating disruption along with other types of behavioral manipulations. For example, Eq. 2 might be extended to estimation of absolute moth density in crops. This use might require estimates of trap findability in the presence and absence of females; however, the competitive effect of females on moth capture by monitoring traps was shown here to be small. Knowledge of the minimal distance traps can be deployed and not compete will also be useful in expanding the utility of Eq. 2.

Data such as those reported here for the Isomate dispenser will point the way toward improvements in both the efficacy and cost-optimization of disruptive formulations. Dispenser density, pheromone release rate, and dispenser specific activity should be manipulated so as to yield the maximum reduction in catch at the lowest economic cost as guided by Eq. 4. For example, an optimized point-source dispenser for codling moth disruption should release the minimal amount of pheromone required to quickly and reliably deactivate an arriving male for a full diel cycle. Expected savings in pheromone per dispenser might then be redirected toward increasing dispenser density or lowering product price (see SI Text 1E for further comment).

Future work will test Eq. 3, where traps, females, and dispensers all compete simultaneously for males. But already, projected three-way outcomes can be calculated by using parameter values reported here for two-way tests. Finally, Eq. 4 can be generalized as (SI Text 1F) for application across and beyond biology.

Materials and Methods

Known densities of codling moth males were released into replicated 19 × 19 × 3.5 m-high field cages (20 cages were built), each enclosing 12 ≈2.8 m-high cultivated “Jonagold” bearing apple trees within a 3 ha recently neglected orchard just north of Leslie, MI. Ten ≈12-cm-diameter rot-resistant wooden posts concreted into the ground supported a trellis-wire superstructure covered by 40% white shade cloth (International Greenhouse) woven with a porosity of 2 × 4 mm from polypropylene fibers. Laboratory-reared C. pomonella pupae were supplied by the US Department of Agriculture-Agricultural Research Service (USDA-ARS) facility in Wapato, WA, as well as purchased from Benzon Research (Carlisle, PA). Segregated male moths emerging into 30 cm³ screened holding cages were provided 10% sucrose solution and held under laboratory conditions on the natural Michigan photoperiod. Batches of 1- to 4-day-old males were transported to the field in small glass vials (1–3 males per vial). These were randomized before males were ejected from handheld vials opened individually. The vast preponderance of flights led directly into the dense canopy of the closest trees, permitting males to be initially distributed uniformly throughout the field cages. Males incapable of horizontal or upward flight (<2%) were destroyed whenever possible and replaced by able individuals. Releases occurred in the early afternoon.

The Pherocon VI delta (triangle) traps (Trécé, Adair, OK) monitoring catch were hung in the upper third of tree canopies and baited with 0.1 mg of codling moth sex pheromone ((E,E)-8,10-dodecadien-1-ol) on a red rubber-septa (Trécé) pinned beneath the trap roof. Lures were used for no more than 14 d. This trapping system is as effective as any known. Moth capture was recorded for 7 d after any release of moths. But, it always became negligible after 4 d, which apparently represents male codling moth reproductive lifespan under these given experimental conditions. Males survive somewhat longer without effective traps in the vicinity. The units for temporal results reported are in fractions of the male codling moth’s sexual lifespan. The window for sexual activity by C. pomonella opens for ≈150 min/d in the summertime; over 4 d, this sums to ≈600 min.

The experimental design was randomized complete block; three replicates were accumulated for all experiments, usually over time. Expt. 1 was conducted between Aug. 27 and Sept. 15, 2007; lower temperatures due to lateness in the season were probably responsible for the low trap findability × efficiency (0.5) relative to that of other experiments. One replicate used six cages simultaneously. Expt. 2 was conducted between June 4 and Aug. 4, 2008. One replicate used 12 cages simultaneously: 6 densities × 2 dispenser types. Total males released per cage and per replicate in 3–6 batches were 94, 95, and 122. Expt. 3 occurred between July 23 and Aug. 27, 2007, whereas Expt. 4 spanned July 1 to Aug. 15, 2008. Expts. 4 and 2 used common methods and, through time, shared the same set of cages, but were never ongoing simultaneously. All statistical tests were two-tailed and with alpha level of 0.05. All error bars represent SEM.