Cost and color of photosynthesis

Abstract

The question of why plants are green has been revisited in several articles recently. A common theme in the discussions is to explain why photosynthesis appears to absorb less of the available green sunlight than expected. The expectation is incorrect, however, because it fails to take the energy cost of the photosynthetic apparatus into account. Depending on that cost, the red absorption band of the chlorophylls may be closely optimized to provide maximum growth power. The optimization predicts a strong influence of Fraunhofer lines in the solar irradiance on the spectral shape of the optimized absorption band, which appears to be correct. It does not predict any absorption at other wavelengths.

Electronic supplementary material

The online version of this article (doi:10.1007/s11120-009-9522-3) contains supplementary material, which is available to authorized users.

Introduction

Photovoltaic solar power converters are usually designed to absorb as much of the solar irradiance above the bandgap energy as possible, because maximum power output per surface area is considered to be most profitable. The photosynthetic solar power converters that maintain life on earth all have approximately the same characteristic absorption spectrum due to chlorophylls and carotenoids in their light-harvesting protein complexes. The existence of exceptions, spectrally different photosynthetic organisms adapted to the available irradiance at the bottom of the photic zone in deep or muddy waters (Stomp et al. 2007), merely adds weight to the question of why, at the top of the photic zone and especially on land, photosynthetic organisms are green, not black, in spite of two billion years of evolution.

Probably inspired by increasing concern about our future energy supply, this unanswered question is attracting renewed interest (Terashima et al. 2009; Björn et al. 2009; Raven 2009). It is often pointed out that a mature leaf, especially that of a shade plant, does effectively intercept nearly all visible light. Some suggest that photosynthesis is not optimized for light absorption because other limiting factors prevail during most of the day. Another proposal is that chlorophyll was selected because of its redox properties rather than its absorption spectrum. It has even been proposed that chlorophyll-based photosynthesis evolved on account of shading by green-absorbing bacteriorhodopsin-based photosynthetic organisms (Goldsworthy 1987). To our knowledge, no one has challenged the assumption that black, or gray, would be better, with the exception of Lars Olof Björn in 1976 (Björn1976). The present study extends his analysis to optically thick systems and takes their energy cost into account.

Theory

By analogy to minimal models used to describe the competition for light in aquatic photosynthesis, terrestrial photosynthesis may be modeled as a suspension of cells under constant illumination from above, but with two key differences: both light absorption by liquid water and the vertical mixing rate of the suspension become negligible. Only the species whose photosynthetic apparatus provides the most growth power at the top of the suspension will remain on top. As its population grows, it pushes its average down into its own shade until the lowest cells receive insufficient power for their maintenance. This will be partially compensated for by adjustment of the amount of photosynthetic apparatus per cell, but its genetic modification to optimize the average growth power of the population will not be selected for, because the species would lose dominance at the top and be replaced.

Solar irradiance provides an input of power in the antenna pigment systems that is the product of the excitation rate in light, J _L, and the free energy, μ:

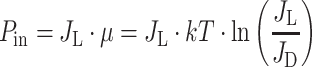where kT is the thermal energy and J _D the thermal excitation rate at ambient temperature (Ross and Calvin 1967). Photosynthesis stores this absorbed power in chemical form with an efficiency P _out/P _in. The proteins involved in light-harvesting and CO₂ assimilation constitute a substantial part of photosynthetic cells and their production costs must be correspondingly high. The net growth power gained by the organism, P _G, is only the fraction of P _out that is not spent on reproduction of the growth generating equipment:

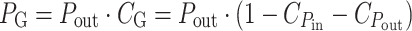Here 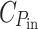denotes the energy cost of power input (light-harvesting) and 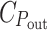the cost of power output (chemical storage of the absorbed power), and C _G the cost of the rest of the cell, all expressed as a fraction of the total energy cost of the cell.

A simple hyperbolic dependence of power output on power input will be assumed, saturating at a maximum P _sat that is proportional to the amount of, and hence to the energy invested in producing, the required machinery:

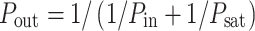As a function of P _sat, maximum growth power results when dP _G/dP _sat = 0, which leads to the condition:

In words: the fraction of saturation reached equals the fraction of output power invested in the machinery for chemical storage of the absorbed power.

Likewise, if P _in were proportional to the energy invested in the light-harvesting apparatus and no losses occur, maximum growth power would result when P _out/P _in = 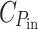: the yield of chemical storage of the absorbed power equals the fraction of output power invested in the light-harvesting apparatus. However, adding pigments to a black cell would not help, so this can only be true as long as the attenuation of the light intensity by the pigments remains negligible. In reality, self-shading will cause diminishing returns and an optimal distribution of the absorbers over the spectrum of the incident light must be sought.

The question is what spectral distribution would optimize P _G if the organism could freely tune the resonance frequency of the electronic transition dipoles that make up its absorption spectrum. In order to express P _G in terms of the absorber distribution, we divide the relevant part of the spectrum into n sufficiently small frequency steps with index i. At a light intensity (photon flux density) I _sol(ν) the excitation rate becomes:

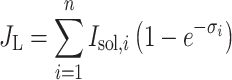The absorption cross-section σ_i is defined here per unit area like I _sol, so it is dimensionless and exp(−σ_i) is the transmittance. The thermal excitation rate at an energy density of black body radiation ρ_bb(ν) at ambient temperature is:

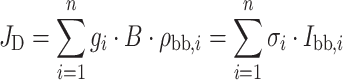where B is the Einstein coefficient, which is proportional to dipole strength, and g _i the number of dipoles. As indicated, the thermal excitation rate of a dipole Bρ can be written as σI, where I is the light intensity (photon flux density), ρ·c/hν, so that its absorption cross-section σ = B·hν/c, with hν the photon energy and c the speed of light (the weak spectral dependence of the refractive index, and hence of c, in the region of interest will be neglected). The σ_i used above, therefore, equals g _i·hν_i·B/c.

No spectral dependence will be imposed on the energy cost of the molecular structures required to create an electronic transition dipole or on the resulting dipole strength, so the cost of light-harvesting is assumed to be proportional to the total number of dipoles Σg _i and, therefore, proportional to Σσ_i/hν_i.

P _G can now be expressed as a function of the parameters g _i and the optimum is then found by setting its gradient to zero, i.e., equating the partial derivatives of P _G with respect to all g _i to zero, and solving the resulting n equations, which have the form:

with the proviso that the transmittance e ^−σ ≤ 1. The term on the left-hand side is the transmitted power spectrum. The σ_i cannot be retrieved directly from this equation as they appear in summed form on the right-hand side as well. This fixed point equation can be solved by the method of iterative mapping. The derivation of the equation and a description of the method for solving it is given in the S.M.

The first term on the right-hand side of the equation is just the black body radiation at ambient temperature multiplied by a very large number (for μ values in the relevant range) and effectively causes an abrupt rise of the transmittance to 1 below a certain photon energy, a condition that is almost perfectly met by the bandgap in semiconductor photovoltaic cells.

The second term on the right is spectrally constant, so at photon energies above the bandgap the dipoles should be distributed such that they absorb all power above a constant level that is determined by their energy cost. This level is spectrally constant due to the diminishing returns caused by Beer’s law. It is constant transmitted power rather than intensity because the absorption cross-section of a dipole is proportional to its resonance frequency, and does not indicate that photon energies in excess of the bandgap have been used. The cost of chemical storage of the absorbed power, 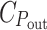, has no influence (the equation implies that P _sat is optimized accordingly) and the level depends only on the ratio between the cost of light harvesting, 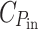, and that of “the rest of the cell”, C _G.

Results and discussion

Figure 1 illustrates what fraction of the solar irradiance spectrum would be transmitted by a photosynthetic cell optimized for growth power, for a few values of the relative cost 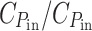 + C _G). At zero cost, the second term in the transmitted power equation is zero and only the power at photon energies below about 1.14 eV is transmitted (shown in black). The corresponding absorptance (1 − e ^−σ) spectrum plotted on a wavelength scale is the outermost curve in Fig. 2, showing 50% cut-off at 1,090 nm. This is the supposedly ideal absorptance spectrum of a single-bandgap photovoltaic cell in full sunlight.

Fig. 1.

Solar irradiance transmitted by a photosynthetic cell optimized for growth power at different costs. The spectra were calculated with the transmitted power equation given in the text, for the standard solar irradiance spectrum at sea level, air mass 1.5, from ASTM [http://rredc.nrel.gov/solar/spectra/am1.5/]. The relative cost parameter  + C _G) was 0 (black), 0.55, 0.82, 0.95, or 1 (white)

Fig. 2.

Growth power-optimized absorptance (1 − T) spectrum as a function of cost. The spectra were obtained from transmitted power spectra like those in Fig. 1 and smoothed on a wavelength scale by convolution with a 10 nm wide Gaussian function. Progressively lighter gray shades correspond to increasing relative costs of light-harvesting

For increasing values of the relative cost, shown in progressively lighter shades, the bandgap shifts stepwise to higher energy/shorter wavelength, jumping the strong atmospheric absorption lines in the infra-red, while the spectrally constant level of transmitted power at higher photon energies gradually increases and its intersection with the irradiance spectrum, beyond which no absorption occurs, shifts to lower photon energy/longer wavelength. As the price of light-harvesting complexes (in energy cost of synthesis per unit of integrated dipole strength) increases, the relative cost approaches unity while the total amount of dipoles approaches zero, until the “single pigment” situation studied by Björn (1976) is obtained.

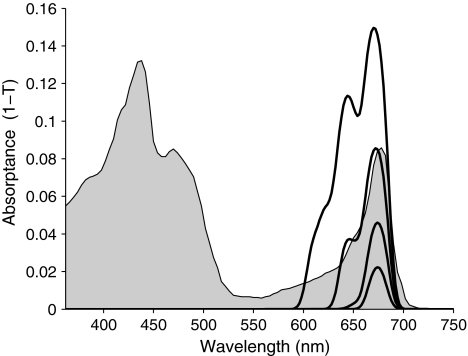
Focusing on the spectra at high cost, Figs. 3 and 4 show that at the highest costs only in the 670–680 nm region some absorption remains, which corresponds to the position of the red absorption band of chlorophyll a in vivo. At lower costs a second band appears, close to the position of that of chlorophyll b, and the spectral shape becomes quite similar to the red absorption band of the photosynthetic apparatus, shown in gray.

Fig. 3.

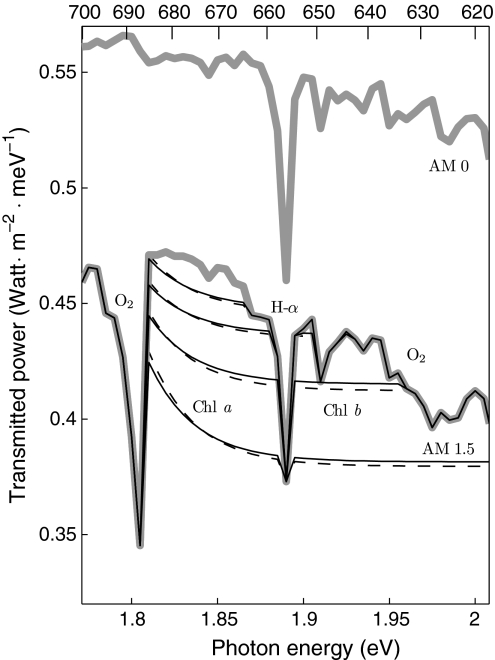
Detail of Fig. 1 for high costs. The solid lines represent the transmitted power spectra corresponding to relative costs of 0.934, 0.962, 0.978, 0.986 (in upward direction for increasing costs), corresponding to an increase in energy cost per dipole by a factor of 5 for each step. The dashed lines represent the same calculations performed with only 1% of the solar irradiance and multiplied by 100 to fit the same scale. The heavy gray line is the solar irradiance. For reference also the extra-terrestrial irradiance (air mass 0, from the same source [http://rredc.nrel.gov/solar/spectra/am0/]) is shown

Fig. 4.

Detail of Fig. 2 for high costs. Absorptance spectra corresponding to the transmitted power spectra shown in Fig. 3. The gray shaded spectrum is an absorptance plot of the absorption spectrum of spinach chloroplasts, corrected for scattering and flattening (Latimer and Eubanks 1962) and arbitrarily normalized to obtain an absorptance at the red maximum corresponding to that of the most similar theoretical curve

The relative costs used for calculating the solid curves in Figs. 3 and 4 are the same and were chosen so that the energy costs per dipole are spaced by a factor 5, showing that a dramatic reduction in the energy cost of producing light-harvesting proteins would be needed to change the optimized absorptance spectrum substantially. The result is also quite insensitive to light intensity. If the sunlight is attenuated without spectral change, the bandgap shifts to a shorter wavelength, but the absorptance spectra at higher costs remain essentially unaltered, as shown by the dashed lines in Fig. 3 calculated for 1% of full sunlight. They do shift to shorter wavelengths if attenuation is carried out using a (smooth) black-body irradiance spectrum, in accordance with the findings of Björn (1976), but the irregular shape of the actual solar spectrum at sealevel keeps the optimal absorption bands at high costs fixed in the same position. The Q_Y absorption bands of chlorophyll a and b cover the spectral range between the 687 and 628 nm absorption bands of atmospheric O₂, and are separated by the 656 nm H-α absorption line in the solar spectrum. When these O₂ absorption bands were removed from the AM 1.5 spectrum, using the local shape of the AM 0 spectrum with a slope correction, the optimized absorptance band at high cost was still at the Chl a position, but jumped to the Chl b position when optimized at 1% of the light intensity.

In order to determine if the similarity between real and predicted spectra in Fig. 4 is merely a coincidence, we applied the same analysis to one of the “colorful spectral niches” at the bottom of the photic zone described by Stomp et al. (2007). Figure 5 shows the solar irradiance under 5 cm of water with a high concentration of organic matter. At the same relative cost that yielded a good approximation of the red band of photosynthesis in non-attenuated sunlight, optimization for growth power in this spectral niche yields an absorptance spectrum that resembles the Q_Y absorption of bacteriochlorophyll A in purple non-sulfur bacteria (Fig. 6). The lower and upper bounds of the spectral range depend on the arbitrary choice of water depth and organic matter concentration. The fact that the deep trough around 820 nm is reproduced by the effect of a minor atmospheric H₂O absorption band on the optimization, however, does provide independent evidence for the validity of the analysis presented here.

Fig. 5.

The transmitted power spectra of Fig. 1 calculated for the irradiance in a muddy pool. To select the spectral range absorbed by bacteriochlorophyll A, the solar irradiance was attenuated by 5 cm water (Hale and Query 1973) with a “gilvin and tripton” attenuation coefficient K _GT(440) = 11 cm⁻¹ as described by Stomp et al. (2007). The same relative cost values as in Fig. 1 were used

Fig. 6.

The absorptance spectra of Fig. 4 calculated for the irradiance spectrum selected in Fig. 5. Growth power optimized absorptance spectra for the same relative cost values as in Figs. 3 and 4. The gray shaded spectrum is an absorptance plot of the absorption spectrum of Rhodobacter sphaeroides chromatophores, arbitrarily normalized to obtain an absorptance at the red maximum corresponding to that of the most similar theoretical curve

At the relative cost of 0.96 that gives a realistic spectral shape in the red region, C _G is at most barely enough to account for a cell’s DNA, even though the parameter that is maximized by the optimization, P _G, is proportional to it. If the total energy cost of the light harvesting system is about 1/3 of that of the cell (Raven 1984), 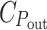would be nearly 2/3. 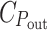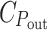Apparently, the assumed hyperbolic saturation of P _out with P _in at a level proportional to /C _G implies that represents the cost of everything needed for growth (except light harvesting), rather than just the photosynthetic apparatus.

Conclusion

The analysis presented here shows that the red absorption band of the photosynthetic apparatus may well be optimized for maximum growth power in spectrally undistorted sunlight, given the energy cost of light harvesting complexes. If so, however, the same optimization does not predict any absorption at other wavelengths. In the blue, such absorption is strong because of the chlorophylls required to shape the red absorption band and the carotenoids required to quench triplet states inevitably formed in those chlorophylls. This blue absorption should probably be regarded as a consequence rather than a cause of the evolutionary selection of the molecular structures responsible, and no special significance should be attached to the fact that they absorb much less in the green region of the spectrum.

Electronic supplementary material

Below is the link to the electronic supplementary material.