Skip to main content
NCBI home page
Acta Crystallographica Section D: Biological Crystallography logoLink to Acta Crystallographica Section D: Biological Crystallography
. 2007 Oct 17;63(Pt 11):1194–1197. doi: 10.1107/S0907444907046148

On macromolecular refinement at subatomic resolution with interatomic scatterers

Pavel V Afonine a,*, Ralf W Grosse-Kunstleve a, Paul D Adams a, Vladimir Y Lunin b, Alexandre Urzhumtsev c,d
PMCID: PMC2808317  PMID: 18007035

Modelling deformation electron density using interatomic scatters is simpler than multipolar methods, produces comparable results at subatomic resolution and can easily be applied to macromolecules.

Keywords: structure refinement, subatomic resolution, deformation density, interatomic scatterers, PHENIX

Abstract

A study of the accurate electron-density distribution in molecular crystals at subatomic resolution (better than ∼1.0 Å) requires more detailed models than those based on independent spherical atoms. A tool that is conventionally used in small-molecule crystallography is the multipolar model. Even at upper resolution limits of 0.8–1.0 Å, the number of experimental data is insufficient for full multipolar model refinement. As an alternative, a simpler model composed of conventional independent spherical atoms augmented by additional scatterers to model bonding effects has been proposed. Refinement of these mixed models for several benchmark data sets gave results that were comparable in quality with the results of multipolar refinement and superior to those for conventional models. Applications to several data sets of both small molecules and macromolecules are shown. These refinements were performed using the general-purpose macromolecular refinement module phenix.refine of the PHENIX package.

1. Introduction

The growing number of macromolecular crystals diffracting to subatomic resolution (53 models in 2003; currently 270) requires the development of appropriate methods and software to model them best. The new information obtained from such macromolecular studies has been discussed in a number of articles (see, for example, the reviews by Dauter et al., 1995 ▶, 1997 ▶; Vrielink & Sampson, 2003 ▶; Petrova & Podjarny, 2004 ▶, and numerous references therein). Afonine et al. (2004 ▶) have shown that information about the density deformation of individual atoms can be extracted from macromolecular data at resolutions of 0.9 Å or better. As a consequence, conventional models for macromolecular structures, in which the electron density of the molecule is a simple sum of contributions from spherical atoms smeared by individual anisotropic displacements, are incomplete and provide inaccurate values for ADPs (atomic displace­ment parameters). Following previous publications, we refer to these models as IAM (independent-atom models).

Model refinement of small molecules at subatomic resolution largely uses the multipolar formalism of Hansen & Coppens (1978 ▶). For these models, the electron density is a sum of atomic contributions in which the density is no longer spherical but depends upon the chemical environment. Such a nonspherical distribution is described by a linear combination of spherical harmonics (Hansen & Coppens, 1978 ▶). Refinement of parameters of multipolar models is monitored mainly by decrease of the crystallographic R factor, improvement of the residual Fourier syntheses, the rigid-bond test (RBT) and other characteristics.

Lecomte and coworkers have reported a number of multipolar refinements of amino acids and nucleic acids to determine a database of multipole parameters and have described several cases of polypeptide and protein refinement using this database (for a review, see Jelsch et al., 2005 ▶). Recently, the group of Coppens (Volkov et al., 2007 ▶) also reported an application of the multipolar refinement to polypeptides, but using their own database of multipolar parameters.

Volkov et al. (2007 ▶) concluded that the applicability of multipolar models in macromolecular studies ‘is in general not warranted, unless exceptionally high-resolution data of ∼0.6 Å or better with satisfactory completeness’ are available. Also it was stated that ‘for macromolecular crystal such data are generally not available, … the number of reflections is not sufficient’. A possible solution to overcome this obstacle is a direct transfer of library parameters without their refinement as discussed by Brock et al. (1991 ▶), Pichon-Pesme et al. (1995 ▶), Jelsch et al. (1998 ▶), Dittrich et al. (2005 ▶), Volkov et al. (2007 ▶) and Zarychta et al. (2007 ▶). However, since the quality of macromolecular X-ray data is generally lower than that for small-molecule crystals, an alternative solution is to introduce a model of intermediate complexity that is more detailed than IAM but simpler than a multipolar model (Afonine et al., 2004 ▶). A possible approach is to complete the IAM with spherical scatterers between the atoms (IAS, interatomic scatterers). It should be noted that the use of the IAM–IAS model is much more runtime-efficient and can be straightforwardly implemented in macromolecular crystallographic packages. Here, we use IAS instead of the previous name DBE (dummy bond electron model; Afonine et al., 2004 ▶), as it better reflects the features of the model.

In this paper, we compare the results obtained with different types of electron-density models for several benchmark data sets. The implementation of IAS modelling into the general-purpose crystallographic program suite PHENIX (Adams et al., 2002 ▶) has allowed the corresponding refinements with phenix.refine (Afonine et al., 2005 ▶) to be performed quickly and in a fully automated fashion.

2. Comparative refinement at subatomic resolution

The modelling of structures at subatomic resolution with multipolar models takes into account the delocalization of electron density from atomic centres owing to the formation of interatomic bonds. The IAM–IAS model (Afonine et al., 2004 ▶) instead treats this delocalized density as spherical Gaussian scatterers located at the centroid of the delocalized density and keeps the conventional spherical atoms unchanged. The multipolar model requires that existing IAM atoms be replaced, while the IAS models complete them with specifically constructed scatterers. Also, the IAM–IAS model may be gradually extended once the new features become visible. Some details of the construction and refinement of IAM–IAS models and the development of the corresponding library of parameters were originally outlined by Afonine et al. (2004 ▶). The current tests were aimed to demonstrate that IAM–IAS models can improve conventional IAM models by lowering the R and R free factors, correcting the ADP parameters and producing clearer residual maps to the same degree as multipolar models and yet are significantly simpler to work with. In this short communication, we do not have the possibility of discussing applications other than map improvement (see, for example, Afonine et al., 2002 ▶). For the same reason, the complete methodology and implementation details of IAS in PHENIX, including the choice of refinement targets, the role of data completeness and the efficient resolution, will be discussed separately in a full-length paper (Afonine et al., in preparation).

To estimate the quality of IAM–IAS models, we built and refined such models for YGG and P2A4 (Table 1 ▶), for which a comparative refinement has been reported by Volkov et al. (2007 ▶). Similarly to Volkov et al. (2007 ▶), refinement was performed at two different resolutions. The highest available resolution (0.44 and 0.37 Å, respectively; for YGG the data completeness is below 50% at a resolution higher than 0.57 Å) was considered as ‘high resolution’, where the data-to-parameter ratio is high enough even for the use of a multipolar model, and a resolution of 0.80 Å was the ‘low resolution’ where this ratio becomes too low. In addition to the standard R factor and rigid-bond test (Hirshfeld, 1976 ▶), R free (Brünger, 1992 ▶) was used as a refinement-quality indicator.

Table 1. Data used for refinements.

N nonH, N H and N IAS give the number of non-H, H and IAS atoms in corresponding models. d high is the highest resolution for the data set, N high is the corresponding number of reflections. N low is the number of reflections for the data sets truncated to lower resolution (d low = 0.80 Å; YGG and P2A4 only).

Molecule Space group and unit-cell parameters (Å, °) NnonH NH NIAS dhigh (Å) Nhigh Nlow Reference
YGG P212121, a = 7.98, b = 9.54, c = 18.32 22 19 39 0.43 4766 1358 Volkov et al. (2007 ▶)
P2A4 P212121, a = 10.13, b = 12.50, c = 19.50 35 36 71 0.37 21475 2513 Volkov et al. (2007 ▶)
Antifreeze protein (KW03) P212121, a = 32.50, b = 39.50, c = 44.64 650 518 367 0.62 118501 — Ko et al. (2003 ▶)
Trypsin P1, a = 32.87, b = 37.02, c = 39.78, α = 102.89, β = 104.59, γ = 102.37 2231 1515 1362 0.80 163918 — Schmidt et al. (2003 ▶)
Phospholipase C2, a = 44.73, b = 59.09, c = 45.31, α = 90.00, β = 117.43, γ = 90.00 1324 956 679 0.80 77695 — Liu et al. (2003 ▶)
Scorpion toxin P212121, a = 45.90, b = 40.70, c = 30.10 647 441 335 0.96 31001 — Housset et al. (2000 ▶)
Open in a new tab

Unfortunately, the YGG and P2A4 models had been refined previously against the full set of data [in fact, the set selected with I > 3σ(I), which is not explicitly stated in Volkov et al., 2007 ▶], making the conventional R free analysis biased. Therefore, when performing the IAS refinements we only note that R free is lower than the corresponding values for the refined IAM models.

The IAM–IAS models were generated and refined completely automatically in PHENIX. Table 2 ▶ shows principal refinement information. All stereochemical and ADP restraints on atomic parameters were removed for both the small molecules and macromolecules used in this study (Dauter et al., 1997 ▶; Schmidt et al., 2003 ▶; Petrova et al., 2006 ▶). Since the starting models were previously refined to a high quality, no stereochemical distortions arising from the unrestrained refinement were observed. A decrease in the R free shows that refinement of IAS did not overfit the experimental data and indeed improved the models. When refining at ‘low resolution’, the ADP values obtained with the IAS are smaller than those from the refinement of corresponding IAMs. Based on previous work (Afonine et al., 2004 ▶; Petrova et al., 2006 ▶), we believe that they are closer to the correct values of the ADPs, which will otherwise tend to increase to model the deformation density along the bonds (Coppens, 1967 ▶; Dunitz & Seiler, 1973 ▶). The rigid-bond test also confirms that the introduction of IAS improved the model. In fact, the IAS refinement with the maximum-likelihood target (Lunin et al., 2002 ▶; to our knowledge never previously applied in this context) improved the models further as measured by the rigid-bond test; however, analysis of this is beyond the scope of this paper. For ‘high-resolution refinement’, mean ADP values are similar with and without IAS, as noted previously by Afonine et al. (2004 ▶). This indicates that the highest resolution data contain sufficient information to deconvolute the deformation-density and atomic uncertainty effects and to estimate the ADPs correctly even without IAS.

Table 2. Comparative statistics for refinement of IAS and multipolar models.

Mt and Mr represent multipolar models with transferred and refined parameters (refinements ‘3’ and ‘5’ in Volkov et al., 2007 ▶). 〈B nonH〉 is the mean value of the equivalent isotropic ADP calculated for non-H atoms. RBT is the rigid-bond-test value (the same as DMSDA, differences in mean-squared displacement amplitudes, in Volkov et al., 2007 ▶). 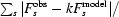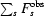R work and R free are the standard crystallographic R and R free factors between experimental F obs and model-based calculated structure-factor magnitudes F model (Afonine et al., 2005 ▶) calculated as Inline graphic Inline graphic.

Data set Model Ndata/Npar† Rwork Rfree 〈BnonH〉 (Å2) RBT (104 Å2)
YGG, low resolution IAM‡ 4.9 2.16 — — 17.76
  Mt‡ 6.2 1.22 — — 12.85
  IAM 6.2 2.35 2.62 1.23 18.99
  IAS 4.0 1.57 2.00 1.05 12.23
YGG, high resolution IAM‡ 17.3 4.51 — — 8.77
  Mt‡ 21.9 3.66 — — 7.38
  Mr‡ 10.6§ 3.42 — — 6.38
  IAM 21.9 4.57 4.72 1.04 8.62
  IAS 14.2 3.75 4.06 1.07 7.68
P2A4, low resolution IAM‡ 5.5 2.98 — — 15.64
  Mt‡ 7.1 1.84 — — 7.09
  IAM 7.1 3.51 3.79 1.24 20.77
  IAS 4.5 2.45 3.27 1.07 16.77
P2A4, high resolution IAM‡ 46.7 3.44 — — 3.67
  Mt‡ 61.0 2.67 — — 2.65
  Mr‡ 43.6§ 2.53 — — 3.09
  IAM 61.1 3.72 3.63 1.14 3.66
  IAS 38.1 3.06 3.23 1.14 4.79
Antifreeze protein IAM 18.6 12.77 15.37 7.84 208.4
  IAS 14.3 11.76 14.44 7.40 195.7
Trypsin IAM 7.6 10.30 13.79 5.79 149.3
  IAS 5.8 9.19 13.35 5.52 126.0
Phospholipase IAM 6.0 8.99 12.80 9.88 250.6
  IAS 4.7 8.31 12.64 9.11 213.5
Scorpion toxin IAM 4.9 9.40 15.47 10.30 365.8
  IAS 3.9 8.78 15.23 10.42 363.1
Open in a new tab
†

For multipolar refinement a number of parameters were fixed or linked by constraints. N par is the number of parameters at each step and does not include the number of parameters refined previously. In contrast to Volkov et al. (2007 ▶), in the current project the ratio N data/N par was calculated for the total number of refined parameters even when at each particular moment only a subset of them were refined; a direct comparison of this information with that reported in Volkov et al. (2007 ▶) is not straightforward.

‡

Refined by Volkov et al. (2007 ▶); corresponding numbers are cited from there.

§

An estimate obtained if the same set of parameters were used for refinement at ‘high’ resolution.

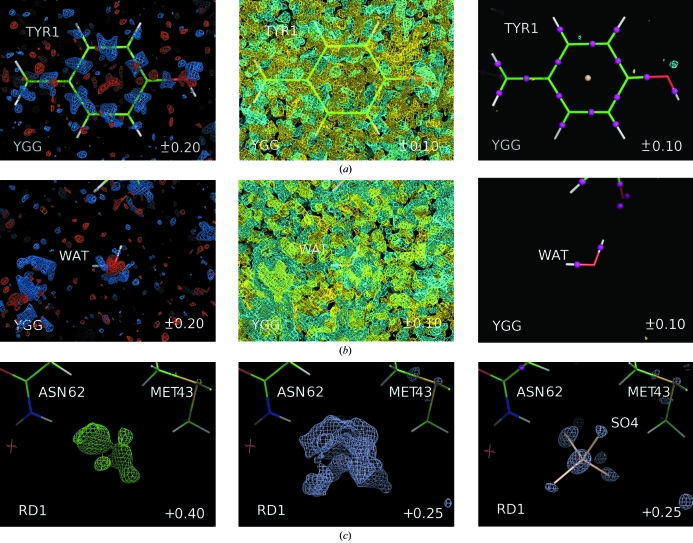
Fig. 1 ▶ illustrates the improvement of the difference F obs − F calc maps, reducing the residual peaks to the same level as for multipolar models (compare with Figs. 2 and 3 in Volkov et al., 2007 ▶). Overall, for the whole set of monitoring parameters the results show the comparable quality of the IAM–IAS and multipolar models despite the simplicity of the former.

Figure 1.

Figure 1

Open in a new tab

Residual Fourier maps calculated on an absolute scale. IAS are shown as small spheres in magenta (IAS with positive occupancy) and in brown (IAS with negative occupancy). (a, b) Maps at 0.43 Å resolution for YGG. Left and middle, IAM-phased maps; right, IAM–IAS-phased maps. Contour colours are +0.20 e Å−3 (marine), +0.10 e Å−3 (cyan), −0.10 e Å−3 (yellow) and −0.20 e Å−3 (red). Views are similar to those in Figs. 2 and 3 of Volkov et al. (2007 ▶). (c) Maps at 0.62 Å resolution for the antifreeze protein RD1. Left and middle, IAM-phased maps shown at cutoff levels of 0.40 e Å−3 (green) and 0.25 e Å−3 (light blue); right, IAM–IAS-phased map shown at a cutoff level of 0.25 e Å−3 (light blue). The sulfate ion inserted instead of the previously located water nicely fits the residual density (shown in brown).

Several macromolecular structures were used as another benchmark (Table 1 ▶). Previously, refinement at subatomic resolution using multipolar models has been reported for crambin (Fernandez-Serra et al., 2000 ▶; 0.54 Å), trypsin (Schmidt et al., 2003 ▶; 0.80 Å), phospholipase (Liu et al., 2003 ▶; 0.80 Å; for resolution higher than 0.86 Å the data completeness is below 50%) and scorpion toxin (Housset et al., 2000 ▶; 0.96 Å). The corresponding models were extracted from the PDB (Bernstein et al., 1977 ▶; Berman et al., 2000 ▶). Unfortunately, the models available in the PDB did not allow exact reproduction of the results reported, making comparative analysis of the IAS refinement impossible. In particular, this completely excluded the crambin data from our tests. To complete the picture at higher resolution, we additionally performed an IAS refinement of the antifreeze protein RD1 at 0.62 Å (Ko et al., 2003 ▶). Table 2 ▶ summarizes the results of the refinement of these models. In all cases, the residual maps became much clearer. In particular, this map improvement highlighted the double conformation of the S—S bonds for the phospholipase and trypsin structures, which were otherwise hidden in the noise, and identified two ions previously interpreted as waters (Fig. 1 ▶ c illustrates this for RD1).

In all cases, the full round of completely automated IAS model building and IAS–IAM refinement, with no manual intervention, took from a few minutes to 1 h on a modern Linux computer. For all protein refinements, completing IAM by IAS decreases the R factors; the R free factors are lower for IAS–IAM than for IAM. The RBT value systematically decreases after the introduction of IAS. We observe that the mean ADP slightly increased for the scorpion toxin data, which may indicate that the resolution (0.96 Å) approaches the limit for the use of the IAM–IAS method.

3. Conclusion

Currently, multipolar modelling is the most precise and powerful tool for crystallographic studies at subatomic resolution when the crystals diffract to ultrahigh resolution of about 0.6 Å or higher and the data-to-parameter ratio justifies refinement of the model parameters. At a resolution near 0.8–0.9 Å, which is more common for macromolecular crystals at sub-angstrom resolutions, multipolar modelling typically requires too many parameters to be refined. As an alternative to the multipolar method, IAM–IAS models may be used, where IAM atoms are augmented by small interatomic scatterers. This approach makes model building and refinement a very transparent and easily monitored procedure. The results of automated refinement of such models for both small molecules and macromolecules at subatomic resolution confirm the efficiency of these models both in terms of model quality and CPU resources required. The tests show that these models can be used even at ultrahigh resolution, producing results that are comparable with those obtained with multipolar models.

Acknowledgments

This work was supported in part by the US Department of Energy under Contract No. DE-AC03-76SF00098 and a grant to PDA from NIH/NIGMS (1P01GM063210). VYL was supported by RFBR grants 05-01-22002_CNRS-a and 07-07-00313-A. All results presented are based on the CCI Apps source-code bundle with version tag 2007_08_10_0051. PyMOL (DeLano, 2002 ▶) was used to present the maps and structures.

References

  1. Adams, P. D., Grosse-Kunstleve, R. W., Hung, L.-W., Ioerger, T. R., McCoy, A. J., Moriarty, N. W., Read, R. J., Sacchettini, J. C., Sauter, N. K. & Terwilliger, T. C. (2002). Acta Cryst. D58, 1948–1954. [DOI] [PubMed]
  2. Afonine, P. V., Grosse-Kunstleve, R. W. & Adams, P. D. (2005). CCP4 Newsl.42, contribution 8.
  3. Afonine, P. V., Lunin, V. Y., Muzet, N. & Urzhumtsev, A. (2004). Acta Cryst. D60, 260–274. [DOI] [PubMed]
  4. Afonine, P. V., Pichon-Pesme, V., Muzet, N., Jelsch, C., Lecomte, C. & Urzhumtsev, A. (2002). CCP4 Newsl.41, contribution 6.
  5. Bernstein, F. C., Koetzle, T. F., Williams, G. J., Meyer, E. F. Jr, Brice, M. D., Rodgers, J. R., Kennard, O., Shimanouchi, T. & Tasumi, M. (1977). J. Mol. Biol.112, 535–542. [DOI] [PubMed]
  6. Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res.28, 235–242. [DOI] [PMC free article] [PubMed]
  7. Brock, C. P., Dunitz, J. D. & Hirshfeld, F. L. (1991). Acta Cryst. B47, 789–797.
  8. Brünger, A. (1992). Nature (London), 355, 472–475. [DOI] [PubMed]
  9. Coppens, P. (1967). Science, 158, 1577–1579. [DOI] [PubMed]
  10. Dauter, Z., Lamzin, V. S. & Wilson, K. S. (1995). Curr. Opin. Struct. Biol.5, 784–790. [DOI] [PubMed]
  11. Dauter, Z., Lamzin, V. S. & Wilson, K. S. (1997). Curr. Opin. Struct. Biol.7, 681–688. [DOI] [PubMed]
  12. DeLano, W. L. (2002). The PyMOL Molecular Graphics System. DeLano Scientific, San Carlos, CA, USA. http://www.pymol.org.
  13. Dittrich, B., Hübschle, C. B., Messerschmidt, M., Kalinowski, R., Girnt, D. & Luger, P. (2005). Acta Cryst. A61, 314–320. [DOI] [PubMed]
  14. Dunitz, J. D. & Seiler, P. (1973). Acta Cryst. B29, 589–595.
  15. Fernandez-Serra, M. V., Junquera, J., Jelsch, C., Lecomte, C. & Artacho, E. (2000). Solid State Commun.116, 395–400.
  16. Hansen, N. K. & Coppens, P. (1978). Acta Cryst. A34, 909–921.
  17. Hirshfeld, F. L. (1976). Acta Cryst. A32, 239–244.
  18. Housset, D., Benabicha, F., Pichon-Pesme, V., Jelsch, C., Maierhofer, A., David, S., Fontecilla-Camps, J. C. & Lecomte, C. (2000). Acta Cryst. D56, 151–160. [DOI] [PubMed]
  19. Jelsch, C., Guillot, B., Lagoutte, A. & Lecomte, C. (2005). J. Appl. Cryst.38, 38–54.
  20. Jelsch, C., Pichon-Pesme, V., Lecomte, C. & Aubry, A. (1998). Acta Cryst. D54, 1306–1318. [DOI] [PubMed]
  21. Jelsch, C., Teeter, M. M., Lamzin, V. S., Pichon-Pesme, V., Blessing, R. H. & Lecomte, C. (2000). Proc. Natl Acad. Sci. USA, 97, 31731–3176. [DOI] [PMC free article] [PubMed]
  22. Ko, T.-P., Robinson, H., Gao, Y.-G., Cheng, C.-H. C., DeVries, A. L. & Wang, A. H.-J. (2003). Biophys. J.84, 1228–1237. [DOI] [PMC free article] [PubMed]
  23. Liu, Q., Huang, Q., Teng, M., Weeks, C. M., Jelsch, C., Zhang, R. & Niu, L. (2003). J. Biol. Chem.278, 41400–41408. [DOI] [PubMed]
  24. Lunin, V. Y., Afonine, P. V. & Urzhumtsev, A. G. (2002). Acta Cryst. A58, 270–­282. [DOI] [PubMed]
  25. Petrova, T., Ginell, S., Mitschler, A., Hazemann, I., Schneider, T., Cousido, A., Lunin, V. Y., Joachimiak, A. & Podjarny, A. (2006). Acta Cryst. D62, 1535–1544. [DOI] [PubMed]
  26. Petrova, T. E. & Podjarny, A. D. (2004). Rep. Prog. Phys.67, 1565–1605.
  27. Pichon-Pesme, V., Lecomte, C. & Lachekar, H. (1995). J. Phys. Chem.99, 6242–6250.
  28. Schmidt, A., Jelsch, C., Østergaard, P., Rypniewski, W. & Lamzin, V. S. (2003). J. Biol. Chem.278, 43357–43362. [DOI] [PubMed]
  29. Volkov, A., Messerschmidt, M. & Coppens, P. (2007). Acta Cryst. D63, 160–­170. [DOI] [PubMed]
  30. Vrielink, A. & Sampson, N. (2003). Curr. Opin. Struct. Biol.13, 709–715. [DOI] [PubMed]
  31. Zarychta, B., Pichon-Pesme, V., Guillot, B., Lecomte, C. & Jelsch, C. (2007). Acta Cryst. A63, 108–125. [DOI] [PubMed]

Articles from Acta Crystallographica Section D: Biological Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES