FRET Fluctuation Spectroscopy of Diffusing Biopolymers: Contributions of Conformational Dynamics and Translational Diffusion

Abstract

The use of Fluorescence Correlation Spectroscopy (FCS) to study conformational dynamics in diffusing biopolymers requires that the contributions to the signal due to translational diffusion are separated from those due to conformational dynamics. A simple approach that has been proposed to achieve this goal involves the analysis of fluctuations in Fluorescence Resonance Energy Transfer (FRET) efficiency. In this work, we investigate the applicability of this methodology by combining Monte Carlo simulations and experiments. Results show that diffusion does not contribute to the measured fluctuations in FRET efficiency in conditions where the relaxation time of the kinetic process is much shorter than the mean transit time of the molecules in the optical observation volume. However, in contrast to what has been suggested in previous work, the contributions of diffusion are otherwise significant. Neglecting the contributions of diffusion can potentially lead to an erroneous interpretation of the kinetic mechanisms. As an example, we demonstrate that the analysis of FRET fluctuations in terms of a purely kinetic model would generally lead to the conclusion that the system presents complex kinetic behavior even for an idealized two-state system

Introduction

Fluorescence correlation spectroscopy (FCS) is a technique based on the measurement of the spontaneous fluctuations of the fluorescence signal of a small number of molecules.^1–5 Fluorescence fluctuations are usually measured in an optically restricted sub-micron observation volume, and then analyzed statistically to reveal kinetic information about the processes that lead to these fluctuations. Such processes include concentration fluctuations via molecular diffusion in vitro and in vivo^6–9, chemical reactions^10,11, photophysical processes^12–14, conformational dynamics^15–17, etc. Fluorescence fluctuations are mathematically defined as deviations of the intensities from the mean (δI(t) =I(t) − 〈I(t)〉), and are quantified by their normalized auto (x = y) or cross (x ≠ y) correlation functions (eq. 1), which are a measure of the similarity between the fluorescence intensity measured at a given time t in detector x and the intensity measured after a certain lag time τ in detector y. The auto- and cross-correlation functions of the fluorescence fluctuations are related to the corresponding correlation functions of the fluorescence intensities as shown in eq. 1. In FCS, the correlation decays are measured experimentally and the kinetic parameters of the processes of interest are then extracted by fitting the results with the appropriate physical models.

$$G_{xy}(\tau )=\frac{\langle \delta I_x(t)\delta I_y(t+\tau )\rangle }{\langle I_x(t)\rangle \langle I_y(t)\rangle }=\frac{\langle I_x(t)I_y(t+\tau )\rangle }{\langle I_x(t)\rangle \langle I_y(t)\rangle }-1$$ (1)

The use of FCS to study conformational dynamics in biological macromolecules has increased in popularity in the last decade. In essence, the approach involves labeling the biopolymer with a fluorophore-quencher or donor-acceptor Fluorescence Resonance Energy Transfer (FRET) pair, so that the intensity of fluorescence of these reporters is a direct measure of the distance between them.^18,19 Conformational changes in the biopolymer result in fluctuations in florescence intensity, and therefore the fluorescence correlation functions contain information about the characteristic timescales of the process. FCS has been used to study conformational dynamics in nucleic acids^20–25, proteins^26–30 and protein-DNA complexes^19,31.

However, an important limitation of FCS when used to study conformational dynamics is the fact that translational diffusion is also a source of fluorescence fluctuations, since the number of photons emitted by a molecule depends on its position within the observation volume created by the optical setup. The measured intensity in both the donor and acceptor detectors will then fluctuate not only as a consequence of conformational dynamics, but also as molecules diffuse in and out of the observation volume. The interpretation of the auto- and cross- correlation curves will therefore depend on the relative timescales of the dynamics one wishes to study and the residence time of the molecule in the observation volume (τ_D), which is dictated by translational diffusion. For typical biological polymers (D ~ 10⁻¹⁰ − 10⁻¹¹ m²s⁻¹), the residence time in the confocal volume is of the order of 100 μs − 1 ms. Therefore, the contributions of conformational dynamics are temporally separated from the contributions due to diffusion only if the relaxation time of the kinetic process (τ_R) is lower than approximately 1μs.²⁴ For slower processes, additional analysis has to be carried out in order to deal with the overlap of these two timescales.

A variety of approaches have been proposed to address the issue of separating the contributions of translational diffusion and conformational dynamics to the experimentally measured correlation decays^18,22,32,33. Bonnet et al.¹⁸ were the first to address the problem, and proposed a method that involves comparing the autocorrelation decay of the donor-acceptor (or fluorophore-quencher) double-labeled biomolecule with the corresponding decay of a control consisting of a donor-only (or fluorophore-only) sample. For the control, the autocorrelation function consists of the diffusion contribution only, while the autocorrelation decay of the double-labeled sample can be described as the product of the same diffusion term and a kinetic term that depends on the relaxation time of the reaction. The latter can be then isolated from the ratio of the autocorrelation decay of the two samples. Although seemingly simple, this procedure suffers from a series of limitations due to the fact that it relies on the need of performing two independent measurements under identical optical and chemical conditions (see ref. 32 for a more thorough discussion). To overcome these issues, other methods that do not require a control measurement were subsequently proposed.

One simple alternative proposed by Klenerman and coworkers^22,34 involves the analysis of the fluctuations of the so-called proximity ratio, a function related to the FRET efficiency. The rationale behind this approach is that in contrast to the individual acceptor and donor intensities (I_A and I_D), the calculated proximity ratio (p)

$$p=\frac{I_A}{I_A+I_D}$$ (2)

depends strongly on the separation between the donor and acceptor molecules, but not on the position of the molecule in the observation volume. Therefore, the correlation function G_p(τ) (eq.3) of the proximity ratio p is expected in principle to have contributions only from conformational dynamics, but not from molecular diffusion.

$$G_p(\tau )=\frac{\langle \delta p(t)\delta p(t+\tau )\rangle }{{\langle p(t)\rangle }^2}$$ (3)

It is important to note that the same can be argued for any other function that represents ratios of fluorescence intensities, such as the ratiometric function proposed by Li et al.³⁵

In this work, we demonstrate that although the above arguments regarding the ability of G_p to eliminate diffusion contributions are intuitively true at first sight, they are erroneous unless diffusion is significantly slower than kinetics (τ_D ≫ τ_R). We support this claim with the results of Monte Carlo simulations and experiments, and discuss the limitations and consequences of using this approach in biophysical studies.

Materials and Methods

Simulations

Diffusion

A three dimensional random walk was used to simulate translational diffusion as follows. Initially, N molecules are placed randomly inside a box with semiaxis L_x = L_y = L_z/s, where s is a shape factor that depends on the optical setup defined as s = ω₂/ω₁, and ω₁ and ω₂ are the radial and axial semiaxes of the observation volume. Each molecule moves based on its diffusion coefficient (D), so that the length of one step (dr) is given by³⁶:

$$dr={(6\mathit{Ddt})}^{1/2}$$ (4)

where dt is the simulation step time. Each step of the simulation involves moving each individual molecule a distance dr in a random direction determined by two random angles generated for each particle: 0 ≤ θ ≤ π and 0 ≤ φ ≤ 2π.

$$\begin{array}{l}x(t+dt)=x(t)+\mathit{dr}cos(\phi )sin(\theta )\\ y(t+dt)=y(t)+\mathit{dr}sin(\phi )sin(\theta )\\ z(t+dt)=z(t)+\mathit{dr}cos(\theta )\end{array}$$ (5)

This method produces results consistent with theoretical predictions as long as dr is small compared with the size of the observation volume and dt is small with the relevant timescales of the physical processes being considered.³⁷

Conformational Dynamics

To simulate the kinetic contributions, each molecule is allowed to be in one of two states (1, 2). Initially, the state of the N molecules is chosen randomly taking into account that the probability that a molecule exists in state 1 is (K+1)⁻¹, where K is the equilibrium constant of the process. The reaction is simulated by a Poisson process with rates k₁₂ and k₂₁ for the forward and backward reaction respectively. Such process can be approximated using a discrete Bernoulli approximation so that the probability of ‘success’ (the reaction occurs) in each interval dt is given by p = k.dt, where k depends on whether the forward or backward reaction is considered. Thus, for each simulation step, molecules in state 1 change to state 2 with a probability k₁₂.dt and molecules in state 2 change to 1 with probability k₂₁.dt. This method approximates a Poisson process as long as p is small so the probability of two or more ‘successes’ in an interval is negligible.³⁸

Fluorescence Intensity

The intensities in detectors D,A (donor, acceptor) were calculated for each molecule and each simulation step as

$$\begin{array}{l}{I}_D=j_{1,2}{e}^{-2(x^2+y^2)/{\omega }_1^2}{e}^{-2z^2/{\omega }_2^2}\\ I_A=h_{1,2}{e}^{-2(x^2+y^2)/{\omega }_1^2}{e}^{-2z^2/{\omega }_2^2}\end{array}$$ (6)

where j_1,2 and h_1,2 represent the intensity measured in the donor and acceptor detectors when a molecule in state 1 or 2 is exactly at the center of the observation volume. These values define the proximity ratios in each state: p_1,2 = h_1,2/(h_1,2 + j_1,2).

The recorded fluorescence intensity in each detector is then calculated as the sum of the contributions of all molecules in the box. Shot noise was simulated by determining the final measured intensity randomly from a Poisson distribution with a mean value that equals the calculated fluorescence intensity from all molecules. Although shot noise has a clear impact in the signal-to-noise ratio of the simulated FCS decays, it is not an important variable in the analysis of their shapes and amplitudes, which is the focus of this paper.

The approach described above was tested using a variety of input parameters that are typically encountered in FCS experiments, and the results were always consistent with the well-established physical models for the auto- and cross-correlation functions of the fluorescence intensities (see Supporting Information for details and examples).

Experiments

FCS measurements were carried out using a custom confocal optical setup. A 532 nm CW laser (Crystalaser, Reno NV) was attenuated to approximately 50 μW and focused into a 1.4 NA objective lens (Olympus PlanApo 100X/1.4NA Oil). The same objective was used to collect the emitted light, which was passed through a 100 μm-pinhole to reject out-of-focus light, and further split into the donor and acceptor signals with a dichroic mirror (Omega XF2021). Donor and acceptor intensities were measured with 1 μs time resolution using two independent avalanche photodiodes (Perkin Elmer Optoelectronics, SPCM-AQR14). Band pass filters were used in front of each detector to further reduce background and crosstalk (Omega 3RD560-620 for the donor, and Chroma BP670/40 for the acceptor). The experimental conditions of the measurements with nucleosomes have been described elsewhere.¹⁹

Results and Discussion

Consider a system that contains two populations of molecules. Molecules can exist in state 1 (with proximity ratio p₁) or state 2 (with proximity ratio p₂ > p₁), but they interconvert only in timescales that are much slower than their average residence in the observation volume (i.e. τ_R ≫ τ_D). In other words, molecules diffuse in either state 1 or 2, but never interconvert during their transit through the observation volume. Typically, FCS experiments are carried out in conditions such that there are about 10 molecules on average in the observation volume at the time. According to the arguments presented by Klenerman and coworkers^22,34, the donor and acceptor intensities will fluctuate as molecules diffuse closer or further away from the focal point, but because the donor-acceptor distance for each molecule would remain fixed throughout the experiment (molecules do not interconvert), the proximity ratio will be constant except for experimental uncorrelated noise. Therefore, it follows from this argument that the Gp decay is expected to be zero at all lag times for systems in which τ_R ≫ τ_D.

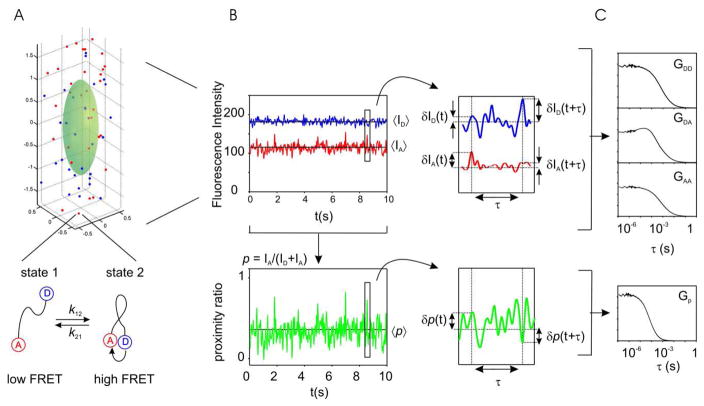
Here, we challenge the validity of these arguments, and claim that such a system will present fluctuations in the measured proximity factor in the timescales of molecular diffusion. The key aspect of the discussion is that the observation volume is inhomogeneous, and as a consequence the proximity ratio will actually depend on the position of all molecules. A typical optical setup using one-photon excitation, a high numerical aperture objective, and a pinhole in the detection path has an observation volume which is approximately Gaussian (fig. 1 and eq. 6).³⁹ Consequently, molecules closer to the focal point are excited and detected more efficiently, dominating the contributions to the measured fluorescence intensity. At any time, the proximity ratio is calculated from the measured acceptor and donor intensities, which depend on the position of all molecules in the observation volume (r). The measured proximity ratio is therefore

Figure 1.

A: schematics of the FCS simulation and idealized experimental measurement. Point molecules diffuse freely throughout a Gaussian observation volume (green surface). The fluorescence intensity of a given molecule depends on its location as $I\propto exp\left[-2(x^2+y^2)/{\omega }_1^2\right]exp\left[-2z^2/{\omega }_2^2\right]$ (see eq. 6), where ω₁ and ω₂ represent the radial and axial dimensions of the observation volume. Molecules contain a donor-acceptor FRET pair, and interconvert between two different states with rates k₁₂ and k₂₁ for the forward and backward reaction respectively. The two states are distinguishable by their different proximity ratio. B: The fluorescence intensity, which is the sum of the contributions of all molecules, is measured in two independent detectors (blue: donor, red: acceptor). The proximity ratio (p, green trace) is calculated point-by-point as p = (I_A/(I_A + I_B)). Fluctuations in intensity or in proximity ratio are calculated as deviations from the mean: δf (t) = f (t) − 〈f (t)〉, where f (t) is an intensity or proximity factor time series. C: Fluctuations are analyzed in terms of their auto- or cross-correlation functions (eqs. 1 and 3).

$$p=\frac{{\displaystyle \sum _i}{I}_{Ai}({\mathbf{r}}_i)}{{\displaystyle \sum _i}{I}_{Ai}({\mathbf{r}}_i)+{\displaystyle \sum _i}{I}_{Di}({\mathbf{r}}_i)}$$ (7)

where I_Ai (r) and I_Di (r) are the acceptor and donor intensities of molecule i, r_i represents the molecule position, and the sum is performed over all molecules present in the sample. In reality, contributions are negligible for molecules at distances much larger than the dimensions of the observation volume (defined by ω₁ and ω₂).

It is then clear that the experimentally measured p will fluctuate as molecules diffuse throughout the observation volume: even if it is true that the individual proximity ratios remain constant as molecules diffuse, high values will be measured when molecules in state 2 are close to the focal point by chance, while low values will be measured when molecules in state 1 are in that region. Note that this is true only because the sample is heterogeneous (i.e. at a given time different molecules have different p values).

The proximity ratio will therefore fluctuate in the timescale of diffusion in situations in which the diffusion time is much faster than the relaxation time of the kinetic process. In general, it is expected that both diffusion and conformational dynamics will contribute to the G_p decay unless fluctuations are dominated by kinetics (τ_D ≫ τ_R). In this case, fluctuations in FRET efficiency occur at timescales much shorter than diffusion, so the system appears static at the timescales comparable with the relaxation time of the system. In addition, at the timescales relevant for diffusion, the two-state system can be approximated as a homogeneous one-state system with a proximity factor that is the average of the individual p values weighted by the relative lifetimes of the two states. Such a system will therefore show no contributions from diffusion in any timescale.

All statements in this discussion were verified by Monte Carlo simulations and experiments as described below.

The case τ_R ≫ τ_D

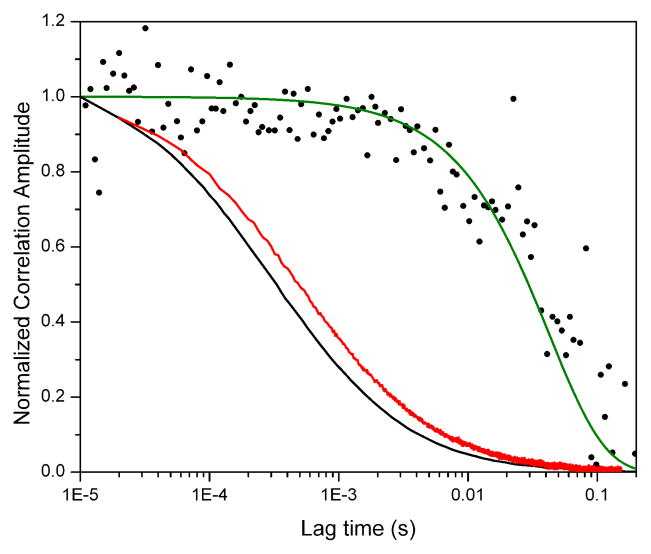
In this section, we analyze the situation in which diffusion is much faster than conformational dynamics. Our motivation for this analysis relies on our interest in applying FCS techniques to the study of conformational dynamics in nucleosomes. In these studies, we consider the equilibrium between two states: a high FRET state in which the DNA is tightly wrapped around the protein core, and a low FRET state in which the DNA has partially unwrapped in a spontaneous way. For all practical purposes, this system can be represented by an equilibrium between two species that can be distinguished by their different proximity ratio. In earlier work, we determined that the relaxation time of the conformational transition is about 50 ms for this particular type of nucleosomes, while the average residence time of these particles in the observation volume is of the order of 1ms.^19,32 The kinetic relaxation time of the process was determined by two independent methods. In the first study¹⁹, we followed the methodology introduced by Bonnet et al described above, which uses a donor-only sample as a control. In this case, we calculated the relaxation time from the ratio of the donor autocorrelation function of the donor-acceptor sample and the corresponding function measured for a donor-only nucleosome. The result is shown in figure 2 as black circles together with a fit to a two-state model (green curve) from which we obtained the relaxation time. In the second study³², we obtained very similar results by applying a method developed in our laboratory that relies on the analysis of the ratio of the donor autocorrelation and the donor-acceptor cross-correlation. In this case, we proved that because the auto- and cross-correlation decays share the same diffusion contributions, their ratio depends only on the kinetic terms that one wishes to isolate.

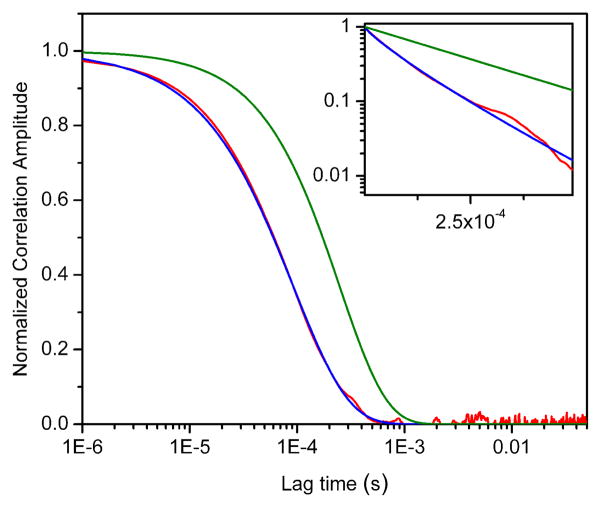
Figure 2.

Black circles (●): Ratio of the donor autocorrelation functions of donor-acceptor and donor-only nucleosomes. Green curve: Fit to a two-state model giving 50 ms as the relaxation time (see ref. 19). Black curve: experimental donor autocorrelation function (G_DD) of donor-acceptor double-labeled nucleosomes. Red curve: experimental proximity ratio correlation (G_p) of donor-acceptor nucleosome calculated from the same data as G_DD. All curves have been arbitrarily normalized for clarity.

Because nucleosomes present dynamics in the 50 ms-timescale, one would in principle expect the proximity ratio correlation to decay in the same timescale. However, the analysis of the same data according to equations 2 and 3 yielded dramatically different results (figure 2, red curve). Not only the measured Gp decays at much shorter timescales, but it also closely resembles the decay of the donor autocorrelation (G_DD, figure 2), which in this case is a very good approximation of the diffusion contributions of the system. It is therefore clear that in this situation Gp does not reflect the timescales of conformational dynamics, but rather the timescales of diffusion.

Monte Carlo simulations were then performed to confirm this result and discard the possibility of artifacts related to the experimental optical arrangement. Briefly, the simulation involves a two-state system diffusing freely in a box containing a Gaussian observation volume at the center. The two states (1 and 2) are distinguishable by their different proximity ratio values. The number of photons per unit time emitted by a molecule depends on its state, and on its position within the observation volume. The measured intensity in each detector (donor, acceptor) is calculated as the sum of the contributions of all molecules in the box. Details are given in the Materials and Methods section.

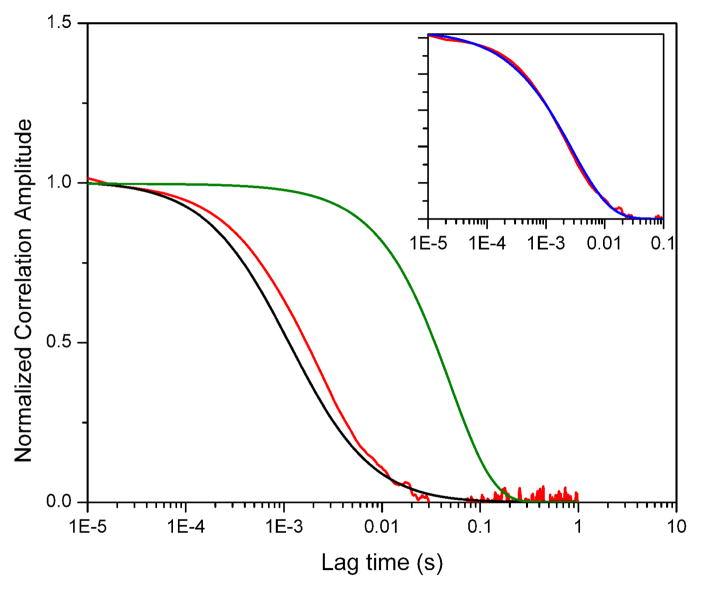
Figure 3 shows the result of a simulation with τ_R = 50 ms and τ_D = 1.1 ms (all other parameters used in this and all other simulations are listed in the Supporting Information). In this plot, the green curve represents the kinetic term (Aexp(−τ/τ_R)), the black curve the diffusion term (eq. 9), and the red curve is the Gp decay obtained in the simulation. It is evident that the decay of the proximity function correlation does not represent the kinetic term as was originally suggested in the original publications. In fact, the Gp decay is very close to the decay expected for pure diffusion contributions, as we observed experimentally with the nucleosome samples as described above. An attempt to fit the Gp decay with a kinetic model (blue curve, inset) has serious consequences, as discussed next.

Figure 3.

Results of a computer simulation with parameters τ_R = 50 ms and τ_D = 1.1 ms. Red curve: proximity ratio correlation (G_p). Black curve: Diffusion model according to Eq. 9. Green curve: two-state kinetic model (exp[−τ/τ_R]). Inset: G_p decay in red, together with a stretched exponential decay (Eq. 8.) with parameters τ_R = 2.8 ms and β = 0.67 (blue curve). All curves have been arbitrarily normalized for clarity.

The assumption that the correlation function of the proximity ratio does not depend on diffusion can lead to serious artifacts. This approach has been mostly used to investigate the kinetic behavior of DNA hairpins containing a donor-acceptor pair.^22,34,35 In these works, experimentally measured Gp decays were fitted to a purely kinetic model described by a stretched exponential:

$$G_p(\tau )=G_p(0)exp\left[-{(\tau /{\tau }_R)}^{\beta }\right]$$ (8)

The conclusion of these experiments was that DNA hairpins do not behave as a two-state system (i.e. they present non-Arrhenius kinetics) because β values around ~0.4–0.5 were needed to fit the decays under a large variety of conditions. These results contradicted the early work of Bonnet et al., who measured Arrhenius behavior (β = 1) for the same system using the ‘control’ method described above (i.e. the ratio of the autocorrelation functions of the double-labeled hairpin and the donor-only hairpin). Interestingly, Klenerman and coworkers also measured a β-value very close to 1 using Bonnet’s approach, in disagreement with the lower values that the same group obtained for the same sample using the proximity ratio correlation method.³⁵

The disagreement between the different methods of analysis can be explained taking into account the contributions of diffusion to the Gp decay described above. In the limit τ_R ≫ τ_D, the Gp decay will be dominated by diffusion, and thus described mathematically by the well-known equation derived by Elson and Madge in their early work.²

$$G(\tau )=\frac{1}{\langle N\rangle }\left(\frac{1}{1+\tau /{\tau }_d}\right){\left(\frac{1}{1+\tau {\omega }_1^2/{\tau }_d{\omega }_2^2}\right)}^{1/2}$$ (9)

Here, 〈N〉 is a measure of the average number of molecules in the observation volume, defined as 〈N〉 = Cπ^3/2ω₁²ω₂, where C is the sample concentration in units of number of particles per unit volume.³ An attempt to analyze this decay in terms of a kinetic model will undoubtedly lead to the need of using a stretched parameter β < 1. As an example, we fitted the experimentally measured G_p decay of the nucleosome sample described above (fig 2, red curve), and obtained τ_R = 0.67ms and β=0.37. The relaxation time obtained in this analysis is about two orders of magnitude shorter than the one measured by other methods of analysis, and very close to the diffusion time of this sample. A similar result was obtained in the simulations. The blue curve in the inset of figure 3 is a trace according to eq. 8 with β=0.67 and τ_R= 2.8 ms (more than one order of magnitude shorter than the actual τ_R), showing that this type of analysis would lead to the conclusion that the kinetic behavior of the system is complex, even in the highly idealized 2-state system used in the simulation. The measured relaxation time will be much shorter than the actual relaxation time (k₁₂ + k₂₁)⁻¹, and will in fact be a measure of the diffusion time. The value of β needed to fit the experimental results is lower than the value needed to fit the simulation results due to deviations from a perfect Gaussian observation volume in the actual optical apparatus. As an example, we have fitted the experimental autocorrelation function of tetramethylrhodamine diffusing freely in aqueous buffer with a stretched exponential (eq. 8) and also obtained β =0.37 (see supplemental information).

The case τ_D ≫ τ_R

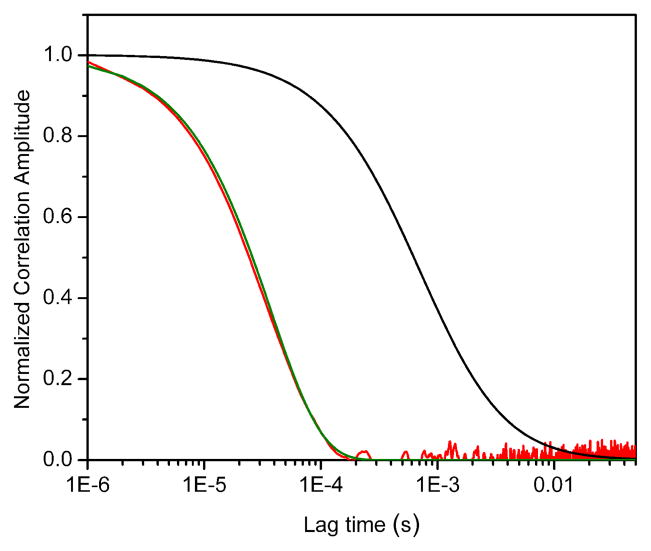
Diffusion is not expected to contribute significantly to the Gp decay when the relaxation time of the reaction is much shorter than the mean residence time of the particle in the observation volume. Figure 4 shows the result of a simulation with τ_R = 37 μs and τ_D = 0.94 ms, where it is clear that the Gp decay (red curve) can be adequately described by a monoexponential function with a relaxation time that equals the reciprocal of the sum of the rates used in the simulation (green curve).

Figure 4.

Results of a computer simulation with parameters τ_R = 37 μs and τ_D = 0.94 ms. Red curve: proximity ratio correlation (G_p). Black curve: Diffusion model according to Eq. 9. Green curve: two-state kinetic model (exp[−τ/τ_R]). All curves have been arbitrarily normalized for clarity.

Evidently, a non-monoexponential decay in this case would be truly indicative of complex kinetics. Experimentally, a safe way of testing that the Gp decay is not contaminated with diffusion contributions would be to perform experiments under different optical conditions. The size and shape of the observation volume (given by ω₁ and ω₂) can be modified by changing the numerical aperture of the objective and the size of the detection pinhole. These parameters will affect τ_D, but should have no influence on the measured relaxation time provided that Gp is determined exclusively by kinetic contributions. It should be noted that temporal resolution is lost in the calculation of Gp in this type of analysis because fluorescence intensities need to be binned so that there are enough photons in both the donor and acceptor channels (the proximity ratio cannot be calculated when no photons are recorded in both detectors). Experimentally, this requires a binning time of ~20 μs, making it hard to determine relaxation times in a similar timescale.²² Consequently, even when the G_p decay describes the kinetic term adequately when τ_D ≫ τ_R, the relaxation times accessible experimentally by this approach are limited by the low intensities measured in the experiment. In contrast, intensity correlation functions (G_DD, G_DA and G_AA) can be determined with much better time-resolution, allowing the study of much faster processes.^24,27

The case τ_D ≈ τ_R

In the most general case the G_p decay will have contributions of both diffusion and conformational dynamics. Because diffusion can be described with a stretched exponential with β ~0.7 (lower values are expected for non-ideal optical setups as described above), its contributions are expected to result in a non-monoexponential G_p decay even for an idealized two-state system. As an example, figure 5 shows the result of a simulation with τ_D = 150 μs and τ_R = 250 μs. The simulated G_p decay (red line) can be successfully fitted with a stretched exponential with β = 0.85 and τ_R = 0.37(k₁₂ + k₂₁)⁻¹ (blue line). The kinetic contribution (exp[−t(k₁₂ + k₂₁)]) is plotted in green for comparison. The contributions of diffusion not only distort the monoexponential behavior of the kinetic component but also influence the relaxation time obtained from the analysis. The non-exponential nature of the G_p decay is visibly obvious from the curvature of the data in a linear-log plot (inset).

Figure 5.

Results of a computer simulation with parameters τ_R = 250 μs and τ_D = 150 μs. Red curve: proximity ratio correlation (G_p). Green curve: two-state kinetic model (exp[−τ(k₁₂ + k₂₁)]). Blue curve: A stretched exponential with τ_R = 0.37(k₁₂ + k₂₁)⁻¹ and β = 0.85. All curves have been arbitrarily normalized for clarity. Inset: same data in a linear-log plot to stress the non-exponential behavior of the G_p decay.

The case of DNA hairpins

The idea of measuring and analyzing fluctuations in the proximity ratio as a way of isolating kinetic contributions was proposed in the context of studies of the kinetics of loop closure in DNA hairpins. A stretched exponential model (eq. 8) was used to analyze the results, and β-values in the range 0.4–0.5 were consistently obtained in all experiments. In all cases, the relaxation times obtained from the fits were in the range 100–350 μs, very close to the τ_D values expected for these molecules in a typical FCS setup.^22,34,35 The results of these studies were interpreted as being a consequence of the existence of a complex energy landscape, in disagreement with other FCS studies¹⁸ and transient spectroscopy T-jump experiments^40–42.

The results and discussion presented so far suggest that the Gp decays measured in these studies may have significant diffusion contributions. Because these contributions were overlooked in the interpretation of the proximity ratio fluctuations, it is likely that the reported relaxation times and β-values do not represent the true kinetic behavior of DNA hairpins. It is crucial to stress that the kinetic behavior of these samples might be indeed complex, and we are not implying that a simple 2-state model necessarily describes the system appropriately. Non-exponential kinetics has been reported by Kim et al.²⁴, who investigated the kinetics of the initial step of DNA hairpin folding by monitoring fluorescence fluctuations in a DNA hairpin containing a fluorophore susceptible to quenching by proximity to guanosine residues. Jung et al.⁴³ investigated the unfolding kinetics of DNA hairpins in flowing solution and observed stretched exponentials with β-parameters of the order of 0.7 for hairpins containing polythymine loops. However, we do not believe these conclusions regarding the non-exponential behavior of hairpins can be derived from the proximity ratio experiments, which are likely to be influenced by translational diffusion.

The amplitude of the Gp decay

So far, we have established that the characteristic timescale of the G_p decay is given by the relaxation time of the reaction in conditions in which τ_D ≫ τ_R (i.e. the Gp decay is dominated by the kinetic contributions). The actual determination of k₁₂ and k₂₁ requires that the equilibrium constant of the process is known. This information is contained in the amplitude of the Gp decay (Gp(0)).

The value of Gp(0) depends on the mean number of molecules in the observation volume (〈N〉), the equilibrium constant of the reaction (K = f₂/f₁), and the ratio of the proximity ratios of the two states (Q = p₂/p₁).

Wallace et al. reported that the amplitude of the G_p decay can be expressed as G_p(0) = K× [(1 − Q²)/(1 + QK)]²/〈N〉. However, here we present a revised expression, which we verified through Monte Carlo simulations.

In the case of a single-molecule, and in conditions so that τ_D ≫ τ_R, it is expected that the proximity ratio will fluctuate between p₁ and p₂ as the molecule changes conformation. Therefore, the amplitude of the decay under these conditions is:

$$G_p(0)=\frac{\langle p{(t)}^2\rangle }{{\langle p(t)\rangle }^2}-1=\frac{f_1{p}_1^2+f_2{p}_2^2}{{(f_1{p}_1+f_2{p}_2)}^2}-1=\frac{K{(1-Q)}^2}{{(1+QK)}^2}$$ (10)

Note that the numerator in the previously published equation was K(1− Q²)², which would erroneously predict that Gp → ∞ as p₁ →0.

More importantly, the expression in reference ²² predicts that Gp increases indefinitely as 〈N〈 decreases. It is critical to stress that 〈N〉 = 1 does not represent single-molecule conditions in a system in which molecules diffuse freely, as a Poisson distribution with a mean of 1 predicts that the probability of observing more than one molecule at the time is about 0.26. Therefore, eq. 10 should be valid in the limit 〈N〉 → 0, which ensures that no more than one molecule contributes to the fluctuations in proximity ratio. As 〈N〉 increases, the fluctuations in the proximity ratio about its mean value are expected to decrease, and the measured proximity ratio will ultimately equal the mean at all times at large concentrations (〈p²〉 = 〈p〉² when 〈N〉 →∞). Thus, the maximum measurable amplitude is given by equation 10, and G_p(0) is expected to decrease to zero as 〈N〉 →∞. Mathematically:

$$G_p(0)=\frac{1}{\langle N\rangle +1}\frac{K{(1-Q)}^2}{{(1+QK)}^2}$$ (11)

Note that the difference between 〈N〉 and 〈N〉 + 1 can be significant at the low concentrations used in FCS (〈N〉 ~10). Equation 11 is consistent with the result of dozens of simulations using different 〈N〉, Q and K values. All results are included as Supporting Information.

Other considerations

In this work, we demonstrated that the autocorrelation function of the proximity factor will in general depend on both diffusion and kinetics, even for the idealized two-state system of the figure. In practice, the G_P decay will also be affected by other experimental issues including optical artifacts due to non-overlapping confocal volumes for the donor and acceptor detectors, and contributions from fluorophore photophysics. For instance, single-molecule experiments have shown that the existence of photoinduced dark states contributes to broadening in FRET distributions.⁴⁴ The efficiency of formation of these dark states depends on laser intensity, and will thus depend on the particular trajectory of the molecule through the observation volume. The existence of these dark states will therefore contribute to further diffusion-dependent fluctuations in FRET efficiency.

Equation 11 suggests that equilibrium constants can be in principle determined by FCS, but in practice such determinations are often difficult due to the presence of background, and the fact that the value of the parameter Q is usually not known. Background can be a problem, particularly at the low sample concentrations used in these experiments. It has been well-established that the presence of non-correlated background does not distort the shape of the correlation decays of the fluorescence intensities, but just affects their amplitudes.⁴⁵ Simulations show that the same is true for the G_p decay only at sample concentrations high enough so that the observation volume contains several fluorescently labeled molecules at all times. Under these conditions, background just decreases the amplitude of the G_p decay, but because the shape is not distorted the determination of τ_R in the presence of background would still be possible in principle if τ_D ≫ τ_R. However, our simulations show that background can contaminate the G_P decay when experimental conditions are such that the observation volume does not contain any fluorescent molecule a significant fraction of the time. We demonstrated that diffusion contributions appear in the Gp decay under these conditions, even when τ_D ≫ τ_R. A thorough discussion of the effects of background is included as Supporting Information.

Conclusions

We have investigated the applicability of the proximity ratio correlation function to the study of conformational dynamics in biopolymers diffusing in solution. Our results show that, in contrast to what had been previously established in other studies, the proximity ratio correlation decay has significant contributions from translational diffusion. These conclusions are supported by the results of experiments and Monte Carlo simulations. Diffusion contributions are negligible only when the relaxation time of the process is much shorter than the mean transit time of the biomolecules through the optical observation volume. In all other cases, both conformational dynamics and translational diffusion contribute to the fluctuations in the proximity ratio and FRET efficiency. Neglecting the contributions of diffusion has therefore the potential of introducing significant artifacts in the analysis of the kinetic behavior of the polymer.