Myosin II Is Essential for the Spatiotemporal Organization of Traction Forces during Cell Motility

Amoeboid motility results from pseudopod protrusions and retractions driven by traction forces of cells. We propose that the motor and actin-crosslinking functions of MyoII differentially control the temporal and spatial distribution of the traction forces, and establish mechanistic relationships between these distributions, enabling cells to move.

Abstract

Amoeboid motility requires spatiotemporal coordination of biochemical pathways regulating force generation and consists of the quasi-periodic repetition of a motility cycle driven by actin polymerization and actomyosin contraction. Using new analytical tools and statistical methods, we provide, for the first time, a statistically significant quantification of the spatial distribution of the traction forces generated at each phase of the cycle (protrusion, contraction, retraction, and relaxation). We show that cells are constantly under tensional stress and that wild-type cells develop two opposing “pole” forces pulling the front and back toward the center whose strength is modulated up and down periodically in each cycle. We demonstrate that nonmuscular myosin II complex (MyoII) cross-linking and motor functions have different roles in controlling the spatiotemporal distribution of traction forces, the changes in cell shape, and the duration of all the phases. We show that the time required to complete each phase is dramatically increased in cells with altered MyoII motor function, demonstrating that it is required not only for contraction but also for protrusion. Concomitant loss of MyoII actin cross-linking leads to a force redistribution throughout the cell perimeter pulling inward toward the center. However, it does not reduce significantly the magnitude of the traction forces, uncovering a non–MyoII-mediated mechanism for the contractility of the cell.

INTRODUCTION

Amoeboid motility is a prototypic mode of cell motility that has been most extensively studied in lymphocytes (Zigmond and Hirsch, 1973; Miller et al., 2002) and Dictyostelium (Varnum and Soll, 1984; Yumura et al., 1984; Segall, 1987; Soll et al., 1988; Fisher et al., 1989). Amoeboid cells moving on a planar substrate exhibit oscillations in cell velocity and shape (Abercrombie et al., 1970; Wessels et al., 1988). Cells protrude a pseudopod in the front that attaches to the substrate, forming new adhesions. The ensuing contraction breaks the adhesion at the back of the cell causing its retraction, and the cycle repeats with a well-defined average period, T (Lauffenburger and Horwitz, 1996).

This process is mainly driven by the coordinated turnover of filamentous actin (F-actin) and the F-actin–directed nonmuscular myosin II complex (MyoII) (Condeelis et al., 1988; Fukui et al., 1991; Iwadate and Yumura, 2008). Actin filament length is regulated by capping proteins, and the mechanical properties of F-actin are modulated by actin binding and cross-linking proteins (Wear et al., 2000; Pollard and Borisy, 2003; Iwasa and Mullins, 2007), among them MyoII. The MyoII complex contains two heavy chains (MhcA) (Delozanne and Spudich, 1987), two regulatory light chains (MlcR) (Chen et al., 1994), and two essential light chains (MlcE) (Chen et al., 1995; de la Roche and Cote, 2001; Bosgraaf and van Haastert, 2006). MyoII motor activity is regulated by phosphorylation of the regulatory light chain (Griffith, 1987) and requires the essential light chain (Pollenz et al., 1992; Liu et al., 1998). The MyoII complexes can assemble into antiparallel bundles with motor head groups at both ends. These bipolar filaments bind and cross-link actin filaments to form a cortical meshwork that increases in density from the front to the rear of the cell (Fukui and Yumura, 1986). This cytoskeletal structure is important for the mechanical stiffness of the cell (cortical tension) (Laevsky and Knecht, 2003) and can also generate the contractile forces required for efficient cell motility (Jay et al., 1995; Stites et al., 1998). In addition to motors, translocation requires cell–substrate adhesions to transmit traction forces to the substrate (Huttenlocher et al., 1995; Zaidel-Bar et al., 2004).

In migrating wild-type Dictyostelium amoebae, both the substrate contact area and the traction forces are coupled to the specific phase of the migration cycle (Weber et al., 1995; Uchida et al., 2003; Del Alamo et al., 2007; Lombardi et al., 2007). We and others have shown that the traction forces have a defined spatial organization, with a region of rearward-directed stresses near the front and a region with forward-directed stresses near the back (Uchida et al., 2003; Ladam et al., 2005; Del Alamo et al., 2007; Iwadate and Yumura, 2008). The proper spatiotemporal coordination of traction forces is probably an important determinant of migration speed, as suggested previously (Lombardi et al., 2007; Smith et al., 2007) and also supported by our earlier study (Del Alamo et al., 2007). The magnitude of the traction forces is important for motility on highly adhesive substrates and in environments in which cells are unable to move if they cannot develop sufficiently large contractile forces for rear detachment (Jay et al., 1995). Thus, the mechanisms that control the spatiotemporal organization and strength of these forces play essential roles in the regulation of cell movement.

Despite the enormous recent advances in our knowledge about the biochemical processes controlling cell motility, our understanding of the spatiotemporal coordination of the mechanical processes on the cellular scale remains limited. Current approaches to this question are based on the measurement of parameters such as cell shape or traction forces and the analysis of their changes in different mutant strains with altered biochemical properties (Uchida et al., 2003; Uchida and Yumura, 2004; Heid et al., 2005; Stepanovic et al., 2005; Lombardi et al., 2007; Wessels et al., 2007; Iwadate and Yumura, 2008; Volk et al., 2008). Cells are plastic and dynamic objects, which makes capturing and describing their entire range of motion and shapes challenging (Wessels et al., 1994). In addition, there is a substantial level of variability in the properties of individual cells, even in a clonal population (Keren et al., 2008). A common way to ameliorate this problem is to select a limited number of cells that can represent the population. However, the identification of such “prototypical” cells is subjective and is often lacking statistical validation.

In this report, we show that the chemotactic migration of single, isolated Dictyostelium cells is made up of a repetitive sequence of canonical steps. Our analysis of the temporal evolution of the length of the cell and the strain energy transmitted to the substrate as well as of the area fluxes (defined in Materials and Methods) shows that these quantities vary periodically. Taking advantage of the periodicity of the cell migration cycle, we have implemented a novel statistical methodology that allows us to systematically dissect the motility cycle into four canonical phases (protrusion, contraction, retraction, and relaxation) and to compute average maps of traction forces for each phase. We have also applied this analysis to the area fluxes that arise when the cells move. The development of this conditional sampling technique enabled us to systematically compile large data sets of high-resolution time-lapse recordings of shapes and traction forces during chemotaxis and obtain a statistically significant quantification of the spatiotemporal distribution of the traction forces the cell exerts at the different stages in the motility cycle. We have used this approach to compare the motility characteristics of wild-type and mutant strains with impaired MyoII function. We then related the molecular properties of MyoII with the spatiotemporal organization of the traction stresses and analyzed how these stresses govern the motility cycle (Yumura et al., 1984; Fukui and Yumura, 1986; Delozanne and Spudich, 1987; Wessels et al., 1988; Pollenz et al., 1992; Jay et al., 1995; Shelden and Knecht, 1995; Xu et al., 1996). Our study provides new insight into the molecular basis of MyoII function for cellular organization, in particular, how the cross-linking and motor properties of MyoII affect the spatiotemporal distribution of traction forces and the ability of cells to move. These insights should be applicable to a wide range of cell types.

MATERIALS AND METHODS

Dictyostelium Culture and Microscopy

Axenically grown Dictyostelium wild-type and mutant cells were prepared for chemotaxis and seeded onto a flat elastic gelatin gel as described previously (Meili et al., 1999; Del Alamo et al., 2007). Time-lapse sequences of chemotaxing cells were acquired on an inverted microscope controlled by MetaMorph software (Molecular Devices, Sunnyvale, CA).

Traction Cytometry

The traction stresses exerted by the cells, $\overrightarrow{\tau }$, were determined from measurements of the deformation of their substrate after solving the equation of static equilibrium for an elastic substrate, as described previously (Del Alamo et al., 2007). This method is an extension of unconstrained Fourier transform traction cytometry (FTTC; Butler et al., 2002) that considers 1) three-dimensional substrates of finite thickness, 2) arbitrary Poisson ratios, and 3) the gap between the measurement plane and the free surface of the substrate. As a consequence of these improvements, the traction cytometry technique of del Álamo et al. (2007) also determines the net traction force exerted by the cell, which allowed us to test the quality of the results by comparing it with Newton's second law prediction that this force should be negligibly small (see analysis of measured net forces in the Supplemental Data). Previous traction cytometry techniques did not permit this comparison because they imposed a zero-net force by design. The substrate deformation field was obtained from the lateral displacements of 0.1-μm fluorescent latex beads embedded in the gel. The lateral displacements were determined by comparing each instantaneous image with a reference image of relaxed substrate. The comparison was performed by dividing the instantaneous and reference images into interrogation windows and computing the cross-correlation between each pair of interrogation windows. This procedure was performed using custom correlation procedures written in MATLAB (The Mathworks, Natick, MA). An ensemble average of the correlation between each image and several reference images (typically 3) increased the signal-to-noise ratio and allowed us to reduce the size of the interrogation window to 16 × 16 pixels (compare to the 64 × 64 pixels used in Butler et al., 2002), leading to a Nyquist spatial resolution of 1.37 μm. The Young's modulus of the gel was determined from the indentation of a tungsten carbide sphere (Keer, 1964). The pole forces exerted at the front and back halves of the cell, ${\overrightarrow{F}}_f$ and ${\overrightarrow{F}}_b$, where

the subspace ξ > 0 indicates the front of the cell (see Eq. 12) and ∫()dS represents a surface integral. The integral for ξ < 0 yields ${\overrightarrow{F}}_b$. The strain energy U_s that the cells exert on their substrate, assuming it is a hookean solid, is given by

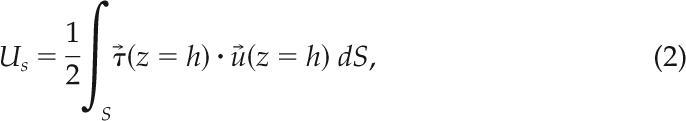where $\overrightarrow{u}$ is the measured displacement vector field on the free surface of the substrate (Butler et al., 2002).

Statistical Tools

We used conditional statistics to characterize the average traction stresses exerted by wild-type, mlcE⁻, and mhcA⁻ cells during different phases of their motility cycles. These phase averages were calculated from instantaneous maps of traction stresses after arranging the experimental time-lapse data series by phases. The sorting procedure had three steps as sketched in Figure 3A. First, we recorded the quasi-periodic time evolution of the length of the cell, L(t). Second, a human user selected the peaks and valleys of each time history of L(t). Third, a computer algorithm automatically divided each cycle of L(t) into the phases during which the cell length is increasing (phase 1, protrusion), is near to a local maximum (phase 2, contraction), is decreasing (phase 3, retraction), or is near to a local minimum (phase 4, relaxation). This algorithm worked by applying the following adaptive threshold on L(t)

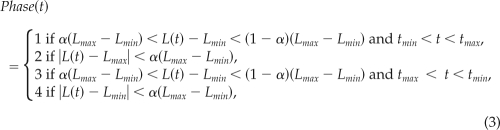where t_min and t_max are the instants of time associated with the nearest local minimum and maximum of L(t) and L_min = L(t_min) and L_max = L(t_max). Once a phase had been assigned to each time point of our time-lapse experiments, we calculated the average maps of traction stresses based on the conditions that Phase(t) = 1,…,4. Note that the threshold needs to be 0 < α < 0.5 to avoid overlap of adjacent phases. Figures 3, 5, and 6 were calculated using α = 0.2. The selection of a threshold for separating the motility cycle into stages was shown to have a negligible effect on the phase-averaged traction maps. To check whether our results are independent of α, we recalculated Figure 5 for values of the threshold parameter lower and higher than α = 0.2. The resulting stress maps (Supplemental Figures S2 and S3) are highly similar to those in Figure 5, confirming that our results are robust irrespective of the threshold.

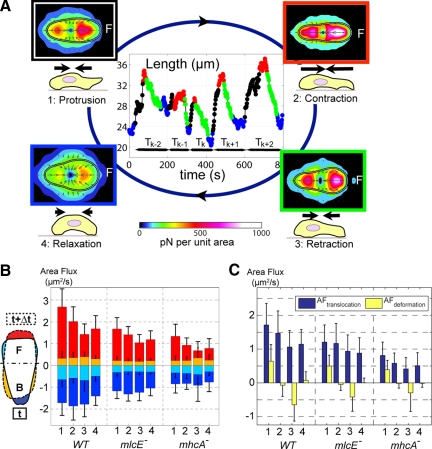
Figure 3.

Analysis of the four phases of the motility cycle using phase statistics. (A) Assignment of individual time points to the four phases of the motility cycle based on increasing length (black), maximal length (red), decreasing length (green), and minimal length (blue). Normalization yields average stress maps (color map) and cell shape (black-white-black outline) for each phase. The bar plots in B show average area fluxes during each phase as determined by phase statistical analysis. The insert sketch represents the contour of a cell at time t (solid line) and at time t + Δt (dashed) and illustrates the origin of each of the different area fluxes represented in the bar plots in this panel. Red stands for area increase in the front and yellow for increase in the back. Dark blue stands for area decrease in the back and light blue for area decrease in the front. (C) Area flux due to cell shape change (see Eq. 1) in yellow area flux attributable to continuous translocation in dark blue (see Eq. 2).

Figure 5.

Spatiotemporal mapping of the traction stresses exerted by wild-type and MyoII mutant cells. (A) Phase-averaged traction stresses and cell shape corresponding to the four stereotypical stages defined in Figure 3 for wild-type (first column, N = 31), mlcE⁻ (second column, N = 14), and mhcA⁻ (third column, N = 27) cells. The contour maps show the average traction stress field, measured in a reference frame rotated to coincide with the instantaneous principal axes of the cells and scaled with their half-length, L(t)/2. The colors indicate the magnitude of the stresses in pN per unit area and the arrows indicate their direction. The white contours show the average shape of the cells in this reference frame. The front (F) of the cell corresponds to x > 0 and the back (B) corresponds to x < 0. (B) Components of the traction stresses parallel and perpendicular to the major axis of the cell averaged over the entire motility cycle. An estimation of the average stresses in Pa (= pN/μm²) can be obtained by dividing the values of traction stresses shown in this figure (in pN) by the squared average of L(t)/2 (in square micrometers). Average values for the length of each cell line during each phase of the motility cycle are given in Table 1.

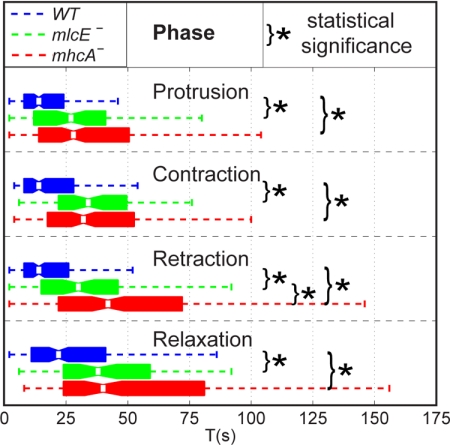
Figure 6.

Box plot of the durations T₁, T₂, T₃, and T₄ of the stereotypical stages of the motility cycle defined in Figure 3: 1) protrusion, 2) contraction, 3) retraction, and 4) relaxation.

Mathematically, we define the average map of traction stresses corresponding to the ith phase of the motility cycle of a set {j = 1,…,N} of cells, using M_j temporal observations for the jth cell, as

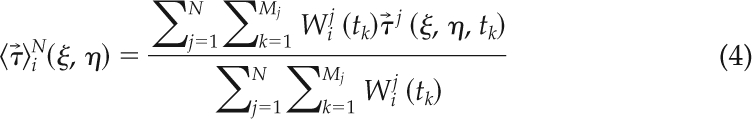where (ξ, η) are the spatial coordinates and ${\overrightarrow{\tau }}^j$(ξ, η, t_k) is the instantaneous traction stress field generated by the jth cell at time t_k. The weight function W_i^j(t_k) is set equal to 1 when the jth cell is in the ith phase of the motility cycle at time t = t_k and equal to zero otherwise. In the results section, we show that, when N becomes sufficiently large, ($\overrightarrow{\tau }$)_i^N converges to a uniquely defined function characteristic for each cell line, independently of the particular cells used to compile the average.

Before computing the phase averages, we converted the instantaneous traction stress fields into a cell-based, dimensionless coordinate system (ξ, η) that took into account that the shape and the orientation of the cells was changing and could adapt to these changes. The cell-based representation involves aligning the longitudinal axis of the cell with the horizontal (ξ) axis and rescaling the coordinates with the half-length of the cell. This coordinate system allowed us to compile statistics coming from different cells at different instants of time. The origin of the cell-based coordinate system was located at the instantaneous centroid of each cell, whose instantaneous coordinates in the laboratory frame were (x_c(t),y_c(t)). The (ξ,η) coordinates were expressed mathematically as

where x and y were the coordinates in the laboratory reference frame, and θ(t) was the angle between the longitudinal axis of the cell and the x-axis of the laboratory reference frame. Because the distances were scaled with the instantaneous half-length of the cell, L(t)/2, in the cell-based reference frame, the longitudinal axis of the cell always spanned from ξ = −1 to ξ = 1. The dimensions of the traction stresses in this coordinate system need to be consistent with the fact that their surface integral is a force. Because ξ and η are nondimensional, these traction stresses are scaled with (L(t)/2)² and therefore, they have dimensions of force (e.g., pN per unit nondimensional area). Supplemental Figure S4 illustrates the alignment and scaling of the traction stresses that is performed before averaging for three time-lapse frames of the same cell.

To calculate the phase-averaged contour of the cell, we applied the procedures described above (phase conditioning, aligning, scaling and averaging) to a scalar function P^j(ξ,η,t) so that, at each instant of time, P = 1 inside the two-dimensional projection of the cell and P = 0 outside of it. The conditional average of this function for a set {j = 1,…,N} of cells (calculated similar to the average traction stresses of Eq. 4), 〈P(ξ, η)〉_i^N, yielded the probability that a given point belonged to a cell during the ith phase of the motility cycle in cell-based coordinates. We defined the phase-averaged contour of the cell as the isocontour 〈P(ξ, η)〉_i^N=Pau_i^N that enclosed an area equal to the average area of the cell during the same phase. Supplemental Figure S5 illustrates the calculation of the average cell outline by showing a contour map of 〈P(ξ, η)〉_i^N measured for the protrusion phase of wild-type cells, and the resulting average cell contour, which corresponds to the probability level that encloses an area equal to the average area of all cells in this case, Pav_iN = 41%. Because Pav_iN corresponds to a nonzero probability, it is to be expected that the instantaneous contour of a given cell does not match the average cell contour due to variability in cell shape. In particular, the instantaneous contour of a given cell often exceeds the average cell contour in some locations. When this occurs, the cell may instantaneously exert traction stresses outside of the average cell outline, which can account for the small, nonzero values of the average stresses outside the average contour observed in Figure 5. This statistical effect is caused by the natural variability of cell shape and is observed even when the instantaneous traction stresses outside of the instantaneous cell outline are forced to be zero by using a constrained traction cytometry method (see Supplemental Data).

Area Fluxes

The differential area flux at each element of area of the plane is defined as the rate of change of the probability that the considered element belongs inside a cell weighted with the differential area of the element,

where (ξ, η) are calculated from Eq. 5 with respect to x_c(t_k−1) and y_c(t_k−1) and L(t_k−1) both for P(ξ, η, t_k−1) and P(ξ, η, t_k). According to the definition of P given above, P(ξ, η, t_k) − P(ξ, η, t_k-1) will be equal to 1 wherever the cell has gained area, −1 wherever the cell has lost area, and 0 if the cell was present at both times t_k−1 and t_k. Therefore, the integral AF = ∫daf in a region of the (ξ, η) plane represents the change of cell area measured in that region per unit time: if AF > 0 in a certain region of space, then the cell is adding material at that region and vice versa.

RESULTS

The Mechanical Process of Amoeboid Cell Motility Is Characterized by Quasi-periodic Changes of Cell Length and Strain Energy Exerted on the Substrate

To investigate the mechanical underpinnings of the motility cycle, we analyzed recordings of single Dictyostelium cells undergoing chemotactic migration on an elastic substrate embedded with carboxylate-modified yellow-green 0.1-μm fluorescent latex beads for three strains: wild-type (KAx-3), MyoII null (mhcA⁻; lacks MyoII cross-linking and motor function), and MyoII essential light chain null (mlcE⁻, with altered MyoII motor function; see Discussion) cells. The time-lapse images of a cell and the displacement of the microbeads as a cell moves allow us to determine the changes in the cell shape as well as to calculate the distribution of traction stresses from the measured deformation of the elastic substrate (Del Alamo et al., 2007). The quasi-periodic time evolution of both cell length, L, and total strain energy exerted by the cell on the elastic substrate, U_s (Eq. 2), suggests that stereotypical elements of chemotactic cell movement such as protrusion or contraction are repeated sequentially, consistent with previous observations of other groups on a range of cell types (Figure 1B; Abercrombie et al., 1970; Wessels et al., 1988; Lauffenburger and Horwitz, 1996).

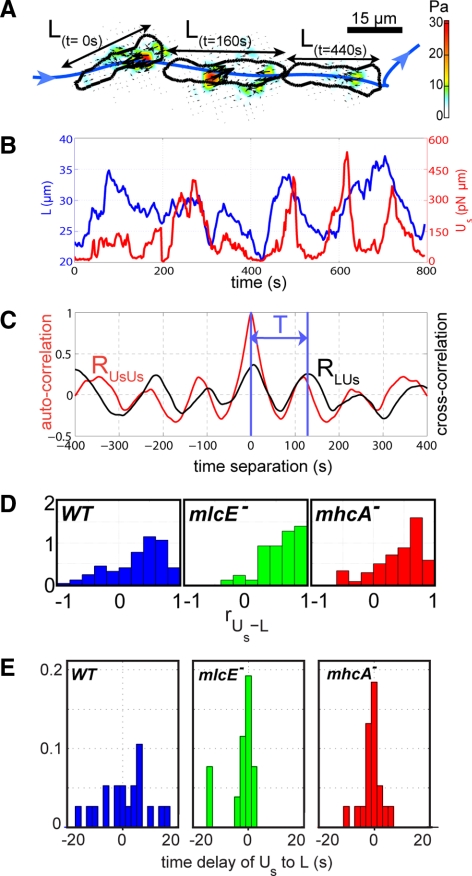
Figure 1.

Periodicity of amoeboid motility. (A) Outline of a wild-type cell moving left to right at three different instances of time and the corresponding traction stresses it imposes on the elastic substrate. The graph in B shows the quasi-periodic time evolution of the length of such a cell (L) in blue and the time evolution of the total strain energy it deposits into the substrate in red (U_s). The graph in C further illustrates the periodic nature of the cellular motility process by plotting the cross-correlation between cell length and strain energy (R_UsL) in black and the autocorrelation of the strain energy in red (R_UsUs). (D) Histograms of the correlation coefficients between U_s and L within each motility cycle for wild-type (blue, N = 31 cells, 122 cycles), mlcE⁻ (green, N = 14 cells, 46 cycles), and mhcA⁻ (red, N = 27 cells, 119 cycles) cells. (E) Histograms of the phase shift between the peaks of R_UsL and R_UsUs, measured in seconds. The histograms in D and E are normalized to integrate to unit area.

The existence and degree of periodicity of a force-regulated motility cycle were studied in more detail by analyzing the autocorrelations and cross-correlation of L and U_s (Figure 1C). The autocorrelation of U_s, R_UsUs, and the cross-correlation between L and U_s, R_LUs, show a high degree of periodicity and can be used to more unambiguously determine the period of the motility cycle, T. Another important aspect is the duration of the correlation, which in the cell presented in Figure 1 is maintained for four complete cycles as indicated by the sustained magnitude of the peaks of R_UsUs and R_LUs, instead of rapidly decaying to zero as would be expected for an irregular signal. The observed correlations are consistent with the notion that the oscillations in L and U_s are caused by a recurring organized process rather than by random fluctuations. The magnitudes of the peaks for both R_UsUs and R_LUs are very similar, meaning that U_s is correlated as closely with itself as it is with L. Physically, this means that the cell length and the level of stresses transmitted to the substrate are highly correlated. Although the analysis shown in Figure 1 is for a single wild-type cell, similar periodicity was statistically confirmed for three strains studied. The histograms of the r between U_s and L, R_LUs, for the three strains (Figure 1D) indicate that L and U_s are strongly correlated for the majority of the wild-type, mhcA⁻, and mlcE⁻ cells analyzed. The percentage of cells showing a correlation coefficient R_UsL > 0.5 is 44% for wild-type, 58% for mlcE⁻, and 55% for mhcA⁻ cells. Further evidence is provided by the statistics of the probability of the null hypothesis that U_s and L are independent versus the alternative that they show positive correlation. The percentage of cells with a p value lower than 0.05 is 58% for wild-type, 89% for mlcE⁻, and 72% for mhcA⁻ cells, which confirms that in the majority of cases U_s and L are positively correlated. The histograms of the time delay between the peaks of R_UsL and R_UsUs, shown in Figure 1E are narrow and symmetric with respect to zero, indicating that the time evolutions of cell length and strain energy are statistically in phase.

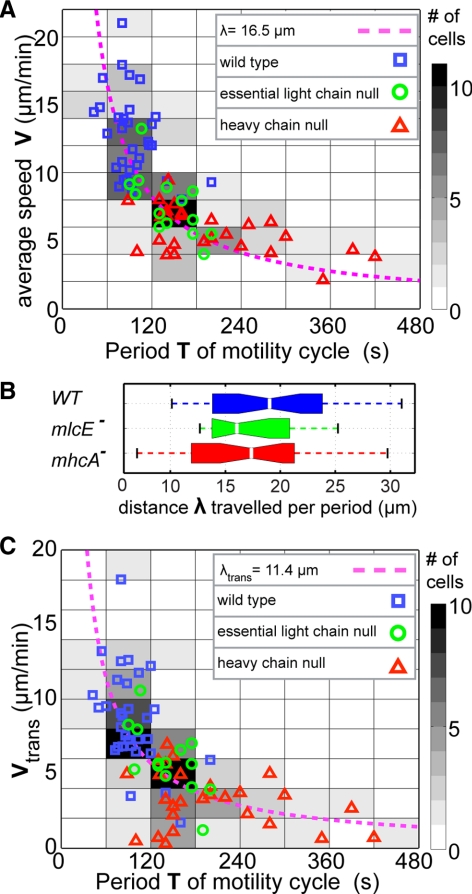
Our previous study suggested that the rate at which Dictyostelium cells are able to repeat the strain energy cycle on a flat surface determines their velocity (Del Alamo et al., 2007). The relationship between the average velocity of the cell (V) and the period of the strain energy cycle (T) is well approximated by the hyperbola VT = λ, where λ is a constant with units of length (Figure 2A). The r between V and 1/T is R = 0.71. The probability of the null hypothesis that V and 1/T are independent versus the alternative that they show positive correlation, p = 2.3 × 10⁻¹⁴ is extremely low. One important aspect of this empirical relationship is that it holds for a wide range of velocities (2–18 μm/min) and is conserved in mutants we have tested that have contractility defects. Wild-type cells (p = 0.0045) have the fastest velocities and shortest periods, whereas mhcA⁻ cells (p = 0.011) have the slowest velocities and the longest periods and mlcE⁻ cells (p = 0.0029) have velocities and periods falling between the periods measured for wild-type and mhcA⁻ cells.

Figure 2.

Dictyostelium motility on gelatin substrates is pace limited. (A) Scatter plot of the average velocity of N = 72 chemotaxing Dictyostelium cells versus the period of their motility cycle (determined from the time evolution of L). The data points come from three different cell lines: N = 31 wild-type cells (blue squares), N = 14 mlcE⁻ cells (green circles), and N = 27 mhcA⁻ cells (red triangles). The dashed magenta hyperbola (V = λ/T) is a least square fit to the data, yielding λ = 18 μm. The V − T plane has been divided into tiles that have been colored according to the number of cells whose speed and motility period lie within each tile. Darker tiles contain more cells, as indicated in the color. (B) Box plot of the product V·T for wild-type, mhcA⁻, and mlcE⁻ cells. (C) Scatter plot of the continuous translocation velocity V_trans (see Eq. 3) of the same cells as in A versus the period of their motility cycle. The dashed magenta hyperbola (V_trans = λ/T) is a least square fit to the data, yielding λ = 12 μm.

To test the robustness of the above-mentioned empirical relationship across these three strains, a nonparametric, one-way analysis of variance test was performed on the values of λ measured for the wild-type, mlcE⁻, and mhcA⁻ cells. The resulting p values of the null hypothesis that the distributions of λ from different strains have different averages (p = 0.36 for wild-type/mlcE⁻, p = 0.22 for wild-type/mhcA⁻, and p = 0.97 for mlcE⁻/mhcA⁻) indicate that these distributions are similar. Figure 2B depicts a box plot of the distributions of λ for wild-type, mlcE⁻, and mhcA⁻ cells. The measured average and standard deviations of λ for wild-type, mlcE⁻, and mhcA⁻ cells are λ = 19.5 ± 6.0, 17.6 ± 6.2, and 17.4 ± 4.0 μm, respectively. These values are of the order of the length of the cells, indicating that, on average, during each motility cycle these cells move a distance comparable to their length. This similarity in values of λ suggests that, despite their differences, the implementation of the motility cycle of these three strains should not differ substantially.

A Phase Statistical Analysis of the Motility Cycle Provides a Unified Description of the Behavior of Wild-Type and Mutant Cells

We developed a statistical method that enables us to determine the spatiotemporal mechanical organization of the average cell during locomotion (see Materials and Methods). The method first divides the motility cycle into a number of canonical stages (or phases) and then computes the phase-average maps of the traction forces. For this purpose, we developed an unbiased, automatic procedure that is capable of identifying the canonical stages of the motility cycle in each experimental time-lapse record. This is possible for amoeboid cells because they move following a series of well-defined steps that translate into periodic oscillations of L and U_s, as discussed previously. We used a cell-based reference system with the origin at the instantaneous centroid of each cell and the horizontal axis coinciding with the longitudinal major axis of the cell (see Materials and Methods). Comparing sequential time points enabled us to determine the shape changes. We divided the motility cycle into four stages (or bins) according to the criteria indicated in Figure 3A, and we named these stages based on the properties of the cell at each stage: 1) protrusion, defined as the fraction of each cycle during which the cell length is increasing; 2) contraction, defined as the fraction of each cycle during which the cell length is near a local maximum (our force measurements have shown this phase to coincide with maximum strain energy; Figure 1); 3) retraction, defined as the fraction of each cycle during which the cell length decreases; and 4) relaxation, defined as the fraction of each cycle during which the cell length is at a minimum (our force measurements have shown this phase to coincide with minimum strain energy; Figure 1). We used the assigned phases to sort the data obtained from different cells at different instants of time and to compile average maps of stress and cell shape. More information about this methodology, including the algorithm for the dissection of the motility cycle into phases and other statistical tools used in this study, can be found in Materials and Methods and Supplemental Data. Our method is robust, and relatively insensitive to the algorithm used to sort out the four phases of the motility cycle (see Materials and Methods and Supplemental Data).

The changes in cell shape during the cycle can be analyzed by determining the area fluxes (for the definition, see Materials and Methods). The bar plot in Figure 3B shows the integrated positive area flux in the front, AF_front⁺, the integrated negative area flux in the back, AF_back⁻, the integrated negative area flux in the front, AF_front⁻, and the integrated positive area flux in the back, AF_back⁺. The inset sketch in Figure 3B is a graphical representation of each of these contributions. The absolute values of the integrated area fluxes vary between 1 and 5 μm²/s and are in good agreement with previous measurements of average and instantaneous area gain or loss for single cells (Wessels et al., 1988, 1994; Heid et al., 2005; Yoshida and Soldati, 2006). If a cell simply moved forward while maintaining a constant shape, then AF_front⁺ and AF_back⁻ would have the same magnitude and opposite signs, and the sum of AF_front⁻ and AF_back⁺ would be equal to zero. In reality, amoeboid motility involves an additional component of deformation. To distinguish kinematically between shape preserving translocation and the component of the cell movement that is associated with deformation, we define the area flux of deformation, AF_def, and the area flux of translocation of the cells, AF_trans, as follows:

These parameters are defined so that AF_def = 0 when a cell is undergoing shape preserving translocation and AF_trans = 0 when the front and back area fluxes are balanced so that the centroid of the cell does not change position. Figure 3C shows a bar plot with the values of AF_def and AF_trans for wild-type, mlcE⁻, and mhcA⁻ cells during the four stages of the motility cycle. This plot confirms that our stage-sorting methodology captures the physical events defining the motility cycle for the three cell lines under study. AF_def indicates that during protrusion, cells, on average, mainly deform by gaining area at the front, whereas they lose area at the back during retraction. Conversely, the cells undergo little deformation during contraction and relaxation. The substantial contribution of AF_trans to each phase means that part of the locomotion of Dictyostelium cells occurs independent of deformation or area change on the time scale of the period T. This could potentially be due to events of protrusion/retraction with a period much shorter than T. However, considerably shorter period fluctuations of cell length are absent from the time-lapse movies of individual migrating cells, which suggests a shape preserving translocation due to continuous contraction of the actomyosin network at the back of the cell (Wessels et al., 1988; Fukui et al., 2000; Langridge and Kay, 2006; Yoshida and Soldati, 2006). To isolate the component of the velocity coming from continuous translation of the cell rather than from its deformation, we have estimated the average velocity of continuous translocation, by dividing the area flux of translocation with the average width of the cell, W. This estimation is expressed as follows:

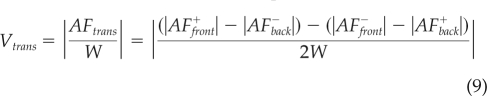Figure 2C illustrates that V_trans shares the same correlation with the period of the motility cycle as the total cell velocity. This result is expected, as we find that continuous translocation is a substantial contributor to the total velocity of the cell. However, this correlation suggests the existence of a coupling mechanism through which the period T of the cell deformation cycle for the inchworm-like contribution to cell motility is linked to the continuous translocation.

Finally, it should be noted that, although the magnitudes of AF_trans and AF_def are lower in mhcA⁻ and mlcE⁻ cells than in wild-type cells, the time evolutions of the parameters for all of the cell lines parallel each other, indicating that the cells from the three strains implement the motility cycle in a similar manner, despite the defects in actomyosin contractility of the mutants. This result is consistent with the observation noted above that all of the cell lines have similar values of λ, the distance moved per cycle (Figure 2).

Measurements of Individual Cells Are Variable but the Phase Averages Converge Rapidly and Reproducibly

For any sample of cells, the statistical significance of the cell-based phase averages introduced in Materials and Methods is limited by sources of uncertainty such as cell-to-cell variability, measurement errors, or the reproducibility of the experimental conditions. These random contributions eventually cancel out as one increases number N of measured cells. Figure 4 quantifies the relative uncertainty of the phase-averaged traction stresses defined in Eq. 4 as a function of N. We estimate this uncertainty from the ratio

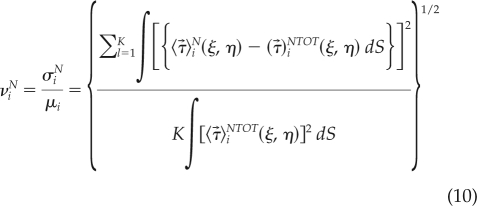where 〈($\overrightarrow{\tau }$ξ, η)〉_i^N is the average traction stress field for the ith phase of the motility cycle, and ∫()ds represents a surface integral in the cell-based coordinate system. The numerator of Eq. 10, σ_i^N, is the SD of the distribution {〈($\overrightarrow{\tau }$ξ, η)〉_i^N} of the ith phase average traction stresses obtained for all the subsets of N cells (a total of K) that exist within in a set of N_TOT > N cells [i.e., for N = 2 cells and N_TOT = 3 cells, we would calculate K = 3 partial averages with cells (1,2), (2,3), and (1,3) and compare them with the total average obtained with cells (1,2,3)]. We note that σ_i¹ is the SD of the distribution of instantaneous traction stresses observed on single cells. The denominator of Eq. 4, μ_I, represents the average traction stresses for the ith phase and is used to normalize σ_i^N, so that ν_i^N indicates the variability of 〈($\overrightarrow{\tau }$ξ, η)〉_i^N relative to its expected value.

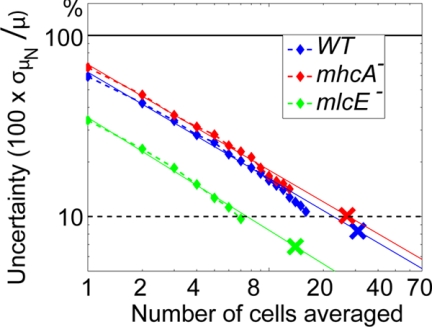
Figure 4.

Percentage of error (two-dimensional L2 norm) of the phase averaged traction fields as a function of the number of cells compiled in the statistics. Blue, wild-type cells; red, mhcA⁻ cells; green, mlcE⁻ cells. The plots show the standard deviations, σ_μ^N, of the distributions of phase-averages μ^N obtained for all possible combinations of N cells that can be formed within a population of N_TOT > N cells. The results are normalized with the total average, μ^NTOT, and represented as a function of N. The straight lines are projections of the data from each cell strain. The color crosses on the projections correspond to N = N_TOT (N_TOT = 31, 14, and 27 for wild-type, mlcE⁻, and mhcA⁻ cells, respectively). These crosses therefore estimate the uncertainty of the phase averages in Figure 5.

Equation 4 is a precise estimation of the uncertainty of the measurements only when N_TOT ≫ N and the average, 〈($\overrightarrow{\tau }$ξ, η)〉_i^Ntot, can be considered as “exact” in comparison with 〈($\overrightarrow{\tau }$ξ, η)〉_i^N. However, N_TOT is necessarily limited in practice by the finite number of experiments performed, which in our case is N_TOT = 31, 14, and 27 for wild-type, mlcE⁻, and mhcA⁻ cells. For this reason, we have only plotted ν_i^N for N < N_TOT/2 in Figure 4. Even for these moderate numbers, the combinations that need to be considered for the calculation of σ_i^N are overwhelmingly large, so we have estimated this quantity by performing a Monte-Carlo simulation with n = 1000 iterations. The result shows that the relative uncertainty of 〈($\overrightarrow{\tau }$ξ, η)〉_i^N decreases with the number of cells as σ_i^N/μ_i ∝ N^−1/2, as expected for the SD of the sum of independent statistical distributions (Grinstead and Snell, 1997). The accuracy of the phase-averaged traction stresses given in this article can be estimated by extrapolating the ν_i^N ∝ N−1/2 behavior to N = N_TOT. This extrapolation yields the colored crosses in Figure 4, which correspond respectively to ν_i^N = 10% for the three cell lines. A similar extrapolation also can be carried out to estimate the number of cells that would be necessary to reach any desired level of statistical convergence. For example, Figure 4 indicates that ν_i^N = 30% − 70% for N = 1, implying that observations made on the basis of single-cell traction maps have a high inherent uncertainty, which makes the need for statistical analysis obvious.

MyoII Is Required for the Proper Spatial Organization of the Traction Stresses

Comparison of the contour and traction stress maps of wild-type, mlcE⁻, and mhcA⁻ cells should provide insights into the different function of MyoII in controlling the distribution of traction forces during the chemotaxis motility cycle. Figure 5A includes contour maps of the phase-averaged traction stresses generated by these three strains during the four stereotypical phases as defined in this study: protrusion, contraction, retraction, and relaxation. In all strains, the cells contract from the periphery inward toward the cell center throughout the cycle, as indicated by the black arrows. It should be noted that Figure 5 shows average maps of traction forces and average cell contours. Because the instantaneous contour of the cell does not need to be equal to the average contour, it is perfectly possible to observe nonzero average traction stresses outside of the average cell contour (for details, see Materials and Methods and Supplemental Data). Supplemental Movies M1, M2, and M3 illustrate how the contour and stress maps of each of the three strains change as the cell moves.

Wild-type cells produce the highest traction stresses (see color map), which are concentrated in two well-defined areas in the front and the back of the cell and which probably correspond to the two discontinuous regions of cell substrate adhesion observed by Weber et al. (1995). The overall spatial distribution of stresses in mlcE⁻ cells is similar to that of wild-type cells, although their magnitude is lower by a factor of ∼2. MyoII motor activity has been proposed to be mostly abrogated in mlcE⁻ cells (Chen et al., 1995), but MyoII still can cross-link F-actin (Xu et al., 2001). The stresses produced by mhcA⁻ cells, which lack the myosin II heavy chain and thus all MyoII functions, are similar in magnitude to those of mlcE⁻ cells. We therefore suggest that the loss/reduction of MyoII-mediated contraction results, unexpectedly, in only modestly depressed peak values of stress, suggesting that similar stress levels can be maintained by other mechanisms. In mhcA⁻ cells, the stress pattern is qualitatively different due to not being focused in two separate areas and being situated closer to the cell boundaries than in wild-type or mlcE⁻ cells. The differences between the mhcA⁻ and mlcE⁻ strains suggest that the lack of organization in the stress patterns of the mhcA⁻ cells may result from the loss of MyoII's F-actin cross-linking function and not be due to an inability to generate shape-preserving forces that play a role during mitosis (Effler et al., 2006). The importance of MyoII for the organization of the stresses is even more evident in a different view of the traction stress data presented in Figure 5B. Here, the vectors of traction stress fields averaged over the entire cycle period are decomposed into their components parallel and perpendicular to the main cell axis. This view emphasizes that in wild-type and mlcE⁻ cells, the contribution of the parallel stress components to the total stress field is much higher than that of the perpendicular components. This is not true for mhcA⁻ cells, in which the proportion of the perpendicular components is much larger, consistent with a key role of the MyoII F-actin–cross-linking function in regulating the spatial organization of the stress forces.

The Mechanical Cycle of Traction Stresses and Cell Shapes Remains Similar but Is Slowed down When MyoII Function Is Lost

We then applied the phase averaging method to examine the forces that cells exert during each stage of the motility cycle, enabling us to compare the mechanics of their locomotion. In Figure 5A, each strain is represented by four distinct phase-averaged stress maps and cell shapes. Table 1 contains the measured average speed and duration corresponding to each phase and strain described in Figure 5A. Remarkably, the wild-type and the two mutant strains that affect MyoII function move continuously during all phases with relatively small changes in speed, as shown in Figure 3B and discussed above. In addition, the cells always contract. Comparison of the three strains shows that although the magnitudes of the stresses are different, the overall time evolutions of the stress patterns during the phases of the motility cycle are similar: they are minimal during the relaxation phase (minimal cell length), increase during protrusion, reach their maximum during contraction (maximal length), and decrease during retraction. Theses observations support the hypothesis that wild-type, mlcE⁻, and mhcA⁻ cells move by implementing a similar motility cycle in which the cell length and the mechanical energy deposited by the cell on the substrate evolve similarly in time, which is consistent with the data presented in Figures 2 and 3.

Table 1.

Numerical values obtained from the statistical analysis of the motility cycle of wild-type, mclE⁻, and mhcA⁻ cell lines. The table lists the averages and standard deviations for each phase of the motility cycle as well as for the whole cycle. Values are given for cell length (L), cell aspect ratio (AR), cell speed (V), the translational component of area flux (AF_trans), the component of area flux attributable to deformation (AF_defor), the total duration of the motility cycle (T) and the duration of individual phases (T₁, T₄, T₃ and T₄), pole force (F_p), and strain energy (U_s). The number N of cells used for this statistical analysis: wild-type (N = 31), micE⁻ (N = 14), and mhcA⁻ (N = 27).

			L (μm)	AR	v (μm/min)	AFtrans (μm2/s)	AFdefor (μm2/s)	T (s)	Fp (pN)	Us (pN μm)
wild-type	Whole Cycle	mean	21.85	2.53	12.71	1.27	0.01	94.10	387.5	68.1
		std	4.51	0.66	3.12	0.41	0.10	29.15	305.6	94.6
	Protrusion	mean	22.14	2.56	15.11	1.65	0.65	22.01	404.5	73.4
		std	4.57	0.60	4.00	0.54	0.50	11.52	350.8	118.9
	Contraction	mean	24.88	3.14	14.40	1.38	−0.03	23.19	482.4	86.3
		std	5.14	0.80	4.19	0.59	0.26	14.00	448.0	121.0
	Retraction	mean	22.10	2.55	11.47	1.02	−0.56	22.93	393.5	64.4
		std	4.52	0.70	3.12	0.40	0.42	10.84	286.0	74.5
	Relaxation	mean	19.13	2.02	10.97	1.05	0.04	29.96	313.7	57.8
		std	3.64	0.52	2.65	0.35	0.21	14.93	235.4	88.9
mlcE-	Whole Cycle	mean	22.32	2.03	7.62	1.01	0.02	143.64	348.5	38.2
		std	3.31	0.29	2.30	0.36	0.09	36.22	132.9	19.1
	Protrusion	mean	22.34	2.02	8.55	1.14	0.41	32.80	344.3	38.5
		std	3.17	0.29	2.70	0.50	0.27	12.09	142.0	23.0
	Contraction	mean	24.76	2.39	8.50	1.13	−0.02	38.01	416.6	47.5
		std	2.98	0.35	2.58	0.40	0.18	7.75	162.1	25.9
	Retraction	mean	22.62	2.09	7.03	0.94	−0.31	39.30	363.1	40.4
		std	3.15	0.31	2.33	0.42	0.26	16.97	140.3	23.2
	Relaxation	mean	19.98	1.68	6.70	0.86	0.05	42.54	265.7	26.4
		std	3.55	0.29	2.23	0.39	0.11	18.76	119.2	14.4
mhcA-	Whole Cycle	mean	19.98	2.08	5.64	0.58	0.00	190.81	284.6	48.8
		std	5.72	0.39	1.68	0.33	0.04	83.29	159.9	50.0
	Protrusion	mean	20.47	2.16	7.21	0.87	0.41	35.50	302.8	53.1
		std	5.78	0.44	2.08	0.40	0.25	19.27	205.4	61.1
	Contraction	mean	22.95	2.54	6.27	0.61	−0.03	41.22	364.4	64.5
		std	6.41	0.53	1.93	0.31	0.15	21.10	222.0	59.8
	Retraction	mean	20.24	2.13	4.90	0.40	−0.21	50.01	281.8	47.0
		std	5.41	0.38	1.62	0.34	0.24	28.14	174.8	51.6
	Relaxation	mean	17.57	1.72	5.20	0.56	−0.02	58.81	241.6	40.0
		std	5.11	0.32	1.65	0.41	0.12	30.83	141.3	48.3

Despite these overall similarities, we observe differences between the three cell lines that can be correlated with the molecular properties of the MyoII complex. One of the most obvious differences between wild-type and MyoII mutant strains is the increased duration of all four phases T₁, T₂, T₃, and T₄ (Figure 6). The durations of each of the four phases of wild-type cells are considerably shorter than those of mhcA⁻ cells and are also far shorter than those of mlcE⁻ cells for protrusion, contraction, and retraction and slightly shorter for the relaxation phase. This finding suggests that the contractile function of MyoII is important during all phases of motility and is an important factor in determining the overall speed.

We then examined the mechanical function of MyoII during each stage of the motility cycle in more detail by comparing the stress patterns and cell shapes. In wild-type cells, we observe that the region of concentrated stresses at the front is close to the centroid of the cell during protrusion, suggesting that the frontal part of the cell (the pseudopod) glides over the substrate (consistent with previous studies (Wessels et al., 1994). During contraction, this region of concentrated stresses seems to have moved closer to the front edge of the cell, suggesting the formation of new adhesion regions. Likewise, the region of concentrated stresses in the posterior part of the cell is located closer to the centroid of the cell during retraction, consistent with the back of the cell gliding forward. During protrusion, mhcA⁻ cells produce comparatively low, spread-out traction stresses at their back, which indicates a dilated shape compared with wild-type and mlcE⁻ cells. These differences could be due to an inability of mhcA⁻ cells to compensate for the increase in cytoskeletal compression in response to F-actin polymerization at the front through myosin contraction at the back of the cell. Instead, the bulge that appears at the back of mhcA⁻ cells during this phase suggests that this compression is compensated for by an increase in membrane tension at the back. This implies that mhcA⁻ cells are less effective in controlling the stability of protruding pseudopodia, which may explain the reduced frequency of pseudopod protrusion in mhcA⁻ cells observed by Wessels et al. (1988). Consistent with these ideas, Fukui et al. (2000) reported reduced stability of protruding pseudopodia in mhcA⁻ cells subjected to centrifugal force. During retraction, the shape of wild-type and mlcE⁻ cells becomes much wider at the front than at the back due to the accumulation of mass coming from the retraction of the rear part of the cell. This shape is consistent with the cortical tension being lower at the front than at the back, probably due to MyoII contracting at the back and generating a pressure gradient. A similar, although less pronounced, frontal dilatation is observed in mlcE⁻ cells during retraction, suggesting that these cells can still partially control their cortical tension, presumably through the cross-linking action of MyoII. However, this mechanism seems to be less efficient in cells with reduced or modified MyoII-based motor function because this phase is prolonged in mlcE⁻ mutants compared with wild-type cells (Figure 6). Cells lacking MyoII cannot take advantage of either of these two mechanisms. They display a reduced dilatation of their front and their retraction is prolonged considerably. The relaxation time in mlcE⁻ cells is longer than that in wild-type cells but shorter than that in mhcA⁻ cells, indicating that both the contractile and the noncontractile activities of MyoII help to determine how fast a cell can finish retraction and protrude again to start the next motility cycle.

DISCUSSION

We have expanded previous descriptions of the amoeboid motility cycle (Lauffenburger and Horwitz, 1996) and have elucidated the functions that MyoII plays in controlling the spatial distribution of traction forces that regulate this process. We have used a new phase-averaging statistical method to analyze the measurement of the temporal evolution of the traction forces and cell shapes changes during chemotaxis that does not depend on the subjective identification of representative cells. Our statistical analysis provides a quantitative representation of the motility cycle of the average cell with detailed spatial and temporal information and provides statistically significant evidence for the existence of a coherent motility cycle, as was proposed previously based on microscopic observations (Zigmond and Hirsch, 1973; Devreotes and Zigmond, 1988; Weber et al., 1995). Our analysis of the area fluxes of the plane view of the cells undergoing chemotaxis clearly shows that the overall cell movement is the result of a combination of a continuous translocation with a superimposed periodic cycle of front protrusion and rear retraction. These results provide clear evidence against an alternative possibility in which cells move continuously, undergoing random changes in cell shape, traction stresses, and length.

We show that when amoeboid cells undergo chemotaxis on elastic substrates, the largest fraction of the variations in the strain energy transmitted to the substrate are “periodic” and coordinated with the changes in cell length, rather than the superposition of chaotic “random” changes. Owing to the periodic nature of this process, we have been able to implement a novel statistical methodology that dissects the motility cycle into four “canonical” stages and to compute average maps of traction forces for each stage of the cycle. This phase-average analysis has allowed us to quantify the main differences in the cell shape changes and generation of traction forces among wild-type, mlcE⁻, and mhcA⁻ strains. These maps provide new insights into how MyoII cross-linking and contractility functions contribute to the generation of the traction forces that cells exerts on the substratum as they move. We show that wild-type cells and cells with altered MyoII function exhibit important and significant differences, providing insight into the complex roles MyoII plays in regulating these forces. We note that there are specific differences between wild-type and mlcE⁻ cells. In vitro, MyoII lacking the essential light chain, while retaining ATPase activity, lacks motor activity, although it still binds and cross-links F-actin (for discussion, see Chen et al., 1995; Xu et al., 2001). However, the behavior of this myosin has not been fully characterized, particularly the force–velocity relationship and how this myosin behaves in response to mechanical stress. For example, the MyoII complex lacking the essential light chains may behave similar to MyoII^S456L in that it is able to undergo translocation under conditions when mechanical stress is applied (Ren et al., 2009). The differences between the strains can at least partially be explained by a possible altered responsiveness of the MyoII motor activity or reduced motor activity in mlcE⁻ cell, while retaining the ability to cross-link F-actin or, in mhcA⁻ cells, the absence of MyoII function (Wessels et al., 1988). Comparison of phase-averaged stress force maps of wild-type or mlcE⁻ cells to those of mhcA⁻ cells show that mhcA⁻ cells are overall of more rounded shape at all stages of the motility cycle. More importantly, we show that mhcA⁻ cells are still able to contract continuously, but unlike the other cell types, mhcA⁻ cells do not mainly contract by exerting opposing pole forces front to back, but rather they contract all around the cell periphery. This difference in the stress distribution reveals an important role of MyoII for cytoskeletal integrity through its F-actin cross-linking function. In addition to the loss of myosin motor activity, which impairs rear retraction, this reduced organization of the stress forces may contribute to the observed increase in the periods of the motility cycle of mhcA⁻ cells. Additional evidence for the role of MyoII in cytoskeletal integrity becomes apparent in the protrusion phase in which, in mhcA⁻ cells, the back is wider than the front, suggesting that the cytoskeletal integrity at the back of the cell may be insufficient to balance the backward forces produced by actin polymerization during protrusion (Condeelis et al., 1988; Fukui et al., 1991; Iwadate and Yumura, 2008). A reduced ability to compensate for these forces also may be connected with the reduced frequency of pseudopod protrusion in mhcA⁻ cells, which has been reported previously (Wessels et al., 1988; Fukui et al., 1991, 2000). Our detailed analysis of the temporal and spatial distribution of stress forces also suggests that both MyoII actin cross-linking and contractility functions play an important role in increasing the level of intracellular tension at the back of the cell to promote retraction.

It should be noted that MyoII may determine the stresses transmitted to the substrate not only by setting the level of cytoskeletal tension through its cross-linking and contraction functions but also by modulating the number and area of the cell substrate adhesions. Therefore, a more detailed dissection of the mechanical function of MyoII would require measuring jointly the cell traction forces and substrate attachment regions. Nevertheless, our pole force measurements (Table 1), which represent the integrated effect of the stresses in the front and back of the cell (Del Alamo et al., 2007), provide a quantification of the overall level of cytoskeletal contraction in the cell independent of the number and area of the adhesions. These pole force measurements show no significant differences between wild-type and mlcE⁻ cells but are 27% lower in mhcA⁻ cells, consistent with prior observations that the cortical resistance to compression is reduced by 32% in mhcA⁻ cells (Pasternak et al., 1989), and supporting an important role of MyoII for cytoskeletal integrity through its F-actin cross-linking function. In contrast, these data indicate that roughly 70% of the magnitude of cellular stresses comes from molecules other than MyoII. For example, we know that other actin cross-linking proteins, including α-actinin, cortexillin, and gelation factor (ABP120), make a significant contribution to maintaining cytoskeletal integrity and cortical stiffness (Witke et al., 1992; Faix et al., 1996; Reichl et al., 2008). It is therefore reasonable to assume that in the mhcA⁻ cells, where our measurements show that contractile forces are more uniformly distributed throughout the cortex, some of these cross-linkers are relocalized and possibly partially compensate for the lack of MyoII cross-linking function.

We gained further insight into the conserved motility cycle by decomposing our measurements of the movement of Dictyostelium cells into two distinct kinematical components: an inchworm-like motility component consisting only of protrusion and retraction and a shape-preserving component consisting only of continuous translocation. These events are not necessarily driven by different biochemical processes but are characterized by a different level of spatial and temporal coherence. We argue that the shape-preserving component is the result of continuous contributions from events occurring at a length scale much shorter than the cell length and at a time scale much shorter than the measured period of the motility cycle (T), possibly at the level of a single protein or molecular complex. Our MyoII mutant data suggest a direct involvement of continuous actomyosin contraction in this component and therefore indicate that MyoII makes an important contribution to cell speed during all phases of motility. Such a contribution may be related to its previously described role in frontal blebbing, which is sometimes observed in highly motile Dictyostelium cells (Langridge and Kay, 2006; Yoshida and Soldati, 2006) and other cell types (Charras, 2008). Interestingly, both the total migration speed and its inchworm-like and shape-preserving components are inversely proportional to the period of T. This dependence on the period of the cycle for the shape-preserving portion is unexpected and strongly suggests the existence of a coupling mechanism. The “inchworm” component presumably modulates the overall shape of the cell as well as other cellular properties like the global level of stress that drives the continuous, shape-preserving translocation of the cell. Recently, two components have also been found to play a role in leukocyte motility, but, rather than contributing to motility simultaneously, they have been described as a switch from deformation to gliding when MyoII activity is suppressed, or when substrate adhesiveness is increased (Jacobelli et al., 2009). Further work is needed to understand the exact relationship between our results and this observation, but the two findings suggest the existence of evolutionarily conserved mechanical aspects of amoeboid motility.

Our phase-averaged maps also shed light on the mechanical process of motility and reflect on the role of MyoII in this process. Our traction cytometry measurements reveal that cells migrating under conditions of normal adhesiveness generate opposing traction “pole forces” much greater than those required to overcome the external resistance of the environment (Del Alamo et al., 2007). Basic mechanical principles suggest that the speed of amoeboid cells is limited by the amount of propulsive power that they are able to generate through their traction forces. The average propulsive power generated per motility cycle can be represented as P = Fv ∼ F λ/T, where F is the characteristic traction force, λ is the distance traveled per cycle, and T is the characteristic period or duration of the cycle. Two extreme regimes of motion can arise when the propulsive power is limited either by the strength of the forces that the cells can produce to overcome the resistance of their environment (strength limited motility) or by the pace at which they can repeat their motility cycle (pace limited motility). Strength limited motility is realized experimentally in highly adhesive substrates, in restrictive environments such as multicellular aggregates or under an agar overlay, or when cells are moving against an external force generated by a micropipette. Previous studies have established the importance of MyoII for cell motility under these conditions (Wessels et al., 1988; Jay et al., 1995; Shelden and Knecht, 1995, 1996; Xu et al., 1996; Effler et al., 2006; Reichl et al., 2008). Our study provides an analysis of the role of MyoII in motility under nonrestrictive conditions and helps define specific roles for MyoII functions in controlling traction forces and cell motility.

Because the net traction forces required to drive the motion of the cell were measured to be much smaller than the forces that the cell applies locally to the substrate in all of cases that we studied (Supplemental Table S1 and Supplemental Figure S1), we suggest that the motility of wild-type and mutant cells on flat surfaces is not strength limited, in contrast to the case of cells moving in highly adhesive substrates, in restrictive environments, or against external forces. Instead, we propose that amoeboid motility on flat surfaces is pace limited. Consistent with this regime, we measure that a cell's mean velocity of migration V and the period T of its motility cycle are related by a rather simple proportionality as V = λ/T, where λ ≈ 18 μm (similar to our previous analyses, λ ≈ 16 μm) is a “stride” length. Furthermore, we find that the stride length is conserved between wild-type cells and strains with modified MyoII contractility or even in cells with reduced adhesion. The finding that, for wild-type cells and these specific mutants, regardless of the speed of migration, a cell on the average advances a fixed length per cycle, suggests that the mechanochemical processes that define λ are conserved in all of these strains. Consistent with the above findings, we propose that the stride length may be controlled by the regulation of F-actin polymerization either via intrinsic properties of F-actin polymerization, such as an average duration controlled by biochemical feedback loops, or via adaptable sensors of physical parameters. We further postulate that such a control mechanism is more likely than the determination of a set stride length by direct physical constraints such as membrane stiffness, because wild-type and MyoII mutant strains differ greatly in their cytoskeletal properties (Wessels and Soll, 1990; Feneberg et al., 2001; Girard et al., 2006), yet vary little in their characteristic step length. Moreover, in agreement with previous reports (Wessels et al., 1988; Uchida et al., 2003; Del Alamo et al., 2007; Lombardi et al., 2007), we find that the period T of the motility cycle is partially determined by altered properties of actomyosin contractility (lacking in mlcE⁻ and mhcA⁻ cells) and by the actin cross-linking function of MyoII (lacking in mhcA⁻ cells). In particular, we show quantitatively that the actomyosin contractility is important for efficient progress through all of the phases of the motility cycle. We find that the F-actin cross-linking by MyoII is as important for the initiation of the protrusion of the front as for the retraction of the rear, possibly by indirectly stabilizing the cytoskeletal organization along the lateral sides and posterior of the cell where cortical MyoII is distributed along an anterior–posterior gradient (Yumura et al., 1984).

Abbreviations used:

F-actin

filamentous actin

MyoII

nonmuscular myosin II complex

MhcA

MyoII heavy chain

MlcE

myoII essential light chain

MlcR

MyoII regulatory light chain

mIcE⁻

mlcE null

mhcA⁻

mhcA null

wild-type

wild type

V

average velocity of a cell

T

duration of the motility cycle of a cell

T₁

average duration of the protrusion phase

T₂

average duration of the contraction phase

T₃

average duration of the retraction phase

T₄

average duration of the relaxation phase

λ

average distance traveled by a cell during one motility cycle

L

length of a cell

Us

strain energy deposited by a cell on its substrate

R_UsUs

auto correlation coefficient of the time evolution of Us

R_Lus

cross correlation coefficient of the time evolution of Us

AF_front⁺

overall positive area flux (rate of area gain) in the front of a cell

AF_back⁺

overall positive area flux (rate of area gain) in the back of a cell

AF_front⁻

overall negative area flux (rate of area loss) in the front of a cell

AF_back⁻

overall negative area flux (rate of area loss) in the back of a cell

AF_def

area flux (rate of area change) of deformation

AF_trans

area flux (rate of area change) of shape-preserving translocation

V_trans

velocity of shape-preserving translocation.