A new gene selection procedure based on the covariance distance

Abstract

Motivation: Very little attention has been given to gene selection procedures based on intergene correlation structure, which is often neglected in the context of differential gene expression analysis. We propose a statistical procedure to select genes that have different associations with others across different phenotypes. This procedure is based on a new gene association score, called the covariance distance.

Results: We apply the proposed method, along with two alternative methods, to several simulated datasets and find out that our method is much more powerful than the other two. For biological data, we demonstrate that the analysis of differentially associated genes complements the analysis of differentially expressed genes. Combining both procedures provides a more comprehensive functional interpretation of the experimental results.

Availability: The code is downloadable from http://www.urmc.rochester.edu/biostat/people/faculty/hu.cfm

Contact: huruizg@hotmail.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Microarray technology has become a routine gene expression analysis tool in recent years. Biomedical researchers rely on this technology to identify potentially ‘interesting’ genes. Typically, individual genes are tested for their differential expressions between phenotypes by the two-sample Student's t-test or its non-parametric counterpart. The resulting P-values are adjusted by a chosen multiple testing procedure (MTP) in order to control certain group-wise Type I errors. In depth reviews of MTPs used in microarray analysis can be found in Dudoit et al. (2003) and Simon et al. (2003). Popular choices include the Bonferroni procedure, which controls the familywise error rate (FWER), and the Benjamini–Hochberg procedure (Benjamini and Hochberg, 1995), which controls the false discovery rate (FDR). Despite the inherently different designing philosophy, the empirical Bayes methodology (Efron, 2003) can be considered as one of the MTPs since it controls a local version of FDR.

All of the above MTPs were first designed for independent tests. However, it might be inappropriate to model gene expressions as independent random variables because gene expressions are correlated in groups of functionally linked genes (e.g. gene ontology, biological pathways). Long-range, inter-pathway correlation has also been documented recently (Almudevar et al., 2006; Klebanov and Yakovlev, 2008; Qiu et al., 2005a). Ignoring the dependence between gene expressions leads to the loss of control of type I errors and poor reproducibility (high instability) of outcomes (Qiu and Yakovlev, 2006; Qiu et al., 2005b, 2006).

Several extensions to the MTPs have thus been proposed in order to address this ‘dependence problem’. For example, the Westfall–Young permutation procedure (Westfall and Young, 1993) can be seen as an extension of the Šidák procedure for dependent tests; and a variant of the original Benjamini–Hochberg procedure lends itself to the control of FDR with gene dependence (Benjamini and Yekutieli, 2001); and a data-driven variable transformation called the δ-sequence method (Klebanov et al., 2008; Klebanov and Yakovlev, 2008) de-correlates gene expressions and thus improves the power and stability of the non-parametric empirical Bayes method significantly.

Although the invention of these new MTPs has mitigated the adverse effect of intergene dependence in differential expression analyses, none of them were designed to select candidate genes by utilizing the rich information contained in the intergene dependence structure. Several other approaches have been proposed to capitalize on this dependence structure:

1. Incorporating the existing biological gene sets information into statistical procedures. One such example is the gene set enrichment analysis (Mootha et al., 2003; Subramanian et al., 2005), which has gained considerable momentum in the past few years. The main drawback of this approach is that it is not suitable for searching new functionally linked gene sets.

2. A multitude of cluster analysis methods including several variants of principal components analysis (Liu et al., 2002; Raychaudhuri et al., 2000; Wang and Gehan, 2005), hierarchical clustering (Eisen et al., 1998), self-organizing maps (Törönen et al., 1999), support vector machines (Brown et al., 2000; Furey et al., 2000), etc. These methods can be used as exploratory tools to highlight the possible hidden relationship between genes, or as means to reduce the vast dimensionality of the multiple testing problem. Like the methods in the first approach, these methods do not select genes by their dependence structure directly. Instead, they group genes in the form of either principal components or gene clusters, so the selection step (which is still based on statistical inference of mean values) can be more efficient.

3. Another approach is to select genes based on the phenotypic changes of their dependence structure directly. The standard practice is to compute an association score for each gene pair which represents the change of their association in different phenotypes and then compute its P-value by a resampling method. Choices of this score include liquid association (Li, 2002), biweight midcorrelation (a robust correlation coefficient) (Shedden and Taylor, 2005), or simply the Pearson correlation with Fisher transformation (Choi et al., 2005). One major obstacle of this method is the daunting magnitude of multiple testing. If we denote m as the number of genes, then there are 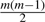distinct gene pairs. It renders most MTPs powerless. Consequently, these proposed methods either rely on unadjusted P-values (Li, 2002) thus totally abandoning control over group-wise type I error, or resort to some ad hoc criteria such as selecting top n% of gene pairs (Choi et al., 2005) or genes that have scores greater than a prespecified threshold (Shedden and Taylor, 2005).

The persistent interest in incorporating dependence structure into gene selection procedure stems from the interdependence of all biological processes. Transcriptional regulatory circuits, called network motifs, with a set of transcription factors regulating a set of target genes in a multi-layer, auto-correlated manner is the basic example of the interlocked biological processes (Alon, 2006). In these circuits, expression of target genes depends on the expression of regulator genes. Changes in these associations in different cellular states can be indicative of changes in regulatory programs which motivates association studies (Dettling et al., 2005; Lai et al., 2004; Li, 2002). On the other hand, induced changes of the cellular states can also be reflected in changes of the dependence structure. For example, histone deacetylases (HDACs) dynamically affect transcription of many genes; HDAC inhibitors downregulate HDACs and consequently affect the transcription of up to 20% of the entire genome (Menegola et al., 2006; Stamatopoulos et al., 2009). Disentangling the subset of genes, differentially associated (DA) with HDACs under inhibitors treatment, can be informative in carcinogenesis studies, given recent success of HDAC inhibitors as anticancer drugs (Bots and Johnstone, 2009).

A procedure, specifically designed to select genes changing their associations with other genes was recently suggested (Hu et al., 2009). This procedure also overcomes the multiplicity problem of differential association analysis based on gene pairs. Instead of searching for DA gene pairs in a sea of potential candidates by univariate tests, they propose to test whether the joint distributions of the correlation vectors (CVs) change across different phenotypes. CV is defined as the Fisher transformation of the Pearson correlation coefficients between a given gene and the rest. The multiplicity of this method is m, so MTPs commonly used in differential expression analysis can be applied to control group-wise type I errors. This approach utilizes the joint distributions of CVs. Consequently, it can detect genes which are differentially correlated (DC) with a large number of genes, yet each individual correlation change is too small to be detected by a pairwise method. The main caveat of this approach is the low testing power. One likely culprit is the use of the Fisher transformed Pearson's correlation coefficient as the association score. In this article, we propose a new gene selection procedure based on a new association score, the covariance distance, together with a trimming algorithm. Through several simulation studies, we demonstrate that it is a better choice for selecting DC genes compared with the CV method based on the Pearson's correlation coefficients. In addition to testing gene correlation coefficient changes, this new method can also detect gene variance changes across phenotypes.

2 METHODS

2.1 Biological data used in the study

The biological dataset used in this study is the childhood leukemia dataset from the St Jude Children's Research Hospital (SJCRH) Database (Yeoh et al., 2002). We select two groups of data: 88 patients (arrays) with hyperdiploid acute lymphoblastic leukemia (HYPERDIP) and 79 patients (arrays) with a special translocation type of acute lymphoblastic leukemia (TEL). To make two data groups comparable, only the first 79 arrays in HYPERDIP are used.

Since the original probe set definitions in Affymetrix GeneChip data are known to be inaccurate (Dai et al., 2005), we update them by using a custom CDF file to produce values of gene expressions. The CDF file was downloaded from http://brainarray.mbni.med.umich.edu. Each slide is then represented by an array reporting the logarithm (base 2) of expression level on the set of 7084 genes. To avoid introducing false standard deviations (SDs) when performing permutations, each gene is centered by subtracting its sample mean. For convenience, the words ‘gene’ and ‘gene expression’ are used interchangeably to refer to these log-transformed and mean-centered gene expressions in this article.

2.2 The covariance distance vector

Let c=A,B be two different phenotypes or biological conditions, m be the total number of genes and n be the number of arrays sampled from each phenotype group. Denote X^c=(X^c₁,…, X^c_m) as the m-dimensional random vector from which n independent observations (arrays), x^c_i=(x^c_i1,…, x^c_in, i=1,…, m, are sampled in the phenotype c. As a special case, if X^c is a multi-normal random vector, its joint distribution function, F_X^c(x), is completely characterized by its first-order moments (the means) and second-order moments (the covariances).

Univariate gene selection methods select genes that have different marginal distributions (usually in terms of different mean values) under different biological conditions: selected genes are called differentially expressed (DE) genes. For the distributional changes caused by the changes of the second-order moments, we suggest a different hypothesis testing framework.

We define the covariance distance between two genes x^c_i and x^c_j to be 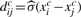, where 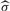is the function of sample SD. Like the sample correlation coefficient, this distance is a measure of the similarity between two random variables in terms of their second-order moments. We also define the covariance distance vector for the i-th gene as D^c_i=(d^c_i1,…, d^c_im), with its joint distribution denoted by F_D^ci(x).

We propose to test the following hypotheses

The i-th gene is selected if H_i is rejected.

This approach is closely related to a similar method proposed by Hu and colleagues (2009). The main difference lies in the choice of association score: the covariance distance is used in place of the Pearson's correlation coefficient (with Fisher transformation). The covariance distance approach has two distinctive advantages: (i) the covariance distance is more sensitive to small changes (differences) of corr(x_i, x_j) when x_i and x_j are highly correlated (see Section 4 of the Supplementary Materials for more details); (ii) it can also reflect the changes of the variances of x_i and x_j (see Section 2 of the Supplementary Materials for more details). If the association scores between a fixed gene and the others are different across phenotypes, it is called DA. As a special case, if the correlation coefficients between one gene and the rest are different across phenotypes, it is called DC.

2.3 The trimmed covariance distance vector

We choose the N-distance (also known as the N-statistic) with Euclidean kernel as the multivariate summary statistic for testing hypotheses (see Section 3 of the Supplementary Materials for details). This statistic has been successfully employed to select DE genes, DC genes and gene combinations in microarray data analysis (Hu et al., 2009; Szabo et al., 2002, 2003; Xiao et al., 2004; ?).

In order to test the hypotheses, we need to create samples of the covariance distance vectors. We may divide the arrays in each phenotype into n_s subgroups, each containing 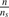arrays. By computing the covariance distance vectors from each subgroup, we obtain a sample of vectors with size n_s for each phenotype. We have tested different choices of n_s (n_s=1, 4, 8, 16) and found that the results are consistent. Therefore, we choose n_s=1 to save computing time.

We compute covariance distance vectors for the i-th gene in both phenotypes (D^A_i and D^B_i), and then calculate N_i, the sample N-distance between D^A_i and D^B_i. This is a measure of the difference between two covariance distance vectors. A list of significant genes can be selected as the DA genes based on this measure.

An adaptation to the above approach can make it more practical, which is illustrated by the following example. Suppose there are 10 genes in a study. In one phenotype all 10 genes are independent; in the other phenotype the first gene becomes highly correlated with the rest but the other nine genes are still independent with each other. With a large enough sample size, the above approach will call all genes DA. In fact, the selection of the first gene is straightforward because it has completely different dependence structures with nine other genes in two phenotypes. Genes 2,…, 10 have the same dependence structures with all but the first genes in two phenotypes, which leads to a relatively small, albeit none-zero change of the N-distance of its covariance distance vectors. The first gene is the ‘reason’ for the correlation structure change. Therefore, it is reasonable to expect a sensible statistical procedure to select the first gene as the only DA gene. In other words, our criterion here is to select genes which change their associations with most of the other genes. This selection criterion can be achieved by excluding a subset of genes that induce large changes of the covariance distance before computing the N-distance.

For the fixed i-th gene, we can sort all m genes in descending order by |d^A_ij−d^B_ij|, j=1,…, m, which reflects the j-th gene's ‘contribution’ to N_i. If we omit the top K genes, the remaining covariance distance vector is called the trimmed covariance distance vector (TCDV) and denoted by D_i^c,K where c=A or B. Here, K is a parameter which indicates how many genes (covariance distances) need to be trimmed. Trimming is a widely used technique in robust inference (see e.g. Wilcox, 2005). A good K should be large enough so genes with only a few changed covariance distances (possibly due to the presence of DA genes) have near-zero difference of TCDV, and small enough so that true DA genes can still be detected effectively.

Instead of testing H_i, we can test the following hypotheses based on the TCDV

where F_D^A,Ki(x) and F_D^A,Ki(x) are the joint distributions of D_i^A,K and D_i^B,K, respectively. The i-th gene is declared to be DA if H^′_i is rejected.

2.4 Resampling P-values through permutations

By using the TCDV in place of the covariance distance vector, we can compute a resampling-based P-value for the i-th gene as follows:¹

1. Compute d^A_ij and d^B_ij, its covariance distances with all other genes in two phenotypes.

2. Sort genes by |d^A_ij−d^B_ij| in descending order, j=1,…, m.

3. Omit the first K genes (covariance distances) in the covariance distance vectors D_i^A and D_i^B to get the TCDVs D_i^A,K and D_i^B,K in two phenotypes.

4. Compute N_i^K, the N-statistic of D_i^A,K and D_i^B,K.

5. Randomly shuffle the arrays in two different conditions, then split them into two groups with equal size.

6. Compute the TCDVs and the N-distance for this permuted dataset. If computationally feasible (e.g. n≤10), this step is repeated for all possible permutations of arrays. Otherwise L random permutations will be used. Record these resampling-based N-statistics as N^K_il, i=1,…, m, l=1,…, L.

7. Obtain the resampling-based P-value, p_i, by comparing N^K_i with N^K_il: .

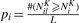Finally, we apply the extended Bonferroni adjustment (Gordon et al., 2007) with threshold 1.0 to control the per-family error rate (PFER). Extended Bonferroni adjustment is less conservative than the FWER controlling procedures and more stable than the FDR controlling procedures in the context of microarray analysis.

2.5 Trim number

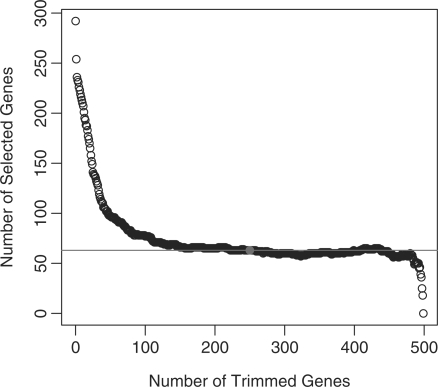
Ideally, K, the number of trimmed genes, should be chosen such that just the true DA genes are trimmed, no more, no less. As expected, this is a Catch-22. In reality, it is a classical trade-off between type I error and the power of the test, so a good choice of K depends on how it affects the selection power. We conduct the following experiment to answer this question. We randomly choose 500 genes from the leukemia dataset and vary K from 0 to 499. For each fixed K, by applying the above algorithm with permutation number L=10 000, we obtain resampling-based P-values, and then we select DA genes by controlling the PFER at 1.0 level with the extended Bonferroni procedure (Gordon et al., 2007). The relationship between the trim number K and the number of selected DA genes is summarized in Figure 1. It shows that the number of selected DA genes decreases as K becomes larger. When K stays between 100 and 480, the number of selected DA genes is very close to the case when K=250 (half of total number of genes), marked by the horizontal line in Figure 1. It implies that a conservative (large) choice of K does not decrease the testing power too much. Together with the simulation results below, we suggest trimming half of the total number of genes in practice. If the computation resources permit, we encourage researchers to produce a figure similar to Figure 1 and select the appropriate trim number accordingly.

Fig. 1.

Number of selected DA genes as a function of K, number of trimmed genes. The horizontal line marks the case when K=250, the trimming strategy used in this study.

2.6 Correlation coefficient vector and covariance vector gene selection method

We compare the performances of the new TCDV method and the method proposed in Hu et al. (2009) (CV in what follows). In fact, the main improvement of the TCDV method is the choice of the correlation distance over the Pearson's correlation coefficient as the association score to quantify changes of between-gene dependence. Because the covariance distance is defined as the SD of the difference between gene expressions, it has the ability to detect changes of both correlation coefficients and variance (technical details including two illustrations can be found in Section 2 of the Supplementary Materials). Therefore, it makes sense to compare the TCDV method to a third method, which uses the covariance between genes as the association score. We denote this method as the COV method.

2.7 Simulation studies

We simulate several sets of data, each containing m=708 genes in two groups which represent two different phenotypes (phenotypes A and B). Both groups contain 80 arrays (replications). Since the covariance distance is sensitive to the changes of both correlation coefficient and SD, we have the following two simulated datasets:

• SIMU1: for phenotype A, any two distinct genes have correlation coefficient 0.9 and all the genes have SDs 0.35. Therefore, the (population) covariance distance between genes i and j is 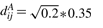where 1≤i<j≤708. For phenotype B, all the genes still have the same SDs 0.35, but the correlation coefficients are changed to

  

  Here, corr(i, j) stands for the correlation coefficients between the i-th and the j-th genes and ρ_d is a constant taking value in {0.01, 0.02, 0.03, 0.04}. Therefore, the covariance distance between the i-th and j-th gene is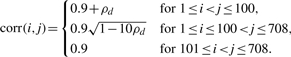

  

  SIMU1 is designed to mimic the changes of the correlation coefficients across two phenotypes. The first 100 genes are DC.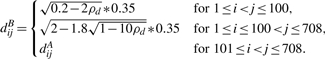
• SIMU2: for phenotype A, any two distinct genes have correlation coefficient 0.9 and all the genes have SDs 0.35. As in SIMU1, the covariance distance between genes i and j is 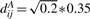where 1≤i<j≤708. For phenotype B, any two distinct genes still have the same correlation coefficients 0.9 as in phenotype A, but the first 100 genes have the SDs 0.35+s_d and all the other genes have the SDs 0.35. Here, s_d is a constant taking value in {0.04, 0.08, 0.12, 0.16}. The covariance distance between the i-th and jth genes is

  

  SIMU2 is designed to mimic the changes of the variance across two phenotypes.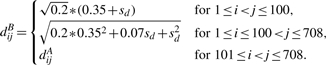

In both simulated studies, the first 100 genes are set to be DA genes. ρ_d and s_d quantify how much covariance distances are different across two phenotypes. The choices of 0.9 as the base correlation coefficient and 0.35 as the base SD are to match the mean sample correlation coefficient and mean (SD) in the leukemia dataset.

Another way to simulate the covariance structure of the biological data is through a resampling method. More precisely, we randomly choose 708 genes from the leukemia dataset and permute the arrays in both HYPERDIP and TEL. Then we split the arrays into two groups with equal size of arrays (79) in each group. These two groups mimic two biological conditions without DA genes. Next, we introduce changes to the first 100 genes in the first group. We denote the expressions in the first group by x^A_ij, 1≤i≤708 and 1≤j≤79, and generate the dataset as follows:

• SIMU3: we multiply the gene expressions x^A_ij (1≤i≤50, 1≤j≤79) by s_d where s_d=1.3 if 1≤i≤25 and s_d=1.6 if 26≤i≤50. As a result, the SDs of the first 50 genes are increased by small (s_d=1.3) or large (s_d=1.6) amounts. Next, we generate 50 79-dimensional random vector a_i (1≤i≤50) with i.i.d. standard normal components {a_ij}, 1≤j≤79 and add them to the gene expressions x_i+50,j, respectively (1≤i≤50) with a tuning parameter ρ_d defined as follows: x_i+50,j+ρ_da_ij where ρ_d=0.1 if 1≤i≤25 and ρ_d=0.2 if 26≤i≤50. Evidently, the covariance distances associated to the second 50 genes are different in two groups and the differences are mainly caused by the changes of the correlation coefficients. Again, the first 25 of them have smaller effect size comparing to the next 25.

In SIMU3, the first 100 genes are considered DA genes of which the last 50 are DC.

3 RESULTS

3.1 Simulation results

We apply the TCDV, CV and COV methods to 20 randomly generated SIMU1 and SIMU2 datasets. The mean and the SD of the true positive (TP)/false positive (FP) of each method are reported in Tables 1–3. When applying the TCDV method, we use three different trimming strategies: (i) under-trim (K=50), (ii) exact-trim (K=100) and (iii) over-trim (K=354, or half of the total number of genes).

Table 2.

SIMU2, TP and FP with the TCDV method.

	Effect size	K=50	K=100	K=354
	sd	Mean (SD)	Mean (SD)	Mean (SD)
TP	0.04	3.75 (1.92)	3.75 (1.95)	3.85 (2.13)
	0.08	44.25 (9.55)	44.65 (9.6)	45.1 (10.11)
	0.12	91.6 (5.17)	91.55 (5.15)	92.3 (5.03)
	0.16	99.7 (0.95)	99.75 (0.89)	99.8 (0.68)
FP	0.04	1.65 (1.24)	1.55 (1.24)	1.3 (1.23)
	0.08	4.55 (2.64)	2.6 (1.46)	1.6 (0.86)
	0.12	22.75 (11.97)	5.56 (2.54)	2.35 (1.19)
	0.16	251.5 (118.78)	7.75 (2.12)	2.25 (1.22)

Total number of genes: 708. Number of DA genes: 100. The extended Bonferroni threshold 1.0.

Table 1.

SIMU1, TP and FP with the TCDV method

	Effect size	K=50	K=100	K=354
	ρd	Mean (SD)	Mean (SD)	Mean (SD)
TP	0.01	30 (15.48)	30 (15.58)	27.55 (15.35)
	0.02	89.65 (10.11)	89.8 (10.33)	90.1 (11.12)
	0.03	99.8 (0.68)	99.8 (0.68)	100 (0)
	0.04	100 (0)	100 (0)	100 (0)
FP	0.01	4.65 (2.15)	2.75 (1.58)	2.1 (1.22)
	0.02	29.45 (25.86)	5.6 (2.29)	2.35 (1.28)
	0.03	271.8 (139.59)	7.1 (2.83)	2.65 (1.49)
	0.04	446.25 (120.54)	5.85 (2.13)	1.55 (1.2)

Total number of genes: 708. Number of DA genes: 100. The extended Bonferroni threshold 1.0.

Table 3.

SIMU1 and SIMU2, TP and FP with the CV and COV methods

Effect size		CV method		COV method
		TP	FP	TP	FP
		Mean (SD)	Mean (SD)	Mean (SD)	Mean (SD)
ρd	0.01	4.05 (13.88)	0.6 (2.61)	0 (0)	0 (0)
	0.02	24.5 (33.96)	3.5 (9.29)	0.3 (1.31)	0 (0)
	0.03	63.35 (35.89)	1.6 (4.78)	0 (0)	0.05 (0.22)
	0.04	82.35 (27.37)	6.65 (21.54)	0 (0)	0 (0)
sd	0.04	0.05 (0.22)	0.1 (0.44)	0 (0)	0 (0)
	0.08	0 (0)	0.4 (1.32)	0.05 (0.22)	0 (0)
	0.12	0.15 (0.48)	1.05 (4.13)	8.45 (22.25)	0.85 (3.71)
	0.16	0 (0)	0.05 (0.22)	4.2 (14.91)	0 (0)

Total number of genes: 708. Number of DA genes: 100. The extended Bonferroni threshold 1.0.

For SIMU1, both the TCDV and CV method select the DA genes while the COV method does not. The TCDV method performs better than the CV method in terms of testing power. It shows that the TCDV method is a better choice than the CV method for testing the pure correlation coefficient changes when genes are highly correlated (see Section 4 of the Supplementary Materials for a mathematical explanation). For SIMU2, the TCDV method detects the DA genes successfully, whereas the CV method does not. The COV method catches only a few TPs. It demonstrates that using covariance is not the main reason why the TCDV method performs better than the CV method. As for the TCDV method, the more genes we trim, the less FPs we get. As expected, the under-trim strategy (K=50) leads to considerable FPs, but fortunately, both the exact-trim (K=100) and the over-trim (K=354) strategies largely reduce the FPs and the difference between the two is minor. In practice, the true number of DA gene is not available to us, therefore we suggest to be always conservative and trim half of the number of genes.

Since COV method does not show acceptable power in the simulation study, we only apply the TCDV method and CV method to SIMU3. Again, the above two procedures are applied to 20 SIMU3 datasets (obtained from different choices of 708 genes). The mean and SD of the TP/FP are summarized in Table 4.

Table 4.

SIMU3, TP and FP in simulations of biological data with the TCDV method and the CV method.

	Effect size	TCDV method			CV method
		K=50	K=100	K=354
		Mean (SD)	Mean (SD)	Mean (SD)	Mean (SD)
TP	sd=1.3	20.3 (3.62)	19.9 (3.95)	18.95 (4.99)	0 (0)
	sd=1.6	24.4 (0.92)	24.35 (1.06)	24.3 (1.23)	0.35 (0.73)
	ρd=0.1	14.75 (3.71)	13.25 (4.04)	12.4 (5.12)	7.9 (4.0)
	ρd=0.2	21.6 (0.92)	21.6 (0.92)	21.45 (1.16)	18.95 (1.86)
	Total	81.05 (8.38)	79.1 (8.88)	77.1 (11.26)	27.2 (5.85)
FP		76.25 (82.95)	12.6 (31.69)	2.2 (5.52)	0.05 (0.22)

Total number of genes: 708. Number of DA genes: 100. The extended Bonferroni threshold 1.0.

The TCDV method selects 70–80% of the DA genes. When we trim conservatively (K=354), it has a good control of the FPs. On the other hand, the CV method fails to select the DA but non-DC genes altogether and performs poorly in selecting the DC genes.

3.2 The analysis of biological data

We apply both the TCDV method (K=3542) and the CV method to the biological datasets. It takes approximately 98 and 18 h to analyze the biological dataset with L=1 00 000 permutations by the TCDV and CV methods, respectively. All computations were done on four nodes of a cluster computer which has six nodes each with 8 × Intel E5450 3.0 GHz processors and 8 × 2 GB SDRAM. By controlling the PFER at 1.0 level with the extended Bonferroni procedure, the TCDV method selects 293 unique genes while the CV method selects only 14. Furthermore, we have tested the pure variance differences for all the genes. With extended Bonferroni threshold 1.0, there are only five unique genes that significantly change their variances across phenotypes. Compared with 293 DA genes we detect with TCDV method, this number is quite small. Therefore, it is reasonable to believe that the majority of gene DA is induced by changes of correlation coefficients.

The choice of a gene selection method should be determined by the biological relevance of the produced genes list. In what follows we demonstrate that the analysis of DA genes is a valuable addition to the analysis of DE genes. Taking together both procedures provides a more comprehensive functional interpretation of the experimental results.

• We compare the lists of DA (obtained using TCDV) and DE (obtained using Wilcoxon rank sum test and controlling PFER with the extended Bonferroni adjustment at level 1.0) genes between HYPERDIP and TEL groups. DA list has 293 and DE list has 98 unique genes. There are only 40 genes shared between two lists. To explore the functional differences between these gene lists we further construct small molecular interaction networks for each of the lists separately using the Ingenuity software (Redwood City, CA, USA; http://www.ingenuity.com/index.html). For every list we select five top-scored networks (Supplementary Figs 1 and 2). Supplementary Table 1 illustrates that the major functional difference between these two lists lies in the presence of ‘DNA Replication, Recombination, and Repair’ biological function in the DA gene list, while other processes in which genes from both lists are involved are more similar. ‘DNA Replication, Recombination, and Repair’ network, among others, include histone, cyclin-dependent kinase, heat shock protein, minichromosome maintenance protein, modulator of apoptosis, proteosomal subunits, replication protein, transcription regulator TP53 and ubiquilin. We list these proteins here because they reflect the general functional trend of the DA genes, i.e. at the protein level these genes mostly regulate and modify the activities of other genes/proteins. To illustrate how the analysis of DA genes complements the analysis of DE genes, we merge² two small interaction networks: ‘Cell Cycle, Cancer, Reproductive System Disease’ resulted from the list of DE genes and ‘DNA Replication, Recombination, and Repair’ resulted from the list of DA genes (Supplementary Fig. 3). The integration of two networks leads to appearance of new connections between nodes, which were hidden before integration (compare Supplementary Figs 1b, 2a and 3). The connections represent molecular interactions already known from the literature. This experiment demonstrates that indeed genes from DE and DA lists are interacting partners in biological processes and the analyses of DE and DA genes are complementing each other. The search of Canonical Pathways significantly enriched in genes from either list (using Ingenuity software) reveals that there is only one such a pathway, ‘Cell Cycle: G1/S Checkpoint Regulation’, which includes genes from DA list (Supplementary Fig. 4). Interestingly, AML1 is involved in the regulation of the G1 to S cell cycle transition and regulates p21 (G1/S pathway member) (Bernardin-Fried et al., 2004; Strom et al., 2000). In contrast, in TEL group TEL/AML1 fusion converts AML1 from functioning as a transcriptional activator to a transcriptional repressor (Hiebert et al., 1996). We would expect that the enrichment of G1/S checkpoint with DA genes results from their differential association with the new fusion TEL/AML1 gene in TEL, as compared with HYPERDIP group.

• The TEL-AML1 group is different from other leukemia subtypes by the presence of t(12;21)(p13;q22) translocation, generating the TEL/AML1 fusion gene. We are interested in whether this cytological abnormality can be monitored throughout the overrepresentation of either DA or DE genes in chromosomal bands in the comparison of TEL/AML1 and HYPERDIP groups. We apply a conditional test for overrepresentation of DE and DA genes in chromosomal bands. After correction for multiple testing there are no chromosomal bands significant for the enrichment in DE genes. However, bands 21q, Xp, 21q22.3, Xp11.23, 6p25.1 come as significant in the analysis of DA genes. It should be noted that the band 21q22.3 contains the fusion TEL/AML1 gene and one can hypothesize that either the translocation itself or TEL/AML1 fusion protein affects other genes in this band. Among others, 21q22.3 band includes ubiquitin-conjugating enzyme and SUMO protein, which post-translationally modify TEL protein, leading to its compartmentalization to specific nuclear speckles (Chakrabarti et al., 2000). Ubiquitin-conjugating enzyme and SUMO also interact with TEL/AML1 fusion, leading to its compartmentalization in the same speckles about 10 times less frequently, whereas TEL/AML1 and AML1 occupy non-overlapping sites in the nucleus (Chakrabarti et al., 2000). These observations suggest that ubiquitin-conjugating enzyme and SUMO are DA between TEL and HYPERDIP groups because they interact differently with TEL/AML1, TEL and AML1 proteins. Still the question remains, whether other genes in this band are called DA because the translocation somehow influences their expression or because they interact differently with fusion and fusion's partners. The appearance of four other significant bands is difficult to explain. Although in the original analysis (Yeoh et al., 2002) it was noted that chromosomes 21 and X contained almost 70% of genes, defining HYPERDIP group, the biological explanation of this phenomenon is still lacking. Here, we simply note that the analysis of DA genes provides some additional information about cytogenetic abnormalities as compared with the analysis of DE genes.

4 DISCUSSIONS AND CONCLUSIONS

Thanks to the recent advances of microarray technology, conducting large-scale microarray experiments is now much more affordable. With larger datasets, it is natural for biologists to ask questions about the changes of the dependence structure between genes in addition to changes of the marginal distributions. Unfortunately, the ‘large p, small n’ nature of the microarray data makes it very difficult to select co-expressed gene pairs directly, because the multiplicity of the correlation/covariance matrix is in the range of millions thus it is hard to distinguish meaningful biological changes from the ‘background noise’. From the multiple testing perspective, it is advantageous to put the focus on genes instead of gene pairs (Hu et al., 2009; Hudson et al., 2009) because it reduces the multiplicity dramatically (from 25 087 986 to 7084 in our real data analysis) so that standard MTPs can be employed to control group-wise type I errors, just as in the case of differential expression analysis. While procedures based on this approach are much more efficient than those based on gene pairs, their selection power is still a major concern. In Hu et al.'s study, the number of DA genes selected by the CV method is one magnitude of order less than the DE genes. We have found in this study that the covariance distance is a better summary statistic for detecting changes of the dependence structure between gene expressions. Consequently, the TCDV procedure selects far more DA genes than the CV procedure. In fact, DA genes selected by the TCDV procedure even outnumber DE genes selected by a comparable non-parametric differential analysis procedure. With the application of the TCDV method to more gene expression datasets, we believe that the DA genes along with the DE genes will provide us more comprehensive information for the biological research. Meanwhile, improvement of the selection power and the reduction of the computational cost of the TCDV are certainly worth further investigation. More quantitative insights into the gene dependence structures will definitely help us better understand the true underlying biological mechanism.

5 AUTHORS CONTRIBUTIONS

The basic idea was first proposed by R.H. and X.Q. who also developed the detailed study design. R.H. carried out the needed computations and simulations and the majority of the software development. G.G. conducted the gene functional analysis for DE and DA genes. R.H. and X.Q. were responsible for most of the composition of the findings.