Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2010 Jan;184(1):233–241. doi: 10.1534/genetics.109.110510

Human Triallelic Sites: Evidence for a New Mutational Mechanism?

Alan Hodgkinson 1,1, Adam Eyre-Walker 1
PMCID: PMC2815919  PMID: 19884308

Abstract

Most SNPs in the human genome are biallelic; however, there are some sites that are triallelic. We show here that there are approximately twice as many triallelic sites as we would expect by chance. This excess does not appear to be caused by natural selection or mutational hotspots. Instead we propose that a new mutation can induce another mutation either within the same individual or subsequently during recombination. We provide evidence for this model by showing that the rarer two alleles at triallelic sites tend to cluster on phylogenetic trees of human haplotypes. However, we find no association between the density of triallelic sites and the rate of recombination, which leads us to suggest that triallelic sites might be generated by the simultaneous production of two new mutations within the same individual on the same genetic background. Under this model we estimate that simultaneous mutation contributes ∼3% of all distinct SNPs. We also show that there is a twofold excess of adjacent SNPs. Approximately half of these seem to be generated simultaneously since they have identical minor allele frequencies. We estimate that the mutation of adjacent nucleotides accounts for a little less than 1% of all SNPs.

ALTHOUGH the density of biallelic SNPs in the human genome is reasonably low, there are some sites that have three (triallelic sites) or even four nucleotides segregating in the human population. We show here that there are approximately twice as many triallelic sites as we would expect by chance. There are at least three mutational mechanisms that could potentially generate such an excess of triallelic sites. First, some sites may be hypermutable, and if the mutation rate of at least two pathways (e.g., C → T and C → A) is elevated at such sites, then there will be an excess of triallelic sites. The mutation rate of a site is known to depend upon the adjacent nucleotides, the best known example being the CpG dinucleotide (Coulondre et al. 1978; Bird 1980) at which the frequency of both transition and transversion mutations is elevated. However, other adjacent nucleotides also influence the mutation rate (Blake et al. 1992; Zhao et al. 2003; Hwang and Green 2004). Furthermore, we have recently shown that there is variation in the mutation rate that does not depend upon the identity of the adjacent nucleotides or any specific context (Hodgkinson et al. 2009).

Second, it is possible that two of the alleles at a triallelic site are generated simultaneously within a single individual. Point mutations are generally assumed to involve the production of a single new allele per mutation event at a rate that is governed by the effects mentioned above. However, it is not difficult to imagine mechanisms that might induce mutations on both strands of the DNA duplex; for example, the presence of a base mismatch may itself be unstable, so we might go from a G-C base pair to a G-A, which then may mutate to C-A; if DNA replication reads through this mismatch, the G allele will have mutated to both C and T. Alternatively, the mutation may occur across both strands of the duplex at the same time, possibly as a result of a chemical or radiation event. Third, in a similar manner, we might imagine a single SNP inducing subsequent mutations if base mismatches are formed during recombination in heteroduplex DNA.

Here we attempt to identify the cause of the excess of triallelic sites by analyzing sequence data around triallelic sites.

MATERIALS AND METHODS

The expected number of triallelic sites in nuclear DNA was estimated as follows. We downloaded human SNP data from the Environmental Genome Project (NIEHS SNPs 2008) and the SeattleSNPs project (SeattleSNPs 2008). High-quality sequence data were used to identify SNPs (Q > 25), and each SNP reported was confirmed in multiple individuals and/or multiple reactions. Assuming the same Q-value for resequencing, the error rate is expected to be at least 1 × 10−5. We masked all CpG and coding sites; coding sites were removed since it is difficult to calculate the expected number of triallelic sites in coding sequences because of selection. Sites were designated as CpG if the site, or any of the SNPs at the site, would yield a CpG dinucleotide. We started by tallying the number of each type of nucleotide within each intron and across all genes, ignoring any regions that were not scanned for variation. We then calculated the frequency of each type of SNP, μX−Y, where X and Y are A, C, T, or G, by orientating the SNP using orthologous chimpanzee sequences and then dividing the number of human sites where X was inferred to be the ancestral allele and Y was inferred to be the derived state by the total number of X sites. For example, μA−G was estimated by dividing the number of sites where the inferred mutation was from A to G (i.e., A was the allele present at the orthologous chimpanzee position and G was the second allele at the SNP site) by the total number of sites that were A. Orthologous chimpanzee sequences were found and downloaded using Ensembl Biomart (http://www.ensembl.org/biomart/martview/) and then aligned to human sequences using FSA (Bradley et al. 2009), which incorporates Exonerate (Slater and Birney 2005) and MUMmer (Kurtz et al. 2004). We were unable to find a small number of orthologous chimpanzee sequences and there were occasional gaps in alignments. In total, ∼94% of human SNP sites had an orthologous nucleotide in chimpanzee; the ancestral state was inferred from the major allele at sites with no orthologous chimp nucleotide. At triallelic sites, two mutations were assumed to have occurred. The expected number of triallelic sites (Etri) was then found by multiplying each mutation rate by the total frequency of nucleotides with the same allele (n(X)),

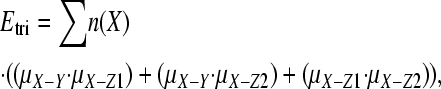graphic file with name M1.gif (1)

where the summation is across X, and Z1 and Z2 are A, C, T, or G, and X, Y, Z1, and Z2 are all different nucleotides in each case.

We also downloaded >5000 complete mitochondrial sequences from GenBank (http://www.ncbi.nlm.nih.gov) and aligned the protein-coding sequences. Sequences in which genes were of different length to the consensus were removed, leaving 4764 complete alignments. We considered fourfold synonymous sites only. The expected number of triallelic sites in mitochondrial sequences was found in much the same way, using the same formula as that used for nuclear DNA (Equation 1). However, in this case the ancestral state was inferred from the major allele at each site, as orientation of SNPs using the chimp sequence is impossible because of the large divergence between humans and chimps for mtDNA. Although the use of frequency data will lead to some level of misinference, this is likely to be very small because when the population size is stationary, the level of misinference is expected to be ∼7% for 5000 sequences. mtDNA also shows a skew toward rare alleles, which will further reduce the level of misinference.

The expected distances between SNPs were estimated by randomly distributing SNPs within each intron across the intron sequence. SNPs were not allowed to fall on CpG dinucleotides, as these would have been discarded as CpG SNPs (as stated above). The expected number of triallelic sites within this analysis was the number of times a site was hit by two SNPs multiplied by a factor K, which reflects the fact that when two mutations occur at the same site they will not necessarily generate a triallelic SNP, for example, if two transitions occur at the same site. Let the proportion of SNPs that are transitions be fts and the proportion of transversions that are G ↔ T or C ↔ A be ftv1 and the proportion that are G ↔ C or A ↔ T be ftv2. Then, the expected number of triallelic sites is 2x2 · fts(ftv1 + ftv2) + 2x2 · ftv1 · ftv2, where x is the density of SNPs, and the expected number of times two SNPs are expected to fall at the same site is x2. Thus K = 2(fts(ftv1 + ftv2) + (2 ftv1 · ftv2)). In the human genome fts = 0.66, ftv1 = 0.183, and ftv2 = 0.163 (http://www.ncbi.nlm.nih.gov/), which means that K = 0.516.

The expected number of triallelic SNPs incorporating the effects of adjacent nucleotides on the rate of mutation was calculated using Equation 1, but by summing X over triplets rather than nucleotides. For example, if the site in question is TTT, then the three possible mutations are TTT → TCT, TTT → TGT, and TTT → TAT and the relative frequency of each SNP is μTTT-C, μTTT-G, and μTTT-A, respectively. The likelihood of a triallelic SNP being observed at this site is then simply

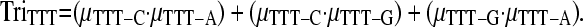graphic file with name M2.gif

This probability is then multiplied by the total number of TTT sites and repeated in a similar fashion across all triplet types to give the total number of triallelic sites expected. The process was repeated using estimated mutation rates from each gene rather than across all sites in the data set. This incorporates the effects of any regional variation in triplet mutation rates.

To investigate the effects of cryptic variation in the mutation rate on the number of triallelic sites we used the method described in Hodgkinson et al. (2009), but we considered only non-CpG human triallelic SNPs against chimpanzee non-CpG biallelic SNPs. We did not correct for the effects of adjacent nucleotides on the mutation rate since there are not enough data to estimate these for triallelic sites and the effects are small for biallelic sites (Hodgkinson et al. 2009). As such, the expected number of coincident SNPs is simply the total number of alignments divided by the number of positions in the alignment that were not part of a CpG dinucleotide.

To test whether triallelic SNPs in autosomal data could have been produced by a simultaneous mutation event or by an event linked to recombination we considered whether the minor alleles were significantly closer together on a phylogenetic tree of human haplotypes than would be expected by chance. For each triallelic site we took the 100 biallelic SNPs on either side of the site from each of the individuals sampled in the Environmental Genome Project and SeattleSNPs studies, not including the triallelic SNP itself. Where there were not 100 SNPs on either side of the triallelic site within each gene, we used extended data on either side of the triallelic site up to a total of 200 SNPs where possible. We then used PHASE (Stephens et al. 2001) to construct haplotypes from the variation data. The biallelic sites were bootstrapped 1000 times and each bootstrap data set was used to build a phylogenetic tree, using the neighbor-joining method in Phylip (Felsenstein 2005). The triallelic site was then placed back on this tree. The distances between the minor alleles in the triallelic site were found by summing the lengths of branches on each tree separating the terminal nodes containing the alleles; if either one of the minor alleles was not a singleton, the distances between every pair of haplotypes containing the minor alleles were averaged. The expected distance between minor alleles was estimated by randomly placing two mutation events on two branches of each tree inferred from the bootstrapped data according to the inferred length of the branches; simulations in which the two mutations fell on the same branch, or on the two branches descending from the root, were discarded since they would not generate a triallelic SNP. Minor alleles were designated as those at the lowest frequency and the average distance between them was calculated as before. The process was repeated across the 1000 bootstrapped trees for each triallelic SNP, and an estimated P-value was calculated as the proportion of trees in which the observed distance between minor alleles was smaller than the distance between the minor alleles of the simulated data. Fisher's combined probability test was used to calculate whether the P-values across all triallelic sites were significant.

To test whether the randomization procedure and analysis of phylogenetic trees were satisfactory we also derived the expected distance between a random pair of nonadjacent biallelic SNPs from within the set of haplotypes generated for each triallelic SNP and then calculated whether these mutations fell significantly closer on the phylogenetic tree of haplotypes than we would expect by chance. In each case, phylogenetic trees were reconstructed as before, excluding the two randomly chosen biallelic SNPs. Where a single haplotype contained both minor alleles for the two SNPs chosen, the allele at lower frequency was used, thus generating three different alleles across all haplotypes for comparison. We found no significant difference between the real data and the simulated data (P = 0.28) for the distances between minor alleles at the biallelic sites. We therefore conclude that our analysis procedure for phylogenetic trees is satisfactory and does not lead to artificial clustering of SNPs.

A second test was performed to judge whether the minor alleles of triallelic sites tended to cluster on a phylogenetic tree of haplotypes in the population. The distances between minor alleles of triallelic sites were calculated as above; however, on this occasion they were compared to the distances between minor alleles of triallelic sites that were generated by coalescent simulations. For each triallelic site the recombination rate was calculated using the Pairwise program in LDhat (McVean et al. 2002), considering all haplotypes in the population and assuming a constant rate of recombination. A coalescent simulation was then performed using MS (Hudson 2002), which incorporated a model of demographic history as outlined by Adams and Hudson (2004) and the recombination rate and population structure for each particular triallelic site. Individuals were considered to be either African or non-African in the simulation. Finally, the program Seq-Gen (Rambaut and Grassly 1997) was used to generate haplotypes for each population under a finite sites model, with the mutation rate set such that the average nucleotide diversity would be 0.0015 (-s option). This is slightly higher than the average nucleotide diversity in humans, but was increased to reduce computing time. The process was repeated for each triallelic site until 100 data sets had been generated that contained a triallelic site; for each of these simulated triallelic sites we extracted the same number of biallelic SNPs as were present in the original data. Each set of sequences was then used as above, with the triallelic site removed, to generate a phylogenetic tree; the triallelic site was then placed back on the tree and the distance between minor alleles computed as above. The distribution of distances was then compared to the distribution of distances from the bootstrapped trees of the original data. The P-value was calculated by randomly pairing a value from the original bootstrapped data, with a value from the coalescent simulations; the P-value was the number of times the former was less than the latter. The coalescent simulations depend upon the demographic model, but ethnic information for the DNA samples was available only for 60 of the 113 triallelic sites; we therefore considered only these.

To test whether triallelic SNPs are linked to recombination we calculated the average recombination rate across each gene in our data set, using data from Kong et al. (2002). We split the genes into quartiles on the basis of the average recombination rate and tested whether the density of triallelic sites was significantly different between the upper and lower quartiles, using a z-test.

The expected number of triallelic SNPs that fall within immediately adjacent SNPs was calculated by multiplying the frequency of triallelic SNP sites by the frequency of immediately adjacent SNP sites (two per pair of SNPs) within each intron.

We estimate the relative contributions of single and simultaneous mutation events to the production of variation as follows. We assume the mutations are neutral, the population is stationary in size, and the organism being considered is diploid. First, let us consider single biallelic SNPs. The expected number of biallelic sites in a sample of n sequences is

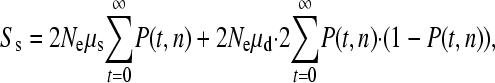graphic file with name M3.gif (2)

where μs is the rate of single mutations, μd is the rate for simultaneous double mutations during the mitotic phase of germ-line development, and P(t, n) is the probability of observing a mutation that was produced t generations in the past in a sample of n sequences. Note that only simultaneous mutation events during mitosis are likely to generate two mutations that can both be inherited; this is because only one meiotic product generates an egg in females so only one mutation from a simultaneous event during meiosis will be inherited. Furthermore, human females typically have only one offspring at a time; hence, only one product from a simultaneous event in male meiosis will be transmitted. The first summation denotes the probability of observing a SNP produced by a normal mutational event, and the second summation denotes the probability of observing a biallelic SNP that was originally produced by a simultaneous event, with one allele being lost through genetic drift and therefore contributing only a biallelic SNP to the population.

The expected number of triallelic SNPs is approximately

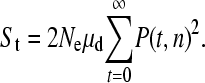graphic file with name M4.gif (3)

This is only an approximation because it assumes that the frequencies of the two mutations are independent, whereas they are not; for example, if one allele goes to fixation, then the other allele can no longer exist. However, this approximation is likely to be good since the new mutations will generally be rare.

The probability of observing a SNP in the population, P(t, n), can be split into two components: the probability that a SNP is segregating in the population, y(j, t, N), where j is the number of copies of the new allele in the population of size N, and the probability that it is sampled in our data, z(n). We can estimate y(j, t, N) using a transition matrix approach as follows. We initially introduce a single mutation into our population: y(1, 0, N) = 1 and y(j, 0, N) = 0 for j > 1. The probability of the mutation being at a frequency j given that we had i copies in the previous generation can be calculated from the binomial distribution

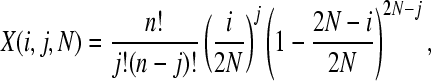graphic file with name M5.gif

so

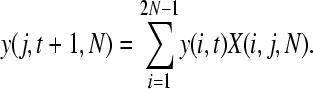graphic file with name M6.gif

The chance of sampling a SNP is

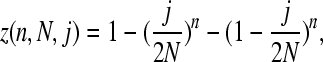graphic file with name M7.gif

where n is our sample size, (j/2N)n is the chance that one of the minor alleles gets sampled in all cases, and (1 − j/2N)n is the chance that the other allele gets sampled in all cases. The likelihood of observing the SNP is therefore

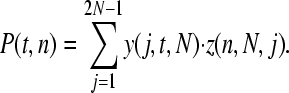graphic file with name M8.gif

Both Equations 2 and 3 involve infinite sums; to determine a reasonable limit of this summation we note that ∑P(t, n) should be equal to ∑(2/i) as given by Watterson's classic formula for the number of neutral polymorphisms segregating in a sample of sequences (Watterson 1975):

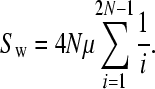graphic file with name M9.gif

The convergence of ∑P(t, n) depends upon the number of chromosomes sampled; we required that ∑P(t, n) was within 1% of ∑(2/i).

From Equations 2 and 3 it is straightforward to estimate the relative rates of single and simultaneous mutation, μs and μd, from the observed numbers of biallelic and triallelic sites, Ss/St.

RESULTS

Excess of triallelic sites:

We used data from 896 nuclear genes that had been resequenced in between 90 and 95 human individuals to search for triallelic sites. After removing CpG and coding sites, we had a total of 36,702 transitions, 20,375 transversions, and 113 sites that had three alleles segregating in the human population (supporting information, Table S1). This is significantly greater than the 61.15 triallelic sites expected by chance if mutations are randomly distributed across non-CpG sites (ratio of observed over expected = 1.85, with a standard error of 0.17, P < 0.001 under the null hypothesis that the ratio is one). We also searched for triallelic SNPs at fourfold synonymous sites in human mitochondrial genes in 4764 complete sequences. We found 1125 transitions, 173 transversions, and 126 triallelic sites. In this case we found no significant excess of triallelic sites above that expected by chance (observed over expected = 1.20, P > 0.05). We did not consider the results from mtDNA further. The excess of triallelic SNPs in nuclear DNA could be caused by one of three processes: natural selection, mutation hotspots, or another mutational mechanism. It is important to note at this stage that the excess is unlikely to be the result of sequencing errors as each SNP in the Environmental Genome Project and SeattleSNPs data sets has been confirmed in multiple individuals and/or in multiple reactions (NIEHS SNPs 2008; SeattleSNPs 2008).

Natural selection:

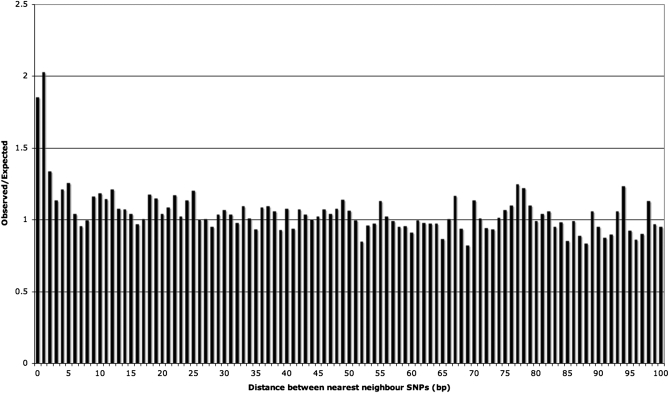
Selection is expected to lead to an apparent excess of triallelic sites because SNPs will not tend to segregate within regions under selection, and therefore SNPs will appear to be clustered between these areas. First, this is unlikely to be the case here as all of the sequences considered are intronic, and although selection is known to act in these regions, it is thought to affect only a small percentage of sites (Waterston et al. 2002; Dermitzakis et al. 2005; Asthana et al. 2007). Furthermore, if selection were responsible for the excess of triallelic SNPs, we would expect to see SNPs clustering more generally. However, if we look at the distances between SNPs, and compare this to the results from simulations in which SNPs are randomly distributed, then we see no evidence of clustering except an excess of triallelic sites and an excess of immediately adjacent SNPs (Figure 1). We consider the excess of adjacent SNPs separately below. The distances between SNPs suggest that selection is not affecting the number of triallelic sites present.

Figure 1.—

Figure 1.—

Open in a new tab

Observed over expected values for the distance to the nearest neighbor SNP within each intron.

Mutation hotspots:

The excess of triallelic SNPs could be a result of local variation in the mutation rate in the human genome. It has previously been shown that the mutation rate varies as a function of local context effects, particularly depending upon the adjacent nucleotides (Blake et al. 1992; Zhao et al. 2003; Hwang and Green 2004). Such variation in the mutation rate could lead to an increased number of triallelic SNPs if some sites have an elevated mutation in two or more pathways, e.g., if both C → T and C → A occur at higher rates. To investigate whether neighboring nucleotide effects could cause the excess of triallelic sites, we estimated the probability of observing a SNP at the central nucleotide of each triplet, ignoring CpGs, and used these to estimate the expected number of triallelic sites. If we estimate the probabilities across all our genes, we infer the expected number of triallelic sites to be 61.88; this is only slightly larger than the estimate ignoring adjacent nucleotide effects and is significantly less than the number observed (observed/expected = 1.83, standard error = 0.17, P < 0.001). If we estimate probabilities within genes, thus controlling for any regional variation in mutation rates within chromosomes, this expectation increases slightly to 69.03, but this is still highly significantly different from the observed number (P < 0.001). Local context effects are therefore not the cause of the excess of triallelic sites. We do not consider the effects of nucleotides farther away, as these have been shown to have a much smaller effect on mutation rates than adjacent nucleotides (Krawczak et al. 1998; Zhao et al. 2003), which themselves have little impact on the expected number of triallelic SNPs.

It is also possible that the excess of triallelic SNPs is caused by CpG alleles that were subsequently lost from the population. If we consider a CpG site that mutates at a high rate to produce a TpG and an ApG, and if the CpG is then lost from the population and either the TpG or the ApG then mutates to a GpG, this generates a triallelic site that was in part caused by the increased mutation rate associated with a CpG. To test for this we repeated the analysis and excluded all sites preceded by a C or followed by a G; we find that the effect is still significant (observed/expected = 1.77, standard error = 0.18, P < 0.001). Therefore, CpGs that have been lost are not causing the excess of triallelic sites.

However, we have previously shown that the mutation rate varies across the human genome in a cryptic nature that is not associated with any specific context effect (Hodgkinson et al. 2009). This was demonstrated by showing that there is an excess of sites with a SNP at the orthologous position in humans and chimpanzees (coincident SNPs). Such cryptic variation could potentially lead to an excess of triallelic sites, should at least two mutational pathways be elevated at particular sites (e.g., a transition and a transversion). However, we note that this cryptic variation seems to largely elevate the rate of mutation of a single mutational pathway: there is a large excess of cases in which an X ↔ Y SNP in humans is coincident with an X ↔ Y SNP in chimps, but little or no excess of X ↔ Y in humans and X ↔ Z in chimpanzees (where X, Y, and Z can be A, T, G, or C) (Hodgkinson et al. 2009). Cryptic variation would therefore not tend to generate triallelic sites. However, to investigate the matter further we considered whether triallelic sites in humans also tended to have a SNP at the orthologous position in chimpanzee and calculated the number expected assuming that chimpanzee SNPs and triallelic sites were randomly distributed relative to one another. As an excess of triallelic SNPs requires an increased level of mutation along two pathways, we would expect the ratio of coincident triallelic SNPs to their expected number to be far in excess of that found for coincident single SNPs. Because we are not interested in the excess of triallelic sites per se, we can take advantage of triallelic sites found in dbSNP; there are ∼50,000 examples. These were BLASTed against a data set of chimpanzee SNPs to yield a data set of 548 alignments of 81 bp with the chimpanzee SNP in the central position and the human triallelic SNP elsewhere within the alignment. Of these alignments, 17 have the human and chimpanzee SNPs in the same position, as opposed to the 6.96 we would expect were the SNPs distributed at random (observed over expected ratio = 2.44); this is not significantly different from the ratio for non-CpG single SNPs in which local context effects are ignored, which is 2.40 (Hodgkinson et al. 2009). There is therefore no evidence that cryptic variation in the mutation rate tends to generate an excess of triallelic sites.

There are a number of additional mutation hotspot mechanisms that could cause an excess of triallelic sites, which need to be considered. First, it has been suggested that sequences adjacent to indel events may have elevated rates of mutation; this is most evident up to 100 bp from the indel, but effects decline away from indels across several hundred base pairs (Tian et al. 2008). It is unlikely that an increase in the rate of mutation in these areas could cause the excess of triallelic SNPs in our data because if the effect were sufficiently large, we would expect to see a clustering of SNPs in certain parts of the genome. It is clear from Figure 1 (discussed in the Natural selection section) that this is not the case. Furthermore, α-polymerase pause sites are also thought to mutate at a higher than normal rate (Todorova and Danieli 1997) and could cause an excess of triallelic sites. In our data, however, there is only one occurrence of the motif associated with a pause site in the region immediately upstream of triallelic sites and thus the motif does not affect our results.

Recombination and simultaneous mutation:

The evidence above suggests that it is not particular sites that tend to produce triallelic SNPs; so maybe triallelic sites are generated by a mechanism that can occur at all sites with a similar probability, but one in which one mutation generates the second mutation. There are at least two related potential mechanisms. First, it is possible that a mutation could induce a subsequent mutation, possibly through the formation of heteroduplex DNA during recombination. The lack of an excess of triallelic sites in mitochondrial DNA, in which recombination is rare or absent, would be consistent with this model. Second, it might be possible that two mutations occur within a single DNA duplex; for example, a G = C base pair might become an A = C mismatch, which then becomes an A = G. If replication runs through this mismatch before it is repaired, we would end up with the G = C allele being mutated to A = T and C = G; so two new mutations have been generated within a single event. Alternatively, it may be possible that both strands of DNA are mutated simultaneously, perhaps as a result of a chemical or radiation event. This process of simultaneous mutation would need to occur in the mitotic phase of germ-line development for the two new alleles to be potentially transmitted to the next generation. We refer to these as the “recombination” and “simultaneous mutation” models, respectively.

To investigate whether one of these two mechanisms generates the excess of triallelic sites we can potentially test a prediction that both models make for recombining data: they both predict that new mutations should cluster together on a phylogenetic tree of human haplotypes. We expect this clustering under the simultaneous mutation model because we hypothesize that both new mutations will be produced on the same genetic background. The clustering is also expected under the recombination model because the first mutation should induce the second mutation equally as often on the original haplotype as it does on another haplotype in the population. To investigate whether we could detect clustering in recombining autosomal loci we took each of our triallelic sites and 200 biallelic SNPs surrounding the site where possible; using the biallelic SNPs, we constructed haplotypes and inferred the phylogenetic relationships between them. We then calculated the average distance between haplotypes containing the minor alleles. Among our 113 triallelic sites we find 6 cases in which the minor alleles are significantly closer to each other at the 5% level than if mutations are placed on the phylogenetic trees at random, approximately what we would expect by chance alone; however, if we combine probabilities across all triallelic sites, we find significant evidence for proximity of the minor alleles (P < 0.05). Nevertheless, comparing the observed distances between minor alleles with those generated by randomly placing mutations on the same phylogenetic tree may not be the most appropriate way to detect clustering. There may be some genealogies that tend to produce triallelic sites by double mutation, where the minor alleles tend to be clustered together on deeper branches of the phylogenetic tree. As a consequence, the method above may average across several genealogies if there has been recombination and so produce an average genealogy that does not tend to lead to an excess of triallelic sites. Thus we performed coalescent simulations under a realistic demographic model, with the rate of recombination estimated from the biallelic sites, to generate a set of simulated triallelic sites for each observed triallelic site. We then compared the observed distances between the minor alleles of triallelic sites with those produced from the coalescent simulations. We knew the ethnicities of the individuals sequenced only for 60 of the triallelic sites and so could perform simulations only for those sites because of the need to incorporate demography; in 12 cases the minor alleles are significantly closer to each other at the 5% level than those generated from coalescent simulations. If we combine probabilities across all 60 triallelic sites, we find highly significant evidence of proximity (P < 0.001). This is consistent with both the simultaneous mutation and recombination pathways.

In principle it is possible to differentiate between the recombination and simultaneous models by considering nonrecombining nuclear DNA, such as the nonrecombining portion of the Y chromosome (NRY). In the NRY, under the simultaneous mutation hypothesis we expect both mutations to appear at the same time on the same genetic background in about half the triallelic sites, the other half being a consequence of chance alone. The simultaneous generation of two mutations will manifest itself as two new alleles emanating from a single node in the phylogenetic tree of human haplotypes. Unfortunately, to our knowledge only a single non-CpG triallelic SNP has been reported for the NRY: this is an A, T, C triallelic SNP termed M116 (Underhill et al. 2001). In this case, the two minor alleles, T and C, are found in different haplogroups and as such cannot have been caused by a simultaneous mutation event. This does not disprove that triallelic sites are produced by simultaneous mutation since we infer that ∼50% of triallelic sites are due to chance alone (see above).

Alternatively, we may be able to differentiate between the two models by considering the prediction that under the recombination model, triallelic SNPs and recombination rates should be correlated. We have already shown that there is no excess of triallelic sites in human mitochondrial DNA and clearly there is a prediction under the recombination model that there should be no excess in nonrecombining sequences. However, in mtDNA a lack of triallelic sites does not necessarily point to triallelic SNPs being generated during recombination, as there are many other factors that differentiate the mutation process in mtDNA and nDNA that could be equally likely to generate the result. Consequently, we tested for a correlation between triallelic SNPs and recombination rates in the autosomal data sets. We separated our data set of introns from genes into quartiles on the basis of the average recombination rate across the gene (rates taken from Kong et al. 2002) and found that there was no significant difference between the number of triallelic SNPs per sampled site in genes that were in the upper and lower 25% of recombination rates (P = 0.77). We also tested for a correlation between recombination rate and the presence/absence of a triallelic site across genes, using logistic regression: there was no evidence of a significant correlation (P = 0.99). It should be noted at this point that our test for a correlation between triallelic SNPs and recombination may not include all gene conversion events, as the genetic map measures only crossover rates and our hypothetical recombination mechanism would also apply to gene conversion events. However, as gene conversion and crossover hotspots tend to coincide (Jeffreys and May 2004), it is likely that the result would be mirrored when considering gene conversion as an indicator of triallelic SNP density. There is therefore no evidence that triallelic sites are linked to recombination. This leads us to believe that the simultaneous mutation model most likely explains the excess of triallelic SNPs in the human genome.

Adjacent mutations:

As we noted above, besides an excess of triallelic sites there is also an excess of adjacent SNPs. It has been previously noted that adjacent substitutions are more common than one would expect by chance (Averof et al. 2000) and it has been suggested that this is due to the simultaneous mutation of adjacent nucleotides. To investigate whether this is the case we compared the absolute difference in minor allele frequency (MAF) between adjacent SNPs. If adjacent SNPs are produced simultaneously, then we expect many adjacent SNPs to have identical MAF since they can differ in frequency only if they are broken up through recombination. This is what we observe: approximately half of all adjacent SNPs have identical MAFs (252/506), which is consistent with the observation that adjacent SNPs are approximately twice as common as expected by chance. We also note that the absolute difference in MAF between adjacent SNPs is significantly smaller than the absolute difference in MAF between one of the adjacent SNPs (randomly chosen) and the next nonadjacent SNP (P < 0.001, average difference in MAF for adjacent SNPs = 0.073, average difference in MAF for nonadjacent SNP = 0.107). Thus, it seems that there is a process that produces adjacent SNPs simultaneously, and it therefore seems possible that a similar process could also generate triallelic sites if a mutation event that causes a doublet mutation along a strand can also cause a double mutation across strands, which could occasionally occur at the same time. To investigate this we searched our data for any case in which a triallelic site was adjacent to another SNP. We found one case, and although this feature is rare, this is significantly higher than the 0.008 we expect by chance alone (P < 0.01). The coincidence of a triallelic site and an adjacent SNP could be due either to some sites having a greater chance of producing adjacent and triallelic sites or to the generation of both simultaneously.

DISCUSSION

We have shown that there is an excess of sites in the human genome that have three alleles segregating in the population. The excess cannot be explained by natural selection or an increased mutation rate at particular sites. Instead, there is some evidence that a proportion of triallelic sites may be caused by a single mutation mechanism in which two new alleles are produced at the same or a similar time, on the same or a similar genetic background; the minor alleles at a triallelic SNP tend to be closer together on the phylogenetic tree than one would expect by chance. We show that the clustering is unlikely to be caused by a mutational mechanism linked to recombination as there is no association between recombination rates and genes that contain triallelic SNPs. We have also shown that there may be an association between triallelic and immediately adjacent SNPs. None of these lines of evidence is individually particularly strong, but collectively they suggest that a proportion of triallelic sites are a consequence of simultaneous mutation. A conclusive test can be made using Y chromosome data, and the 1000 human genome project is likely to provide sufficient information to resolve the problem since the project will produce long nonrecombining Y chromosome sequences from many males. However, these data are unlikely to be available for another 12–18 months (G. McVean, personal communication).

The available evidence suggests that the excess of triallelic sites is caused by the simultaneous production of two new alleles in a single individual. If this is the case, then we can estimate the frequency of this process using Equations 2 and 3. To a first approximation the relative numbers of biallelic and triallelic SNPs depend upon their mutation rates and the relative probabilities of detecting a single SNP (∑P(t, n)) and two SNPs generated simultaneously (∑P(t, n)2). Surprisingly we find that ∑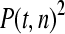Inline graphic is only about 15-fold lower than ∑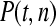Inline graphic when large numbers of chromosomes have been sampled (Table 1); so the chance of sampling two mutations produced in the same generation is actually quite high in the data we have analyzed.

TABLE 1.

The summed probabilities that a single SNP is sampled in n chromosomes until it is fixed or lost and the summed probabilities that two mutations produced simultaneously are sampled, together with a ratio of the two values across different numbers of sampled chromosomes

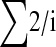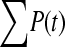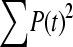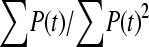No. of chromosomes Inline graphic Inline graphic Inline graphic Inline graphic
4 3.66 3.62 0.017 212.02
10 5.65 5.58 0.049 112.70
40 8.51 8.29 0.190 43.73
100 10.35 9.88 0.419 23.61
200
 11.75
 10.90
 0.698
 15.61
Open in a new tab

We can use Equations 2 and 3 to estimate the ratio of the rates of single and simultaneous mutation, 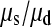Inline graphic as follows. We infer that approximately half of all triallelic sites are a consequence of simultaneous mutation; hence 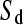Inline graphic = 51.13 and 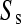Inline graphic = 57,077. In our data between 180 and 190 chromosomes have been sampled so ∑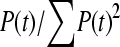Inline graphic is between 16.05 and 16.54 and hence 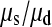Inline graphic is between 65.6 and 67.7; so single mutations occur ∼65 times more frequently than simultaneous mutations and since each simultaneous event produces two new mutations, we estimate that ∼3% of all distinct SNPs are generated in this fashion.

We have also shown that there is an excess of adjacent SNPs and that at least half of these adjacent SNPs appear to be generated simultaneously. If we assume that the doublet mutations remained linked throughout their life, i.e., there is no recombination between them, then we can directly estimate the rate of adjacent mutation (μa) by considering the ratio of single SNPs to adjacent SNPs; using this approach we estimate 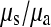Inline graphic as 225.6, assuming that approximately half of all immediately adjacent mutations occur simultaneously. As adjacent mutation events contribute two new SNPs, we estimate that ∼0.89% of all distinct SNPs are generated in this fashion. So although adjacent SNPs are slightly more common than triallelic sites, the rate at which they are produced is actually lower, and this is because the probability that two independent SNPs survive to be sampled is considerably lower than the probability that two linked SNPs survive (Table 1). Of course, this number depends on the rate of recombination between adjacent SNPs: should this rate be extremely high, there will be almost no linkage between adjacent SNPs; if it is low, adjacent SNPs will behave in the manner of single SNPs. In this case it is reasonable to suggest that the latter is most probably more realistic. Our estimate of the ratio of single over doublet mutation rates of 225.6 is closer to the ∼1000 estimated by Kondrashov (2003) than the ∼10 estimated by Averof et al. (2000). We believe that our estimate is likely to be the most accurate as it uses the most direct approach to compare mutation rates in neutral sequences.

Acknowledgments

We are very grateful to Phil Green, Mike Zody, and an anonymous referee for comments. A.H. and A.E.-W. were funded by the Biotechnology and Biological Sciences Research Council and A.E.-W. by the European Community and the National Evolutionary Synthesis Center.

The authors declare that they have no competing interests.

Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.109.110510/DC1.

References

  1. Adams, A. M., and R. R. Hudson, 2004. Maximum-likelihood estimation of demographic parameters using the frequency spectrum of unlinked single-nucleotide polymorphisms. Genetics 168 1699–1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Asthana, S., W. S. Noble, G. Kryukov, C. E. Grantt, S. Sunyaev et al., 2007. Widely distributed noncoding purifying selection in the human genome. Proc. Natl. Acad. Sci. USA 104 12410–12415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Averof, M., A. Rokas, K. H. Wolfe and P. M. Sharp, 2000. Evidence for a high frequency of simultaneous double-nucleotide substitutions. Science 287 1283–1286. [DOI] [PubMed] [Google Scholar]
  4. Bird, A. P., 1980. DNA methylation and the frequency of Cpg in animal DNA. Nucleic Acids Res. 8 1499–1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Blake, R. D., S. T. Hess and J. Nicholsontuell, 1992. The influence of nearest neighbors on the rate and pattern of spontaneous point mutations. J. Mol. Evol. 34 189–200. [DOI] [PubMed] [Google Scholar]
  6. Bradley, R. K., A. Roberts, M. Smoot, S. Juvekar, J. Do et al., 2009. Fast statistical alignment. PLoS Comput. Biol. 5 e1000392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Coulondre, C., J. H. Miller, P. J. Farabaugh and W. Gilbert, 1978. Molecular-basis of base substitution hotspots in Escherichia-coli. Nature 274 775–780. [DOI] [PubMed] [Google Scholar]
  8. Dermitzakis, E. T., A. Reymond and S. E. Antonarakis, 2005. Conserved non-genic sequences: an unexpected feature of mammalian genomes. Nat. Rev. Genet. 6 151–157. [DOI] [PubMed] [Google Scholar]
  9. Felsenstein, J., 2005. PHYLIP (Phylogeny Inference Package) Version 3.6. Distributed by the author. Department of Genome Sciences, University of Washington, Seattle.
  10. Hodgkinson, A., E. Ladoukakis and A. Eyre-Walker, 2009. Cryptic variation in the human mutation rate. PLoS Biol. 7 e27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hudson, R. R., 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18 337–338. [DOI] [PubMed] [Google Scholar]
  12. Hwang, D. G., and P. Green, 2004. Bayesian Markov chain Monte Carlo sequence analysis reveals varying neutral substitution patterns in mammalian evolution. Proc. Natl. Acad. Sci. USA 101 13994–14001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Jeffreys, A. J., and C. A. May, 2004. Intense and highly localized gene conversion activity in human meiotic crossover hot spots. Nat. Genet. 36 151–156. [DOI] [PubMed] [Google Scholar]
  14. Kondrashov, A. S., 2003. Direct estimates of human per nucleotide mutation rates at 20 loci causing Mendelian diseases. Hum. Mutat. 21 12–27. [DOI] [PubMed] [Google Scholar]
  15. Kong, A., D. F. Gudbjartsson, J. Sainz, G. M. Jonsdottir, S. A. Gudjonsson et al., 2002. A high-resolution recombination map of the human genome. Nat. Genet. 31 241–247. [DOI] [PubMed] [Google Scholar]
  16. Krawczak, M., E. V. Ball and D. N. Cooper, 1998. Neighboring-nucleotide effects on the rates of germ-line single-base-pair substitution in human genes. Am. J. Hum. Genet. 63 474–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kurtz, S., A. Phillippy, A. L. Delcher, M. Smoot, M. Shumway et al., 2004. Versatile and open software for comparing large genomes. Genome Biol. 5 R12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. McVean, G., P. Awadalla and P. Fearnhead, 2002. A coalescent-based method for detecting and estimating recombination from gene sequences. Genetics 160 1231–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. NIEHS SNPs, 2008. NIEHS Environmental Genome Project. University of Washington, Seattle. http://egp.gs.washington.edu.
  20. Rambaut, A., and N. C. Grassly, 1997. Seq-Gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosci. 13 235–238. [DOI] [PubMed] [Google Scholar]
  21. SeattleSNPs, 2008. NHLBI Program for Genomic Applications. SeattleSNPs, Seattle. http://pga.gs.washington.edu.
  22. Slater, G. S., and E. Birney, 2005. Automated generation of heuristics for biological sequence comparison. BMC Bioinformatics 6 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Stephens, M., N. J. Smith and P. Donnelly, 2001. A new statistical method for haplotype reconstruction from population data. Am. J. Hum. Genet. 68 978–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Tian, D. C., Q. Wang, P. F. Zhang, H. Araki, S. H. Yang et al., 2008. Single-nucleotide mutation rate increases close to insertions/deletions in eukaryotes. Nature 455 105–108. [DOI] [PubMed] [Google Scholar]
  25. Todorova, A., and G. A. Danieli, 1997. Large majority of single-nucleotide mutations along the dystrophin gene can be explained by more than one mechanism of mutagenesis. Hum. Mutat. 9 537–547. [DOI] [PubMed] [Google Scholar]
  26. Underhill, P. A., G. Passarino, A. A. Lin, P. Shen, M. M. Lahr et al., 2001. The phylogeography of Y chromosome binary haplotypes and the origins of modern human populations. Ann. Hum. Genet. 65 43–62. [DOI] [PubMed] [Google Scholar]
  27. Waterston, R. H. K., E. Lindblad-Toh, J. Birney, J. F. Rogers, P. Abril et al., 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420 520–562. [DOI] [PubMed] [Google Scholar]
  28. Watterson, G. A., 1975. Number of segregating sites in genetic models without recombination. Theor. Popul. Biol. 7 256–276. [DOI] [PubMed] [Google Scholar]
  29. Zhao, Z. M., Y. X. Fu, D. Hewett-Emmett and E. Boerwinkle, 2003. Investigating single nucleotide polymorphism (SNP) density in the human genome and its implications for molecular evolution. Gene 312 207–213. [DOI] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES